从立体或多视航空航天遥感图像重建地面三维场景一直是摄影测量与遥感中的核心问题。自动获取立体像对中每个像素的同名点是:三维重建的关键技术,通常称为“图像密集匹配”。图像密集匹配可分为4个过程[1]。第1步是匹配代价的计算。像素值的亮度差、相关系数及互信息是一些经典的匹配代价。这些代价主要基于灰度、梯度或信息熵,以待匹配图像块作为模板,按照给定的相似性度量在搜索区域内逐像素遍历计算。这些匹配代价虽然实现简单,但易受无纹理区域、表面镜反射、单一结构和重复图案的影响[2]。第2步是匹配代价聚合。代价聚合通常是对匹配点邻域内所有匹配代价加权求和。代价聚合能达到局部滤波的效果。但传统的算法中,包括半全局匹配法和图割法(GraphCut)[3],都对代价聚合做了不同程度的简化。第3步是视差值计算。最小匹配代价对应的视差值即为最优结果。通常采用能量函数的方法计算最优视差值。最后一步是视差精化。该步骤是对视差值执行优化的过程,包括一系列后处理技术,如左右一致性检验、中值滤波、子像素增强等。最后可由密集匹配获得视差图,转换为深度信息,从而重建三维场景。
在各个阶段,经典匹配算法都或多或少地采用了经验性的方法而非严格的数学模型,如设计特征、测度、聚合方式等,并做了不同程度的简化,如认为邻域内像素的匹配代价独立,因此难以达到数学上的最优。采用深度学习算法,是否能够克服上述传统方法中的难点、进一步提高匹配精度,是值得深入研究的问题。
密集匹配作为三维重建的核心内容,受到广泛的重视。图割法[3]是一种经典的全局立体匹配算法。利用图论的思想,将求解图的最小割算法作为核心技术,以求解二维区域的能量最小问题。PMVS(patch-based multi-view stereo)算法[4]首先提取特征点并进行匹配,然后以特征点为中心扩张到周围面块,对面块匹配,得到准密集匹配点。在效率上,图割法等全局匹配算法采用近似最优的优化方法,计算量大,运行时间过长,不太适合大容量的遥感影像。2008年提出了效率更高的半全局匹配方法(semi-global matching, SGM)[5]。SGM将匹配点邻域的二维代价聚合替代为多个简单的一维代价聚合,对当前区域的16个一维方向进行动态规划计算,以求解最小代价。影像块匹配算法[6](patch-match method)利用图像的局部相关性,认为匹配点周围的区域也相互匹配。文献[7]开发的SURE软件是基于SGM的多视影像匹配算法。
随着机器学习的普及,深度学习[8-11]在各个研究领域都得到了广泛的应用。尤其是卷积神经网络(convolutional neural networks, CNN),不仅提高了图像识别和分类的准确性,提升了在线运算效率,更关键的是它避免了各类特征设计。一些研究者逐渐将深度学习引入到立体匹配中,在计算机视觉标准测试集上的匹配结果逐渐超过传统匹配方法,展示了一定的优越性。
基于深度学习的密集匹配有两种策略:只学习立体匹配4个标准步骤中的一部分和端到端学习。前者的例子包括MC-CNN网络[12],只用于学习匹配代价,以及SGM-Net网络[13],在SGM中引入CNN学习惩罚项,以解决惩罚参数调整困难的问题。
端到端的学习策略是直接从立体像对预测视差图。DispNet[14]是一种用于视差图预测的普适的全卷积网络。GC-Net(geometry and context network)[2]利用像素间的几何信息和语义信息构建3D张量,从3D特征中学习视差图。PSM-Net(pyramid stereo matching network)[15]是由空间金字塔池和三维卷积层组成的网络,将全局的背景信息纳入立体匹配中,以实现遮挡区域、无纹理或重复区域的可靠估计。CRL(cascade residual learning)[16]串联了两个改进的DispNet[14]网络,第1个网络得到立体像对间的初始化视差值,第2个网络利用第1个网络的残差值进一步精化。文献[17]提出一种Highway网络结构,引入多级加权残差的跳接,利用复合损失函数进行训练。以上方法均在监督方式下运行。文献[18]设计了一种卷积神经元网络,利用左右图像(和右左图像)的视差一致性学习视差图,无需真实视差图作为训练。
深度学习方法已经较成功地应用于计算机视觉标准测试集的立体匹配,但是应用于遥感影像的处理尚不成熟。本文研究了深度学习的方法在航空遥感影像密集匹配上的性能,并在多个数据集上与经典方法和商业软件进行比较。此外,本文还评估了深度学习在航空遥感图像匹配中的泛化能力,即在计算机视觉标准数据集上训练的模型,是否能直接应用到航空遥感影像中。
1 方法 1.1 MC-CNNMC-CNN通过深度卷积神经元网络的自我学习,得到最优的相似性测度,用于匹配代价的计算,而取代相关系数、灰度差等经验设计的方法。
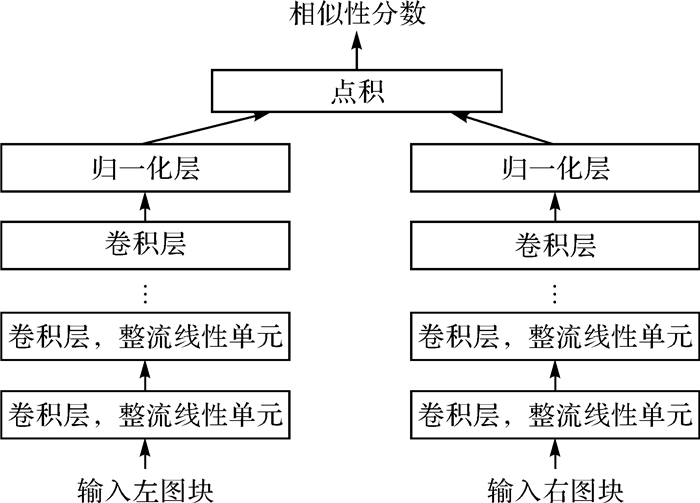
MC-CNN中包括两种不同结构的网络:Fast结构和Slow结构,前者比后者的处理速度更快,但得到的视差值精度稍逊于后者。两种结构均利用一系列卷积层从输入图块中提取特征向量,依据特征向量计算图块间的相似性。Fast结构采用固定的余弦度量(即点积)比较提取出的两个特征向量是否相似,Slow结构尝试用一系列全连接层学习出特征向量间的相似性分数。由于Slow网络对训练数据集容量和内存均有较高要求,本文采用Fast网络作为试验网络。网络框架如图 1所示。
|
| 图 1 MC-CNN Fast网络框架 Fig. 1 The structure of Fast MC-CNN |
Fast结构是一种连体(siamese)网络,两个子网络分别由多个卷积层组成,且共享参数,分别用于提取左图块和右图块中的特征向量。在本文中,卷积层数设置为4,卷积核大小为3×3。两个归一化特征向量通过点积得到相似性分数。MC-CNN每次输入一对正负样本,计算损失值,并通过最小化Hinge Loss函数训练网络。设s+、s-分别为正负样本的输出,限差为m,则Hinge Loss定义为max(0, m+s--s+)。在本文试验中,m设置为0.2。
MC-CNN只用于学习代价函数,诸如代价聚合[19]、半全局匹配、左右一致性检验、子像素增强、中值滤波和双边滤波等后处理步骤参考了SGM的相关流程。
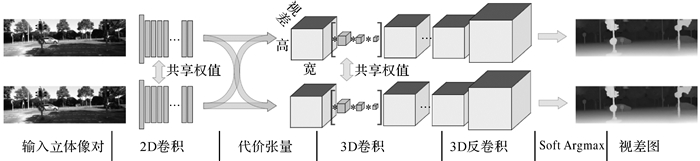
1.2 GC-NetGC-Net采用端到端的学习策略,直接学习从核线立体像对到深度图的可微映射函数。GC-Net将视差看作第3维,构建图像-视差张量。由3D卷积学习特征,得到最优视差图(即3D张量中的一个曲面)。在图 2中,立体像对首先通过一系列共享的2D卷积核提取特征图。第2步,将特征图串联并构建代价立方体(cost volume)。具体的,以左片特征图为例,设其宽度和长度分别为w和h,右片相对于左片的最大视差为n。将对应的右片特征图每次平移一个像素,即共生成n张图。左片特征图与平移后的n张右片特征图逐个串联,得到w×h×(n+1)的3D张量。第3步,利用3D卷积和3D反卷积学习一系列的3D特征图,其最终的大小为W×H×n。H和W分别为原始图像的长宽。第4步,通过定义一个SoftArgmin函数,将3D特征图压缩为2D视差图d′。最后,采用d′与参考视差图d之间的一次范式误差作为代价函数,反向传播并迭代得到最优参数。
|
| 图 2 GC-Net网络结构 Fig. 2 The structure of GC-Net |
在试验中,2D卷积部分包含18个卷积层,每一层含32个卷积核,其中第1层的卷积核大小为5×5,剩余17层均为3×3。3D卷积部分包含14个卷积层,卷积核大小均为3×3×3。前两层的卷积核个数为32,后3层为128,剩余3D卷积层的卷积核个数为64。反卷积部分由5层反卷积组成,反卷积核大小为3×3×3,每一层的反卷积核个数分别为64/64/64/32/1。
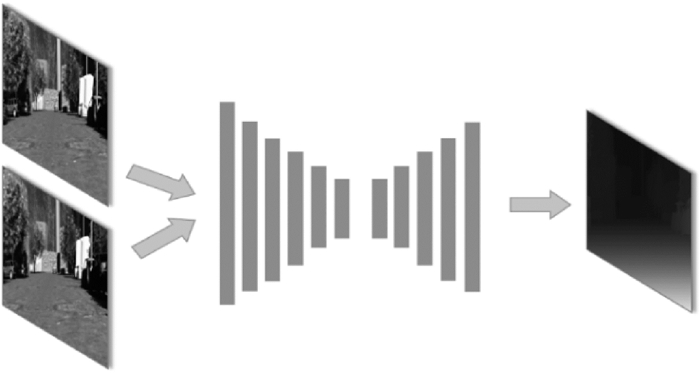
1.3 DispNetDispNet网络以FlowNet(flow estimation network)[20]网络为基础,是一种通用的全卷积神经元网络,由编码和解码两阶段组成,以核线影像对为输入,直接输出对应的视差图。其中编码阶段由6个卷积层组成,前两层的卷积核大小分别为7×7和5×5,其余层均为3×3。解码部分由5个上卷积层组成,卷积核大小为4×4。每一尺度的特征图都与真实视差图比较,得到对应的损失值。在训练过程中采用加权的方式赋予这些损失值不同的重要程度。DispNet网络的示意图如图 3所示。DispNet网络采用Adam优化器调整模型中的权值,学习速率设置为1e-4,且每200 k次迭代学习速率减半。
|
| 图 3 DispNet网络结构 Fig. 3 The structure of DispNet |
1.4 迁移学习
迁移学习(transfer learning)[21]是一种将从源数据集学习的模型应用于新的目标数据集的策略。如果已有模型能够直接应用于目标数据集上,将避免大量工作,特别是在目标集样本不充足的情况下。迁移学习可分为直推式迁移和模型微调(fine-tuning)。
直推式迁移学习使用源数据集的训练模型,在不进行任何参数调整的情况下,直接对目标数据集进行预测。该方法要求模型本身具有良好的泛化能力,且要求源任务和目标任务是同一类问题。
利用少量目标数据集样本进行模型微调是另一种常见的迁移学习模式。将预训练模型的参数作为初值,用目标数据集的样本进行精调整,以减少新模型训练需要的迭代次数,并弥补样本量不足带来的弊端。
参数迁移可分为两种:一种是微调所有层的参数;另一种是仅调整最后几层,并冻结具有普遍性和重用性底层特征。由于本文涉及的网络层数较浅,统一采用前一种方式。

|
| 图 4 参数迁移 Fig. 4 Parameter transfer |
2 数据集
为全面评价深度学习方法在航空遥感立体像对密集匹配中的性能,本文试验中共采用5套数据集,其中KITTI、Driving是开源的近景数据集,Hangzhou、München、Vaihingen 3套是采集自无人机平台和传统航摄平台的完整航空遥感数据集。
2.1 KITTI数据集KITTI街景数据集[22]采集自汽车车顶上安装的两个高分辨率立体相机。真实深度值是由一个旋转激光扫描仪记录所得,点云密度约为影像像素的30%。KITTI数据集包括KITTI2012和KITTI2015。KITTI2012数据集为灰度核线影像,平均大小为1240×376像素,包含194对训练图像和195对测试图像。KITTI2015数据集包含灰度影像和彩色影像,平均大小为1242×375像素;包括200对训练图像和200对测试图像。KITTI数据集只提供训练集的真实深度图参考,因此,本文将训练集中的80%作为训练集,剩余20%作为测试集以统计精度。这也是其他文献通行的方法。
2.2 Driving数据集Driving数据集[23]是一套虚拟的街景影像集。它是由一个汽车模型动态行驶在虚拟街景模型中,每一帧获取一对立体像对。Driving数据集提供多种参数设置下的共超过4000对数据,并提供密集的真实视差图。其数据量比现有的其他数据集多几个数量级,有效促进了大型卷积神经元网络的训练。Driving数据集中的左右像对为核线影像,影像大小固定为960×540。本文试验中选取了300对数据,其中80%作为测试集,其余20%作为测试集。
2.3 Hangzhou数据集Hangzhou数据集由无人机采集。无人机在距地面约640 m的低空拍摄,记录了2017年8月杭州附近山村地区的场景。包括4条航带20张9000×6732像素的像片,具有80%的航向重叠度和60%的旁向重叠度。影像中包括高速公路、低矮房屋、工业厂房、裸露田地、树林,以及裸露山体等地物类型。由LiDAR获得的该地区的激光点云作为地面真实深度值。
本文在空中三角测量解算后,将原始影像两两纠正为核线影像,并由激光点云得到对应每个同名像素点的视差值。受计算机显卡容量的限制,原始大小的航空影像不能直接用于训练,因此将核线影像裁剪为1325×354像素的子图像。通过手工挑选的方式去除一部分山区不理想的影像对(主要是LiDAR点云误差),剩余的328对影像作为训练集,40对作为测试集。
2.4 München与Vaihingen数据集München数据集和Vaihingen数据集采集自航摄飞机拍摄的标准航空遥感影像。两套影像均为德国地区的场景。其中München包含3条航带15张14 114×15 552像素的航空影像,具有80%的航向重叠度和80%的旁向重叠度。影像中的主要地物类型为城市建筑、道路、绿化带等。Vaihingen为3条航带36张乡村影像,大小为9420×14 430像素;航向重叠度60%,旁向重叠度60%。影像中的地物多为平坦的种植区,其余为密集低矮的房屋以及树林、河流等。两套数据分辨率高,地物清晰,分别作为城市和乡村的典型,具有较强的代表性。
两套数据中,作为参考的地面高程信息以半密集的DSM形式提供。该DSM由7种商业软件生成,取中值作为最终深度值,目视精度较高。
与Hangzhou数据处理过程类似,将纠正后的核线影像分别裁剪为1150×435像素和955×360像素大小的子图像。经筛选后,最终得到由540对影像构成的München数据集以及由740对影像构成的Vaihingen数据集。训练集和测试集的比例设置为4:1。
3 试验与结果分析为全面评价深度学习在航空遥感影像中的性能和泛化能力,本文设计了两类试验。第1类是利用3套航空数据集Hangzhou、München、Vaihingen测试各种深度学习方法的性能,并与经典的SGM和主流摄影测量软件SURE作对比。第2类是测试深度学习模型的泛化性能。包括将计算机视觉标准测试集上训练的模型直接应用于航空影像,以及测试基于目标集小样本训练的迁移学习。
所有试验均以训练后的网络模型在测试集上的结果作为评价依据。本文采用三像素误差(three-pixel-error,3PE)和一像素误差(one-pixel-error,1PE)作为评价标准。如3PE指点位误差小于3个像素的个数占所有像素的百分比。
所有的深度学习算法均在Linux系统下实现。其中MC-CNN在深度学习框架torch下实现,采用Lua语言编写核心代码。GC-Net模型和DispNet模型分别在Keras和Tensorflow下实现,采用Python作为主要语言。所有模型的训练和测试均在NVIDIA Titan Xp 12 G GPU上运行。
3.1 深度学习方法与传统方法的比较试验评估了3种网络模型MC-CNN、GC-Net、DispNet在密集匹配上的表现,并与SGM、商业软件SURE比较。各种方法/软件的设定如下:
(1) MC-CNN:MC-CNN的训练输入是以匹配点为中心的9×9窗口。在训练阶段,模型每次输入128对正负样本,采用小批量梯度下降法最小化损失,动量设置为0.9。所有数据迭代14次,学习速率设置为0.002。第11次迭代后,学习速率调整至0.000 2。预测阶段,输入一对核线立体像对,输出相似性分数,通过一系列后处理过程得到最终的视差图。
(2) GC-Net:训练输入为整幅核线像对及对应的视差图。GC-Net在稀疏的视差图上训练效果较差,因此只在3套密集型的数据集上训练模型(不能处理的数据集在表 1中统一以“—”表示)。输入数据的批量大小设置为1,所有数据迭代50次,学习速率设置为0.001。测试阶段直接输出视差图及精度。
| methods | 精度(3PE/1PE) | ||||
| KITTI2015 | Driving | Hangzhou | München | Vaihingen | |
| MC-CNN | 0.960/0.778 | — | 0.953/0.816 | 0.965/0.867 | 0.992/0.932 |
| GC-Net | — | 0.926/0.857 | — | 0.984/0.953 | 0.997/0.980 |
| DispNet | 0.937/0.737 | 0.835/0.547 | 0.923/0.591 | 0.883/0.532 | 0.950/0.710 |
| SGM | 0.893/0.732 | 0.713/0.505 | 0.896/0.739 | 0.921/0.859 | 0.987/0.925 |
| SURE | — | — | 0.968/0.831 | 0.932/0.879 | 0.990/0.969 |
(3) DispNet:整幅核线影像对作为输入。批量大小设置为32。所有数据迭代1500次,学习速率设置为0.000 1,并在训练过程中逐渐下降。输出视差图及精度。
(4) SGM:采用Opencv3.0库中自带函数,并附加高斯平滑、中值滤波等后处理过程。以批处理的方式对每一套测试集进行处理,由生成的视差图和真实视差图比较计算点位误差并统计精度。
(5) SURE:作为商业软件,输入为所有原始影像及外方位元素信息,输出为OSGB格式的三维模型。因此只在3套航空影像数据集上进行试验。该软件输出的三维模型反映的是地物点的真实坐标,为了参与精度评定,由三维坐标计算每个点在核线影像上对应的视差值,并与真实视差值比较。
传统方法和深度学习方法在5套数据集上的表现见表 1。
从表 1可见,第1,在3种深度学习方法中,端到端的GC-Net模型表现最好。在3套数据集上均优于其他方法,在地势平坦的Vaihingen数据集上精度达到99.7%(98.0%)。在地物高差变化较大的München数据集上,3PE比第2名的MC-CNN模型高2%左右,1PE高出近9%。在效果较差的Driving数据集上,92.6%的测试精度远超其他方法。
第2,MC-CNN模型表现良好且稳定,在各套数据集上的精度均远超SGM,在KITTI2015和Hangzhou数据集上优势最明显。在München和Vaihingen两套航空影像数据集上,与基于多视匹配的SURE相当。在Hangzhou数据集上稍逊色于SURE。
第3,DispNet模型在遥感影像数据集上表现最差,甚至弱于SGM。DispNet网络结构属于通用架构,而非专门为立体匹配设计。在1PE标准上较差的结果反映了通用模型架构在密集匹配任务上的局限性。
第4,GC-Net在所有方法中表现最优;MC-CNN与基于多视匹配的商业软件SURE相当,且远优于SGM;DispNet表现最差。本文预测:若在GC-Net或MC-CNN中加入多视约束,基于深度学习的方法将可能明显超越传统方法。
图 5分别展示了两种深度学习方法和一种传统方法在3套航空影像数据集上的预测视差图。从上到下分别是立体像对的左图、右图、参考深度图、MC-CNN、GC-Net、SGM方法的预测结果。可见GC-Net表现最为优秀,与参考图最为相似;而传统方法SGM效果略差。

|
| 图 5 3种方法在3套数据集上的预测视差图 Fig. 5 Disparity maps of 3 methods used on the 3 data sets |
图 6是由4种方法的视差图恢复得到的三维立体场景。从上到下分别是左图、参考三维场景、MC-CNN、GC-Net、SGM和SURE的预测结果。由图 6可见,SURE在Hangzhou数据集上有一定的扭曲,其他方法则表现相对较好。在München数据集上,各种方法均较为接近参考三维场景,但SURE的侧面纹理更加细致。在地势平坦的Vaihingen数据集上,所有方法都达到了很好的水平。

|
| 图 6 由4种方法的密集视差图恢复出的三维场景 Fig. 6 3D scenes recovered from disparity maps of 4 methods |
3.2 迁移学习 3.2.1 直接迁移学习
直接迁移学习是将预训练得到的模型,直接应用于目标数据集的预测。表 2是基于MC-CNN的预训练模型在目标集上的测试结果。训练集表示用于模型训练的源数据集,测试集表示目标数据集。例如,对于Hangzhou目标数据集,若用自身作为源数据集训练,其精度为95.3%(加粗的对角线元素);若采用KITTI2012作为源数据集,则其精度为94.4%。
| 测试集 | 精度(3PE/1PE) | ||||
| 训练集 | |||||
| KITTI2012 | KITTI2015 | Hangzhou | München | Vaihingen | |
| KITTI2012 | 0.963/0.866 | 0.957/0.848 | 0.941/0.856 | 0.945/0.797 | 0.946/0.813 |
| KITTI2015 | 0.958/0.768 | 0.960/0.778 | 0.951/0.761 | 0.955/0.751 | 0.953/0.750 |
| Hangzhou | 0.944/0.808 | 0.942/0.805 | 0.953/0.816 | 0.948/0.770 | 0.940/0.760 |
| München | 0.960/0.854 | 0.960/0.851 | 0.960/0.844 | 0.965/0.867 | 0.959/0.850 |
| Vaihingen | 0.988/0.919 | 0.987/0.912 | 0.987/0.916 | 0.989/0.922 | 0.992/0.932 |
试验的测试精度同样由3PE和1PE评价。总体而言,基于MC-CNN的深度学习方法具有良好的泛化能力,3PE标准上其模型退化程度(即采用其他数据源进行训练导致的精度降低)为0.2%~2.2%,在1PE标准上为0.8%~5.6%。即使用预训练的模型直接预测而不进行任何新的学习,MC-CNN依然远超SGM,并与SURE软件几乎相当。
表 3是基于GC-Net直接迁移学习的结果。由于只有Driving、München、Vaihingen 3套数据具有密集的深度图标签,因此将这3套数据作为源数据集训练模型。其数据的表示方法与表 2相同。
| 测试集 | 精度(3PE/1PE) | ||
| 训练集 | |||
| Driving | München | Vaihingen | |
| Driving | 0.926/0.857 | 0.895/0.808 | 0.895/0.793 |
| München | 0.969/0.893 | 0.984/0.953 | 0.964/0.922 |
| Vaihingen | 0.980/0.881 | 0.979/0.943 | 0.997/0.980 |
| KITTI2015 | 0.934/0.739 | 0.881/0.705 | 0.942/0.743 |
| Hangzhou | 0.911/0.779 | 0.940/0.799 | 0.949/0.841 |
GC-Net同样具有很强的泛化能力,但稍弱于MC-CNN。迁移学习时,3PE标准下模型退化程度约为1.5%~3%(1PE标准下为3.1%~9.9%)。测试精度平均下降2%,而MC-CNN只有0.6%。这是可以预料的,因为MC-CNN只用来学习更底层的相似测度。
3.2.2 参数微调在目标集含有少量样本的前提下,可以采用第2种迁移学习策略:以预训练模型作为初值,利用目标样本进一步微调。
表 4和表 5分别为基于MC-CNN方法和基于GC-Net方法的参数微调结果。“目标训练集”表示参与训练的目标集样本数量,DT方法表示直接在目标集上的训练,模型参数随机初始化;TL方法表示参数迁移学习并微调。“相对提升”是在同样大小的训练集下,TL相对于DL的精度提高。在表 4中,KITTI2015为源数据集,预训练了MC-CNN模型,Hangzhou为目标集;在表 5中,Vaihingen为源数据集,预训练了GC-Net模型,München为目标集。
| 数据集大小/对 | 25 | 50 | 100 | 200 | 300 | |||||
| 方法 | DT | TL | DT | TL | DT | TL | DT | TL | DT | TL |
| 3PE | 0.943 | 0.949 | 0.944 | 0.948 | 0.946 | 0.948 | 0.951 | 0.952 | 0.952 | 0.953 |
| 相对提升/(%) | 0.50 | 0.37 | 0.14 | 0.12 | 0.11 | |||||
| 数据集大小/对 | 25 | 50 | 100 | 200 | 250 | |||||
| 方法 | DT | TL | DT | TL | DT | TL | DT | TL | DT | TL |
| 3PE | 0.783 | 0.965 | 0.902 | 0.947 | 0.928 | 0.961 | 0.959 | 0.977 | 0.972 | 0.978 |
| 相对提升/(%) | 18.1 | 4.5 | 3.2 | 1.8 | 0.6 | |||||
表 4中,当用25对训练集直接训练模型时,可达到94.4%的精度;样本量增加一倍时,测试精度提高0.09%左右。可见,MC-CNN方法对训练样本的数量要求不高,少量样本的微调也能得到较好的训练模型。当采用迁移学习策略时,25对训练样本可达到94.9%的精度,相比于随机初值的直接训练,具有0.5%的优势。
在表 5的GC-Net方法中,只用25对训练样本时,直接训练模型(DT)仅有78.3%的测试精度;样本量增加一倍时,测试精度达到90.2%,提高11.9%。当样本量逐渐增加,最终达到97.2%。可见,相比于MC-CNN,端到端的GC-Net需要更多的训练样本。而采用迁移学习并微调的策略(TL),25对训练样本即可达到96.5%的精度。
从以上统计结果可见,迁移学习并微调对于模型精度的提高提供了较好的帮助。样本量越少,迁移学习的作用越大。同时在试验中发现,迁移学习不仅能提高精度,还可以减少在目标集上训练新模型的迭代次数,以更短的时间得到更优的结果。因此,本文建议:在基于深度学习的密集匹配中,尽量以训练好的模型作为目标数据集的初值,以得到效率和精度上的提升。
4 结论本文将深度学习方法引入到航空影像的密集匹配中,在多个数据集上与传统方法做了详细的比较,并分析了深度学习的泛化能力。首先,验证了深度学习方法与商业软件SURE相比略有优势,且远远好于SGM。其次,在深度学习方法中,GC-Net作为端到端的方法,取得了最好的效果,只学习相似性测度的MC-CNN次之。最后,测试了深度学习在立体密集匹配中的泛化能力并发现:MC-CNN和GC-Net具有较强的泛化能力,在标准数据库上训练的模型,可直接用于航空数据集,且3PE精度下降并不明显,尤其以MC-CNN表现最佳。这种泛化能力来自图像匹配只依赖于底层特征,而这些特征无论在近景、航空甚至模拟场景都是通用的。此外,通过迁移学习和参数微调,深度学习方法可实现效率和性能的同时提升。
| [1] | SCHARSTEIN D, SZELISKI R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J]. International Journal of Computer Vision, 2002, 47(1-3): 7–42. |
| [2] | KENDALL A, MARTIROSYAN H, DASGUPTA S, et al. End-to-end learning of geometry and context for deep stereo regression[C]//Proceedings of 2007 IEEE International Conference on Computer Vision. Venice, Italy: IEEE, 2017: 66-75. |
| [3] | BOYKOV Y Y, JOLLY M P. Interactive graph cuts for optimal boundary & region segmentation of objects in N-D images[C]//Proceedings of the 8th IEEE International Conference on Computer Vision. Vancouver, BC, Canada: IEEE, 2001: 105-112. |
| [4] | FURUKAWA Y, PONCE J. Accurate, dense, and robust multiview stereopsis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(8): 1362–1376. DOI:10.1109/TPAMI.2009.161 |
| [5] | HIRSCHMULLER H. Stereo processing by semiglobal matching and mutual information[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(2): 328–341. DOI:10.1109/TPAMI.2007.1166 |
| [6] | BLEYER M, RHEMANN C, ROTHER C. Patchmatch stereo-stereo matching with slanted support windows[C]//Proceedings of the British Machine Vision Conference. Dundee: BMVA Press, 2011: 14.1-14.11. |
| [7] | ROTHERMEL M, WENZEL K, FRITSCH D, et al. SURE: photogrammetric surface reconstruction from imagery[C]//Proceedings of 2012 LC3D Workshop. Berlin: [s.n.], 2012: 29. |
| [8] | GOODFELLOW I, BENGIO Y, COURVILLE A. Deep learning[M]. Cambridge: MIT Press, 2016. |
| [9] |
郑卓, 方芳, 刘袁缘, 等.
高分辨率遥感影像场景的多尺度神经网络分类法[J]. 测绘学报, 2018, 47(5): 620–630.
ZHENG Zhuo, FANG Fang, LIU Yuanyuan, et al. Joint multi-scale convolution neural network for scene classification of high resolution remote sensing imagery[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(5): 620–630. DOI:10.11947/j.AGCS.2018.20170191 |
| [10] |
龚健雅, 季顺平.
摄影测量与深度学习[J]. 测绘学报, 2018, 47(6): 693–704.
GONG Jianya, JI Shunping. Photogrammetry and deep learning[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(6): 693–704. DOI:10.11947/j.AGCS.2018.20170640 |
| [11] |
范大昭, 董杨, 张永生.
卫星影像匹配的深度卷积神经网络方法[J]. 测绘学报, 2018, 47(6): 844–853.
FAN Dazhao, DONG Yang, ZHANG Yongsheng. Satellite image matching method based on deep convolution neural network[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(6): 844–853. DOI:10.11947/j.AGCS.2018.20170627 |
| [12] | ŽBONTAR J, LECUN Y. Computing the stereo matching cost with a convolutional neural network[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 1592-1599. |
| [13] | SEKI A, POLLEFEYS M. SGM-Nets: Semi-global matching with neural networks[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI: IEEE, 2017: 6640-6649. |
| [14] | MAYER N, ILG E, HÄUSSER P, et al. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV: IEEE, 2016: 4040-4048. |
| [15] | CHANG Jiaren, CHEN Yongsheng. Pyramid stereo matching network[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT: IEEE, 2018: 5410-5418. |
| [16] | PANG Jiahao, SUN Wenxiu, REN J S, et al. Cascade residual learning: A two-stage convolutional neural network for stereo matching[C]//Proceedings of 2017 IEEE International Conference on Computer Vision Workshops. Venice, Italy: IEEE, 2017: 878-886. |
| [17] | SHAKED A, WOLF L. Improved stereo matching with constant highway networks and reflective confidence learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI: IEEE, 2017: 6901-6910. |
| [18] | ZHONG Yiran, DAI Yuchao, LI Hongdong. Self-supervised learning for stereo matching with self-improving ability[J]. arXiv: 1709.00930, 2017. https://arxiv.org/abs/1709.00930 |
| [19] | ZHANG Ke, LU Jiangbo, LAFRUIT G. Cross-based local stereo matching using orthogonal integral images[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2009, 19(7): 1073–1079. DOI:10.1109/TCSVT.2009.2020478 |
| [20] | DOSOVITSKIY A, FISCHER P, ILG E, et al. FlowNet: Learning optical flow with convolutional networks[C]//Proceedings of the IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015: 2758-2766. |
| [21] | PAN S J, YANG Qiang. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345–1359. DOI:10.1109/TKDE.2009.191 |
| [22] | MENZE M, GEIGER A. Object scene flow for autonomous vehicles[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 3061-3070. |
| [23] | MAYER N, ILG E, HÄUSSER P, et al. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV: IEEE, 2016: 4040-4048. |
| [24] | FUSIELLO A, TRUCCO E, VERRI A. A compact algorithm for rectification of stereo pairs[J]. Machine Vision and Applications, 2000, 12(1): 16–22. DOI:10.1007/s001380050120 |
| [25] | LIANG Zhengfa, FENG Yiliu, GUO Yulan, et al. Learning for disparity estimation through feature constancy[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT: IEEE, 2018: 2811-2820. |
| [26] | OQUAB M, BOTTOU L, LAPTEV I, et al. Learning and transferring mid-level image representations using convolutional neural networks[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH: IEEE, 2014: 1717-1724. |



