2. 东华理工大学测绘工程学院, 江西 南昌 330013
2. School of Geomatics, East China University of Technology, Nanchang 330013, China
影像匹配是遥感影像处理与应用的关键步骤之一。经过数十年的发展,研究人员提出了许多适用于不同类型影像的匹配方法[1-5]。现有影像匹配方法大体上可分为两类:基于灰度的匹配方法和基于特征的匹配方法[6-7]。基于灰度的匹配方法能够获得亚像素级精度,但对影像灰度变化和几何变形比较敏感[8]。相对而言,基于特征的匹配方法能够较好地克服基于灰度的匹配方法对影像灰度变化和几何变形稳健性不足的问题。随着SIFT(scale invariant feature transform)算法[9]的成功,基于特征的匹配方法受到了越来越多的关注[10-11]。
针对影像视角变化,研究人员通过模拟影像仿射或投影空间,并在模拟空间进行特征匹配,获得了较好的匹配结果[12]。但这类方法时间效率较低,在实际应用中受到限制。在摄影测量领域,高精度POS(position and orientation system)数据通常被用来辅助大视角变化影像(如倾斜影像)的匹配,即利用POS信息对影像进行粗纠正,整体上降低影像几何变形的影响,再采用传统方法进行特征点匹配[13-17]。这类方法能够在一定程度上改善影像匹配的效果,但全局变换难以准确描述影像之间的局部几何变形。针对这个问题,将整幅影像分成多个子区域,分别对子区域进行特征点检测和匹配,可以克服全局影像几何纠正的不足,增加匹配点的数量[18-19]。对于无高精度POS数据的情况,可通过初匹配获取一定数量的匹配点来估计立体像对之间的几何变换模型,进而对影像进行粗纠正[19-21]。基于影像粗纠正的方法虽然能够改善影像匹配效果,但仍然存在以下问题:①影像纠正只能在一定程度上缓解平面场景的几何变形,城区影像由于存在显著的遮挡问题,对于位于视差不连续处的特征点(如建筑物角点或边缘附近的特征点),无论经过影像全局几何纠正还是分区域处理,都难以在同名点之间获得影像内容一致的特征区域,进而产生错误匹配;②通过影像初匹配进行几何纠正的方法依赖于初始匹配结果,对于存在大视角变化的城区宽基线影像,现有方法难以获得可靠的初匹配结果,导致最终匹配结果不可靠。
为此,本文面向无高精度POS信息的城区宽基线影像,针对传统方法为同名点计算的特征区域影像内容不一致,导致同名点特征描述符相似度低、匹配失败的问题,充分挖掘特征点邻域几何结构信息,提出结构自适应的特征区域计算方法,在不同视角情况下获得影像内容一致性的同名特征区域和相似特征描述符,并设计可靠的特征点匹配算法,提高正确匹配点对的数量和匹配正确率。
1 本文方法城区影像场景多为人工建筑物,能够提取大量的点特征和直线特征。本文方法通过挖掘点特征与直线特征之间的几何关系来实现城区宽基线影像特征点匹配:首先,对立体像对提取点特征和直线特征,利用特征点邻域内的直线特征表达特征点的几何结构方向信息,为特征点计算结构自适应的不变特征区域和特征描述符,通过双向匹配策略获取可靠的初匹配点,并估计立体像对核线几何关系;其次,针对部分特征点难以仅利用几何结构方向信息构建视角不变特征区域的问题,联合特征点几何结构方向信息和核线几何约束,构建视角不变特征区域进行特征匹配;最后,设计特征匹配扩展算法增加匹配点数量,提高特征匹配率,并通过RANSAC(random sample consensus)算法[22]剔除错误匹配。本文方法的整体流程如图 1所示,其中斜体标记步骤为本文方法的关键步骤。

|
| 图 1 本文方法整体流程 Fig. 1 Flow chart of the proposed method |
1.1 结构自适应特征点双向匹配
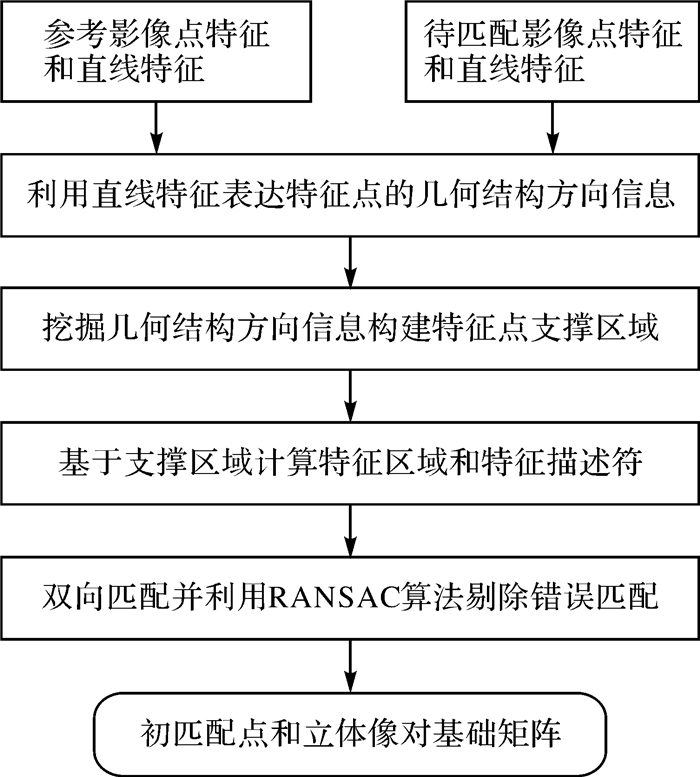
结构自适应的特征点双向匹配是本文方法的初匹配步骤,目的是获取一定数量的匹配点并估计立体像对核线几何关系,其算法流程如图 2所示。
|
| 图 2 结构自适应特征点双向匹配流程 Fig. 2 Flow chart of the structure adaptive bidirectional feature point matching method |
具体匹配方法如下:
(1) 利用直线特征表达特征点的几何结构方向信息。如图 3所示,以特征点pi为中心,确定大小为m×m的局部邻域Ri,提取与Ri相交的非平行直线特征。以特征点为原点,以与直线特征平行的方向向量表示该特征点的几何结构方向。在每个方向上,以邻域内与该方向一致且最长的直线特征的长度,作为该几何结构方向的向量长度。

|
| 图 3 特征点几何结构方向的表达 Fig. 3 Interest point structure orientation |
(2) 挖掘几何结构方向信息构建特征点支撑区域。根据几何结构方向数量差异,将特征点分以下3种情况进行处理:
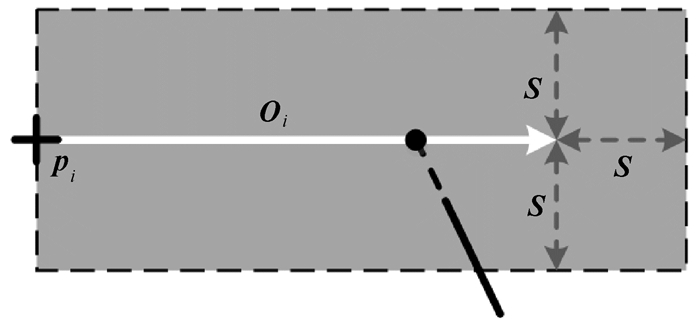
1) 如果特征点具有3个及以上几何结构方向,对其中任意两个满足夹角α∈ [θ, π-θ]的几何结构方向,分别在对应的几何结构方向上寻找显著点。其中,在每个方向上寻找显著点的方法如图 4所示[23]。图 4中,pi为特征点,Oi表示pi的一个几何结构方向,为Oi确定一个长度为|Oi|+S,宽度为2S的向量支撑区域(其中,|Oi|表示向量Oi的模,参数S用于控制向量支撑区域的尺寸)。如果向量支撑区域内存在直线特征且与该几何结构方向的交点也位于向量支撑区域内,则认为该交点是该几何结构方向上的一个显著点。由两个方向上的显著点与特征点构成平行四边形区域,即为特征点支撑区域(图 5(a))。如果在一个几何结构方向上存在多个显著点,则每个显著点分别用于构建特征点支撑区域,得到多个支撑区域。
|
| 图 4 几何结构方向显著点的确定 Fig. 4 Stable point determination on astructure orientation |
|
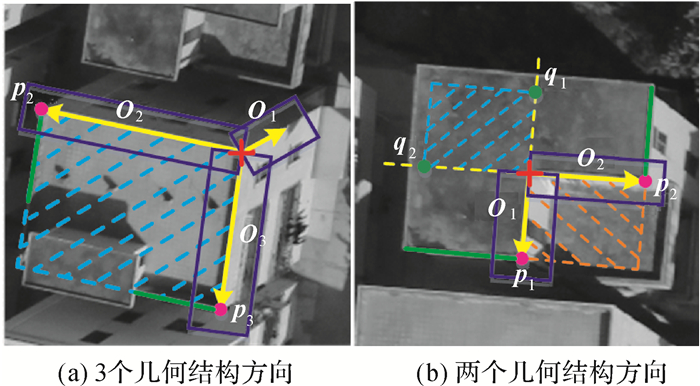
| 图 5 特征点支撑区域 Fig. 5 Interest point support region |
2) 如果特征点具有两个几何结构方向,首先沿各个方向寻找显著点,然后以特征点为中心,在几何结构方向的反方向确定对称点作为虚拟显著点,最后分别由显著点、虚拟显著点和特征点确定支撑区域(图 5(b))。
3) 如果特征点少于两个几何结构方向,则无法利用上述方法构建视角不变支撑区域。后续1.3节的特征点匹配扩展步骤将对这类特征点进行处理。
图 5所示为构建特征点支撑区域示意图。图 5(a)所示为特征点具有3个几何结构方向的情况,由于O1的向量支撑区域内没有直线特征,即该方向上没有显著点,因此无法与其他几何结构方向一起构建特征点支撑区域。O2和O3的向量支撑区域内分别存在直线特征且交点也位于向量支撑区域内,因此可以在O2和O3所夹范围内确定一个特征点支撑区域(蓝色虚线标记区域)。图 5(b)所示为特征点具有两个几何结构方向的情况,获得显著点p1和p2以后,分别在几何结构方向的反方向确定对称点q1和q2作为虚拟显著点,形成两个特征点支撑区域(橙色和蓝色虚线标记区域)。分别由显著点和虚拟显著点确定特征点支撑区域可以保证当特征点位于视差不连续区域时至少有一个支撑区域具备视角不变性。在图 5(b)所示情况中,显著点确定的支撑区域(橙色虚线标记区域)的影像内容不具备视角不变性,而虚拟显著点确定的支撑区域(蓝色虚线标记区域)的影像内容具备视角不变性。
(3) 基于特征点支撑区域计算特征区域和特征描述符。如果一个特征点存在多个支撑区域,将该特征点视作多个不同的特征点分别分配一个支撑区域。将平行四边形支撑区域归一化得到正方形特征区域。在支撑区域归一化时,为所有特征点设置相同的特征区域尺寸Tr×Tr,并分别将支撑区域中特征点及其对角线顶点映射到正方形特征区域的左下角和右上角顶点。由支撑区域与特征区域4个顶点的对应关系计算单应性矩阵进行特征区域归一化。将特征区域划分为16个子区域,在每个子区域内计算8个方向的梯度方向直方图,得到128维特征描述符。最后,对特征描述符进行归一化处理,提高特征描述符对影像光照变化的稳健性[9]。
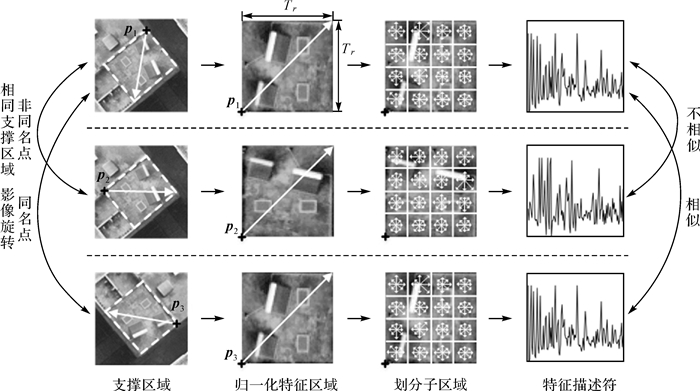
通过本文提出的特征区域归一化处理,一方面可以避免建筑物同一顶(侧)面上不同位置的角点因为对应于同一个支撑区域而产生错误匹配,另一方面能够消除影像旋转变化的影响。如图 6所示,特征点p1和p2虽然支撑区域相同,但是经过本文方法得到的特征区域和特征描述符具有较强的可区分性,能够避免错误匹配。虽然特征点p1和p3所在的影像存在旋转变化,但是本文提出的特征区域归一化方法能够消除影像旋转变化,得到相似的特征区域和特征描述符,提高特征匹配率。
|
| 图 6 特征区域和特征描述符计算过程 Fig. 6 Feature region and descriptor computation |
(4) 利用双向的NNDR(nearest neighbor distance ratio)匹配策略[24]进行特征点匹配,并结合RANSAC算法剔除错误匹配,得到初匹配集合MSet1和基础矩阵F。
虽然初匹配能够正确匹配部分特征点,但是该方法只对满足以下条件的特征点有效:特征点具有至少两个满足夹角约束条件并且能够获得显著点(图 4所示方法)的几何结构方向。该条件导致初匹配步骤获得的匹配点数量有限。为了提高匹配点数量,本文方法在初匹配之后分别设计双重核线约束的结构自适应特征点匹配(1.2节)和特征点匹配扩展(1.3节)算法。前者用于处理具有两个及两个以上几何结构方向的未匹配特征点;后者用于处理经过前面两个匹配步骤仍然未匹配成功的特征点。
1.2 双重核线约束的结构自适应特征点匹配首先,对于参考影像上未匹配且具有两个及以上几何结构方向的特征点pi,由特征点与任意两个夹角α∈[θ, π-θ]的几何结构方向的终点s1和s2确定一个平行四边形,作为特征点pi的支撑区域(图 7(a))。其次,基于基础矩阵F分别计算点pi、s1和s2在搜索影像上对应的核线epi= Fpi、es1= Fs1和es2= Fs2。然后,在搜索影像上筛选到核线epi的距离小于阈值Te,并且具有两个及以上几何结构方向的特征点,得到候选匹配点集合Cio。最后,对候选匹配点qj∈Cio,取其任意两个夹角β∈ [θ, π-θ]的几何结构方向,分别计算几何结构方向与核线es1和es2的交点Qs1和Qs2,由点qj、Qs1和Qs2为qj确定一个平行四边形支撑区域。由于在匹配之前特征点pi和qj的几何结构方向对应关系未知,本文方法在计算交点Qs1和Qs2时分别考虑如图 7(b)和(c)所示的两种情况,构建两个相应的支撑区域,避免由错误的几何结构方向对应关系造成同名特征点支撑区域不一致的问题。此外,鉴于核线估计存在误差导致计算的交点不可靠,本文方法在交点Qs1和Qs2的邻域内(邻域大小为2Te)计算显著点来代替Qs1和Qs2作为支撑区域顶点。显著点计算方法为:对交点邻域内任意像素gk,按式(1)计算其像素显著性S(gk),交点邻域中显著性值最大的像素即为显著点
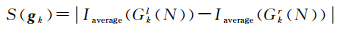 (1)
(1)

|
| 图 7 核线约束的特征点支撑区域 Fig. 7 Feature support region computation based on epipolar geometric constraint |
式中,Gkl(N)和Gkr(N)分别表示以点gk为中心,沿对应的几何结构方向两侧N个像素的集合(本文方法中参数N设置为5);Iaverage()表示像素集合的灰度值均值。
获得参考影像特征点及其候选同名特征点的支撑区域以后,采用1.1节提出的方法计算特征区域和特征描述符,并基于NNDR匹配策略[25]得到特征点匹配集合MSet2。
1.3 特征点匹配扩展根据特征点是否位于某个已匹配的特征点支撑区域内,将未匹配的特征点分成两类(第1类:是;第2类:否),并分别进行匹配:
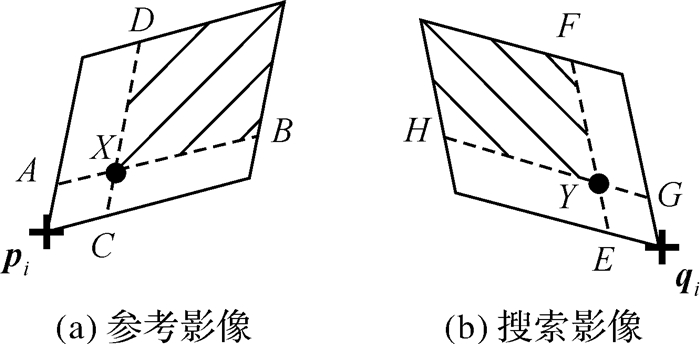
1.3.1 结合几何约束和特征描述符相似性匹配第1类特征点在几何约束方面,如图 8所示,假设(pi, qi)为一对已匹配的特征点,图中实线平行四边形区域为其支撑区域。X为参考影像上位于点pi支撑区域内的一个未匹配特征点,由搜索影像上所有位于特征点qi支撑区域内的未匹配特征点构成X的候选匹配点集合CX。由于特征点支撑区域是基于直线特征确定的局部区域,可以近似为平面区域。由仿射几何可知,如果特征点X与特征点Y ∈CX为一对同名点,则|XA| /|XB|=|YE|/|YF|,且|XC|/|XD|=|YG|/|YH|。其中,点A、B、C、D分别为过特征点X且与点pi的支撑区域的边平行的直线与点pi的支撑区域的交点;点E、F、G、H分别为过特征点Y且与点qi的支撑区域的边平行的直线与点qi的支撑区域的交点。
|
| 图 8 第1类未匹配特征点匹配扩展 Fig. 8 The matching expansion for the unmatched point in the first class |
计算特征描述符时,首先,根据X在pi的支撑区域中的位置确定X的支撑区域:如果|XA|≤|XB|,则点B被视作一个显著点,否则点A被视作显著点;如果|XC|≤|XD|,则点D被视作第2个显著点,否则点C被视作第2个显著点。由点X与两个显著点共同确定特征点X的支撑区域;然后,根据显著点的对应关系(A→E、B→F、C→G和D→H),确定候选匹配点对应的显著点及支撑区域;最后,采用1.1节所述方法计算特征点X及其候选匹配点的特征区域和特征描述符。
按式(2)计算参考影像特征点与所有候选同名特征点的相似性度量值sim(X, Y),并寻找最相似的候选匹配点,如果其相似性度量值大于阈值Tsim,则认为该特征点与参考特征点为一对匹配点。完成第1类特征点匹配以后,得到匹配集合MSet3。
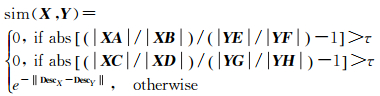 (2)
(2)
式中,τ为仿射不变量阈值;DescX和DescY分别为特征点X及其候选匹配点Y的特征描述符。
1.3.2 基于单应变换匹配第2类特征点首先,基于前面所有匹配结果{MSeti, i=1, 2, 3}估计影像之间的单应矩阵H;然后,为参考影像上所有第2类未匹配特征点确定以特征点为中心的正方形特征区域,基于单应变换为搜索影像上所有第2类未匹配特征点确定以特征点为中心的四边形特征区域,并将四边形特征区域归一化为正方形区域;最后,计算所有未匹配特征点的特征描述符,并在核线约束下通过NNDR匹配策略得到匹配集合MSet4。利用RANSAC算法对所有匹配结果{MSeti, i=1, …, 4}剔除错误匹配,得到最终匹配结果。
2 试验及结果分析 2.1 试验数据为了验证本文算法的有效性,分别采用6对典型的局部影像块、一组原始大小的三视航空倾斜影像和一组原始大小的三视无人机影像进行特征点匹配试验。如图 9所示:(a)和(b)所示分别为平房和广场区域倾斜像对,其中参考影像为下视影像,搜索影像为斜视影像;(c)所示为无人机影像对;(d)—(f)所示均为倾斜影像,其中(d)和(e)中参考影像为下视影像,搜索影像为斜视影像,(f)中参考影像和搜索影像均为斜视影像;(g)所示为三视航空倾斜影像;(h)所示为三视无人机影像。试验数据详细信息见表 1。

|
| 图 9 试验数据 Fig. 9 Experimental datasets |
| 编号 | 拍摄系统 | 拍摄地点 | 相对航高/m | 地面采样间隔/cm | 交会角/(°) | 影像大小/pixel |
| 影像对1 | IQ180 | 深圳 | 800 | 8 | 51.4 | 1000×1000 |
| 影像对2 | IQ180 | 深圳 | 800 | 8 | 53.6 | 1000×1000 |
| 影像对3 | Nikon D810 | 深圳 | 300 | 6 | 36.9 | 1024×1024 |
| 影像对4 | SWDC-5 | 贵阳 | 600 | 8 | 49.6 | 1000×1000 |
| 影像对5 | SWDC-5 | 贵阳 | 600 | 8 | 47.7 | 1200×1200 |
| 影像对6 | SWDC-5 | 贵阳 | 600 | 8 | 94.4 | 1200×1200 |
| 三视影像1 | SWDC-5 | 贵阳 | 600 | 8 | — | 8176×6132 |
| 三视影像2 | Canon IXUS127 | 南昌 | 240 | 8 | — | 4608×3456 |
2.2 参数设置
本文方法相关参数设置为:构建特征点邻域几何结构方向向量时,特征点邻域大小m×m=11×11像素;邻域几何结构方向向量支撑区域参数s=20像素;邻域几何结构方向向量夹角阈值θ=10°;归一化特征区域尺寸Tr×Tr=65×65像素;点到核线的距离阈值Te=20像素;特征匹配扩展算法中,仿射不变量阈值τ=0.3,特征描述符相似性阈值Tsim=0.65。在本文试验中,Harris算子[27]和LSD算子[28]分别被用于提取点特征和直线特征。本文试验中所有对比方法的参数均按原文献作者推荐的参数值进行设置。本文所有试验均在相同平台环境(Windows 10,Intel Core i7 3.6 GHz,RAM 32 GB)下完成。
2.3 试验结果分析 2.3.1 局部影像像对匹配结果分析本文试验首先基于局部影像对(图 9(a)—(f))进行两两匹配,将本文方法与多种匹配算法进行对比分析以验证本文方法对典型影像区域的有效性。对比方法包括:分别将Harris-Affine算子[25]、Hessian-Affine算子[25]、MSER算子[26]和DoG算子[9]与SIFT特征描述符和NNDR匹配策略组合而成的4种特征匹配算法(HarAff、HesAff、MSER和SIFT算法)、ASIFT算法[12],以及基于影像粗纠正的ISIFT算法[19-20]。
在这部分试验中,以正确匹配特征对数和匹配正确率(正确匹配特征对数/总匹配对数)为评价指标,统计结果如图 10所示。其中,通过人工检查的方式来统计正确匹配特征对数。

|
| 图 10 对比试验统计结果 Fig. 10 Statistic results of the comparative experiments |
从图 10(a)所示的正确匹配对数可以看出,HarAff、HesAff、MSER和SIFT 4种方法在所有像对上都只能获得少量的匹配对,表明这4种方法难以适用于视角变化较大且存在遮挡问题的城区宽基线影像。相对于上述4种方法,ASIFT和ISIFT算法通过改进匹配策略来提高算法的稳健性。其中,ASIFT算法通过模拟影像仿射空间来消除影像之间的几何变形,获得了更好的匹配效果。影像对2中场景深度变化不显著,ASIFT算法模拟的仿射空间能够较好地拟合影像局部区域,因此ASIFT算法在影像对2上获得了最多的匹配对。但是ASIFT方法中模拟的仿射空间不连续,在影像视角变化和场景深度变化较大的影像对4、5和6上,许多局部区域没有被模拟的仿射空间所覆盖,即难以通过模拟仿射空间来消除这些局部区域的几何变形,因此ASIFT方法在这3对影像上获得的特征对数较少。此外,ASIFT算法为特征点分配规则特征区域的方法难以适用于地物遮挡和视差不连续的情况。ISIFT算法也是基于影像模拟和粗纠正的思想,但是ISIFT算法只对整幅影像进行一次模拟,当参考影像与待匹配影像视角变化大且影像场景深度变化较大时,整幅影像之间不服从同一个全局变换模型,ISIFT方法获得的几何变换模型只能纠正影像中的部分区域。因此ISIFT方法虽然能够改善SIFT方法的匹配结果,但是其改善程度有限。此外,ISIFT算法依赖于初匹配的结果。如图中所示影像对5的匹配结果,ISIFT算法因为初匹配结果难以准确估计影像之间的几何变换模型,最终匹配失败。
相对于以上方法,本文方法在除影像对2以外的所有5对影像上都得到了最多的正确匹配。这主要得益于本文方法能够根据特征点邻域结构自适应地获取影像内容一致的特征区域。无论特征点位于平面区域或是视差不连续区域,本文方法得到的同名特征区域之间都具有较高的相似度,更容易在特征匹配过程中被正确识别出来。此外,本文方法中的特征匹配扩展算法有助于获得更多的匹配对。
从图 10(b)所示的匹配正确率可以看出,本文方法和ASIFT算法的匹配正确率优于其他方法。当影像初匹配能够获得一定数量的正确匹配用于估计影像几何变换模型时,ISIFT算法也能获得较高的匹配正确率,但是当影像视角变化导致无法通过初匹配来估计影像几何变换模型时,ISIFT算法将匹配失败。
2.3.2 完整三视影像匹配结果分析除了采用局部影像像对进行算法验证以外,本文试验还利用两组三视影像测试本文方法的匹配性能。鉴于SIFT算法的广泛应用以及ASIFT算法对影像视角变化的稳健性,这部分试验将本文方法与SIFT算法和ASIFT算法进行对比分析。在具体实施时,考虑到原始SIFT算法和ASIFT算法在处理较大尺寸影像时计算内存开销非常大,且算法时间效率极低,本文采用更加高效的GPU版本的SIFT算法(SIFTGPU[29])以及下采样模式的ASIFT算法(先将原始影像下采样为800×600像素大小的影像进行匹配,再将匹配结果反算回原始影像[30])。此部分试验以三度重叠匹配数量和匹配效率为评价指标。3种方法在两组三视影像上匹配的统计结果如下表 2所示,三度重叠匹配如图 11和图 12所示。由于ASIFT方法的三度重叠匹配数量为0,因此图 11中只列出SIFTGPU方法和本文方法的结果。
| SIFTGPU | ASIFT | 本文方法 | ||
| 三视影像1 | 三度重叠匹配数量 | 10 | 0 | 463 |
| 运算时间/s | 15 | 2392 | 1537 | |
| 三视影像2 | 三度重叠匹配数量 | 593 | 327 | 1303 |
| 运算时间/s | 10 | 227 | 139 | |

|
| 图 11 三视影像1的三度重叠匹配结果 Fig. 11 Three-time overlapped matches on three-view image dataset 1 |

|
| 图 12 三视影像2的三度重叠匹配结果 Fig. 12 Three-time overlapped matches on three-view image dataset 2 |
从表 2统计结果可以看出,在三度重叠匹配数量方面,本文方法在两组数据上获得的三度重叠匹配数量都远超SIFTGPU和ASIFT算法。尤其在三视影像1上,影像之间视角变化大,且影像场景为密集建筑区域,大量特征点位于视差不连续的边缘附近,SIFTGPU和ASIFT算法几乎匹配失败,而本文方法仍然能够获得463个三度重叠匹配;在算法时间效率方面,SIFTGPU算法的时间效率最高。本文方法在分步匹配中利用初匹配估计同名核线来约束后续匹配过程,时间效率优于ASIFT算法,但相对于SIFTGPU而言,运算效率仍然较低。
此外,表 2统计结果显示ASIFT方法获得的三度重叠匹配少于SIFTGPU方法,尤其在三视影像1上的三度重叠匹配数量为0。对ASIFT方法在该数据集上的匹配结果进行仔细检查发现:ASIFT方法在三视影像集1中三对立体像对之间获得的两两匹配数量分别为108对、33对和222对,如图 13所示。其中,影像1和影像3由于视角差异太大(图 13(b)),ASIFT方法获得的匹配点数量非常少,直接影响了三度重叠匹配的数量。

|
| 图 13 ASIFT方法(下采样模式)在三视影像1上的两两匹配结果 Fig. 13 Matches of ASIFT (down-sampling mode) on image pairs in three-view image dataset 1 |
为了进一步验证ASIFT算法在三视影像1上的匹配效果,使用普通模式(直接在原始影像上进行匹配)的ASIFT方法对三视影像1进行匹配试验。具体实施时,采用OpenCV中的ASIFT算子,分别在三视影像1中的3幅影像上提取了2 523 709、3 746 247和3 402 273个特征点。数百万个特征点进行盲匹配和穷举搜索带来了巨大的时间开销(约67个小时),然而三度重叠匹配数量仍然是0。3幅影像两两匹配的结果如图 14所示。从图 14(b)可以看出,对于视角变化非常大的影像1和影像3,ASIFT算法获得的匹配点非常少,与图 13(b)的结果一致。此外,从图 14(a)和图 14(c)所示匹配结果可以看出,虽然ASIFT方法在两两影像之间能够获得一些匹配点,但是匹配点在多视影像上的重复率非常低。

|
| 图 14 ASIFT方法(普通模式)在三视影像1上的两两匹配结果 Fig. 14 Matches of ASIFT (general mode) on image pairs in three-view image dataset 1 |
综上所述,本文方法在匹配效果方面优于SIFTGPU方法和ASIFT方法,在匹配时间效率方面优于ASIFT方法,但低于SIFTGPU方法。笔者将在后续研究中通过算法和程序优化提高本文方法的时间效率。
3 结论本文针对城区宽基线影像视角变化导致传统方法难以为同名点计算影像内容一致的特征区域和相似特征描述符,进而导致匹配失败的问题,提出了一种结构自适应的特征点匹配方法。本文方法的创新之处在于利用城区影像点特征与直线特征的几何关系定义了特征点几何结构方向信息,构建了结构自适应的特征区域和特征描述符,在此基础上设计特征匹配和扩展算法,实现了城区宽基线影像的可靠匹配。以上改进使得本文方法能够较好地处理因影像视角变化导致的几何变形和遮挡问题,对于大视角变化的城区宽基线影像能够获得较好的匹配结果。但是,由于本文方法在特征匹配时利用了粗略的核线约束,因此匹配结果中的误匹配都满足该约束条件。在后续剔除误匹配时,部分误匹配难以通过(基于基础矩阵的)RANSAC算法来剔除。此外,本文方法的运算效率仍需进一步提高。后续工作将研究如何有效剔除错误匹配,并通过算法和程序优化提高本文方法的运算效率。
| [1] |
戴激光, 宋伟东, 贾永红, 等.
一种新的异源高分辨率光学卫星遥感影像自动匹配算法[J]. 测绘学报, 2013, 42(1): 80–86.
DAI Jiguang, SONG Weidong, JIA Yonghong, et al. A new automatically matching algorithm for multi-source high resolution optical satellite images[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 80–86. |
| [2] |
叶沅鑫, 单杰, 彭剑威, 等.
利用局部自相似进行多光谱遥感图像自动配准[J]. 测绘学报, 2014, 43(3): 268–275.
YE Yuanxin, SHAN Jie, PENG Jianwei, et al. Automated multispectral remote sensing image registration using local self-similarity[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 268–275. DOI:10.13485/j.cnki.11-2089.2014.0039 |
| [3] |
岳春宇, 江万寿.
几何约束和改进SIFT的SAR影像和光学影像自动配准方法[J]. 测绘学报, 2012, 41(4): 570–576.
YUE Chunyu, JIANG Wanshou. An automatic registration algorithm for SAR and optical images based on geometry constraint and improved SIFT[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 570–576. |
| [4] |
陈敏, 朱庆, 朱军, 等.
SAR影像与光学影像的高斯伽玛型边缘强度特征匹配法[J]. 测绘学报, 2016, 45(3): 318–325.
CHEN Min, ZHU Qing, ZHU Jun, et al. Feature matching for SAR and optical images based on Gaussian-Gamma-shaped edge strength map[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 318–325. DOI:10.11947/j.AGCS.2016.20150084 |
| [5] |
梁焕青, 谢意, 付四洲.
颜色不变量与AKAZE特征相结合的无人机影像匹配算法[J]. 测绘学报, 2017, 46(7): 900–909.
LIANG Huanqing, XIE Yi, FU Sizhou. UAV image registration algorithm using color invariant and AKAZE feature[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 900–909. DOI:10.11947/j.AGCS.2017.20160436 |
| [6] | ZITOV B, FLUSSER J. Image registration methods: a survey[J]. Image and Vision Computing, 2003, 21(11): 977–1000. DOI:10.1016/S0262-8856(03)00137-9 |
| [7] | XIONG Zhen, ZHANG Yun. A novel interest-point-matching algorithm for high-resolution satellite images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(12): 4189–4200. DOI:10.1109/TGRS.2009.2023794 |
| [8] | GRUEN A. Development and status of image matching in photogrammetry[J]. The Photogrammetric Record, 2012, 27(137): 36–57. DOI:10.1111/j.1477-9730.2011.00671.x |
| [9] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. |
| [10] | BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346–359. DOI:10.1016/j.cviu.2007.09.014 |
| [11] | TOLA E, LEPETIT V, FUA P. Daisy: an efficient dense descriptor applied to wide-baseline stereo[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 815–830. DOI:10.1109/TPAMI.2009.77 |
| [12] | MOREL J M, YU Guoshen. ASIFT: a new framework for fully affine invariant image comparison[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 438–469. DOI:10.1137/080732730 |
| [13] | HU Han, ZHU Qing, DU Zhiqiang, et al. Reliable spatial relationship constrained feature point matching of oblique aerial images[J]. Photogrammetric Engineering & Remote Sensing, 2015, 81(1): 49–58. |
| [14] |
肖雄武, 郭丙轩, 李德仁, 等.
一种具有仿射不变性的倾斜影像快速匹配方法[J]. 测绘学报, 2015, 44(4): 414–421.
XIAO Xiongwu, GUO Bingxuan, LI Deren, et al. A quick and affine invariance matching method for oblique images[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 414–421. DOI:10.11947/j.AGCS.2015.20140048 |
| [15] |
肖雄武, 李德仁, 郭丙轩, 等.
一种具有视点不变性的倾斜影像快速匹配方法[J]. 武汉大学学报(信息科学版), 2016, 41(9): 1151–1159.
XIAO Xiongwu, LI Deren, GUO Bingxuan, et al. A robust and rapid viewpoint-invariant matching method for oblique images[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1151–1159. |
| [16] |
闫利, 费亮, 叶志云, 等.
大范围倾斜多视影像连接点自动提取的区域网平差法[J]. 测绘学报, 2016, 45(3): 310–317.
YAN Li, FEI Liang, YE Zhiyun, et al. Automatic tie-points extraction for triangulation of large-scale oblique multi-view images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 310–317. DOI:10.11947/j.AGCS.2016.20140673 |
| [17] |
张力, 艾海滨, 许彪, 等.
基于多视影像匹配模型的倾斜航空影像自动连接点提取及区域网平差方法[J]. 测绘学报, 2017, 46(5): 554–564.
ZHANG Li, AI Haibin, XU Biao, et al. Automatic tie-point extraction based on multiple-image matching and bundle adjustment of large block of oblique aerial images[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 554–564. DOI:10.11947/j.AGCS.2017.20160571 |
| [18] | SUN Yanbiao, ZHAO Liang, HUANG Shoudong, et al. L2-SIFT: SIFT feature extraction and matching for large images in large-scale aerial photogrammetry[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014(91): 1–16. |
| [19] | JIANG San, JIANG Wanshou. On-board GNSS/IMU assisted feature extraction and matching for oblique UAV images[J]. Remote Sensing, 2017, 9(8): 813. DOI:10.3390/rs9080813 |
| [20] | YU Yinan, HUANG Kaiqi, CHEN Wei, et al. A novel algorithm for view and illumination invariant image matching[J]. IEEE Transactions on Image Processing, 2012, 21(1): 229–240. DOI:10.1109/TIP.2011.2160271 |
| [21] |
仇春平, 于瑞鹏, 丁翠, 等.
面向倾斜立体影像的尺度不变特征匹配[J]. 遥感信息, 2016, 31(1): 43–47.
QIU Chunping, YU Ruipeng, DING Cui, et al. Oblique stereo image matching based on scale invariant feature[J]. Remote Sensing Information, 2016, 31(1): 43–47. DOI:10.3969/j.issn.1000-3177.2016.01.007 |
| [22] | FISCHLER M A, BOLLES R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381–395. DOI:10.1145/358669.358692 |
| [23] | LI Kai, YAO Jian. Line segment matching and recon struction via exploiting coplanar cues[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017(125): 33–49. |
| [24] | CHEN Min, QIN Rongjun, HE Haiqing, et al. A local distinctive features matching method for remote sensing images with repetitive patterns[J]. Photogrammetric Engineering & Remote Sensing, 2018, 84(8): 513–524. |
| [25] | MIKOLAJCZYK K, SCHMID C. Scale & affine invariant interest point detectors[J]. International Journal of Computer Vision, 2004, 60(1): 63–86. |
| [26] | MATAS J, CHUM O, URBAN M, et al. Robust wide-baseline stereo from maximally stable extremal regions[J]. Image and Vision Computing, 2004, 22(10): 761–767. DOI:10.1016/j.imavis.2004.02.006 |
| [27] | HARRIS C, STEPHENS M. A combined corner and edge detector[C]//Proceedings of the 4th Alvey Vision Conference. Manchester, Britain: [s.n.], 1988: 147-152. |
| [28] | VON GIOI R G, JAKUBOWICZ J, MOREL J M, et al. LSD: a fast line segment detector with a false detection control[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(4): 722–732. DOI:10.1109/TPAMI.2008.300 |
| [29] | WU Changchang. SiftGPU: a GPU implementation of scale invariant feature transform[EB/OL]. (2011). http://ccwu.me/code.html. |
| [30] | YU Guoshen, MOREL J M. ASIFT: an algorithm for fully affine invariant comparison[J]. Image Processing On Line, 2011(1): 11–38. |


