2. 西南石油大学土木工程与建筑学院, 四川 成都 610500;
3. 广州市市政工程试验检测有限公司, 广东 广州 510520;
4. 中铁二院工程集团有限责任公司, 四川 成都 610031
2. School of Civil Engineering and Architecture, Southwest Petroleum University, Chengdu 610500, China;
3. Guangzhou Municipal Engineering Testing Co. Ltd., Guangzhou 510520, China;
4. China Railway Eryuan Engineering Group Co. Ltd., Chengdu 610031, China
受水文特征、地质地貌等条件的影响,海平面变化具有显著的区域性特征。相较于全球海平面变化,区域海平面变化影响着沿海区域的气候环境,更为直接地影响着人们的生产生活[1]。红海北部通过苏伊士运河与地中海连接,南部通过曼德拉湾与阿拉伯海相连,是典型的半封闭式海域。许多学者对红海的海平面变化及特征进行了研究。文献[2]使用MICOM海洋环流模式研究了红海与印度洋间的季节性质量交换机制,表明红海与印度洋间的季节性质量交换是曼德海峡风驱动与温盐驱动共同作用的结果。文献[3]使用海洋模式数据研究了红海1958—2001年间海平面变化,发现准两年振荡、厄尔尼诺/南方涛动和太阳黑子事件可能对红海海平面变化有重要影响。文献[4]利用卫星重力、卫星测高和温盐数据研究发现质量迁移引起的海平面变化是红海海平面变化的主导因素。
GRACE卫星重力数据提供了高空间、高时间分辨率的时变重力场模型,为研究全球或者区域质量迁移提供了高精度的观测资料[5]。受卫星轨道和测距误差等因素的影响,GRACE地表质量变化受南北条带状噪声影响较为显著,需要采用空间平滑滤波削弱条带误差的影响[6-7]。但空间平滑滤波会引起地球物理信号的泄漏,该误差对狭长型的红海区域的影响十分显著。文献[4]利用尺度因子改正滤波引起的泄漏误差,但改正后的红海质量变化仍明显小于海底压力实测数据。文献[8]提出了顾及高斯平滑的流域核函数,并通过迭代确定最佳流域核函数,从而减小空间平滑引起的泄漏误差,但该方法仍因迭代收敛条件的不同存在差异且流程繁琐。同时,红海地区温盐数据存在覆盖不全或质量不佳的问题,前期研究采用的温盐数据过于单一,影响着比容海平面变化的估算及其精度。针对红海区域的泄漏误差,本文提出了顾及红海真实形态的改进尺度因子,并利用卫星测高、GRACE以及多种温盐数据分析2003—2014年间红海海平面变化特征。
1 数据与方法海平面变化根据成因可分为温度/盐度引起的比容海平面变化和海水质量变化引起的海平面变化。比容海平面变化是由于温度和盐度变化引起的海水体积变化,可通过海洋实测温盐数据估算,海水质量变化引起的海平面变化主要与全球质量迁移有关[9-11]。本文采用GRACE卫星重力数据和温盐数据估算质量变化和比容海平面变化,利用卫星测高数据监测总海平面变化。
1.1 GRACE卫星重力数据采用美国得克萨斯大学空间研究中心CSR(Center for Space Research)发布的GRACE RL05版本球谐系数时变重力场模型估算2003—2014年间红海质量变化。为获得地表质量变化需扣除平均重力场模型,同时增加一阶项球谐系数[12],利用SLR反演的C20系数替换原始的低精度数据[13],并扣除冰后回弹模型[14]。将球谐系数模型截断至60阶,并使用300 km高斯滤波抑制条带误差和高频噪声。为获得完整的海洋质量变化信号,加回GAD海洋模型,并扣除大气质量在海洋上的月时变部分的影响[15]。针对截断与平滑引起的泄漏误差,其可分为两类:研究区域信号泄漏到周边区域(外泄漏)和周边区域信号泄漏至研究区域(内泄漏)[16]。利用GLDAS(global land data assimilation systems)水文模型与ECCO(estimating circulation and climate of the ocean general model)海洋模式数据构建全球表面质量变化模型(通过在海洋上平铺一层海水的形式保证全球质量守恒),将研究区域内的模型值设为零,然后将模型转化为球谐系数,截断至60阶并进行与GRACE数据相同的滤波处理,得到研究区域的內泄漏信号并加以扣除[4],再采用尺度因子改正红海信号泄漏至周边区域的外泄漏误差。
1.2 温盐数据采用多种海洋温盐数据集估算比容海平面变化,包括CORA(coriolis ocean dataset for reanalysis)[17]、SODA(simple ocean data assimilation)[18]、ORAS4(ocean reanalysis system 4)[19]、WOA09(world ocean atlas 2009)[20]、WOA18(world ocean atlas 2018)[21]与Ishii海洋温盐数据集[22]。比容海平面变化主要受海洋中上层0~1500 m的温盐变化影响[23],因此使用Thermodynamic Equation of Seawater-2010软件[24]计算红海2003—2014年间0~1500 m深度的比容海平面变化。
1.3 卫星测高数据采用法国AVISO(archiving, validation and interpretation of satellite oceanographic data)提供的2003—2014年间的月均海平面高度异常数据(mean sea level anomaly, MSLA)计算总海平面变化。该数据集综合了TOPEX/Poseidon、Jason-1/2、ERS-1/2、Geosat Follow-On等多颗测高卫星资料,格网空间分辨率为0.25°×0.25°,并已进行必要的标准地球物理改正及大气改正(海洋潮汐及其负荷改正、极潮改正、电磁偏差改正和反变气压改正等)。但该数据集并未考虑部分地球物理信号改正,本文使用GRACE数据估算质量变化引起的海底地壳垂向负荷形变以改正卫星测高数据中负荷影响,并扣除冰后回弹模型[14]。
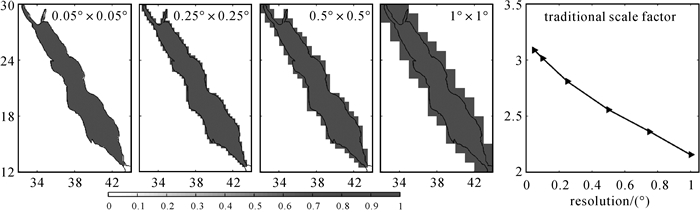
2 改进尺度因子方法及其验证 2.1 改进尺度因子针对截断与滤波引起的外泄漏误差,可采用尺度因子进行改正。通常使用理想盆地核函数求取尺度因子:假设研究区域内的质量变化是均匀一致的,研究区域内信号为1,区域外信号为0,对该格网进行球谐展开,截断至一定阶次,采取与GRACE数据相同的滤波处理,得到研究区域内的剩余信号,尺度因子即为1/(剩余信号)。格网型的理想盆地核函数边界与真实地理边界并不完全一致,通常选取覆盖整个研究区域的格网以防止遗漏信号,这会使边界格网包含非研究区域,导致根据传统理想盆地核函数估算的尺度因子偏小。当研究区域范围较大时该影响较弱,但对于中小范围研究区域其影响较为明显。假定0.05°× 0.05°格网边界与红海真实地理边界一致,在此基础上得到其他低空间分辨率格网。图 1为不同空间分辨率的理想盆地核函数及估算的300 km高斯滤波对应的尺度因子。随着空间分辨率的降低,边界格网所包含的非红海区域的面积增大,导致估算的尺度因子迅速减小。
|
| 图 1 不同空间分辨率的理想盆地核函数及估算的300 km高斯滤波尺度因子 Fig. 1 Basin kernel function in different spatial resolution and estimated scale factors corresponding to 300 km Gaussian filter |
GRACE球谐系数模型截断阶次有限(通常截断至60阶次),故大多数情况下采用1°或者0.5°的理想盆地核函数估算尺度因子,但受边界格网中非研究区域的影响,其与真实红海范围的理想盆地核函数估算结果存在较大差异。为了减小该影响,改进理想盆地核函数

式中,Sinside为边界格网内的研究区域面积;S为格网面积。将利用改进理想盆地核函数计算的尺度因子称之为改进尺度因子。图 2为不同空间分辨率的改进理想盆地核函数以及估算的300 km高斯滤波对应的改进尺度因子。改进的理想盆地核函数内部为1,边界格网值与格网内红海的面积有关,其他格网则为0;不同空间分辨率估算的改进尺度因子基本一致,表明改进的尺度因子能够获得稳定的估算结果。

|
| 图 2 不同空间分辨率的改进理想盆地核函数及估算的300 km高斯滤波尺度因子 Fig. 2 Improved basin kernel function in different spatial resolution and estimated scale factors corresponding to 300 km Gaussian filter |
2.2 改进尺度因子的验证
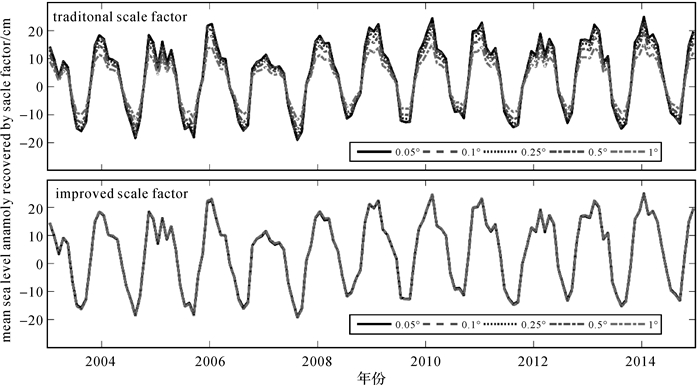
为验证改进尺度因子的有效性以及相较于传统尺度因子的优势,利用红海2003—2014年间的卫星测高数据进行模拟实验,分析改进尺度因子恢复真实信号的能力。将卫星测高数据插值成0.05°×0.05°格网,球谐展开至60阶并做300 km高斯滤波,进而转换成不同空间分辨率的格网数据。分别利用传统尺度因子与改进尺度因子改正泄漏误差来恢复真实信号,其恢复的红海卫星测高海平面变化时间序列如图 3所示,同时表 1给出了不同时间序列的周年信号及与原始信号的均方根误差。传统尺度因子恢复信号的时间序列与周年振幅随空间分辨率的降低而显著减小,与真实信号的均方根误差迅速增大。而不同空间分辨率的改进尺度因子恢复信号与真实信号的时间序列基本一致,周年振幅与真实信号偏差最大不超过0.5 cm,均方根误差最大仅为0.4 cm。综合分析表明改进尺度因子能够有效恢复红海地区真实信号,明显优于传统的尺度因子恢复结果。
|
| 图 3 基于传统与改进尺度因子的卫星测高恢复信号时间序列 Fig. 3 Time series of simulated signals (satellite altimetry data) recovered by traditional and improved scale factor |
| 格网分辨率 | 周年振幅/cm | 周年相位/(°) | 与真实信号的差异RMS/cm | |
| 原始信号 | 0.05° | 16.2±0.9 | 57±3 | — |
| 传统尺度因子 | 0.1° | 15.9±0.9 | 57±3 | 0.3 |
| 0.25° | 14.9±0.8 | 57±3 | 1.1 | |
| 0.5° | 13.1±0.7 | 57±3 | 2.5 | |
| 1° | 10.4±0.6 | 57±3 | 4.8 | |
| 改进尺度因子 | 0.1° | 16.4±0.9 | 57±3 | 0.2 |
| 0.25° | 16.4±0.9 | 57±3 | 0.2 | |
| 0.5° | 16.5±0.9 | 57±3 | 0.2 | |
| 1° | 16.6±0.9 | 57±3 | 0.4 |
3 红海海平面变化分析 3.1 温盐数据质量分析
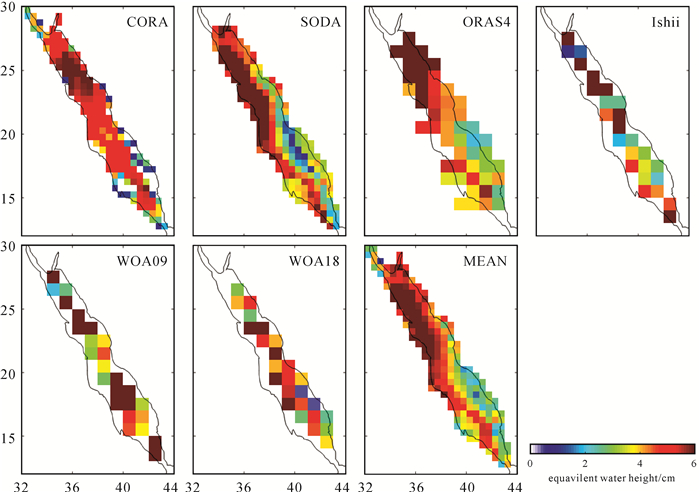
图 4为不同温盐数据估算的2003—2014年红海比容海平面变化周年振幅的空间分布,其中Ishii数据时间段为2003—2012年。Ishii、WOA09与WOA18数据在红海区域存在严重的数据缺失,CORA和ORAS4数据也存在部分缺失,SODA数据的覆盖率良好。不同温盐数据的估算结果均表明红海北部比容信号的周年振幅大于南部区域,但对于局部区域而言,不同温盐数据结果的空间分布仍存在较大差异。
|
| 图 4 红海比容海平面变化周年振幅空间分布 Fig. 4 Spatial pattern of annual amplitude of steric sea level variations in the Red Sea |
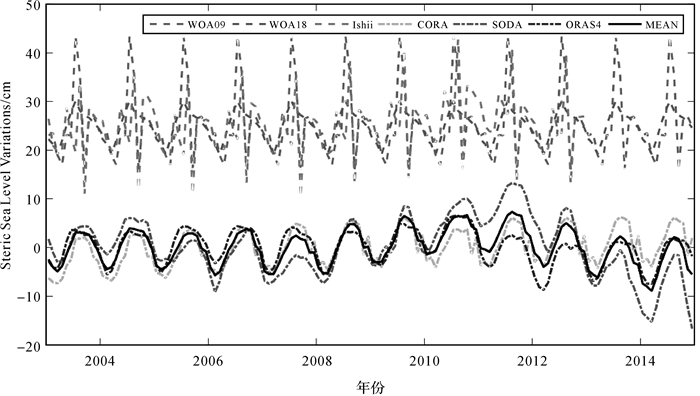
图 5为不同温盐数据估算的红海比容海平面变化时间序列,表 2为各数据估算的温比容、盐比容及温盐比容效应引起的海平面变化的周年信号统计数据。CORA、ORAS4与SODA数据估算的比容海平面变化周年振幅基本一致,同时CORA和ORAS4数据无明显的年际信号,而SODA数据的年际变化较为明显。WOA09与WOA18为多年月均值数据,不包含年际信号,其中WOA09盐度数据在红海地区质量较差[8],其盐比容结果存在异常值,进而影响估算的温盐比容海平面变化信号;WOA18数据质量在红海地区相较于WOA09模型有较大提升[21],其估算的总比容信号的周年振幅与CORA、ORAS4及SODA估算结果基本一致。Ishii周年振幅明显小于其他数据,其时间序列存在异常极值,热比容周年振幅与其他数据差异不大,Ishii数据集采用WOA05数据作为背景模型,因此在红海地区盐度数据误差较大,故Ishii盐度数据质量不佳是造成差异的主要原因。红海地区单一的温盐数据存在覆盖不全或质量不佳的问题,为了改善比容海平面变化的精度,综合CORA、SODA与ORAS4温盐数据估算结果得到平均比容海平面变化,其空间分布以及时间序列如图 4和图 5中所示,平均比容信号能够有效覆盖红海区域,且时间序列与CORA及ORAS4一致性较好。
|
| 图 5 红海比容海平面变化时间序列 Fig. 5 Time series of the steric sea level variations in the Red Sea |
| 数据 | 总比容周年信号 | 热比容周年信号 | 盐比容周年信号 | |||||
| 振幅/cm | 相位/(°) | 振幅/cm | 相位/(°) | 振幅/cm | 相位/(°) | |||
| CORA | 4.5±0.3 | 213±8 | 4.4±0.2 | 212±3 | 0.1±0.2 | 244±5 | ||
| SODA | 4.2±0.4 | 215±5 | 4.1±0.7 | 213±11 | 0.3±0.6 | 271±55 | ||
| ORAS4 | 4.3±1.2 | 217±16 | 4.1±0.2 | 203±3 | 0.9±0.2 | 296±17 | ||
| Ishii | 1.9±1.5 | 196±46 | 3.6±0.3 | 210±5 | 1.9±1.4 | 44±44 | ||
| WOA09 | 5.1±1.2 | 221±13 | 4.1±0.1 | 202±1 | 1.9±1.1 | 268±35 | ||
| WOA18 | 4.1±0.1 | 220±1 | 4.9±0.1 | 209±1 | 1.2±0.1 | 347±5 | ||
| MEAN (CORA+SODA+ORAS4) | 4.3±0.4 | 215±6 | 4.2±0.3 | 209±4 | 0.4±0.2 | 285±35 | ||
3.2 海平面变化对比分析
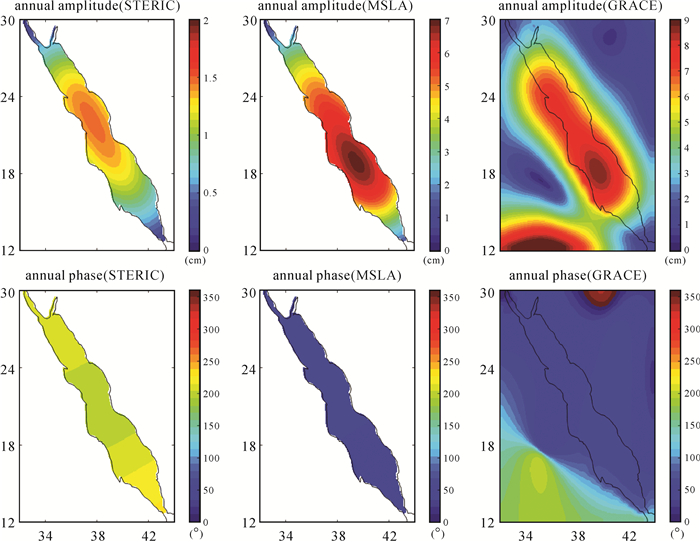
GRACE时变重力场模型可直接确定全球海洋质量变化及其空间分布,与卫星测高确定的总海平面变化(MSLA)和温盐比容海平面变化(STERIC)构成了海平面变化闭合验证环[15]。由于流域尺度因子无法恢复信号的空间分布,采用300 km高斯平滑结果分析GRACE红海质量变化空间特征。同时为保证不同数据的一致性,将卫星测高与比容数据球谐展开至60阶,并进行300 km高斯平滑。图 6为红海2003—2014年总海平面、质量与比容海平面变化周年信号的空间分布,红海总海平面与质量变化的周年振幅均在红海中部区域达到最大,并沿两端方向递减,这是由阶数截断与高斯平滑导致的[4]。总海平面变化与比容海平面变化的周年相位近似相反,与质量变化的周年相位基本一致。
|
| 图 6 红海总海平面、比容海平面与质量变化周年信号空间分布 Fig. 6 Spatial pattern of annual signals of total sea level, steric sea level and mass-induced sea level variations in the Red Sea |
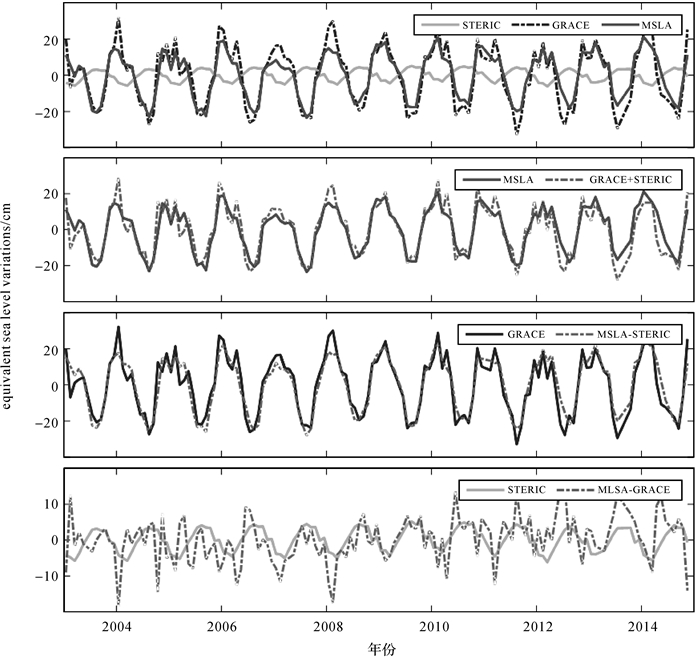
表 3为红海2003—2014年总海平面、质量与比容海平面变化的季节性信号统计表,图 7为各时间序列曲线(其中GRACE数据为改进尺度因子的恢复结果)。红海总海平面变化季节性信号显著,冬季海平面呈上升趋势,夏季呈下降趋势。比容海平面变化的周年与半周年振幅(4.3±0.4/0.2±0.5 cm)均明显小于质量变化结果(20.5±1.7/4.4±1.7 cm),表明红海总海平面的季节性变化主要受质量变化影响。利用改进尺度因子估算的红海质量变化的周年振幅明显大于传统尺度因子恢复结果(16.1±1.3 cm),周年振幅信号量增加了21%。同时改进尺度因子恢复结果和联合卫星“测高—温盐”数据估算的红海质量变化的周年振幅(20.2±1.0 cm)基本一致,表明改进尺度因子能有效削弱红海地区泄漏误差的影响,改善GRACE数据反演红海质量变化的精度。
| 周年信号 | 半周年信号 | ||||
| 振幅/cm | 相位/(°) | 振幅/cm | 相位/(°) | ||
| GRACE(传统尺度因子) | 16.1±1.3 | 57±5 | 3.4±1.3 | 173±22 | |
| GRACE(改进尺度因子) | 20.5±1.7 | 57±5 | 4.4±1.7 | 174±22 | |
| STERIC | 4.3±0.4 | 215±6 | 0.2±0.5 | 127±120 | |
| MSLA | 16.2±0.9 | 57±3 | 4.5±0.9 | 167±11 | |
| MSLA-STERIC | 20.2±1.0 | 52±3 | 4.4±1.0 | 169±11 | |
| MSLA-GRACE | 4.3±1.4 | 238±18 | 0.5±1.4 | 87±158 | |
| GRACE+STERIC | 16.6±1.7 | 63±6 | 4.5±1.7 | 172±22 | |
|
| 图 7 红海总海平面、比容海平面和质量变化时间序列 Fig. 7 Time series of total sea level, steric sea level and mass-induced sea level variations in the Red Sea |
“GRACE+温盐”数据估算的红海综合海平面变化的周年与半周年振幅分别为16.6±1.7/4.5±1.7 cm,与卫星测高数据监测的总海平面变化的周年与半周年振幅(16.2±0.9/4.5±0.9 cm)基本一致,两者时间序列相关系数为0.91,表明卫星测高、卫星重力与温盐数据具有较好的一致性,多源数据可构成完整的红海海平面的监测手段。“测高-比容”估算的红海质量变化的季节性信号也与GRACE数据估算结果一致,两者时间序列的相关系数为0.93,表明GRACE数据能有效监测红海质量变化,多源数据可用于GRACE卫星重力数据验证以及GRACE数据后处理方法的评价。“测高-GRACE”估算的红海比容海平面变化时间序列受随机误差影响较大,其与温盐数据估算的比容海平面变化的相关系数仅为0.4。但“测高-GRACE”数据同样具有较为明显的季节性特征,其周年振幅与温盐数据的估算结果仍符合较好,表明利用卫星测高与GRACE数据可估算红海比容海平面变化季节性信号[8],但因单月数据易受卫星测高与卫星重力数据的误差影响,导致其精度低于温盐数据的估算结果。同时,“测高-GRACE”数据估算的周年振幅与CORA、SODA、ORAS4及WOA18温盐数据模型基本一致,也表明WOA09和Ishii温盐数据模型在红海地区的适用性较差。
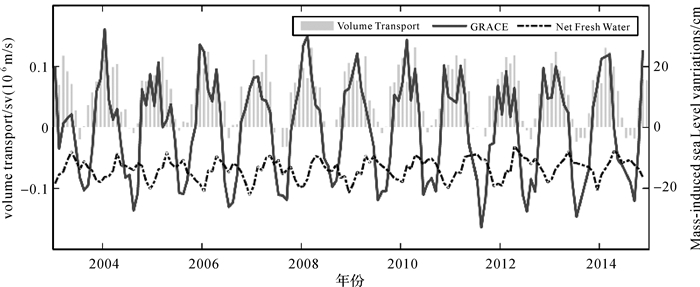
3.3 红海质量变化成因分析由于红海周边为沙漠区域,陆地水与红海质量交换作用可忽略不计[25],红海质量变化来源于降水-蒸发及红海与亚丁湾的海水质量交换。本文使用OAFlux(objectively analyzed air-sea fluxes)蒸发数据[26]与GPCP(global precipitation climatology project)降水数据[27]估算红海净淡水通量(降水-蒸发),结果如图 8所示,净淡水通量全年为负,且与总质量变化负相关。利用HYCOM(hybrid coordinate ocean model)海水流速数据[28]估算红海与亚丁湾间的海水质量交换,海水体积输运方向以亚丁湾至红海为主,仅在6至9月间为红海流向亚丁湾[2]。红海与亚丁湾间的水交换与红海总质量变化具有明显的相关性,其相关系数为0.83,表明与亚丁湾的海水质量交换是红海质量变化季节性信号的主要成因。
|
| 图 8 红海降水-蒸发作用、曼德海峡体积通量及质量变化时间序列 Fig. 8 Time series of precipitation-evaporation effect, volume flux and mass-induced sea level variations in the Red Sea |
4 结论
本文利用卫星测高、GRACE卫星重力与温盐数据研究2003—2014年间红海总海平面、质量与比容海平面变化,并结合气象与海洋资料探讨了红海质量变化成因。主要研究结论如下:
(1) 红海形状狭长,受截断和滤波引起的泄漏误差影响较大,分析了不同空间分辨率的理想盆地核函数对应的300 km高斯滤波的尺度因子的变化。随着空间分辨率的降低,估算的传统尺度因子迅速减小,表明传统尺度因子不能有效恢复红海地区真实信号。为此提出改进尺度因子方法改正泄漏误差,利用卫星测高数据进行模拟实验,结果表明不同空间分辨率的改进理想盆地核函数估算的尺度因子基本一致,且恢复信号与模拟数据相符。利用改进尺度因子估算的红海质量变化周年振幅为20.5±1.7 cm,大于传统尺度因子的16.1±1.3 cm,与测高-比容估算的红海质量变化周年振幅(20.2±1.0 cm)相当,表明改进尺度因子可有效削弱泄漏误差的影响,改善GRACE数据反演红海质量变化的精度。
(2) 红海地区温盐数据存在覆盖不全或质量不佳的问题,分析了多种红海温盐数据估算的比容海平面变化。CORA、ORAS4、SODA及WOA18温盐数据估算的比容海平面变化的季节性信号一致性较好,而Ishii和WOA09温盐数据在红海地区适用性较差,且时间序列存在异常极值。综合CORA、ORAS4与SODA温盐数据估算的比容海平面变化得到平均比容海平面变化,可改善红海地区比容信号的空间分布与精度。
(3) 温盐变化与质量变化引起的综合海平面变化与卫星测高数据监测结果基本一致,“测高-比容”估算的红海质量变化也与GRACE数据估算结果相当,表明卫星测高、卫星重力与温盐数据具有较好的一致性,多源数据可构成完整的红海海平面的监测手段,并可用于GRACE卫星重力数据验证与GRACE数据后处理方法的评价。卫星“测高-GRACE”估算的比容信号噪声较大,但季节性信号仍与温盐数据的估算结果符合较好。曼德海峡体积通量与红海质量变化的相关系数为0.83,表明红海与亚丁湾的海水质量交换主导了红海质量的季节性变化。
致谢: 感谢CSR提供的GRACE RL 5月时变重力场模型数据,AVISO提供的月均海平面高度异常数据,NASA提供的陆地水文模型数据与JPL提供的海底压力数据。
| [1] | LYU K, ZHANG Xuebin, CHURCH J A, et al. Time of emergence for regional sea-level change[J]. Nature Climate Change, 2014, 4(11): 1006–1010. DOI:10.1038/nclimate2397 |
| [2] | SOFIANOS S S, JOHNS W E. An Oceanic General Circulation Model (OGCM) investigation of the Red Sea circulation, 1. Exchange between the Red Sea and the Indian Ocean[J]. Journal of Geophysical Research, 2002, 107(C11): 3196. DOI:10.1029/2001JC001184 |
| [3] | MANASRAH R, HASANEAN H M, AL-ROUSAN S. Spatial and seasonal variations of sea level in the Red Sea, 1958—2001[J]. Ocean Science Journal, 2009, 44(3): 145–159. |
| [4] | FENG W, LEMOINE J M, ZHONG M, et al. Mass-induced sea level variations in the Red Sea from GRACE, steric-corrected altimetry, in situ bottom pressure records, and hydrographic observations[J]. Journal of Geodynamics, 2014(78): 1–7. |
| [5] | TAPLEY B D, BETTADPUR S, RIES J C, et al. GRACE measurements of mass variability in the earth system[J]. Science, 2004, 305(5683): 503–505. DOI:10.1126/science.1099192 |
| [6] | WAHR J, SWENSON S, VELICOGNA I. Accuracy of GRACE mass estimates[J]. Geophysical Research Letters, 2006, 33(6): L06401. |
| [7] | SWENSON S, WAHR J. Post-processing removal of correlated errors in GRACE data[J]. Geophysical Research Letters, 2006, 33(8): L08402. |
| [8] | WAHR J, SMEED D A, LEULIETTE E, et al. Seasonal variability of the Red Sea, from satellite gravity, radar altimetry, and in situ observations[J]. Journal of Geophysical Research, 2014, 119(8): 5091–5104. |
| [9] |
文汉江, 李洪超, 蔡艳辉, 等.
联合Argo浮标、卫星测高和GRACE数据研究海平面变化[J]. 测绘学报, 2012, 41(5): 696–702.
WEN Hanjiang, LI Hongchao, CAI Yanhui, et al. The study of global sea level change by combining Argo floats data、satellite altimetry and GRACE observations[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 696–702. |
| [10] |
蒋涛, 李建成, 王正涛, 等.
联合Jason-1与GRACE卫星数据研究全球海平面变化[J]. 测绘学报, 2010, 39(2): 135–140.
JIANG Tao, LI Jiancheng, WANG Zhengtao, et al. Global sea level variations from combined Jason-1 and GRACE data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 135–140. |
| [11] |
卢飞, 游为, 范东明, 等.
由GRACE RL05数据反演近10年中国大陆水储量及海水质量变化[J]. 测绘学报, 2015, 44(2): 160–167.
LU Fei, YOU Wei, FAN Dongming, et al. Chinese continental water storage and ocean water mass variations analysis in recent ten years based on GRACE RL05 data[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 160–167. |
| [12] | SWENSON S, CHAMBERS D, WAHR J. Estimating geocenter variations from a combination of GRACE and ocean model output[J]. Journal of Geophysical Research, 2008, 113(B8): B08410. |
| [13] | CHENG Minkang, RIES J C, TAPLEY B D. Variations of the Earth's figure axis from satellite laser ranging and GRACE[J]. Journal of Geophysical Research, 2011, 116(B1): B01409. |
| [14] | A G, WAHR J, ZHONG Shijie. Computations of the viscoelastic response of a 3-D compressible earth to surface loading:An application to Glacial Isostatic Adjustment in Antarctica and Canada[J]. Geophysical Journal International, 2013, 192(2): 557–572. DOI:10.1093/gji/ggs030 |
| [15] | CHAMBERS D P, WILLIS J K. A global evaluation of ocean bottom pressure from GRACE, OMCT, and steric-corrected altimetry[J]. Journal of Atmospheric and Oceanic Technology, 2010, 27(8): 1395–1402. DOI:10.1175/2010JTECHO738.1 |
| [16] | SWENSON S, WAHR J. Multi-sensor analysis of water storage variations of the Caspian Sea[J]. Geophysical Research Letters, 2007, 34(16): L16401. |
| [17] | CABANES C, GROUAZEL A, VON SCHUCKMANN K, et al. The CORA dataset:Validation and diagnostics of in-situ ocean temperature and salinity measurements[J]. Ocean Science, 2013, 9(1): 1–18. |
| [18] | CARTON J A, GIESE B S. A reanalysis of ocean climate using simple ocean data assimilation (SODA)[J]. Monthly Weather Review, 2008, 136(8): 2999–3017. DOI:10.1175/2007MWR1978.1 |
| [19] | BALMASEDA M A, MOGENSEN K, WEAVER A T. Evaluation of the ECMWF ocean reanalysis system ORAS4[J]. Quarterly Journal of the Royal Meteorological Society, 2013, 139(674): 1132–1161. DOI:10.1002/qj.2063 |
| [20] | SHOWSTACK R. World ocean database[J]. Eos, Transactions American Geophysical Union, 2009, 90(49): 472–472. |
| [21] | BOYER T P, LOCARNINI R A, BARANOVA O K, et al. The world ocean atlas 2018: improvements and uses of climatological mean fields[C]//AGU Fall Meeting Abstracts. 2018. |
| [22] | ISHⅡ M, KIMOTO M, SAKAMOTO K, et al. Steric sea level changes estimated from historical ocean subsurface temperature and salinity analyses[J]. Journal of Oceanography, 2006, 62(2): 155–170. DOI:10.1007/s10872-006-0041-y |
| [23] |
陈美香, 常曼, 张雯皓, 等.
全球比容海平面低频变化特征研究[J]. 海洋科学进展, 2016, 34(2): 162–174.
CHEN Meixiang, CHANG Man, ZHANG Wenhao, et al. Characteristics of low-frequency variation of global steric sea level[J]. Advances in Marine Science, 2016, 34(2): 162–174. DOI:10.3969/j.issn.1671-6647.2016.02.002 |
| [24] | Intergovernmental Oceanographic Commission. The international thermodynamic equation of seawater-2010: Calculation and use of thermodynamic properties[R]. Paris: IOC, 2010. |
| [25] | SIDDALL M, SMEED D A, HEMLEBEN C, et al. Understanding the Red Sea response to sea level[J]. Earth and Planetary Science Letters, 2004, 225(3-4): 421–434. DOI:10.1016/j.epsl.2004.06.008 |
| [26] | YU Lisan, JIN Xiangze, WELLER R A. Multidecade global flux datasets from the objectively analyzed air-sea fluxes (OAFlux) project: latent and sensible heat fluxes, ocean evaporation, and related surface meteorological variables[R]. [S.l.]: Woods Hole Oceanographic Institution, 2008. |
| [27] | ADLER R F, HUFFMAN G J, CHANG A, et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present)[J]. Journal of Hydrometeorology, 2003, 4(6): 1147–1167. DOI:10.1175/1525-7541(2003)004<1147:TVGPCP>2.0.CO;2 |
| [28] | CHASSIGNET E P, HURLBURT H E, SMEDSTAD O M, et al. The HYCOM (hybrid coordinate ocean model) data assimilative system[J]. Journal of Marine Systems, 2007, 65(1-4): 60–83. DOI:10.1016/j.jmarsys.2005.09.016 |



