2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 陆军工程大学, 江苏 南京 210007;
4. 信息工程大学, 河南 郑州 450052
2. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China;
3. Army Engineering University, Nanjing 210007, China;
4. Information Engineering University, Zhengzhou 450052, China
GNSS载波相位观测量具有毫米级的精度,远高于伪距观测量,由文献[1]提出的Hatch滤波算法组合了载波相位和伪距两种观测量,以历元间电离层延迟变化较小为前提,通过多历元的叠加求出平均模糊度和电离层延迟量,并用于改进伪距观测值的精度。这种方法在短时段内可以显著提高伪距观测值精度,但是当历元间电离层变化较大或平滑时段较长时,平滑结果将产生严重的系统误差。基于此,国内外一些学者对算法进行改进。文献[2]利用差分基站提供的电离层物理信息,考虑到电离层在不同区域,日、季节的电离层变化和卫星仰角等因素,建立电离层模型并提出一种最优平滑伪距的DGPS单频接收机算法,比传统的Hatch滤波具有更高的定位精度和稳健性。文献[3]利用线性回归模型化电离层延迟的变化率,并综合考虑卫星高度截止角和多路径噪声的特性,提出一种自适应滤波算法,通过成本函数计算最优平滑时间,能够在一定程度上提高GPS静态定位和动态定位的精度。文献[4]利用Klobuchar模型补偿电离层延迟变化的变化率,提出了一种改进的单频载波相位平滑伪距方法,仿真算例表明其精度明显优于传统单频载波相位平滑伪距法。文献[5]利用Kalman滤波的新息向量,调整了噪声方差矩阵并得到最优平滑时间窗口的时间常数。此算法在仿真算例中有效改善了定位精度和稳定性。文献[6-7]指出在动态飞行器上搭载的单频WAAS和LAAS接收机,其载波相位平滑观测量经常受到电离层变化的影响,尤其在赤道和极地区域,并提出了减轻TEC影响的算法。文献[8]针对地基增强系统中载波相位平滑存在的误差问题,采用由卫星仰角、电离层变化及用户到参考站的距离坐标变量实时确定平滑窗口的宽度,其结果比传统的100 s Hatch滤波器的误差减少了68%。文献[9]为了应对传统Hatch滤波器的发散问题,提出利用电离层延迟变化量和卫星高度角自适应改变平滑窗口的宽度,其结果比经典的Hatch滤波器提高了约21%。为了应对电离层延迟的影响以及增强结果的稳定性,也有不少学者采用多频或差分数据来避免常规单频载波平滑伪距所带来的发散问题[10-13],但是单频或非差分用户无法使用。
由于电离层延迟变化是影响单频载波相位平滑伪距精度变差的主要原因,因此解决平滑伪距精度发散的关键在于准确计算并扣除历元间的电离层延迟变化值。目前存在的研究结果,部分是利用窗口减弱电离层影响,部分是利用外部的差分信息对电离层延迟进行改正,也有研究根据外部的物理和几何参数对电离层改正窗口的宽度进行估计,但大多需要依赖外部环境或数据,并且改正效果有限。
本文通过研究发现,历元间单频载波相位和伪距观测值本身所包含的电离层信息足以提供厘米级别的电离层延迟改正,因此提出一种自模型化的单频载波平滑伪距算法,实现在不依赖外部数据的情况下,大幅减弱原始Hatch滤波的系统误差。本文首先推导了顾及电离层变化的载波相位平滑伪距模型,根据实测数据分析了电离层延迟演化规律,采用最小二乘多项式拟合法对历元间的电离层延迟信息进行拟合计算,在此基础上,提出了自模型化载波相位平滑伪距算法;然后对自模型化平滑伪距进行了实现,并通过与伪距的残差分析与原始算法进行了比较,证明有效地消除了电离层影响;最后通过静态和动态定位试验验证了算法的正确性。
1 顾及电离层延迟变化的载波相位平滑伪距忽略对伪距码和载波相位观测量影响基本相同的对流层延迟、接收机钟差、卫星钟差,以及在一定卫星高度截止角或多历元后均值后,可忽略不计的多路径效应等,k历元时某一频点的相位和伪距观测方程可以简化为
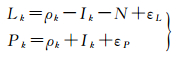 (1)
(1)
式中,Lk和Pk分别表示载波相位距离观测值和伪距观测值;ρk为站星几何距离;N为以距离为单位的模糊度参数;Ik为该频率的电离层距离延迟;εL、εP为载波相位距离和伪距观测的观测噪声。
令第1历元的电离层延迟为I1,第k历元与第1历元电离层延迟差为ΔIk, 1=Ik-I1,将式(1)中两方程相减,并将观测噪声吸收在观测量中,则
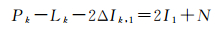 (2)
(2)
为方便表达,引入常数A=2I1+N。在模糊度和电离层延迟未知的情况下,A需要由观测值来计算。考虑到各历元观测值存在噪声,在k历元内,可以求得A的估值Ak
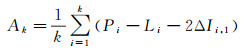 (3)
(3)
式中,i为历元序号。由式(2)和式(3)可得到指定频点第k历元顾及电离层延迟变化的平滑伪距
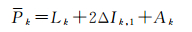 (4)
(4)
相邻两历元相减,得到顾及电离层延迟变化的载波相位平滑伪距的递推公式
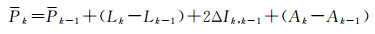 (5)
(5)
式中
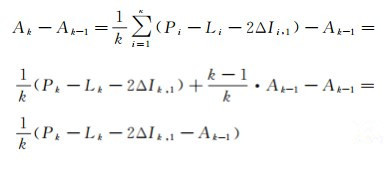 (6)
(6)
将其代入式(5),有
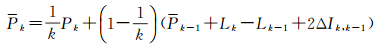 (7)
(7)
式(7)与式(5)等价,但是减少了Ak的迭代计算,具有更高的计算效率。如果整个时段中电离层变化为0,即对于任意历元i有ΔIi, 1=0,那么式(7)就变成了经典的Hatch滤波,也是众多文献中所指的载波平滑伪距加权平均公式[1, 4, 14],即经典Hatch滤波是顾及电离层延迟变化的载波平滑伪距的特殊形式。可以发现式(7)右边最后1项右括号内的内容与式(5)右边前3项是相同的,只包括前k-1历元的平滑值和当前历元载波变化改正值,称之为平滑伪距Pk的推估值Pk,即
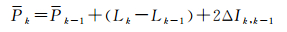 (8)
(8)
式中,顾及电离层延迟变化的载波相位平滑伪距推估模型。若历元间电离层延迟变化为0,则是经典Hatch滤波的推估模型。式(7)可以写为
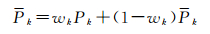 (9)
(9)
式中,wk是第k历元实测伪距Pk对应的权,此处为历元数量的倒数wk=1/k。经典Hatch滤波为了抑制由电离层变化而导致的平滑伪距偏差,通常将wk设定为一个固定的参数m,即当k>m时,wk=1/m。本文称该方法为固定窗口加权法或加权Hatch滤波。这种通过降低平滑伪距权值来降低电离层延迟积累误差的影响的方法,虽然可以消除部分系统偏差,但是也降低了平滑伪距的精度。
由式(3)和式(4)可知,历元间电离层延迟变化对于传统Hatch滤波在第k历元的平滑伪距,造成的偏差为
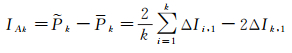 (10)
(10)
式中,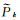
由于常规的载波平滑伪距算法忽略了电离层延迟历元间变化的影响,当平滑时段变长,电离层延迟变化增加到一定程度后,式(10)的积累值变大,平滑伪距存在着发散的情况。
如果指定站星间的电离层延迟变化连续,即不存在跳变或其变化率比较稳定,在指定时段内电离层延迟可采用最小二乘拟合计算,且其拟合等效距离精度优于伪距观测噪声,那么就可以计算出历元间电离层延迟的变化率,并对各历元伪距和载波进行改正,达到消除或减弱电离层影响的目的。这种方法本文称之为顾及电离层变化的平滑伪距法,简称电离层改正法。本文首先对电离层延迟演化规律进行分析,验证本文算法的先验条件,然后介绍单频观测数据的电离层延迟自模型化求解算法。
2 电离层延迟的演化规律与自模型化求解 2.1 电离层延迟规律分析由于电离层延迟的变化是导致传统载波相位平滑伪距发散的主要原因,因此要想消除或减弱电离层的影响,获得较为准确的分析数据作为自模型化建模的基础,必须对电离层影响的规律和数值大小进行分析。在站星电离层延迟的求解方面具有多种算法,包括各种电离层预报模型[15-17],如NeQuick、Klobuchar等;IGS(international GNSS service)也定期发布电离层产品,如格网电离层产品,球谐函数模型产品等。但是对于特定测站和特定时段而言,这种通用预报模型和全球性产品的精度有限[18]。目前,最精确的方法是采用多频载波测量数据实测计算的结果,包括双频、三频电离层组合模型等,考虑到三频组合观测噪声过分放大[19-20],且双频载波组合已经能够满足用于分析载波平滑伪距电离层改正的精度需求,因此本文采用双频载波观测数据进行研究。
2.1.1 采用双频载波计算电离层变化对于L1和L2双频GNSS载波,考虑一阶电离层影响,其具有如下观测方程
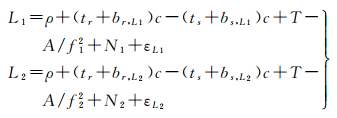 (11)
(11)
式中,A为与传播路径电子总数相关的电离层参数A=-40.28 cTEC[19];T为对流层延迟;br、bs为对应频点的接收机和卫星的未校准相位偏差,其他符号与式(1)相同。需要注意的是:这里的下标指的是对应的频点,而非历元编号。
令ΔL=L1-L2、Δb=bL1-bL2、ΔN=N1-N2、ΔB=(Δbr-Δbs)c+ΔN、ΔIA=A(1/f12-1/f22),将式(11)中两个频率的载波观测值相减,可得
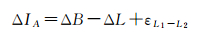 (12)
(12)
即频率间电离层延迟差分值可以通过载波距离观测值作差获得。由于短期内的硬件延迟通常变化很小[21-23],在不发生周跳的情况下,可以将式(12)中ΔB视为常量,与ΔI一起考虑。
将式(12)两边同时乘以ΔIA的系数,可得各频率电离层和相位偏差及模糊度的距离总和,以变量IB表示,这里只考虑L1载波的情况
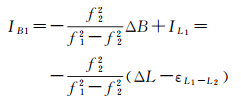 (13)
(13)
历元作差,可以求得电离层历元间的变化值
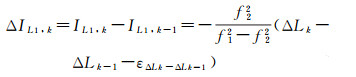 (14)
(14)
通过两个载波测量值作差,可以消除大部分观测误差,只剩下电离层延迟、未校准相位偏差和模糊度。由误差传播定律可知,求出的电离层和相位偏差总和IB与载波相位观测量L属于同一数量级的测量精度,可达毫米级别。其中,如果不发生周跳,变化的只有电离层延迟。
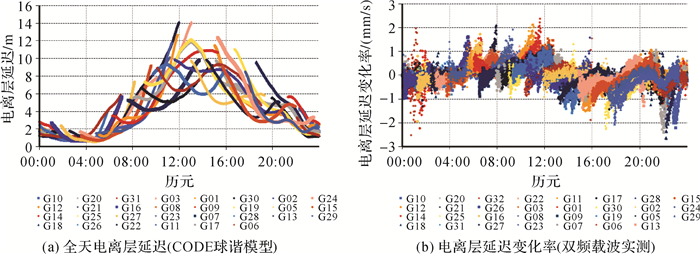
2.1.2 电离层延迟变化计算试验选取4个IGS观测站,其中两个赤道附近站(KIRI、NKLG),一个高纬度站(LAMA)和一个中纬度站(SHAO),采用全天观测数据,采样率为30 s,高度截止角为15°,计算GPS L1频率的电离层延迟变化率,其中NKLG的电离层延迟及其变化如图 1所示。
|
| 图 1 NKLG站全天电离层延迟及其变化率 Fig. 1 All-day ionospheric delay and its rate of change at the NKLG station |
4个站点电离层延迟变化的统计数据见表 1。
| mm/s | |||||
| 站名 | 最大值 | 最小值 | 平均值(×10-8) | 中误差 | 总历元数 |
| KIRI | 2.90 | -3.04 | 3.603 | 0.423 | 25 422 |
| NKLG | 3.46 | -2.66 | 1.760 | 0.401 | 25 121 |
| LAMA | 1.78 | -1.99 | 1.519 | 0.265 | 22 515 |
| SHAO | 2.19 | -2.06 | -0.854 | 0.281 | 22 630 |
图 1(a)采用CODE球谐函数模型绘制[24],这里用于查看总体趋势。可以看出对于指定的站点,站星电离层具有明显的时间特性,在本地时间12—16时达到最大值,但是由于卫星的相对运动,各颗卫星信号的电离层延迟看上去连续,变化平缓,但是没有明显的运动规律;从实测数据的图 1(b)和从表 1可以看出电离层延迟变化量基本都在3 mm/s内与载波观测量噪声相当,且变化基本连续,可以认为各历元间的电离层延迟是连续变化的,因此在一定的时段内可以采用最小二乘拟合的方法求取其近似值。
2.2 电离层延迟变化的自模型化求解本文采用单频载波和伪距观测值组合,对站星电离层延迟变化进行估计,不依赖任何外部数据,因此称之为自模型化。由式(2)可知,伪距减去载波距离则为2倍电离层和模糊度之和INk
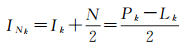 (15)
(15)
在没有周跳的情况下,INk数值的变化直接体现为电离层延迟的变化。从式(15)中可以看出,采用伪距和载波作差获得的电离层延迟的精度比伪距精度高一倍。采用多个历元,通过最小二乘多项式拟合[25],可以精化其精度,从而求出站星电离层延迟变化的估值。在实时计算时,采用最近的时段窗口数据拟合;在事后或准实时处理时,拟合时段窗口中心历元。具体方法为:将各历元INk作为观测值,以时间作为自变量,连续多历元观测后,就可以组成误差方程进行平差计算,从而求得拟合系数,进而求得每个历元的拟合值及其变化。具体的拟合阶次和采用时间窗口大小,可以根据拟合残差大小进行判定。
2.3 电离层延迟自模型化效果分析为了验证电离层延迟自模型化的效果,确定拟合阶次和窗口大小,采用两个IGS参考站:赤道站MBAR和中纬度站SHAO,在2018年001日,分别采用电离层延迟最活跃的赤道正午前后和最不活跃的中纬度夜间时段,采用不同拟合阶次(1~3),采样率分别为10 s和1 s的实测卫星观测数据,进行逐历元移动开窗最小二乘多项式事后拟合计算,将双频载波计算数值作为真值,统计并比较不同参数下计算结果的中误差。
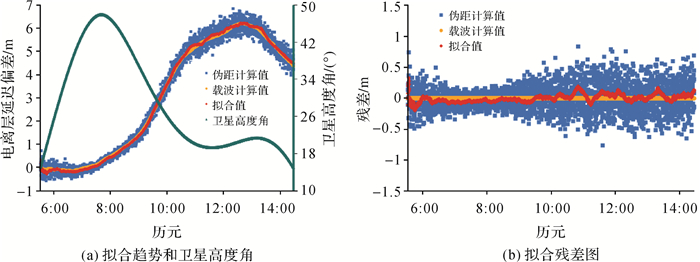
2.3.1 赤道MBAR早上到午后G23MBAR站G23卫星,有效观测时段从2018-01-01 05:31到2018-01-01 14:27,跨度达9 h,由于地处赤道且包含正午时段,该段数据受电离层延迟影响大且变化剧烈。图 2是G23卫星电离层延迟偏差的拟合情况,其中黄色载波计算值作为真值,蓝色是伪距计算值,红色曲线是依据伪距值拟合的结果,深绿色是卫星高度角对应的图(a)的次竖轴。1 s采样率和10 s采样率在不同拟合阶次和不同时段窗口下的拟合统计结果见表 2,其中加粗字体表示当前数值为最小值。
|
| 图 2 G23 30 min窗口线性拟合电离层延迟 Fig. 2 Ionospheric delay of G23 with a linear fit of 10 s sampling rate using a 30-minute window |
| 时段窗口/m | 1 s采样率(32 141历元) | 10 s采样率(3214历元) | |||||||
| 历元数 | 线性 | 2次 | 3次 | 历元数 | 线性 | 2次 | 3次 | ||
| 10 | 600 | 0.071 | 0.072 | 0.208 | 600 | 0.059 | 0.070 | 0.163 | |
| 20 | 1200 | 0.069 | 0.069 | 0.070 | 1200 | 0.050 | 0.056 | 0.062 | |
| 30 | 1800 | 0.068 | 0.069 | 0.070 | 1800 | 0.045 | 0.057 | 0.059 | |
| 40 | 2400 | 0.070 | 0.069 | 0.069 | 2400 | 0.044 | 0.044 | 0.054 | |
| 60 | 3600 | 0.076 | 0.067 | 0.067 | 3600 | 0.047 | 0.041 | 0.046 | |
| 90 | 5400 | 0.095 | 0.072 | 0.068 | 5400 | 0.066 | 0.047 | 0.045 | |
| 120 | 7200 | 0.134 | 0.079 | 0.070 | 7200 | 0.085 | 0.043 | 0.039 | |
2.3.2 中纬度SHAO夜间到早上G17
SHAO站的G17卫星的时段为:UTC 16:30—23:00,对应本地时间为夜间到早上,22:30—7:00,共7 h,由于地处中纬度在夜间时段,该段数据电离层延迟较小且变化缓慢。表 3显示了该星在1 s采样率和10 s采样率在不同拟合阶次和不同时段窗口下的拟合统计结果。
| 时段窗口/m | 1 s采样率(32 141历元) | 10 s采样率(3214历元) | |||||||
| 历元数 | 线性 | 2次 | 3次 | 历元数 | 线性 | 2次 | 3次 | ||
| 10 | 600 | 0.059 | 0.070 | 0.163 | 600 | 0.076 | 0.101 | 9.313 | |
| 20 | 1200 | 0.050 | 0.056 | 0.062 | 1200 | 0.058 | 0.071 | 0.081 | |
| 30 | 1800 | 0.045 | 0.057 | 0.059 | 1800 | 0.050 | 0.060 | 0.068 | |
| 40 | 2400 | 0.044 | 0.044 | 0.054 | 2400 | 0.046 | 0.055 | 0.061 | |
| 60 | 3600 | 0.047 | 0.041 | 0.046 | 3600 | 0.039 | 0.047 | 0.056 | |
| 90 | 5400 | 0.066 | 0.047 | 0.045 | 5400 | 0.045 | 0.038 | 0.043 | |
| 120 | 7200 | 0.085 | 0.043 | 0.039 | 7200 | 0.055 | 0.038 | 0.039 | |
通过以上试验,可以发现由于短期内站星电离层延迟变化缓慢,采用移动开窗最小二乘多项式对单频伪距和载波组合计算的电离层延迟进行拟合,都取得了厘米级别的精度,但是不同的时段和拟合阶次具有不同结果,概括如下:
(1) 在一定的时段窗口内(本文试验为小于30 min),电离层采用一阶移动开窗拟合法效果较佳,在更长时段后,电离层变化复杂性变强,部分高阶拟合优于线性效果,而太短的拟合时段的拟合效果也会受到影响,且其在高阶拟合时易产生龙格现象。
(2) 由单频载波和伪距计算的电离层延迟,在多项式拟合后整体精度可达4~7 cm,精度高于伪距噪声。
(3) 在相同时段内,采用不同的采样率数据,拟合结果有所区别,但是并不明显,因而可以认为电离层拟合与时段长度相关,与采样率相关不大。
由于在一定电离层延迟精度可达厘米级别,小于伪距噪声,因此预期采用自模型化的电离层延迟改正,可望将电离层延迟引起的载波相位平滑伪距偏差消除到厘米级别。为方便计算,本文对自模型化电离层拟合统一采用20 min窗口的线性拟合值。
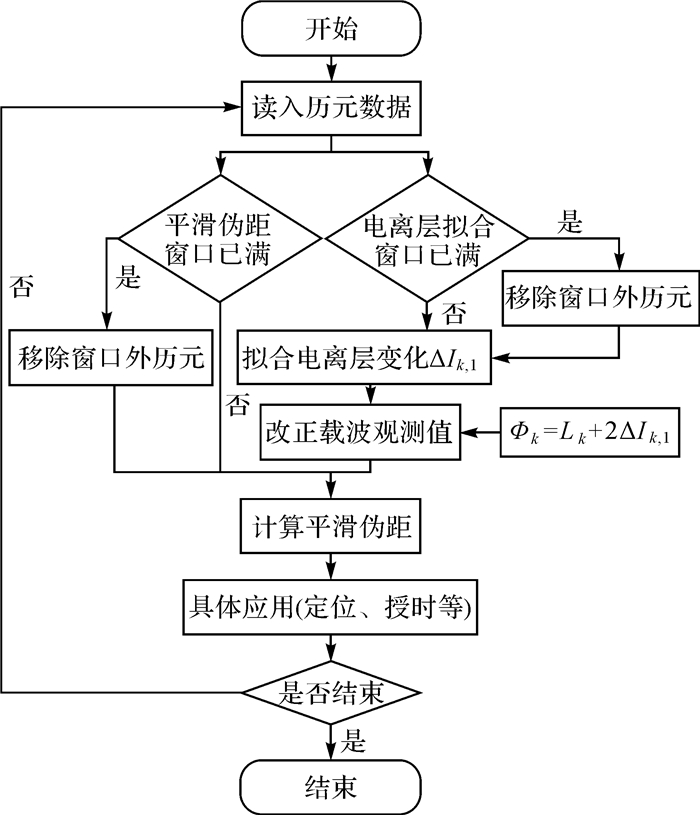
3 自模型化平滑伪距的实现与精度分析 3.1 自模型化平滑伪距的实现电离层自模型化的平滑伪距算法流程如图 3所示,其中需要维护两个历元数据缓存窗口:一个是电离层拟合窗口,如前文所述,本文采用20 min固定窗口;另一个缓存窗口是平滑伪距数值窗口,用于存储原始的载波伪距观测值,如果采用经典Hatch滤波,则不需要此缓存。与常规Hatch滤波主要的区别在于:本文方法通过自身数据拟合出电离层变化,然后直接改正到载波相位观测量,从而实现对电离层延迟变化的改正。实际计算中,可以将原始载波Lk直接加上电离层延迟改正,即Φk=Lk+2ΔIk, 1,替换原始载波Lk。
|
| 图 3 电离层自模型化的平滑伪距算法流程 Fig. 3 Flow chart of the ionospheric self-modeling smooth pseudorange algorithm |
3.2 电离层变化改正的平滑伪距残差分析
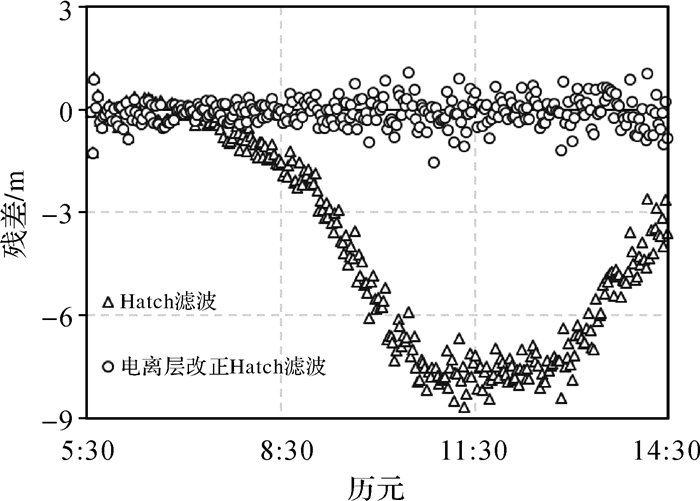
下面通过实测数据检验本文提出的自模型电离层变化改正方法,文中以“电离层改正”代替。通过对改正前后的结果与原始伪距进行作差比较,并统计其残差。数据采用MBAR站的G23星,采样率10 s,电离层变化以20 min移动窗口线性拟合。拟合残差中误差见图 4和表 4。
|
| 图 4 常规Hatch滤波加电离层改正前后的平滑伪距残差 Fig. 4 Residual of smooth pseudorange before and after ionospheric correction of Hatch filter |
| m | |||
| 名称/时段窗口/min | 历元数/权 | 固定权Hatch | 电离层改正(窗口20 min) |
| 常规Hatch | — | 4.977 8 | 0.400 5 |
| 120 | 720 | 3.082 4 | 0.400 3 |
| 60 | 360 | 1.896 5 | 0.400 1 |
| 40 | 240 | 1.390 5 | 0.399 7 |
| 30 | 180 | 1.111 9 | 0.399 5 |
| 20 | 120 | 0.820 8 | 0.398 8 |
| 10 | 60 | 0.541 5 | 0.396 7 |
| 5 | 30 | 0.432 8 | 0.391 8 |
由表 4可以看出,随着时间的积累,受电离层变化影响,常规Hatch滤波产生了较大的系统性偏差。采用加权限制平滑伪距权值后,偏差得到改善,但是在长时段中的改善效果有限。考虑到平滑伪距需要一定的历元数量才能达到较好的平滑效果,因此采用加权窗口的方法,在降低系统误差的同时也降低了平滑精度。采用自模型化数据对电离层变化进行改正后,无论是常规的Hatch滤波,还是开窗加权Hatch滤波,系统性偏差基本得到了消除。本试验中,残差稳定在0.4 m左右。由于此处采用原始伪距作为比较基准,其本身具有较大噪声,因此本数值并不能代表平滑精度。下面通过定位计算对算法进行验证。
4 利用本文算法进行静态和动态定位本文涉及的载波平滑伪距算法在GNSSer(GNSS data parallel processer)软件平台[26]进行了实现。GNSSer是本课题组研制的科研型GNSS数据处理软件,旨在提供高精度、并行化、云模式的GNSS计算服务。下面采用实测数据分别对这几种算法的平滑效果进行对比分析。具体的模型和参数设置见表 5。
4.1 MBAR站静态定位试验
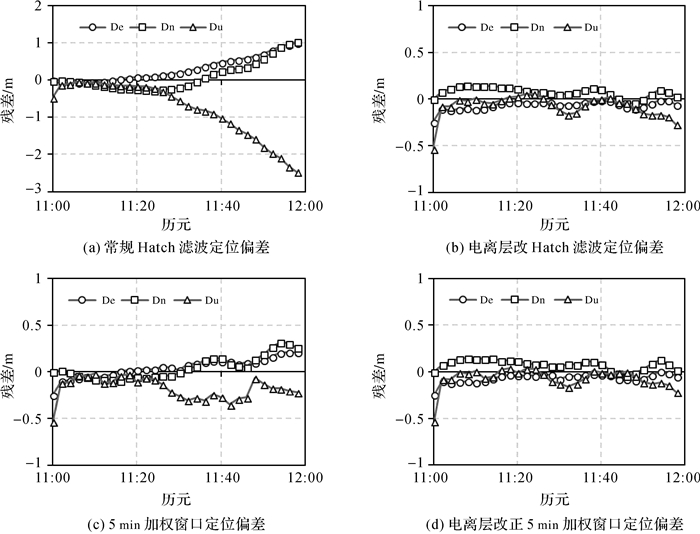
采用MBAR站中午11—12点、采样率为1 s、总计3600历元的数据,进行伪距逐历元4参数平差定位计算,分别采用原始伪距,常规Hatch滤波,加权Hatch滤波以及电离层自模型化改正后的平滑伪距进行定位计算,最后,以IGS发布日解的坐标为真值,将定位结果进行作差比较,每个历元的定位偏差见图 5、图 6和表 6。其中, 符号De、Dn、Du分别是东北天(ENU)3方向的差值。
|
| 图 5 MBAR站电离层改正前后定位偏差 Fig. 5 Positioning deviation before and after ionospheric correction of MBAR station |
|
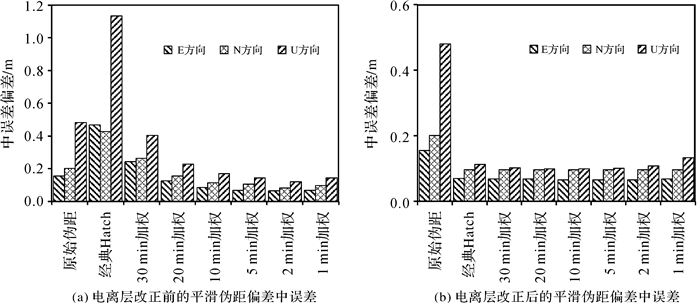
| 图 6 不同算法在ENU 3方向定位中误差 Fig. 6 RMS of ENU in positioning of different algorithms |
| m | ||||||||||
| 算法 | 历元数/权 | 电离层改正前 | 电离层改正后 | |||||||
| E方向 | N方向 | U方向 | 水平 | E方向 | N方向 | U方向 | 水平 | |||
| 原始伪距 | - | 0.156 | 0.201 | 0.481 | 0.254 | - | - | - | - | |
| 常规Hatch | - | 0.466 | 0.425 | 1.132 | 0.631 | 0.07 | 0.096 | 0.113 | 0.119 | |
| 30 m加权 | 1800 | 0.241 | 0.262 | 0.402 | 0.356 | 0.069 | 0.097 | 0.103 | 0.119 | |
| 20 m加权 | 1200 | 0.127 | 0.155 | 0.228 | 0.200 | 0.068 | 0.097 | 0.099 | 0.118 | |
| 10 m加权 | 600 | 0.084 | 0.114 | 0.17 | 0.142 | 0.066 | 0.097 | 0.099 | 0.117 | |
| 5 m加权 | 300 | 0.067 | 0.106 | 0.144 | 0.125 | 0.066 | 0.097 | 0.101 | 0.117 | |
| 2 m加权 | 120 | 0.065 | 0.083 | 0.119 | 0.105 | 0.066 | 0.096 | 0.108 | 0.116 | |
| 1 m加权 | 60 | 0.068 | 0.095 | 0.142 | 0.117 | 0.068 | 0.097 | 0.134 | 0.118 | |
图 5为MBAR站不同伪距定位方法ENU 3方向的定位偏差。可以发现:①载波相位平滑伪距起到了很好的滤波作用,使得历元间的定位结果连续,且窗口越长,定位结果越平滑;②载波相位平滑伪距可以在很短的时间内(10 s),达到分米级别的定位精度;③随着历元窗口的增加,常规Hatch滤波受电离层影响而发散(图 5(a)),高程方程最大偏移达3 m,而采用窗口加权后,系统偏差得到了抑制,但是历元间的定位结果波动变大;④采用自模型化电离层改正后的平滑伪距,无论是常规Hatch滤波,还是加权窗口滤波的电离层系统偏差都得到了很好的消除或减弱,并且定位结果基本稳定。电离层改正前后的定位残差中误差统计见表 6。
从表 6和图 6可以看出,窗口加权的载波平滑伪距,在加权窗口达到2 min(120历元)时,取得了最佳的定位结果,甚至在水平方向略优于电离层改正后的结果,但是这种结果对电离层变化依赖强,实际操作中难以把握;而采用电离层改正后的各种平滑伪距的定位偏差基本没有太大变化,只有在毫米级别有所区别,可以认为结果是一致的。本例中,电离层改正后的平滑伪距定位,以IGS发布坐标为真值,在水平方向和高程方向外符合精度达到了11.6和9.9 cm,分别比原始伪距定位提高了2.2倍和4.9倍。
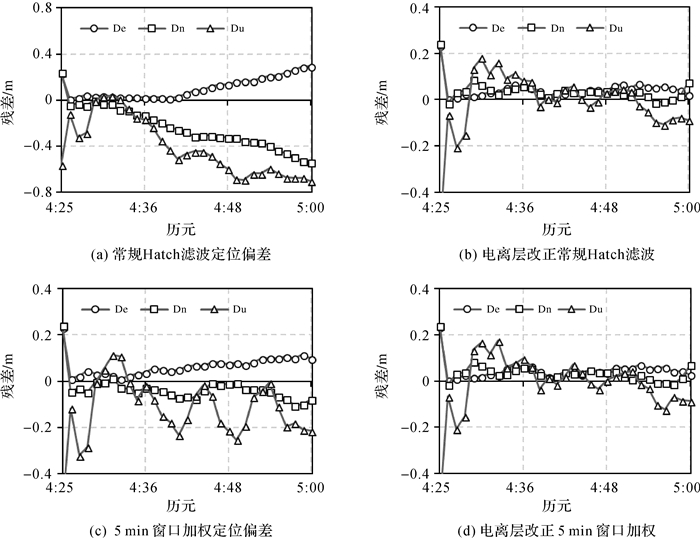
4.2 操场小车动态定位试验动态定位在中纬度的河南省郑州市展开,为一小车围绕一个标准足球运动场运动,一共绕行4.5圈约1.8 km,时间为UTC 4:25—5:00(本地时间为12:25—13:00),共35 min,2101历元,数据采样率1 s,在距离球场中心800 m的东南方向架设了一个静态参考站,二者接收机皆为Trimble Net R9。静态参考站采用全天24 h观测数据和IGS精密产品,作非差精密定位计算,然后与动态站数据组载波双差,该计算结果作为测试的真值;动态小车采用逐历元4参数平差对GPS系统L1频率的伪距进行定位计算,分别采用3种平滑伪距算法定位结果进行定位计算,并与双差解作为动态定位数据的真值进行对比,计算结果如图 7、图 8和表 7所示。
|
| 图 7 操场小车动态定位偏差 Fig. 7 Dynamic positioning deviation of the device on the playground |
|
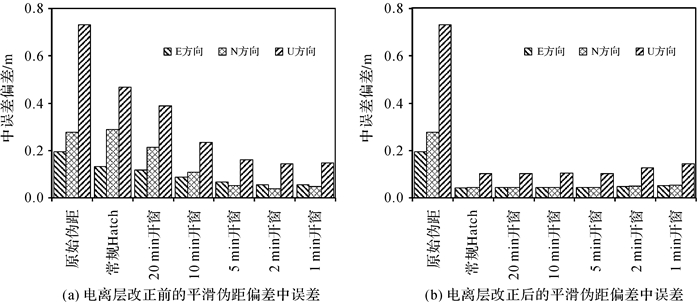
| 图 8 不同算法动态定位在ENU 3方向中误差 Fig. 8 RMS of ENU in dynamic positioning of different algorithms |
| m | |||||||||
| 计算方法 | 电离层改正前 | 电离层改正后 | |||||||
| E方向 | N方向 | U方向 | 水平 | E方向 | N方向 | U方向 | 水平 | ||
| 原始伪距定位 | 0.195 | 0.278 | 0.730 | 0.340 | — | — | — | — | |
| 常规Hatch滤波 | 0.134 | 0.289 | 0.468 | 0.319 | 0.043 9 | 0.044 5 | 0.1037 | 0.062 5 | |
| 20 min窗口 | 0.118 | 0.214 | 0.389 | 0.244 | 0.044 5 | 0.044 5 | 0.103 6 | 0.062 9 | |
| 10 min窗口 | 0.088 | 0.109 | 0.234 | 0.140 | 0.044 5 | 0.044 6 | 0.104 5 | 0.063 0 | |
| 5 min窗口 | 0.068 | 0.052 | 0.161 | 0.086 | 0.045 0 | 0.044 4 | 0.103 4 | 0.063 3 | |
| 2 min窗口 | 0.057 | 0.040 | 0.145 | 0.069 | 0.048 8 | 0.049 7 | 0.128 5 | 0.069 7 | |
| 1 min窗口 | 0.056 | 0.048 | 0.149 | 0.074 | 0.052 3 | 0.054 9 | 0.144 4 | 0.075 8 | |
可以看出,尽管只有35 min时间且地处中纬度地区,采用常规Hatch滤波仍然受到了较大的电离层影响(图 7(a)),高程方向最大偏离了0.7 m,随着加权窗口的减小,系统偏差得到减小,但是历元间的平滑程度也减弱了;采用自模型化改正后的伪距平滑,没有表现出明显的系统偏差,得到了较为平稳的结果。
从本文试验可以看出,采用固定窗口加权,窗口不宜太大,本文试验中在2 min窗口加权取得较好结果,但是历元间结果的平滑程度受到了较大影响;电离层改正平滑伪距后,常规Hatch滤波和各个加权窗口的滤波定位精度基本相当,结果非常稳定,差距在毫米级别,但是更长时段的平滑伪距的计算结果其历元间偏差更小,即偏差曲线更为平滑和一致。本文中,直接对常规Hatch滤波进行改正取得了最好的计算结果,其中水平精度达到了6.3 cm,高程精度达到了10.4 cm,分别比原始伪距提高5.4和3.3倍。
5 结语本文推导了顾及电离层变化的载波相位平滑伪距模型,并证明常规Hatch滤波是改模型电离层变化为0的特殊形式,在分析电离层延迟规律的基础上,提出采用自模型化求解电离层延迟变化的方法,并对实现了一种自模型化平滑伪距的算法。为了证明算法的有效性,同时进行了静态和动态定位试验进行验证。可以得到如下结论:
(1) 自模型化电离层变化的载波相位平滑伪距可以大幅降低伪距观测噪声,获得较为稳定的亚分米甚至厘米级别的定位精度,相比原始伪距,本文试验定位结果提高2.2~7.0倍的精度。
(2) 在1 s采样率的观测数据下,平滑伪距的结果可以在10 s内收敛到分米级别,其中,静态算法在ENU方向精度达分别到6.6、9.7、9.9 cm,动态算法在ENU方向精度达分别到4.4、4.5、10.4 cm,结果表明文中提出的算法同时适用于静态和动态定位。
(3) 本文提出的自模型化电离层变化的载波相位平滑伪距,在不依赖外部观测数据的条件下,只需要自身单频伪距和载波观测值,就可以有效地纠正常规Hatch滤波受电离层影响而带来的系统性偏差,使得常规平滑伪距变得更为稳定和可靠,为获得更高精度的伪距观测值提供了更多的选择。
| [1] | HATCH R.The synergism of GPS code and carrier measurements[C]//Proceedings of the 3rd International Geodetic Symposium on Satellite Doppler Positioning.Las Cruces, NM: New Mexico State University, 1982: 1213-1232. https://www.researchgate.net/publication/234386882_The_Synergism_of_GPS_Code_and_Carrier_Measurements |
| [2] | PARK B, SOHN K, KEE C. Optimal Hatch filter with an adaptive smoothing window width[J]. The Journal of Navigation, 2008, 61(3): 435–454. DOI:10.1017/S0373463308004694 |
| [3] | KIM E, WALTER T, POWELL J D.Adaptive carrier smoothing using code and carrier divergence[C]//Proceedings of 2007 International Technical Meeting of the Institute of Navigation.San Diego, CA: ION, 2007. |
| [4] |
徐博, 刘文祥, 廖鸣.
一种基于电离层变化率的单频载波相位平滑伪距改进方法[J]. 中南大学学报(自然科学版), 2014, 45(2): 464–467.
XU Bo, LIU Wenxiang, LIAO Ming. An improved method of single frequency carrier phase smoothing pseudo[J]. Journal of Central South University (Science and Technology), 2014, 45(2): 464–467. |
| [5] |
赵琳, 李亮, 黄卫权.
自适应卡尔曼滤波在载波相位平滑伪距中的应用[J]. 哈尔滨工程大学学报, 2010, 31(12): 1636–1641.
ZHAO Lin, LI Liang, HUANG Weiquan. An adaptive Kalman filtering algorithm for carrier smoothed code[J]. Journal of Harbin Engineering University, 2010, 31(12): 1636–1641. DOI:10.3969/j.issn.1006-7043.2010.12.013 |
| [6] | WALTER T, DATTA-BARUA S, BLANCH J, et al.The effects of large ionospheric gradients on single frequency airborne smoothing filters for WAAS and LAAS[C]//Proceedings of 2004 International Technical Meeting of the Institute of Navigation.San Diego, CA: ION, 2004: 103-109. |
| [7] | LUO Ming, PULLEN S, DENNIS J, et al.LAAS ionosphere spatial gradient threat model and impact of LGF and airborne monitoring[C]//Proceedings of 2003 ION GPS/GNSS.Portland, OR: ION, 2003. |
| [8] | HUANG Zhenggang, HUANG Zhigang, ZHU Yanbo. A new optimal Hatch filter to minimize the effects of ionosphere gradients for GBAS[J]. Chinese Journal of Aeronautics, 2008, 21(6): 526–532. DOI:10.1016/S1000-9361(08)60170-3 |
| [9] | ZHANG Xiao, HUANG Pan.Optimal Hatch filter with an adaptive smoothing time based on SBAS[C]//Proceedings of the 2nd International Conference on Soft Computing in Information Communication Technology.Taipei, China: Atlantis Press, 2014. |
| [10] | KONNO H.Dual-frequency smoothing for CAT Ⅲ LAAS: performance assessment considering ionosphere anomalies[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation.Forth Worth, TX: ION, 2007. |
| [11] | MCGRAW G. Generalized divergence-free carrier smoothing with applications to dual frequency differential GPS[J]. Navigation, 2009, 56(2): 115–122. DOI:10.1002/j.2161-4296.2009.tb01748.x |
| [12] | HWANG P Y, MCGRAW G A, BADER J R. Enhanced differential GPS carrier-smoothed code processing using dual-frequency measurements[J]. Navigation, 1999, 46(2): 127–137. DOI:10.1002/j.2161-4296.1999.tb02401.x |
| [13] |
邝英才, 吕志平, 李林阳, 等.
GPS/BDS/Galileo相位平滑伪距单点定位性能分析[J]. 导航定位学报, 2018, 6(2): 68–76.
KUANG Yingcai, LV Zhiping, LI Linyang, et al. Performance analysis of GPS/BDS/Galileo phase-smoothed pseudorange point positioning[J]. Journal of Navigation and Positioning, 2018, 6(2): 68–76. |
| [14] |
吴富梅, 唐颖哲.
基于载波相位平滑伪距技术的GPS/INS组合导航[J]. 大地测量与地球动力学, 2010, 30(1): 130–135.
WU Fumei, TANG Yingzhe. GPS/INS integrated navigation based on phase smoothing pseudorange[J]. Journal of Geodesy and Geodynamics, 2010, 30(1): 130–135. |
| [15] | RADICELLA S M, NAVA B.NeQuick model: origin and evolution[C]//Proceedings of the 9th International Symposium on Antennas, Propagation and EM Theory.Guangzhou, China: IEEE, 2010: 422-425. https: //www.researchgate.net/publication/261352103_NeQuick_model_Origin_and_evolution |
| [16] |
方涵先, 翁利斌, 杨升高.
IRI、NeQuick和Klobuchar模式比较研究[J]. 地球物理学进展, 2012, 27(1): 1–7.
FANG Hanxian, WENG Libin, YANG Shenggao, et al. The research of IRI、NeQuick and Klobuchar models[J]. Progress in Geophysics, 2012, 27(1): 1–7. |
| [17] | KLOBUCHAR J A. Ionospheric time-delay algorithm for single-frequency GPS users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(3): 325–331. DOI:10.1109/TAES.1987.310829 |
| [18] |
李子申, 王宁波, 李敏, 等.
国际GNSS服务组织全球电离层TEC格网精度评估与分析[J]. 地球物理学报, 2017, 60(10): 3718–3729.
LI Zishen, WANG Ningbo, LI Min, et al. Evaluation and analysis of the global ionospheric TEC map in the frame of international GNSS services[J]. Chinese Journal of Geophysics, 2017, 60(10): 3718–3729. DOI:10.6038/cjg20171003 |
| [19] |
袁运斌, 霍星亮, 张宝成.
近年来我国GNSS电离层延迟精确建模及修正研究进展[J]. 测绘学报, 2017, 46(10): 1364–1378.
YUAN Yunbin, HUO Xingliang, ZHANG Baocheng. Research progress of precise models and correction for GNSS ionospheric delay in China over recent years[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1364–1378. DOI:10.11947/j.AGCS.2017.20170349 |
| [20] |
刘西风.电离层二阶项延迟及其对GNSS定位结果影响的研究[D].武汉: 中国科学院测量与地球物理研究所, 2009. LIU Xifeng.Study of second order ionospheric delay and its effect on GNSS positioning solution[D]. Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2009. http://www.irgrid.ac.cn/handle/1471x/681604?mode=full&submit_simple=Show+full+item+record |
| [21] |
常青, 张东和, 萧佐, 等.
GPS系统硬件延迟估计方法及其在TEC计算中的应用[J]. 地球物理学报, 2001, 44(5): 596–601.
CHANG Qing, ZHANG Donghe, XIAO Zuo, et al. A method for estimating GPS instrumental biases and its application in TEC calculation[J]. Chinese Journal of Geophysics, 2001, 44(5): 596–601. DOI:10.3321/j.issn:0001-5733.2001.05.003 |
| [22] |
宋小勇, 杨志强, 焦文海, 等.
GPS接收机码间偏差(DCB)的确定[J]. 大地测量与地球动力学, 2009, 29(1): 127–131.
SONG Xiaoyong, YANG Zhiqiang, JIAO Wenhai, et al. Determination of GPS receiver's DCB[J]. Journal of Geodesy and Geodynamics, 2009, 29(1): 127–131. |
| [23] |
张宝成, 袁运斌, 欧吉坤.
GPS接收机仪器偏差的短期时变特征提取与建模[J]. 地球物理学报, 2016, 59(1): 101–115.
ZHANG Baocheng, YUAN Yunbin, OU Jikun. Short-term temporal variability of GPS receiver's differential code biases (DCB): retrieving and modeling[J]. Chinese Journal of Geophysics, 2016, 59(1): 101–115. |
| [24] | JEE G, LEE H B, KIM Y H, et al. Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: ionospheric perspective[J]. Journal of Geophysical Research, 2010, 115(A10): A10319. |
| [25] |
陈桂秀.
用程序求解最小二乘拟合多项式的系数[J]. 青海师范大学学报(自然科学版), 2010, 26(3): 14–17.
CHEN Guixiu. Solve the least square curve fitting polynomial coefficient with program[J]. Journal of Qinghai Normal University (Natural Science), 2010, 26(3): 14–17. DOI:10.3969/j.issn.1001-7542.2010.03.004 |
| [26] | LI Linyang, LV Zhiping, CHEN Zhengsheng, et al. GNSSer: objected-oriented and design pattern-based software for GNSS data parallel processing[J]. Journal of Spatial Science, 2019. DOI:10.1080/14498596.2019.1574245 |
| [27] |
张宝成.
GNSS非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报, 2014, 43(10): 1099.
ZHANG Baocheng. Study on the theoretical methodology and applications of precise point positioning using undifferenced and uncombined GNSS data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1099. DOI:10.13485/j.cnki.11-2089.2014.0155 |
| [28] |
姚宜斌, 曹娜, 许超钤, 等.
GPT2模型的精度检验与分析[J]. 测绘学报, 2015, 44(7): 726–733.
YAO Yibin, CAO Na, XU Chaoqian, et al. Accuracy assessment and analysis for GPT2[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 726–733. |



