2. 中国测绘科学研究院, 北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
CORS站坐标运动特征预测分析是维持2000中国大地坐标系统(China geodetic coordinate system 2000,CGCS2000)框架准确性和现势性的重要基础[1]。通过对国内多个CORS站高程坐标分量序列特征分析发现,CORS站在垂直方向表现出明显的非线性和周期性特征,并且不同的CORS站对应周期性变化模式和运动规律也不尽相同[2]。影响全球定位系统(global positioning system,GPS)高程分量周期性变化的因素很多,主要包括地壳运动、冰雪、土壤水分、大气压负载以及CORS站测量技术的高低等[3-4]。在分析CORS站高程坐标分量运动特征时,只考虑线性运动,直接在线性最小二乘拟合模型中对周期项赋予固定数值[5],而忽略其非线性运动特征,导致建立的CORS站高程线性速度场模型对于垂向速率估计和误差估计存在很大的偏差[6-8]。同时CORS站周围存在物理、地理因素及测量仪器等产生的噪声,也会影响CORS站高程运动的规律。在对我国CORS站高程时间序列数据噪声模型研究时,文献[9]利用功率谱分析CORS高程序列的噪声性质,并采用极大似然法定量地估计噪声序列中有色噪声的分量。文献[10]利用不同组合的噪声模型对CORS站坐标时间序列的噪声进行分析,并计算了积雪深度、大气压负载、土壤湿度负载等对CORS站位移的影响,得到中国区域CORS站坐标序列的噪声特性主要表现为白噪声+闪烁噪声和白噪声+带通幂律噪声。文献[11]利用AR模型对CORS站高程噪声序列建模,并与CORS站高程非线性拟合模型结合进行高程运动的预报。
研究结果表明,CORS站高程分量建模的残差序列表现为有色噪声,从统计意义上是否为非平稳的随机过程,需要进一步研究。统计学采用异方差法分析时间序列的平稳性特性,如果存在异方差特性,则时间序列是非平稳的随机过程。统计学中对时间序列是否存在异方差特性进行了研究,大多数研究者对截面数据产生的异方差给予了足够多的关注而放松了对时间序列数据也会产生异方差的警惕[12-13]。文献[14]于1982年提出了在时间序列背景下也有可能出现异方差性的观点,并从理论上提出了一种观测时间序列方差变动的方法,自回归条件异方差(autoregressive conditional heteroskedasticity,ARCH)检验。ARCH检验认为时间序列存在的异方差性为ARCH过程,通过检验该过程是否成立去判断时间序列是否存在异方差[15]。除了ARCH方法检验异方差外,还有残差平方图分析法、帕克检验法、等级相关系数检验法、White检验法等[16]。
国内外CORS站已经积累了20余年的连续观测数据,为研究地壳运动、地震活动等提供了重要的信息。本文采用SOPAC(scripps orbit and permanent array center)全球数据中心6个国内外CORS站20余年的高程时间序列数据,设计非线性周期模型迭代算法,建立CORS站高程坐标分量非线性最小二乘拟合模型,并以均方根误差(root mean square error,RMSE)和拟合优度(goodness of fit,目前没有固定的简写形式,文中记为RNEW)为精度指标衡量模型的优劣。建立CORS站高程非线性拟合模型后,以残差平方序列为研究对象[17],利用ARCH检验法、残差平方序列图分析法判断残差平方序列的异方差特性,对具有异方差特性的残差平方序列建立广义自回归条件异方差(generalized autoregressive conditional heteroskedasticity,GARCH)波动模型,描述其随着时间变化的非平稳波动情况[18],验证GARCH模型对非平稳残差平方序列建模的可行性,为CORS站高程残差序列有色噪声建模提供一种途径。
1 CORS站高程时间序列非线性建模方法经典的CORS站高程时间序列线性周期拟合模型采用固定周期项。例如式(1)包含了年、半年和两年周期项,对应周期值分别为T1=1、T2=0.5、T3=2,利用线性最小二乘法求解模型未知参数M =[a b A1 A2 A3]T, 其中a为常数项,b为线性速度,A1、A2、A3为对应不同周期项的振幅值。
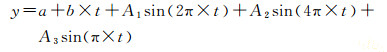 (1)
(1)
非线性最小二乘模型将各个周期项作为未知值,加入了每个未知周期项对应的初相和频率未知数,例如式(2)中,M =[a b A1 f1 φ1 A2 f2 φ2 A3 f3 φ3]T是模型的未知参数。
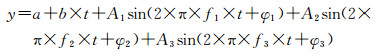 (2)
(2)
线性模型(1)的解作为非线性模型(2)的初值,记为M0。将模型(2)在初值M0处按泰勒级数展开至一阶项,得到线性化后的误差方程式为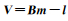
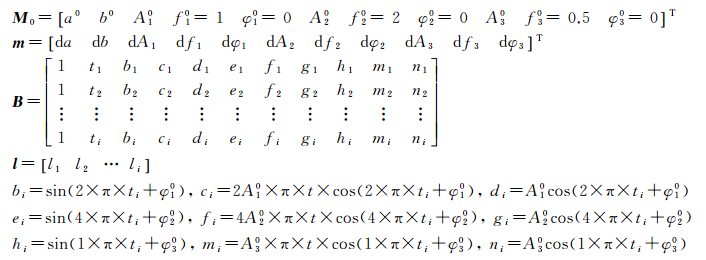
LS求解非线性模型时,给定未知参数初值的精度不同,一次平差结果可能不满足参数的精度要求,采用高斯-牛顿迭代算法,计算流程如图 1所示,其中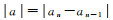

|
| 图 1 CORS站高程非线性建模流程 Fig. 1 The nonlinear modeling process of CORS stations height |
为了评价CORS站高程时间序列非线性建模的效果,采用均方根误差RMSE、可决系数(coefficient of determination,记为R2)、拟合优度RNEW 3个精度评价指标。
均方根误差RMSE反映了测量值与真实值之间的偏离程度[19]
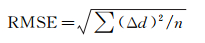 (3)
(3)
式中,n为测量次数;Δd为测量值与真实值之间的偏差。
可决系数R2是线性回归方程对观测值的拟合程度[20]
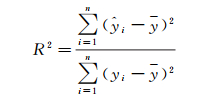 (4)
(4)
式中,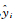
拟合优度在统计学中用于判定非线性回归方程对观测值的拟合程度[21],在对回归方程拟合程度的解释上,RNEW与R2意义相同,当RNEW越接近于1,非线性模型拟合程度越高
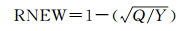 (5)
(5)
式中,Q=∑r2;Y=∑y2;r是拟合残差;y是序列观测值。
2 CORS站高程非线性建模试验从SOPAC全球数据中心获得国内外6个CORS站20余年干净的带有趋势项的高程坐标时间序列数据,对于缺值数据,使用三次样条法进行插值处理[22]。采用线性模型(1)和非线性模型(2)分别建立CORS站高程分量拟合模型。
表 1是线性模型(1)的未知参数估计值。作为CORS站高程非线性高斯-牛顿迭代的初值,其中YAR2和AUCK两站只给出了一年和半年周期项的初值,这两个站的两年周期项振幅估计值均小于0.1 mm,两年周期项在高程分量运动模型中所占的比重可以忽略不计。
| 参数 | BJFS | KUNM | SHAO | BOGO | YAR2 | AUCK |
| a/m | 0.001 90 | 0.005 90 | 0.005 70 | 0.000 65 | -0.000 99 | -0.000 22 |
| b/ma-1 | 0.002 20 | -0.001 00 | -0.001 10 | -0.000 28 | 0.000 43 | -0.000 28 |
| A1/m | 0.005 20 | 0.005 80 | 0.005 70 | 0.004 30 | 0.005 40 | 0.005 90 |
| A2/m | 0.001 20 | 0.001 60 | 0.001 80 | 0.000 90 | 0.000 80 | 0.000 94 |
| A3/m | 0.000 25 | 0.001 30 | 0.001 20 | 0.000 64 | — | — |
| f1/a-1 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 |
| f2/a-1 | 2.000 00 | 2.000 00 | 2.000 00 | 2.000 00 | 2.000 00 | 2.000 00 |
| f3/a-1 | 0.500 00 | 0.500 00 | 0.500 00 | 0.500 00 | — | — |
| φ1/rad | 0.000 00 | 0.000 00 | 0.000 00 | 0.000 00 | 0.000 00 | 0.000 00 |
| φ2/rad | 0.000 00 | 0.000 00 | 0.000 00 | 0.000 00 | 0.000 00 | 0.000 00 |
| φ3/rad | 0.000 00 | 0.000 00 | 0.000 00 | 0.000 00 | — | — |
表 2是非线性模型(2)的未知参数估计值及精度评价指标。为了便于对比线性和非线性模型拟合结果的差异,将线性模型的建模精度指标结果也放在了表 2,其中(nl)rmse和(l)rmse分别表示非线性建模与线性建模的均方根误差指标。周期方面:6个CORS站高程非线性建模的周期值(频率f的倒数)均不是整数,其周期性变化并不是经典的CORS站高程时间序列模型所采用的固定整年、整半年或两年;近似年周期的估计误差,除了AUCK站达到12%外,其他5个站均在1%;近似半年周期的估计误差不超过18%;近似两年周期的估计误差不超过6%。振幅方面:近似年周期项对应的振幅值介于5~8 mm,近似半年周期项的振幅介于1~2 mm,近似两年周期项对应的振幅值介于0.1~1.3 mm,说明6个CORS站的高程方向以近似年和半年周期性变化为主,近似两年周期性变化基本忽略不计。精度评价指标方面:6个CORS站的非线性模型RMSE精度在5 mm水平,低于线性模型1~2 mm,线性模型R2明显低于非线性模型RNEW指标0.1左右,非线性建模精度整体优于线性模型。
| 参数 | BJFS | KUNM | SHAO | BOGO | YAR2 | AUCK |
| a/m | 0.001 80 | 0.006 00 | 0.006 80 | 0.000 66 | -0.001 00 | -0.000 23 |
| b/ma-1 | 0.002 20 | -0.001 10 | -0.001 00 | -0.000 28 | 0.000 42 | -0.000 28 |
| A1/m | 0.006 90 | 0.007 50 | 0.007 60 | 0.005 00 | 0.006 30 | 0.006 80 |
| f1/a-1 | 0.988 70 | 1.01 250 | 1.012 80 | 0.998 00 | 1.01000 | 1.120 40 |
| φ1/rad | -1.674 40 | 0.073 50 | 0.082 90 | -1.470 40 | -0.408 70 | -0.146 00 |
| A2/m | 0.001 00 | 0.001 30 | 0.001 50 | 0.000 70 | 0.000 75 | 0.001 00 |
| f2/a-1 | 1.990 50 | 1.870 70 | 1.816 80 | 1.981 80 | 2.020 00 | 2.042 80 |
| φ2/rad | 3.353 70 | 1.501 50 | 1.438 40 | 2.940 80 | 2.448 90 | 1.068 50 |
| A3/m | 0.000 23 | 0.001 10 | 0.001 30 | 0.000 60 | — | — |
| f3/a-1 | 0.470 90 | 0.486 00 | 0.48700 | 0.437 60 | — | — |
| φ3/rad | 2.279 40 | 0.979 90 | 0.550 20 | 2.105 24 | — | — |
| (nl)rmse/m | 0.006 00 | 0.007 90 | 0.007 88 | 0.004 90 | 0.006 03 | 0.005 31 |
| (l)rmse/m | 0.008 10 | 0.009 22 | 0.009 30 | 0.006 41 | 0.008 14 | 0.007 71 |
| rnew | 0.976 64 | 0.952 31 | 0.952 46 | 0.965 23 | 0.953 64 | 0.964 85 |
| R2 | 0.852 30 | 0.823 45 | 0.819 95 | 0.886 52 | 0.852 32 | 0.886 58 |
图 2是6个CORS站高程分量线性和非线性建模结果,纵轴表示CORS站高程坐标值,横轴表示高程坐标对应的时间值,纵轴单位是mm,横轴单位是年;绿色散点代表CORS站原始高程值,黑色粗实线代表线性模型拟合曲线,红色粗实线代表非线性模型拟合曲线。从图 2可以看出,各个CORS站建立的非线性模型拟合效果优于线性模型。
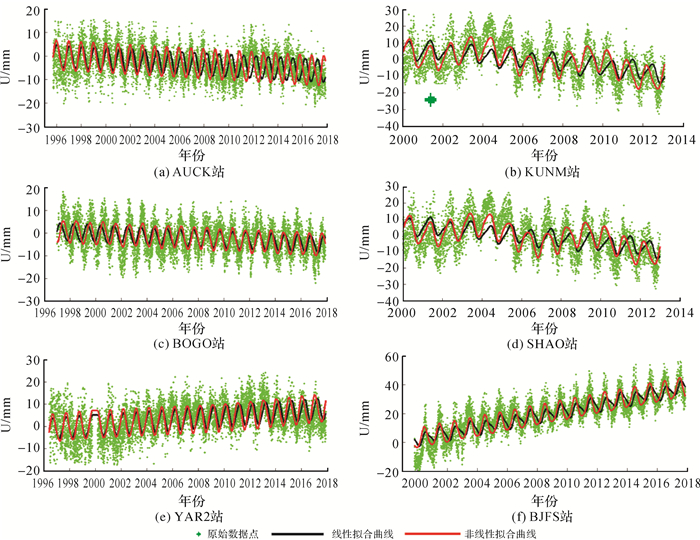
|
| 图 2 6个CORS站高程数据建模结果 Fig. 2 The height data modeling results of 6 CORS stations |
3 ARCH效应检验与GARCH(p, q)波动模型
为了克服AR模型只能对平稳序列数据建模的不足,引入经济学的序列波动分析方法对非平稳序列数据建模,验证序列波动GARCH分析方法对CORS站高程非平稳残差平方序列建模的可行性,为CORS站高程残差序列建模和非线性速度场重构奠定基础。
3.1 ARCH效应检验方法异方差性是相对于同方差而言,若一个残差平方序列随时间的变化其值波动幅度较大,则称该残差平方序列具有异方差性。对CORS站高程非线性建模后的残差平方序列检验其异方差性是否存在,即残差平方序列是否存在ARCH效应[23]。图 3是CORS站高程残差平方序列ARCH效应检验流程,分为两步:首先检验残差平方序列自相关特性,利用Q检验法及残差平方序列自相关系数(autocorrelation coefficient,ACF)检验如图 4所示;接着检验残差平方序列的异方差性,构造t统计量检验流程如图 5所示。若CORS站高程非线性建模后的残差平方序列同时存在自相关性和异方差性,则其具有ARCH效应,即CORS站高程非线性建模后的残差平方序列具有非平稳性[24]。
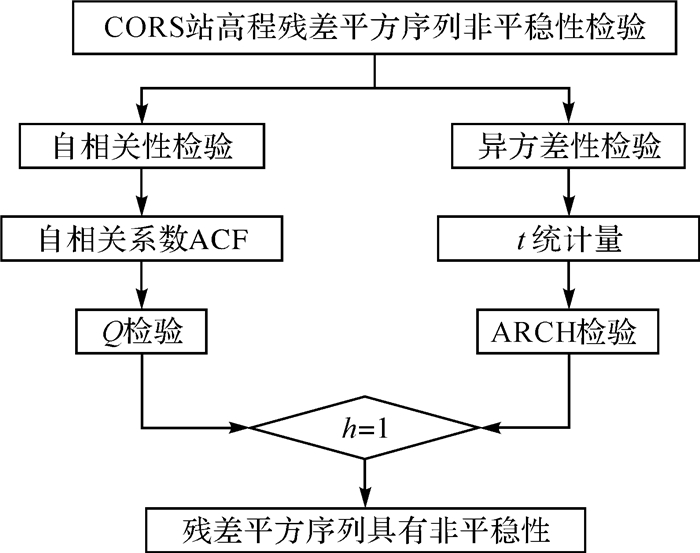
|
| 图 3 CORS站高程残差平方序列非平稳性检验流程 Fig. 3 The nonstationarity test procedure of CORS stations height residual square sequence |
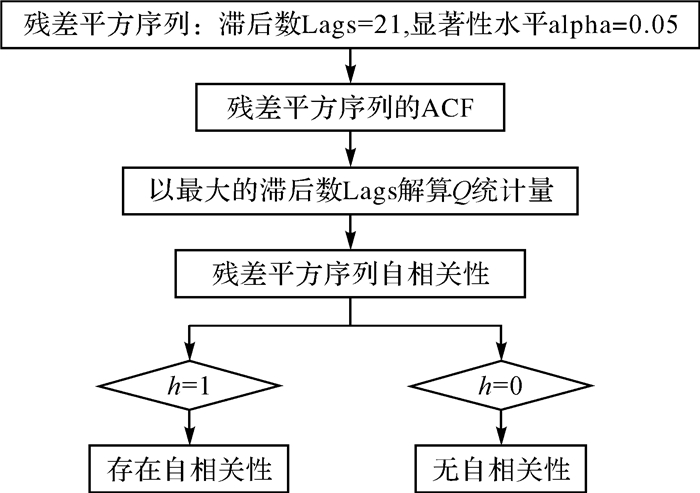
|
| 图 4 自相关性Q检验流程 Fig. 4 The autocorrelation of Q test procedure |

|
| 图 5 异方差性ARCH检验流程 Fig. 5 The ARCH test procedure of heteroscedasticity |
图 4和图 5中,滞后数Lags值由残差平方序列自相关系数值对应的最大滞后数确定,试验选择的BJFS和BOGO两个CORS站时间序列长度为21年,其残差平方序列的自相关系数值对应的最大滞后数均为21,即Lags=21。自相关性检验的原假设为残差平方序列不存在自相关性,异方差性检验的原假设为残差平方序列不存在异方差性,显著性水平alpha=0.05,表示残差平方序列相关性和异方差性的检验置信度为95%,h为检验残差平方序列自相关性和异方差性程序中设置的逻辑值,若h=1表示拒绝原假设,h=0表示接受原假设。
自相关性检验的Q统计量可表示为
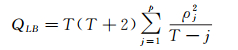 (6)
(6)
式中,ρj是残差平方序列的j阶自相关系数;T是残差平方序列的总长度;p是设定的滞后阶数。
残差平方序列的自相关系数定义为
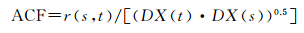 (7)
(7)
式中,ACF表示残差平方的自相关系数值;r(s, t)为序列自协方差;DX(t)和DX(s)表示不同时刻方差。其中,序列自协方差、不同时刻方差定义为
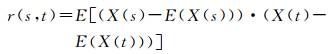 (8)
(8)
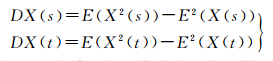 (9)
(9)
残差平方序列的偏自相关系数(partial autocorrelation coefficient,PACF)定义如式(10),φkk表示滞后数为k的偏自相关系数,由克莱姆法则求得,D为系数行列式,ρi为样本的自相关系数,Dk为将D的第k列换为常数项。
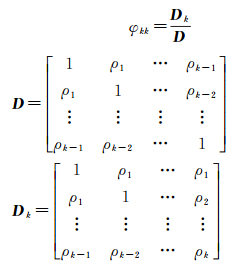 (10)
(10)
图 5异方差性t检验时,回归统计矩阵X由残差平方序列值对应的时间构成,反应变量y为残差平方序列值,预测响应yhat为残差平方预测值。t统计量stat定义为
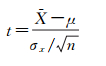 (11)
(11)
式中,X为样本平均数;μ为总体残差平方序列值的平均数;σx为样本标准差;n为样本容量。本文研究中样本容量选取为总体的0.2倍。
3.1.1 残差平方序列自相关性检验自相关性指序列之间不是完全相互独立的,而是存在某种相互关系[25]。BJFS和BOGO两站的残差平方序列如图 6所示,纵轴表示高程时间序列数据非线性建模后的残差平方值,横轴表示时间。为了检验CORS站高程残差平方序列的自相关性,绘制两个CORS站的残差平方序列自相关如图 7所示,纵坐标ACF表示CORS站残差平方序列的自相关系数,横坐标Lags表示自相关系数对应的滞后阶数值。自相关系数ACF随滞后阶数Lags的变化并不是快速趋近于0,而是缓慢地变化为0,即残差平方序列在不同时刻存在某种相互关系,并不是相互独立的,通过自相关图定性地判断出两站残差平方序列具有自相关性。

|
| 图 6 两个CORS站高程的残差平方序列 Fig. 6 The residual squared sequence of two CORS stations height |

|
| 图 7 两个CORS站高程残差平方序列的自相关图 Fig. 7 The autocorrelation graph of two CORS stations height residual square sequences |
为了定量地判断两站残差平方序列的自相关性,采用Q检验法对两站的残差平方序列自相关性进行检验,利用式(7)计算残差平方序列的自相关系数ACF,以最大滞后数(Lags=21)计算式(6)的Q统计量,得到BJFS、BOGO两站的Q统计量分别为4.12和4.23,均大于显著性水平为0.05时的Q临界值3.48,故拒绝原假设,即逻辑量h=1,两站的残差平方序列具有自相关性。
3.1.2 残差平方序列异方差性检验由残差平方序列图 6定性的判断残差平方序列的异方差性[26]:两站的残差平方序列随时间变化,并不是一个常数,并且每隔一年左右都会出现集聚现象(尖峰厚尾),即残差平方序列随时间波动幅度较大,定性的判断出了两站残差平方序列具有异方差特性。
采用ARCH检验方法定量地判定残差平方序列的异方差特性。ARCH过程如式(12),i为ARCH过程的阶数;α0为常数项;αi为ARCH过程阶数对应残差平方值的系数;υt为随机误差;α0>0, αi≥0(i=1, 2, …, p)
 (12)
(12)
由图 5计算两站残差平方序列的t统计量stat:BJFS站stat=2.98、BOGO站stat=2.81,均大于显著性水平为0.05时的t临界值2.10,故拒绝原假设,即逻辑值h=1,残差平方序列存在异方差性,证明了两站高程残差平方序列是非平稳随机过程。
3.2 残差平方序列GARCH(p, q)波动模型为了定量描述残差平方序列的波动,引入GARCH(p, q)模型对CORS站高程非平稳残差平方序列建模,GARCH模型可以有效地拟合具有长期记忆性的异方差函数,而ARCH模型是GARCH模型的一个特例[27],即p=0的GARCH(p, q)模型。GARCH (p, q)模型定义如式(13)所示,i=1, 2, …, p,j=1, 2, …, q,其中p是模型拖尾值,它的阈值由序列自相关系数值基本趋于稳定时对应的滞后数Lags确定;q是模型截尾值,它的阈值由序列偏自相关系数值基本趋于稳定时对应的滞后数Lags确定
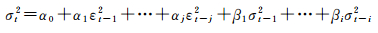 (13)
(13)
根据残差平方序列自相关图 7判断拖尾值p:BJFS站ACF在滞后阶数Lags=6后趋于稳定,模型拖尾值p的阈值为6,即p≤6;BOGO站ACF在滞后阶数Lags=10后趋于稳定,模型拖尾值p的阈值为10,即p≤10。
图 8是残差平方序列偏自相关图:纵坐标PACF表示CORS站残差平方序列的偏自相关系数值,横坐标Lags表示偏自相关系数值对应的滞后阶数值。BJFS站PACF在滞后阶数Lags=5后趋于稳定,模型截尾值q的阈值为5,即q≤5。BOGO站PACF在滞后阶数Lags=4后趋于稳定,模型截尾值q的阈值为4,即q≤4。

|
| 图 8 两个CORS站高程残差平方序列的偏相关图 Fig. 8 The partial correlogram graph of two CORS stations height residual square sequences |
由残差平方序列自相关图和偏自相关图综合判断出了两站GARCH模型的拖尾值p和截尾值q的阈值:BJFS站(p≤6,q≤5),BOGO站(p≤10,q≤4)。
为了求出GARCH模型最佳的(p,q)值,本文参考文献[28]中引用的赤池信息量准则(Akaike information criterion,AIC)选取最佳模型拖尾和截尾值
 (14)
(14)
式中,K是参数的数量(GARCH(p,q)模型的组合个数);L是似然函数,即残差平方序列之和除以GARCH(p,q)模型的组合个数。
根据AIC准则求出了最佳(p, q)值,BJFS站(p=1, q=1),BOGO站(p=1, q=1),并对两站的残差平方序列建立GARCH(1,1)波动模型
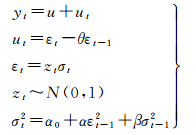 (15)
(15)
式中,yt=u+ut为均值方程;ut=εt-θεt-1方差方程;zt为服从标准正态分布的随机变量;σt2为εt的条件方差;εt-12为ARCH项;σt-12为GARCH项;α0为常数项;u是残差平方序列均值;α为ARCH项系数;β为GARCH项系数;模型待求的未知参数是M =(α0, α, β, u)。
由极大似然估计准则求解BJFS和BOGO站波动模型GARCH(1,1)的未知参数[29-30]分别见表 3和表 4,constant代表未知参数M中的常数项α0,GARCH(1)代表β,ARCH(1)代表α,offset代表u,由于4个值为常数或某项的系数,故无单位。
| parameter | value | standard error | t statistic |
| constant | 0.000 000 20 | 0.000 006 15 | 0.132 911 00 |
| GARCH(1) | 0.688 887 00 | 0.375 217 00 | 1.835 970 00 |
| ARCH(1) | 0.167 274 00 | 0.906 637 00 | 0.184 500 00 |
| offset | 0.000 048 96 | 0.000 138 28 | 0.354 015 00 |
| parameter | value | standard error | t statistic |
| constant | 0.000 000 20 | 0.000 001 70 | 0.117 767 00 |
| GARCH(1) | 0.521 826 00 | 0.648 599 00 | 0.804 54200 |
| ARCH(1) | 0.214 017 00 | 0.012 011 80 | 17.817 200 0 |
| offset | 0.000 026 29 | 0.000 118 60 | 0.221 713 00 |
将表 3和表 4残差平方序列GARCH(1, 1)模型参数值分别代入式(15),解算两站的条件方差序列值,如图 9所示,纵轴表示残差平方值与条件方差值,横轴表示时间,黑色实线代表残差平方序列,绿色点线代表条件方差序列。条件方差是在残差平方基础上描述的残差平方序列波动情况,其数值比残差平方值小,为了直观地反映条件方差与残差平方随时间的变化规律,图 9将条件方差扩大到100倍,与残差平方值在同一个数量等级。从图 9可知,条件方差序列随时间的变化趋势会在某一段时间急剧升高或降低,与残差平方序列随时间的变化趋势一致,利用GARCH(1, 1)模型可以对CORS站高程非平稳的残差平方序列波动情况进行描述。
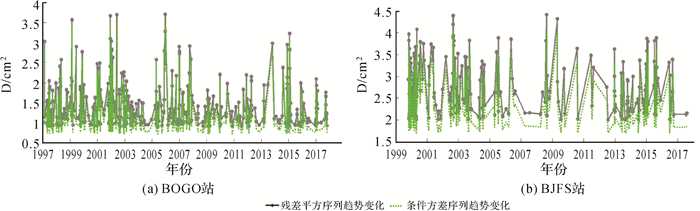
|
| 图 9 残差平方序列与条件方差序列趋势变化比较 Fig. 9 Comparison of the trend between the residual squared sequence and the conditional variance sequence |
4 结论
(1) 建立了CORS站高程分量非线性速度场周期拟合模型。CORS站高程分量周期性运动以近似年周期项为主,近似半年周期项次之,近似两年变化的比重几乎可以忽略不计。周期项并不是严格的年、半年或两年,固定周期项的线性建模估计结果存在偏差,采用非线性模型对CORS站高程数据建模精度明显优于传统固定周期项的线性模型。
(2) 建立了描述CORS站高程残差平方序列非平稳波动的GARCH(1, 1)模型。非线性建模后的CORS站高程残差平方序列自相关性和异方差性检验结果表明,残差平方序列是非平稳的随机过程,即非线性建模后的CORS站高程残差序列具有非平稳性。GARCH(p,q)模型克服了AR模型只能对平稳序列建模的不足,为下一步基于GARCH(p,q)模型对CORS站高程非平稳残差序列建模和非线性速度场重构提供了思路。
| [1] |
程鹏飞.
2000国家大地坐标系建立的理论与方法[M]. 北京: 测绘出版社, 2014.
CHENG Pengfei. Theory and method for establishment of the China Geodetic Coordinate System 2000[M]. Beijing: Surveying and Mapping Press, 2014. |
| [2] |
张鹏, 蒋志浩, 秘金钟, 等.
我国GPS跟踪站数据处理与时间序列特征分析[J]. 武汉大学学报(信息科学版), 2007, 32(3): 251–254.
ZHANG Peng, JIANG Zhihao, BEI Jinzhong, et al. Data processing and time series analysis for GPS fiducial stations in China[J]. Geomatics and Information Science of Wuhan University, 2007, 32(3): 251–254. |
| [3] |
程鹏飞, 成英燕, 秘金钟, 等.
CGCS2000板块模型构建[J]. 测绘学报, 2013, 42(2): 159–167.
CHENG Pengfei, CHENG Yingyan, BEI Jinzhong, et al. CGCS2000 plate motion model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 159–167. |
| [4] | YAKUBU I, KUMI-BOATENG B. Control position fix using single frequency global positioning system receiver technique:a case study[J]. Research Journal of Environmental and Earth Sciences, 2011, 3(1): 32–37. |
| [5] |
鲁铁定, 陶本藻, 周世健.
基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报(信息科学版), 2008, 33(5): 504–507.
LU Tieding, TAO Benzao, ZHOU Shijian. Modeling and algorithm of linear regression based on total least squares[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 504–507. |
| [6] |
曾波, 张彦芬, 姜卫平, 等.
山西CORS网基准站速度场分析[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1401–1404.
ZENG Bo, ZHANG Yanfen, JIANG Weiping, et al. Velocity analysis of Shanxi CORS fiducial station[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1401–1404. |
| [7] |
蒋志浩, 张鹏, 秘金钟, 等.
基于CGCS2000的中国地壳水平运动速度场模型研究[J]. 测绘学报, 2009, 38(6): 471–476.
JIANG Zhihao, ZHANG Peng, BEI Jinzhong, et al. The model of crustal horizontal movement based on CGCS2000 frame[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 471–476. DOI:10.3321/j.issn:1001-1595.2009.06.001 |
| [8] |
张荣斗, 黄丁发, 廖华, 等.
基于GPS的四川地区现时地壳形变分析[J]. 测绘科学, 2008, 33(6): 30–32.
ZHANG Rongdou, HUANG Dingfa, LIAO Hua, et al. The analysis of present-day crustal deformation in Sichuan based on GPS[J]. Science of Surveying and Mapping, 2008, 33(6): 30–32. DOI:10.3771/j.issn.1009-2307.2008.06.009 |
| [9] |
蒋志浩, 张鹏, 秘金钟, 等.
顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J]. 测绘学报, 2010, 39(4): 355–363.
JIANG Zhihao, ZHANG Peng, BEI Jinzhong, et al. Velocity estimation on the colored noise properties of CORS network in China based on the CGCS2000 frame[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 355–363. |
| [10] |
李昭, 姜卫平, 刘鸿飞, 等.
中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496–503.
LI Zhao, JIANG Weiping, LIU Hongfei, et al. Noise model establishment and analysis of IGS reference station coordinate time series inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496–503. |
| [11] |
王晓明. CGCS2000坐标框架动态特性及非线性建模方法研究[D].北京: 中国测绘科学研究院, 2013. WANG Xiaoming. The study on movement characteristics and non-linear model of CGCS2000 framework[D]. Beijing: Chinese Academy of Surveying and Mapping, 2013. http://cdmd.cnki.com.cn/Article/CDMD-86001-1013373834.htm |
| [12] |
林金官, 韦博成.
非线性随机效应模型的异方差性检验[J]. 系统科学与数学, 2002, 22(2): 245–256.
LIN Jinguan, WEI Bocheng. Testing for heterogeneity in nonlinear models with random effects[J]. Journal of Systems Science and Mathematical Sciences, 2002, 22(2): 245–256. DOI:10.3969/j.issn.1000-0577.2002.02.015 |
| [13] |
陈敏, 安鸿志.
时间序列中条件异方差性的检验[J]. 中国科学(A辑), 1998, 28(11): 961–971.
CHEN Min, AN Hongzhi. A test of conditional heteroscedasticity in time series[J]. Science in China Series A:Mathematics, 1998, 28(11): 961–971. |
| [14] | ENGLE R F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J]. Econometrica, 1982, 50(4): 987–1007. DOI:10.2307/1912773 |
| [15] |
解静.劳动力对经济增长的贡献研究[D].南京: 南京大学, 2015. XIE Jing. Research on the contribution of labour force to the growth of economy[D]. Nanjing: Nanjing University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10284-1015315138.htm |
| [16] |
徐生霞, 潘海涛.
截面数据异方差问题检验技术的比较[J]. 统计与决策, 2017(5): 16–20.
XU Shengxia, PAN Haitao. Comparative study of heteroscedasticity test technology for section data[J]. Statistics and Decision, 2017(5): 16–20. |
| [17] |
尹群.基于GARCH模型和VaR的我国创业板市场风险应用研究[D].哈尔滨: 哈尔滨工业大学, 2017. YIN Qun. Study on the risk application of China's growth enterprise market based on GARCH models and VaR[D]. Harbin: Harbin Institute of Technology, 2017. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D760473 |
| [18] |
姜翔程, 熊亚敏.
基于GARCH族模型的我国股市波动性研究[J]. 西南师范大学学报(自然科学版), 2017, 42(2): 115–119.
JIANG Xiangcheng, XIONG Yamin. On analysis of the volatility of Chinese stock market based on GARCH model[J]. Journal of Southwest China Normal University (Natural Science Edition), 2017, 42(2): 115–119. |
| [19] |
张恒璟, 改健.
CORS站高程非线性速度场估计方法[J]. 测绘科学, 2017, 42(12): 146–150.
ZHANG Hengjing, GAI Jian. Estimation method of elevation nonlinear speed field of CORS station[J]. Science of Surveying and Mapping, 2017, 42(12): 146–150. |
| [20] |
杨龙光, 吴晶妹.
基于统计与聚类的信用评级新方法[J]. 统计与决策, 2016(3): 13–16.
YANG Longguang, WU Jingmei. A new method of credit rating based on statistics and clustering[J]. Statistics and Decision, 2016(3): 13–16. |
| [21] |
苏雅芳.宏观经济校准模型的拟合优度研究[D].南京: 南京大学, 2014. SU Yafang. Measures of fit for the macroeconomic calibrated models[D]. Nanjing: Nanjing University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2944132 |
| [22] |
田慧, 程鹏飞, 秘金钟.
不同插值方法对CORS高程时间序列的影响分析[J]. 测绘科学, 2013, 38(1): 16–17, 46.
TIAN Hui, CHENG Pengfei, BEI Jinzhong. Effect analysis of different interpolation methods on height time series of CORS[J]. Science of Surveying and Mapping, 2013, 38(1): 16–17, 46. |
| [23] |
蒋学雷, 陈敏, 吴国富.
中国股市的羊群效应的ARCH检验模型与实证分析[J]. 数学的实践与认识, 2003, 33(3): 56–63.
JIANG Xuelei, CHEN Min, WU Guofu. The ARCH model and its empirical analysis of herding behavior on the Chinese stock market[J]. Mathematics in Practice and Theory, 2003, 33(3): 56–63. DOI:10.3969/j.issn.1000-0984.2003.03.011 |
| [24] |
傅彦博, 孙付平, 朱新慧, 等.
全球GPS测站垂向周年变化统计改正模型的建立[J]. 测绘学报, 2018, 47(10): 1337–1345.
FU Yanbo, SUN Fuping, ZHU Xinhui, et al. Establishment of statistical correction model for vertical annual variations of global GPS stations[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(10): 1337–1345. DOI:10.11947/j.AGCS.2018.20170616 |
| [25] |
罗秋菊, 罗倩文.
中国省域展览业与经济相关关系及其空间溢出研究[J]. 地理科学, 2016, 36(11): 1729–1735.
LUO Qiuju, LUO Qianwen. Cross-province analysis on exhibition industry and economic development level, and the spatial spillover effects[J]. Scientia Geogarphica Sinica, 2016, 36(11): 1729–1735. |
| [26] |
张晓琴, 王佳鸣.
基于正交表的异方差估计方法改进[J]. 数理统计与管理, 2016, 35(2): 225–231.
ZHANG Xiaoqin, WANG Jiaming. An improved estimation method of the variance with orthogonal table in the heteroskedastic model[J]. Journal of Applied Statistics and Management, 2016, 35(2): 225–231. |
| [27] | BOLLERSLEV T. Generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics, 1986, 31(3): 307–327. DOI:10.1016/0304-4076(86)90063-1 |
| [28] |
杨贵军, 于洋, 孟杰.
基于AIC的粗糙集择优方法[J]. 模糊系统与数学, 2018, 32(1): 165–171.
YANG Guijun, YU Yang, MENG Jie. Selection of better rough set based on AIC[J]. Fuzzy Systems and Mathematics, 2018, 32(1): 165–171. |
| [29] |
吴思鑫, 冯牧, 张虎, 等.
基于高频数据的非平稳GARCH(1, 1)模型的拟极大指数似然估计[J]. 中国科学:数学, 2018, 48(3): 443–456.
WU Sixin, FENG Mu, ZHANG Hu, et al. Quasi-maximum exponential likelihood estimation for non-stationary GARCH (1, 1) models with high-frequency data[J]. Scientia Sinica Mathematica, 2018, 48(3): 443–456. |
| [30] |
宋鹏, 胡永宏, 朱颖颖.
GARCH(1, 1)模型的稳健估计比较及应用[J]. 数学的实践与认识, 2017, 47(8): 181–189.
SONG Peng, HU Yonghong, ZHU Yingying. The comparison of robust estimates for GARCH (1, 1) model and application of example[J]. Mathematics in Practice and Theory, 2017, 47(8): 181–189. |


