2. 皇家墨尔本理工大学空间科学研究中心, 澳大利亚 维多利亚州 墨尔本 3001
2. Space Research Centre, RMIT University, Australia VIC 3001
随着现代测量技术的发展,测量数据处理的对象已经由单一同类观测数据转变为多源、多类或同类多因素的异方差结构观测数据,在这种情况下随机模型的准确性对参数解估计的统计特性具有重要影响[1-2]。方差-协方差分量估计能够极大地改善随机模型不精确的问题,从而成为国内外学者关注的焦点,并形成了一整套的理论框架[3-8]。近年来主要理论研究包括:①以平差结果之一的残差向量为基本输入量的残差型VCE方法,如Helmert法[1-2, 7]、最小二乘方差分量估计法(简称LS-VCE)[9-11]、MINQUE法[12]、BIQUE法[13]、MLE-VCE法[14]、等效残差法[15-16]及EIV模型的VCE方法[4, 8]等;②以等价条件闭合差为基本输入量的解析型VCE方法,如VCE-ECM法[17-18]。近年来的主要应用研究有:文献[19— 20]研究了常规导线控制网中角度观测值与距离观测值的定权问题;文献[21—22]探讨了GNSS观测值随机模型的精化问题;文献[23—24]研究了坐标转换中不同公共点坐标的精度问题;文献[11, 25—26]开展了GNSS站坐标时间序列的噪声估计及评价研究。
大量研究表明,LS-VCE方法[9-10, 15]可导出Helmert、MINQUE、MLE-VCE等方法的方差-协方差分量估计公式,具有最优无偏特性。与此同时,基于等价条件平差模型的VCE-ECM法[17-18]以等价条件闭合差作为基本输入量,摒弃了平差值求解或残差估计过程。鉴于此,本文从方差-协方差分量最小二乘估计准则和等价条件平差模型出发,利用等价条件闭合差的二次型构造方差分量估计公式,进而将方差分量估计方程变换为线性Gauss-Markov形式并建立了基本估计方程;然后,顾及矩阵拉直、半拉直算子和Kronecker积的性质进行化简,导出了基于等价条件闭合差的方差-协方差分量最小二乘估计公式(least-square variance-covariance estimation based on the equivalent condition misclosure),简称为LSV-ECM法。在此基础上,证明了本文LSV-ECM法与残差型VCE方法的等价性,定量分析了LSV-ECM法、Helmert法和LS-VCE法的计算复杂度,以边角网平差和中国区域GNSS站坐标时序建模实例验证本文方法的正确性和高效性。
1 等价条件闭合差的方差分量最小二乘估计 1.1 等价条件平差模型设概括平差模型为
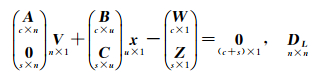 (1)
(1)
式中,A、[BT CT]均为行满秩系数矩阵;W为具有参数的条件方程闭合差;Z为限制条件方程闭合差;DL为观测值L的方差阵;V、x分别为待求的残差与参数向量;下标c、s分别为条件方程个数和限制条件方程个数;n、u分别为观测数和参数个数;平差模型自由度r=(c+s)-u。
令矩阵BT=[BT C T],利用正交投影矩阵H消去参数向量,即
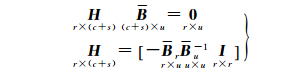 (2)
(2)
式中,H称为零空间算子;Bu、B r为B的上u行与下r行分块矩阵,即BT= [BuT BrT];式(1)等式两边均左乘H,根据式(1)可将式(2)概括平差模型化为等价的条件平差模型
 (3)
(3)
式中,A= HcA、w= HcW + HsZ称为等价条件闭合差。其中,Hc、Hs为H的左c列与右s列分块矩阵,即H = [Hc Hs]。
1.2 方差-协方差分量最小二乘估计方法假设概括平差模型式(1)中随机模型DL可表示为
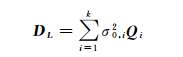 (4)
(4)
式中,∑(·)表示累加运算;k为方差-协方差分量的个数;Qi为第i个协因数分量矩阵。
由式(3)可将等价条件闭合差W的随机模型表示为
 (5)
(5)
令F = DW,根据式(4)、式(5)可得
 (6)
(6)
式中,Qi=AQiAT。
进一步令θ=[σ0, 12 σ0, 22 … σ0, k2] T,并顾及F、Qi的矩阵对称性质,利用下三角矩阵拉直算子(简称半拉直算子)vh(·)对式(6)等式两端F, Qi进行变换,可得
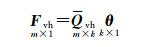 (7)
(7)
式中,m=r(r+1)/2;Fvh=vh(F);Qvh=[vh(Q1) vh(Q2) … vh(Qk)]。
记向量Fvh的方差阵为Σvh,N令=2QvhTΣvh-1Qvh;U=2QvhTΣvh-1Fvh,则由最小二乘准则可得式(7)的方差-协方差分量估计式
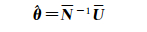 (8)
(8)
 (9)
(9)
式中,D为复制矩阵(duplication matrix)[9],也即半拉直算子与拉直算子的映射矩阵
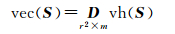 (10)
(10)
分析可知,式(8)—式(10)含有大量的高维矩阵迭代运算(r2阶),因而需进一步简化矩阵运算。考虑到矩阵拉直算子vec(·)、Kronecker积⊗和矩阵迹算子tr(·)具有如下性质[9]
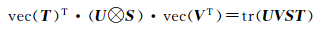 (11)
(11)
利用式(9)—式(11)对方差-协方差分量估计式N、U中的元素进行简化,整理可得
 (12)
(12)
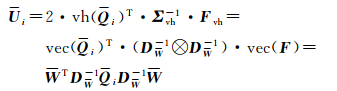 (13)
(13)
式(8)和式(12)—式(13)构成了本文方法方差-协方差分量估计式的最终形式。由上述推导过程可知,本文方法仅含等价条件平差模型的DW、Qi和W三类输入量,降低了矩阵运算维数(由r2阶降为r阶),且在最小二乘迭代估计过程中仅需更新DW(Qi和W为已知量)。对于特定的平差模型,只需变换DW、Qi和W计算式便可得到相应的方差-协方差分量估计公式(表 1)。因此,本文称为等价条件闭合差的方差-协方差最小二乘估计方法,简称LSV-ECM方法。该方法采用概括平差模型导出的等价条件闭合差进行表达,不同于Helmert型通用VCE法[7]等采用基于平差因子的残差向量表示,也区别于等效残差型VCE法[15-16]采用基于正交矩阵分解的等效残差表示,所得估计公式具有更好的模型通用性和形式简洁性。其次,本文LSV-ECM方法利用矩阵半拉直算子将方差-协方差分量估计方程变换为线性Gauss-Markov形式,并利用最小二乘准则进行方差-协方差分量估计,从而保证了估计结果具有无偏性和最优性。
| 参量 | 模型 | ||||||
| 条件平差 | 具有参数的条件平差 | 间接平差 | 附有限制的间接平差 | ||||
| B=0, C=0 | C=0 | A=-I, C=0 | A=-I | ||||
| Qi | AQiAT | HAQiATHT | HQiHT | HcQiHcT | |||
| W | W | HW | HW | HcW+HsZ | |||
| DW | ADLAT | HADLATHT | HDLHT | HcDLHcT | |||
现有文献已证明残差型VCE方法之间的等价性,并形成了一套较为完整的理论框架。通过概括平差因子矩阵R也可以证明本文LSV-ECM方法与残差型VCE方法的等价性。对于概括平差模型,LSV-ECM法与Helmert型通用VCE方法[7](简称通用Helmert法)等价;对于间接平差模型,LSV-ECM法与LS-VCE法[9, 11]、基于等效残差的LS-VCE法[15]等价;对于具有参数的条件平差模型,LSV-ECM法与文献[10]相应算法等价。为节省篇幅,这里仅给出LSV-ECM法与通用Helmert法[7]等价关系的证明过程。
根据概括平差模型,
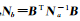
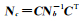
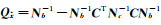
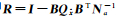
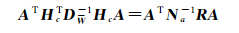 (14)
(14)
顾及式(14)及Qi= HcAQiATHcT和W=HcAV,可将式(12)—式(13)表达式Nij、Ui化简整理为关于概括平差因子矩阵R的表达式
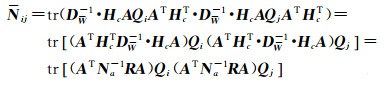 (15)
(15)
 (16)
(16)
分析对比式(15)—式(16)和式(12)—式(13)可知,LSV-ECM方法可以导出通用Helmert法[7],等价性得证。其次,残差型VCE方法(如Helmert法、LS-VCE法等)均以残差向量为输入量,而本文LSV-ECM法以等价条件闭合差为输入量,后者实现了平差值求解(残差为平差结果之一)与随机模型估计的分离。再次,等价条件闭合差维数低于残差向量维数,且前者为不需求解的已知量,因此计算效率方面明显优于前者。
表 2以间接平差模型为例分析了3种方法在构建N、U时所需的计算复杂度(迭代一次所需的加法乘法和求逆复杂度[27])。由表 2可看出,通用Helmert法与LS-VCE法以残差向量作为基本输入量,故二者的矩阵求逆复杂度完全相同,仅在加法乘法复杂度方面略有差异,故通用Helmert法和LS-VCE法在计算效率方面基本相等;而本文LSV-ECM法以等价条件闭合差为基本输入量,矩阵求逆复杂度和加法乘法复杂度均小于通用Helmert法和LS-VCE法,因此LSV-ECM法的计算效率高于通用Helmert法和LS-VCE法。
2 应用结果及分析 2.1 边角网平差
为验证本文方法的正确性和有效性,利用边角网实例进行方差分量估计和参数平差计算。设有边角网[17],其中A、B、C是已知点,P1、P2是待定点,网中观测了12个角度,编号为1~12,观测了6条边长,编号为13~18。采用间接平差模型,先验测角中误差为1.5″,测边中误差为2 cm,记后验测角方差为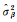
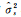
方案1:分别采用通用Helmert法[7]、LS-VCE法[9, 11]、本文LSV-ECM法进行方差分量估计和参数平差计算。其中测角和测边单位权中误差的迭代初值均取先验中误差,迭代终止条件为测角和测边的单位权中误差相等。
方案2:在方案1的基础上,剔除含有粗差的12号角度观测值和16号边长观测值[18],基于余下的16个观测值进行方差分量估计和参数平差计算。
按上述方案分别进行计算,统计不同方法迭代收敛时的方差分量估值、参数估值及其中误差。另外,为避免单次计算的随机误差,将上述方案重复计算100次,并统计LS-VCE法和本文LSV-ECM法相对于通用Helmert法的耗时比值Tratio,所得结果如表 3所示。
| 结果 | 方案1 | 方案2 | |||||
| Helmert | LS-VCE | LSV-ECM | Helmert | LS-VCE | LSV-ECM | ||
 |
3.64, 5.92 | 3.64, 5.92 | 3.64, 5.92 | 0.79, 3.07 | 0.79, 3.07 | 0.79, 3.07 | |
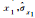 |
-1.56, 0.98 | -1.56, 0.98 | -1.56, 0.98 | -2.90, 0.53 | -2.90, 0.53 | -2.90, 0.53 | |

|
0.89.1.03 | 0.89.1.03 | 0.89.1.03 | 0.09, 0.55 | 0.09, 0.55 | 0.09, 0.55 | |
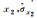
|
5.64, 1.64 | 5.64, 1.64 | 5.64, 1.64 | 3.48, 1.20 | 3.48, 1.20 | 3.48, 1.20 | |
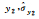
|
-12.38, 1.86 | -12.38, 1.86 | -12.38, 1.86 | -17.80, 1.28 | -17.80, 1.28 | -17.80, 1.28 | |
| Tratio | 1 | 96% | 65% | 1 | 97% | 71% | |
从方案1方差分量和待估参数的估计结果看,3种结果完全相同,表明3种方法均能获得一致的估计结果。同时比较3种方法的计算效率,通用Helmert法和LS-VCE的计算效率处于同一水平,本文所提出的LSV-ECM法的计算效率最高,其计算时间约为通用Helmert法的65%,较通用Helmert法和LS-VCE法均有明显提升,从而验证本文方法的有效性。
方案2中同样可以验证本文所提方法的正确性和有效性,不再赘述。同时,方案2在剔除两个粗差观测值以后,两类观测值的单位权方差、参数的估计精度均有较大提升,表明3种方差分量估计方法都无法抑制粗差影响,必须引入质量控制方法进行粗差识别与剔除。
2.2 GNSS站坐标时序建模为进一步检验本文LSV-ECM法的正确性和高效性,选用中国大陆构造环境监测网络(crustal movement observation network of China,CMONOC)中16个长期线性趋势稳定的GNSS基准站2005.0014(DOY)~2015.0014(DOY)共10年的原始坐标时间序列进行噪声特性分析(方差-协方差分量估计)和三维运动速度估计(平差参数计算),测站位置分布如图 1所示。

|
| 图 1 CMONOC所选测站分布 Fig. 1 Geographical distribution of selected stations in the CMONOC network |
GNSS站坐标时序的观测方程和随机模型分别为[11]
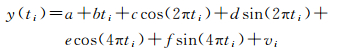 (17)
(17)
 (18)
(18)
式中,ti是以年为单位的时间序列历元点;a为常数项;b为线性速度项;c、d组合表示全年性周期运动;e、f组合表示半年性周期运动;vi为残差;σWN、σFN为所求的噪声分量大小;Q WN、Q FN分别为白噪声和闪烁噪声的协因数阵,具体形式见文献[11]。
基于上述间接平差模型,分别利用通用Helmert法[7]、LS-VCE法[9, 11]和本文LSV-ECM法进行方差分量估计和参数平差计算,并统计北(N)、东(E)、竖直(U)3个方向的噪声分量
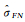
| mm | |||||||||||
| 站点 | N | E | U | ||||||||
| Helmert | LS-VCE | LSV-ECM | Helmert | LS-VCE | LSV-ECM | Helmert | LS-VCE | LSV-ECM | |||
| WN, FN | WN, FN | WN, FN | WN, FN | WN, FN | WN, FN | WN, FN | WN, FN | WN, FN | |||
| ZHZC | 0.80, 2.11 | 0.80, 2.11 | 0.80, 2.11 | 0.78, 2.98 | 0.78, 2.98 | 0.78, 2.98 | 3.43, 9.73 | 3.43, 9.73 | 3.43, 9.73 | ||
| YANC | 0.52, 1.67 | 0.52, 1.67 | 0.52, 1.67 | 0.45, 1.87 | 0.45, 1.87 | 0.45, 1.87 | 2.10, 6.73 | 2.10, 6.73 | 2.10, 6.73 | ||
| XIAM | 0.79, 3.57 | 0.79, 3.57 | 0.79, 3.57 | 0.93, 3.19 | 0.93, 3.19 | 0.93, 3.19 | 3.78, 13.13 | 3.78, 13.13 | 3.78, 13.13 | ||
| WUHN | 0.76, 3.23 | 0.76, 3.23 | 0.76, 3.23 | 0.77, 3.03 | 0.77, 3.03 | 0.77, 3.03 | 3.01, 13.03 | 3.01, 13.03 | 3.01, 13.03 | ||
| TAIN | 0.96, 2.31 | 0.96, 2.31 | 0.96, 2.31 | 0.92, 3.10 | 0.92, 3.10 | 0.92, 3.10 | 3.18, 8.77 | 3.18, 8.77 | 3.18, 8.77 | ||
| QION | 0.98, 5.20 | 0.98, 5.20 | 0.98, 5.20 | 1.27, 4.63 | 1.27, 4.63 | 1.27, 4.63 | 4.7, 15.01 | 4.7, 15.01 | 4.7, 15.01 | ||
| LUZH | 0.68, 2.19 | 0.68, 2.19 | 0.68, 2.19 | 0.62, 2.63 | 0.62, 2.63 | 0.62, 2.63 | 2.73, 12.19 | 2.73, 12.19 | 2.73, 12.19 | ||
| KMIN | 0.67, 3.73 | 0.67, 3.73 | 0.67, 3.73 | 0.65, 4.94 | 0.65, 4.94 | 0.65, 4.94 | 3.29, 14.57 | 3.29, 14.57 | 3.29, 14.57 | ||
| JIXN | 0.58, 2.52 | 0.58, 2.52 | 0.58, 2.52 | 0.61, 1.98 | 0.61, 1.98 | 0.61, 1.98 | 2.37, 6.75 | 2.37, 6.75 | 2.37, 6.75 | ||
| HRBN | 0.61, 3.15 | 0.61, 3.15 | 0.61, 3.15 | 0.33, 3.45 | 0.33, 3.45 | 0.33, 3.45 | 1.50, 11.83 | 1.50, 11.83 | 1.50, 11.83 | ||
| HLAR | 0.75, 2.97 | 0.75, 2.97 | 0.75, 2.97 | 0.70, 2.65 | 0.70, 2.65 | 0.70, 2.65 | 2.32, 11.50 | 2.32, 11.50 | 2.32, 11.50 | ||
| GUAN | 1.07, 3.41 | 1.07, 3.41 | 1.07, 3.41 | 1.21, 5.08 | 1.21, 5.08 | 1.21, 5.08 | 5.23, 16.22 | 5.23, 16.22 | 5.23, 16.22 | ||
| DLHA | 0.41, 2.50 | 0.41, 2.50 | 0.41, 2.50 | 0.51, 2.31 | 0.51, 2.31 | 0.51, 2.31 | 1.51, 10.49 | 1.51, 10.49 | 1.51, 10.49 | ||
| CHUN | 0.55, 3.09 | 0.55, 3.09 | 0.55, 3.09 | 0.44, 3.05 | 0.44, 3.05 | 0.44, 3.05 | 1.92, 13.27 | 1.92, 13.27 | 1.92, 13.27 | ||
| BJSH | 0.76, 1.99 | 0.76, 1.99 | 0.76, 1.99 | 0.76, 1.35 | 0.76, 1.35 | 0.76, 1.35 | 2.81, 7.45 | 2.81, 7.45 | 2.81, 7.45 | ||
| BJFS | 0.61, 3.49 | 0.61, 3.49 | 0.61, 3.49 | 0.62, 2.19 | 0.62, 2.19 | 0.62, 2.19 | 2.73, 7.31 | 2.73, 7.31 | 2.73, 7.31 | ||
| Tratio(WN) | 1 | 99.5% | 74.0% | 1 | 99.8% | 73.8% | 1 | 99.9% | 72.1% | ||
| Tratio(FN) | 1 | 99.5% | 74.0% | 1 | 99.8% | 73.8% | 1 | 99.9% | 72.1% | ||
| 注:高斯白噪声(WN)的单位为mm;闪烁噪声(FN)的单位为mm/a0.25 | |||||||||||
对比表 4中通用Helmert法、LS-VCE法和LSV-ECM法的计算结果可知,3种方法所得的噪声分量结果完全相同,验证了本文方法的正确性。同时,对比3种方法的计算效率可知,通用Helmert法与LS-VCE法基本一致,而本文LSV-ECM法有较大提高,三维方向计算时间比分别为通用Helmert法的74.0%、73.8%、72.1%,表明本文方法的高效性。
由表 4噪声分量的估计结果可知,白噪声分量均远小于闪烁噪声分量,表明有色噪声为中国区域GNSS站坐标时间序列的主要噪声,在参数估计时若直接采用白噪声模型会导致估计结果有偏,并会产生较高的虚假估计精度。另外,对比不同方向的噪声分量估计结果,北方向和东方向的噪声分量相差不大,且量级较小,94%和88%的测站白噪声分量在1 mm以内,50%的测站闪烁噪声分量在3 mm/a0.25以内,而竖直方向的噪声分量远高于水平方向,这与现有结论相一致,约有56%的测站白噪声分量在3 mm以内,31%的测站闪烁噪声分量在9 mm/a0.25以内。
为进一步分析噪声大小与经纬度之间的关系,绘制了白噪声分量和闪烁噪声分量随经纬度的变化情况。由于噪声大小与纬度相关性较强、与经度相关性较弱,为节省篇幅,此处仅讨论噪声大小与纬度变化的关系,见图 2。从图 2可以看出,水平方向的白噪声和闪烁噪声分量大小较为平稳,竖直方向的噪声大小波动较大。从整体趋势上看,白噪声和闪烁噪声大小随纬度变化的趋势较为明显。具体表现为:噪声大小随纬度增加而逐渐减小,减少过程中有轻微波动,且在中纬度地区有翘尾现象。该现象原因分析可能是GNSS的GDOP值随纬度增大而降低[28],从而使噪声分量表现出随纬度增加而减小的现象,而且噪声分量在中纬度地区呈现一定的翘尾现象。

|
| 图 2 噪声分量大小与纬度的关系 Fig. 2 The relationship between noise components and latitude |
此外,为检验方差-协方差分量估计结果的正确性和有效性,以CMONOC的公布数据(http://www.cgps.ac.cn/cgs/index.action)作为对比参考值,表 5统计了中国区域GNSS站的三维运动速度和不确定度。由该表可知,中国区域不同站点水平方向均呈现东南方向运动趋势,这与亚欧板块的整体运动趋势相一致,但竖直方向运动变化差异性较大,其中约40%的测站呈现下沉趋势。对比本文结果与CMONOC的公布结果,除JIXN、HLAR站N方向,KMIN、GUAN站E方向,CHUN、BJFS站U方向以外,其余计算结果均在2倍中误差范围内。此外,参照文献[29]的计算结果,对比发现除CHUN站U方向外,其余测站的计算结果与本文结果具有较好的相符性,进一步验证了本文方法的正确性。需要指出的是,CHUN站U方向的差异性可能是数据预处理和共模误差提取策略不同所致。
| mm/a | ||||||||
| 站点 | N | E | U | |||||
| 本文方法 | CMONOC | 本文方法 | CMONOC | 本文方法 | CMONOC | |||
| ZHNZ | -11.35±0.07 | -11.18±0.15 | 32.90±0.11 | 33.17±0.23 | 1.21±0.31 | 1.24±0.38 | ||
| YANC | -9.30±0.05 | -8.69±0.14 | 32.57±0.10 | 32.46±0.05 | 1.06±0.22 | 1.02±0.13 | ||
| XIAM | -12.16±0.11 | -12.48±0.17 | 32.47±0.06 | 32.82±0.17 | 1.4±0.42 | 0.78±0.36 | ||
| WUHN | -10.93±0.10 | -11.08±-0.12 | 32.50±0.11 | 33.60±0.74 | -0.79±0.42 | 0.47±0.41 | ||
| TAIN | -11.54±0.07 | -11.58±0.37 | 30.98±0.10 | 31.38±0.16 | 0.92±0.28 | 1.21±0.30 | ||
| QION | -11.98±0.17 | -10.24±0.78 | 31.57±0.10 | 31.94±0.15 | -0.6±0.48 | -0.46±0.32 | ||
| LUZH | -9.75±0.070 | -9.61±0.13 | 34.96±0.15 | 35.76±0.28 | 0.46±0.39 | 0.35±0.30 | ||
| KMIN | -17.23±0.12 | -16.18±0.87 | 33.09±0.08 | 31.13±0.53 | -1.23±0.47 | -0.48±0.31 | ||
| JIXN | -9.72±0.08 | -10.35±0.06 | 29.13±0.16 | 28.66±0.11 | 1.79±0.22 | 1.53±0.17 | ||
| HRBN | -12.56±0.10 | -12.38±-0.21 | 25.79±0.06 | 25.95±0.51 | -0.49±0.38 | -0.09±0.21 | ||
| HLAR | -10.51±0.09 | -11.35±0.04 | 25.76±0.11 | 25.88±0.07 | 2.05±0.37 | 1.44±0.16 | ||
| GUAN | -11.11±0.11 | -11.23±0.10 | 31.30±0.10 | 33.11±0.19 | -0.33±0.52 | -1.97±0.46 | ||
| CHUN | -11.58±0.10 | -12.21±0.14 | 27.37±0.07 | 26.53±0.52 | -1.81±0.42 | -0.15±0.29 | ||
| BJSH | -11.45±0.06 | -11.28±0.18 | 30.10±0.10 | 29.94±0.13 | 1.36±0.24 | 1.05±0.29 | ||
| BJFS | -9.94±0.11 | -10.18±0.14 | 30.58±0.04 | 30.10±0.19 | 2.63±0.24 | -0.11±0.63 | ||
3 结论
本文基于等价条件平差模型和最小二乘准则,利用等价条件闭合差的二次型构建方差-协方差分量估计方程,并通过矩阵半拉直算子将其变换为线性Gauss-Markov形式,进而顾及矩阵拉直算子、半拉直算子和Kronecker积运算性质,导出了基于等价条件平差模型的方差-协方差分量最小二乘估计公式,简称LSV-ECM法。该方法实现了平差值求解(残差为平差结果之一)与随机模型估计的分离,有效兼顾了等价条件闭合差(已知)和最小二乘的特性。边角网平差实例的结果表明,本文的LSV-ECM法与通用Helmert法、LS-VCE法的结果完全相同,但计算效率更高,验证了该方法与残差型VCE方法的等价性和计算高效性。
分析指出了方差-协方差分量估计方法相较于常规GNSS-MLE法进行GNSS站坐标时间序列噪声分析的优势,并利用LSV-ECM法、通用Helmert法、LS-VCE法计算分析了中国区域16个GNSS站坐标时间序列在WN+FN模型下的噪声估计和站点速度。估计结果表明,有色噪声是中国GNSS站坐标时序的主要噪声,且白噪声和有色噪声分量随纬度增大而减小,速度估计结果与陆态网络的公布结果基本一致,水平方向的整体运动趋势呈东南方向,而竖直方向的运动趋势差异性较大。因此,计算结果也进一步验证了本文LSV-ECM法的正确性和高效性。
| [1] |
崔希璋, 於宗俦, 陶本藻, 等.
广义测量平差[M]. 2版. 武汉: 武汉大学出版社, 2009.
CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized surveying adjustment[M]. 2nd ed. Wuhan: Wuhan University Publishing House, 2009. |
| [2] | KOCH K R. Parameter estimation and hypothesis testing in linear models[M]. Berlin: Springer-Verlag, 1999. |
| [3] |
王志忠, 朱建军.
非线性模型中方差和协方差分量的估计[J]. 测绘学报, 2005, 34(4): 288–293.
WANG Zhizhong, ZHU Jianjun. Estimation of variance and covariance components in the nonlinear model[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(4): 288–293. DOI:10.3321/j.issn:1001-1595.2005.04.002 |
| [4] | XU Peiliang. The effect of incorrect weights on estimating the variance of unit weight[J]. Studia Geophysica et Geodaetica, 2013, 57(3): 339–352. DOI:10.1007/s11200-012-0665-x |
| [5] |
独知行, 欧吉坤, 靳奉祥, 等.
联合反演模型中相对权比的优化反演[J]. 测绘学报, 2003, 32(1): 15–19.
DU Zhixing, OU Jikun, JIN Fengxiang, et al. Optimization inversion of the relative weight ratio λ in the joint inversion models[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 15–19. DOI:10.3321/j.issn:1001-1595.2003.01.004 |
| [6] | XU Peiliang, LIU Yumei, SHEN Yunzhong, et al. Estimability analysis of variance and covariance components[J]. Journal of Geodesy, 2007, 81(9): 593–602. DOI:10.1007/s00190-006-0122-0 |
| [7] |
於宗俦.
Helmert型方差—协方差分量估计的通用公式[J]. 武汉测绘科技大学学报, 1991, 16(2): 8–17.
YU Zongchou. Thegoneral formulas of Helmerttype for estimating variance and covariance components[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1991, 16(2): 8–17. |
| [8] |
王乐洋, 温贵森.
Partial EIV模型的非负最小二乘方差分量估计[J]. 测绘学报, 2017, 46(7): 857–865.
WANG Leyang, WEN Guisen. Non-negative least squares variance component estimation of Partial EIV model[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 857–865. DOI:10.11947/j.AGCS.2017.20160501 |
| [9] | TEUNISSEN P J G, AMIRI-SIMKOOEI A R. Least-squares variance component estimation[J]. Journal of Geodesy, 2008, 82(2): 65–82. DOI:10.1007/s00190-007-0157-x |
| [10] |
赵俊, 郭建锋.
方差分量估计的通用公式[J]. 武汉大学学报(信息科学版), 2013, 38(5): 580–583, 588.
ZHAO Jun, GUO Jianfeng. Auniversal formula of variance component estimation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 580–583, 588. |
| [11] | AMIRI-SIMKOOEI A R, TIBERIUS C C J M, TEUNISSEN P J G. Assessment of noise in GPS coordinate time series: methodology and results[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B7): B07413. DOI:10.1029/2006JB004913 |
| [12] | RAO C R. Estimation of variance and covariance components —MINQUE theory[J]. Journal of Multivariate Analysis, 1971, 1(3): 257–275. DOI:10.1016/0047-259X(71)90001-7 |
| [13] | CROCETTO N, GATTI M, RUSSO P. Simplified formulae for the BIQUE estimation of variance components in disjunctive observation groups[J]. Journal of Geodesy, 2000, 74(6): 447–457. DOI:10.1007/s001900000109 |
| [14] | YUZ C. A universal formula of maximum likelihood estimation of variance-covariance components[J]. Journal of Geodesy, 1996, 70(4): 233–240. DOI:10.1007/BF00873704 |
| [15] |
李博峰, 沈云中, 楼立志.
基于等效残差的方差-协方差分量估计[J]. 测绘学报, 2010, 39(4): 349–354, 363.
LI Bofeng, SHEN Yunzhong, LOU Lizhi. Variance-covariance component estimation based on the equivalent residuals[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 349–354, 363. |
| [16] |
李博峰, 沈云中.
基于等效残差积探测粗差的方差-协方差分量估计[J]. 测绘学报, 2011, 40(1): 10–14, 32.
LI Bofeng, SHEN Yunzhong. Equivalent residual product based outlier detection for variance and covariance component estimation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 10–14, 32. |
| [17] |
刘志平.
等价条件闭合差的方差-协方差分量估计解析法[J]. 测绘学报, 2013, 42(5): 648–653.
LIU Zhiping. Analytical method for VCE using equivalent condition misclosure[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 648–653. |
| [18] |
刘志平, 张书毕.
方差-协方差分量估计的概括平差因子法[J]. 武汉大学学报(信息科学版), 2013, 38(8): 925–929.
LIU Zhiping, ZHANG Shubi. Variance-covariance component estimation method based on generalization adjustment factor[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 925–929. |
| [19] | PENG Junhuan, SHI Yun, LI Shuhui, et al. MINQUE of Variance-covariance components in linear Gauss-Markov models[J]. Journal of Surveying Engineering, 2011, 137(4): 129–139. DOI:10.1061/(ASCE)SU.1943-5428.0000050 |
| [20] |
杨恒山.
边角网平差中方差分量估计改进算法[J]. 测绘通报, 2008(3): 5–7.
YANG Hengshan. An improved algorithm of variance component estimate in side-angular network adjustment[J]. Bulletin of Surveying and Mapping, 2008(3): 5–7. |
| [21] | SHU Yuanming, FANG Rongxin, LIU Jingnan. Stochastic models of very high-rate (50 Hz) GPS/BeiDou code and phase observations[J]. Remote Sensing, 2017, 9(11): 1188. DOI:10.3390/rs9111188 |
| [22] | LI Bofeng. Stochastic modeling of triple-frequency BeiDou signals: estimation, assessment and impact analysis[J]. Journal of Geodesy, 2016, 90(7): 593–610. DOI:10.1007/s00190-016-0896-7 |
| [23] | AMIRI-SIMKOOEI A R. Parameter estimation in3D affine and similarity transformation: implementation of variance component estimation[J]. Journal of Geodesy, 2018, 92(11): 1285–1297. DOI:10.1007/s00190-018-1119-1 |
| [24] | WANG Leyang, XU Guangyu. Variance component estimation for partial errors-in-variables models[J]. Studia Geophysica et Geodaetica, 2016, 60(1): 35–55. DOI:10.1007/s11200-014-0975-2 |
| [25] | AMIRI-SIMKOOEI A R. Non-negative least-squares variance component estimation with application to GPS time series[J]. Journal of Geodesy, 2016, 90(5): 451–466. DOI:10.1007/s00190-016-0886-9 |
| [26] | ZANGENEH-NEJAD F, AMIRI-SIMKOOEI A R, SHARIFIMA, et al. Recursive least squares with real time stochastic modeling: application to GPS relative positioning[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XLⅡ-4/W4. Tehran, Iran: ISPRS, 2017: 531-536. |
| [27] | RAZ R. On the complexity of matrix product[J]. SIAM Journal on Computing, 2002, 32(5): 1356–1369. |
| [28] |
丁朋辉, 程鹏飞, 蔡艳辉.
GPS/GALILEO组合系统可见卫星与GDOP的区域和时序分析[J]. 测绘科学, 2008, 33(6): 5–8.
DING Penghui, CHENG Pengfei, CAI Yanhui. The regional and sequential analysis of visible satellite and GDOP value for GPS/Galileo combination system[J]. Science of Surveying and Mapping, 2008, 33(6): 5–8. DOI:10.3771/j.issn.1009-2307.2008.06.001 |
| [29] |
田云锋, 沈正康, 李鹏.
连续GPS观测中的相关噪声分析[J]. 地震学报, 2010, 32(6): 696–704.
TIAN Yunfeng, SHEN Zhengkang, LI Peng. Analysis oncorrelated noise in continuous GPS observations[J]. Acta Seismologica Sinica, 2010, 32(6): 696–704. |


