2. 西安石油大学计算机学院, 陕西 西安 710065
2. School of Computer Science, Xi'an Shiyou University, Xi'an 710065, China
现有的端元提取算法大多只是利用高光谱影像的光谱信息,把高光谱数据当作空间无序的光谱矢量来处理,对图像的空间信息利用不足。实际上,地物在图像空间上的分布是有规律的,是具有一定的几何形状的,充分利用图像的空间信息有益于提高端元提取的效率和精度[1-4]。文献[5]提出的自动形态学端元提取(automated morphological endmember extraction,AMEE)算法同时利用了图像的光谱信息和空间信息,在试验中取得了不错的效果。
数学形态学的两个基本操作是膨胀和腐蚀,灰度图像的膨胀和腐蚀操作是在结构元素内寻找像元的灰度最大值和最小值来取代目标像元的灰度值[6]。而高光谱图像是一个数据立方体,采用寻找灰度最大值和最小值进行膨胀和腐蚀操作显然是不合理的。AMEE算法对高光谱图像的膨胀和腐蚀操作进行了拓展性定义,高光谱图像的膨胀和腐蚀不再是寻找像元的灰度最大值和最小值,而是寻找结构元素内的最纯像元和混合度最大像元。AMEE算法通过计算和比较结构元素内像元之间或者像元与凸面单形体中心之间的光谱角距离来定量化衡量像元的相对纯度,它将最纯像元与混合程度最大像元的光谱角距离定义为离心率指数(morphological eccentricity index,MEI),并赋值给结构元素内的最纯像元,扩大结构元素并不断迭代更新,最后得到一幅MEI图像,根据MEI值由高到低在像元中选取端元。
然而AMEE算法也存在一些缺陷。首先,AMEE算法将结构元素内所有像元的均值光谱作为混合程度最大的像元,这在结构元素内混合像元占大多数时是合理的,但结构元素内的纯净像元较多时,像元的均值光谱将更接近纯像元,此时距离均值光谱较远的是混合程度较大的像元,而不是纯像元,此时的膨胀和腐蚀操作就是不正确的。其次,AMEE算法将结构元素内最纯像元与混合程度最大像元之间的光谱角距离定义为MEI来表示像元纯度,但不同结构元素内混合程度最大的像元也是不一样的,因此计算MEI值时的参考标准是不同的,MEI值的大小也就无法真实有效地表示像元的纯度[7]。
另外,从现有的纯像元指数(pure pixel index,PPI)端元提取算法的角度来看,PPI算法将特征空间中所有的样本点在随机生成的直线上进行投影,然后统计每个像元投影落在直线两端的次数来选取端元[8-11]。这种方法只是把高光谱图像看成是无序光谱向量的集合,仅仅利用了图像的光谱信息,而忽略了图像中地物分布的空间结构信息。
受AMEE算法启发,如果能在结构元素内运用PPI算法寻找最纯净像元,并给像元赋值相应的纯净指数,拓展定义形态学中的膨胀操作和腐蚀操作对整幅图像进行处理,扩大结构元素不断迭代运算并累计更新像元的PPI值,最终可得到一幅PPI值图像,那么端元就可以在PPI累计值较大的像元中选取。这种方法可以弥补上述AMEE算法存在的不足,改善AMEE算法的性能。
1 现有的AMEE算法与PPI算法 1.1 AMEE算法AMEE算法将传统数学形态学理论进行了拓展性定义,给出了高光谱图像的形态学膨胀和腐蚀操作方法。AMEE算法中定义了两种腐蚀和膨胀操作[5]。
(1) 将结构元素内某像元到其他像元的距离累计之和作为纯度指标。结构元素K内某个像元f(x, y)到其他像元的距离累计之和用式(1)表示
 (1)
(1)
此时,膨胀和腐蚀操作的拓展定义如下
 (2)
(2)
 (3)
(3)
式中,d(x, y)、e(x, y)是结构元素K内的像元,d(x, y)与K内其他像元的距离累计之和最大,是K中最纯的像元;e(x, y)与K内其他像元的距离累计之和最小,是K中混合度最大的像元。
(2) 将结构元素内像元到结构元素中心的距离作为纯度指标。假设结构元素K像元数量为M,那么K的中心可定义为
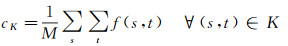 (4)
(4)
结构元素K内像元f(x, y)到K的中心的距离可表示为
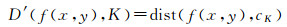 (5)
(5)
此时膨胀和腐蚀操作可分别拓展定义为
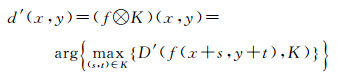 (6)
(6)
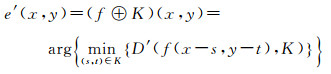 (7)
(7)
式中,d′(x, y)是距离K的中心最远的像元,即相对最纯的像元;e′(x, y)是距离K的中心最近的像元,即混合度最大的像元。
AMEE算法将d(x, y)与e(x, y)之间的光谱夹角距离定义为MEI,MEI用来定量表示像元的相对纯度,并赋值给结构元素中最纯的像元,计算公式如式(8)所示
 (8)
(8)
AMEE算法可以描述如下:从最小结构元素Kmin开始,在整幅影像中移动,每移动一次,都会在结构元素内找到一个最纯净像元和一个混合度最大的像元,计算MEI值并将其赋给最纯净像元。然后逐渐增大结构元素的尺寸,并重复执行上述操作,达到预设的最大迭代次数Imax后终止,最终获得一幅MEI图像,参考MEI的值由高到低选取端元。
1.2 PPI算法PPI算法的思想是基于凸面几何学理论。凸面几何学理论认为高光谱影像的所有像元在高维光谱特征空间中对应的样本点呈散点图分布,所有样本点包含在一个凸面单形体内部,那些纯净像元(端元)位于凸面单形体的顶点处[12-17]。
凸面单形体的特点决定了位于单形体顶点的样本点在特征空间中任意直线上的投影必直线的两端。以二维空间为例,如图 1所示,端元e1、e2、e3位于三角形的顶点,混合像元是由端元混合而成,都位于三角形的内部。在这个二维空间中随机生成一条直线,将所有样本点投影到直线上,三角形的顶点必将投影到线段的两端,三角形内部的点会投影到线段的内部[18]。

|
| 图 1 PPI算法中像元投影原理 Fig. 1 Schematic diagram of pixel projection principle in PPI algorithm |
在特征空间中生成大量的随机直线进行投影,统计每个像元落在线段两个端点的次数作为像元纯净指数,用来定量表示该像元的纯净度。显然,某个像元对应的像元纯净指数越大,它是纯像元的可能性就越高[19-22]。
PPI算法虽然原理比较简单直观,但有PPI算法没有利用图像的空间信息,需要利用可视化工具手动选择端元,自动化程度不高,而且投影直线都是随机生成的,导致每次算法运行所提取的端元并不一定相同。
2 PPI-AMEE算法膨胀和腐蚀操作的目的是找出结构元素内最纯像元和混合度最大的像元。AMEE算法通过计算结构元素内的最纯像元与混合度最大像元之间的光谱角距离作为MEI表示像元的纯度。而PPI算法利用端元位于凸面单形体顶点的特性,将所有样本点投影到在特征空间中随机生成的直线上,统计样本点投影在直线两端的次数作为纯像元指数来表示像元的纯度。鉴于此,如果在结构元素内部用PPI代替MEI来寻找最纯净像元和混合程度最严重的像元,进而拓展性地定义形态学中的膨胀和腐蚀操作,也能达到同样甚至更优的端元提取效果。本文结合PPI算法和AMEE算法提出一种PPI-AMEE端元提取方法。
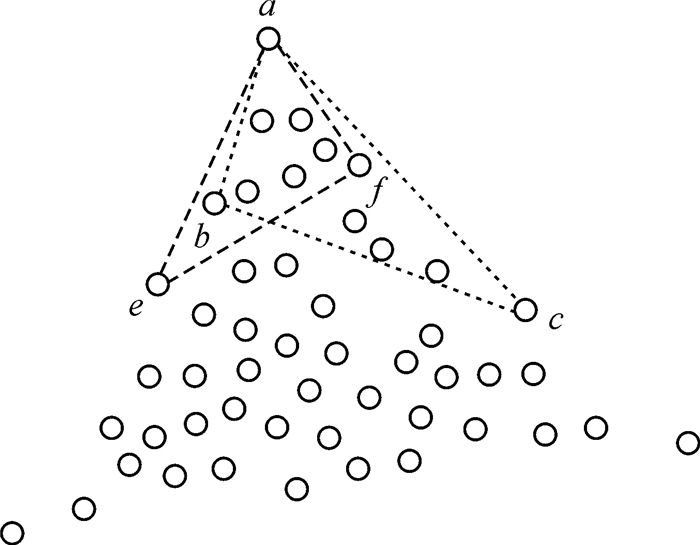
以二维空间为例,图 2所示为像元在特征空间中的点云分布,结构元素覆盖范围内的像元只是其中的一小部分。图 2中三角形框abc和aef分别代表不同的结构元素所覆盖的像元。根据AMEE方法,需要在结构元素范围内寻找距离中心最远的像元作为最纯像元,然而观察三角形框abc和aef,距离中心最远的像元分别是伪端元c和e,并不是实际的端元a,因此AMEE方法在局部范围内膨胀所得的最纯像元可能并不准确。
|
| 图 2 不同结构元素覆盖像元的空间分布 Fig. 2 Spatial distribution of pixels covered by different structural elements |
如果在结果元素范围内采用PPI算法寻找最纯像元,三角形框abc和aef的3个顶点均能被投影到随机生成的直线的两端,但每个顶点投影到直线两端的次数并不相同,真实端元a投影到直线两端的次数不一定是最多。但如果在图像上移动结构元素,比如从三角形框abc变化到三角形框aef,原来的顶点b、c变为了e、f,也就是说随着结构元素的变化,伪端元也是变化的,但真实端元a却依旧能够投影到线段两端。也就说只要结构元素内存在真实的纯像元,就一定能被PPI算法投影到直线的两端,而伪端元则随着结构元素的改变可能不会再次被PPI算法找到。
如果对结构元素内的像元采用PPI算法,记录每个像元的纯度指数,那么随着结果元素的增大和改变,伪纯像元的纯度指数不会累计增大,而实际纯像元的纯度指数则不断累计增大。因此,可以利用PPI指数代替AMEE算法中的MEI指数来对形态学中的膨胀和腐蚀操作重新进行拓展定义。
膨胀操作:将结构元素覆盖范围内的像元在随机生成的直线上投影,统计每个像元落在线段两端的次数,次数最多者被认为纯度最高,并把这个次数作为纯度指标赋给对应的像元。
腐蚀操作:统计每次投影距离线段中点最近的像元,并记录次数,次数最多者被认为混合程度最严重。
本文提出的方法不需要进行腐蚀操作,只需要进行膨胀操作。记录结构元素内每一个像元投影到直线两端的次数,并赋值给对应像元作为纯度指数。如前所述,随着结构元素的增大和变化,只有真实的纯像元的PPI值在不断累计增大,伪端元的PPI值不会持续增大,最终形成一幅类似于AMEE方法中的MEI图像的PPI图像,端元就从具有较大PPI值的像元中选取。
传统的PPI算法需要随机性地生成投影直线,算法执行过程中需要用户主观介入观察,具体生成多少投影向量,需要由用户主观设定,没有统一的标准。本文提出的PPI-AMEE算法只在结构元素内部运行PPI算法,将结构元素的像元在特征空间中两两连线生成投影向量,这样使得投影向量尽可能地分布在不同方向上,而不会像传统PPI算法那样在对整幅图像的所有像元投影时,由于生成的投影向量是完全随机的,有可能使得生成的投影向量主要集中在某些特定方向上,而使得最终结果并不准确。而且由于结构元素所包含的像元数量是确定的,因此两两连线生成投影向量的数量是确定的,而且随着结构元素的扩大,像元数目增多,生成的投影向量也相应地自动增多。这样以来,算法运行过程中不再需要用户主观设定投影向量的数目,在一定程度上提高了算法的自动程度。
在结构元素内运行PPI算法时,首先生成投影向量βk,假设结构元素内有n个像元,当结构元素内的像元两两连线生成投影向量时,根据排列组合的数学知识,一共可以生成n(n-1)/2个投影向量。计算结构元素的像元在向量βk上的投影F′k=βkFk,找到F′k中最大值和最小值的位置imax=argmax(F′k),imax=argmin(F′k), 并不断累计更新对应像元纯度指数pimax=pimax+1,pimin=pimin+1。
这里定义结构元素K内某个像元f(x, y)投影后所得PPI值的累计之和为
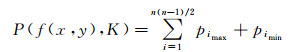 (9)
(9)
相应的膨胀和腐蚀操作可以分别拓展性地定义为
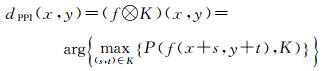 (10)
(10)
 (11)
(11)
PPI-AMEE算法的具体步骤如下:
(1) 先对整幅图像进行最小噪声分离变换(minimum noise fraction,MNF)变换进行降维和去噪处理,估算端元数目m;
(2) 设定结构元素的最小尺寸Kmin和最大尺寸Kmax,得出最大迭代次数Imax;
(3) 令i=1,所有像元的PPI初值P(f(x, y), K)=0,从最小结构元素Kmin开始执行;
(4) 按照PPI算法拓展定义的形态学结构算子进行膨胀操作,得到结构元素内各像元的纯度指数;
(5) i=i+1,如果i=Imax,顺序执行步骤(6),否则增大结构元素K,跳回步骤(4)执行;
(6) 输出PPI图像,参考PPI值较大的m个像元确定为端元。
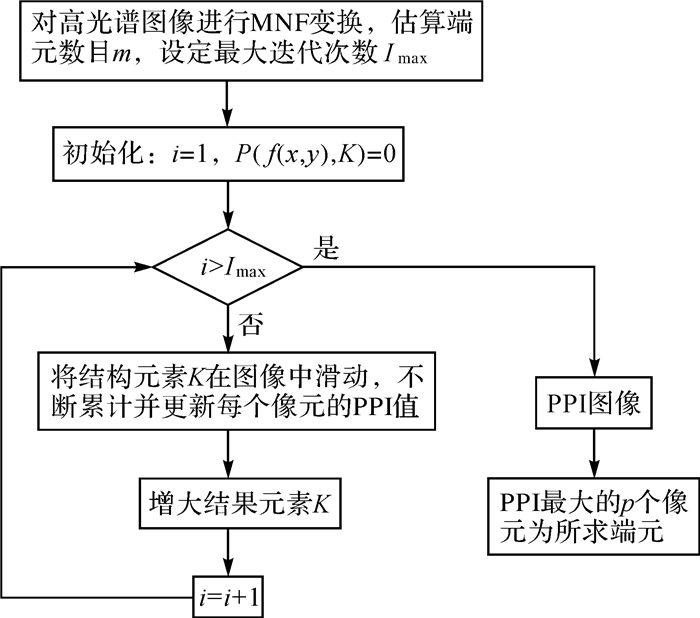
算法的流程如图 3所示。
|
| 图 3 PPI-AMEE算法流程 Fig. 3 Flow chart of PPI-AMEE algorithm |
3 试验结果与分析
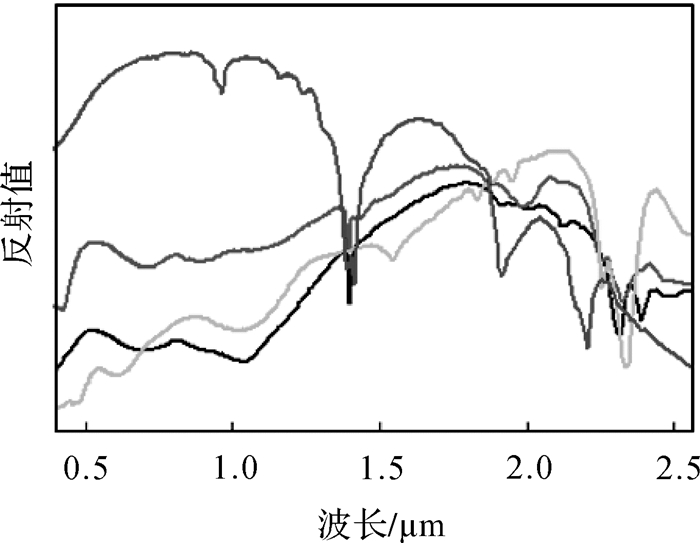
首先采用模拟数据比较PPI、AMEE、PPI-AMEE这3种算法的性能,选取美国地质勘探局(United States Geological Survey,USGS)光谱库中的4种矿物光谱,如图 4所示,按照Dirichlet分布生成一个随机数字序列来构造混合像元的丰度矩阵,生成大小为200×200的模拟图像,并在模拟图像中分别添加信噪比(SNR)分别为10 db、20 db、30 db、40 db、50 db的高斯噪声。表 1给对比分析了不同信噪比情况下,PPI、AMEE、PPI-AMEE所提取的4个端元与USGS光谱库中对应光谱之间的光谱角距离(spectral angle distance, SAD)的均值、光谱信息散度(spectral information divergence, SID)的均值。
|
| 图 4 构建模拟数据的4种光谱 Fig. 4 Four spectra of simulated data |
| SNB/db | PPI | AMEE | PPI-AMEE | |||||||
| SAD/rad | SID/bit | SAD/rad | SID/bit | 时间/s | SAD/rad | SID/bit | 时间/s | |||
| 10 | 0.158 | 0.052 | 0.149 | 0.050 | 65.26 | 0.142 | 0.048 | 72.53 | ||
| 20 | 0.113 | 0.041 | 0.132 | 0.047 | 64.83 | 0.126 | 0.043 | 66.78 | ||
| 30 | 0.107 | 0.037 | 0.127 | 0.042 | 61.62 | 0.109 | 0.038 | 55.96 | ||
| 40 | 0.102 | 0.035 | 0.102 | 0.033 | 60.59 | 0.093 | 0.030 | 52.67 | ||
| 50 | 0.092 | 0.028 | 0.096 | 0.031 | 59.93 | 0.086 | 0.026 | 51.98 | ||
本文的PPI算法进行了1000次随机投影,由于PPI算法运行时间与随机投影的次数有关,投影次数越多,运行时间越长,因此比较PPI算法与其他算法的运行效率不具有意义。试验中,AMEE算法和PPI-AMEE算法迭代时,设置它们的最小结构元素和最大结构元素均为3×3和15×15,比较它们不同信噪比情况下的运行时间,试验结果见表 1。
表 1显示,随着信噪比的提高,3种算法所提取的4个端元与USGS光谱库对应光谱之间的光谱角距离均值、光谱信息散度均值逐渐变小,也就是说端元提取精度逐渐变高。从算法运行时间来看,在信噪比较低时PPI-AMEE的运行效率比AMEE稍低,但随着信噪比的提高PPI-AMEE的运行效率逐渐优于AMEE。
真实高光谱数据试验中采用的是美国内华达州Cuprite地区的AVIRIS高光谱数据,该地区有详细的地物调查报告,是检验各种分类算法和混合像元分解算法的典型数据[23-25]。该数据包含224个波段,波长范围为400~2500 nm,去除其中受水蒸气影响较大和信噪比较低的波段,剩余188个波段。选择15、69、157波段作为红、绿、蓝通道合成假彩色图像,如图 5所示。

|
| 图 5 Cuprite地区的AVIRIS数据假彩色合成图 Fig. 5 False-color composition image of AVIRIS data in Cuprite region |
利用Hysime算法[26]估计端元的数目为9。这里重点研究对比4种矿物:明矾石(alunite)、钙芒硝(buddingtonite)、方解石(calcite)和高岭石(kaolinite),因为这4种矿物都有比较明显的纯像元分布区域。
试验中分别采用AMEE算法、PPI算法和PPI-AMEE算法提取9个端元,然后计算其与USGS光谱库中的4种矿物alunite、buddingtonite、calcite、kaolinite标准光谱的光谱角。AMEE算法和PPI-AMEE算法中最小结构元素和最大结构元素分别设置为3×3和15×15。用PA1、PA2,…,PA9表示PPI-AMEE算法提取的9个端元,表 2所示为PPI-AMEE算法提取端元与USGS标准光谱之间的光谱角混淆矩阵。
| 矿物种类 | PA1 | PA2 | PA3 | PA4 | PA5 | PA6 | PA7 | PA8 | PA9 |
| alunite | 0.173 | 0.185 | 0.049 | 0.205 | 0.156 | 0.253 | 0.262 | 0.166 | 0.172 |
| buddingtonite | 0.196 | 0.233 | 0.272 | 0.183 | 0.123 | 0.178 | 0.212 | 0.231 | 0.196 |
| calcite | 0.229 | 0.234 | 0.237 | 0.062 | 0.167 | 0.196 | 0.182 | 0.239 | 0.217 |
| kaolinite | 0.156 | 0.243 | 0.236 | 0.193 | 0.184 | 0.198 | 0.217 | 0.249 | 0.053 |
从表 2中看出,PA3与alunite标准光谱的光谱角最小,因此PA3即被确认为PPI-AMEE算法提取的对应alunite的端元。同理,PA5、PA4、PA9分别对应buddingtonite、calcite、kaolinite。
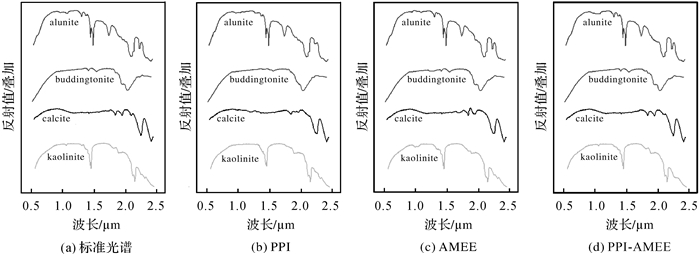
然后,分别单独采用AMEE算法和PPI算法提取Cuprite地区alunite、buddingtonite、calcite、kaolinite的端元光谱,连同上述PPI-AMEE算法所提取的端元光谱曲线一起示于图 6中,并与USGS光谱库中标准光谱曲线进行对比。
|
| 图 6 PPI、AMEE、PPI-AMEE提取的端元与USGS标准光谱的对比 Fig. 6 Comparison of enmembers extracted by PPI, AMEE, PPI-AMEE with USGS standard spectra |
表 3中的试验数据比较了PPI、AMEE、PPI-AMEE这3种算法所提取的4个端元光谱与各自对应的标准光谱之间的光谱角距离、光谱信息散度。
| 矿物种类 | PPI | AMEE | PPI-AMEE | |||||
| SAD /rad |
SID /bit |
SAD /rad |
SID /bit |
SAD /rad |
SID /bit |
|||
| alunite | 0.074 | 0.022 | 0.052 | 0.020 | 0.049 | 0.019 | ||
| buddingtonite | 0.165 | 0.053 | 0.136 | 0.047 | 0.123 | 0.043 | ||
| calcite | 0.085 | 0.029 | 0.070 | 0.025 | 0.062 | 0.023 | ||
| kaolinite | 0.095 | 0.031 | 0.061 | 0.022 | 0.053 | 0.020 | ||
真实数据的试验结果表明,与AMEE算法和PPI算法相比,PPI-AMEE算法端元与USGS标准光谱之间的光谱角距离和光谱信息散度最小,其端元提取精度总体上优于其他两种算法。
4 结论本文提出的PPI-AMEE算法融合了AMEE算法和PPI算法的设计思想,采用PPI算法对数学形态学中的膨胀和腐蚀操作作了拓展性的定义,在结构元素内通过累计各像元的PPI指数寻找最纯像元。PPI算法只是把整幅高光谱影像当作无序向量进行投影的,仅仅利用了图像的光谱信息。PPI-AMEE算法在结构元素局部范围内运行PPI算法,然后结合数学形态学的膨胀操作对整幅图像进行处理,同时兼顾了图像的空间信息和光谱信息。试验结果表明,本文提出的PPI-AMEE算法的端元提取精度优于AMEE算法和PPI算法。
| [1] |
蓝金辉, 邹金霖, 郝彦爽, 等.
高光谱遥感影像混合像元分解研究进展[J]. 遥感学报, 2018, 22(1): 13–27.
LAN Jinhui, ZOU Jinlin, HAO Yanshuang, et al. Research progress on unmixing of hyperspectral remote sensing imagery[J]. Journal of Remote Sensing, 2018, 22(1): 13–27. |
| [2] |
张春森, 郑艺惟, 黄小兵, 等.
高光谱影像光谱-空间多特征加权概率融合分类[J]. 测绘学报, 2015, 44(8): 909–918.
ZHANG Chunsen, ZHENG Yiwei, HUANG Xiaobing, et al. Hyperspectral image classification based on the weighted probabilistic fusion of multiple spectral-spatial features[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 909–918. DOI:10.11947/j.AGCS.2015.20140544 |
| [3] |
王俊淑, 江南, 张国明, 等.
融合光谱-空间信息的高光谱遥感影像增量分类算法[J]. 测绘学报, 2015, 44(9): 1003–1013.
WANG Junshu, JIANG Nan, ZHANG Guoming, et al. Incremental classification algorithm of hyperspectral remote sensing images based on spectral-spatial information[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 1003–1013. DOI:10.11947/j.AGCS.2015.20140388 |
| [4] | DELGADO J, MARTÍN G, PLAZA J, et al. Fast spatial preprocessing for spectral unmixing of hyperspectral data on graphics processing units[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(2): 952–961. DOI:10.1109/JSTARS.2015.2495128 |
| [5] | PLAZA A, MARTÍNZE P, PÉREZ R, et al. Spatial/spectral endmember extraction by multidimensional morphological operations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(9): 2025–2041. DOI:10.1109/TGRS.2002.802494 |
| [6] | JIMÉNEZ L I, PLAZA J, PLAZA A. Efficient implementation of morphological index for building/shadow extraction from remotely sensed images[J]. Journal of Supercomputing, 2017, 73(1): 482–494. DOI:10.1007/s11227-016-1890-9 |
| [7] |
方俊龙.高光谱像元解混技术研究[D].杭州: 杭州电子科技大学, 2016. FANG Junlong. Research on hyperspectral unmixing techniques[D]. Hangzhou: Hangzhou Dianzi University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10336-1016074027.htm |
| [8] | CHANG C I, PLAZA A. A fast iterative algorithm for implementation of pixel purity index[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(1): 63–67. DOI:10.1109/LGRS.2005.856701 |
| [9] | LU Xiaoqiang, WU Hao, YUAN Yuan, et al. Manifold regularized sparse NMF for hyperspectral unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 2815–2826. DOI:10.1109/TGRS.2012.2213825 |
| [10] | HEYLEN R, PARENTE M, GADER P. A review of nonlinear hyperspectral unmixing methods[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6): 1844–1868. DOI:10.1109/JSTARS.2014.2320576 |
| [11] | CHANG C I, WU Chaocheng. Design and development of iterative pixel purity index[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2676–2695. DOI:10.1109/JSTARS.2015.2403259 |
| [12] | ZARE A, GADER P, CASELLA G. Sampling piecewise convex unmixing and endmember extraction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1655–1665. DOI:10.1109/TGRS.2012.2207905 |
| [13] | LI H C, CHANG C I. Recursive orthogonal projection-based simplex growing algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 3780–3793. DOI:10.1109/TGRS.2016.2527737 |
| [14] | ZHANG Shaoquan, AGATHOS A, LI Jun. Robust minimum volume simplex analysis for hyperspectral unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(11): 6431–6439. DOI:10.1109/TGRS.2017.2728104 |
| [15] | LI H C, CHANG C I. Geometric simplex growing algorithm for finding endmembers in hyperspectral imagery[C]//Proceedings of 2016 IEEE International Geoscience and Remote Sensing Symposium. Beijing: IEEE, 2016. |
| [16] |
李琳, 孟令博, 孙康, 等.
基于代数余子式的N-FINDR快速端元提取算法[J]. 电子与信息学报, 2015, 37(5): 1128–1134.
LI Ling, MENG Lingbo, SUN Kang, et al. A fast N-FINDR algorithm based on cofactor of a determinant[J]. Journal of Electronics and Information Technology, 2015, 37(5): 1128–1134. |
| [17] | GENG Xiurui, SUN Kang, JI Luyan, et al. Optimizing the endmembers using volume invariant constrained model[J]. IEEE Transactions on Image Processing, 2015, 24(11): 3441–3449. DOI:10.1109/TIP.2015.2446196 |
| [18] |
徐君, 徐富红, 蔡体健, 等.
一种基于最大距离的纯像元指数端元提取算法[J]. 地球信息科学学报, 2015, 17(1): 86–90.
XU Jun, XU Fuhong, CAI Tijian, et al. A novel pure pixel index endmember extraction algorithm based on the maximum distance[J]. Journal of Geo-Information Science, 2015, 17(1): 86–90. |
| [19] | CHANG C I, WU C C, LIU W, et al. A new growing method for simplex-based endmember extraction algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2804–2819. DOI:10.1109/TGRS.2006.881803 |
| [20] | CHANG C I, WU Chaocheng, LO C S, et al. Real-time simplex growing algorithms for hyperspectral endmember extraction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 1834–1850. DOI:10.1109/TGRS.2009.2034979 |
| [21] | CHAN T H, CHI C Y, HUANG Y M, et al. A convex analysis-based minimum-volume enclosing simplex algorithm for hyperspectral unmixing[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4418–4432. DOI:10.1109/TSP.2009.2025802 |
| [22] | LIU Junmin, ZHANG Jiangshe. A new maximum simplex volume method based on householder transformation for endmember extraction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 104–118. DOI:10.1109/TGRS.2011.2158829 |
| [23] |
王瀛, 梁楠, 郭雷.
一种基于修正扩展形态学算子的高光谱遥感图像端元提取算法[J]. 光子学报, 2012, 41(6): 672–677.
WANG Ying, LIANG Nan, GUO Lei. A hyperspectral remote sensing image endmember extraction algorithm based on modified extended-morphological operator[J]. Acta Photonica Sinica, 2012, 41(6): 672–677. |
| [24] | SWAYZE G A. The hydrothermal and structural history of the cuprite mining district, southwestern Nevada: An integrated geological and geophysical approach[D]. Boulder: University of Colorado, 1997: 399. |
| [25] | CLARK R N, SWAYZE G A. Automated spectral analysis: Mapping minerals, amorphous materials, environmental materials, vegetation, water, ice and snow, and other materials: The USGS tricorder algorithm[C]//Proceedings of the 5th Annual JPL Airborne Earth Science Workshop. Pasadena: JPL Publication, 1995. |
| [26] | BIOUCAS-DIAS J M, NASCIMENTO J M P. Hyperspectral Subspace Identification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(8): 2435–2445. DOI:10.1109/TGRS.2008.918089 |


