2. 32023部队, 辽宁 大连 116000
2. 32023 Troops, Dalian 116000, China
近年来,随着遥感平台和传感器的不断进步,人们获取高光谱遥感影像的能力不断提高。但在完成数据获取以后,数据的处理与分析将真正决定地物探测的水平。高光谱影像分类能够为高光谱影像的进一步应用提供基础,是高光谱遥感中的关键技术和研究热点之一[1]。高光谱影像中可以获取每个像素近似连续的光谱曲线,这些光谱曲线能够较好地反映地物的属性信息,这就为地物的精细分类提供了可能。但近似连续的光谱曲线导致了高光谱影像具有高维的数据特点,且在高光谱影像中获取标记数据较为困难,可用于训练的标记样本数量较少。高维的数据结构和较少的训练样本数量给高光谱影像分类带来了极大的挑战[2]。
早期的高光谱影像分类方法通过提取光谱特征,并结合支持向量机、决策树、逻辑回归等分类器进行分类[3]。但在高光谱影像中“同谱异物”和“同物异谱”的现象广泛存在,这就导致仅仅利用光谱信息进行分类具有一定的局限性。高光谱影像具有“图谱合一”的特点,在提供光谱特征的同时,也提供了丰富的空间信息。而大量的研究表明,在分类过程中引入空间信息能够降低地物分类的不确定性,从而能够提高高光谱影像分类的精度[4]。拓展形态学属性剖面[5](extended morphological profile,EMP)通过形态学操作提取高光谱影像的空间结构信息,并与光谱特征结合进行分类,有效地改善了高光谱影像的分类效果。除了EMP,还可以应用滤波半径依次增加的引导滤波器来获得影像不同尺度的结构信息,进而提高分类精度[6]。纹理特征也是一种能够有效利用空间信息的方法,常用于高光谱影像分类的纹理特征有Gabor特征[7]、局部二值模式[8]纹理特征等。除了上述在特征提取过程中考虑空间邻域信息,也可以利用聚类获得的空间信息来提高高光谱影像的分类精度。文献[9]利用聚类信息对支持向量机的分类结果进行后处理,进一步提高了高光谱影像的分类精度。文献[10]在利用支持向量机对Gabor特征进行分类的基础上,采用多数投票策略进一步融合超像素分割结果,在训练样本数量较少的情况下取得了较为理想的分类精度。文献[11]提出利用边缘保持滤波对分类结果进行处理,既能滤除分类结果中孤立的分类噪声,又能较好地保持分类结果的边缘,因此能够提高分类精度。
近年来,随着计算能力和数据获取能力的不断提高,深度学习方法得到了快速发展,已经被广泛应用于自然语言处理、图像分类识别、高分辨率遥感影像处理、高光谱影像分类等领域。最早用于高光谱影像分类的深度学习模型是堆栈式自编码器,该方法先利用主成分分析对高光谱影像进行降维处理,然后选取一定的邻域范围,并展成一维特征向量输入到堆栈式自编码器中进行分类[12]。随后,利用光谱特征的一维卷积神经网络模型也被引入到了高光谱分类领域中[13]。为了进一步提高高光谱影像的分类精度,二维卷积神经网络被用于提取高光谱影像的空间特征,并将空间特征与光谱特征结合进行分类,取得了较为理想的分类结果[14-16]。此外,研究人员还利用三维卷积神经网络[17]和循环神经网络[18]提取高光谱影像的空-谱特征进行分类。基于深度学习的高光谱影像分类方法能够自动从数据中学习如何提取特征,简化了高光谱影像分类的处理流程,但仍然面临小样本问题的挑战。
视觉显著性是人类视觉系统的重要机制, 其能够快速准确地提取场景中最感兴趣的区域,并忽略冗余的信息[19]。视觉显著性估计已经被广泛应用于遥感图像处理和分析中,例如文献[20]联合显著性和多层卷积神经网络进行高分辨率遥感影像场景分类;文献[21]对高光谱影像进行显著性波段选择,从而提高高光谱影像的分类精度。为充分利用空间信息提高高光谱影像分类精度,本文以显著性滤波器为基础,提出了一种用于高光谱影像分类的显著性特征提取方法,并进一步结合光谱特征进行分类。最后利用Pavia大学、Indian Pines和Salinas 3组高光谱数据集验证了本文算法的有效性。
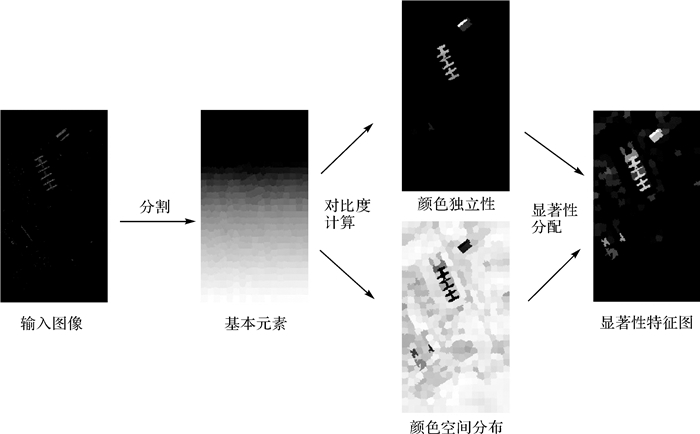
1 高光谱影像显著性特征提取与分类视觉显著性估计中通常以彩色图像为输入[22],因此,本文以3个相邻波段的高光谱影像为输入,进行显著性特征提取,然后沿光谱维度利用滑窗法获取各个波段的显著性特征,最后将各个波段的显著性特征进行堆叠形成最终用于分类的显著性特征。如图 1所示,3个相邻波段的高光谱影像显著性特征提取主要包括超像素分割、对比度计算和显著性分配3个步骤。
|
| 图 1 3个波段显著性特征提取流程 Fig. 1 Salient feature extraction of three adjacent bands |
1.1 SLIC超像素分割
基于像素的视觉显著性估计方法对噪声较为敏感,而超像素以相对简单的方式表示图像并能减少图像的冗余,同时每个超像素块具有相同的性质[23]。为了更加有效地提取显著性特征,首先将输入的三波段高光谱影像根据颜色相似性分割为若干个超像素,每个超像素由区域内的颜色均值表示,进而以超像素为基础进行视觉显著性估计。本文采用SLIC[24](simple linear iterative cluster)方法对输入的三波段高光谱影像进行超像素分割。
SLIC算法是基于k-means聚类设计的超像素分割算法,其根据CIE LAB颜色空间和二维坐标构成的5维特征向量进行局部聚类,并将搜索空间限制在与超像素大小成比例的区域内来提高计算效率[25]。SLIC算法接受一个参数K(K为超像素分割的个数),首先初始化K个种子点,并在每个种子点的邻域空间内搜索距离该种子点最近的若干像素,将它们与该种子点归为一类,直到所有像素点都归类完毕;然后计算这K个超像素里所有像素点的平均向量值作为新的聚类中心;再根据更新后的K个聚类中心重复上述步骤,迭代直到收敛。K个种子之间的初始距离定义为S=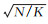
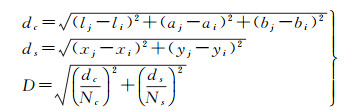 (1)
(1)
式中,l、a、b为CIE LAB颜色空间对应的3个通道变量;i和j为超像素的索引;Nc和Ns分别为最大的颜色距离和种子点之间最大的距离。
SLIC算法能够有效地将图像分割为若干个超像素块,每个超像素块内部像素属性趋于一致,并由颜色均值表示。这样可以在特征提取的过程中充分考虑像素周围的局部空间信息,同时能够降低噪声对特征提取的影响。
1.2 对比度计算视觉显著性检测中通常通过计算对比度来进行显著性估计,为了更加充分地利用全局空间信息,以分割后的超像素为基础,定义颜色独立性和空间颜色分布两种对比度。颜色独立性定义如下
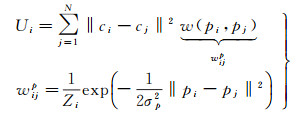 (2)
(2)
式中,cj=[lj, ajbj]和pj=[xj, yj]分别为第j个超像素的颜色和位置;wijp表示局部或全局对比的控制变量,权重与超像素空间位置的距离有关;Zi为归一化因子,用于保证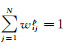
进一步可将式(2)改写为
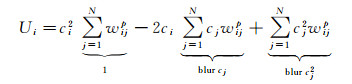 (3)
(3)
式中,第1项的结果是1;第2和第3项可以通过以w为核的滤波器,分别对cj和cj2进行滤波加以实现。
空间颜色分布定义如下
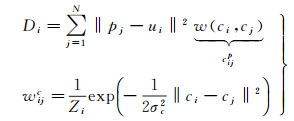 (4)
(4)
式中,cj=[lj, ajbj]和pj=[xj, yj]分别为第j个超像素的颜色和位置;wijc表示表示i和j个超像素的颜色相似度; Zi为归一化因子;σc为参数;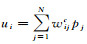
式(4)可以改写为
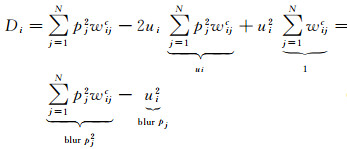 (5)
(5)
与式(2)类似,式(4)可以通过对pj2和pj进行滤波的方式加以实现。
1.3 显著性分配根据颜色独立性和空间颜色分布计算每个超像素的显著性为
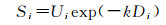 (6)
(6)
由式(6)可知空间颜色分布Di越大即颜色分布越广,对应显著性值越小;颜色独立性Ui越大,则对应显著性值越大。最终定义每个像素的显著性如下
 (7)
(7)
式中,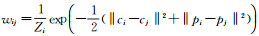
由于高光谱影像具有众多波段,因此需要沿光谱方向依次获取各个波段的显著性特征。最后将各个波段获得的显著性特征图进行堆叠,形成维度为B-2的显著性特征向量,其中B为波段数。为进一步提高分类精度,将每个像素的显著性特征向量和光谱特征向量进行连接形成最终用于分类的特征。
大量的研究已经表明支持向量机是一种快速可靠的分类器,因此本文采用支持向量机作为最终的分类器。其中支持向量机的核函数采用高斯核函数,核函数参数和惩罚系数在2-2, 2-1, …, 27范围内通过5折交叉验证确定。
2 试验结果与分析 2.1 试验数据参照文献[26],采用Pavia大学、Indian Pines和Salinas 3组高光谱数据集进行分类试验来验证显著性特征提取方法的有效性。Pavia大学数据集由ROSIS传感器获得,Indian Pines和Salinas数据集由AVIRIS传感器获得。Pavia大学数据集的影像大小为610×340像素,空间分辨率为1.3 m,光谱覆盖范围为430~860 nm,有103个有效波段可用于分类试验。Indian Pines数据集的影像大小为145×145像素,空间分辨率为20 m,光谱覆盖范围为400~2500 nm,有200个有效波段可用于分类。Salinas数据集的影像大小为512×217像素,空间分辨率为3.7 m,光谱覆盖范围为430~860 nm,有204个有效波段可用于分类。3组高光谱影像数据集的地物类别、选取的训练样本数量和测试样本数量分别如表 1-表 3所示。
| 序号 | 地物类别 | 训练样本 | 确认样本 | 测试样本 |
| 1 | 柏油路面 | 180 | 20 | 6631 |
| 2 | 草地 | 180 | 20 | 18 649 |
| 3 | 砖块砂砾 | 180 | 20 | 2099 |
| 4 | 树木 | 180 | 20 | 3064 |
| 5 | 金属板 | 180 | 20 | 1345 |
| 6 | 裸土 | 180 | 20 | 5029 |
| 7 | 沥青屋顶 | 180 | 20 | 1330 |
| 8 | 砖块 | 180 | 20 | 3682 |
| 9 | 阴影 | 180 | 20 | 947 |
| 总数 | 1620 | 180 | 42 776 |
| 序号 | 地物类别 | 训练样本 | 确认样本 | 测试样本 |
| 1 | 未耕玉米地 | 180 | 20 | 1428 |
| 2 | 玉米幼苗 | 180 | 20 | 830 |
| 3 | 草地/牧场 | 180 | 20 | 483 |
| 4 | 草地树木 | 180 | 20 | 730 |
| 5 | 干草/料堆 | 180 | 20 | 478 |
| 6 | 未耕大豆地 | 180 | 20 | 972 |
| 7 | 大豆幼苗 | 180 | 20 | 2455 |
| 8 | 整理过的大豆 | 180 | 20 | 593 |
| 9 | 木材 | 180 | 20 | 1265 |
| 总数 | 1620 | 180 | 9234 |
| 序号 | 地物类别 | 训练样本 | 确认样本 | 测试样本 |
| 1 | 椰菜_绿_野草1 | 180 | 20 | 2009 |
| 2 | 椰菜_绿_野草2 | 180 | 20 | 3726 |
| 3 | 休耕地 | 180 | 20 | 1976 |
| 4 | 粗糙的休耕地 | 180 | 20 | 1394 |
| 5 | 平滑的休耕地 | 180 | 20 | 2678 |
| 6 | 残株 | 180 | 20 | 3959 |
| 7 | 芹菜 | 180 | 20 | 3579 |
| 8 | 未结果实的葡萄 | 180 | 20 | 11 271 |
| 9 | 正在开发的葡萄园土壤 | 180 | 20 | 6203 |
| 10 | 开始衰老的玉米 | 180 | 20 | 3278 |
| 11 | 长叶莴苣4 wk | 180 | 20 | 1068 |
| 12 | 长叶莴苣5 wk | 180 | 20 | 1927 |
| 13 | 长叶莴苣6 wk | 180 | 20 | 916 |
| 14 | 长叶莴苣7 wk | 180 | 20 | 1070 |
| 15 | 未结果实的葡萄园 | 180 | 20 | 7268 |
| 16 | 葡萄园小路 | 180 | 20 | 1807 |
| 总数 | 2880 | 320 | 54 129 |
2.2 参数设置
本文提出的高光谱影像显著性特征提取涉及的参数主要包括:颜色独立性调节参数σp、空间颜色分布调节参数σc和分割超像素的个数K。本小节以Pavia大学数据集为例分析不同的参数设置对最终分类结果的影响。需要指出的是本小节的分类试验没有结合光谱特征,仅采用了显著性特征。
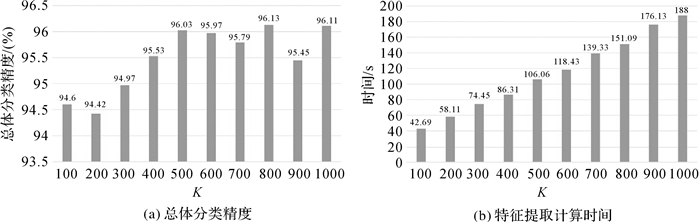
图 2所示为在Pavia大学数据集中设置不同的K值对应的总体分类精度和特征提取所需时间。由图 2可知,当K值较少时(例如100、200),分类精度较低;而当K值大于500时,均能够取得较为理想的分类精度;但随着K值的增大,特征提取所需时间也相应增加,而分类精度提升却不明显。在实际应用过程中应该根据高光谱影像大小适当增大K。本文综合考虑分类精度和计算效率统一设置K=500。
|
| 图 2 Pavia大学数据集不同的K值对应的总体分类精度和计算时间 Fig. 2 Overall accuracy and computing time with different number of elements decomposed by SLIC on the University of Pavia dataset |
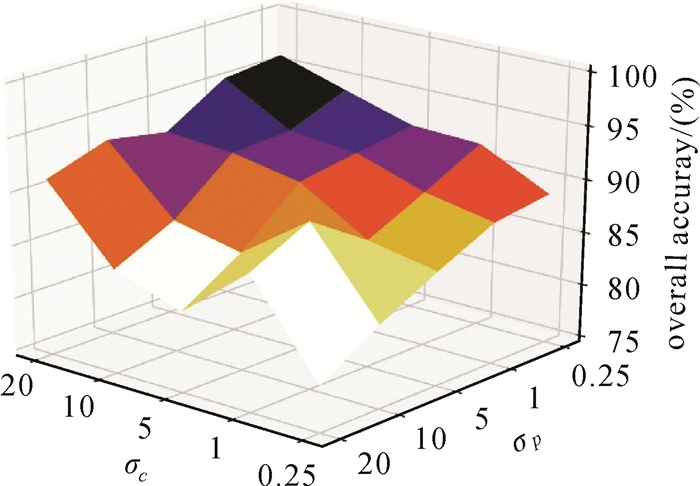
为了分析σc和σp对最终分类精度的影响,分别设置σc和σp为0.25、1、5、10、20。图 3所示为在Pavia大学数据集中设置不同的σc和σp值对应的总体分类精度。分析图 3可知,当σp值固定时,总体分类精度随着σc的增加而增加,而当σc固定时,总体分类精度大体上随着σp的减小而增加。这说明为了获取更高的分类精度,应该设置较大σc的值和较小σp的值。根据图 3,最终设置σc=20、σp=0.25。
|
| 图 3 Pavia大学数据集不同的σc和σp值对应的总体分类精度 Fig. 3 Overall accuracy with different σc and σp on the University of Pavia dataset |
通过以上分析,本文提出的高光谱影像显著性特征提取方法对于分割超像素的个数K、颜色独立性调节参数σp、空间颜色分布调节参数σc 3个参数较为敏感。实际应用中应该根据高光谱影像的大小适当调节K值的大小,即影像越大,K的值也越大。需要指出的是,过小的K值会导致精度下降,根据本文结果建议设置K≥500较为合理。对于σc和σp,应该设置较大的σc值和较小的σp值。根据本文试验结果设置σc=20、σp=0.25较为合理。
表 4给出了分别利用颜色独立性和颜色空间分布特征以及综合利用颜色独立性和颜色空间分布特征进行分类的总体分类精度。由表 4可知综合利用两种对比度有利于提高分类精度。
| (%) | |||
| 颜色独立性 | 颜色空间分布 | 颜色独立性+颜色空间分布 | |
| 总体分类精度 | 93.91 | 87.53 | 96.03 |
通常来说对高光谱影像进行特征提取前,可以进行波段随机排序、PCA变换等预处理操作,以期进一步提高分类精度。表 5给出了采用不同的波段数量进行超像素分割和采用不同预处理操作,进而提取显著性特征对应的总体分类精度。其中“PCA”表示对高光谱数据进行PCA变换后,再选取相邻波段进行显著性特征提取;“随机排列”表示对高光谱影像不同波段进行随机排列后再选取相邻波段进行显著性特征提取。
| (%) | |||
| PCA | 随机排列 | 直接选择 | |
| 1波段 | 89.71 | 93.38 | 95.24 |
| 3波段 | 92.22 | 95.86 | 96.03 |
| 5波段 | 92.13 | 96.07 | 96.11 |
观察表 5可知采用单波段进行显著性特征提取的分类精度略低于采用3个连续波段进行显著性特征提取的分类精度。这是由于采用单波段进行显著性特征提取仅仅考虑了空间邻域信息,而采用3个连续的波段进行显著性特征提取不仅在特征提取的过程中引入了邻域空间信息,还能够充分考虑相邻波段的影响。进一步采用5个相邻波段进行显著性特征提取对于分类精度的提升效果不明显,且会极大地增加特征提取的时间。此外,事先对高光谱数据进行PCA变换,使各波段相互独立,再进行显著性特征提取,会极大地降低分类精度。而波段随机排列操作对于分类精度的提升并没有帮助。为了简化特征提取过程,本文不对高光谱影像进行随机排序或PCA变换等预处理操作。且最终采用3个连续的波段进行显著性特征提取,即沿着光谱方向采用大小为3、步长为1的滑窗法获得所有波段的显著性特征。
2.3 试验结果与分析为了验证显著性特征(SF+SVM)的有效性,分别与SVM、EMPs[5]、Gabor[27]、2D-CNN[11]和3D-CNN[26, 28]、Gabor+SVM+SLIC[10]算法进行对比分析,并进一步将显著性特征和光谱特征结合输入到SVM中进行分类(Spec-SF+SVM)。SVM采用光谱特征进行分类;EMPs取前3个主成分波段进行特征提取,每个波段分别利用4个开运算和4个闭运算构建形态学属性剖面特征,开闭运算的半径分别为3、5、7、9;Gabor滤波器的带宽设置为1,波长设置为1.4,方向角分别取0°、30°、60°、90°,偏移相位为0,滤波窗口大小为11×11;2D-CNN采用3个卷积层和3个池化层,3个卷积层的卷积核大小分别为5×5、6×6、4×4;3D-CNN采用7个三维卷积层、2个三维池化层和1个全连接层,且引入了两个残差模块,三维卷积层的卷积核大小设置为3×3×3;Gabor+SVM+SLIC中的SLIC分割数设置为500。SVM、EMPs、Gabor、Gabor+SVM+SLIC、SF+SVM和Spec-SF+SVM均采用支持向量机作为分类器,支持向量机核函数采用高斯核函数,核函数参数和惩罚系数通过5折交叉验证确定;2D-CNN和3D-CNN均从训练样本中随机选取10%的样本作为确认样本,并选择在确认样本上分类精度最高的模型进行测试。
表 6-表 8给出了不同算法在3组高光谱数据集上的分类结果。观察分类结果可知,采用空间特征进行分类的EMPs、Gabor、2D-CNN、3D-CNN和SF+SVM的总体分类精度、平均分类精度、Kappa系数均优于仅利用光谱特征进行分类的SVM,这说明在分类过程中引入空间信息有助于提高高光谱影像分类精度;2D-CNN和3D-CNN由于训练样本数量较少,其分类精度较EMPs和Gabor并无明显优势;Gabor+SVM+SLIC除了使用SVM对Gabor特征进行分类,还利用SLIC超像素分割结果采用多数投票的策略对分类结果进行修正,因此能够获得较其他对比方法更高的分类精度。SF+SVM在Pavia大学数据集上的分类精度高于SVM、EMPs、Gabor和2D-CNN,略低于3D-CNN和Gabor+SVM+SLIC,且在Indian Pines和Salinas数据上均能获得较其他方法更高的分类精度。这说明了本文所提出的显著性特征是一种有效的特征提取方法,能够提高高光谱影像的分类精度,且将显著性特征与光谱特征结合(Spec-SF+SVM)能够进一步提高高光谱影像的分类精度。
| (%) | ||||||||
| 序号 | SVM | EMPs | Gabor | 2D-CNN | 3D-CNN | Gabor+SVM+SLIC | SF+SVM | Spec-SF+SVM |
| 1 | 91.24 | 86.17 | 95.54 | 88.80 | 95.23 | 97.06 | 97.03 | 96.46 |
| 2 | 85.37 | 91.57 | 90.71 | 90.33 | 96.88 | 96.63 | 95.71 | 98.05 |
| 3 | 90.66 | 88.61 | 97.98 | 91.19 | 94.85 | 95.65 | 96.95 | 97.78 |
| 4 | 98.07 | 95.07 | 100.0 | 99.71 | 98.43 | 99.86 | 91.19 | 100.0 |
| 5 | 100.0 | 99.03 | 97.32 | 100.0 | 99.85 | 100.0 | 99.70 | 96.14 |
| 6 | 87.25 | 94.35 | 98.35 | 92.22 | 93.28 | 93.72 | 95.37 | 99.32 |
| 7 | 96.32 | 95.79 | 91.04 | 95.56 | 97.67 | 94.70 | 99.47 | 96.69 |
| 8 | 89.65 | 83.24 | 99.89 | 95.17 | 95.71 | 97.13 | 96.66 | 99.89 |
| 9 | 100.0 | 99.89 | 90.30 | 99.58 | 100.0 | 99.45 | 99.89 | 98.42 |
| OA | 89.16 | 91.00 | 94.81 | 92.11 | 96.30 | 96.68 | 96.03 | 97.19 |
| AA | 93.17 | 92.64 | 95.68 | 94.73 | 96.88 | 97.13 | 96.89 | 98.08 |
| Kappa | 85.96 | 88.24 | 93.18 | 89.72 | 95.11 | 95.89 | 94.77 | 96.31 |
| (%) | ||||||||
| 序号 | SVM | EMPs | Gabor | 2D-CNN | 3D-CNN | Gabor+SVM+SLIC | SF+SVM | Spec-SF+SVM |
| 1 | 82.49 | 69.75 | 94.10 | 83.75 | 86.55 | 90.24 | 94.96 | 99.75 |
| 2 | 85.54 | 87.71 | 99.79 | 96.14 | 94.58 | 97.25 | 94.34 | 99.38 |
| 3 | 96.89 | 97.93 | 99.59 | 98.96 | 98.96 | 97.42 | 97.52 | 99.86 |
| 4 | 99.59 | 98.77 | 100.0 | 98.77 | 99.86 | 89.55 | 99.73 | 99.79 |
| 5 | 100.0 | 99.79 | 95.99 | 98.74 | 100.0 | 99.70 | 99.79 | 97.74 |
| 6 | 82.82 | 91.87 | 87.05 | 93.93 | 94.75 | 99.22 | 95.78 | 98.45 |
| 7 | 73.93 | 82.57 | 93.93 | 77.72 | 86.97 | 99.32 | 96.74 | 98.31 |
| 8 | 91.74 | 90.56 | 99.84 | 98.65 | 96.46 | 97.55 | 98.31 | 99.76 |
| 9 | 98.66 | 95.10 | 88.38 | 98.02 | 99.84 | 99.68 | 99.84 | 95.66 |
| OA | 86.34 | 87.23 | 93.35 | 90.00 | 93.10 | 95.92 | 97.11 | 98.30 |
| AA | 90.18 | 90.45 | 95.41 | 93.86 | 95.33 | 96.66 | 97.45 | 98.55 |
| Kappa | 84.12 | 85.11 | 92.24 | 88.39 | 91.94 | 94.71 | 96.61 | 98.00 |
| (%) | ||||||||
| 序号 | SVM | EMPs | Gabor | 2D-CNN | 3D-CNN | Gabor+SVM+SLIC | SF+SVM | Spec-SF+SVM |
| 1 | 99.40 | 99.85 | 99.85 | 98.11 | 99.70 | 98.16 | 99.95 | 99.57 |
| 2 | 99.54 | 99.49 | 99.81 | 99.54 | 100.0 | 99.25 | 99.62 | 100.0 |
| 3 | 99.90 | 100.00 | 99.75 | 98.03 | 98.73 | 99.69 | 100.0 | 99.64 |
| 4 | 99.71 | 99.78 | 99.50 | 100.0 | 99.78 | 99.57 | 98.64 | 98.81 |
| 5 | 97.80 | 97.46 | 98.36 | 98.21 | 99.22 | 95.37 | 95.97 | 99.47 |
| 6 | 99.60 | 99.70 | 98.84 | 100.0 | 100.0 | 100.0 | 99.32 | 99.83 |
| 7 | 99.44 | 98.91 | 99.78 | 97.85 | 99.89 | 97.51 | 99.75 | 97.52 |
| 8 | 79.24 | 81.60 | 86.36 | 87.82 | 89.51 | 92.32 | 98.38 | 99.87 |
| 9 | 99.69 | 98.03 | 99.77 | 96.70 | 99.81 | 99.77 | 99.69 | 99.15 |
| 10 | 94.02 | 97.04 | 96.67 | 96.28 | 97.04 | 96.37 | 98.99 | 99.34 |
| 11 | 99.91 | 98.78 | 97.85 | 98.03 | 98.03 | 100.0 | 99.72 | 100.0 |
| 12 | 99.64 | 100.0 | 100.0 | 99.90 | 100.0 | 99.95 | 95.49 | 99.24 |
| 13 | 98.14 | 99.02 | 99.89 | 100.0 | 99.78 | 100.0 | 98.69 | 98.79 |
| 14 | 99.07 | 99.72 | 98.76 | 99.72 | 99.91 | 99.25 | 98.50 | 99.71 |
| 15 | 75.15 | 85.90 | 86.13 | 79.43 | 85.13 | 98.25 | 99.97 | 99.23 |
| 16 | 98.95 | 99.39 | 99.17 | 94.80 | 99.94 | 98.78 | 100.0 | 99.95 |
| OA | 91.60 | 93.54 | 94.76 | 93.47 | 95.46 | 97.33 | 99.02 | 99.15 |
| AA | 96.20 | 97.17 | 97.54 | 96.53 | 97.90 | 98.39 | 98.92 | 99.38 |
| Kappa | 90.67 | 92.82 | 94.17 | 92.73 | 94.95 | 96.79 | 98.90 | 99.06 |
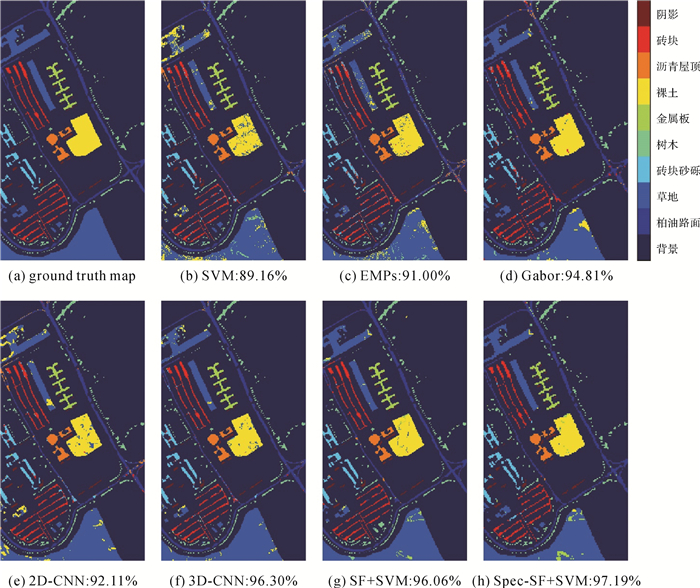
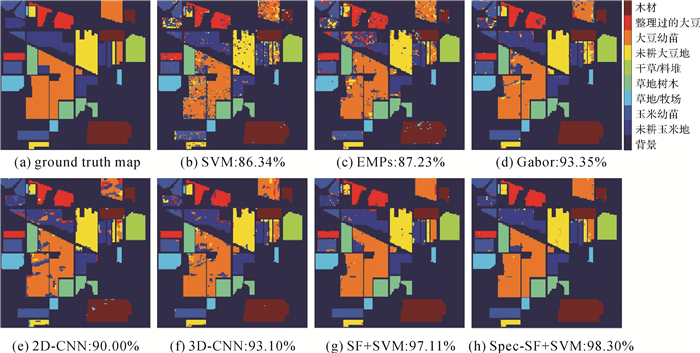
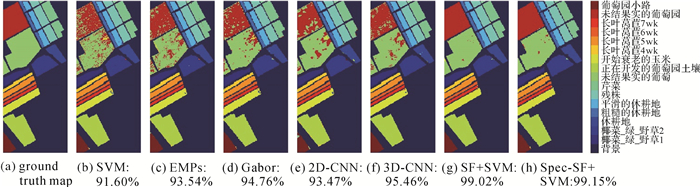
为了更好地观察分类结果,图 4-图 6给出了3组高光谱影像数据采用不同的算法获得的分类图。观察图 4-图 6可知,SF+SVM和Spec-SF+SVM获得的分类图噪声明显少于其他对比算法,具有更好的视觉效果。这也进一步说明了本文算法的有效性。
|
| 图 4 各算法在Pavia大学数据集上的分类结果及其对应的总体分类精度 Fig. 4 Classification maps and overall accuracy with different methods on the University of Pavia dataset |
|
| 图 5 各算法在Indian Pines数据集上的分类结果及其对应的总体分类精度 Fig. 5 Classification maps and overall accuracy with different methods on the Indian Pines dataset |
|
| 图 6 各算法在Salinas数据集上的分类结果图及其对应的总体分类精度 Fig. 6 Classification maps and overall accuracy with different methods on the Salinas dataset |
2.4 训练样本数量适宜性分析
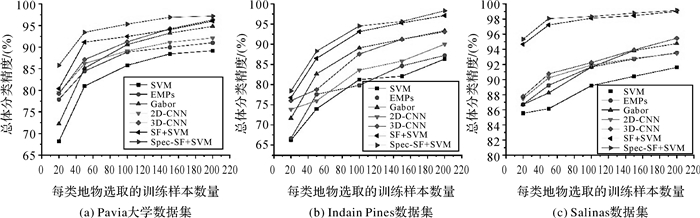
高光谱影像中可用于分类的标记样本数量通常较少,因此小样本问题是高光谱影像分类面临的主要挑战之一。本小节进一步减少训练样本数量进行试验分析,以验证所提出算法在小样本情况下的有效性。如图 7所示为3组高光谱数据集中选取不同数量的训练样本对应的分类结果。观察图 7可知,不同算法的分类精度均随着训练样本数量的减少而降低,但SF+SVM和Spec-SF+SVM均能取得较SVM、EMPs、Gabor、2D-CNN和3D-CNN更高的分类精度,尤其是当每类地物选取20个训练样本时,SF+SVM和Spec-SF+SVM的分类精度依然高于其他对比算法,这证明了所提出方法在小样本情况下的有效性。
|
| 图 7 不同训练样本数目对应的总体分类精度 Fig. 7 Overall accuracy with different number of training samples |
3 总结与展望
本文提出了一种高光谱影像显著性特征提取方法,能够充分地利用局部和全局的空间信息来提高高光谱影像分类的精度。采用Pavia大学、Indian Pines和Salinas 3组高光谱影像数据集进行试验验证。试验结果表明:①与EMPs、Gabor、2D-CNN、3D-CNN等空间特征提取方法相比,采用显著性特征进行分类能够获取更高的分类精度,且将显著性特征与光谱特征结合能够进一步提高分类精度;②本文提出的显著性特征提取方法对小样本有较好的适应性,在训练样本较少的情况下,采用显著性特征进行分类仍然能够取得较为理想的分类结果。
| [1] |
杜培军, 夏俊士, 薛朝辉, 等.
高光谱遥感影像分类研究进展[J]. 遥感学报, 2016, 20(2): 236–256.
DU Peijun, XIA Junshi, XUE Chaohui, et al. Review of hyperspectral remote sensing image classification[J]. Journal of Remote Sensing, 2016, 20(2): 236–256. |
| [2] |
刘冰, 余旭初, 张鹏强, 等.
面对高光谱影像分类的半监督阶梯网络[J]. 测绘科学技术学报, 2017, 34(6): 576–581.
LIU Bing, YU Xuchu, ZHANG Pengqiang, et al. Semi-supervised ladder network for hyperspectral image classification[J]. Journal of Geomatics Science and Technology, 2017, 34(6): 576–581. |
| [3] | GHAMISI P, PLAZA J, CHEN Yushi, et al. Advanced spectral classifiers for hyperspectral images:a review[J]. IEEE Geoscience and Remote Sensing Magazine, 2017, 5(1): 8–32. |
| [4] | GHAMISI P, MURA M D, BENEDIKTSSON J A. A survey on spectral-spatial classification techniques based on attribute profiles[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2335–2353. DOI:10.1109/TGRS.2014.2358934 |
| [5] | BENEDIKTSSON J A, PALMASON J A, SVEINSSON J R. Classification of hyperspectral data from urban areas based on extended morphological profiles[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 480–491. |
| [6] |
王雷光, 曹小汪, 郑雅兰, 等.
高光谱影像的引导滤波多尺度特征提取[J]. 遥感学报, 2018, 22(2): 293–303.
WANG Leiguang, CAO Xiaowang, ZHENG Yalan, et al. Multi-scale feature extraction of hyperspectral image with guided filtering[J]. Journal of Remote Sensing, 2018, 22(2): 293–303. |
| [7] | SHEN Linlin, JIA Sen. Three-dimensional Gabor wavelets for pixel-based hyperspectral imagery classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(12): 5039–5046. DOI:10.1109/TGRS.2011.2157166 |
| [8] | LI Wei, CHEN Chen, SU Hongjun, et al. Local binary patterns and extreme learning machine for hyperspectral imagery classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(7): 3681–3693. DOI:10.1109/TGRS.2014.2381602 |
| [9] | TARABALKA Y, BENEDIKTSSON J A, CHANUSSOT J. Spectral-spatial classification of hyperspectral imagery based on partitional clustering techniques[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2973–2987. DOI:10.1109/TGRS.2009.2016214 |
| [10] |
贾森, 吴奎霖, 朱家松, 等.
面向高光谱图像分类的超像素级Gabor特征融合方法研究[J]. 南京信息工程大学学报(自然科学版), 2018, 10(1): 72–80.
JIA Sen, WU Kuilin, ZHU Jiasong, et al. Superpixel-level Gabor feature fusion method for hyperspectral image classification[J]. Journal of Nanjing University of Information Science and Technology (Natural Science Edition), 2018, 10(1): 72–80. |
| [11] | KANG Xudong, LI Shutao, BENEDIKTSSON J A. Spectral-spatial hyperspectral image classification with edge-preserving filtering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2666–2677. DOI:10.1109/TGRS.2013.2264508 |
| [12] | CHEN Yushi, LIN Zhouhan, ZHAO Xing, et al. Deep learning-based classification of hyperspectral data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6): 2094–2107. DOI:10.1109/JSTARS.2014.2329330 |
| [13] | LIU Bing, YU Xuchu, ZHANG Pengqiang, et al. A semi-supervised convolutional neural network for hyperspectral image classification[J]. Remote Sensing Letters, 2017, 8(9): 839–848. DOI:10.1080/2150704X.2017.1331053 |
| [14] | YUE Jun, ZHAO Wenzhi, MAO Shanjun, et al. Spectral-spatial classification of hyperspectral images using deep convolutional neural networks[J]. Remote Sensing Letters, 2015, 6(6): 468–477. |
| [15] | LIU Bing, YU Xuchu, ZHANG Pengqiang, et al. Supervised deep feature extraction for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 1909–1921. DOI:10.1109/TGRS.2017.2769673 |
| [16] | MEI Shaohui, JI Jingyu, HOU Junhui, et al. Learning sensor-specific spatial-spectral features of hyperspectral images via convolutional neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(8): 4520–4533. DOI:10.1109/TGRS.2017.2693346 |
| [17] | LIU Bing, YU Xuchu, ZHANG Pengqiang, et al. Spectral-spatial classification of hyperspectral image using three-dimensional convolution network[J]. Journal of Applied Remote Sensing, 2018, 12(1): 016005. |
| [18] | LIU Bing, YU Xuchu, YU Anzhu, et al. Spectral-spatial classification of hyperspectral imagery based on recurrent neural networks[J]. Remote Sensing Letters, 2018, 9(12): 1118–1127. DOI:10.1080/2150704X.2018.1511933 |
| [19] |
崔丽群, 赵越, 胡志毅, 等.
复合域的显著性目标检测方法[J]. 中国图象图形学报, 2018, 23(6): 846–856.
CUI Liqun, ZHAO Yue, HU Zhiyi, et al. Saliency object detection method based on complex domains[J]. Journal of Image and Graphics, 2018, 23(6): 846–856. |
| [20] |
何小飞, 邹峥嵘, 陶超, 等.
联合显著性和多层卷积神经网络的高分影像场景分类[J]. 测绘学报, 2016, 45(9): 1073–1080.
HE Xiaofei, ZOU Zhengrong, TAO Chao, et al. Combined saliency with multi-convolutional neural network for high resolution remote sensing scene classification[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1073–1080. DOI:10.11947/j.AGCS.2016.20150612 |
| [21] | SU Peifeng, LIU Daizhi, LI Xihai, et al. A saliency-based band selection approach for hyperspectral imagery inspired by scale selection[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(4): 572–576. DOI:10.1109/LGRS.2018.2800034 |
| [22] | PERAZZI F, KRÄHENBVHL P, PRITCH Y, et al. Saliency filters: contrast based filtering for salient region detection[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA: IEEE, 2012: 733-740. |
| [23] | LIU Tie, YUAN Zejian, SUN Jian, et al. Learning to detect a salient object[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(2): 353–367. DOI:10.1109/TPAMI.2010.70 |
| [24] | ACHANTA R, SHAJI A, SMITH K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274–2282. DOI:10.1109/TPAMI.2012.120 |
| [25] |
崔玲玲, 许金兰, 徐岗, 等.
融合双特征图信息的图像显著性检测方法[J]. 中国图象图形学报, 2018, 23(4): 583–594.
CUI Lingling, XU Jinlan, XU Gang, et al. Image saliency detection method based on a pair of feature maps[J]. Journal of Image and Graphics, 2018, 23(4): 583–594. |
| [26] |
刘冰, 余旭初, 张鹏强, 等.
联合空-谱信息的高光谱影像深度三维卷积网络分类[J]. 测绘学报, 2019, 48(1): 53–63.
LIU Bing, YU Xuchu, ZHANG Pengqiang, et al. Deep 3D convolutional network combined with spatial-spectral features for hyperspectral image classification[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(1): 53–63. DOI:10.11947/j.AGCS.2019.20170578 |
| [27] |
余旭初, 谭熊, 付琼莹, 等.
联合纹理和光谱特征的高光谱影像多核分类方法[J]. 测绘通报, 2014(9): 38–42.
YU Xuchu, TAN Xiong, FU Qiongying, et al. Combined texture-spectral feature for multiple kernel classification of hyperspectral images[J]. Bulletin of Surveying and Mapping, 2014(9): 38–42. DOI:10.13474/j.cnki.11-2246.2014.0289 |
| [28] | LIU Bing, YU Xuchu, YU Anzhu, et al. Deep few-shot learning for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(4): 2290–2304. |



