在地图上,河流常常不单独存在,而是由一条主流和若干级支流组成一个河系。根据平面图形特点,河系类型可分为树枝状、羽毛状、格状、扇状、辐射状等,其中树状河系最为常见,即主流有若干支流,而各条支流又可能拥有若干亚支流等[1]。树状河系具有明显的层次结构,主流、支流蕴含着空间上的“父子关系”,对其进行综合应充分反映河流的主、支流关系,强调支流注入主流处的图形特点[2]。因此,河流分级是树状河系综合的关键所在,也是研究的重点和难点。
对此,已有不少学者进行了富有成效的探索与研究。大致可分为两类:
(1) 通过河段的局部空间关系分析来确定主、支流关系。文献[3]提出了E关系、EC关系和序关系的河系目标基本关系;文献[4]通过缓冲区检索来建立河网的主支流父子关系。该类方法缺少属性特征的参与,难以对河段的主支流特征进行量化评价。
(2) 通过多指标综合评价方法来确定主支流关系。文献[5]通过计算主支流夹角等来确定各河段的流向和主支流关系;文献[6]通过提取河流的高差、集水面积等属性信息进行权重判别来自动判别河流的主支流;在此基础上,文献[7]使用了支流级别建立水系的Horton码来完成分级;文献[8]则采用最大隶属度带权平均规划法来确定权重;文献[9-10]分别顾及节点处分支河段的累计河段数、累计长度和河段深度、最大长度上游河段来识别河系主流;文献[11]根据河流语义、长度、角度约束的树状河系Stroke连接来构成树状河系层次关系。该类方法较少考虑到河系的整体结构特征,易出现局部的主支流判别错误。
以上研究使用了不同方法对河系进行河流分级,取得了较好的成果。然而,河系的分级是从人的认知角度出发赋予客观事物的属性,自然界并不存在固有的河系等级。专家对河系的分级兼顾了局部、整体、几何、语义等多个角度,是主观经验和客观事实进行综合的结果。因此,单采用固定的模型和算法难以对其进行描述,还需要专家的经验知识进行辅助判断。
针对上述现有方法的不足,本文从案例学习的角度出发,提出一种基于朴素贝叶斯的树状河系自动分级方法。该方法从现有的分级案例提取知识,通过训练分类模型来指导河段的主支流分类,从而得到更符合专家分类意图的结果。
1 朴素贝叶斯的原理与应用策略 1.1 朴素贝叶斯的原理朴素贝叶斯分类模型(naive Bayes classifier, NBC),发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率,并在实际应用中十分成功[12]。该分类模型基于贝叶斯定理与特征条件独立假设。设有变量集U={x, y},假设所有的条件属性x都作为类变量y的子节点。其中x={x1, x2, …, xn}包括n个条件属性,y={y1, y2, …, yk}包括k个类标签,将一个样本划分到yk的可能性P(yk|x1, x2, …, xn)为
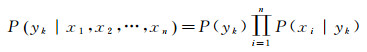 (1)
(1)
朴素贝叶斯分类模型的优点有:算法逻辑简单,易于实现;算法实施的时间、空间开销小;算法性能稳定,对于不同特点的数据其分类性能差别不大,即模型的健壮性比较好[13]。
1.2 基于朴素贝叶斯的树状河系自动分级策略河系结构可以概括为“河系-河流-河段”的三级结构,且每个河段由交汇点相连。从该结构可以得出,河段间的主支流关系识别是河流主支流关系识别的基础,河流主支流关系的识别则是河系层次结构化实现分级的基础。基于此思想,本文从河口出发,自下游向上游依次对交汇点处各相连河段进行主支流关系识别,由河段的主支流关系逐级构建河流实体,完成河系的层次结构化,从而实现自动分级。
河段间主支流识别的难点在于多个主流特征的综合考虑,即在量化表达时如何科学有效地选取相关指标和设定各指标的权重。对此,专家综合知识的有效利用是解决该问题的有效途径[14]。近年来,基于案例学习的方法利用机器学习算法有效获取和利用了专家综合案例中隐含的综合知识,在制图综合领域取得了较好的成效[15-18]。本文从案例学习的角度出发,从已有专家制图成果中获取主支流案例,从案例中获取综合知识,即利用机器学习算法训练生成分类模型指导新树状河系的主支流识别。
下游河段的多个上游河段中有且只有一个河段是主流河段,其他则是支流河段。主支流识别实际上是将上游河段中最符合主流特征的分类为主流河段,其他的分类为支流河段的过程。故常用的机器学习分类方法并不完全适用于主支流识别过程,可能会出现上游河段中不存在或者同时存在多个河段被分类为主流河段的情况。但是在分类过程中,计算得出分类为主流类别的概率能定量评价各上游河段的主流特征,可以根据分类概率值排序得出最优(即最符合主流特征)河段作为上游河段。由于朴素贝叶斯算法基于贝叶斯定理能科学定量地计算出分类概率,易于实现,且分类性能和稳健性较好。因此,本文选用朴素贝叶斯分类模型计算上游河段分类为主流类别的概率,选取概率值最大的上游河段作为主流河段,其他则全部分类为支流河段。
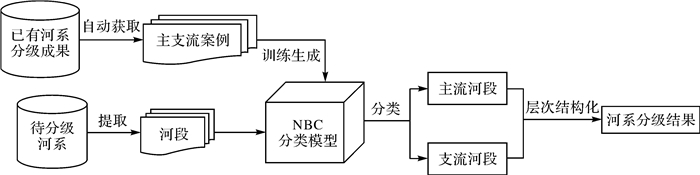
综上,本文提出基于朴素贝叶斯的树状河系自动分级方法,从已有的树状河系分级成果中自动获取主支流案例,采用朴素贝叶斯的方法对主支流案例进行学习来得到NBC分类模型,使用分类模型自下而上对上游河段识别得到主流河流,对各级河流进行层次结构化实现河系自动分级。其具体流程如图 1所示。具体步骤如下:
|
| 图 1 基于朴素贝叶斯的树状河系自动分级方法流程 Fig. 1 Flow chart of automatic classification method of tree-like river network based on NBC |
步骤1:主支流案例的定义与获取。对河段计算特征描述项作为主支流案例的属性空间,把专家分级成果中对上游河段的主支流分类结果作为主支流案例的标记。
步骤2:NBC分类模型的训练。采用朴素贝叶斯的机器学习方法对主支流案例进行训练得到NBC分类模型。
步骤3:利用NBC分类模型对新的待分级树状河系的河段计算分类为主流类别的概率,对每个交汇点处将主流概率最大的上游河段分类为主流河段,其余分类为支流河段。
步骤4:连接各级主流河段构成各级河流实体,进行层次结构化完成河系分级。
2 主支流案例的设计和获取 2.1 主支流案例设计本文将主支流案例定义为:由主支流案例对象(object)、案例特征(feature)以及案例标记(lable)组成的一条记录。采用三元表示法对主支流案例进行描述,每个案例由3部分组成,其形式化的表示为
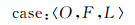 (2)
(2)
式中,案例对象(O)是指具体的河段对象及其唯一序号,如河段_ID_001;案例特征(F)中包含多项对河段的主流特征进行描述的量化指标,特征的确定与表达是案例设计的难点;案例标记(L)是指对河段的分类标记,即主流(1)、支流(0)。
2.2 主支流案例特征提取主支流案例设计中案例特征的提取是关键所在,只有选择正确的案例特征来充分反映河段的主流特征,才能获取隐含的主支流分类知识,从而利用机器学习算法训练得到行之有效的分类模型。
主流上,在河流的汇合处,上下游河段的流向几乎在一条直线上,常被称为“180°假设”[19];主流往往是最长的河流,在汇合点处也符合180°假设[20]。另外,主流一般也拥有最多的支流数[8]。本文参考相关文献,顾及语义特征、河段的局部几何特征和河流、河系的整体结构特征,选择以下6项指标作为主支流案例的案例特征(F),即NBC主支流分类模型的条件属性:
(1) 语义一致性。语义一致性指河段间的名称是否相同。属于同一条河流的河段名称往往具有语义一致性,而主流与支流的河段名称一般不同。本文对该指标值的计算方式如下:若下游河段与上游河段名称相同,则赋值为1,否则赋值为0。
(2) 汇入角度。上下游河段的汇入角度是主支流识别的重要依据,汇入角度越接近180°,作为主流河段的可能性越大。本文在计算上下游河段间夹角时,采用从交汇点处分别往外延伸3个节点所得钝角夹角的平均值作为最后的汇入角度(若少于3个节点则使用该河段全部节点)。
(3) 河段长度。河段长度指河段的长度,长度值越大,作为主流河段的可能性越大。本文计算上游河段两端节点(即交汇点)间的线要素距离作为河段长度值。
(4) 河段分叉数。河段分叉数是指河段的上游河段数量。一般来说河段分叉数越多,作为主流河段的可能性越大。
(5) 最大河流长度。河流最大长度指从河段的交汇点向上游追溯所有河源点中的最大长度。河流最大长度越多,作为主流河段的可能性越大。
(6) 上游河源数。上游河源数指河段上游所有河源口的数量。上游河源数越多,作为主流河段的可能性越大。
2.3 主支流案例获取主支流案例自动获取流程如图 2所示,具体步骤如下。

|
| 图 2 主支流案例自动获取方法流程 Fig. 2 Flow chart of automatic acquisition of main-tributary case |
步骤1:预处理。为避免原始数据中的河流流向错误,本文从河源出发,自上游向下游逐个河段检查河流流向是否一致,若上下游河段存在不一致,则改正下游河段的河流流向。然后以河段为基本单元自动构建树结构;
步骤2:案例特征和标记计算。遍历所有河段单元,计算其上游河段如2.2节所述的特征指标值;判断其上游河段的等级与该河段是否相同,如果相同则案例标记为1(主流),否则案例标记为0(支流)。
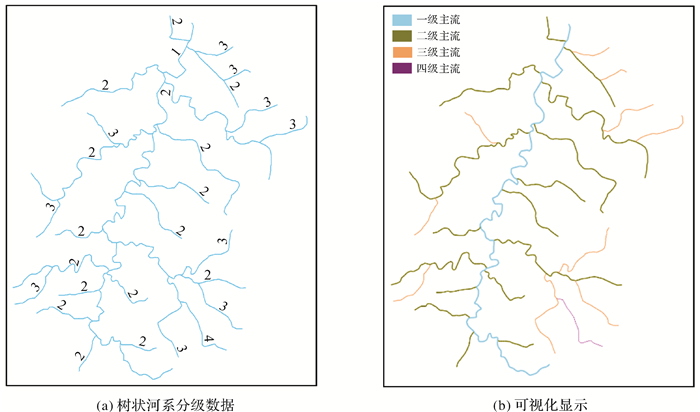
为验证本节主支流案例自动获取方法的有效性,本文通过人工筛选出某流域河系分级地图中的所有树状河系专家已分级数据作为主支流案例获取的数据源,该流域范围内的树状河系种类复杂,不同树状河系具有不同的结构和特征,能较好地反映主支流的一般关系和代表树状河系总体,其中部分河系如图 3(a)所示,图 3(b)为各级主流赋以不同颜色和宽度的可视化显示。
|
| 图 3 某流域树状河系分级数据 Fig. 3 Classification data of tree-like river network |
对该数据源使用本文案例获取方法一共得到446个主支流案例,其中主流案例为223个,支流案例为223个,部分案例如表 1所示。
| 案例对象(O) ID |
案例特征(F) | ||||||
| 语义一致性 | 汇入角度/(°) | 河段长度/m | 河段分叉数 | 最大河流长度/m | 上游河源数 | 案例标记(L) | |
| 1 | 0 | 173.40 | 2 868.21 | 2 | 5 029.39 | 2 | 1 |
| 2 | 0 | 142.57 | 2 865.67 | 0 | 2 865.67 | 1 | 0 |
| 3 | 1 | 151.93 | 221.74 | 2 | 14 650.78 | 6 | 1 |
| 4 | 0 | 100.91 | 6 421.30 | 2 | 10 478.25 | 2 | 0 |
| 5 | 1 | 161.02 | 3 859.36 | 2 | 37 165.81 | 20 | 1 |
| 6 | 0 | 129.53 | 8 712.62 | 2 | 16 279.63 | 3 | 0 |
| | | | | | | | |
3 主支流朴素贝叶斯分类模型的训练和测试
将2.3节中获取的主支流案例作为训练样本利用朴素贝叶斯算法进行训练生成主支流朴素贝叶斯分类模型。训练样本的数据总量为446个,其中主流案例样本为223个,支流案例样本为223个,并按2:1的比例随机分为训练集和测试集。
建立朴素贝叶斯分类器有3种常用模型:高斯模型、多项式模型和多元伯努利模型。
高斯模型中,每个特征都是连续的,并且都呈高斯分布。由于特征的所有属于某个类别的观测值被假设符合高斯分布,其条件概率函数为
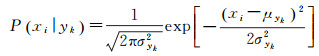 (3)
(3)
多项式模型中,特征向量表示由多项式分布生成的特定事件的频率,其条件概率函数为: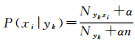
多元伯努利模型中,特征是独立的布尔(二进制变量)类型来描述输入。如果特征值xi为1,则P(xi|yk)=P(xi=1|yk);如果特征值xi为0,则P(xi|yk)=1-P(xi=1|yk)。
本文对3个模型使用相同的数据样本进行训练和测试,从中选择分类效果最好的模型,其中对模型分类效果通过训练集分类正确率、测试集分类正确率和主流识别正确率3项指标进行衡量。训练集分类正确率和测试集分类正确率分别是分类模型在训练集和测试集上的分类正确率,主流识别正确率是指分类模型在测试集上能正确识别出上游的主流河段的比率。其中对主流识别正确的定义为主流河段分类为主流类别的概率大于其他任何上游河段。经训练,对不同模型的分类效果指标统计如表 2所示。
| (%) | |||
| 朴素贝叶斯模型 | 训练集分类正确率 | 测试集分类正确率 | 主流识别正确率 |
| 高斯模型 | 85.382 | 82.759 | 96.552 |
| 多项式模型 | 86.379 | 80.670 | 84.828 |
| 多元伯努利模型 | 79.070 | 73.793 | 81.379 |
需要说明的是,测试集分类正确率不高,但并不影响本文方法的主支流识别结果,其相对不高的原因是由于主支流分类的特殊性。因为主支流分类是相对的,并无绝对的分类标准,主支流识别实际上是将上游河段中最符合主流特征的分类为主流河段,其他的分类为支流河段的过程。故存在较多主流特征不明显的主流河段(同一交汇处的支流河段主流特征更不明显)和主流特征较为明显的支流河段(同一交汇处的主流河段主流特征更加明显)。而这些河段同样也作为案例出现在训练集和测试集中,从而导致主流特征不明显的主流河段被分类为“支流”,与主流特征较为明显的支流河段被分类为“主流”,因而测试集的分类正确率不高。例如,表 3中同一交汇处上游的5号和6号河段由于汇入角度、河段长度等主流特征均不明显,均被直接分类为支流河段;相反,另一交汇处上游的8号、17号河段由于主流特征明显,均被直接分类为主流河段。该直接分类结果与案例原始的标记不符,所以造成了测试集分类正确率不高。
| ID | 上游河段ID | 语义一致性 | 汇入角度 /(°) |
河段长度 /m |
河段分叉数 | 最大河流长度 /m |
上游河源数 | 标记 | 直接分类结果 | 支流分类概率 | 主流分类概率 | 概率分类结果 |
| 5 | 1 | 0 | 116.87 | 3 335.21 | 0 | 3 335.21 | 1 | 主流 | 支流 | 0.997 617 67 | 0.002 382 33 | 支流 |
| 6 | 1 | 0 | 122.65 | 2 531.75 | 0 | 2 531.75 | 1 | 支流 | 支流 | 0.996 337 73 | 0.003 662 27 | 主流 |
| 8 | 7 | 0 | 159.98 | 2 107.89 | 2 | 10 554.61 | 3 | 支流 | 主流 | 0.474 085 7 | 0.525 914 3 | 支流 |
| 17 | 7 | 1 | 138.95 | 8 156.74 | 2 | 17 336.21 | 2 | 主流 | 主流 | 0.014 561 19 | 0.985 438 81 | 主流 |
也正是因为主支流分类的特殊性,本文方法不是通过简单的直接分类来识别主支流,而是使用分类模型对待分类树状河系中的河段计算其分类为主流的概率,在每个交汇点处以概率最大的上游河段作为主流河段。例如,上表中的5号和6号河段二者计算所得的主流分类概率分别为0.002 382 33和0.003 662 27,通过比较概率将原本直接分类为“支流”的6号河段最终分类为“主流”,而8号、17号河段分别为0.525 914 3和0.985 438 81,则将原本分类为“主流”的8号河段最终分类为“支流”,从而避免了主支流分类模型直接分类所导致的错误识别结果。因此,较训练集分类正确率和测试集分类正确率而言,主流识别正确率指标能更好地衡量本文方法中分类模型对主支流识别效果。
由统计数据可以看出,多元伯努利模型的3项指标均为最低,说明其在主支流分类效果最差;多项式模型虽然其训练集分类正确率最高,但测试集分类正确率却略低于高斯模型,且主流识别正确率远低于高斯模型,这说明高斯模型的主支流分类的实用效果要强于多项式模型。因此,本文选用高斯模型训练得到主支流朴素贝叶斯分类模型。
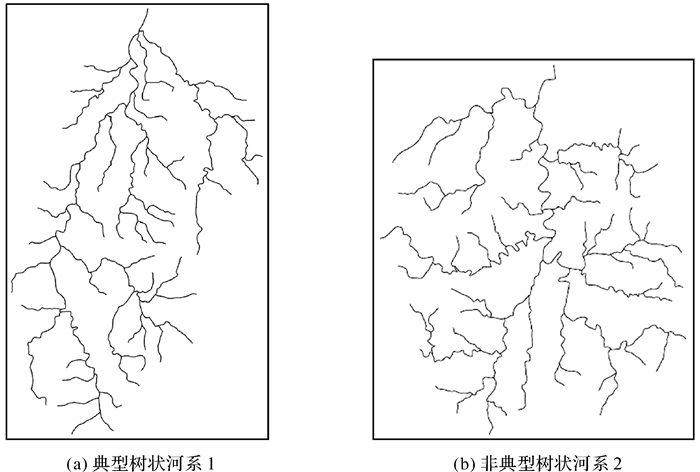
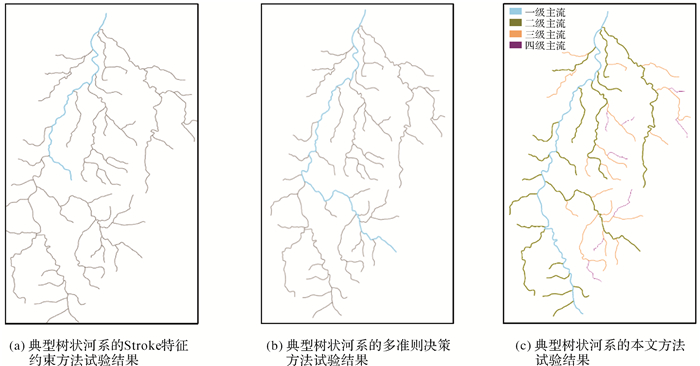
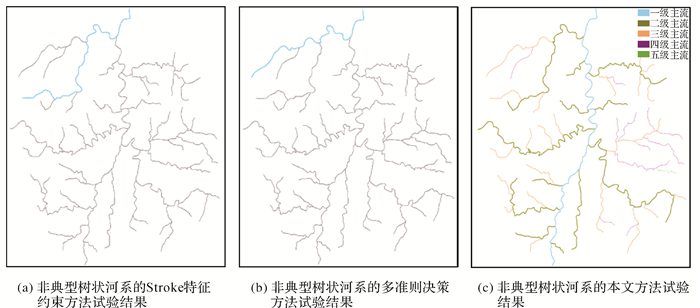
4 试验与分析为验证本文方法的有效性和实用性,分别对某流域未分级的树状河系1和树状河系2(如图 4所示)进行主支流识别的试验(河系1为典型树状河系,即河系的主流现象较为明显,各级河流之间的主流特征差别较大,共拥有89个河段;河系2为非典型树状河系,即河系的主流现象不明显,各级河流之间的主流特征差别较小,共拥有97个河段),其中部分计算过程和数值如表 4所示。同时选用多准则决策方法(文献[8])和Stroke特征约束方法(文献[11])作为对比,试验结果如图 5和图 6所示。图 5(a)、图 6(a)分别是典型树状河系和非典型树状河系的Stroke特征约束方法一级主流识别结果,图 5(b)、图 6(b)分别是典型树状河系和非典型树状河系的多准则决策方法一级主流识别结果,图 5(c)、图 6(c)分别为典型树状河系和非典型树状河系的本文方法分级结果,其中蓝色线条为一级主流。
|
| 图 4 河系1和河系2分级试验数据 Fig. 4 River network 1&2 experimental data |
| ID | 上游河段ID | 语义一致性 | 汇入角度 /(°) |
河段长度 /m |
河段分叉数 | 最大河流长度 /m |
上游河源数 | 支流分类概率 | 主流分类概率 | 分类结果 |
| 63 | 89 | 1 | 156.81 | 405.21 | 2 | 55 564.07 | 39 | 0 | 1 | 主流 |
| 2 | 89 | 0 | 110.91 | 9 313.63 | 2 | 32 123.43 | 6 | 0.000 000 08 | 0.999 999 92 | 支流 |
| 1 | 63 | 0 | 128.26 | 5 728.15 | 2 | 9 063.36 | 2 | 0.940 453 04 | 0.059 546 96 | 支流 |
| 64 | 63 | 1 | 155.48 | 2 870.18 | 2 | 55 158.86 | 37 | 0 | 1 | 主流 |
| 5 | 2 | 0 | 166.58 | 7 956.68 | 0 | 7 956.68 | 1 | 0.981 121 18 | 0.018 878 82 | 主流 |
| 21 | 2 | 0 | 141.57 | 9 914.59 | 0 | 9 914.59 | 1 | 0.989 512 52 | 0.010 487 48 | 支流 |
| | | | | | | | | | | |
|
| 图 5 典型树状河系的不同方法试验结果 Fig. 5 Results of different methods(atypical tree-like river network) |
|
| 图 6 非典型树状河系的不同方法试验结果 Fig. 6 Results of different methods(atypical tree-like river network) |
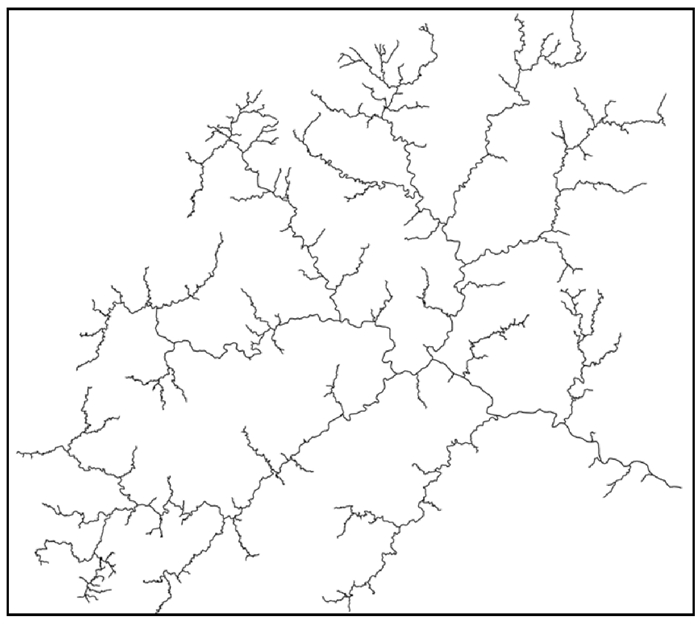
为进一步验证本文方法对复杂树状河系的分级效果,选用树状河系3(某流域全部树状河系,共拥有424个河段,如图 7所示)进行分级试验,分级结果如图 8所示。
|
| 图 7 河系3试验数据 Fig. 7 River network 3 experimental data |
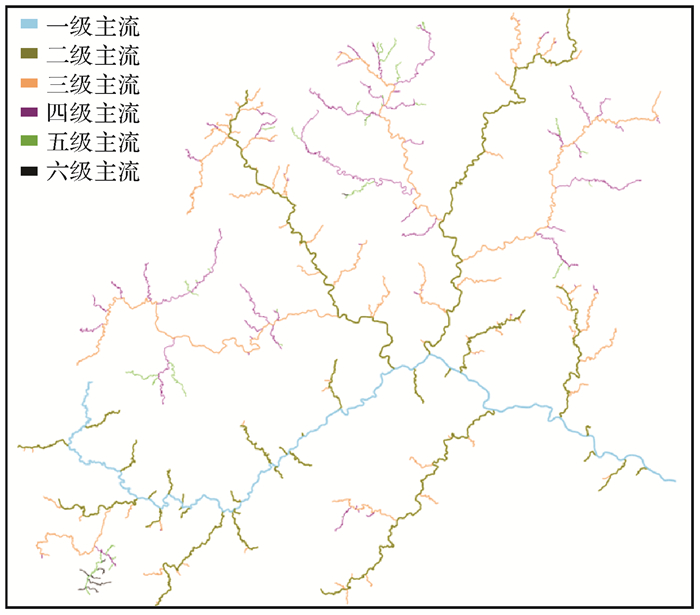
|
| 图 8 河系3的分级试验结果 Fig. 8 Classification result of river network 3 |
由主流识别结果可以看出:
(1) Stroke特征约束方法通过长度优先性和方向一致性来确定主流,仅考虑上游河段的局部几何特征,而忽略了河流的整体结构特征,导致其主流识别趋向于局部的长度最大和方向一致。在典型树状河系和非典型树状河系中都存在有将较长的支流河段误分类为主流河段的情况,其主流识别结果并不符合主流拥有最多、最复杂的支流的整体结构特征。
(2) 多准则决策方法仅包含长度、角度、支流数3项指标,没有考虑到最大河流长度、上游河源数等反映整体结构特征的指标,导致其主流识别结果在复杂情况下容易出现判断错误,尤其是对于主流与支流差异较小的非典型树状河系时误分类现象较为明显。且该方法识别每一级主流时都需要遍历河系全部河流造成计算开销较大,主流识别效率较低。
(3) 本文方法的主流识别结果则有效兼顾了长度最大、角度最平缓和支流最多的主流特征,识别效果较上述方法更好,在典型树状河系、较为复杂的非典型树状河系和更为复杂的整幅流域河系中都能正确识别主支流,分类后所得主流的主流特征明显,与人工识别结果较为一致。
由分级结果可以看出:由于主支流识别合理,本文对于典型树状河系和非典型树状河系的自动分级方法都取得了良好的效果,河系层次结构合理,各级主流等级关系分明,父子关系和左右支关系清晰,满足制图要求。
经分析总结,本文树状河系自动分级方法的特点如下:
(1) 本文使用语义一致性、汇入角度、河段长度、河段分叉数、最大河流长度和上游河源数6项指标来描述河段的主流特征,兼顾了局部几何特征和整体结构特征,使NBC分类模型能更好地识别出主流河段。
(2) 本文方法基于案例学习,采用了朴素贝叶斯的机器学习方法对从已有分级成果中获取的主支流案例进行训练,较好地利用了专家分级经验和知识,有效解决了多指标综合评价的权重设定模糊问题,提高了河系分级的智能化和知识化水平。
(3) 本文方法具有较强的学习能力,随着案例样本数据质量和数量的增加以及对河段主流特征的属性描述项的完善,本文方法将会进一步提升获取主支流分类的综合知识的质量和数量,从而提高对河段的主支流分类性能,实现更好的分级效果。
5 结论本文提出了一种基于朴素贝叶斯的树状河系自动分级方法,通过对上游河段分类为主流类别的概率来确定主流河段。首先从已有分级成果中获取主支流案例,案例特征项对河段的主流特征描述兼顾了局部几何特征和整体结构特征,然后使用朴素贝叶斯的机器学习方法训练得到NBC分类模型,将待分级河系中的河段自下游向上游进行主支流分类识别,最后完成层次结构化实现自动分级。本文方法NBC分类模型的分类正确率较高,主支流识别结果有效反映了长度最大、角度最平缓和支流最多的主流特征,较好地还原了专家意图,分级结果等级清晰,层次分明。整个分级过程实现了河系分级知识由专家分级成果至专家主支流案例再到主支流分类NBC分类模型的有效获取和表达,提高了树状河系分级的智能化和知识化水平。
本文进一步的研究工作是:对河系中河流方向错误的自动判别方法研究;结合图论等数学方法继续挖掘更能反映主流特征的主支流案例特征项和获取更多高质量主支流案例以增强NBC分类模型的分类性能。
| [1] |
郭庆胜.
地图自动综合理论与方法[M]. 北京: 测绘出版社, 2002.
GUO Qingsheng. Theory and method of automatic map generalization[M]. Beijing: Surveying and Mapping Press, 2002. |
| [2] |
王家耀.
普通地图制图综合原理[M]. 北京: 测绘出版社, 1993.
WANG Jiayao. Principles of cartographic generalization of map[M]. Beijing: Surveying and Mapping Press, 1993. |
| [3] |
杜清运.
地图数据库中的结构化河网及其自动建立[J]. 武汉测绘科技大学学报, 1988, 13(2): 70–77.
DU Qingyun. The automatic establishment of structured river network in cartographic database[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1988, 13(2): 70–77. |
| [4] |
毋河海.
河系树结构的自动建立[J]. 武汉测绘科技大学学报, 1995, 20(S1): 7–14.
WU Hehai. Automatic establishment of river tee structure[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1995, 20(S1): 7–14. |
| [5] |
郭庆胜.
河系的特征分析和树状河系的自动结构化[J]. 地矿测绘, 1999(4): 7–9.
GUO Qingsheng. Analysing the characters of the networks of rivers and structuralizing the tree-like network of rivers automatically[J]. Surveying and Mapping of Geology and Mineral Resources, 1999(4): 7–9. |
| [6] |
沈涛, 苏山舞.
基于DEM的河流多尺度显示研究[J]. 测绘科学, 2003, 28(2): 20–22.
SHEN Tao, SU Shanwu. Study of the multi-scale display of river based on DEM[J]. Science of Surveying and Mapping, 2003, 28(2): 20–22. DOI:10.3771/j.issn.1009-2307.2003.02.006 |
| [7] |
赵春燕.水系河网的Horton编码与图形综合研究[D].武汉: 武汉大学, 2004. ZHAO Chunyan. Research on Horton code and graphic generalization of catchment[D]. Wuhan: Wuhan University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10486-2006035679.htm |
| [8] |
谭笑, 武芳, 黄琦, 等.
主流识别的多准则决策模型及其在河系结构化中的应用[J]. 测绘学报, 2005, 34(2): 154–160.
TAN Xiao, WU Fang, HUANG Qi, et al. A multi-criteria decision model for identifying master river and its application in river system construction[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 154–160. DOI:10.3321/j.issn:1001-1595.2005.02.012 |
| [9] |
郭庆胜, 黄远林.
树状河系主流的自动推理[J]. 武汉大学学报(信息科学版), 2008, 33(9): 978–981.
GUO Qingsheng, HUANG Yuanlin. Automatic reasoning on main streams of tree river networks[J]. Geomatics and Information Science of Wuhan University, 2008, 33(9): 978–981. |
| [10] |
翟仁健, 薛本新.
面向自动综合的河系结构化模型研究[J]. 测绘科学技术学报, 2007, 24(4): 294–298, 302.
ZHAI Renjian, XUE Benxin. A structural river network data model for automated river generalization[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2007, 24(4): 294–298, 302. DOI:10.3969/j.issn.1673-6338.2007.04.017 |
| [11] |
李成名, 殷勇, 吴伟, 等.
Stroke特征约束的树状河系层次关系构建及简化方法[J]. 测绘学报, 2018, 47(4): 537–546.
LI Chengming, YIN Yong, WU Wei, et al. Method of tree-like river networks hierarchical relation establishing and generalization considering Stroke properties[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(4): 537–546. DOI:10.11947/j.AGCS.2018.20170141 |
| [12] |
周志华.
机器学习[M]. 北京: 清华大学出版社, 2016.
ZHOU Zhihua. Machine learning[M]. Beijing: Tsinghua University Press, 2016. |
| [13] |
王峻.朴素贝叶斯分类模型的研究与应用[D].合肥: 合肥工业大学, 2006. WANG Jun. Research and application of naive Bayesian classification model[D]. Hefei: Hefei University of Technology, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10359-2006072733.htm |
| [14] |
钱海忠, 武芳, 王家耀.
自动制图综合及其过程控制的智能化研究[M]. 北京: 测绘出版社, 2012.
QIAN Haizhong, WU Fang, WANG Jiayao. Study of automated cartographic generalization and intelligentized generalization process control[M]. Beijing: Surveying and Mapping Press, 2012. |
| [15] |
郭敏, 钱海忠, 黄智深, 等.
道路网智能选取的案例类比推理法[J]. 测绘学报, 2014, 43(7): 761–770.
GUO Min, QIAN Haizhong, HUANG Zhishen, et al. Intelligent road-network selection using cases based reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 761–770. DOI:10.13485/j.cnki.11-2089.2014.0120 |
| [16] |
何海威, 钱海忠, 刘闯, 等.
采用决策树算法进行居民地自动综合[J]. 测绘科学技术学报, 2016, 33(6): 623–628.
HE Haiwei, QIAN Haizhong, LIU Chuang, et al. Auto generalization of settlement by using decision tree algorithm[J]. Journal of Geomatics Science and Technology, 2016, 33(6): 623–628. |
| [17] |
谢丽敏, 钱海忠, 何海威, 等.
基于案例推理的居民地选取方法[J]. 测绘学报, 2017, 46(11): 1910–1918.
XIE Limin, QIAN Haizhong, HE Haiwei, et al. A habitation selection method by using case-based reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11): 1910–1918. DOI:10.11947/j.AGCS.2017.20170061 |
| [18] |
何海威, 钱海忠, 谢丽敏, 等.
立交桥识别的CNN卷积神经网络法[J]. 测绘学报, 2018, 47(3): 385–395.
HE Haiwei, QIAN Haizhong, XIE Limin, et al. Interchange recognition method based on CNN[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 385–395. DOI:10.11947/j.AGCS.2018.20170265 |
| [19] | PAIVA J, EGENHOFER M J, FRANK A U. Spatial reasoning about flow directions: towards an ontology for river networks[C]//Proceedings of the ⅩⅤⅡ International Congress for Photogrammetry and Remote Sensing.[S.l.]: ISPRS, 1992: 224-318. |
| [20] |
郝志伟, 李成名, 殷勇, 等.
一种启发式有环河系自动分级算法[J]. 测绘通报, 2017(10): 68–73.
HAO Zhiwei, LI Chengming, YIN Yong, et al. A heuristic algorithm for automatic classification of river system with ring[J]. Bulletin of Surveying and Mapping, 2017(10): 68–73. DOI:10.13474/j.cnki.11-2246.2017.0318 |



