2. 中国测绘科学研究院, 北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
抽样检验是质量管理中的重要统计技术手段,特别是在破坏性检验、可靠性检验以及寿命试验、连续批检验和散料检验中发挥着巨大的作用。通过抽取一定量的样品进行检验,既可以对一批产品的质量作出判断,同时又不需要付出太大的工作量,对产品的生产管理和分析影响产品质量的因素具有重要意义。针对产品的抽样,国际上普遍采用的是ISO 2859.1-1999标准,国内制定的GB/T2828.1-2012[1]完全采用这一国际标准。该标准也是我国工业产品的质量控制的基础性标准之一。
相比工业产品,测绘地理信息产品无论在产品形态、生产工艺、仪器设备和生产环境,还是在产品管理、流通和产品服务等方面都存在很大的不同。因此,为了适应测绘地理信息产品的特殊要求,国家发布了专门针对测绘地理信息产品质量检验的国家标准GB/T24356-2009与GB/T18316-2008[2-3],对测绘地理信息产品的抽样、质量元素、检验参数、质量评定和判定进行了规定。虽然这两项标准在国家和地方的基础测绘以及各个行业测绘领域中发挥了重要作用,但是随着以新型基础测绘为代表的测绘地理信息智能化的发展,其在抽样方案、产品质量参数、质量评定判定准则等方面逐渐显现出不完善、不适应的现象,特别是在生产中的“小批量分段”和“大批量分批”抽样方案与数字化、信息化和智能化测绘地理信息出现的大批量产品检验非常不适应。同时,国家标准GB/T24356-2009对弃真错误概率给出了“零概率”要求的同时,而未对不合格产品通过合格检验的“纳伪”错误概率给出相应的规定,导致生产管理实际中出现一定风险。
针对测绘地理信息产品质量检验的抽样方案,文献[4]采用OC曲线分析方法,给出了推荐的GIS产品不合格率3%~5%极限质量;文献[5]采用OC曲线分析方法,对连续大批量空间数据质量抽样检验方案进行分析,给出了不同条件下的空间数据质量检验的AQL值;文献[6]提出了GIS数字地图1/m子幅抽样检验概念,采用OC曲线分析方法给出了典型抽样方案。其他相关的研究多数都是从抽样方案的实际操作方面讨论[7],而对测绘地理信息产品质量检验的“弃真”和“纳伪”概率的研究,文献相对较少。学术上研究较多的是测量的不确定性以及不确定性表征[8-19]。这些研究主要是针对给定的地理信息产品如何客观真实反映其自身质量状况,属于抽样检验的检验技术范畴。
本文从假设检验的两类错误概率分布出发,对测绘地理信息产品质量检验的抽样方案进行分析,给出两类错误概率的计算方法,同时计算了典型的抽样方案的两类错误概率,重点对现行的大批量测绘产品分批抽样检验进行了讨论,提出了低不合格率总体条件下,抽样检验自身的高“纳伪”概率将导致抽样检验的失真性,在并通过实际算例计算了导致检验结论失真的质量边界。
1 假设检验的两类错误 1.1 两类错误的定义为了推断总体的某些性质,需要先提出关于总体的假设,然后从总体中随机抽取样本,根据样本的检验和分析,对提出的假设作出判断:是接受还是拒绝。一般可表示为
 (1)
(1)
式中,H1与H0通常为互补条件。针对H1检验H0,H0称为原假设,H1称为备择假设。由于检验结论是根据样本给出的,总有可能出现错误的判断。当假设H0实际上为真,检验拒绝H0,称为第Ⅰ类错误,又叫弃真错误;当H0实际不真,检验接受H0,称为第Ⅱ类错误,又叫纳伪错误。犯第Ⅰ类错误的概率,记为α,又称为生产方风险,即合格批被拒收。犯第Ⅱ类错误的概率,记为β,又称为使用方风险,即不合格批被接受。在实际应用中,应照顾双方的利益,使生产方风险和使用方风险都尽可能控制在一定的范围[20-22]。
1.2 两类错误概率的计算两类错误概率的计算等价于计算检验统计量落入特定拒绝域的概率[22]。对检验问题(H0、H1),构造样本空间Ω的集合分割:W和W=Ω-W, 当定义W为拒绝域,则W为接受域。根据两类错误的定义,则有
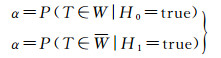 (2)
(2)
式中,P(x)为概率分布函数;T为检验统计量;W为拒绝域。对零假设H0,本来是正确的,由于样本的随机性,统计量落入拒绝域W,错误地将该假设否定,其概率为α;同样,对零假设H0,本来是错误的,由于样本的随机性,统计量落入接受域W,错误地将该假设接受,其概率为β。α值的计算实际上等价于拒绝域W的确定,由给定的分布函数P可直接确定。但β的计算需要另外给定一个样本空间Ω的集合划分:W′和W′=Ω-W′才能唯一确定β(图 1)。故
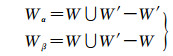 (3)
(3)
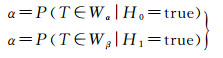 (4)
(4)

|
| 图 1 两类错误拒绝域集合 Fig. 1 The reject sets of two types errors |
图 1显示,对给定的集合总体,压缩拒绝域W,W′必然扩大,同理压缩拒绝域W′,W必然扩大。要想同时减小W、W′,必然扩大集合总体。
2 测绘地理信息产品抽样检验的两类错误 2.1 抽样检验的抽样方案抽样方案是指抽样检验中所用的样本和有关接收准则的组合[23-24]。抽样方案既包括从批量中怎样抽样,又包括对批次合格/不合格的判定准则,因此,必须在抽样检验前定出样本量和鉴别该批产品是否合格的标准(接收准则)。通常采用四元组(N, n, Ac, Re)[1, 23]表示抽样方案模型,其中N为批量,n为抽取的样本量,Ac为可接受的不合格品数,Re为拒绝的不合格品数。
对给定的抽样方案(N, n, Ac, Re),其检测通过的概率服从超几何分布
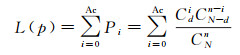 (5)
(5)
式中,Pi为该抽样中不合格品数为i概率。根据产品的不合格率p,d=N×p。当N>10n,且p < 10%(文献[23-24]),对于给定不合格率的计数型大批量简单随机抽样,可近似采用二项分布代替超几何分布,即
 (6)
(6)
由L(p)构成的曲线称为该方案的抽样操作特性曲线[23],即OC曲线。OC曲线反映了抽样方案的检验通过概率与产品不合格率的分布关系。对给定的质量水平p0与p1,在不考虑检验误差的条件下,式(4)即为
 (7)
(7)
GB/24356-2009采用了计数型一次简单随机抽样方法[1, 23-25],并规定当不合格数为0,判定批合格;当不合格数大于等于1,判定批不合格,即Ac=0,Re=1。该抽样方案(N, n, 0, 1)可表述为从批量为N的产品中随机抽取n个样品进行检验,若其中不合格品数为0,就可以较高的概率接受该批产品;若其中不合格品数大于等于1,则以较高的概率拒绝该批产品。表 1为该标准规定的抽样表。当测绘地理信息成果的批量超过200,需要进行均匀分批,再按此表抽样,进行检验。
| 批量 | 样本量 | 批量 | 样本量 |
| 1-20 | 3 | 101-120 | 11 |
| 21-40 | 5 | 121-140 | 12 |
| 41-60 | 7 | 141-160 | 13 |
| 61-80 | 9 | 161-180 | 14 |
| 81-100 | 10 | 181-200 | 15 |
| 201- | 分批次提交,批次数应最小,各批次的批量应均匀 | ||
| 说明 | 当样本量等于或大于批量时,则全数检查 | ||
依据表 1,选取其中的典型抽样方案,计算3种不同质量水平pi情况下的两类错误概率,见表 2(其中,由于表 1中批量相对较小,p1采用不合格数表示,即批量为N的产品中存在p1个不合格品)。
| 序号 | N | n | α(p0=0) | β(p1=1) | β(p1=2) | β(p1=5) |
| 1 | 20 | 3 | 0.00 | 0.850 | 0.716 | 0.399 |
| 2 | 40 | 5 | 0.00 | 0.875 | 0.763 | 0.493 |
| 3 | 60 | 7 | 0.00 | 0.883 | 0.779 | 0.525 |
| 4 | 80 | 9 | 0.00 | 0.887 | 0.786 | 0.542 |
| 5 | 100 | 10 | 0.00 | 0.900 | 0.809 | 0.584 |
| 6 | 120 | 11 | 0.00 | 0.908 | 0.824 | 0.613 |
| 7 | 140 | 12 | 0.00 | 0.914 | 0.835 | 0.635 |
| 8 | 160 | 13 | 0.00 | 0.918 | 0.844 | 0.651 |
| 9 | 180 | 14 | 0.00 | 0.922 | 0.850 | 0.664 |
| 10 | 200 | 15 | 0.00 | 0.925 | 0.855 | 0.674 |
很显然,基于原假设p0=0,依据GB/T24356-2009的检验方案,“弃真”概率α全为0,等价于W为空。对应给定的p1=1, 2, 5等3种情况下,“纳伪”概率表现为:①随着产品的质量的下降而降低,随着批量的增大而增大(实际上由于不合格数不变,等价为产品质量提升);②测绘地理信息产品采用了200为批量的上限,在仅有一个不合格品条件下,“纳伪”概率最小值为0.850,即采用(20,3,0,1)的抽样方案,批量为20个单位,其中存在一个不合格品,被检验为合格品的概率为0.85。表 2反映GB/T24356-2009的检验方案对应的“纳伪”概率普遍较高,使用方风险较大。
3 测绘地理信息产品大批量抽样检验 3.1 大批量产品检验总体通过概率的等价性依据GB/T24356-2009的要求,当批量大于200时,要将总体划分为不同的批,且要求批次最小,各批批量均匀。假设总体为N(N>200)分为批量为Ni(Ni≤200)的k个批次,根据表 1,抽取Ni对应的样本量ni,则根据概率分布规律,有
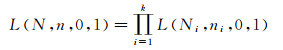 (8)
(8)
式中,
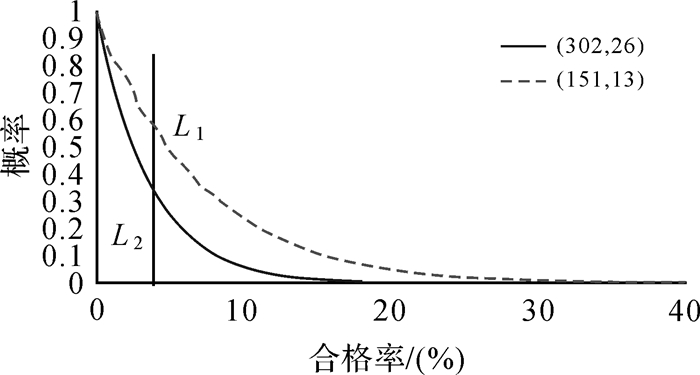
假定总体为302个单位,则需要将该总体分为151个单位的两个批次。根据表 1,需要分别抽取13个单位,则抽样方案(302,26,0,1)和(151,13,0,1)的OC曲线如图 2。图 2显示整体合格的概率L2等于分批概率L1的平方。通过将一个大总体进行分批,每个批次检测通过的概率得到提升,降低了整体被拒绝的风险。同时,对各个批次而言,检测被拒绝,只是拒绝当前批次,当前不合格品的作用范围限定在当前批内。而整体检验,不合格品的作用范围扩展到整个总体。相比而言,采用大批量的分批检验,实际上是实施了放松检验。
|
| 图 2 大总体分批抽样方案的OC曲线 Fig. 2 OC-curve lines of different sampling plans With big lots |
3.2 大批量的质量检验两类错误概率
根据假设检验的定义,原假设为该批产品中无不合格品,即在302个单位产品中p0=0;备择假设为该批产品中有不合格品。假设在302个单位产品中存在p1=2件不合格品,分别计算整体检验和分批检验情况下的两类错误概率如表 3、表 4。
| N | n | α(p0=0) | β(L(p1)(p1=2) | β′(p1=2) |
| 302 | 26 | 0.000 | 0.835 | 0.165 |
| N | n | α (p0=0) |
β(L(p1)) (p1=1) |
β′ (p1=1) |
L(p1)×L(p1) (p1=2) |
β′×β′ (p1=2) |
| 151 | 13 | 0.000 | 0.914 | 0.086 | 0.835 | 0.007 |
表 3给出了整体检验时,两类错误概率的计算值,其中β′为假设备择假设为真、实际检验备择假设也为真的概率。表 4中给出了分批检验时,单批检验的两类错误概率,以及由单批计算的总体检验通概率值和总体检验不通过的概率。数值显示,对相同的抽样样本量,无论整体检验还是分批检验,总体检验通过的概率是等价的。同时,由于分批检验减小了批量,相应单批也减小了样本量,因此,客观上计数型简单随机抽样的整数特性表现为不合格率的降低,所以,单批检验通过概率增大,其代价为“纳伪”概率的增加,整体检验不通过的概率显著减小。
3.3 大批量抽样检验的失真性随着信息化、智能化技术的发展,以DLG、DOM、DEM、DRG为代表的数字化产品大多都是(超)大批量形态。尽管测绘地理信息成果的生产越来越多地采用自动化的手段,但是毕竟生产过程还需要各种设备、人员的参与,生产的工艺流程还存在一定的不完善,所以,随着批量的增大,测绘地理信息产品中出现不合格品必然是一个大概率事件,即测绘地理信息产品的不合格率必然p0>0。则对批量为N的总体,不合格数
 (9)
(9)
对于产品质量均匀的总体,采用简单随机抽样从其中抽取n个样品,则样品不合格率应该与总体一样,则样品中的不合格数
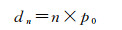 (10)
(10)
因此,随着批量的增大,dn一定大于零。依据GB/T24356-2009的抽样方案(N, n, 0, 1),则必然被拒接。对于总体检验,则拒绝总体,采用分批检验,则拒绝对应的批次。本质上,该现象表现为抽样方案中Ac=0的必然结果,体现了该抽样方案对大批量的总体检验的不合理性。
另一方面,对测绘生产而言,要求所有的产品全部都合格是测绘地理信息服务的客观需要,通过对大批量总体的分批检验处理,人为提高了总体检验通过的概率,必然增加“纳伪”错误概率的风险。表 5显示抽样方案(302,26,0,1)在5种不同假设条件下,原假设的“纳伪”错误的概率值。数据表明,当批量中存在少量不合格品时(整体不合格率小于2%),检验通过表现为一个大概率事件;当批量中存在的不合格品数达到一定量(整体不合格率大于5%),该检验方案能够以较高的概率拒绝该批产品。因此,当整体不合格率处于较低水平时,现行的抽样方案存在一定的失效性,将不能很好反映质量真实状况。
| N | n | β(L(p1)) (p1=2) |
β(L(p1)) (p1=6) |
β(L(p1)) (p1=12) |
β(L(p1)) (p1=18) |
β(L(p1)) (p1=30) |
| 302 | 26 | 0.835 | 0.580 | 0.333 | 0.189 | 0.058 |
这种现象本质上表现为计数型随机抽样检验的固有特性,所以,在要求“弃真”概率α为0的条件。对于存在少量不合格品的批量,随机抽样检验的高“纳伪”错误概率将是不可避免,也意味着需要增大样本量或者采用非随机抽样的检测方法才能准确把握质量状况。
4 结论与展望本文从概率分布的角度,给出了测绘地理信息产品质量检验中的两类错误概率的计算方法,并针对GB/T24356-2009规范中的采用的抽样方案,实际计算了该标准中典型抽样方案的两类错误概率值,分析了该标准中“纳伪”概率控制的不完善性,为使用该标准提供了风险控制的计算方法。
同时结合测绘地理信息质量检验的应用需要,重点对大批量抽样检验进行了讨论,从概率的角度说明了大批量整体检验与分批检验对整体检验通过概率的等价性;基于“纳伪”概率计算,验证了现行抽样方案在低不合格率(小于5%)的条件下,将导致大批量产品检验的高“纳伪”概率。本质上,这种高“纳伪”概率是计数型随机抽样检验的固有特性,也意味着对于存在少量不合格品的批量,随机抽样检验的高“纳伪”错误概率将是不可避免。
因此,一方面,对水准控制点、GNSS控制点为代表的大地测量、工程测量成果,采用抽样检验确定批成果的整体质量是不合适的。因为任何一个点的错误可能带来严重的后果。另一方面,对大批量的图类成果,或者重复生产的地理信息产品,需要根据质量控制指标、检验方式、检验成本等因素,综合优化设计抽样方案。GB/T24356-2009标准中的抽样方案本身就是在综合考虑了特定生产水平和生产方式条件下基础测绘地理信息成果的基本质量要求、人工检验方式和检验费用成本定额的条件下制定的,本文的研究内容只是该优化问题的一个方面,笔者也将在后续的研究中对该问题进行深入分析。
| [1] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 2828.1-2012计数抽样检验程序第1部分: 按接收质量限(AQL)检索的逐批检验抽样计划[S].北京: 中国标准出版社, 2012. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, China National Standardization Management Committee. GB/T 2828.1-2012 Sampling procedures for inspection by attributes-Part 1: Sampling schemes indexed by acceptance quality limit (AQL) for Lot-By-Lot inspection[S]. Beijing: Standard Press of China, 2012. |
| [2] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T24356-2009测绘成果质量检查与验收[S].北京: 中国标准出版社, 2009. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, China National Standardization Management Committee. GB/T24356-2009 Specifications for quality inspection and acceptance of surveying and mapping products[S]. Beijing: Standard Press of China, 2009. |
| [3] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T18316-2008数字测绘成果质量检查与验收[S].北京: 中国标准出版社, 2008, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, China National Standardization Management Committee. GB/T18316-2008 Specifications for inspection and acceptance of quality of digital surveying and mapping achievements[S]. Beijing: Standard Press of China, 2008. |
| [4] |
刘大杰, 刘春.
GIS数字产品质量抽样检验方案探讨[J]. 武汉测绘科技大学学报, 2000, 25(4): 348–352, 361.
LIU Dajie, LIU Chun. Study on sampling inspection schemes to digital products in GIS[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(4): 348–352, 361. |
| [5] |
王振华, 童小华, 梁丹, 等.
连续大批量空间数据质量抽样检验方案[J]. 同济大学学报(自然科学版), 2010, 38(5): 749–752.
WANG Zhenhua, TONG Xiaohua, LIANG Dan, et al. Sampling inspection schemes for continuous lot spatial data[J]. Journal of Tongji University (Natural Science), 2010, 38(5): 749–752. DOI:10.3969/j.issn.0253-374x.2010.05.021 |
| [6] |
刘春, 刘大杰, 史文中.
GIS数字地图质量子幅抽样方案的探讨[J]. 测绘学报, 2002, 31(S1): 99–102.
LIU Chun, LIU Dajie, SHI Wenzhong. Study of quality sampling inspection with seed-map to digital products in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(S1): 99–102. DOI:10.3321/j.issn:1001-1595.2002.z1.021 |
| [7] | GLASER B G, STRAUSS A L. The discovery of grounded theory:strategies for qualitative research[M]. Chicago: Aldine, 1967. |
| [8] | ALKHATIB H, NEUMANN I, KUTTERER H. Uncertainty modeling of random and systematic errors by means of monte carlo and fuzzy techniques[J]. Journal of Applied Geodesy, 2009, 3(2): 67–79. |
| [9] |
杨元喜.
卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646–650.
YANG Yuanxi. Some notes on uncertainty, uncertainty measure and accuracy in satellite navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646–650. |
| [10] | HELTON J C, JOHNSON J D, SALLABERRY C J, et al. Survey of sampling-based methods for uncertainty and sensitivity analysis[J]. Reliability Engineering & System Safety, 2006, 91(10-11): 1175–1209. |
| [11] |
史文中.
空间数据与空间分析不确定性原理[M]. 北京: 科学出版社, 2005.
SHI Wenzhong. Principle of Modelling Uncertainties in spatial data and analysis[M]. Beijing: Science Press, 2005. |
| [12] |
李德仁.
对空间数据不确定性研究的思考[J]. 测绘科学技术学报, 2006, 23(6): 391–392.
LI Deren. Some Thoughts on spatial data uncertainty in GIS[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(6): 391–392. DOI:10.3969/j.issn.1673-6338.2006.06.001 |
| [13] |
承继成, 金江军.
地理数据的不确定性研究[J]. 地球信息科学, 2007, 9(4): 1–4.
CHENG Jicheng, JIN Jiangjun. The uncertainty of geographic data[J]. Geo-Information Science, 2007, 9(4): 1–4. DOI:10.3969/j.issn.1560-8999.2007.04.001 |
| [14] |
舒红, 齐翠红.
地理信息时态不确定性的语义与计算[J]. 武汉大学学报(信息科学版), 2007, 32(7): 633–636.
SHU Hong, QI Cuihong. Semantics and computation of temporal uncertainty in geographical information[J]. Geomatics and Information Science of Wuhan University, 2007, 32(7): 633–636. |
| [15] |
邬伦, 承继成, 史文中.
地理信息系统数据的不确定性问题[J]. 测绘科学, 2006, 31(5): 13–17.
WU Lun, CHENG Jicheng, SHI Wenzhong. Data uncertainties in geographic information system[J]. Science of Surveying and Mapping, 2006, 31(5): 13–17. DOI:10.3771/j.issn.1009-2307.2006.05.002 |
| [16] |
林宗坚, 张永红.
遥感与地理信息系统数据的信息量及不确定性[J]. 武汉大学学报(信息科学版), 2006, 31(7): 569–572.
LIN Zongjian, ZHANG Yonghong. Measurement of information and uncertainty of remote sensing and GIS data[J]. Geomatics and Information Science of Wuhan University, 2006, 31(7): 569–572. |
| [17] |
史文中.
地理信息系统中几何特征不确定性的通用模型:从1维到N维[J]. 测绘学报, 1997, 26(2): 160–167.
SHI Wenzhong. A generic statistical approach for handling uncertainties of geometric features in GIS:from 1 to N dimensions[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(2): 160–167. DOI:10.3321/j.issn:1001-1595.1997.02.011 |
| [18] |
史文中, 童小华, 刘大杰.
GIS中一般曲线的不确定性模型[J]. 测绘学报, 2000, 29(1): 52–58.
SHI Wenzhong, TONG Xiaohua, LIU Dajie. An approach for modeling error of generic curve features in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(1): 52–58. DOI:10.3321/j.issn:1001-1595.2000.01.009 |
| [19] |
王金铃, 陈永奇.
论观测值的可靠性度量[J]. 测绘学报, 1994, 23(4): 252–258.
WANG Jinling, CHEN Yongqi. On the reliability measure of observations[J]. Acta Geodaetica et Cartographica Sinica, 1994, 23(4): 252–258. DOI:10.3321/j.issn:1001-1595.1994.04.003 |
| [20] |
盛骤, 谢世千, 潘承毅.
概率论与数理统计[M]. 3版. 北京: 高等教育出版社, 2001.
SHENG Zhou, XIE Shiqian, PAN Chengyi. Probability and statistics[M]. 3rd ed. Beijing: Higher Education Press, 2001. |
| [21] |
刘凤霞.
假设检验中两类错误的几何解释[J]. 渤海大学学报(自然科学版), 2007, 28(3): 251–253.
LIU Fengxia. Geometrical interpretation to two types of errors in hypothesis verification[J]. Journal of Bohai University (Natural Science Edition), 2007, 28(3): 251–253. DOI:10.3969/j.issn.1673-0569.2007.03.014 |
| [22] |
吴光鲁.
统计检验中两类错误与拒绝域的确定[J]. 西安地质学院学报, 1990, 12(1): 115–117.
WU Guanglu. Two kinds of the errors in the statistical inspection and a determination of the rejection region[J]. Journal of Xi'an College of Geology, 1990, 12(1): 115–117. |
| [23] |
信海红.
抽样检验技术[M]. 2版. 北京: 中国计量出版社, 2015.
XIN Haihong. Technology of sampling inspection[M]. 2nd ed. Beijing: Metrological Publishing House of China, 2015. |
| [24] |
宋保维, 毛昭勇, 鲍亚东, 等.
基于质量标准的计数抽样检验优化方法[J]. 计算机工程, 2008, 34(3): 256–257.
SONG Baowei, MAO Zhaoyong, BAO Yadong, et al. Sampling inspection optimization based on quality standard[J]. Computer Engineering, 2008, 34(3): 256–257. DOI:10.3969/j.issn.1000-3428.2008.03.090 |
| [25] |
周富臣.
计数抽样检验及其应用[J]. 实用测试技术, 2000(2): 32–36, 16.
ZHOU Fuchen. Sampling inspection by attributes and its application[J]. Practical Measurement Technology, 2000(2): 32–36, 16. |


