全极化SAR(polarimetric SAR,PolSAR)系统作为传统单极化SAR系统的一种更高级形式,能同时发射、接收水平及垂直的极化雷达波,能够获取地物更为丰富的后向散射信息,更利于地物场景的解译,已在诸多行业领域得到广泛应用。特别是,我国于2016年发射了国内首颗民用全极化SAR卫星--高分3号,进一步推动了PolSAR的应用前景。然而,由于成像机理的限制,使得PolSAR影像不可避免地存在相干斑噪声。相干斑严重降低了SAR影像的质量,也降低了利用SAR数据进行地物解译的能力[1-2]。因此,对于PolSAR数据的后续应用而言,相干斑滤波是必不可少的预处理程序。
对于全极化SAR数据而言,噪声不仅存在于极化协方差矩阵的对角线元素上,同时也存在于非对角线元素上。并且,对角线元素受到乘性噪声的影响,而非对角线元素则受到乘性和加性混合的噪声的影响[3]。这使得全极化SAR的去噪问题要比单极化SAR要复杂得多。早期的全极化SAR去噪的方法大都是基于文献[4]提出的极化白化滤波器。之后,文献[1]提出了一种基于线性最小均方误差(linear minimum mean square error,LMMSE)原则的PolSAR去噪算法(增强Lee滤波)。这一方法极大地推动了对极化SAR去噪的研究,也引领了之后一系列基于LMMSE滤波器的算法[5-6]。除此之外,基于二叉树的算法[7]、各向异性扩散算法[8-9]、变分正则化算法[10-11]、模拟退火算法[12]等也被应用于极化SAR去噪。近年来,基于非局部均值(nonlocal means,NLM)思想的算法已成为了PolSAR影像去噪的研究热点[13-15],并取得了较好的去噪效果。NLM算法最先应用于数字图像处理[16]。其基本思想是认为影像中往往都会存在重复出现的或相似的影像块,因此像素的估计值可由它的非局部搜索窗口中的所有像素加权平均后得到,而其中每一个像素的权重由它的邻域窗口与待处理像素邻域窗口的差异性所获得。差异越大,权重越小。
然而,传统PolSAR非局部均值去噪算法在度量像素或影像块极化相似度时基本利用到的都是含噪声影像的某种统计特性,而没有考虑到原始像素间的差异性。并且,许多PolSAR非局部均值算法仅仅考虑的是强度信息相似性,而未考虑包括极化相位差在内的全极化信息,导致难以获得稳健准确的相似性测度。有鉴于此,本文提出一种迭代优化的PolSAR NLM算法。该算法的核心思想是:在每次迭代去噪过程中,同时考虑原始影像全极化噪声统计特性和前一次迭代所得的相对低噪声度影像的全极化信息,以完善影像块间极化相似性的度量。试验部分的模拟PolSAR和真实PolSAR影像去噪结果都表明,本文提出的算法取得了较好的去噪效果,噪声得到了有效的抑制,影像边缘细节和极化散射特性都得到了较好的保持。
1 非局部均值及PolSAR相干斑统计特性 1.1 非局部均值去噪思想NLM去噪算法滤波过程的通式可表示为
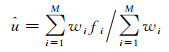 (1)
(1)
式中,f为原始噪声影像;w代表一个权重函数。NLM算法认为目标像素的估计值由它的非局部搜索窗口中的像素加权平均后得到,而其中每一个像素的权重由该像素的邻域窗口与待处理像素邻域窗口的整体差异性所计算获得。图 1展示了NLM的基本思想:对于以像素p为中心的邻域块而言,由于以q1为中心的邻域块的内部结构与之非常相似,所以在对p进行去噪时,像素q1的权重w(p, q1)较大;而由于以q2和q3为中心的邻域块的内部结构与之相差较大,所以在对p进行去噪时,像素q2和q3的权重很小。可以看到,由于NLM算法不仅考虑了单一像素间影像值的接近性,还考虑到了两个像素邻域块的结构布局的相似性,这使其比起传统的邻域滤波方法更能取得稳定有效的滤波效果。显而易见,决定NLM算法滤波效果的一个重要因素就是影像块间相似性的度量,本文的主要创新就是提出了一种迭代优化的全极化影像块相似性度量方式。

|
| 图 1 NLM算法的思路 Fig. 1 The diagram of the idea of nonlocal means |
1.2 PolSAR相干斑统计特性
对于PolSAR系统而言,在满足散射互易性的条件下,每个分辨率单元的后向散射雷达信号可以用一个三维目标矢量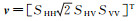
众所周知,对于SAR的强度数据而言,其噪声是一种服从Gamma分布的乘性噪声[17]。然而,全极化数据的噪声模型要复杂得多。对于噪声完全发育的视数为L的PolSAR影像而言,其极化协方差矩阵CL服从如下的复Wishart分布[18]
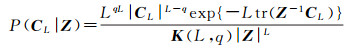 (2)
(2)
式中,tr(·)和|·|分别表示矩阵的迹和行列式;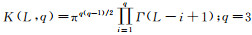
要完善影像块间极化相似性的度量,就必须要考虑到全极化信息。本文提出的PolSAR NLM算法的创新性是在每次迭代去噪过程中,同时考虑原始影像全极化噪声统计特性和前一次迭代所得的相对低噪声度影像的全极化信息。因此,如何度量原始影像块全极化相似性及迭代所得影像块全极化相似性是本文的主要关注点。
2.1 迭代优化的PolSAR影像块相似性度量在第1次迭代去噪时,为了计算原始含噪声像素间的极化相似性,本文采用基于复Wishart分布的似然比检验法[19]。假设两个3×3的极化协方差矩阵X和Y满足Wishart分布,给定假设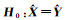
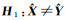
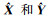
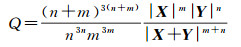 (3)
(3)
式中,m=n为影像的视数。对以上公式取自然对数并简化常数项,可得到
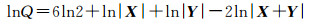 (4)
(4)
式中,lnQ的取值范围是(-∞, 0]。像素越相似,则lnQ越大。
随着影像迭代去噪过程的进行,所得影像的噪声程度会逐渐减弱。因此,在每次迭代的过程中,都可以利用上一次迭代所得影像的信息来完善像素的相似性测度。这一迭代优化的相似性度量思想可以表示为
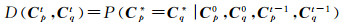 (5)
(5)
式中,C*和C0分别代表影像真实和原始观测到的极化协方差矩阵;Ct-1是在t-1次迭代滤波所得影像的极化协方差矩阵。以上公式代表的是在同时已知原始观测值C0及上次迭代所得值Ct-1的前提下,p和q两个像素有同一真实值的概率。假设事件Cp*=Cq*|C0及Cp*=Cq*|Ct-1相互独立,则式(5)可转化为
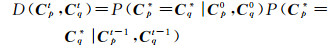 (6)
(6)
接下来可利用贝叶斯定理对式(6)右边第1项进行变化。贝叶斯公式如下
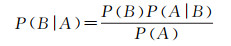 (7)
(7)
式中,P(B|A)代表条件A发生的前提下B发生的概率。据此,有
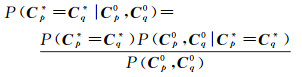 (8)
(8)
又由于缺乏事件Cp*=Cq*及Cp0、Cq0的先验知识,也即对任意的两个像素p和q而言,这两个事件是随机的,所以P(Cp*=Cq*)和P(Cp0, Cq0)均可假定是定值。因此,式(8)简化为
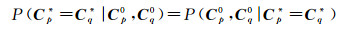 (9)
(9)
迭代相似性测度最终表示为
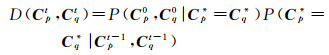 (10)
(10)
对于上式右边第1项,其反映的是假设p和q真实值相同的条件下,两像素受噪声干扰后取值为Cp0和Cq0的概率。显然,这一思想与式(4)的似然比检验的思想契合,故可采用式(4)的方式计算获得。对于第2项,本文不再选择使用基于Wishart分布的似然比方法进行计算,这是因为去噪后影像的噪声特性不再满足Wishart分布。为此,本文采用经过Wishart距离[21]推导而来的Kullback-Leibler测度来对第2项进行计算。需要指出的是,正如文献[18]中的论证,虽然去噪后影像的噪声特性不满足Wishart分布,但Wishart距离仍然适用于滤波处理后的PolSAR数据。
对于PolSAR数据而言,Wishart距离可表示为[18]
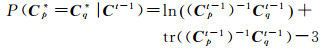 (11)
(11)
若考虑上述Wishart距离的对称性,对其进行调整即可得到如下的Kullback-Leibler散度距离度量公式[20]
 (12)
(12)
最终可推得,式(12)所示的相似测度值仍为负值。值越大,代表像素间越相似。需要说明的是:本文提出的迭代去噪方法的主要思路是在每次迭代的过程中完善权重的计算,而迭代时仍然将像素的原始值同权重结合进行加权平均,所以本质上并不属于“二次滤波”。
值得注意的是,由于式(4)中涉及矩阵行列式的对数,为了避免奇异值的出现,就应当保证|C|≠0,也即保证满秩性。然而,当影像视数小于协方差矩阵的维度时(即L < 3),影像中的一些像素的极化协方差矩阵将不再是满秩的,此时就会导致数学计算的问题。为了解决这一问题,本文算法加入一种对待去噪影像进行预处理的方法[22],保证影像所有像素的协方差矩阵达到满秩。这一协方差矩阵的预变换步骤可以表示为
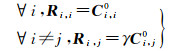 (13)
(13)
式中,i和j代表协方差矩阵中元素的位置;γ=min(L/3, 1)。这一过程的实质就是保持协方差对角元素(即各通道的强度值)不变,而根据影像的视数对非对角元素进行线性变换。研究表明[22],以上步骤处理后的影像仍然满足复Wishart分布,也即基于复Wishart分布的似然比检验法依然适用于变换后的影像。这里需要说明的是,以上预处理过程只是用于计算每个像素的权重,而在加权平均过程中使用的仍然是原始的数据。因此,不会存在改变数据极化信息的弊端。
2.2 权重及滤波参数的设置每次迭代滤波过程中,对于每个参考影像块x而言,窗口内其他影像块y的权重为
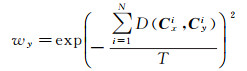 (14)
(14)
式中,N为影像块的像素数;T在每次迭代时为一个固定参数,本文采用文献[23]提出的“噪声估算器”来确定T的取值:每一次迭代时,计算影像上所有相邻像素的相似度,构建由这些相似度所组成的直方图,然后计算直方图的90%分位数,即将此值当作当前时刻的参数T。最终,对于某个像素而言,其极化协方差矩阵的估计值为
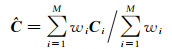 (15)
(15)
式中,M为滤波窗口的大小。
本文提出的PolSAR NLM算法有3个参数需要预先设定,分别是迭代次数t、影像块大小N和滤波窗口大小M。理论而言,随着迭代次数增加,影像的去噪效果会越加优化。但是,迭代次数增加也会带来计算时间的增加。试验发现,对于大多数影像,当迭代次数达到3次时,就能达到优良的去噪效果且继续迭代后的效果提升非常有限。因此,本文提出的PolSAR NLM算法的迭代次数固定为3次。对于NLM算法而言,影像块大小通常设置为3×3到7×7之间,而滤波窗口大小则通常设置为13×13到21×21之间。研究表明[14],随着影像块和滤波窗口大小的增加,影像的噪声会得到更明显地抑制,但细节丢失会逐渐加重。因此,为了达到去噪与保持影像细节之间的折中,本文试验部分将算法的影像块和滤波窗口大小分别设为5×5和17×17。
3 试验结果和分析为了验证本文提出的算法的滤波效果,本文采用一幅模拟的PolSAR数据和两幅真实的PolSAR影像进行去噪的试验。作为对比,试验部分也展示了增强Lee滤波[1]、IDAN滤波[5]及Pretest NLM滤波算法[14]的去噪效果。为了达到去噪与影像细节保持的平衡,本文所有试验中增强Lee滤波的滤波窗口大小设为文献[1]中所推荐的7×7;IDAN滤波的像素搜索窗口大小设置为15×15;Pretest NLM方法的影像块和滤波窗口大小同本文方法设置一致。
3.1 模拟试验模拟试验部分利用Monte Carlo方法[18]生成了一幅PolSAR影像。为了定量评价算法对噪声的抑制及边缘保持的效果,本文采用等效视数(equivalent number of looks,ENL)[24]和基于平均比的边缘保持度(edge preservation degree based on ratio of the average, EPD-ROA)[25]这两个指数。
ENL指数的定义为
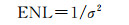 (16)
(16)
式中,σ代表强度影像在同质区的方差系数。ENL的估计方法一般都是人工选取影像内几块大的同质区域,利用以上公式求得每块区域的等效视数后,取平均得到影像全局的等效视数。ENL越大,代表影像的噪声水平越低。
EPD-ROA的定义如下
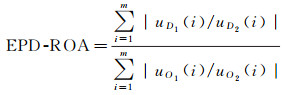 (17)
(17)
式中,m代表影像的大小;uD1(i)和uD2(i)分别表示去噪所得影像的某个方向上两相邻像素的强度值;类似地,uO1(i)和uO2(i)分别表示原始影像的某个方向上两相邻像素的强度值。EPD-ROA指数越接近于1,意味着滤波算法有着越好的边缘保持能力。
一个优良的PolSAR滤波方法不仅能够显著滤除噪声和保持影像纹理细节信息,还应当有效地保持数据极化散射特性,从而保证后续场景解译或物理参数反演的可靠性。为了定量评价散射特性的保持性能,模拟试验部分采用文献[26]中提出的绝对相对误差指数(absolute relative bias, ARB)。对于模拟影像中的每一种地物类别而言,已知某种散射参量θ的真实值θ*,计算去噪后该类每个像素的这一参量的取值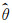
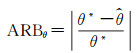 (18)
(18)
最后对所有地物所有像素的ARB指数求均值即为参量θ最终的ARB指数。试验部分所采用的极化参数为Cloude极化分解参数(极化散射熵H,平均alpha角α,极化反熵A)[27],原因是该分解模型能够直观地反映地物的物理散射特性。
图 2展示了几种去噪算法的处理结果,表 1为其定量评价结果。增强Lee滤波在较大程度上抑制了影像的噪声。然而,仔细观察可以发现,这一算法处理后影像呈现出一定的斑块效应,直接导致点目标及边缘受到轻度的模糊。产生这一问题的原因在于,该算法在滤波的过程中采用了一种选择滤波窗口方向的策略,而非通常采用的方形窗口。与增强Lee滤波相比,虽然表 1所示的ENL显示出IDAN方法对噪声的抑制能力有所提升,但其对于影像细节信息的模糊和弱化现象较为明显。很显然,与前面两种传统的局部滤波器相比,Pretest NLM滤波方法在噪声抑制方面有了质的提升,并且实现了对边缘信息的优良保持。然而,可以较明显观察到的是,Pretest NLM处理后的影像的点目标模糊严重。相比之下,本文提出的去噪方法虽然ENL指数略微低于Pretest NLM算法,但影像的边缘和细节信息都得到了较好的保持。就影像极化散射信息的保持性能而言,Pretest NLM方法和本文方法要明显优于其他两种方法,并且这两种方法对不同极化参数的估计精度各有优劣。

|
| 图 2 模拟影像去噪结果 Fig. 2 Filtering results on the simulated image |
| 评价指数 | 增强Lee滤波 | IDAN | PretestNLM | 本文算法 |
| ENL | 24.4 | 42.7 | 82.3 | 80.7 |
| EPD-ROA | 0.78 | 0.70 | 0.88 | 0.90 |
| ARBH | 0.199 | 0.187 | 0.154 | 0.150 |
| ARBα | 0.275 | 0.280 | 0.223 | 0.237 |
| ARBA | 0.240 | 0.246 | 0.183 | 0.171 |
3.2 真实试验
除了模拟的PolSAR数据,两幅真实的PolSAR影像也被用来验证去噪算法的优劣。这两幅影像分别为C波段和L波段的AirSAR传感器所获得的数据,视数为4。
图 3展示了几种去噪算法对C波段AirSAR数据的去噪结果。可以看到,这幅影像场景较为复杂,既包括以表面散射为主的水体,也包含以体散射为主的森林以及散射机制较为复杂的城区。对于这类的影像,一个优良的去噪方法应当在削弱噪声的同时保持影像大部分的细节信息。很显然,与模拟试验结果一样,增强Lee滤波处理后的影像在同质区存在着较明显的斑块效应,部分边缘和点目标丢失;IDAN虽然更好地抑制了影像的噪声水平,但是过平滑问题较为严重;Pretest NLM算法的噪声抑制能力在4种算法当中表现最佳,但也存在轻微的斑块效应,导致处理后影像城区部分一些纹理(主要是细小的道路)以及部分强散射点目标丢失。相反,本文算法虽然噪声去除能力略微逊于Pretest NLM,但细节保持能力有了较大的提升。值得注意的是,同Pretest NLM处理的结果相比,影像中机场跑道处的线状地物(图 3(f)箭头所指)随着迭代的进行反而变得更为模糊。出现这一问题的原因是:目视来看,该线状目标极化散射特性同机场周边植被较为相近,因此初次滤波中大量权重略高的植被像素会参与对线状地物的去噪。然而,初次滤波后这一目标和植被像素的可区分性不仅没有加大,目视来看反而变得更加接近。在这种情况下,迭代的后果就是这些像素的权重反而会提高,模糊问题不断加深。可以看出,对于影像中的一些零星的细节目标,如果本文提出的方法在初次去噪过程中不能较好地将它们与其他异质地物“区分”开来,反而有可能会出现不断过平滑的问题。因此,如何完善初始估计的精确性是本文方法未来值得改进之处。

|
| 图 3 C波段AirSAR影像去噪结果 Fig. 3 Filtering results on the C band AirSAR image |
图 4展示了几种去噪算法对一景L波段PolSAR影像的去噪结果。与之前的试验结果相似,增强Lee滤波带来的块状效应制约了其滤波效果;IDAN能更好地抑制噪声,但影像细节信息出现了严重的丢失;Pretest NLM算法不仅更好地抑制了噪声,而且对于影像边缘的保持有了一定的提升;相比之下,本文提出的算法虽然ENL指标不如PolSAR NLM方法,但EPD-ROA指标反映出本文算法在边缘和细节保持方面相比于前者的优势性。显然,本文提出的算法更好地实现了去噪和细节保持之间的平衡。表 2为几种算法对C波段和L波段影像滤波的评价结果。

|
| 图 4 L波段AirSAR影像去噪结果 Fig. 4 Filtering results on the L band AirSAR image |
| 滤波算法 | C波段影像 | L波段影像 | ||
| ENL | EPD-ROA | ENL | EPD-ROA | |
| 增强Lee滤波 | 42.3 | 0.71 | 39.4 | 0.77 |
| IDAN | 60.9 | 0.70 | 50.4 | 0.75 |
| Pretest NLM | 103.5 | 0.78 | 88.8 | 0.84 |
| 本文算法 | 97.8 | 0.84 | 76.5 | 0.89 |
4 结论
相干斑滤波是PolSAR数据预处理中重要的一环。传统PolSAR非局部均值滤波算法在度量像素或影像块相似度时基本利用到的都是含噪声影像的统计特性,而没有考虑到原始像素间的差异性,而且往往无法利用到全极化信息,因此难以获得稳健准确的相似性测度。本文提出了一种迭代优化的PolSAR非局部均值方法。该方法的创新之处在于:在每次迭代去噪过程中,同时考虑原始影像全极化噪声统计特性和前一次迭代所得的相对低噪声度影像的全极化信息,以完善影像块间极化相似性的度量。模拟的PolSAR数据和不同波段的真实PolSAR影像的去噪试验都表明,本文提出的算法既能有效地抑制相干斑噪声,又能较好地保持影像的边缘、强散射点目标、极化散射特性等细节信息。最后需要指出的是,相比较于传统的局部滤波器,运行效率相对较低是非局部滤波方法的一大弊端,特别是,本文方法还采取了迭代去噪的策略。因此,如何加速算法的运行效率从而提升算法的实用性,是未来值得研究的方向之一。
| [1] | LEE J S, GRUNES M R, DE GRANDI G. Polarimetric SAR speckle filtering and its implication for classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2363–2373. DOI:10.1109/36.789635 |
| [2] |
王建明, 史文中, 邵攀.
自适应距离和模糊拓扑优化的模糊聚类SAR影像变化检测[J]. 测绘学报, 2018, 47(5): 611–619.
WANG Jianming, SHI Wenzhong, SHAO Pan. Change-detection method for SAR image using adaptive distance and fuzzy topology optimization-based fuzzy clustering[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(5): 611–619. DOI:10.11947/j.AGCS.2018.20160607 |
| [3] | LOPEZ-MARTINEZ C, FABREGAS X. Polarimetric SAR speckle noise model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(10): 2232–2242. DOI:10.1109/TGRS.2003.815240 |
| [4] | NOVAK L M, BURL M C, IRVING W W. Optimal polarimetric processing for enhanced target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(1): 234–244. DOI:10.1109/7.249129 |
| [5] |
马晓双, 沈焕锋, 杨杰, 等.
极化SAR相干斑抑制的非局部加权最小均方误差滤波算法[J]. 中国图象图形学报, 2015, 20(1): 140–150.
MA Xiaoshuang, SHEN Huanfeng, YANG Jie, et al. Polarimetric SAR speckle filtering using a nonlocal weighted minimum mean squared error filter[J]. Journal of Image and Graphics, 2015, 20(1): 140–150. |
| [6] | LEE J S, GRUNES M R, SCHULER D L, et al. Scattering-model-based speckle filtering of polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(1): 176–187. DOI:10.1109/TGRS.2005.859338 |
| [7] | ALONSO-GONZALEZ A, LOPEZ-MARTINEZ C, SALEMBIER P. Filtering and segmentation of polarimetric SAR data based on binary partition trees[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2): 593–605. DOI:10.1109/TGRS.2011.2160647 |
| [8] | MA Xiaoshuang, SHEN Huanfeng, ZHANG Liangpei, et al. Adaptive anisotropic diffusion method for polarimetric SAR speckle filtering[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(3): 1041–1050. DOI:10.1109/JSTARS.2014.2328332 |
| [9] | MA Xiaoshuang, SHEN Huanfeng, ZHANG Liangpei. PolSAR anisotropic diffusion filter with a refined similarity measure and an adaptive fidelity constraint[J]. International Journal of Remote Sensing, 2016, 37(24): 5988–6011. DOI:10.1080/01431161.2016.1253893 |
| [10] | NIE Xiangli, QIAO Hong, ZHANG Bo. A variational model for PolSAR data speckle reduction based on the wishart distribution[J]. IEEE Transactions on Image Processing, 2015, 24(4): 1209–1222. |
| [11] | NIE Xiangli, QIAO Hong, ZHANG Bo, et al. A nonlocal TV-based variational method for PolSAR data speckle reduction[J]. IEEE Transactions on Image Processing, 2016, 25(6): 2620–2634. DOI:10.1109/TIP.2016.2552402 |
| [12] | SCHOU J, SKRIVER H. Restoration of polarimetric SAR images using simulated annealing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(9): 2005–2016. DOI:10.1109/36.951091 |
| [13] |
陈建宏, 赵拥军, 黄洁, 等.
改进的多视PolSAR非局部均值滤波算法[J]. 测绘科学技术学报, 2014, 31(5): 496–500, 504.
CHEN Jianhong, ZHAO Yongjun, HUANG Jie, et al. Improved non-local means filter algorithm of multilook polarimetric SAR image[J]. Journal of Geomatics Science and Technology, 2014, 31(5): 496–500, 504. DOI:10.3969/j.issn.1673-6338.2014.05.012 |
| [14] | CHEN Jiong, CHEN Yilun, AN Wentao, et al. Nonlocal filtering for polarimetric SAR data:a pretest approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(5): 1744–1754. DOI:10.1109/TGRS.2010.2087763 |
| [15] |
杨国辉.基于非局部均值的极化SAR降斑研究[D].西安: 西安电子科技大学, 2012. YANG Guohui. Study of polarimetric SAR despeckling based on nonlocal means[D]. Xi'an: Xidian University, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2067859 |
| [16] | BUADES A, COLL B, MOREL J M. A non-local algorithm for image denoising[C]//Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). San Diego, CA: IEEE, 2005, 2: 60-65. https://www.researchgate.net/publication/4156453_A_non-local_algorithm_for_image_denoising |
| [17] | GOODMAN N R. Statistical analysis based on a certain multivariate complex gaussian distribution (an introduction)[J]. Annals of Mathematical Statistics, 1963, 34(1): 152–177. DOI:10.1214/aoms/1177704250 |
| [18] | LEE J S, POTTIER E. Polarimetric radar imaging:from basics to applications[M]. Boca Raton: CRC Press, 2009. |
| [19] | CONRADSEN K, NIELSEN A A, SCHOU J, et al. A test statistic in the complex wishart distribution and its application to change detection in polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(1): 4–19. DOI:10.1109/TGRS.2002.808066 |
| [20] | D'HONDT O, GUILLASO S, HELLWICH O. Iterative bilateral filtering of polarimetric SAR data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3): 1628–1639. DOI:10.1109/JSTARS.2013.2256881 |
| [21] | LEE J S, GRUNES M R, KWOK R. Classification of multi-look polarimetric SAR imagery based on complex wishart distribution[J]. International Journal of Remote Sensing, 1994, 15(11): 2299–2311. DOI:10.1080/01431169408954244 |
| [22] | DELEDALLE C A, DENIS L, TUPIN F, et al. NL-SAR:a unified nonlocal framework for resolution-preserving (Pol)(In)SAR denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2021–2038. DOI:10.1109/TGRS.2014.2352555 |
| [23] | CANNY J. A computational approach to edge detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, PAMI-8(6): 679–698. DOI:10.1109/TPAMI.1986.4767851 |
| [24] | FOUCHER S, BOUCHER J M, BENIE G B. Maximum likelihood estimation of the number of looks in SAR images[C]//Proceedings of the 13th International Conference on Microwaves, Radar and Wireless Communications. Wroclaw, Poland: IEEE, 2000, 2: 657-660. https://www.researchgate.net/publication/3892488_Maximum_likelihood_estimation_of_the_number_of_looks_in_SAR_images |
| [25] | FENG Hongxiao, HOU Biao, GONG Maoguo. SAR Image despeckling based on local homogeneous-region segmentation by using pixel-relativity measurement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(7): 2724–2737. DOI:10.1109/TGRS.2011.2107915 |
| [26] | FOUCHER S, LOPEZ-MARTÍNEZ C. Analysis, evaluation, and comparison of polarimetric SAR speckle filtering techniques[J]. IEEE Transactions on Image Processing, 2014, 23(4): 1751–1764. DOI:10.1109/TIP.2014.2307437 |
| [27] | CLOUDE S R, POTTIER E. A review of target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498–518. DOI:10.1109/36.485127 |


