2. 信息工程大学地理空间信息学院, 河南 郑州 450001;
3. 辽宁生态工程职业学院林学院, 辽宁 沈阳 110101
2. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450001, China;
3. Forestry Institute, Liaoning vocational college of ecological engineering, Shenyang 110101, China
在拍摄遥感影像过程中,受到外界环境及CCD探测器成像机理的影响,遥感影像易受到条带噪声的污染[1-2]。由于条带噪声的存在,严重影响了遥感影像的后续处理工作,因此,急需研究一种能够在不破坏影像细节的情况下有效去除条带噪声的方法。
在过去几十年,研究学者提出了基于滤波方法、基于统计匹配方法及基于全变分优化方法去除条带噪声。基于滤波方法主要包括空间-频率域滤波[3-4]及小波域滤波[5-6]。这类方法虽然可以很好地去除条带噪声,但由于滤波器可能会滤除与条带频率相同或相似的有用信号,从而容易丢失影像细节。为了克服这一缺点,文献[7-8]提出把小波域滤波和频率域滤波组合去除条带噪,并得到了满意的去噪结果;基于统计匹配方法主要以矩匹配方法[9]及直方图匹配方法[10]为典型代表,这类方法是根据各传感器数值统计的差异去除条带噪声[11],去噪效果对统计数据集有很强的依赖性,而且存在收敛速度慢及条带去除不彻底等问题。为了能更有效地去除条带噪声,文献[12]提出了变分法及矩匹配法组合方法去除条带噪声[12];文献[13]通过分析矩匹配法的缺点,提出一种改进行的平滑滤波方法去除条带噪声[13]。
近年来,研究学者提出了基于全变分优化方法去除条带噪声,如文献[14]提出了基于最大后验(MAP)方法去除条带噪声[14];文献[15]从条带噪声具有方向性角度考虑,提出一种复杂的单向变分模型,对去除MODIS影像条带噪声具有很好的效果[15]。虽然上述方法取得了令人满意的去噪效果,但还是会出现丢失影像细节的情况。文献[16]提出一种单向变分框架式正则化条带噪声去除方法,可以达到保留更多影像细节的目的[16];文献[17]提出了一种可以区分条带区域和无条带区域的单向TV-Stokes模型,此方法可以避免对条带噪声过度平滑而丢失影像细节[17];文献[18]提出了一种多尺度变分模型去除MODIS影像的条带噪声,可以去除条带噪声的同时保留更多影像细节[18]。此外,研究人员充分利用了不同波段的光谱相关性来去除多光谱和高光谱影像的条带噪声,从而达到很好的去噪效果[19-25]。
为了去除条带噪声时不破坏影像细节,本文提出一种基于小波的SPVM-DVM条带噪声去除方法。首先,对含有条带噪声的遥感影像进行小波分解,可以了解条带噪声分布的特点。其次,为避免影像细节丢失,构建了条带保留变分模型(stripe preserve variation model, SPVM)和条带去除变分模型(destriping varation model, DVM)。SPVM模型可以有效去除低层高频分量(含条带噪声)中的细节信息而保留条带噪声,从而使条带噪声与细节信息有效分离。DVM模型可以有效去除高层高频分量(含条带噪声)中的条带噪声,并且能有效保留高层高频分量(含条带噪声)中的细节信息。最后,通过小波重构,获得去噪影像。
1 变分法模型构建 1.1 条带噪声的特点分析本文以一幅带有水平方向条带噪声的Landsat影像为例,并对其进行1层小波分解。从图 1可以看到,只有水平方向高频分量(图 1(a))受到条带噪声污染。从图 1(d)及图 1(e)可以看到,水平方向的条带噪声只影响垂直梯度(图 1(e))。

|
| 图 1 高频分量及水平方向高频分量梯度图(为了显示效果,进行对比度拉伸) Fig. 1 High-frequency component and gradient maps of the high-frequency component (contrast stretched for display) |
1.2 条带保留变分模型的构建
在低层高频分量(含条带噪声)中,如果采用单向变分模型去除条带噪声,由于很难控制模型的正则化强度,从而导致影像细节被破坏。针对上述问题,通过在研究单向变分法及条带噪声特点基础上建立一种条带保留变分模型(SPVM),SPVM模型如下
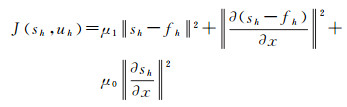 (1)
(1)
式中,等号右边第1项为保真项;第2项是保持条带噪声和水平方向高频分量在水平方向梯度一致;第3项表示惩罚水平方向条带噪声梯度;sh代表条带噪声;fh代表含条带噪声的水平方向高频分量;uh代表水平方向高频分量中的细节信息;μ0、μ1代表正则项惩罚算子。
1.3 条带去除变分模型的构建通过试验分析,如采用SPVM模型去除高层高频分量(含条带噪声)中的细节信息,会导致细节信息去除不彻底,从而无法有效分离出细节信息。因此,构建一种条带去除变分模型(DVM),DVM模型如下
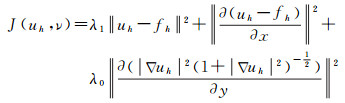 (2)
(2)
式中,等号右边第1项为保真项;第2项是保持去噪后的水平方向高频分量和含条带噪声的水平方向高频分量在水平方向梯度一致;第3项表示惩罚条带噪声垂直方向梯度;uh代表去除条带噪声后的水平方向高频分量;fh代表含条带噪声的水平方向高频分量;ν代表条带噪声;λ0、λ1代表正则项惩罚算子。
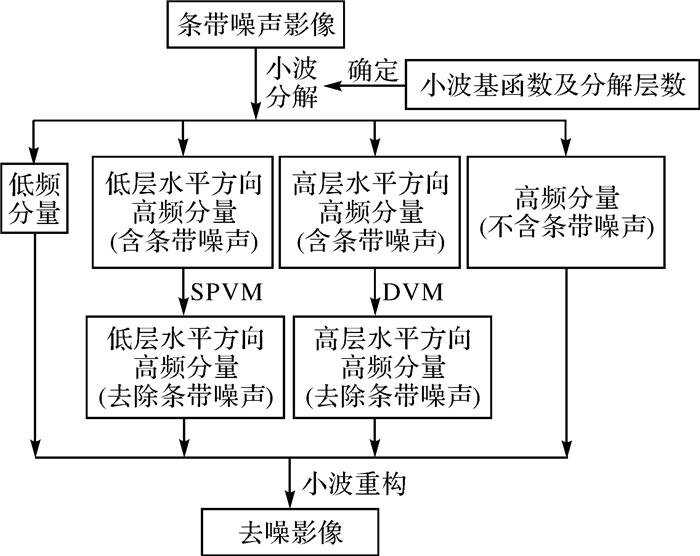
2 试验与分析 2.1 小波变分法去除条带噪声流程小波变分法去除条带噪声流程如图 2所示。
|
| 图 2 小波变分法条带噪声去除流程 Fig. 2 Process diagram of stripe noise removal of remote image based on wavelet variational method |
2.2 小波基函数的选取及分解层数确定
本文根据小波基函数的特性(正交性、支撑长度、消失矩、对称性和正则性等)来确定小波基函数。首先,选取具有紧支撑性及正交性的小波基函数。此小波基函数便于操作,并且能保证较好的时-频局部特性,也利于算法的实现。其次,考虑小波基函数的平滑性(正则性)。如果平滑性差,则随着变换级数的增加,原来平滑的输入信号将很快出现不连续,从而导致重建时失真。综上分析,本文选择haar小波函数。
小波分解的层数主要以经小波分解出的水平方向高频分量是否含有条带噪声为依据来确定的。
2.3 Landsat影像条带噪声去除通过试验分析,本文对含条带噪声的Landsat影像进行4层小波分解。为了避免影像细节丢失,采用SPVM模型和DVM模型分别对1-3层和第4层水平方向高频分量进行去噪处理,其效果最理想。试验结果如图 3所示,其中,h1-h4表示1-4层水平方向高频分量;SPVM_h1-SPVM_h3表示SPVM模型对1-3层水平方向高频分量去噪的结果;DVM_h4表示DVM模型对第4层水平方向高频分量去噪的结果;h1-(SPVM_h1)-h3-(SPVM_h3)表示从1-3层水平方向高频分量中分离出的影像细节;h4-(DVM_h4)表示从第4层水平方向高频分量中分离出的条带噪声。

|
| 图 3 Landsat影像水平方向高频分量去噪结果(为了更好显示,进行对比度拉伸) Fig. 3 Destriped results of the wavelet horizontal direction high-frequency components for Landsat image (contrast stretched for display) |
从图 3可以看到,SPVM模型可以有效去除1-3层水平方向高频分量中的细节信息而只保留条带噪声(图 3(b)、(e)、(h))。再通过1-3层水平方向高频分量(图 3(a)、(d)、(g))分别减去条带噪声(图 3(b)、(e)、(h)),可以有效分离出1-3层水平方向高频分量中的细节信息(图 3(c)、(f)、(i))。而DVM模型对第4层水平方向高频分量去噪后,可以在去除条带噪声的同时有效保留影像细节信息,如图 3(k)所示。
上述低层与高层的划分主要是针对Landsat试验影像而言,而对于不同的遥感影像需要以不破坏影像细节为依据来进行划分。
对低频分量、去噪后的高频分量及不含条带噪声的高频分量进行小波重构,获得去噪影像。并与文献[8]、文献[12]、文献[17]、文献[18]等方法进行比较,试验结果如图 4所示。

|
| 图 4 不同方法的去噪结果及对应的残差图(为了更好显示,残差图进行对比度拉伸) Fig. 4 Destriped results of different algorithms and corresponding residual figure(residual figure contrast stretched for display) |
从图 4(b)-(f)可以看到,本文方法及其他方法都能有效去除条带噪声,但从去噪后影像的视觉效果看,经文献[8]方法去噪后,影像出现模糊,而其他方法去噪后的影像视觉效果较好。从图 5(g)-(k)可以看到,本文方法去除条带噪声的同时基本没有丢失影像细节,而其他方法都丢失少量影像细节。
2.4 去噪效果评定
本文通过主、客观方式来评定去噪效果。在主观上,除影像视觉效果外,还采用行均值曲线及功率谱曲线等评价指标。客观上,采用影像对比度值(image contrast, IC)、影像扭曲(image distortion, ID)[18]、影像辐射质量提升因子(improvement factor, IF)[18]及方法的计算效率(computation efficiency, CE)等评价指标进行评价,试验结果如图 5、图 6及表 1所示。
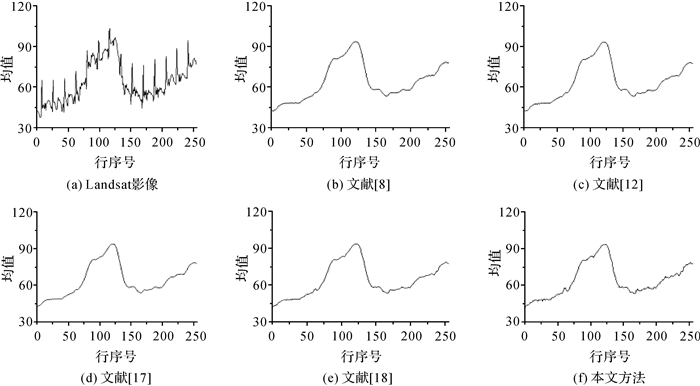
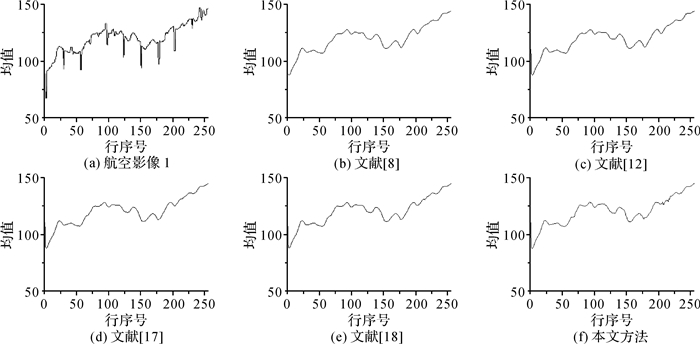
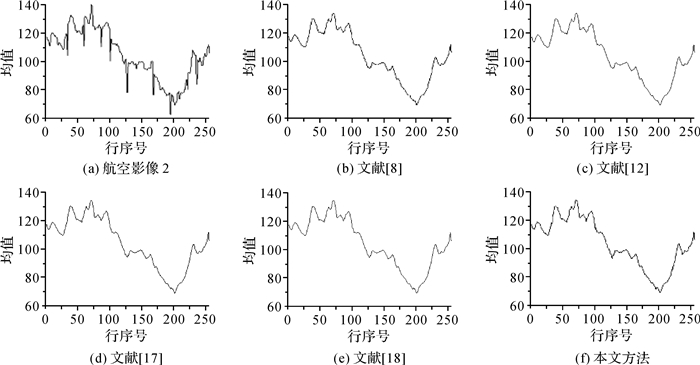
图 5为图 4(a)-(e)的行均值曲线。由于Landsat影像受条带噪声污染,图 5(a)中的行均值曲线出现明显的尖峰现象;而图 5(b)-(f)中的行均值曲线都没有出现尖峰现象,说明本文方法及比较方法都能有效抑制条带噪声。而从行均值曲线粗糙程度看,本文方法的行均值曲线较其他方法粗糙,说明本文方法在保留影像细节方面是最优的。
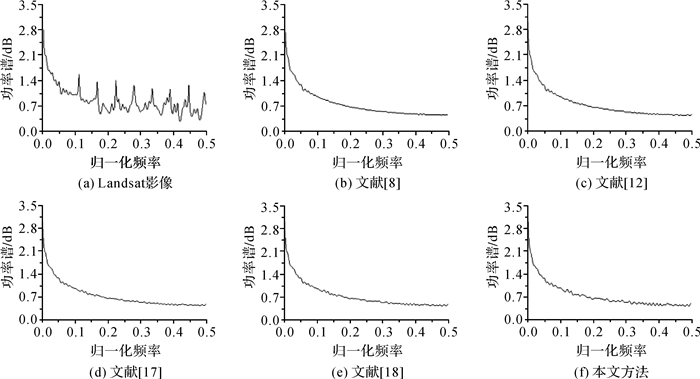
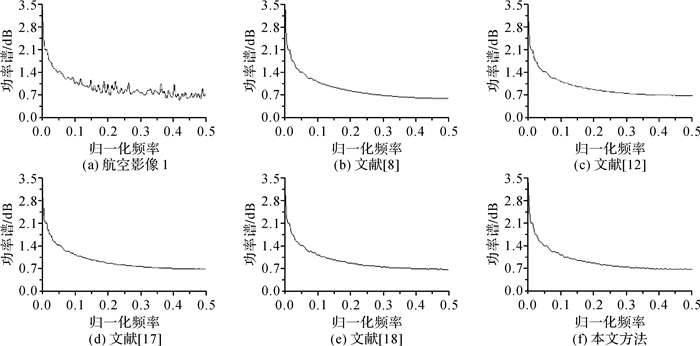
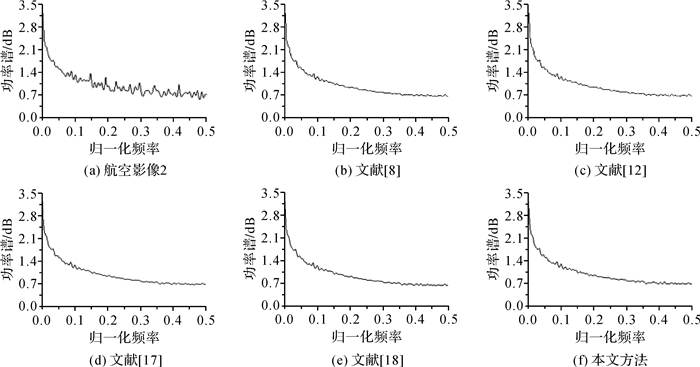
图 6为图 4(a)-(e)的功率谱曲线。由于Landsat影像受条带噪声污染,图 6(a)中的功率谱曲线出现严重震荡及在某些频率点处出现不同程度的尖峰现象;而从图 6(b)-(f)可以看到,本文方法及比较方法的功率谱曲线都无震荡及尖峰现象,说明上述方法都能有效去除条带噪声。但从本文方法功率谱曲线较其他方法粗糙看,本文方法可以达到去除条带噪声的同时保留更多影像细节的目的。
从表 1中的各项评价指标可以看到,本文方法能保证影像扭曲很小的情况下,有效去除条带噪声,并且去噪后影像的对比度及质量都是最优的。
而从CE值可以看到,各种方法运算的效率是不同的。文献[8]方法是采用小波-傅里叶组合滤波法去除条带噪声,由于滤波方法计算简单、效率高,所以去噪时间最短;文献[12]方法是矩匹配法及变分法组合去除条带噪声的,由于矩匹配法计算量大,再加上变分法的计算过程,从而导致文献[12]方法的计算时间最长;文献[18]方法是采用一种多尺度变分方法去除条带噪声,此方法通过多尺度分层分解提取细节信息,所以计算时间要长于文献[17]方法和本文方法;而本文方法是通过小波分解及两种变分模型组合去除条带噪声,其运算过程较文献[17]方法复杂,因此计算时间要长于文献[17]方法。
2.5 方法参数确定采用SPVM模型去除1-3层水平方向高频分量条带噪声时,模型参数确定主要根据水平方向高频分量中的细节信息能否被有效去除来决定的。
通过试验分析,第1层参数μ0、μ1的值一般在0~0.5之间选择。第2层参数μ0、μ1的值一般在0.5~1之间选择。由于第3层水平方向高频分量细节信息能量较第1、2层大,若模型参数选择不当,会导致影像细节去除不彻底,从而无法有效分离出影像细节。因此第3层参数μ0值一般在1~1.5之间选择,而参数μ1值一般在0.5~1之间选择。最后,设定第1层参数值为μ0=0.3,μ1=0.3,第2层参数值为μ0=0.8,μ1=0.8,第3层参数值为μ0=1.1,μ1=0.8。
采用DVM模型去除第4层水平方向高频分量条带噪声时,模型参数选择主要以去除条带噪声时不破坏影像细节为依据。
由于第4层条带噪声的能量较1-3层小。为了避免丢失影像细节,模型参数选择不宜过大。因此参数λ0、λ1值一般在0~0.5之间选择。最后,设定第4层参数值为λ0=0.2,λ1=0.2。
上述参数选择的依据及范围主要是针对Landsat试验影像而言,但可以为其他影像提供借鉴。
2.6 本文方法有效性验证为了检验本文条带噪声去除方法的稳定性,选取两组影像;一组为高光谱影像,包括一幅带有周期性条带噪声的MODIS(moderate-resolution imaging spectroradiometer)第30波段Level-1B遥感数据、一幅带有随机性条带噪声的Hyperion第211波段的遥感数据及一幅带有随机性条带噪声的CHRIS(compact high resolution imaging spectrometer)第1波段Level1遥感数据;另一组为航空影像,包括一幅以建筑物细节为主的航空影像及一幅以植被细节为主的航空影像。
通过试验分析,对5种遥感影像进行小波分解,除CHRIS影像进行5层小波分解外,其余4幅影像都分解4层。影像去噪结果及主客观评价指标见图 7-图 21及表 2。

|
| 图 7 不同方法的去噪结果及对应的残差图(为了更好显示,残差图进行对比度拉伸) Fig. 7 Destriped results of different algorithms and the corresponding residual figure(residual figure contrast stretched for display) |

|
| 图 10 不同方法的去噪结果及对应的残差图(为了更好显示,残差图进行对比度拉伸) Fig. 10 Destriped results of different algorithms and the corresponding residual figure(residual figure contrast stretched for display) |

|
| 图 13 不同方法的去噪结果及对应的残差图(为了更好显示,残差图进行对比度拉伸) Fig. 13 Destriped results of different algorithms and the corresponding residual figure(residual figure contrast stretched for display) |

|
| 图 16 不同方法的去噪结果及对应的残差图(为了更好显示,残差图进行对比度拉伸) Fig. 16 Destriped results of different algorithms and the corresponding residual figure(residual figure contrast stretched for display) |

|
| 图 19 不同方法的去噪结果及对应的残差图(为了更好显示,残差图进行对比度拉伸) Fig. 19 Destriped results of different algorithms and corresponding residual figure(residual figure contrast stretched for display) |
| 方法 | 文献[8] | 文献[12] | 文献[17] | 文献[18] | 本文方法 |
| IF/BD(MODIS30) | 9.665 4 | 12.857 3 | 14.284 2 | 14.460 3 | 14.548 8 |
| ID | 0.954 5 | 0.981 2 | 0.986 2 | 0.988 6 | 0.990 1 |
| IC | 39.083 5 | 41.084 8 | 42.184 8 | 42.456 7 | 42.897 4 |
| CE(unit, s) | 1.45 | 5.56 | 2.25 | 3.33 | 2.78 |
| IF/BD(Hyperion) | 10.351 2 | 13.452 8 | 14.636 9 | 14.9143 | 15.070 5 |
| ID | 0.960 4 | 0.978 4 | 0.983 5 | 0.986 9 | 0.989 2 |
| IC | 33.987 4 | 34.726 3 | 35.425 5 | 35.623 9 | 35.964 7 |
| CE(unit, s) | 0.22 | 4.62 | 0.86 | 1.48 | 1.04 |
| IF/BD(CHRIS) | 22.973 2 | 25.087 8 | 26.184 5 | 26.861 2 | 26.910 4 |
| ID | 0.962 5 | 0.981 1 | 0.986 5 | 0.990 0 | 0.991 4 |
| IC | 49.891 6 | 52.167 6 | 53.313 7 | 53.593 9 | 54.055 2 |
| CE(unit, s) | 2.66 | 7.32 | 3.32 | 4.26 | 3.75 |
| IF/BD(航空影像1) | 8.966 4 | 11.310 3 | 11.488 6 | 11.598 1 | 11.628 7 |
| ID | 0.951 4 | 0.982 4 | 0.986 5 | 0.987 7 | 0.988 4 |
| IC | 42.915 3 | 43.641 8 | 44.642 2 | 45.348 3 | 45.703 2 |
| CE(unit, s) | 0.56 | 5.21 | 1.47 | 2.05 | 1.68 |
| IF/BD(航空影像2) | 10.684 9 | 13.873 2 | 14.523 1 | 14.763 1 | 15.004 5 |
| ID | 0.953 8 | 0.983 1 | 0.987 2 | 0.988 6 | 0.990 8 |
| IC | 42.083 0 | 42.667 8 | 43.257 8 | 43.518 5 | 43.821 6 |
| CE(unit, s) | 0.28 | 4.75 | 0.95 | 1.57 | 1.12 |
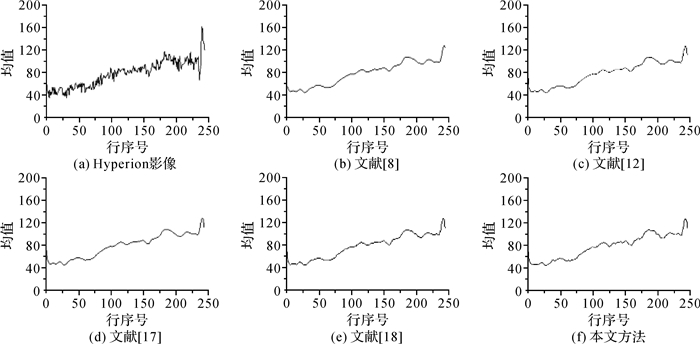
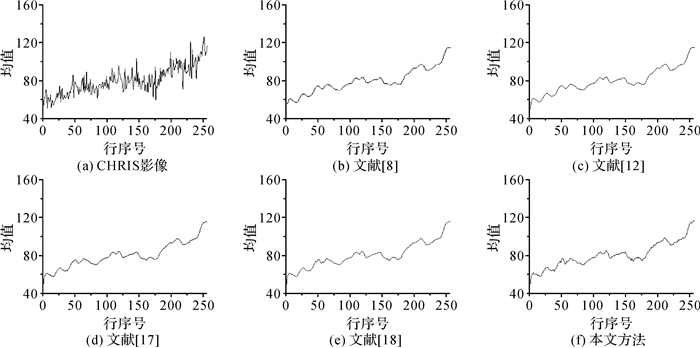
从图 7、图 10、图 13、图 16及图 19可以看到,本文方法在去除条带噪声的同时基本没有丢失影像细节,而其他方法都丢失少量影像细节。
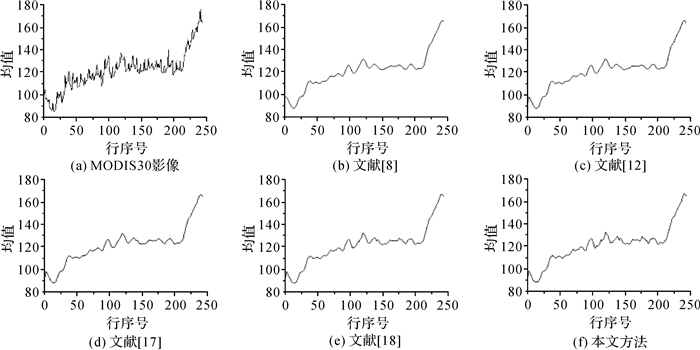
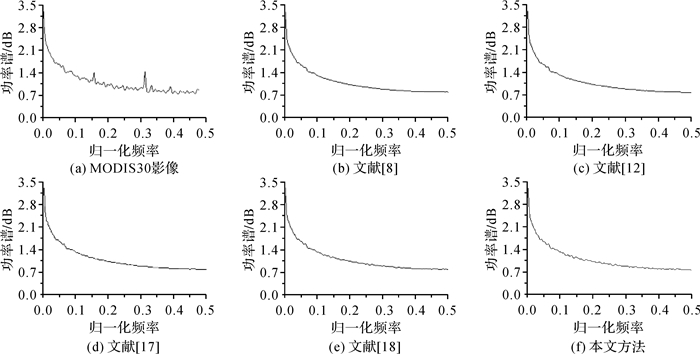
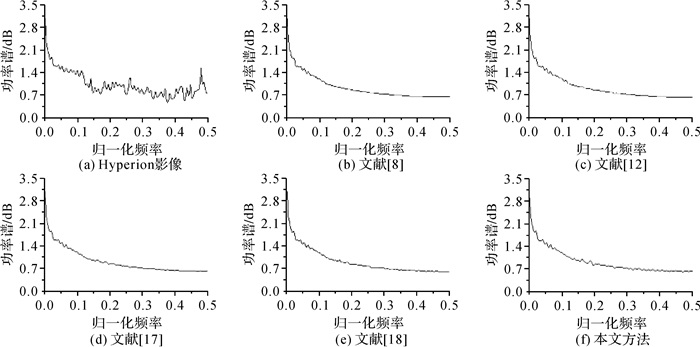
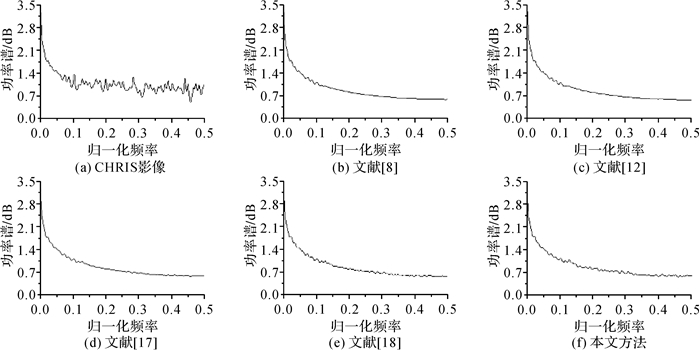
从图 8-图 9、图 11-图 12、图 14-图 15、图 17-图 18及图 20与图 21的对比中可以看到,本文方法的行均值曲线及功率谱曲线都没有出现震荡现象,并且曲线较其他方法粗糙,说明本文方法不仅可以有效去除条带噪声,而且能更好地保留影像细节。
从表 2可以看到,本文方法的ID值、IF值及IC值仍然高于其他方法,说明本文方法的去噪效果仍然是最优的。而从CE值看,本文方法的计算效率仍然低于文献[8]方法及文献[17]方法,但要高于文献[12]方法及文献[18]方法。
3 结论通过对本文条带噪声去除方法的研究,总结以下几点结论:
(1) 本文提出的基于小波的SPVM-DVM条带噪声去除方法不仅可以有效去除高光谱影像及航空影像的周期性及非周期性条带噪声,而且基本没有破坏影像细节,去噪后的影像质量及对比度都是最优的。
(2) 通过对高光谱影像及航空影像条带噪声去除的试验分析,SPVM模型适合处理1~3层高频分量的条带噪声,而DVM模型处理4层以上的高频分量条带噪声比较有效。
| [1] |
孙斌, 李景林, 张星祥, 等.
600mm长焦平面时间延迟积分CCD的交错拼接[J]. 光学精密工程, 2014, 22(11): 2908–2913.
SUN Bin, LI Jinglin, ZHANG Xingxiang, et al. Interleaving assembly of TDICCDs on 600mm focal plane[J]. Optics and Precision Engineering, 2014, 22(11): 2908–2913. |
| [2] |
王任享, 王建荣, 胡莘, 等.
LMCCD相机影像摄影测量首次实践[J]. 测绘学报, 2014, 43(3): 221–225.
WANG Renxiang, WANG Jianrong, HU Xin, et al. First practice of LMCCD camera imagery photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 221–225. DOI:10.13485/j.cnki.11-2089.2014.0032 |
| [3] | CHEN Jinsong, SHAO Yun, GUO Huadong, et al. Destriping CMODIS data by power filtering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(9): 2119–2124. DOI:10.1109/TGRS.2003.817206 |
| [4] | PAN J J, CHANG C I. Destriping of landsat MSS images by filtering techniques[J]. Photogrammetric Engineering and Remote Sensing, 1992, 58(10): 1417–1423. |
| [5] | TORRES J, INFANTE S O. Wavelet analysis for the elimination of striping noise in satellite images[J]. Optical Engineering, 2001, 40(7): 1309–1314. DOI:10.1117/1.1383996 |
| [6] | CHEN Jinsong, LIN Hui, SHAO Yun, et al. Oblique striping removal in remote sensing imagery based on wavelet transform[J]. International Journal of Remote Sensing, 2006, 27(8): 1717–1723. DOI:10.1080/01431160500185516 |
| [7] | PANDE-CHHETRI R, ABD-ELRAHMAN A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(5): 620–636. DOI:10.1016/j.isprsjprs.2011.04.003 |
| [8] | MVNCH B, TRTIK P, MARONE F, et al. Stripe and ring artifact removal with combined wavelet-fourier filtering[J]. Optics Express, 2009, 17(10): 8567–8591. DOI:10.1364/OE.17.008567 |
| [9] | RAKWATIN P, TAKEUCHI W, YASUOKA Y. Stripe noise reduction in MODIS data by combining histogram matching with facet filter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1844–1856. DOI:10.1109/TGRS.2007.895841 |
| [10] | CARFANTAN H, IDIER J. Statistical linear destriping of satellite-based pushbroom-type images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 1860–1871. DOI:10.1109/TGRS.2009.2033587 |
| [11] | SUN Lixin, NEVILLE R, STAENZ K, et al. Automatic destriping of Hyperion imagery based on spectral moment matching[J]. Canadian Journal of Remote Sensing, 2008, 34(S1): S68–S81. |
| [12] |
胡宝彭, 周泽明, 孟勇, 等.
基于矩匹配和变分法的MODIS条带去除模型[J]. 红外, 2014, 35(11): 28–36.
HU Baopeng, ZHOU Zeming, MENG Yong, et al. Destriping model of MODIS images based on moment matching and variational approach[J]. Infrared, 2014, 35(11): 28–36. DOI:10.3969/j.issn.1672-8785.2014.11.007 |
| [13] |
韩玲, 董连凤, 张敏, 等.
基于改进的矩匹配方法高光谱影像条带噪声滤波技术[J]. 光学学报, 2009, 29(12): 3333–3338.
HAN Ling, DONG Lianfeng, ZHANG Min, et al. Destriping hyperspectral image based on an improved moment matching method[J]. Acta Optica Sinica, 2009, 29(12): 3333–3338. |
| [14] | SHEN Huanfeng, ZHANG Liangpei. A MAP-based algorithm for destriping and inpainting of remotely sensed images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(5): 1492–1502. DOI:10.1109/TGRS.2008.2005780 |
| [15] | BOUALI M, LADJAL S. Toward optimal destriping of MODIS data using a unidirectional variational model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(8): 2924–2935. DOI:10.1109/TGRS.2011.2119399 |
| [16] | CHANG Yi, FANG Houzhang, YAN Luxin, et al. Robust destriping method with unidirectional total variation and framelet regularization[J]. Optics Express, 2013, 21(20): 23307–23323. DOI:10.1364/OE.21.023307 |
| [17] | ZHANG Yaozong, ZHOU Gang, YAN Luxin, et al. A destriping algorithm based on TV-Stokes and unidirectional total variation model[J]. Optik, 2016, 127(1): 428–439. |
| [18] |
霍丽君, 何斌, 周达标.
遥感图像条带噪声的多尺度变分模型去除[J]. 光学精密工程, 2017, 25(1): 198–207.
HUO Lijun, HE Bin, ZHOU Dabiao. A destriping method with multi-scale variational model for remote sensing images[J]. Optics and Precision Engineering, 2017, 25(1): 198–207. |
| [19] | JI Tengyun, HUANG Tingzhu, ZHAO Xile, et al. Tensor completion using total variation and low-rank matrix factorization[J]. Information Sciences, 2016(326): 243–257. |
| [20] | LIU Xinxin, LU Xiliang, SHEN Huanfeng, et al. Stripe noise separation and removal in remote sensing images by consideration of the global sparsity and local variational properties[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(5): 3049–3060. DOI:10.1109/TGRS.2015.2510418 |
| [21] | LIU Xinxin, SHEN Huanfeng, YUAN Qiangiang, et al. A universal destriping framework combining 1-D and 2-D variational optimization methods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(2): 808–822. DOI:10.1109/TGRS.2017.2755016 |
| [22] | SONG Qiong, WANG Yuehuan, YAN Xiaoyun, et al. Remote sensing images stripe noise removal by double sparse regulation and region separation[J]. Remote Sensing, 2018, 10(7): 998. DOI:10.3390/rs10070998 |
| [23] | BOUTEMEDJET A, DENG Chenwei, ZHAO Baojun. Edge-aware unidirectional total variation model for stripe non-uniformity correction[J]. Sensors, 2018, 18(4): 1164. DOI:10.3390/s18041164 |
| [24] | CHEN Yong, HUANG Tingzhu, ZHAO Xile, et al. Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint[J]. Remote Sensing, 2017, 9(6): 559. DOI:10.3390/rs9060559 |
| [25] | DOU Hongxia, HUANG Tingzhu, DENG Liangjian, et al. Stripe noise removal of remote sensing image with a directional l0 sparse model[C]//Proceedings of 2017 IEEE International Conference on Image Processing. Beijing: IEEE, 2017: 3505-3509. |