高光谱遥感影像具有图谱合一、光谱波段范围广、分辨率高等特点,增强了遥感对地观测能力和地物鉴别能力,给地物分类带来了机遇[1-3]。但是,高光谱遥感影像同时存在数据量大、波段数多、信息冗余多[4-5],直接对其进行地物分类易导致“维数灾难”问题。因此,如何去除高光谱数据中的冗余信息,挖掘高维数据的潜在本质特征,提取低维鉴别表征,已成为高光谱影像处理中的研究热点[6-7]。
维数约简(dimensionality reduction, DR)是解决这一问题的有效方法,其目的是降低数据维数,得到高维数据有意义的低维表示。近年来,国内外学者提出了一系列维数约简方法,并在许多领域取得了较好的效果。主成分分析(principal component analysis, PCA)[8]、线性判别分析(linear discriminant analysis, LDA)[9]是基于线性子空间的常用方法,但研究表明高光谱影像中存在着非线性的流形结构[10]。流形学习方法能有效发现嵌入高维观测数据中的低维流形结构,代表性方法主要有局部线性嵌入(local linear embedding, LLE)[11]、等距离映射(isometric feature mapping, ISOMAP)[12]和拉普拉斯特征映射(Laplacian eigenmaps, LE)[13]等。然而,这些方法存在“样本外学习”的问题,不能直接得到新样本的低维嵌入特征。为解决此问题,学者对LLE和LE方法进行了线性近似,提出了邻域保持嵌入(neighborhood preserving embedding, NPE)[14]和局部保持投影(locality preserving projection, LPP)[15]等线性方法,取得了不错的分类效果。
上述维数约简方法仅通过利用高光谱数据的光谱信息来实现降维[16],但是高光谱遥感影像具有“图谱合一”的特点,其空间相关性强,即相邻像素点一般具有比较明显的区域一致性[17-21]。因此,学者们开始融合高光谱数据的光谱信息和空间信息来提高地物分类性能[22-23]。文献[24]提出了一种基于空间一致性的邻域保持嵌入(spatial coherence-neighborhood preserving embedding, SC-NPE)算法。该算法通过比较每个像素点周围一定大小环块之间的距离来进行近邻选取,然后通过一个优化的线性嵌入将原始数据映射到低维子空间。文献[25]提出了一种空间域的局部像素近邻保持嵌入(local pixel neighborhood preserving embedding, LPNPE)算法。其目标是寻找一个线性的映射矩阵,使得投影之后局部像素的近邻保持散度矩阵最小化、总体散度矩阵最大化,进而提升分类性能。文献[26]提出了一种鉴别空谱边界(discriminate spectral-spatial margins, DSSM)算法。该算法在每个像素点周围定义一定大小的局部空间区域,通过比较该区域中同类地物与不同地物近邻点之间的差异来挖掘高光谱数据中的空间信息。上述空-谱联合方法在高光谱影像分类中都取得了较好的效果,但仅局限于利用局部空间区域内中心像素与其周围像素之间的空间信息,而忽略了流形重构过程中各像素点与其近邻点之间的空间信息,这些空间信息对于地物分类依然有着重要的作用,尤其在训练样本较少时更为明显。
基于此,本文提出了一种加权空-谱联合保持嵌入(weighted spatial-spectral combined preserving embedding, WSCPE)方法,通过有效利用高光谱影像中的空间-光谱特征信息来提升分类效果。其主要思想是首先采用加权均值滤波(weighted mean filter, WMF)方法对高光谱影像进行空间滤波,以消除噪点和背景点的干扰,然后利用加权空-谱联合距离(weighted spatial-spectral combined distance, WSCD)得到各像素点的空-谱近邻点,并根据各像素点与近邻点空间位置的远近给予不同的权重以进行流形重构,提取出更为有效的鉴别特征,实现高光谱数据降维。在PaviaU和Indian Pines高光谱数据集上的试验结果表明,本文方法能够有效提取出高光谱遥感影像中各类地物的鉴别特征,改善了地物分类性能。
1 NPE算法NPE算法是LLE算法的线性逼近,通过投影矩阵将高维数据投影到低维空间后,保持其局部近邻结构不变。遇有新样本时,可利用得到的投影矩阵计算其嵌入特征。其具体算法步骤包括:
(1) 构建近邻图G。构建图G时可采用K近邻法或ε近邻法得到近邻,若样本点xi和xj为近邻,则在图G中用边连接;否则无边连接。
(2) 计算权重矩阵W。在高维空间中,xi可由它的k个近邻点进行近似线性表示,可通过最小化重构误差进行计算权重,则
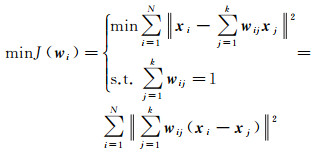 (1)
(1)
式中,wij为xi与xj之间的权值,若xj为xi的近邻点,有wij≠0,否则wij=0。
(3) 求解投影矩阵A。在高维空间中样本xi能够由其近邻点及权重矩阵W进行线性重构,那么其低维映射yi也可以通过W进行重构。因此,投影矩阵A可通过优化以下目标函数而得到
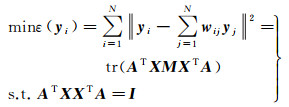 (2)
(2)
式中,M=(I-W)(I-W)T;I=diag(1, …, 1)为单位矩阵。
2 本文算法假设一个高光谱立方体可表示为Z∈RD×l×w,其中l、w分别为高光谱影像的长和宽,D为高光谱数据集的波段数。若高光谱数据集为X=[x1, x2, …, xN]∈RD×N,N为高光谱影像中训练样本的个数,对应的低维嵌入特征可表示为Y=ATX,Y∈RN×d, d≪D,其中A∈RD×d为投影矩阵。
2.1 WMF方法假设数据点xi在原始高光谱影像中的位置坐标为(pi, qi),那么以xi为中心,以w(w为正奇数)为长和宽的近邻空间Ω(xi)可定义为
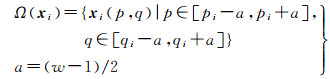 (3)
(3)
由式(3)可得知,近邻空间Ω(xi)中共包含w×w个像素,定义除xi之外的其余w2-1个像素分别为xi1、xi2、…、xi(w-1)2,那么可利用这w×w个像素通过加权求和的方式对xi进行重构,得到重构像素x′i,那么x′i可以表示为
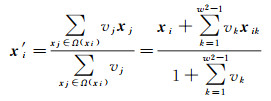 (4)
(4)
式中,vk为像素xik在重构过程中的权重,可通过热核函数进行计算
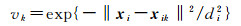 (5)
(5)
式中,di为近邻空间Ω(xi)中所有像素与中心像素xi之间欧氏距离的平均值,可表示为
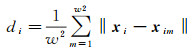 (6)
(6)
WMF方法通过控制参数w的大小来调节滤波窗口的大小,其本质是通过衡量近邻空间中近邻像素与中心像素的光谱相似性来对中心像素进行重构。光谱越相似,所计算出来的权重就越大;相反,若光谱之间的差异越大,其相应的权重就越小。因此,该滤波方法能够有效地消除噪点和背景点的干扰,使得滤波后的图像变得更加平滑。
2.2 WSCPE算法传统NPE算法仅通过像素点之间的光谱相似性来进行近邻点选取,忽略了空间信息。随后提出的SC-NPE算法虽然考虑了一定大小环块之内像素间的空间信息,通过比较各像素点周围环块之间的差异来进行近邻选取,但没有在流形重构过程中利用各像素点与其近邻点之间的空间信息。针对上述问题,本文提出的加权空-谱联合保持嵌入方法(WSCPE)首先采用一种新的加权空-谱联合距离(weighted spatial-spectral combined distance, WSCD)来进行空谱近邻点的选取,然后通过利用各像素点与其空谱近邻点之间的空间关系赋予各空谱近邻点更为合适的重构权重,使得空间位置上越近的像素占据更大的权重,反之权重较小,进而得到空-谱鉴别特征,提高分类性能。
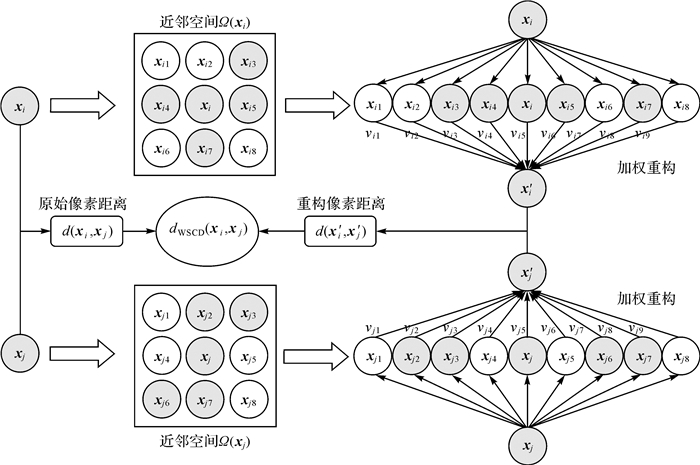
WSCD方法通过对WMF滤波前后的高光谱数据分别计算距离,并对这两种距离进行加权求和以融合像素点的光谱信息和空间信息,可有效度量像素点之间的近邻关系。该方法的具体实现过程如图 1所示。
|
| 图 1 加权空谱联合距离(WSCD)的流程 Fig. 1 Flow chart of weighted spatial-spectral combined distance (WSCD) |
对于任意两个像素点xi和xj,采用WMF方法构造近邻空间对其进行线性重构,得到融合空间近邻信息的重构像素x′i和x′j。在此,定义d(x′i, x′j)为重构像素x′i和x′j之间的欧氏距离、d(xi, xj)为原始像素xi和xj之间的欧氏距离,则加权空-谱联合距离如式(7)所示
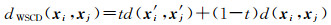 (7)
(7)
式中,0≤t≤1用于调节d(xi, xj)和d(x′i, x′j)两种距离对于加权距离的贡献。
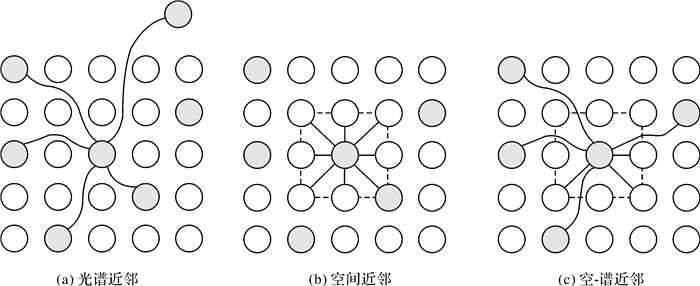
此处用图 2进一步说明不同近邻方法选择的区别。图 2为光谱、空间、空-谱联合近邻选取方式示意图,其中灰色圆圈代表中心像素,黑实线连接的圆圈代表其选取的近邻点。图 2(a)为光谱近邻选取,仅考虑了光谱曲线的相似程度,没有考虑地物一致性原则,因此得到的近邻点来自于影像中较远的位置;图 2(b)表示的是空间近邻选取,由于只考虑了像素在空间位置上的远近关系,因此得到的近邻点可能来自于不同的地物类别,进而影响流形重构效果;图 2(c)表示的是选择空-谱近邻选择,通过利用加权空-谱联合距离,综合考虑了像素间的光谱相似性以及空间远近关系,因此能有效选择真实的近邻点进行流形重构。
|
| 图 2 3种不同近邻点的选取 Fig. 2 Distribution of three different neighbors |
获得空-谱近邻点后,即可构建空-谱近邻图Gss(X, Wss),X为图的顶点,Wss为其权重矩阵。在图Gss中,若两点为近邻,则需连接一条边,否则不连接。根据真实地物成块分布的原则,像素点的近邻点在高光谱图像中空间距离越近,则它们属于同一类的可能性就越大,其重构权重也应该越大;反之,属于同一类的可能性就越小,其重构权重也应该越小。因此,为体现近邻样本的差异性,本文通过引入像素坐标距离dPCDij来表征。在此定义xi和xj在原始图像中坐标分别为(pi, qi)和(pj, qj),则其像素坐标距离dPCDij可以表示为
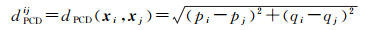 (8)
(8)
通过引入dPCDij,式(1)中的目标函数可重新定义为
 (9)
(9)
式中,(xi-xj)与dPCDij分别为xi和xj之间的光谱距离和像素坐标距离,则(xi-xj)/dPCDij就成了xi和xj之间空间距离和光谱距离的综合性度量。与NPE算法相比,xi的k个近邻点权重w′i1、w′i2、…、w′ik因dPCDij的引入得到不同程度的减小,在空间位置上离xi越近的近邻点,其权重减小的幅度越小,反之则减小的幅度越大,实现对其权重的有效调节。
通过化简,式(9)中目标函数可表示为
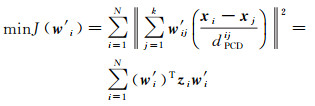 (10)
(10)
式中,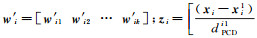
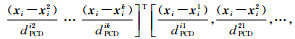
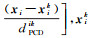
为消除尺度因子的影响,增加样本近邻点权重之和为1的约束条件,目标函数进一步表示为
 (11)
(11)
然后,利用拉格朗日乘子法对式(11)进行求解,可得到
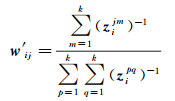 (12)
(12)
在得到空-谱近邻点的权重矩阵W′之后,投影矩阵A可通过求解以下最优化问题得到
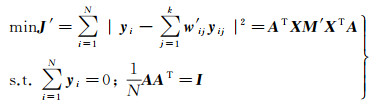 (13)
(13)
式中,M′=(I-W′)(I-W′)T。利用拉格朗日乘子法对式(13)进行求解,可得到
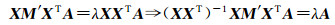 (14)
(14)
通过式(14)求取广义特征值,并对特征值进行升序排序,则前d个特征值所对应的特征向量a1、a2、…、ad就构成了投影矩阵A,则高维数据的低维嵌入特征可表示为Y=ATX。
2.3 WSCPE算法步骤输入:高光谱影像数据集X,低维空间中的近邻个数k,空间窗口w,加权系数t。
输出:映射向量A,高光谱数据的低维嵌入特征Y=[y1 y2 y3…yN]∈RN×d。
步骤1:利用WMF算法对高光谱影像进行滤波。
步骤2:在滤波后的样本集X中根据样本比例随机抽取得到训练样本集,其余作为测试样本。
步骤3:根据WSCD算法计算每个训练样本之间的欧氏距离,并按照从小到大的顺序进行排列,然后选取前k个距离对应的样本点作为其近邻点。
步骤4:根据式(10)计算训练样本的权重矩阵W′。
步骤5:保持权重矩阵W′不变,根据式(13)求出映射向量A以及高维数据的低维表示Y=ATX。
3 试验结果与分析 3.1 试验数据集本文算法主要通过PaviaU和Indian Pines高光谱数据集进行试验论证,下面对其进行简单介绍。
(1) PaviaU数据集:该数据集由西班牙巴斯克大学提供,主要采集于意大利北部的帕维亚大学区域,并且已经对草地、泥土和沥青等9类地物的样本类别进行了事先标注。影像大小为610×340 pixels,空间分辨率为1.3 m,共包含115个波段。由于其中包含的12个波段受水汽的影响较为严重,一般只用其余的103个波段进行研究。图 3(a)、图 3(b)分别为PaviaU数据集的假彩色图和真实地物分布图,其中括号中的数值表示每类地物的样本总数。

|
| 图 3 高光谱图像 Fig. 3 Hyperspectral image |
(2) Indian Pines数据集:该数据集由美国国家宇航局提供,主要采集于美国西北部印第安纳松林,并且事先已经对森林、植被和房屋等16类地物的样本类别进行了事先标注。影像大小为145×145 pixels,空间分辨率为20 m,共包含220个波段。由于其中包含的20个波段受水汽的影响较为严重,一般只用其余的200个波段进行研究。图 3(c)、图 3(d)分别为Indian Pines数据集的假彩色图、真实地物分布图,其中括号中的数值表示每类地物的样本总数。
3.2 试验设置由于高光谱遥感数据中不同波段的数据范围不一致,为了降低不同数据范围对降维的影响,首先对其按波段分别进行归一化处理。在每次试验中,高光谱数据集被随机划分为训练样本和测试样本,利用训练数据得到投影矩阵后,可将样本投影到嵌入空间得到低维特征,利用最近邻分类器(1-nearest neighbor, 1-NN)进行分类,并采用总体分类精度(overall accuracy, OA)、平均分类精度(average accuracy, AA)、Kappa系数3个参数对分类结果进行评价。为了保证试验结果的可靠性,每种条件下的试验均重复进行10次,并取10次结果的平均值作为最终试验结果。
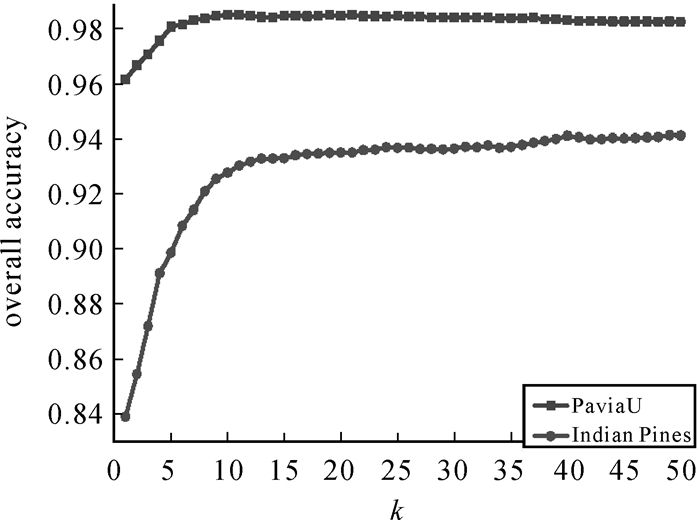
为了论证本文方法在提取高光谱数据集鉴别特征的有效性,试验中选取RAW(表示直接利用原始光谱数据)、PCA、LDA、LPP、NPE、LFDA、DSSM、SC-NPE和LPNPE与本文算法进行对比,其中PCA、LDA、LPP、NPE、LFDA方法仅利用了高光谱数据的光谱信息,而DSSM、SC-NPE、LPNPE等空-谱联合方法则融合了影像的光谱-空间信息。另外,为使LPP、NPE、SC-NPE、LPNPE等方法达到较好的效果,将其参数调整为最佳,低维嵌入特征维数为40维。LDA算法特征维数为c-1维,其中c为类别数。为使WSCPE算法取得最优的近邻数,本文分别从PaviaU和Indian Pines数据集中的从每类地物中随机选取30个样本用于训练,其余样本用于测试,图 4为对应的试验结果。由图 4可知,在PaviaU数据集上可选择k=10,在Indian Pines数据集上可选择k=20。
|
| 图 4 WSCPE在不同k下的分类结果 Fig. 4 Classification result of WSCPE with different k |
3.3 PaviaU试验结果
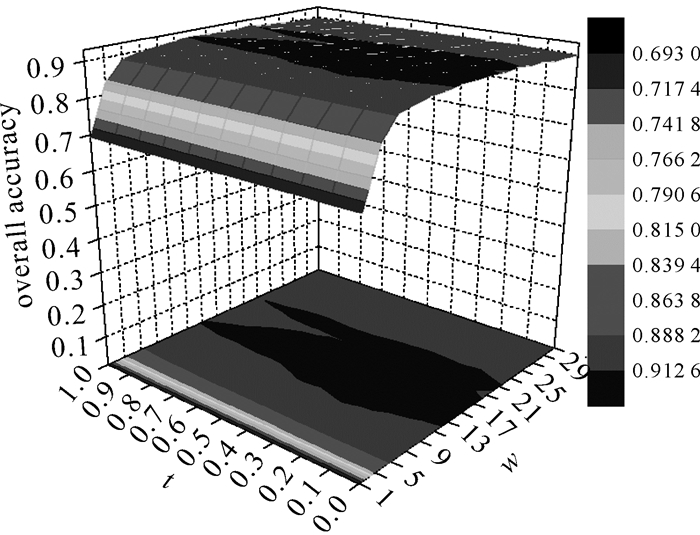
为研究窗口大小w和权重因子t对WSCPE算法性能的影响,首先选用PaviaU数据集进行试验。试验中,从每类地物中随机选取30个样本用于训练,其余样本用于测试,窗口大小w的变化范围为1、3、5、…、31,权重因子t的变化范围为0、0.1、0.2、…、1。图 5为WSCPE算法在不同窗口大小和权重因子下的分类精度。
|
| 图 5 PaviaU数据集中WSCPE在不同w和t下的分类结果 Fig. 5 Classification result of WSCPE with different w and t on PaviaU dataset |
由图 5可知,随着窗口w的增大,本文算法的分类精度随之增加;当w增大到5×5时,增幅开始逐渐减小;当w增大到11×11左右时出现分类精度的峰值;当w继续增大时,分类精度略有下降。这是由于当空间窗口包含了更多的空间近邻时,可利用的空间信息更加丰富,因而能够更好地区分不同地物,提高分类精度。然而,如果选用的窗口太大,得到的近邻点中就会包含来自于其他地物类别的像素点,因此会影响分类性能。综合考虑到算法分类精度以及运行效率,本文选取w=11,t=0.3。
为评估不同算法在不同数目训练样本下的分类性能,从PaviaU数据集中的每类地物中分别随机选取30、40、50、60个样本用于训练,其余样本用于测试。表 1为不同数目训练样本下的分类结果。
| (%) | ||||
| algorithm | 样本数量 | |||
| 30 | 40 | 50 | 60 | |
| RAW | 81.02±1.24 | 83.06±0.75 | 85.29±0.86 | 87.35±0.42 |
| PCA | 81.02±1.25 | 83.06±0.75 | 85.27±0.83 | 87.32±0.41 |
| NPE | 84.95±1.42 | 86.07±0.85 | 87.95±1.34 | 89.53±1.11 |
| LPP | 85.35±1.44 | 87.11±1.59 | 89.57±1.61 | 91.17±0.75 |
| LDA | 90.80±1.14 | 92.44±1.20 | 94.36±1.00 | 95.20±0.30 |
| LFDA | 90.54±1.17 | 92.53±1.28 | 93.38±1.58 | 94.57±0.85 |
| DSSM | 82.16±1.31 | 84.23±1.36 | 86.56±1.28 | 88.51±1.32 |
| SC-NPE | 85.13±1.45 | 86.96±1.23 | 88.63±1.15 | 90.66±1.27 |
| LPNPE | 91.81±1.27 | 93.26±1.25 | 94.29±1.32 | 95.30±1.25 |
| WSCPE | 92.35±1.22 | 94.36±1.29 | 96.48±0.92 | 97.06±1.33 |
由表 1可知,随着训练样本数量的增加,各种算法的分类精度随之提升,这是由于更多的训练样本包含了更丰富的先验信息,更有利于特征提取。在基于光谱特征的维数约简方法中,LDA、LFDA这两种监督算法通过利用训练样本的类别标记信息,其分类精度要明显优于PCA、NPE、LPP等非监督算法。同时,在空-谱联合维数约简方法中,WSCPE算法的分类精度要高于DSSM、SC-NPE、LPNPE方法,并且在各种试验条件下均取得了最好的分类效果。这是因为WSCPE算法分别在近邻点选取和流形重构过程进行了空间信息的挖掘,使得得到的鉴别特征更为丰富和有效,进而提升了分类精度。
为分析各算法在每类地物上的分类性能,试验中随机选取2%的样本用于训练,其余样本用于测试,得到PaviaU数据集中每类地物的分类精度、总体分类精度(OA)、平均分类精度(AA)和Kappa系数如表 2所示。图 6为其相对应的分类结果图。
| (%) | ||||||||||||
| class | train | test | RAW | PCA | NPE | LPP | LDA | LFDA | DSSM | SCNPE | LPNPE | WSCPE |
| 1 | 133 | 6498 | 93.72 | 93.72 | 94.70 | 97.16 | 95.93 | 97.47 | 93.75 | 93.93 | 96.83 | 97.19 |
| 2 | 373 | 18 276 | 97.03 | 97.03 | 97.29 | 99.33 | 99.57 | 99.21 | 97.03 | 98.01 | 99.93 | 99.93 |
| 3 | 42 | 2057 | 80.55 | 80.51 | 85.66 | 94.89 | 87.46 | 88.52 | 80.55 | 84.83 | 89.16 | 95.65 |
| 4 | 61 | 3003 | 84.38 | 84.38 | 85.21 | 81.61 | 96.43 | 94.70 | 85.72 | 88.75 | 88.54 | 92.70 |
| 5 | 27 | 1318 | 99.46 | 99.46 | 95.47 | 99.62 | 99.46 | 99.62 | 99.54 | 99.54 | 99.73 | 99.17 |
| 6 | 101 | 4928 | 88.51 | 88.48 | 88.02 | 97.56 | 96.75 | 97.28 | 89.12 | 91.29 | 99.42 | 99.83 |
| 7 | 27 | 1303 | 84.11 | 84.03 | 88.03 | 99.53 | 100.00 | 98.69 | 84.17 | 91.17 | 93.78 | 100.00 |
| 8 | 74 | 3608 | 93.93 | 93.93 | 83.74 | 95.67 | 93.51 | 93.54 | 94.15 | 94.01 | 91.71 | 95.99 |
| 9 | 19 | 928 | 99.89 | 99.89 | 99.89 | 99.89 | 99.89 | 100.00 | 99.89 | 99.89 | 79.96 | 100.00 |
| OA | - | - | 92.15 | 92.14 | 92.41 | 95.75 | 97.12 | 97.75 | 93.12 | 94.81 | 96.74 | 98.89 |
| AA | - | - | 91.29 | 91.28 | 92.44 | 94.30 | 96.58 | 96.56 | 91.35 | 93.49 | 95.50 | 97.36 |
| Kappa | - | - | 91.05 | 91.04 | 91.87 | 96.38 | 96.51 | 96.54 | 91.48 | 93.10 | 96.59 | 98.21 |

|
| 图 6 各算法在PaviaU数据集上的分类结果 Fig. 6 Classification results of different algorithms on PaviaU data set |
由表 2知,WSCPE算法在大多数类别上都取得了较好的分类结果,尤其是在“gravel”“soil”“bitumen”等区域更为明显,这是因为WSCPE算法在近邻点选取和权重矩阵计算两个过程均引入了像素的空间信息,可有效避免来自不同地物类别中具有相似光谱特征的像素点的影响,因此空间信息的引入可以更好地表征数据本身的内在属性,使得到的鉴别特征更有效地反映出不同地物类别间的本质差异。另外,从图 6可以看出,与其他方法相比,WSCPE的分类结果图更为平滑,错分点更少。
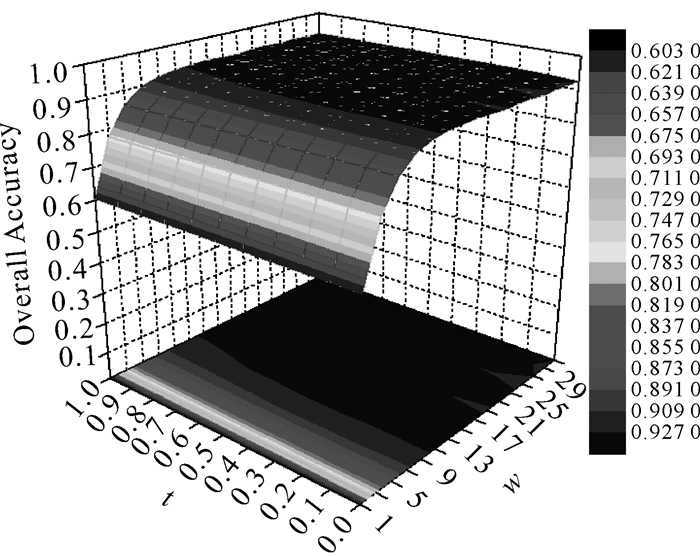
3.4 Indian Pines试验结果试验中,分别从Indian pines数据集每类地物中随机选取30个样本用于训练,剩余样本用于测试。首先对窗口大小w和权重因子t这两个参数进行试验,其中w的变化范围为1、3、5、…、35,t的变化范围为0、0.1、0.2、…、1。图 7为WSCPE算法的分类精度在不同w和t下的试验结果。由于窗口增大到11×11时,算法分类精度已基本稳定,因此在综合考虑到算法分类精度以及算法运行效率的情况下,这里选取w=11,t=0.5。
|
| 图 7 Indian Pines数据集中WSCPE在不同w和t下的分类结果 Fig. 7 Classification result of WSCPE with different w and t on Indian Pines dataset |
表 3为Indian Pines数据集中各算法在不同数目训练样本下的分类结果。可以看出各种算法的分类精度随着训练样本个数的增加而递增,同时WSCPE算法始终取得了最好的分类效果。这是因为WSCPE充分利用高光谱影像的空间一致性原则,将光谱信息和空间信息进行有效的结合,发现高光谱数据内部的鉴别子流形结构,有效提取表征不同地物差异的鉴别特征,从而提升了地物分类效果。
| (%) | ||||
| algorithm | 样本数量 | |||
| 30 | 40 | 50 | 60 | |
| RAW | 78.30±1.04 | 81.12±1.62 | 83.60±0.74 | 84.92±0.36 |
| PCA | 78.23±1.06 | 81.01±1.66 | 83.52±0.77 | 84.79±0.36 |
| NPE | 79.48±1.20 | 82.41±1.90 | 84.18±1.33 | 85.43±0.71 |
| LPP | 80.02±0.46 | 82.95±1.72 | 86.35±1.06 | 88.23±0.63 |
| LDA | 93.06±0.81 | 94.67±1.16 | 96.30±1.30 | 96.93±0.70 |
| LFDA | 90.82±0.71 | 93.29±1.37 | 94.94±0.91 | 95.71±0.42 |
| DSSM | 80.19±0.65 | 84.13±0.81 | 85.42±0.94 | 86.49±0.41 |
| SC-NPE | 80.25±0.51 | 83.98±0.74 | 85.64±0.93 | 87.56±0.39 |
| LPNPE | 91.91±0.64 | 93.94±0.69 | 94.83±0.92 | 96.01±0.81 |
| WSCPE | 93.54±1.03 | 95.62±1.15 | 97.37±0.56 | 98.19±0.73 |
表 4为随机选取3%的训练样本,其余作为测试样本的情况下,在Indian Pines数据集中的不同地物在不同算法下的分类精度,图 8为其相对应的分类结果图。可得知,WSCPE算法的总体分类精度、平均分类精度以及Kappa系数均高于其他算法。同时从图 8中的分类结果图也可看出,WSCPE算法的分类结果图较为平滑,分类效果较好,尤其在“hay-windowed”“soybeans-notill”“wheat”区域更为明显,更加证明了本文算法的有效性。
| (%) | ||||||||||||
| class | train | test | RAW | PCA | NPE | LPP | LDA | LFDA | DSSM | SCNPE | LPNPE | WSCPE |
| 1 | 10 | 36 | 94.44 | 94.44 | 99.89 | 99.89 | 100.00 | 99.89 | 97.22 | 99.89 | 100.00 | 100.00 |
| 2 | 43 | 1385 | 66.57 | 66.57 | 77.40 | 71.84 | 92.71 | 91.41 | 76.75 | 71.19 | 94.44 | 94.30 |
| 3 | 25 | 805 | 73.29 | 72.79 | 75.65 | 66.96 | 82.61 | 79.63 | 78.21 | 76.65 | 80.87 | 94.78 |
| 4 | 10 | 227 | 72.69 | 72.68 | 67.40 | 70.48 | 95.15 | 92.07 | 71.75 | 74.89 | 94.71 | 99.12 |
| 5 | 14 | 469 | 78.89 | 78.89 | 89.77 | 85.71 | 87.21 | 87.42 | 84.36 | 82.73 | 84.43 | 85.71 |
| 6 | 22 | 708 | 95.33 | 95.34 | 98.16 | 94.63 | 98.16 | 95.34 | 95.19 | 93.50 | 98.73 | 92.51 |
| 7 | 10 | 18 | 99.96 | 99.96 | 99.12 | 99.96 | 100.00 | 100.00 | 99.96 | 99.05 | 99.96 | 100.00 |
| 8 | 14 | 464 | 97.63 | 97.84 | 91.38 | 85.34 | 99.57 | 98.71 | 98.89 | 99.57 | 93.53 | 100.00 |
| 9 | 10 | 10 | 99.89 | 99.89 | 99.89 | 100.00 | 99.89 | 99.89 | 80.00 | 100.00 | 99.89 | 100.00 |
| 10 | 29 | 943 | 78.68 | 78.58 | 86.43 | 82.08 | 88.76 | 80.81 | 86.43 | 75.19 | 84.94 | 90.56 |
| 11 | 74 | 2381 | 86.09 | 85.93 | 89.67 | 83.45 | 97.35 | 95.72 | 88.60 | 89.71 | 95.55 | 96.72 |
| 12 | 18 | 575 | 62.43 | 62.09 | 71.83 | 55.13 | 86.78 | 78.78 | 62.30 | 61.39 | 88.35 | 89.74 |
| 13 | 10 | 195 | 93.33 | 93.33 | 96.92 | 97.95 | 100.00 | 100.00 | 98.96 | 93.33 | 99.49 | 100.00 |
| 14 | 38 | 1227 | 96.41 | 96.33 | 96.82 | 94.78 | 98.53 | 96.98 | 97.98 | 99.67 | 91.52 | 98.86 |
| 15 | 12 | 374 | 69.79 | 69.79 | 82.09 | 71.93 | 95.19 | 89.57 | 73.40 | 86.36 | 98.40 | 98.93 |
| 16 | 10 | 83 | 96.39 | 96.39 | 96.39 | 97.59 | 100.00 | 98.80 | 93.98 | 96.39 | 92.77 | 98.80 |
| OA | 81.76 | 81.65 | 86.51 | 80.89 | 93.86 | 91.12 | 85.60 | 84.39 | 92.15 | 95.47 | ||
| AA | 85.12 | 85.06 | 88.74 | 84.87 | 93.42 | 92.83 | 86.48 | 87.54 | 93.61 | 96.25 | ||
| Kappa | 79.18 | 79.05 | 84.61 | 78.21 | 92.97 | 89.82 | 83.58 | 82.10 | 90.93 | 94.38 | ||

|
| 图 8 各算法在Indian Pines数据集上的分类结果 Fig. 8 Classification results of different algorithms on Indian Pines data set |
4 结论
针对传统降维算法单一利用光谱信息,未考虑高光谱影像内部空间结构,提取得到的鉴别特征不够充分有效的问题,本文基于流形学习方法和空间一致性原则,提出一种加权空-谱联合保持嵌入(WSCPE)方法。该方法有效融合影像中的空间-光谱信息,通过加权空-谱距离选择得到各像素点的空-谱近邻,并在流形重构过程中根据各像素点与近邻点空间位置的远近给予不同的权重,提取出更为有效的鉴别特征,进而实现维数约简。在PaviaU和Indian Pines高光谱数据集上的试验结果表明,本文算法可有效提取高光谱遥感影像中各类地物的鉴别特征,改善了地物分类性能,在较少训练样本的情况下其总体分类精度分别达到了98.89%和95.47%。与传统基于光谱以及空-谱联合的降维算法相比,本文提出的WSCPE算法的分类精度有了明显地提升。
| [1] |
黄鸿, 郑新磊.
高光谱影像空-谱协同嵌入的地物分类算法[J]. 测绘学报, 2016, 45(8): 964–972.
HUANG Hong, ZHENG Xinlei. Hyperspectral image land cover classification algorithm based on spatial-spectral coordination embedding[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 964–972. DOI:10.11947/j.AGCS.2016.20150654 |
| [2] | LI Chang, MA Yong, MEI Xiaoguang, et al. Hyperspectral image classification with robust sparse representation[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(5): 641–645. DOI:10.1109/LGRS.2016.2532380 |
| [3] | LI Li, SUN Chao, LIN Lianlei, et al. A dual-layer supervised Mahalanobis kernel for the classification of hyperspectral images[J]. Neurocomputing, 2016, 214: 430–444. DOI:10.1016/j.neucom.2016.06.039 |
| [4] | HU Wei, HUANG Yangyu, WEI Li, et al. Deep convolutional neural networks for hyperspectral image classification[J]. Journal of Sensors, 2015(2): 1–12. |
| [5] |
罗甫林.
高光谱图像稀疏流形学习方法研究[J]. 测绘学报, 2017, 46(3): 400.
LUO Fulin. Sparse manifold learning for hyperspectral imagery[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 400. DOI:10.11947/j.AGCS.2017.20160621 |
| [6] |
侯榜焕, 王锟, 姚敏立, 等.
面向高光谱图像分类的半监督空谱判别分析[J]. 测绘学报, 2017, 46(9): 1098–1106.
HOU Banghuan, WANG Kun, YAO Minli, et al. Semi-supervised spatial-spectral discriminant analysis for hyperspectral image classification[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1098–1106. DOI:10.11947/j.AGCS.2017.20170121 |
| [7] | HUANG Hong, LUO Fulin, LIU Jiamin, et al. Dimensionality reduction of hyperspectral images based on sparse discriminant manifold embedding[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 106(3): 42–54. |
| [8] | BONIFAZI G, CAPOBIANCO G, SERRANTI S. Asbestos containing materials detection and classification by the use of hyperspectral imaging[J]. Journal of Hazardous Materials, 2018, 344(4): 981–993. |
| [9] | LIAO Wenzhi, PIZURICA A, SCHEUNDERS P, et al. Semisupervised local discriminant analysis for feature extraction in hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 184–198. DOI:10.1109/TGRS.2012.2200106 |
| [10] | HUANG Hong, YANG Mei. Dimensionality reduction of hyperspectral images with sparse discriminant embedding[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(9): 5160–5169. DOI:10.1109/TGRS.2015.2418203 |
| [11] | ZHANG Lili, ZHAO Chunhui. Sparsity divergence index based on locally linear embedding for hyperspectral anomaly detection[J]. Journal of Applied Remote Sensing, 2016, 10(2): 025026. DOI:10.1117/1.JRS.10.025026 |
| [12] | LI Wan, ZHANG Liangpei, ZHANG Lefei, et al. GPU parallel implementation of isometric mapping for hyperspectral classification[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(9): 1532–1539. DOI:10.1109/LGRS.2017.2720778 |
| [13] | DORADO-MUNOZ L P, MESSINGER D W. Initial study of Schroedinger eigenmaps for spectral target detection[J]. Optical Engineering, 2016, 55(8): 083101. DOI:10.1117/1.OE.55.8.083101 |
| [14] | LÜ Meng, ZHAO Xinbin, LIU Liming, et al. Discriminant collaborative neighborhood preserving embedding for hyperspectral imagery[J]. Journal of Applied Remote Sensing, 2017, 11(4): 046004. |
| [15] | DENG Yangjun, LI Hengchao, PAN Lei, et al. Modified tensor locality preserving projection for dimensionality reduction of hyperspectral images[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(2): 277–281. DOI:10.1109/LGRS.2017.2786223 |
| [16] | LUO Renbo, LIAO Wenzhi, HUANG Xin, et al. Feature extraction of hyperspectral images with semisupervised graph learning[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(9): 4389–4399. DOI:10.1109/JSTARS.2016.2522564 |
| [17] | TAN Kun, HU Jun, LI Jun, et al. A novel semi-supervised hyperspectral image classification approach based on spatial neighborhood information and classifier combination[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 105(5): 19–29. |
| [18] | WEN Jinhua, FOWLER J E, HE Mingyi, et al. Orthogonal nonnegative matrix factorization combining multiple features for spectral-spatial dimensionality reduction of hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 4272–4286. DOI:10.1109/TGRS.2016.2539154 |
| [19] | XIA Junshi, BOMBRUN L, ADALI T, et al. Spectral-spatial classification of hyperspectral images using ICA and edge-preserving filter via an ensemble strategy[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4971–4982. DOI:10.1109/TGRS.2016.2553842 |
| [20] | XIA Junshi, CHANUSSOT J, DU Peijun, et al. Spectral-spatial classification for hyperspectral data using rotation forests with local feature extraction and Markov random fields[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2532–2546. DOI:10.1109/TGRS.2014.2361618 |
| [21] | DE SOUZA F D M, SARKAR S, SRIVASTAVA A, et al. Spatially coherent interpretations of videos using pattern theory[J]. International Journal of Computer Vision, 2017, 121(1): 5–25. |
| [22] | YUE Jun, ZHAO Wenzhi, MAO Shanjun, et al. Spectral-spatial classification of hyperspectral images using deep convolutional neural networks[J]. Remote Sensing Letters, 2015, 6(6): 468–477. DOI:10.1080/2150704X.2015.1047045 |
| [23] | JIA Sen, ZHANG Xiujun, LI Qingquan. Spectral-spatial hyperspectral image classification using l1/2 regularized low-rank representation and sparse representation-based graph cuts[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2473–2484. DOI:10.1109/JSTARS.2015.2423278 |
| [24] |
魏峰, 何明一, 梅少辉.
空间一致性邻域保留嵌入的高光谱数据特征提取[J]. 红外与激光工程, 2012, 41(5): 1249–1254.
WEI Feng, HE Mingyi, MEI Shaohui. Hyperspectral data feature extraction using spatial coherence based neighborhood preserving embedding[J]. Infrared and Laser Engineering, 2012, 41(5): 1249–1254. DOI:10.3969/j.issn.1007-2276.2012.05.024 |
| [25] | ZHOU Yicong, PENG Jiangtao, CHEN C L P. Dimension reduction using spatial and spectral regularized local discriminant embedding for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 1082–1095. DOI:10.1109/TGRS.2014.2333539 |
| [26] | FENG Zhixi, YANG Shuyuan, WANG Shigang, et al. Discriminative spectral-spatial margin-based semisupervised dimensionality reduction of hyperspectral data[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(2): 224–228. DOI:10.1109/LGRS.2014.2327224 |


