2. 东华理工大学测绘工程学院, 江西南昌 330013;
3. 中国矿业大学环境与测绘学院, 江苏徐州 221116
2. Faculty of Geomatics, East China University of Technology, Nanchang 330013, China;
3. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China
针对EIV(errors-in-variables)模型
 (1)
(1)
式中,L为m×1维观测向量;A为m×u维系数矩阵;e与EA分别为对应L与A的误差项;X为u×1维参数向量。
“加权整体最小二乘EIO模型与算法”一文给出了一种EIV模型的变形——EIO模型,并推导了求解EIO模型及精度评定的方法。EIO函数模型可表示为
 (2)
(2)
式中,V由平差问题中全部观测向量的改正数构成,其维度为n×1;B为改正数向量的m×n阶系数矩阵,具体表述请参见该文。
该文给出的随机模型为
 (3)
(3)
式中,σ02为单位权方差;Q为全部观测向量的协因数阵。
相应的参数解及精度评定公式为
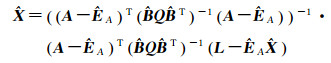 (4)
(4)
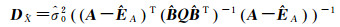 (5)
(5)
式中,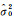
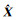
不同的平差问题,函数模型中系数矩阵的结构也不相同。EIV模型中系数矩阵的结构主要分为3类[1]:①由常数元素列和随机元素列组成,如直线拟合模型等;②由随机元素零散分布组成,且随机元素重复出现,如自回归模型等;③由常数元素和随机元素零散分布组成,且随机元素重复出现,如坐标转换模型等。本文将系数矩阵的这些情况统称为系数矩阵的特定结构。
EIO模型及相应的参数估计方法可得到与现有整体最小二乘法(total least squares,TLS)解等价的估计结果。其本质上也是分离EIV函数模型中的非随机(常数)元素和随机元素,进而重构函数模型,达到处理系数矩阵特定结构的目的。针对EIV模型系数矩阵的特定结构,可选择多种不同的模型和方法进行处理。实际应用中,采用何种方法进行数据处理可从模型复杂度、算法计算量、是否易于计算机处理和应用场景等多个方面进行考虑。本文从函数模型和随机模型的角度,罗列出4种EIV模型系数矩阵特定结构的处理方法,从EIV模型参数求解的角度归纳了8种参数估计公式,同时从精度评定的角度讨论了TLS解的一阶及更高阶精度近似评定方法,并且对EIO模型及其参数估计方法作简单分析。
1 EIV模型系数矩阵特定结构的处理方法及分析 1.1 随机模型处理法随机模型处理法也即通过确定系数矩阵元素的协因数,构造特定的权阵来保持系数矩阵的结构。针对系数矩阵A中存在非随机元素、随机元素零散和重复出现等情况,令误差向量

式中,vec(·)为列拉直运算。随机模型处理法是在平差前使v中对应于非随机元素的协因数为0,使重复出现的随机元素的协因数相同,以此逐一确定v的协因数阵中各元素的值[2-3]。将确定后的协因数阵或权阵参与平差计算,保证平差后非随机元素的改正数为0,而重复出现的随机元素的改正数相同,从而保证了系数矩阵误差的结构特征。
1.2 partial EIV模型方法partial EIV模型提取了A中的随机元素项,将非随机元素和随机元素进行了分离,重构后的partial EIV函数模型为[4-5]
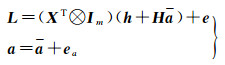 (6)
(6)
式中,h是由vec(A)中的非随机元素和零构成的列向量;H是与A中随机元素有关的固定矩阵;a为系数矩阵中不同随机元素构成的t×1维列向量;a为a的真值;ea为a的误差向量。
由于partial EIV模型将参数向量X与a一同估计,进而保证了系数矩阵A的特定结构。
1.3 通用EIV模型方法通用EIV模型作为一种更广泛的EIV模型,涵盖了间接平差、条件平差、附有参数的条件平差及附有限制条件的间接平差等的基本EIV函数模型形式,其表达式为[6]
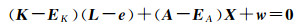 (7)
(7)
式中,K和EK表示观测向量系数矩阵及其改正值;w表示常数向量。
可见当K为单位阵,EK=0且w=0时,通用EIV模型即为文献[3]中等价的表达形式,因此也可处理系数矩阵A中的特定结构问题。
1.4 广义EIV模型方法广义EIV模型为[7]
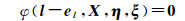 (8)
(8)
式中,φ(·)表示非线性函数;l为模型观测向量;el为其误差向量;η和ξ表示输入、输出向量。
广义EIV模型,也即Gauss-Helmert模型,将各观测数据(无论是出现在系数矩阵中或是观测向量中)进行了统一,本质上也解决了各类模型误差结构化的问题,参数求解可采用Newton法等非线性平差方法。
1.5 各种方法的分析和讨论(1) 针对系数矩阵中随机元素零散、重复出现且存在常数元素等特定结构的EIV模型,主要有两类处理方法:一类是从随机模型的角度去研究和处理,如随机模型处理法;另一类是对EIV模型进行变型,从函数模型的角度进行处理,构造如partial EIV模型、通用EIV模型以及广义EIV模型等更加普适性的函数模型进行参数求解。
(2) 随机模型处理法本质是在平差前充分考虑系数矩阵的结构特点,确定系数矩阵中的各元素及元素间的协因数。因此,在平差结束后,常数元素的误差改正数将为0,而重复出现的随机元素的改正数相等。随机模型处理法其实也是通用EIV模型法处理系数矩阵特定结构的方法,而通用EIV模型具有更为广泛的模型表达能力。
(3) partial EIV模型方法和广义EIV模型方法本质上是从函数模型的角度,考虑系数矩阵的结构性问题。需要指出的是,EIV模型的结构性问题不仅仅是在系数矩阵中,观测向量元素内部、观测向量与系数矩阵之间也会存在该问题,如non-Toeplitz模型[8]、AR模型[1]等。广义EIV模型方法和顾及相关观测的partial EIV模型方法[2]及其他能够处理观测向量和系数矩阵间相关性的方法均能够有效地处理该问题。
(4) EIO模型方法区别于随机模型处理法,是从函数模型的角度处理EIV模型中的结构性问题,也具有明确的可行性,且已在直线拟合、平面四参数解算算例中得到了验证。但EIO模型方法的处理思想本质上也是分离模型中的随机元素与非随机元素,从而达到处理系数矩阵特定结构的目的。笔者研究发现,EIO模型其实可更具普适性,即提取EIV模型中全部观测向量的改正数V实则也可处理观测向量中存在的结构性特点(如non-Toeplitz模型),但遗憾的是这一点并未在“加权整体最小二乘EIO模型与算法”一文的理论与试验中得到体现。
(5) 广义EIV模型涵盖了线性、非线性等各种EIV模型,更适用于采用非线性函数模型表达的应用场景;通用EIV模型则统一了间接平差、条件平差、附有参数的条件平差及附有限制条件的间接平差等的基本EIV函数模型,方便计算机自主选择模型解算;partial EIV模型则更为简洁,且已有文献已将partial EIV模型统一至最小二乘框架下,更加便于编程运算[5]。
2 不同加权整体最小二乘解的等价性证明及分析 2.1 不同加权整体最小二乘解的等价性证明加权整体最小二乘算法的解有多种不同的表达形式,现将8种典型的EIV模型参数估计公式归纳至表 1[9]。表 1中加权整体最小二乘解1至7是根据EIV模型推导得到,解7则是partial EIV模型解,而解8则是采用Gauss-Newton法求解EIV模型的表达式。
| 序号 | 加权整体最小二乘解公式 |
| 解1[3] | 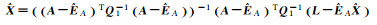 |
| 解2[3] | 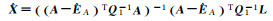 |
| 解3[3] | 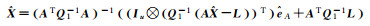 |
| 解4[10] | 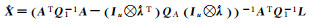 |
| 解5[11] | 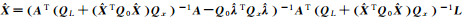 |
| 解6[2] | 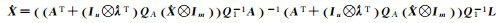 |
| 解7[4] | 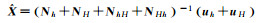 |
| 解8[3] | 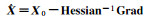 |
注:QL、QA分别为L和A的协因数阵;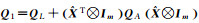 ; ;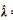 =Q1-1(L-AX);Hessian=∂2(L-AX)TQ1-1(L-AX)/∂X∂XT;Grad=∂(L-AX)TQ1-1(L-AX)/∂X;X0为X的近似值;Nh(i, j)=hiTQL-1hj;NH(i, j)= =Q1-1(L-AX);Hessian=∂2(L-AX)TQ1-1(L-AX)/∂X∂XT;Grad=∂(L-AX)TQ1-1(L-AX)/∂X;X0为X的近似值;Nh(i, j)=hiTQL-1hj;NH(i, j)=  ;NHh(i, j)= ;NHh(i, j)= 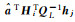 ;NhH(i, j)=hiTQL-1Hj ;NhH(i, j)=hiTQL-1Hj 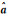 ;uh=[h1 h2 … hu]TQL-1L; ;uh=[h1 h2 … hu]TQL-1L;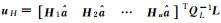 ;hi和hj表示h矩阵中的第i和j行m×1维行向量,同理Hi和Hj表示H矩阵中的第i和j个m×t维矩阵,且h=[h1T h2T … huT]T,H=[H1T H2T …HuT]T。 ;hi和hj表示h矩阵中的第i和j行m×1维行向量,同理Hi和Hj表示H矩阵中的第i和j个m×t维矩阵,且h=[h1T h2T … huT]T,H=[H1T H2T …HuT]T。 | |
(1) 解1与解2形式的等价性:解2表达式等价于
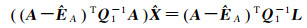 (9)
(9)
对式(9)等式两边同时加上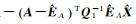
(2) 解1与解3形式的等价性:解3表达式等价于
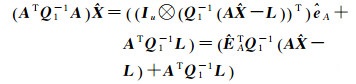 (10)
(10)
式中,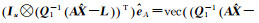
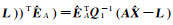
将式(10)最后一个等式展开并适当移项即可得到式(9),证明了解1等价于解2,进而证明了解3也等价于解1。
(3) 解3与解4形式的等价性:考虑到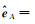

 (11)
(11)
式中,等式左边第2项也即为解3中的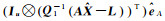
(4) 解4与解5形式的等价性:当系数矩阵协因数阵可表示为Kronecker积形式QA=Q0⊗Qx,则
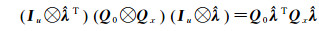 (12)
(12)
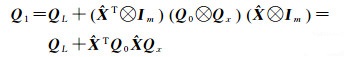 (13)
(13)
将式(12)和式(13)代入解4表达式,则可直接得到解5,证明了解4与解5的等价性,进而解5也等价于解1。
(5) 解6与解4形式的等价性:解6的表达式等价于
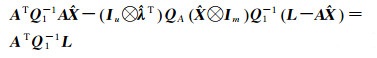 (14)
(14)
考虑到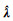
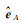
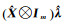
对于解7与解1形式的等价性可参阅文献[5]。而解8实际采用的是Newton法求解EIV模型,具有更快的收敛速度。综上所述,虽然EIV模型的解有多种不同的表达形式,但表 1中不同形式的解(解1至解7)本质是等价的。
2.2 不同加权整体最小二乘解的分析(1) 由表 1可知,解1与解2具有较好的理论意义,其解的形式类似于最小二乘解。因此,相关的抗差整体最小二乘解、整体最小二乘的粗差探测法和整体最小二乘的方差分量估计方法等扩展整体最小二乘方法可以直接依据最小二乘的理论框架导出。解3可以避免矩阵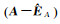
(2) 由式(4)和表 1可知,EIO模型参数估计的表达式实则等价于解1的形式。因此,EIO参数估计方法可以得到与已有加权整体最小二乘解等价的计算结果。在计算效率方面,EIO模型方法中其协因数阵Q是提取观测向量与系数矩阵中随机元素后的随机向量V的协因数阵,其维度将小于对增广矩阵[e EA]拉直后向量的协因数。但从式(4)和解1的法矩阵来看Q1=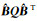
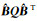
如何对参数估值结果进行精度评定一直是加权整体最小二乘平差的核心问题之一,本文将精度评定分为单位权方差的估计和参数估值协方差阵的计算两个部分进行分析。
3.1 单位权方差的估计尽管EIV模型系数矩阵特定结构的处理方法多种多样,但单位权方差计算方法却较为固定。目前,常用的方法主要有直接计算法和偏差改正计算法。
由观测值改正数及系数矩阵改正数加权计算单位权方差的直接计算法公式为[11]
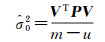 (15)
(15)
式中,P是观测值对应的权矩阵。
式(15)是目前最常用的单位权方差估计式,在形式上与经典最小二乘单位权方差估计式相似,且自由度与经典最小二乘相同,不同的是V的构成。但是,式(15)得到的单位权方差是有偏的,偏差改正计算法的公式为[4]
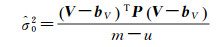 (16)
(16)
式中,bV为改正数向量的偏差。
式(16)顾及到观测值改正数与系数矩阵改正数的偏差,理论上更为准确。
3.2 参数估值协方差阵的计算目前,加权整体最小二乘参数估值协方差阵的计算方法可总结为两类:一类是近似函数表达式法,就是通过导数计算近似非线性函数的表达式,然后进行非线性误差的传播计算,从而得到参数估值的协方差阵,包括一阶近似和二阶近似协方差阵的计算;另一类是近似函数概率分布法,指的是通过采样来生成一定的sigma点(采样点)进而计算非线性函数均值和方差等统计量的方法。
一阶近似协方差阵的计算公式除了上文中列出的式(5),还有以下两种形式[12-13]
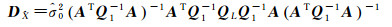 (17)
(17)
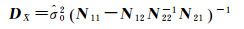 (18)
(18)
式中,

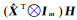
文献[14]利用非线性函数误差传播推导出加权整体最小二乘二阶近似协方差阵的计算公式
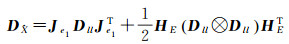 (19)
(19)
式中,ll=[LT aT]T为观测值及系数矩阵中随机元素组成的列向量;e1=[eT eaT]T,e的定义与式(2)相同;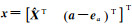
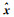
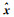
基于采样策略的SUT(scaled unscented transformation)法,将观测值和系数矩阵中随机元素的改正值、观测值和系数矩阵的协方差矩阵作为先验信息,结合相应的比例系数构造sigma点,最后加权计算参数估值的协方差阵[9]
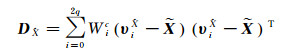 (20)
(20)
式中,i=0, 1,…,q为sigma点的个数,这里q=m+t,q为观测值及系数矩阵中全部随机元素的个数;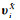

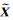
(1) 对于一阶近似协方差阵,式(5)与“加权整体最小二乘EIO模型与算法”一文中的近似精度评定方法等价并且式(5)与该文中的“迭代精确解”在结果上一致[15]。式(5)计算更简单,无须复杂的求导计算,可以更方便地使用。
(2) 对于要求精度评定结果更为准确,或者达到二阶精度,建议使用SUT法[9]等近似函数概率分布法,这些方法无须计算二阶偏导数。式(19)由于需要求解一阶与二阶偏导数,计算复杂度高于SUT法。因此,近似函数概率分布法相比于近似函数表达式法不需要计算复杂的导数,适用性也更强。
(3) 近似函数概率分布法除了SUT法外,还有自适应蒙特卡罗法[16]、刀切法(Jackknife法)[17]等,均可获得参数估值的二阶近似协方差阵。文献[16]结合Gauss-Helmert模型提出了对偶自适应蒙特卡罗精度评定方法,可以在自主选择模拟次数中获得稳定的结果;文献[17]给出了去1刀切法和去d刀切法的加权整体最小二乘精度评定流程,估计出参数估值的后验概率密度并求解协方差矩阵。这些近似函数概率分布法均顾及了参数估值的有偏性及迭代过程中的随机性。
(4) “加权整体最小二乘EIO模型与算法”一文中的单位权方差估计未进行偏差改正,是式(15)的等价表达方式,仍然是有偏的。对精度评定要求不高,且忽略EIV模型非线性以及参数估值随机性带来的影响时,可以使用未偏差改正的直接计算公式求解单位权方差估值。该文的近似精度评定方法在本质上与现有常用的一阶近似协方差阵计算方法没有区别,文中的算例结果也说明了这一点。虽然该文给出了参数估值协方差矩阵的迭代精确解,但本质上仍然只能达到一阶的精度,其迭代策略与文献[15]相同,即通过求解参数估值对其本身的一阶偏导数和参数估值对于观测值以及系数矩阵元素的一阶偏导数,再根据误差传播定律迭代计算参数估计的协方差矩阵。值得注意的是,文献[15]中的计算策略仅求解了关于参数估值的一阶偏导数,并没有求解二阶偏导数,本质上而言仍然属于一阶近似计算方法,该文将此方法视为精确解法似有不妥。
4 结论(1) 针对EIV模型的特定结构,可以从随机模型的角度和函数模型的角度进行研究。随机模型处理法本质是在平差前充分考虑系数矩阵的结构特点,确定系数矩阵中的各元素及元素间的协因数。而函数模型法则是通过对EIV模型进行变型,构造出更具普适性的函数模型。
(2) EIV模型的参数估计方法具有多种不同的表现形式,不同的表现形式具有不同的适用性。等价性证明已表明了不同的整体最小二乘解间的内在联系。
(3) 加权整体最小二乘精度评定涉及非线性误差传播问题,严密的精度评定公式应在非线性误差传播框架下讨论。
(4) 一阶近似的方法求参数估值的协方差信息往往不足以反映参数估值的实际精度,除了上文中提到的两种近似函数概率分布法,Sterling插值法、超球体单行采样法等是通过生成一定的sigma点计算非线性函数均值和方差等统计量的方法,也可用于加权整体最小二乘精度评定。
| [1] |
王乐洋, 许光煜, 温贵森.
一种相关观测的Partial EIV模型求解方法[J]. 测绘学报, 2017, 46(8): 978–987.
WANG Leyang, XU Guangyu, WEN Guisen. A method for partial EIV model with correlated observations[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 978–987. DOI:10.11947/j.AGCS.2017.20160430 |
| [2] | MAHBOUB V. On weighted total least-squares for geodetic transformations[J]. Journal of Geodesy, 2012, 86(5): 359–367. DOI:10.1007/s00190-011-0524-5 |
| [3] | FANG Xing. Weighted total least squares:necessary and sufficient conditions, fixed and random parameters[J]. Journal of Geodesy, 2013, 87(8): 733–749. DOI:10.1007/s00190-013-0643-2 |
| [4] | XU Peiliang, LIU Jingnan, SHI Chuang. Total least squares adjustment in partial errors-in-variables models:algorithm and statistical analysis[J]. Journal of Geodesy, 2012, 86(8): 661–675. DOI:10.1007/s00190-012-0552-9 |
| [5] |
王乐洋, 余航, 陈晓勇.
Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22–29.
WANG Leyang, YU Hang, CHEN Xiaoyong. An algorithm for partial EIV model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22–29. DOI:10.11947/j.AGCS.2016.20140560 |
| [6] |
曾文宪, 方兴, 刘经南, 等.
通用EIV平差模型及其加权整体最小二乘估计[J]. 测绘学报, 2016, 45(8): 890–894.
ZENG Wenxian, FANG Xing, LIU Jingnan, et al. Weighted total least squares of universal EIV adjustment model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 890–894. DOI:10.11947/j.AGCS.2016.20150156 |
| [7] | ZHOU Yongjun, KOU Xinjian, ZHU Jianjun, et al. A Newton algorithm for weighted total least-squares solution to a specific errors-in-variables model with correlated measurements[J]. Studia Geophysica et Geodaetica, 2014, 58(3): 349–375. DOI:10.1007/s11200-013-0254-7 |
| [8] | HAN Jie, ZHANG Songlin, LI Yali, et al. A general partial errors-in-variables model and a corresponding weighted total least-squares algorithm[J]. Survey Review, . DOI:10.1080/00396265.2018.1530332 |
| [9] | WANG Leyang, ZHAO Yingwen. Unscented transformation with scaled symmetric sampling strategy for precision estimation of total least squares[J]. Studia Geophysica et Geodaetica, 2017, 61(3): 385–411. DOI:10.1007/s11200-016-1113-0 |
| [10] | SCHAFFRIN B. Adjusting the errors-in-variables model: linearized least-squares vs. nonlinear total least-squares[C]//SNEEUW N, NOVáK P, CRESPI M, et al. Ⅷ Hotine-Marussi Symposium on Mathematical Geodesy. Cham: Springer International Publishing, 2015: 301-307. |
| [11] | SCHAFFRIN B, WIESER A. On weighted total least-squares adjustment for linear regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [12] | FANG Xing. Weighted total least squares solution for application in geodesy[D]. Hanover: Leibniz University of Hanover, 2011. |
| [13] | AMIRI-SIMKOOEI A, JAZAERI S. Weighted total least squares formulated by standard least squares theory[J]. Journal of Geodetic Science, 2012, 2(2): 113–124. |
| [14] | WANG Leyang, ZHAO Yingwen. Second-order approximation function method for precision estimation of total least squares[J]. Journal of Surveying Engineering, 2019, 145(1): 04018011. DOI:10.1061/(ASCE)SU.1943-5428.0000266 |
| [15] | AMIRI-SIMKOOEI A R, ZANGENEH-NEJAD F, ASGARI J. On the covariance matrix of weighted total least-squares estimates[J]. Journal of Surveying Engineering, 2016, 142(3): 04015014. DOI:10.1061/(ASCE)SU.1943-5428.0000153 |
| [16] |
王乐洋, 赵英文.
非线性平差精度评定的自适应蒙特卡罗法[J]. 武汉大学学报(信息科学版), 2019, 44(2): 206–213, 220.
WANG Leyang, ZHAO Yingwen. Adaptive Monte Carlo method for precision estimation of nonlinear adjustment[J]. Geomatics and Information Science of Wuhan University, 2019, 44(2): 206–213, 220. |
| [17] | WANG Leyang, YU Fengbin. Jackknife resample method for precision estimation of weighted total least squares[J]. Communications in Statistics-Simulation and Computation, . DOI:10.1080/03610918.2019.1580727 |


