2. 重庆大学土木工程学院, 重庆 400044
2. School of Civil Engineering, Chongqing University, Chongqing 400044, China
一些学者认为整体最小二乘EIV模型系数矩阵A存在结构性问题[1-4],一是含有非随机的常数项被误改正;二是含有相同元素被分配不同改正数。针对A中部分变量随机的结构性问题,有人提出采用Partial-EIV模型[4-6],将矩阵分解以避免改正非随机项并缩小计算量。本文研究发现EIV模型结构性问题并不存在,结构性问题是协因数阵QA不正确引起的。EIV模型解与A的结构无关,A的元素可相关,可为常数,可为观测量的函数,其位置可以任意分布。许多算法[7-9]均基于QA定权,但QA阶数是A中所有元素总数的平方,A元素较多时QA阶数过大,因此EIV模型在大数据量平差中迭代计算效率较低。由于EIV模型对矩阵A元素改正处理有缺陷,一些学者提出将观测向量与系数阵A中的随机元素统一至一个向量中进行处理[10-12],提出了TLS牛顿算法[10]、结构化TLS算法[11]、非典型EIV模型算法[12]。本文提出WTLS平差EIO模型,它只对平差问题中的独立观测值进行改正,观测值协因数阵是最简洁的对角阵,适用于独立平差,推导了参数估计迭代公式。由于TLS解具有非线性特征,不能直接求得精确方差,为了获得更精确的精度信息,一些学者提出基于误差传播定律的协因数迭代算法[13],以及基于无味变换原理的非线性误差传播方法[14]。前者是一种确定性方法,计算效率更高。本文基于EIO模型提出了QXX的精确迭代算法。
1 EIO模型 1.1 函数模型误差方程如下
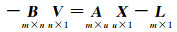 (1)
(1)
式中,L、X、V都是列向量;L为m维观测向量;V是n维(n≥m)独立观测改正数向量;X是u维未知参数向量;A为未知参数X的m×u阶系数矩阵;B为改正数向量V的m×n阶系数矩阵,B=diag([∂f(L, X)/∂Li]1m)= ivec(SBX+B0),SB与B0为常系数阵,ivec表示反拉直运算,由mn×1向量转换为m×n阶矩阵。式(1)由EIV模型演变而来。由EIV模型
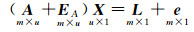 (2)
(2)
将误差矩阵EA及e组成增广矩阵[EA e],归类改写成一个系数矩阵B与独立观测值改正数向量V的矩阵乘积
 (3)
(3)
式(3)反号即得式(1)。L和A的改正矩阵VL和VA与V的关系为
 (4)
(4)
式中,SL和SA为设计系数矩阵。
1.2 随机模型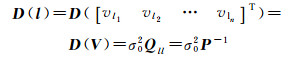 (5)
(5)
式中,l为n阶扩展观测值矩阵;V是l矩阵的改正数向量;σ02是单位权方差;Qll和P分别是l矩阵对应的协因数矩阵及权矩阵
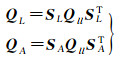 (6)
(6)
式中,QL为观测向量L的协因数矩阵;QA为vec(VA)的协因数矩阵。
2 参数估计 2.1 公式推导目标方程为VTPV= min s.t. L-AX-BV=0,构造拉格朗日极值方程
 (7)
(7)
矩阵A中不含改正数V。由式(3)可知BV=EAX-e。由Φ分别对V、X求偏导,得
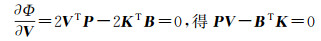 (8)
(8)
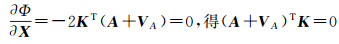 (9)
(9)
设
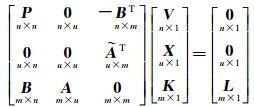 (10)
(10)
式(10)虽可求V、X、K混合矩阵,但需对n+m+u阶矩阵求逆。由式(8)得
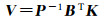 (11)
(11)
将式(11)代入式(1)得
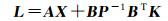 (12)
(12)
设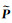
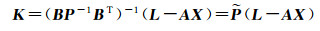 (13)
(13)
将式(13)代入式(9),设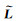
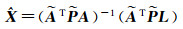 (14a)
(14a)
或
 (14b)
(14b)
其形式与经典LS解和文献[15]算法一致。由式(13)求K矩阵,并代入式(11)求矩阵V
 (15)
(15)
| 项目 | 文献[15]算法 | 本文算法 |
| 函数模型 | EIV、式(2) | EIO、式(1) |
| 随机模型 | 式(6)、QA、QL | 式(5)、Qll |
| Q阶数 | m(u+1)×m(u+1) | n×n |
| Q特征 | 非主对角矩阵 | 主对角矩阵 |
| V定义 | V=[vec(EA) e]T | V=[vl1vl2…vln]T |
| V阶数 | m(u+1)×1 | n×1 |
| B定义 | B=[XT⊗In -In] | B=diag([∂f/∂Li]1m) |
| B阶数 | m×m(u+1) | m×n |
| 平差方法 | 相关平差 | 独立平差 |
| QXX | 近似公式 | 迭代精确解 |
| 计算效率 | 小数据量无差异 | 大数据量时更优 |
2.2 迭代步骤
(1) 线性化形成误差方程式(1);
(2) 设置X初值,改正数V初值为0;矩阵
(3) 将B、P、A、
(4) 将X、V的新值用于更新B、
(5) 重复步骤3—4,‖[X V]i+1-[X V]i‖≤ε(10-18)结束。
3 EIO模型精度评定 3.1 近似精度评定单位权方差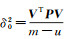
由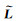

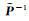
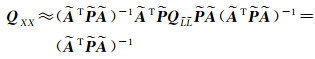 (16)
(16)
设X、L、vec(A)构成(u+m+mu)×1阶矩阵Y,其协因数阵为
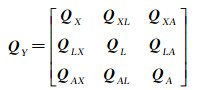 (17)
(17)
式中,A与L不相关,即QLA=QAL=0。若QL、QA已知,则QY为
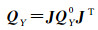 (18)
(18)
QY通过迭代求解,QY0初值虽可设置为0,但QX初值可由式(16)计算,QL与QA初值由式(6)计算,其余协因数初值设为0。J为Jacobi矩阵
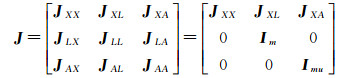 (19)
(19)
式中,因不相关JLX=JLA=JAX=JAL=0;JLL为m阶单位矩阵;JAA为mu阶单位矩阵;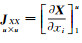
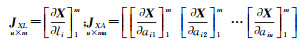
设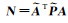
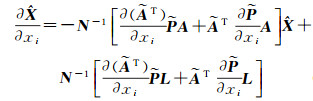 (20)
(20)
式中,由

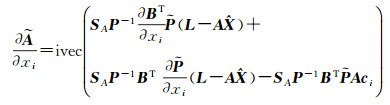
由B=SB·X+B0得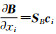

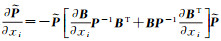
由式(14a)对li求偏导得
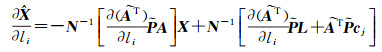 (21)
(21)
式中,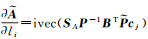
由式(14a)对aij求偏导得
 (22)
(22)
式中,
符号含义:c为规范化单位向量,u阶ci=[0 … 0 1 0 … 0]T,第i行为1,其余为0;m阶cj=[0 … 0 1 0 … 0]T,第j行为1,其余为0;cij为m×u阶矩阵,表示第i行第j列为1,其余为0。
迭代算法求QX精确解的步骤如下:
(1) 设置QY0初值,设置容许误差ε(10-18)及迭代次数Tn(100);
(2) 计算偏导数及Jacobi矩阵J;
(3) 以QY(k+1)=JQY(k)JT更新QY值;
(4) 如果||QY(k+1)-QY(k)||>ε重复步骤3,满足收敛条件步骤5;
(5) 从QY中提取QX。
4 实例计算 4.1 直线拟合本例引自文献[16]直线拟合实例,数据见原文。直线方程为y+vy=k(x+vx)+b,误差方程形式为
本实例来自文献[17],坐标参见原文表4,权数据参见原文式(39)。平面四参数坐标转换模型为
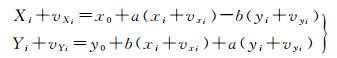
式中,(xi, yi)为源坐标;(Xi, Yi)为目标坐标;x0和y0为平移参数;a和b为旋转参数。误差方程形式为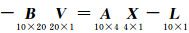
EIO模型只改正独立观测值,协因数阵最简洁,适用于大规模独立平差,可克服EIV模型缺陷。基于EIO模型的参数估计和协因数阵精确迭代算法,实例结果正确,计算效率高。
| [1] |
姚宜斌, 黄书华, 张良, 等.
求解三维坐标转换参数的整体最小二乘新方法[J]. 武汉大学学报(信息科学版), 2015, 40(7): 853–857.
YAO Yibin, HUANG Shuhua, ZHANG Liang, et al. A new method of TLS for solving the parameters of three-dimensional coordinate transformation[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 853–857. |
| [2] |
王乐洋, 郑玄威, 申兴林, 等.
坐标转换Partial-EIV总体最小二乘方法[J]. 测绘工程, 2015, 24(12): 12–16.
WANG Leyang, ZHENG Xuanwei, SHEN Xinglin, et al. Partial-EIV total least squares method for coordinate transformation[J]. Engineering of Surveying and Mapping, 2015, 24(12): 12–16. DOI:10.3969/j.issn.1006-7949.2015.12.003 |
| [3] |
刘经南, 曾文宪, 徐培亮.
整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(5): 505–512.
LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of total least squares methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505–512. |
| [4] |
曾文宪.系数矩阵误差对EIV模型平差结果的影响研究[D].武汉: 武汉大学, 2013: 17-19. ZENG Wenxian. Effect of the random design matrix on adjustment of an EIV model and its reliability theory[D]. Wuhan: Wuhan University, 2013: 17-19. http://cdmd.cnki.com.cn/Article/CDMD-10486-1013210882.htm |
| [5] | XU Peiliang, LIU Jingnan, SHI Chuang. Total least squares adjustment in partial errors-in-variables models:Algorithm and statistical analysis[J]. Journal of Geodesy, 2012, 86(8): 661–675. DOI:10.1007/s00190-012-0552-9 |
| [6] |
王乐洋, 余航, 陈晓勇.
Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22–29.
WANG Leyang, YU Hang, CHEN Xiaoyong. An algorithm for partial EIV model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22–29. DOI:10.11947/j.AGCS.2016.20140560 |
| [7] | FANG Xing. A total least squares solution for geodetic datum transformations[J]. Acta Geodaetica et Geophysica, 2014, 49(2): 189–207. DOI:10.1007/s40328-014-0046-8 |
| [8] | FANG Xing. Weighted total least-squares with constraints:a universal formula for geodetic symmetrical transformations[J]. Journal of Geodesy, 2015, 89(5): 459–469. DOI:10.1007/s00190-015-0790-8 |
| [9] | JAZAERI S, SCHAFFRIN B, SNOW K. On weighted total least-squares adjustment with multiple constraints and singular dispersion matrices[J]. Zfv, 2014, 139(4): 229–240. |
| [10] | ZHOU Yongjun, KOU Xinjian, ZHU Jianjun, et al. A Newton algorithm for weighted total least-squares solution to a specific errors-in-variables model with correlated measurements[J]. Studia Geophysica et Geodaetica, 2014, 58(3): 349–375. DOI:10.1007/s11200-013-0254-7 |
| [11] | ZHOU Yongjun, KOU Xinjian, LI J, et al. Comparison of structured and weighted total least-squares adjustment methods for linearly structured errors-in-variables models[J]. Journal of Surveying Engineering, 2017, 143(1): 04016019. DOI:10.1061/(ASCE)SU.1943-5428.0000190 |
| [12] | MAHBOUB V, ARDALAN A A, EBRAHIMZADEH S. Adjustment of non-typical errors-in-variables models[J]. Acta Geodaetica et Geophysica, 2015, 50(2): 207–218. DOI:10.1007/s40328-015-0109-5 |
| [13] | AMIRI-SIMKOOEI A R, ZANGENEH-NEJAD F, ASGARI J. On the covariance matrix of weighted total least-squares estimates[J]. Journal of Surveying Engineering, 2016, 142(3): 04015013. DOI:10.1061/(ASCE)SU.1943-5428.0000153 |
| [14] | WANG Leyang, ZHAO Yingwen. Unscented transformation with scaled symmetric sampling strategy for precision estimation of total least squares[J]. Studia Geophysica et Geodaetica, 2017, 61(3): 385–411. DOI:10.1007/s11200-016-1113-0 |
| [15] | FANG Xing. Weighted total least squares:necessary and sufficient conditions, fixed and random parameters[J]. Journal of Geodesy, 2013, 87(8): 733–749. DOI:10.1007/s00190-013-0643-2 |
| [16] | NERI F, SAITTA G, CHIOFALO S. An accurate and straightforward approach to line regression analysis of error-affected experimental data[J]. Journal of Physics E:Scientific Instruments, 1989, 22(4): 215–217. DOI:10.1088/0022-3735/22/4/002 |
| [17] | JAZAERI S, AMIRI-SIMKOOEI A R, SHARIFI M A. Iterative algorithm for weighted total least squares adjustment[J]. Survey Review, 2014, 46(334): 19–27. DOI:10.1179/1752270613Y.0000000052 |


