2. 闽江学院海洋学院, 福建 福州 350108;
3. 重庆大学土木工程学院, 重庆 400045
2. Ocean College, Minjiang University, Fuzhou 350108, China;
3. College of Civil Engineering, Chongqing University, Chongqing 400045, China
对工程变形进行准确预报是发现隐患并保障其安全的重要手段。考虑到变形体常受到多种环境因素的影响,而这些影响因素与变形数据间的关联往往具有典型的非线性特征,此时若采用常规的线性预报方法并不能取得较好的预报结果。当前随着机器学习理论的不断发展,BP神经网络(BP neural network,BPNN)、支持向量机(support vector machine,SVM)等非线性理论方法在变形监测数据预报中取得了很多成功的应用[1-5]。
但是,以BPNN模型和SVM模型为代表的非线性变形预报模型本身也存在着不可忽视的缺陷:①BPNN模型存在着训练速度慢、易陷入局部极小、网络结构难以确定等缺陷,而且它基于的是经验风险最小化原则,易导致过学习现象的产生;②近年来被广泛研究的SVM模型尽管基于结构风险最小化原则,但存在模型参数对预报结果极其敏感且难以合理选择的缺点[6-8]。
文献[9]提出了一种极限学习机(extreme learning machine,ELM)方法,它将BPNN模型的参数训练问题转化为解算线性方程组以直接获得输出权值。该方法能避免传统BPNN模型存在的诸多问题,并具有计算效率高的特点,近年来在变形监测领域已获得了一定的应用[10-13]。但是ELM模型的初始输入权值和偏置是随机给定的,这使得模型的稳定性受到较大影响。另外,ELM本质上仍是基于经验风险最小化原则,这将减弱模型的泛化能力。文献[14—15]基于结构风险最小化原则提出了正则化极限学习机(regularized ELM,RELM),可以有效提升模型的泛化能力;但是RELM相对于ELM带来了一个正则化参数,该参数的选取也很难达到最优。为此,结合贝叶斯估计[16],文献[17]提出一种贝叶斯极限学习机(Bayesian ELM,BELM)方法以将包含模型超参数[18]的先验分布转换为后验分布,并通过最大化模型边际似然函数,可以估计得到最优的输出权值。
上述模型用于变形数据预报时,本质上属于静态预报模型。即在持续新增样本数据时,原模型并不发生变化,此时将会产生较大的预报误差。但如果考虑样本数据动态变化的要求,每当新增样本集时,重新训练网络并重新建立新模型,其计算效率将下降,难以应用于在线实时系统[19, 20]。
考虑到当前大部分工程变形监测系统已经可以达到在线实时监测的要求,并且获得的数据量不断增多,本文在BELM模型的基础上,提出一种动态贝叶斯极限学习机(dynamic BELM, DBELM)方法对静态模型参数进行在线更新,以提高变形数据预报的精度和效率。通过对仿真数据和实际变形数据的分析表明,DBELM方法可以适应在线监测系统数据动态增加的需求,相对于静态模型具有更高的预报精度,并且在持续长期预报中具有明显的性能优势。
1 贝叶斯ELM方法BELM方法将贝叶斯线性回归与ELM方法[9, 15]进行结合。对于多输入单输出ELM模型,其满足下列线性回归关系
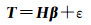 (1)
(1)
式中,T为样本输出矩阵;H为隐含层输出矩阵;β为隐含层输出权值矩阵;ε为噪声项,服从N(0, σ2)高斯正态分布。ELM模型输出的条件分布可以表示为
 (2)
(2)
线性回归模型采用贝叶斯方法进行处理时,引入了模型参数β的先验概率分布,可表示为[20-21]
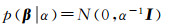 (3)
(3)
式中,α为超参数,可以控制对应分布的方差[22]。当β的先验分布与模型输出的条件分布都为高斯分布时,其后验分布也服从高斯分布[23]。根据贝叶斯估计
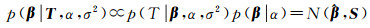 (4)
(4)
后验均值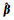
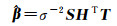 (5)
(5)
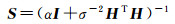 (6)
(6)
式中,超参数α并不是普通意义上的正则化参数,对此本文将在后续内容中进行讨论分析。为了计算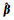
 (7)
(7)
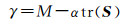 (8)
(8)
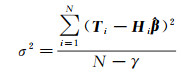 (9)
(9)
式中,M为隐含层节点数目;N为训练样本数目。根据式(5)—式(9)可以迭代求解出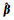
可以看出,采用贝叶斯方法将ELM模型参数的先验估计转换为后验估计,其输出权值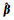
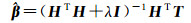 (10)
(10)
式中,λ为正则化参数。对比式(10)与式(5)、式(6),可以发现λ=ασ2。通常,λ需要通过交叉验证的方式来获取,这很难保证其参数选择的最优化;而BELM模型中参数α和σ2的求取是有理论意义的,保证了参数获取的优化特征。所以,与RELM模型相比,BELM模型不仅具有考虑结构风险最小化的特点,而且其参数的选择更加合理准确。
2 动态贝叶斯ELM方法在监测样本数据逐渐增加的情况下,一般可以使用下列两种方式建模:①新增样本后组织所有数据重新建模;②在原有模型的基础上根据新增样本对模型进行动态修正使之适应新情况。显然第1种建模方式需要大量的模型训练时间而难以应用于实时预报;而第2种建模方式耗时较少将更具优势。为此,基于第2种方式,本文采用提出一种动态贝叶斯极限学习机(DBELM)方法以适应于样本集的在线更新。
在BELM模型已计算出初始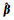
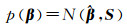 (11)
(11)
当新增样本(x*, t*)时,其参数后验分布也服从高斯正态分布
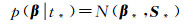 (12)
(12)
式中,x*、t*分别对应新增样本的输入与期望输出。根据文献[24]关于后验参数分布的计算公式,可以推导出
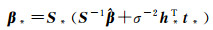 (13)
(13)
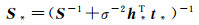 (14)
(14)
式中,h*为新增样本的隐含层输出向量。在计算β*与S*的过程中,初值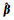
在样本数据增加的过程中,上述方法可以动态更新BELM模型的输出权值,本文将之称为DBELM模型。其用于变形监测数据动态预报的算法流程如下:
(1) 根据已有变形监测数据,在确定模型输入输出的基础上建立训练样本。
(2) 对训练样本使用BELM模型进行学习,获得初始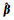
(3) 对新增的样本,由其输入x*根据激活函数计算隐含层输出h*,并根据步骤(2)中的隐含层输出权值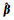
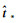
(4) 当样本期望输出t*已知的情况下,使用式(13)、式(14)对初始BELM模型参数进行动态更新。
(5) 逐步增加新样本(x*(i), t*(i)),根据步骤(3)即可逐步动态预测样本输出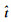
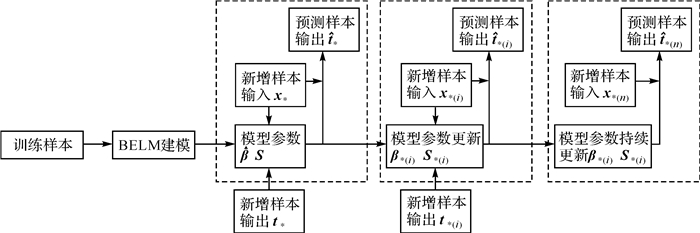
DBELM模型用于变形监测数据动态预报的流程见图 1。
|
| 图 1 DBELM动态预报 Fig. 1 Flow chart of DBELM dynamic prediction |
3 仿真数据分析
仿真数据使用“SinC”函数产生,其表达式为
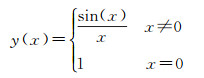
在区间(-10,10)内随机产生5000个训练样本和测试样本。为了模拟变形监测数据的真实性,在所有训练样本上叠加均值为0、方差为0.5的高斯噪声,而测试数据中不添加噪声。
由于DBELM模型是以BELM模型的训练结果为基础,所以为了分析训练样本的学习性能,本文只采用BELM、RELM、ELM 3种模型进行对比。3种模型的激活函数均选择Sigmoid函数,隐含层节点数均设置为20。RELM模型的正则化参数由交叉验证方式进行选取。为了保证建模和预报的稳定性,取20次试验结果的均值作为最终结果。图 2给出了3种模型的训练结果。

|
| 图 2 3种模型的训练结果 Fig. 2 Training results of three models |
由图 2可以看出,ELM的训练曲线有一定的波动性,表明其受到噪声的干扰较大。而RELM、BELM的训练曲线与真实曲线吻合较好,表明其在考虑结构风险最小化后,两种模型都具有一定的抗干扰能力和较好的学习能力。为了评价DBELM、BELM、RELM、ELM这4种模型的预报能力,采用下列两种精度评价指标:
(1) 均方根误差

(2)平均绝对误差
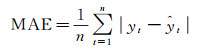
式中,yt为实测值;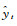
为了检验DBELM模型的性能,对于5000个测试样本集,本文按照每组500个样本逐渐增加的形式进行动态预报分析;而BELM、RELM、ELM这3种模型都是在训练完成的基础上直接对所有测试样本集进行预报。4种模型的预报精度评价指标计算结果见表 1。
| 精度指标 | ELM模型 | RELM模型 | BELM模型 | DBELM模型 |
| RMSE/mm | 0.039 7 | 0.024 1 | 0.022 3 | 0.007 1 |
| MAE/mm | 0.030 5 | 0.021 0 | 0.018 6 | 0.003 0 |
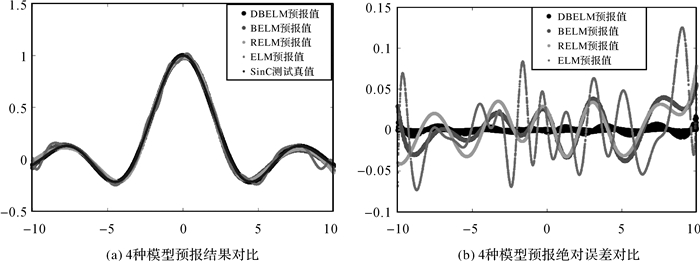
由表 1可以看出,在4种模型中,DBELM模型的预报精度最优,相对于BELM模型有了明显的提升;而BELM模型与RELM模型的预报精度基本相当,但RELM模型中的正则化参数需进行交叉验证选取,耗时相对较长且难以达到最优;ELM模型的预报精度显然最低。图 3给出了4种模型的预报结果对比图和预报绝对误差对比图。
|
| 图 3 4种模型预报结果与预报绝对误差对比 Fig. 3 Comparison of prediction results and absolute errors of four models |
从图 3可以看出,DBELM模型的预报结果与测试真值最为接近,预报的绝对误差也非常小,充分表明所提模型根据新增样本动态更新模型参数,可以有效提高模型的预报精度。
在本节中,使用“SinC”函数中的x作为变形因子、y作为变形量建立样本集来进行仿真预报分析。其预报模型参数的设置与预报分析的结果对后续复杂变形数据分析具有借鉴作用。
4 实例分析本文的实例数据来自湖南省东江大坝的安全监测资料,以具有典型代表性的L9H291垂线测点1999年1月—2003年12月共245期径向位移监测数据为研究对象进行大坝变形预报。
DBELM模型的输入采用温度分量、水压分量和时效分量三者相组合的形式,其中温度分量为6个,水位分量为2个,时效分量为2个[19]。6个温度分量取自位移观测前a到b天的坝址平均气温值,6对a-b值为:1-10,11-20,21-35,36-50,51-70,71-90;2个水位分量为H及H2,H代表坝前水深值;2个时效分量为t1和ln(t1),其中,t1为当前位移数据的观测日期减去首次观测日期并除以100。由于实例数据输入输出的量纲和单位有所不同,为了消除其对预报结果产生的影响,对实例数据的输入输出一律归一化到[-1, 1]。
将245期监测数据分为两块:45期数据为训练样本,剩余200期数据为测试样本。对于DBELM模型,根据第3节的算法处理流程,在采用BELM模型进行训练获得初始模型参数后,以每次20个样本逐次增加的形式进行参数动态更新,并逐步动态预报样本输出。
与仿真数据分析方法类似,对大坝变形预报仍采用上述4种模型进行对比分析,其中4种模型的激活函数类型与隐含层节点数目与仿真数据设置相同。表 2给出了4种模型对实例大坝变形数据的预报精度指标。
| 精度指标 | ELM模型 | RELM模型 | BELM模型 | DBELM模型 |
| RMSE/mm | 1.771 9 | 1.342 8 | 1.256 0 | 0.659 4 |
| MAE/mm | 1.468 5 | 0.974 7 | 0.914 3 | 0.511 1 |
从表 2中可以看出,DBELM模型的预报精度优势明显;而ELM模型的预报精度要劣于RELM、BELM模型,其泛化能力最弱。图 4、图 5分别给出了对于200期大坝变形预报的结果对比图和绝对误差图。

|
| 图 4 预报200期时4种模型结果对比 Fig. 4 Comparison of four models during 200 prediction period |
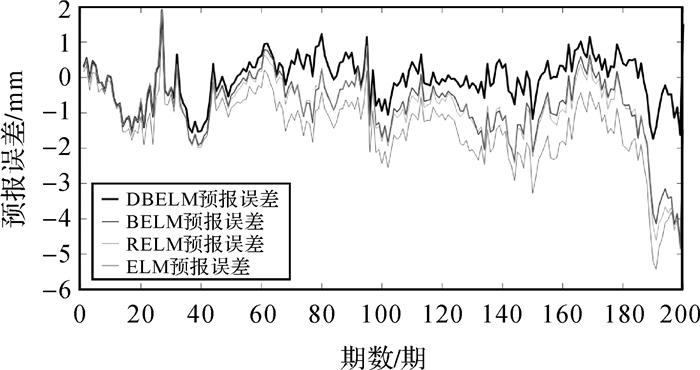
|
| 图 5 预报200期时4种模型绝对误差对比 Fig. 5 Absolute error comparison of four models during 200 prediction period |
从图 4可以看出,DBELM预报曲线与原真实观测曲线吻合最好,而其余3种模型对应的预报曲线都有明显偏离真实数据的趋势。从图 5可以看出,4种预报模型在预报初期其表现都较为理想,但随着预报周期的增加,ELM、RELM、BELM这3种模型的预报误差开始有逐渐增大的趋势,而DBELM模型由于对新增样本的不断更新学习,预报误差明显较小。
在采用上述相对较短的数据(45期)进行训练建模时,DBELM模型取得了较好的预报结果。为了继续检验模型性能,采用145期数据作为训练样本进行建模,而剩余100期数据作为测试样本。4种模型预报的精度指标统计结果见表 3。
| 精度指标 | ELM模型 | RELM模型 | BELM模型 | DBELM模型 |
| RMSE/mm | 0.569 7 | 0.539 3 | 0.524 1 | 0.487 5 |
| MAE/mm | 0.398 0 | 0.383 9 | 0.368 6 | 0.353 9 |
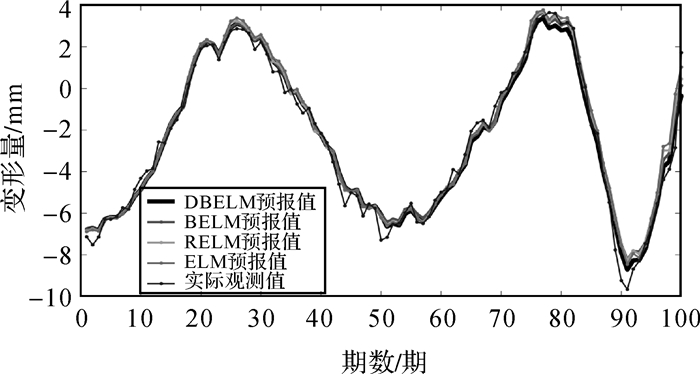
从表 3可以看出,本例中虽然DBELM模型仍可以获得较好的预报结果,但相对于其余3种模型其优势并不明显。这是由于在初始训练样本较多的情况下已可以建立较好的静态模型,此时进行相对短期的预报,静态模型也能取得较为良好的预报结果。图 6、图 7分别给出了对于100期大坝变形预报的结果对比图和绝对误差图。
|
| 图 6 预报100期时4种模型结果对比 Fig. 6 Comparison of four models during 100 prediction period |
|
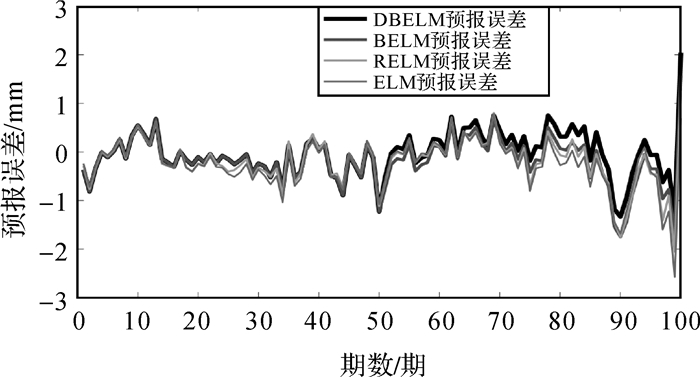
| 图 7 预报100期时4种模型绝对误差对比 Fig. 7 Absolute error comparison of four models during 100 prediction period |
对比图 5与图 7可以看出,DBELM模型在训练样本较少,而测试样本数据不断增多时,其预报误差相对其余3种模型明显较小;而在训练样本较多时,除ELM模型预报误差相对较大外,DBELM、BELM、RELM这3种模型都能取得较好的预报结果,但DBELM模型的预报误差仍然最小。
5 结论(1) 本文所提DBELM模型在BELM模型完成训练的基础上,仅根据新增样本即可对模型参数进行动态更新,无须重复建模,从理论上改善了计算效率,适用于在线变形监测系统的实时预报。
(2) 对仿真数据和实际数据进行分析,结果表明:DBELM模型可以有效提升变形预报精度。特别是在长期持续预报过程中,其预报性能相对于BELM、RELM、ELM 3种模型优势明显。
(3) BELM模型由于采用了贝叶斯方法估计模型参数,具有一定的稳健性。本文中仅在仿真数据中加入了噪声对BELM学习性能进行了分析。考虑到实际变形数据中可能含有粗差的情况,需要研究一种加权DBELM模型以提升模型的稳健性;另外还需根据具体工程监测数据进行变形机理的分析研究。这将是在本文基础上的下一步研究目标。
| [1] | SU Huaizhi, LI Xing, YANG Beibei, et al. Wavelet support vector machine-based prediction model of dam deformation[J]. Mechanical Systems and Signal Processing, 2018, 110: 412–427. DOI:10.1016/j.ymssp.2018.03.022 |
| [2] | CHEN Huangqiong, ZENG Zhigang. Deformation prediction of landslide based on improved back-propagation neural network[J]. Cognitive Computation, 2013, 5(1): 56–62. DOI:10.1007/s12559-012-9148-1 |
| [3] |
王新洲, 范千, 许承权, 等.
基于小波变换和支持向量机的大坝变形预测[J]. 武汉大学学报(信息科学版), 2008, 33(5): 469–471, 507.
WANG Xinzhou, FAN Qian, XU Chengquan, et al. Dam deformation prediction based on wavelet transform and support vector machine[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 469–471, 507. |
| [4] | LIU Haifeng, REN Chao, ZHENG Zhongtian, et al. Study of a gray genetic BP neural network model infault monitoring and a diagnosis system fordam safety[J]. International Journal of Geo-Information, 2018, 7(4): 1–19. |
| [5] | WANG Xiaoyu, KANG Kan, SHEN Changsong. Study on MPGA-BP of gravity dam deformation prediction[J]. Mathematical Problems in Engineering, 2017, 2017: 2586107. |
| [6] |
钱程, 李连基, 周子东.
基于GM-ANN组合模型的大坝变形监测数据分析方法[J]. 中国农村水利水电, 2015(10): 157–159, 162.
QIAN Cheng, LI Lianji, ZHOU Zidong. Dam deformation monitoring data analysis method based on GM-ANN model[J]. China Rural Water and Hydropower, 2015(10): 157–159, 162. DOI:10.3969/j.issn.1007-2284.2015.10.038 |
| [7] |
邢尹, 陈闯, 刘立龙, 等.
改进遗传算法和BP神经网络的大坝变形预测[J]. 计算机工程与设计, 2018, 39(8): 2628–2631, 2686.
XING Yin, CHEN Chuang, LIU Lilong, et al. Dam deformation prediction based on improved genetic algorithm and BP neural network[J]. Computer Engineering and Design, 2018, 39(8): 2628–2631, 2686. |
| [8] |
马琳, 马福恒, 范振东, 等.
SVM大坝变形监测模型研究[J]. 中国农村水利水电, 2015(5): 144–147.
MA Lin, MA Fuheng, FAN Zhendong, et al. Dam deformation monitoring model based on improved MMA-SVM[J]. China Rural Water and Hydropower, 2015(5): 144–147. DOI:10.3969/j.issn.1007-2284.2015.05.036 |
| [9] | HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1/3): 489–501. |
| [10] | LIAN Cheng, ZENG Zhigang, YAO Wei, et al. Extreme learning machine for the displacement prediction of landslide under rainfall and reservoir level[J]. Stochastic Environmental Research and Risk Assessment, 2014, 28(8): 1957–1972. DOI:10.1007/s00477-014-0875-6 |
| [11] | KANG Fei, LIU Jia, LI Junjie, et al. Concrete dam deformation prediction model for health monitoring based on extreme learning machine[J]. Structural Control and Health Monitoring, 2017, 24(10): e1997. DOI:10.1002/stc.v24.10 |
| [12] |
廉城, 曾志刚, 苏义鑫, 等.
基于误差修正EOS-ELM的滑坡位移预测[J]. 华中科技大学学报(信息科学版), 2017, 45(9): 52–57.
LIAN Cheng, ZENG Zhigang, SU Yixin, et al. Landslide displacement prediction based on error correction and ensemble of online sequential extreme learning machine[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2017, 45(9): 52–57. |
| [13] |
张海龙, 范振东.
基于改进PSO-ELM算法的混凝土坝变形非线性监控模型[J]. 水电能源科学, 2018, 36(1): 82–84, 199.
ZHANG Hailong, FAN Zhendong. Nonlinear monitoring model of concrete dam deformation based on improved PSO-ELM algorithm[J]. Water Resources and Power, 2018, 36(1): 82–84, 199. |
| [14] |
邓万宇, 郑庆华, 陈琳, 等.
神经网络极速学习方法研究[J]. 计算机学报, 2010, 33(2): 279–287.
DENG Wanyu, ZHENG Qinghua, CHEN Lin, et al. Research on extreme learning of neural networks[J]. Chinese Journal of Computers, 2010, 33(2): 279–287. |
| [15] | HUANG Guangbin, ZHOU Hongming, DING Xiaojian, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2012, 42(2): 513–529. DOI:10.1109/TSMCB.2011.2168604 |
| [16] |
魏冠军, 党亚民, 章传银, 等.
顾及不确定性影响的变形概率预报法[J]. 测绘学报, 2017, 46(4): 526–532.
WEI Guanjun, DANG Yamin, ZHANG Chuanyin, et al. Method of deformation probability prediction considering the influence of uncertainty factors[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 526–532. DOI:10.11947/j.AGCS.2017.20160531 |
| [17] | SORIA-OLIVAS E, GOMEZ-SANCHIS J, MARTIN J D, et al. BELM:Bayesian extreme learning machine[J]. IEEE Transactions on Neural Networks, 2011, 22(3): 505–509. DOI:10.1109/TNN.2010.2103956 |
| [18] | NING Kefeng, LIU Min, DONG Mingyu. A new robust ELM method based on a Bayesian framework with heavy-tailed distribution and weighted likelihood function[J]. Neurocomputing, 2015, 149: 891–903. DOI:10.1016/j.neucom.2014.07.045 |
| [19] |
邓兴升, 王新洲.
动态模糊神经网络在大坝变形预报中的应用[J]. 水电自动化与大坝监测, 2007, 31(2): 64–67.
DENG Xingsheng, WANG Xinzhou. Application of dynamic fuzzy neural network to dam deformation prediction[J]. Hydropower Automation and Dam Monitoring, 2007, 31(2): 64–67. DOI:10.3969/j.issn.1671-3893.2007.02.019 |
| [20] | MA Junshui, THEILER J, PERKINS S. Accurate on-line support vector regression[J]. Neural Computation, 2003, 15(11): 2683–2703. DOI:10.1162/089976603322385117 |
| [21] | LUO Jiahua, VONG C M, WONG P K. Sparse Bayesian extreme learning machine for multi-classification[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 836–843. DOI:10.1109/TNNLS.2013.2281839 |
| [22] |
韩敏, 李德才.
基于替代函数及贝叶斯框架的1范数ELM算法[J]. 自动化学报, 2011, 37(11): 1344–1350.
HAN Min, LI Decai. An norm 1 regularization term ELM algorithm based on surrogate function and Bayesian framework[J]. Acta Automatica Sinica, 2011, 37(11): 1344–1350. |
| [23] | CHEN Yarui, YANG Jucheng, WANG Chao, et al. Variational Bayesian extreme learning machine[J]. Neural Computing and Applications, 2016, 27(1): 185–196. DOI:10.1007/s00521-014-1710-1 |
| [24] | BISHOP C. Pattern recognition and machine learning[M]. New York: Springer, 2006. |
| [25] | CHEN Tao, MARTIN E. Bayesian linear regression and variable selection for spectroscopic calibration[J]. Analytica Chimica Acta, 2009, 631(1): 13–21. DOI:10.1016/j.aca.2008.10.014 |


