2. 上海市政工程设计研究总院(集团)有限公司, 上海 200082
2. Shanghai Municipal Engineering Design Institute(GROUP) CO., Ltd, Shanghai 200082, China
卫星精密定轨(precise orbit determination, POD)中解算所得的卫星星历是卫星质心的运动轨迹。文献[1—4]指出接收机接收到的观测信号由卫星天线相位中心发出接收机天线的相位中心接收,故在高精度定轨定位中卫星天线和接收机天线相位中心偏差(phase center offset, PCO)及天线相位中心变化(phase center variation, PCV),作为重要的误差源,必须予以改正,即通过卫星天线参数(PCO/PCV)和卫星位置来获取卫星信号发射的相位中心。
自1996年6月30日起,IGS(international GNSS service)的各数据分析中心开始利用相对相位中心改正模型来改正这一误差项。2006年11月后,IGS测站所采用的天线均进行了绝对相位中心模型的改正。地面接收机天线相位中心的绝对与相对校验都是利用露天检定场上的超短基线。文献[5—9]指出相对校验只给出天线相位中心3个坐标轴方向的偏差分量及其随卫星高度角的变化量,绝对天线相位中心检验还给出了天线相位中心改正随卫星方位角的变化。文献[10—12]发现在对地面接收机天线进行绝对相位中心改正时,如不对卫星天线相位中心予以改正,则GNSS(global navigation satellite system)系统测定的参考框架与使用其他观测技术(如VLBI,very long baseline interference和SLR,satellite laser range)得到的结果间存在1.5×10-8的尺度误差。
自北斗卫星导航定位系统于2012年12月27日开始正式提供服务以来,相关学者针对BDS的卫星天线参数作过相关的研究。因目前BDS系统整体性能相较于GPS仍存在一定差距,加上不同的分析中心对BDS轨道处理时使用的各种误差改正模型差异,以及部分误差模型只是简单的借鉴GPS(如光压模型)并不一定能很好地适配BDS,使得相较于GPS,部分分析中心BDS卫星天线参数校验结果差异较大。文献[13—15]指出目前IGS(International GNSS Service)各分析中心除了BDS,均使用相同的卫星天线参数。对于BDS卫星,CODE(Center for Orbit Determination in Europe)使用的是IGS默认的PCO/PCV,GFZ(German Research Centre for Geosciences)使用的是ESA(European Space Agency)发布值,WHU(Wuhan University)则使用的是其通过PANDA(position and navigation data analysist)校验的值。此外,大部分的精密定轨软件都具有估计卫星天线PCO参数的功能,也有相关学者估计过BDS的卫星天线PCO。
本文给出了BDS卫星天线的改正模型并基于上述的4组BDS卫星天线参数,进行了BDS PPP的卫星天线参数与卫星轨道、钟差产品的自洽性论证,并对BDS精密定轨精度、BDS PPP(precise point positioning)精度和收敛时间进行分析。
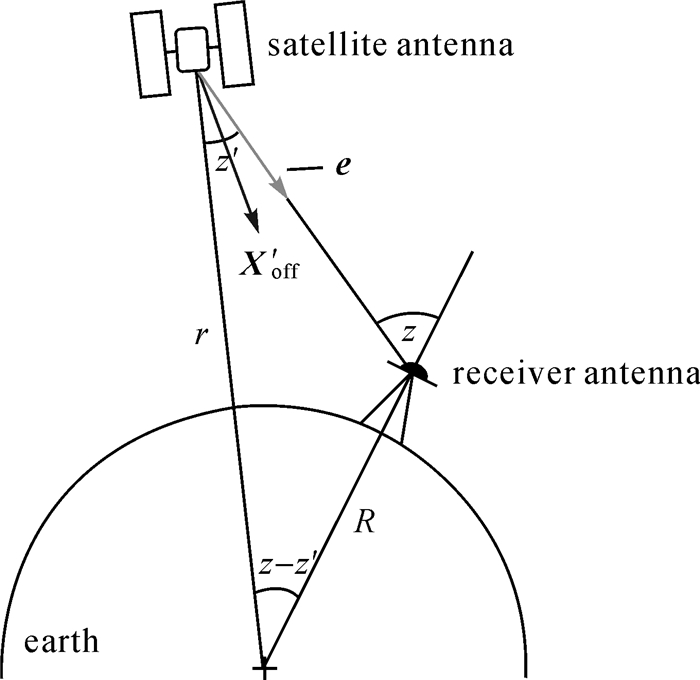
1 导航卫星天线PCO/PCV改正导航卫星天线PCO/PCV通常是在星固系下定义的。PCO表示卫星质心与卫星天线平均信号中心所形成的向量,PCV表示瞬时相位中心与平均相位中心的偏差。如图 1所示,在假设PCV仅与天底角(卫星星固系Z轴与星地连线方向间的夹角)相关的条件下,由卫星天线PCO和PCV所引起的测站至卫星间距离观测值改正Δε′φz′,可表示为
|
| 图 1 卫星天线PCO改正 Fig. 1 Satellite antenna PCO correction diagram |
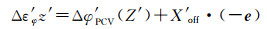 (1)
(1)
式中z′为天底角,其计算公式如下
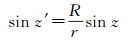 (2)
(2)
式中,R为地球半径;r为卫星到地心距离;z为测站卫星天顶距;Δφ′PCV(z′)表示天底角为z′时卫星天线PCV;X′off表示卫星天线PCO;e表示星固系下卫星至接收机方向的单位向量。
2 BDS PPP卫星天线参数自洽性分析文献[16]指出导航卫星精密定轨需通过卫星天线参数将卫星天线相位中心坐标转换到卫星质心,精密单点定位与之相反,需通过卫星天线参数将精密星历中的卫星质心坐标转换到卫星天线相位中心。由于精密星历的产生一般先于精密单点定位,所以用户在进行精密单点定位时使用的卫星天线参数应该与卫星精密定轨时使用的卫星天线参数保持一致。
选取2018年年积日001和002两天,CEDU站(澳大利亚)和GMSD站(日本)的观测数据,进行两组BDS静态模拟动态精密单点定位,参数设置[17-20]见表 1。
| 参数 | 方案1 | 方案2 |
| BDS卫星轨道钟差 | GFZ事后BDS精密轨道和钟差 | |
| 观测数据 | 伪距和相位 | |
| 截止高度角/(°) | 10 | |
| 电离层 | 无电离层组合B1、B2频点 | |
| 对流层延迟 | Saastamoinen模型+参数估计 | |
| 固体潮、相对论、地球自转 | 模型改正 | |
| 接收机钟差 | 白噪声 | |
| 模糊度 | 浮点解 | |
| 卫星天线参数 | ESA发布值 | IGS默认值 |
两组方案BDS PPP中仅卫星天线参数存在差异,方案1的卫星天线参数与GFZ求解事后BDS精密轨道和钟差使用的卫星天线参数是一致的,为ESA的发布值,方案2使用的是IGS默认值。IGS默认所有BDS卫星PCO的值为(0.6, 0.0, 1.1)m,PCVs的值为0;ESA发布的GEO卫星PCO的值为(0.6, 0.0, 1.1)m,PCVs的值为0;IGSO和MEO的PCO/PCV见表 2和表 3。
| x-PCO | y-PCO | z-PCO | ||||||||
| C06 | C07 | C08 | C09 | C10 | C11 | C12 | C13 | C14 | ||
| 549.0 | 0.0 | 3 049.0 | 3 236.7 | 3 842.6 | 3 973.6 | 3 882.1 | 2 069.5 | 2 313.5 | 3 882.1 | 2 311.7 |
| Nadir/(°) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| IGSO/mm | -3.73 | -0.21 | 2.16 | 0.95 | 0.59 | 0.63 | 0.23 | -0.45 | 0.84 | -1.02 | — | — | — | — |
| MEO/mm | -4.21 | -3.33 | -1.93 | -0.43 | 0.96 | 2.41 | 3.21 | 2.94 | 2.57 | 1.60 | 0.64 | -1.10 | -0.64 | -2.69 |
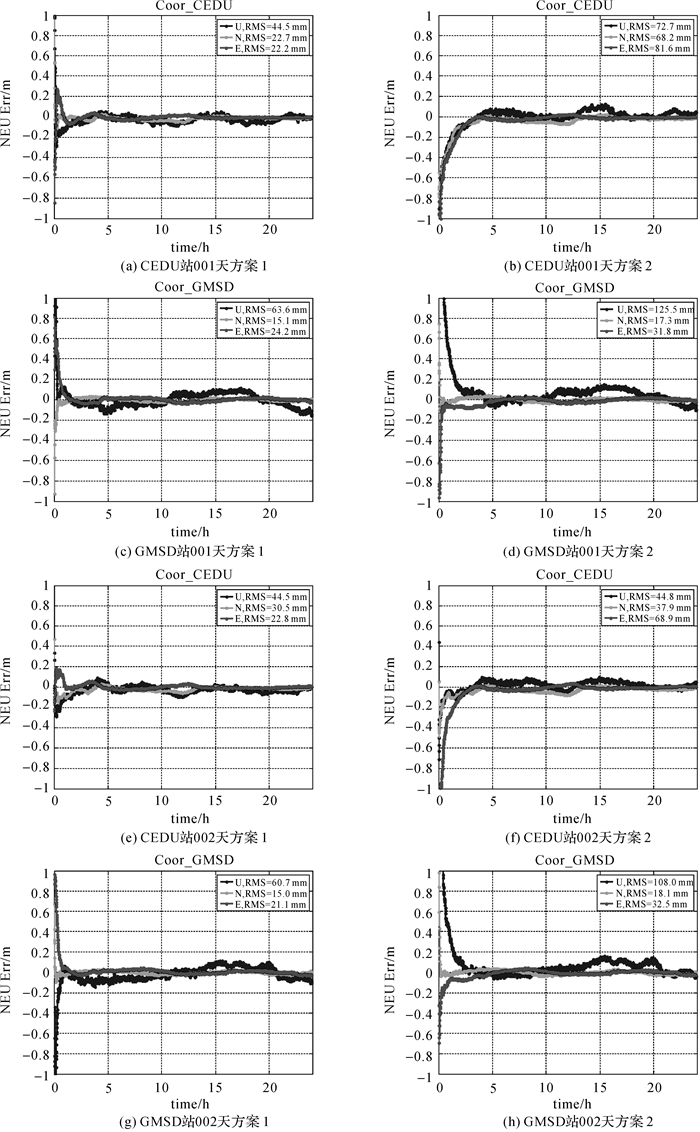
定位结果见图 2,图例中的NEU 3方向上RMS统计对象为收敛后的历元。此处定义当前历元的坐标偏差NE方向小于25 cm,高程方向小于40 cm,且在之后的历元均不超过该阈值认为从该历元开始收敛(下同)。
|
| 图 2 CEDU站和GMSD站BDS定位结果 Fig. 2 BDS PPP results for CEDU and GMSD |
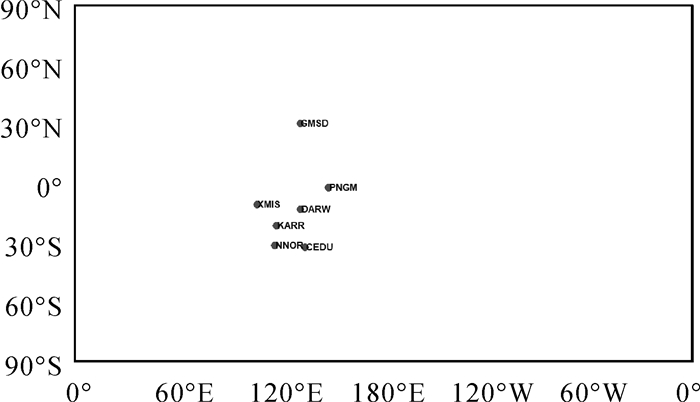
由图 2可知,方案1中的定位结果不论是收敛后精度还是收敛时间都明显优于方案2。选取如图 3中分布的测站,时间为2018年DOY010—DOY050,数据没有发生过中断,且数据质量较好的120个单站单天的数据,进行方案1和2的两组BDS动态PPP定位,并统计收敛时间和收敛后精度,统计结果见表 4。
|
| 图 3 BDS动态PPP测站分布 Fig. 3 Site distribution for BDS kinematic PPP |
| 统计结果 | 方案1 | 方案2 | |
| 收敛时间/min | 19.3 | 44.9 | |
| MEAN/mm | N | -4.9 | -6.7 |
| E | 3.2 | -8.9 | |
| U | 1.6 | 46.0 | |
| RMS/mm | N | 17.1 | 22.3 |
| E | 27.8 | 48.1 | |
| U | 56.9 | 86.0 | |
由表 4可知,方案1相对方案2收敛时间缩短25 min,定位坐标偏差均值NEU 3方向上方案1均优于方案2,RMS在NEU 3方向上方案1相对方案2分别提高5.2、20.3、29.1 mm。
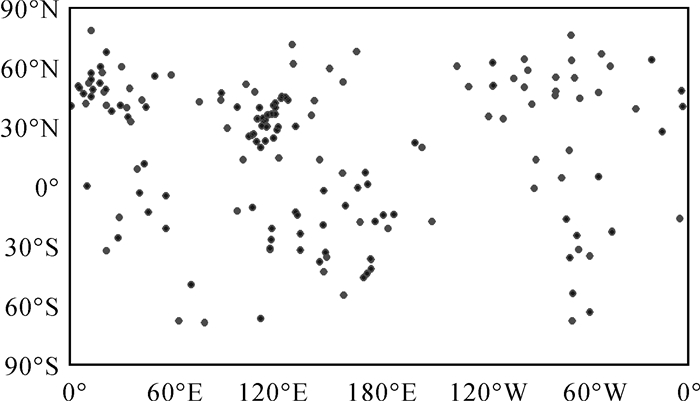
3 基于不同卫星天线参数的BDS轨道精度分析WHU使用的BDS卫星天线参数是通过PANDA软件校验得到,其GEO卫星PCO的值为(0.6, 0.0, 1.1)m,PCVs的值为0;IGSO和MEO的PCO/PCV见表 5和表 6。利用文献[12, 21]中方法,相关学者对BDS卫星的PCO进行过估计,估计时y-PCO固定为0,z-PCO结果为1 100.8 mm,x-pco结果(见表 7),但并没有对PCV进行校验,即PCVs为0。利用上述4组BDS卫星天线参数(分别用ESA,IGS,WHU和EST表示),分别对2018年1月31日—2018年2月5日的BDS精密轨道进行解算,定轨时采用GPS和BDS联合定轨的方式,解算策略[23-25]见表 8,定轨所用的测站分布见图 4。
| mm | ||||||||
| IGSO | x-PCO/mm | y-PCO/mm | z-PCO | |||||
| C06 | C07 | C08 | C09 | C10 | C13 | |||
| 586.4 | 0.0 | 2 513.7 | 2 721.9 | 3 440.0 | 3 551.9 | 4 087.0 | 4 087.0 | |
| MEO | x-PCO/mm | y-PCO/mm | z-PCO | |||||
| C11 | C12 | C14 | — | — | — | |||
| 575.0 | 0.0 | 1 990.7 | 2 249.1 | 2 144.3 | — | — | — | |
| Nadir/(°) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| IGSO/mm | -2.76 | -0.14 | -0.10 | 0.96 | 1.08 | 0.71 | 0.86 | -0.09 | 0.80 | -1.46 | — | — | — | — |
| MEO/mm | -3.98 | -3.42 | -1.89 | -1.08 | 0.68 | 2.24 | 3.08 | 3.17 | 3.07 | 2.16 | 1.14 | -0.63 | -1.00 | -3.43 |
| mm | ||||||||||||||
| PRN | C01 | C02 | C03 | C04 | C05 | C06 | C07 | C08 | C09 | C10 | C11 | C12 | C13 | C14 |
| x-PCO | 842.0 | 842.0 | 656.0 | 651.0 | 651.0 | 793.0 | 793.0 | 791.0 | 638.0 | 640.0 | 640.0 | 600.0 | 640.0 | 640.0 |
| 参数处理策略 | BDS轨道 |
| 观测弧段 | 3 d弧段 |
| 采样率/s | 300 |
| 观测数据 | GPS+BDS非差伪距和相位无电离层组合观测值 |
| 参数估计方式 | 最小二乘 |
| 模糊度 | GPS和IGSO/MEO固定 |
| 观测值加权方式 | 根据高度角加权 |
| 地球自转参数 | 强约束估计 |
| 测站坐标 | 强约束估计 |
| 卫星姿态模型 | GPS:Kouba姿态模型;BDS:GEO采用零偏模型,IGSO/MEO采用动偏和零偏切换的姿态模型 |
| 对流层 | 模型改正+参数估计 |
| 地球重力场 | EGM96模型(12×12) |
| N体引力 | 太阳、月亮和其他行星(采用JPLDE405行星星历) |
| 潮汐 | 地球固体潮、海潮和极潮 |
| 太阳光压 | ECOM5参数模型 |
| 速度脉冲 | 12 h估计一组 |
| 相对论相应 | IERS 2010 |
| 卫星钟差 | 白噪声 |
| 系统间偏差 | 零均值基准,常参数估计 |
|
| 图 4 GPS和BDS联合定轨测站分布 Fig. 4 Sites distribution for GPS and BDS united precise orbit determination |
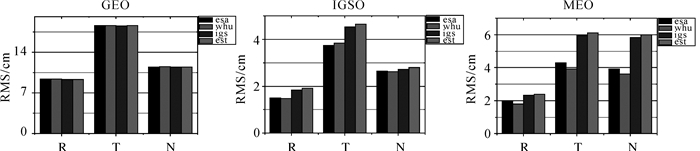
基于不同卫星天线参数的卫星轨道进行重叠弧段比对,比对时进行了七参数转换,比对结果见图 5。由图 5可知,对于不同的卫星天线参数,GEO卫星轨道RTN 3方向上的内符合精度相近,均在9.3、18.6、11.5 cm左右;IGSO卫星ESA和WHU的定轨精度相近在1.5、3.8、2.6 cm左右,IGS和EST的定轨精度相近在1.9、4.6、2.7 cm;MEO卫星ESA卫星定轨精度为2.0、4.3、3.9 cm,WHU为1.8、3.9、3.6 cm,IGS和EST的定轨精度相近在2.3、6.0、5.9 cm左右。
|
| 图 5 基于不同卫星天线参数的卫星轨道内符合精度 Fig. 5 BDS orbit inner accuracy based on different antenna parameters |
基于不同卫星天线参数的卫星轨道与GFZ的事后BDS精密轨道进行比对,比对时进行了七参数转换,比对结果见图 6。由图 6可知,对于不同的卫星天线参数,GEO卫星轨道RTN 3方向上的外符合精度RMS均较大,R方向在40 cm左右,T方向在100~120 cm,N方向在70~80 cm,这是由于GFZ在定轨时GEO卫星的动力学参数求解方式与本文存在较大的差异;IGSO卫星ESA的定轨精度为2.4、5.5、4.3 cm,依次优于WHU、IGS、EST,ESA轨道外符合精度最好是因为GFZ在BDS定轨时也使用了ESA发布的卫星天线参数;MEO卫星ESA和WHU卫星定轨精度相近在2.7、5.6、4.4 cm左右,其中ESA略优于WHU,IGS和EST的定轨精度相近在8.6、10.1、8.9 cm左右。

|
| 图 6 基于不同卫星天线参数的卫星轨道外符合精度 Fig. 6 BDS orbit outer accuracy based on different antenna parameters |
综合,4组天线参数精密定轨内符合精度,ESA、WHU优于IGS、EST。4组天线参数精密定轨外符合精度,排除GEO卫星由于定轨策略不同引起的差异,ESA和WHU同样优于IGS和EST,ESA略优于WHU,ESA优于WHU的部分是由GFZ也采用ESA发布的天线参数所引起,故ESA和WHU的真实优劣并不容易区分,只能通过SLR等其他观测方式来校验。此外由于4组天线参数中GEO卫星天线参数均没有PCV参数,加之GEO卫星轨道高度较大且相对地面静止的特性,PCO参数的差异大部分会被卫星钟差吸收[22],故4组天线参数精密定轨GEO卫星不论内符合精度还是外符合精度,在R方向上的差异均很小。
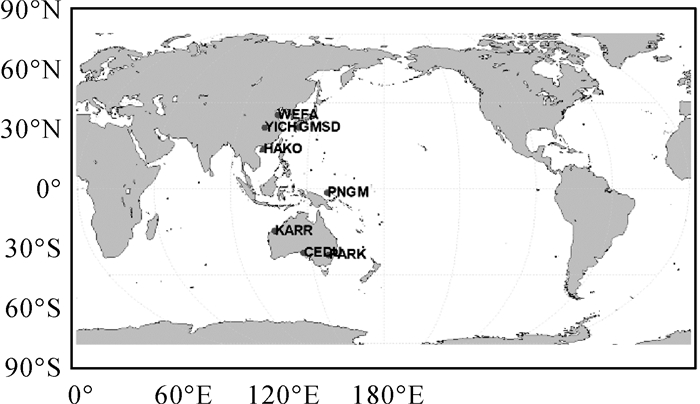
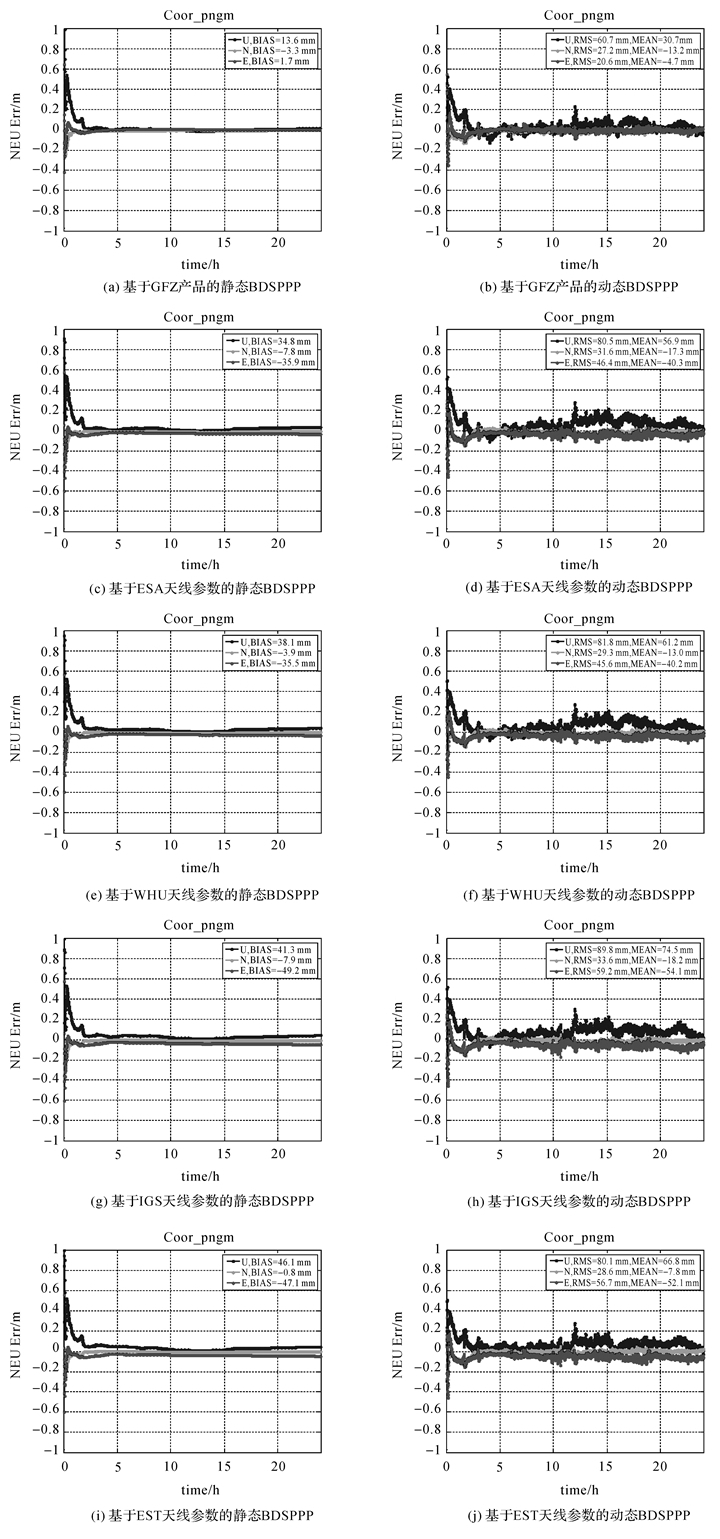
4 基于不同卫星天线参数的BDSPPP精度分析选取如图 7的测站2018年年积日031到036的观测数据,进行5组BDS动态PPP,定位时选用的BDS精密轨道和钟差分别是GFZ事后BDS精密产品和利用2中的策略(采样率改为30 s与GFZ事后精密产品保持一致)和观测数据(去除图 7中的测站)解算所得BDS精密轨道和钟差。定位中使用的卫星天线参数与轨道和钟差产品中使用的保持一致。GMSD站032天5组BDS静态和动态PPP的结果见图 8。
|
| 图 7 BDS PPP测站分布 Fig. 7 Sites distribution for BDS PPP |
|
| 图 8 GMSD站032天5组BDS PPP结果 Fig. 8 Five groups of BDS PPP results for GMSD in DOY 032 |
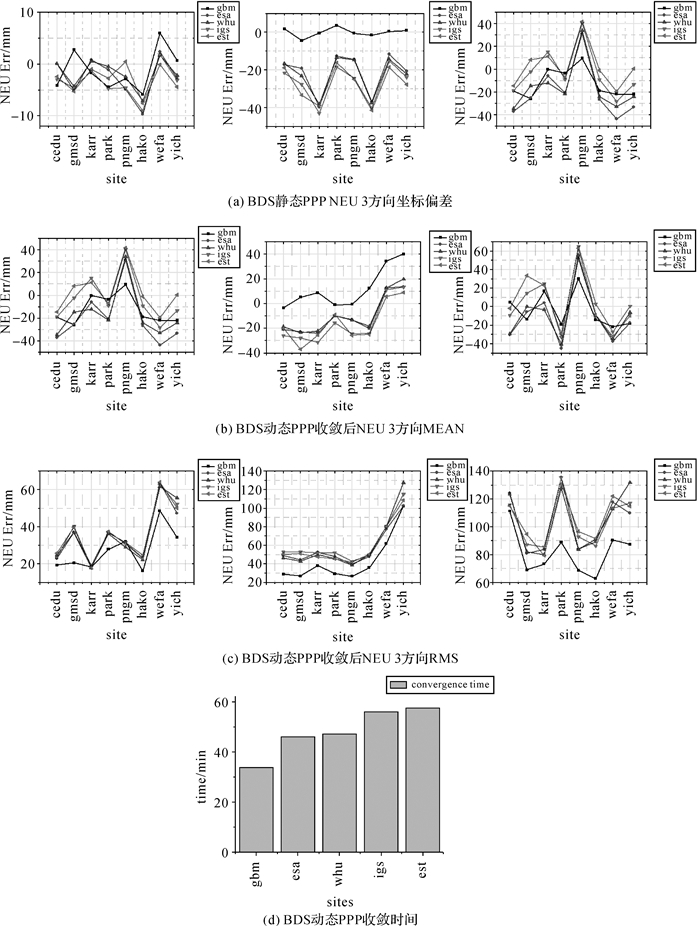
对图 7中8个测站分别进行BDS静态PPP和动态PPP,统计静态PPP最后一个历元定位结果的坐标偏差及动态PPP的收敛时间和收敛后的RMS和MEAN,如图 9所示。
|
| 图 9 基于不同卫星天线参数的BDS PPP统计结果 Fig. 9 BDS PPP results based on different antenna parameters |
由图 8和图 9,不论是BDS静态PPP最后历元坐标偏差还是动态PPP收敛时间和收敛后精度,均是GBM(GFZ的多系统产品)最优,尤其是E方向。主要是因为GFZ BDS轨道钟差解算软件与本文采用的软件不同,且轨道钟差解算策略优于本文。本文基于4组不同BDS卫星天线参数解算的轨道钟差BDSPPP定位结果中,除了动态PPP的收敛时间ESA和WHU优于IGS和EST外,静态PPP定位结果偏差与动态PPP收敛后精度相近,差异较小,均小于3 cm。
5 结论在BDSPPP时使用与精密轨道和钟差相匹配的卫星天线参数,能缩短收敛时间、提高定位精度。使用4组不同的天线参数进行精密定轨,轨道的内符合精度比较接近,见表 9。GEO卫星RTN 3方向内符合精度均在9.3、18.6、11.5 cm左右,IGSO卫星RTN 3方向内符合精度均在1.7、4.2、2.7 cm左右,MEO卫星RTN 3方向内符合精度均在2.1、5.1、4.8 cm左右,除IGSO和MEO卫星在TN方向上ESA与WHU相近优于IGS和EST 1~2 cm,其余差异均在毫米水平。
| cm | |||||
| satellite | direction | ESA | WHU | IGS | EST |
| GEO | R | 9.36 | 9.40 | 9.31 | 9.30 |
| T | 18.55 | 18.61 | 18.54 | 18.60 | |
| N | 11.46 | 11.51 | 11.42 | 11.42 | |
| IGSO | R | 1.50 | 1.48 | 1.83 | 1.92 |
| T | 3.74 | 3.84 | 4.52 | 4.64 | |
| N | 2.63 | 2.62 | 2.72 | 2.79 | |
| MEO | R | 2.01 | 1.81 | 2.32 | 2.39 |
| T | 4.30 | 3.92 | 5.96 | 6.11 | |
| N | 3.93 | 3.63 | 5.83 | 5.99 | |
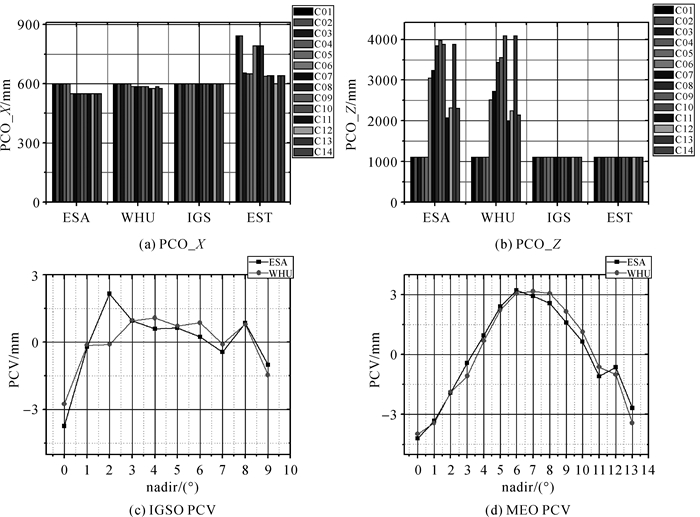
定轨结果与GFZ的事后精密产品比较,剔除定轨时动力学参数求解方式与本文差异的GEO卫星,IGSO和MEO的外符合精度见表 10。IGSO和MEO卫星RTN 3方向外符合精度差异在厘米水平。其中ESA最好,WHU与ESA接近,明显优于IGS和EST。WHU与ESA在各方向上优于IGS与EST 2~9 cm。4组参数的差异主要体现在PCO_X, PCO_Z和PCV,见图 10。ESA和WHU天线参数相似,故轨道外符合精度相似。GFZ使用的天线参数正是ESA,故ESA的外符合精度最好。
| cm | |||||
| satellite | direction | ESA | WHU | IGS | EST |
| IGSO | R | 3.80 | 4.03 | 4.79 | 7.83 |
| T | 6.03 | 7.22 | 12.29 | 16.75 | |
| N | 4.11 | 4.84 | 6.31 | 10.54 | |
| MEO | R | 2.44 | 2.98 | 8.61 | 8.57 |
| T | 5.59 | 5.73 | 9.84 | 10.40 | |
| N | 4.29 | 4.54 | 8.92 | 8.97 | |
|
| 图 10 4组天线参数的差异 Fig. 10 Difference between four sets of antenna parameters |
基于4组天线参数的BDS PPP,不论是动态还是静态,收敛后的精度均相近,差异一般在毫米水平,最大不超过3 cm。基于4组天线参数BDS PPP的差异主要体现在动态PPP的收敛时间上,由于天底角比较小(变化范围[0°,14°]), PCO中的绝大部分会被卫星钟差或者模糊度吸收,而ESA和WHU中的PCV改正对加快收敛起到了重要的作用,两者的PCV相近,故两者收敛时间差异也很小。
| [1] | ROTHACHER M. Comparison of absolute and relative antenna phase center variations[J]. GPS Solutions, 2001, 4(4): 55–60. DOI:10.1007/PL00012867 |
| [2] | SCHMID R, STEIGENBERGER P, GENDT G, et al. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas[J]. Journal of Geodesy, 2007, 81(12): 781–798. DOI:10.1007/s00190-007-0148-y |
| [3] | BILICH A L, MADER G L. GNSS absolute antenna calibration at the national geodetic survey[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR: University of Warmia and Mazury, 2010: 308-312. |
| [4] |
胡一帆.卫星导航天线PCO和PCV在轨标定[D].上海: 同济大学, 2017. HU Yifan. The calibration of antenna PCOPCV based on navigation satellite orbit[D]. Shanghai: Tongji University, 2017. |
| [5] |
胡一帆, 胡弦, 陈俊平, 等.
GPS卫星和接收机天线绝对PCO、PCV对高精度基线解算的影响分析[J]. 测绘通报, 2017(5): 11–16.
HU Yifan, HU Xian, Chen Junping, et al. Analysis of GPS satellite and receiver antenna absolute PCO/PCV influence on high precise baseline resolution[J]. Bulletin of Surveying and Mapping, 2017(5): 11–16. DOI:10.13474/j.cnki.11-2246.2017.0144 |
| [6] |
朱智勤, 李征航, 刘万科.
相位中心改正模式的转变对GPS数据处理的影响[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1301–1304.
ZHU Zhiqin, LI Zhenghang, LIU Wanke. Impact on GPS data processing of changing fom relative phase center corrections to absolute phase center corrections[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1301–1304. |
| [7] | WÜBBENA G, SCHMITZ M, BOETTCHER G, et al. Absolute GNSS antenna calibration with a robot: Repeatability of phase variations, calibration of GLONASS and determination of carrier-to-noise pattern[C]//Proceedings of 2010 IGS Workshop. Darmstadt, Germany: ESOC, 2010. |
| [8] | STEIGENBERGER P, ROTHACHER M, SCHMID R, et al. Effects of different antenna phase center models on GPS-derived reference frames[M]. DREWES H. Geodetic Reference Frames. Berlin, Heidelberg: Springer, 2009: 83-88. |
| [9] | MONTENBRUCK O, SCHMID R, MERCIER F, et al. GNSS satellite geometry and attitude models[J]. Advances in Space Research, 2015, 56(6): 1015–1029. DOI:10.1016/j.asr.2015.06.019 |
| [10] | MADER G L. GPS antenna calibration at the national geodetic survey[J]. GPS Solutions, 1999, 3(1): 50–58. DOI:10.1007/PL00012780 |
| [11] | REBISCHUNG P, GRIFFITHS J, RAY J, et al. IGS08:The IGS realization of ITRF2008[J]. GPS Solutions, 2012, 16(4): 483–494. DOI:10.1007/s10291-011-0248-2 |
| [12] | MENGE F, SEEBER G, VÖLKSEN C, et al. Results of absolute field calibration of GPS antenna PCV[C]//Proceedings of 1998 International Technical Meeting of the Satellite Division of the Institute of Navigation. Nashville, TN: [s.n.], 1998. |
| [13] | DILSSNER F, SPRINGER T, SCHÖNEMANN E, et al. Estimation of satellite antenna phase center corrections for BeiDou[J]. Pasadena, CA:IGS Workshop, 2014. |
| [14] |
郭靖.姿态、光压和函数模型对导航卫星精密定轨影响的研究[D].武汉: 武汉大学, 2014. GUO Jing. The impacts of attitude, solar radiation and function model on precise orbit determination for GNSS satellites[D]. Wuhan: Wuhan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528772.htm |
| [15] | SCHMID R, ROTHACHER M. Estimation of elevation-dependent satellite antenna phase center variations of GPS satellites[J]. Journal of Geodesy, 2003, 77(7-8): 440–446. DOI:10.1007/s00190-003-0339-0 |
| [16] |
张益泽.北斗实时高精度定位服务系统研究[D].上海: 同济大学, 2017. Zhang Yize. Research on real-time high precision BeiDou positioning service system[D]. Shanghai: Tongji University, 2017. http://d.old.wanfangdata.com.cn/Periodical_chxb201809018.aspx |
| [17] |
张小红, 左翔, 李盼, 等.
BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250–256.
ZHANG Xiaohong, ZUO Xiang, LI Pan, et al. Convergence time and positioning accuracy comparison between BDS and GPS precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250–256. |
| [18] |
辜声峰.多频GNSS非差非组合精密数据处理理论及其应用[D].武汉: 武汉大学, 2013. GU Shengfeng. Research on the zero-difference un-combined data processing model for multi-frequency GNSS and its applications[D]. Wuhan: Wuhan University, 2013. |
| [19] |
叶世榕. GPS非差相位精密单点定位理论与实现[D].武汉: 武汉大学, 2002. YE Shirong. Theory and its realization of GPS precise point positioning using un-differenced phase observation[D]. Wuhan: Wuhan University, 2002. http://d.wanfangdata.com.cn/Thesis/Y557920 |
| [20] | SCHMID R, ROTHACHER M, THALLER D, et al. Absolute phase center corrections of satellite and receiver antennas:impact on global GPS solutions and estimation of azimuthal phase center variations of the satellite antenna[J]. GPS Solutions, 2005, 9(4): 283–293. DOI:10.1007/s10291-005-0134-x |
| [21] | GE Maorong, GENDT G. Estimation and validation of the IGS absolute antenna phase center variations[C]//Proceedings of IGS Workshop 2004. Potsdam: GeoForschungsZentrum Potsdam, 2004. |
| [22] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise orbit determination of BeiDou constellation:Method comparison[J]. GPS Solutions, 2016, 20(2): 259–268. DOI:10.1007/s10291-014-0436-y |
| [23] |
施闯, 郑福, 楼益栋.
北斗广域实时精密定位服务系统研究与评估分析[J]. 测绘学报, 2017, 46(10): 1354–1363.
SHI Chuang, ZHENG Fu, LOU Yidong. Research and evaluation of BDS real-time wide-area precise positioning service system[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1354–1363. DOI:10.11947/j.AGCS.2017.20170284 |
| [24] |
楼益栋.导航卫星实时精密轨道与钟差确定[D].武汉: 武汉大学, 2008. LOU Yidong. Research on real-time precise GPS orbitand clock offset determination[D]. Wuhan: Wuhan University, 2008. |
| [25] |
赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D].武汉: 武汉大学, 2004. ZHAO Qile. Research on precision orbit determination theory and software of both GPS navigation constellation and LEO satellites[D]. Wuhan: Wuhan University, 2004. http://d.wanfangdata.com.cn/Periodical_whchkjdxxb200504029.aspx |


