2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054;
4. 西安航天天绘数据技术有限公司, 陕西 西安 710054;
5. 31002部队, 北京 100094
2. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. Xi'an Aerospace Data Technology Co., Ltd, Xi'an 710054, China;
5. Troops 31002, Beijing 100094, China
随着科学技术不断发展,人类对地球认识水平不断提高,有效监测地球环境变化是当今地球科学研究的重要任务之一。地球环境变化与地表物质迁移密切相关,全球海平面上升、冰川消融、陆地水储量变化等全球性环境变化问题,都与地表物质迁移过程有着密切联系[1-2]。因此,开展地表物质迁移研究对监测地球环境变化等具有重要意义。GRACE(gravity recovery and climate experiment)卫星于2002年3月成功发射,开创了高精度全球重力场观测与气候变化试验的新纪元,为连续监测地表物质迁移和重新分布提供了直接观测手段,目前已广泛应用于陆地水储量变化、冰川融化和海水质量变化反演等领域[3-5]。
球谐系数法是利用卫星时变重力场模型反演地表物质迁移研究中应用最广泛的方法。但是,由于卫星载荷的仪器测量误差、混频误差及卫星轨道等因素的影响[6],直接使用时变重力场模型的球谐系数法反演结果存在严重南北条带噪声,必须对球谐系数进行滤波处理。按照滤波思想的不同主要有两类方法,一类方法是高斯滤波[7]、扇形滤波[8]、维纳滤波[9]、均方根(root mean square,RMS)滤波[10]等,这类方法基本思想是通过降低模型高阶次项系数权重以减小短波长分量误差影响;另一类方法则是通过拟合多项式消除球谐系数奇偶次项间的相关误差,主要有滑动多项式拟合方法[11]、PnMm方法[12]及反向延拓滑动多项式拟合方法等[13]。常用的高斯滤波和扇形滤波方法在低纬度地区具有较好的去条带滤波效果,而去相关滤波则在高纬度地区具有较好的去条带效果[4]。因此,为了最大限度消除条带噪声并充分发挥不同滤波方法的各自优势,国外学者提出了组合滤波法,最普遍的组合方式是将高斯滤波或扇形滤波等方法与去相关滤波进行两步滤波处理,其基本思想为:首先对球谐系数进行去相关滤波,分别消除球谐系数奇数和偶数次项之间的相关误差;再对经去相关滤波后的系数进行高斯滤波等滤波处理,削弱高阶次项噪声。研究表明:组合滤波同时削弱了球谐系数高阶次项误差和奇偶次项间相关误差,相比单一滤波方法,去条带噪声效果更好[14]。此外,还有学者提出了两步法各向异性组合滤波[15],该方法分两步分别进行各向异性高斯滤波和RMS滤波,保留了低阶项真实信号并压制高阶项噪声,滤波效果较好。但是,当前的组合滤波方法实质上都是两步处理,不同步骤的滤波方法选取以及滤波参数选取都具有一定经验性,处理较为复杂。
由于对条带噪声的产生机理以及时变重力场模型球谐系数误差特性缺少全面深入的认识,当前国内外对于滤波效果的评判也尚无公认的准则[16],通常根据反演结果图像进行简单判定。国内外学者也有通过反演结果均方根[11, 16]、信噪比[14-15]、趋势项变化[17-18]等方法选取最优滤波参数和评判滤波效果,但不同评判方法都只能在一定程度上评判滤波效果。滤波的目的是消除条带噪声并提高反演结果信噪比,信噪比是指反演结果中信号和噪声的比例,信噪比越大说明混在信号中的噪声越小。因此,以信噪比此作为滤波效果评判指标,能在一定程度上较好反映滤波器的去噪声能力。故本文以信噪比作为滤波效果评判和最优滤波参数选取指标。
本文针对当前GRACE卫星时变重力场滤波研究中存在的不足,分析了时变重力场模型球谐系数误差特性,对不同滤波方法的去条带噪声效果进行试验分析,以信噪比最大为准则,确定了不同方法的最优滤波参数,并在此基础上提出一种新的各向异性组合滤波方法。该方法将各向异性高斯滤波和RMS滤波方法的滤波系数组合使用,不同于传统的两步法组合滤波,仅需一步滤波处理,试验结果表明:本文提出的组合滤波方法计算简单,能够有效消除条带噪声,并提高反演结果信噪比。
1 滤波方法比较分析文献[7]最早提出了球谐系数法,该方法将研究时间段内所有时变重力场模型的平均值作为稳态重力场模型,通过计算相对于稳态重力场模型球谐系数的改变量进而反演得到地表物质迁移,即
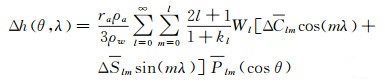 (1)
(1)
式中,ra为地球平均半径;θ、λ为地心余纬和地心经度;l、m为球谐函数的展开阶数和次数;ΔClm、ΔSlm为球谐系数改变量;Plm(cos θ)为完全规格化的勒让德缔合函数;kl为负荷勒夫数;Wl为滤波系数;ρw为水密度;ρa为地球平均密度;Δh为质量变化的等效水柱高。
1.1 高斯滤波文献[19]最早提出空间平滑函数,其本质是将某点的密度变化看成所有点密度变化的加权平均以达到平滑效果。文献[7]首先采用归一化高斯平均核函数,建立了高斯滤波方法,并根据递归关系来计算高斯滤波系数
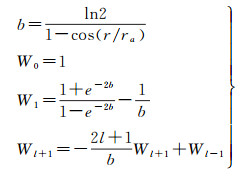 (2)
(2)
式中,r是滤波半径。
1.2 各向异性高斯滤波研究表明:GRACE时变重力场模型高阶高次项系数误差大于高阶低次项系数误差,即时变重力场模型误差是各向异性的[20-21]。因此,仅采用阶相关的高斯滤波会压制高阶低次项的真实信号。针对此,文献[20]提出了滤波系数与所用模型数据的阶和次数都相关的各向异性高斯滤波
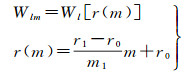 (3)
(3)
式中,W为高斯滤波核函数;r1和r0为滤波半径且r0小于r1;m1为选定的次,且0≤m≤m1。
1.3 扇形滤波文献[8]提出了扇形滤波,该方法对球谐系数的阶和次项同时进行高斯滤波处理
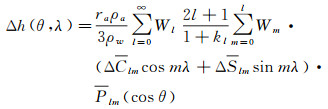 (4)
(4)
式中,Wl和Wm分别为与阶、次数相关的高斯滤波系数。由于其滤波系数在阶-次平面上投影形状为扇形,故称扇形滤波。
1.4 维纳滤波高斯滤波、各向异性高斯滤波及扇形滤波都需要选取合适的滤波半径,滤波半径的选取直接决定了反演结果中条带噪声的去除效果。滤波半径越大,去条带噪声效果越好,但对模型空间分辨率牺牲程度也越大;滤波半径过小,则无法有效消除条带噪声,给真实信号识别带来困难。文献[9]基于信号和噪声的阶方差谱来建立信号和噪声函数,建立了维纳滤波
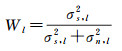 (5)
(5)
式中,σs, l2和σn, l2分别是信号和噪声的阶方差。该方法通过设计滤波函数,对测量信号进行线性卷积得到实际输出信号,使其与期望输出信号满足最小二乘,进而求解得到滤波系数,其滤波系数只依赖于信号和噪声模型的阶方差,属于各向同性滤波。
1.5 RMS滤波由于GRACE卫星观测到的时变重力变化信号在陆地明显高于在海洋,根据该条件可以陆地和海洋信噪比最大为准则建立最优滤波。文献[10]基于该准则得到滤波系数,建立了RMS滤波
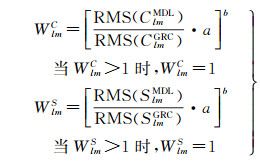 (6)
(6)
式中,MDL为水文模型加上海洋模型的球谐系数,GRC为GRACE时变重力场模型球谐系数,a、b为滤波参数,MASS为质量变化,Err为GRACE测量误差,其中a、b选取满足信噪比RMS_Ratio达到最大值
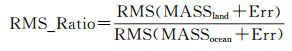 (7)
(7)
研究表明:反演结果呈现条带噪声的重要原因之一是时变重力场模型球谐系数存在系统相关误差[22]。针对此,国外学者提出了去相关滤波方法。该类方法以文献[20]提出的滑动窗口多项式拟合方法为基础,通过消除模型球谐系数奇偶数项间相关误差,从而达到去条带噪声效果。文献[13]对滑动窗口去相关滤波方法上进行了改进,根据相邻高阶系数间具有相关误差的特性,在数据处理时对数据序列的两端各延伸1/2窗口宽度数据,解决了实际去相关改正的系数个数减少的不足,使得该方法可以在更高阶次球谐系数中得到应用。因此,本文后续研究中采用改进的去相关滤波,滤波参数选取为:球谐系数起算阶数为15阶、窗口宽度7为个点、拟合多项式为3阶。
由于去相关滤波仅对高纬度地区具有较好去条带效果,低纬度地区条带噪声无法消除[4]。因此,去相关滤波不能单独使用,需要与其他滤波方法组合使用。当前,最普遍的组合滤波方式是将高斯滤波或扇形滤波与去相关滤波分两步进行滤波处理,即首先采用去相关滤波对球谐系数奇数和偶数阶项之间的相关误差分别进行消除,再对经过去相关滤波后的球谐系数进行高斯滤波或扇形滤波。
1.7 滤波比较分析试验采用GFZ Release 05版本时变重力场模型数据,时间跨度为2004年1月至2010年12月。反演时球谐系数截断至60阶,C20项采用激光测距数据所得结果替换,RMS滤波中的模型数据分别选GLDAS和ECCO模型。试验对不同滤波参数条件下的滤波结果信噪比值进行了统计,以信噪比最大为准则,对滤波参数的最优选取进行了分析。由于不同月份滤波结果类似,受篇幅所限,下文以2010年1月全球陆地水储量变化结果为例进行讨论分析。
图 1所示分别为高斯滤波和扇形滤波结果信噪比值随滤波半径变化。从图中结果可知,反演结果信噪比值均大于1,信噪比值随滤波半径增大先增大后减小;当滤波半径为500 km时,高斯滤波结果信噪比值达到最大值;滤波半径为400 km时,扇形滤波结果信噪比值达到最大值。因此,后续试验中高斯滤波半径取500 km,扇形滤波半径取400 km。
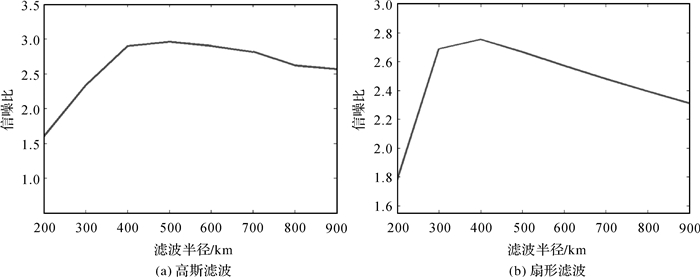
|
| 图 1 不同滤波半径滤波结果信噪比值 Fig. 1 Ratio of filtering results in different radius |
当时变重力场模型球谐系数的次数大于等于15时,球谐系数误差越来越显著[13],故试验中各向异性高斯滤波计算公式(3)中取m1=15。根据图 1结果,滤波半径为500 km时,高斯滤波结果信噪比值达到最大,结合1.2节各向异性高斯滤波系数公式,试验中各向异性高斯滤波半径分别取r0=200、300、400和500 km及r0 < r1≤1000 km。表 1所示为不同滤波半径组合情况下,各向异性高斯滤波结果信噪比值统计,从表 1结果可看出,当r0=200 km、r1=500 km时,各向异性高斯滤波结果信噪比达到最大值。因此,后续试验中各向异性高斯滤波半径r0=200 km、r1=500 km。
| r0 | r1 | |||||||
| 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | |
| 200 | 2.827 | 2.933 | 2.934 | 2.915 | 2.889 | 2.860 | 2.831 | 2.801 |
| 300 | 2.863 | 2.881 | 2.865 | 2.840 | 2.811 | 2.781 | 2.752 | |
| 400 | 2.796 | 2.786 | 2.761 | 2.733 | 2.703 | 2.674 | ||
| 500 | 2.715 | 2.692 | 2.663 | 2.634 | 2.605 | |||
图 2所示为RMS滤波参数a、b分别取1至3时滤波结果信噪比值。从图 2结果可看出,当a=2、b=1.8时,信噪比值达到最大。因此,后续试验中RMS滤波最优参数取为a=2、b=1.8。
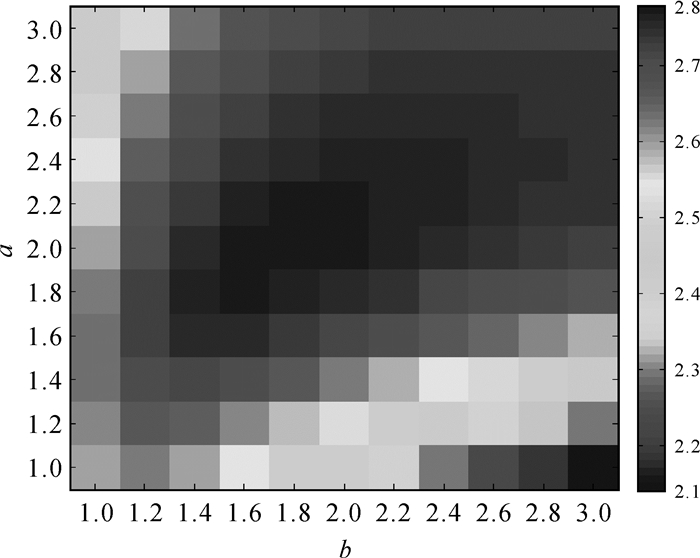
|
| 图 2 不同a、b取值滤波结果信噪比值 Fig. 2 Ratio of filtering results in different a and b |
记组合滤波1为高斯滤波(r=300 km)+去相关滤波,组合滤波2为高斯滤波(r=400 km)+去相关滤波,组合滤波3为高斯滤波(r=500 km)+去相关滤波,组合滤波4为扇形滤波(r=300 km)+去相关滤波,组合滤波5为扇形滤波(r=400 km)+去相关滤波,组合滤波6为扇形滤波(r=500 km)+去相关滤波。
图 3为不同滤波方法所得全球陆地水储量变化反演结果。从图中可以看出,仅采用去相关滤波的反演结果条带噪声严重,其他滤波方法则对条带噪声均具有较好消除效果,各向异性高斯滤波和RMS滤波所得结果信号较强,组合滤波1结果在低纬度海洋区域上存在较为明显条带噪声,组合滤波2结果也在低纬度海洋区域残存少量条带噪声。
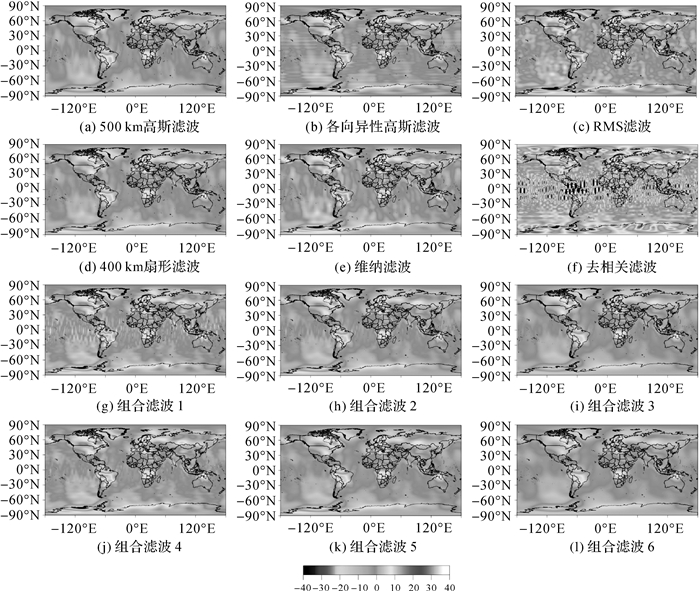
|
| 图 3 不同滤波方法比较 Fig. 3 Comparison of different filtering methods |
表 2为不同滤波方法结果信噪比值统计。从表 2结果可以看出,各向异性滤波结果信噪比值最大,其次分别是组合滤波4、RMS滤波,而组合滤波1结果信噪比值最小;并且,维纳滤波结果信噪比略大于高斯滤波(r=500 km)结果信噪比,与扇形滤波(r=400 km)结果信噪比相当。以上结果表明:单一滤波方法中,各向异性高斯滤波和RMS滤波结果信噪比值最大,在消除条带噪声的同时保留了更多有效真实信号;并且,组合滤波结果的信噪比值大于单一滤波方法结果。
| 滤波方法 | 信噪比值 |
| 高斯滤波(r=500 km) | 2.641 |
| 各向异性高斯滤波(r0=200 km、r1=500 km) | 2.934 |
| 扇形滤波(r=400 km) | 2.754 |
| 维纳滤波 | 2.762 |
| RMS滤波(a=2、b=1.8) | 2.778 |
| 组合滤波1 | 2.359 |
| 组合滤波2 | 2.695 |
| 组合滤波3 | 2.683 |
| 组合滤波4 | 2.836 |
| 组合滤波5 | 2.769 |
| 组合滤波6 | 2.670 |
2 各向异性组合滤波
由上文试验结果可知,单一滤波方法中,各向异性高斯滤波和RMS滤波结果信噪比值最大。图 4(a)和(b)所示分别为各向异性高斯滤波(r0=200 km、r1=500 km)和RMS滤波(a=2、b=1.8)各阶次滤波系数值。从图 4可以看出,各向异性高斯滤波系数在阶数确定的条件下随着次数的增大而减小,对精度较差的高阶高次项权重较小,可有效压制高阶次项噪声;与各向异性高斯滤波相比,RMS滤波则对精度较高的低次项权重更大,更好保留了低次项信号,并且对高阶高次项滤波系数权重也较小,也可有效压制高阶次项噪声。
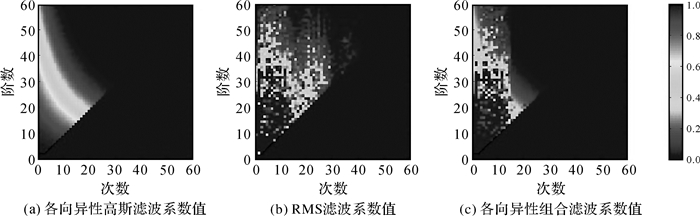
|
| 图 4 不同滤波方法Cnm项各阶次滤波系数值 Fig. 4 Filtering coefficient values of different filtering methods |
研究表明:GRACE时变重力场模型球谐系数误差随着阶数增大而增大,并且高阶高次项系数误差大于高阶低次项系数误差[21]。根据球谐系数的这一误差特性,本文结合各向异性高斯滤波和RMS滤波特点,提出了一种新的各向异性组合滤波方法,该方法不同于传统两步法组合滤波,仅采用一步滤波处理,其基本思想为:以次数mk为分界,当模型球谐系数次数小于mk时,选择RMS滤波和各向异性高斯滤波系数值中较大值,保留低次项信号;当次数大于等于mk时,选择RMS滤波和各向异性高斯滤波系数值中较小值,压制高次项噪声,即
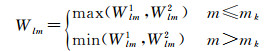 (8)
(8)
式中,Wlm1和Wlm2分别为各向异性高斯滤波和RMS滤波系数值。
图 4(c)为mk=15时本文所提各向异性组合滤波系数值。从图中结果可看出,当分界次数mk=15时,与各向异性高斯滤波和RMS滤波相比,本文所提各向异性组合滤波系数对次数小于15的低次项系数权重更大,保留了更多低次项信号,而对次数大于15以上的高次项系数进行了更强的降权处理,压制了高次项噪声。
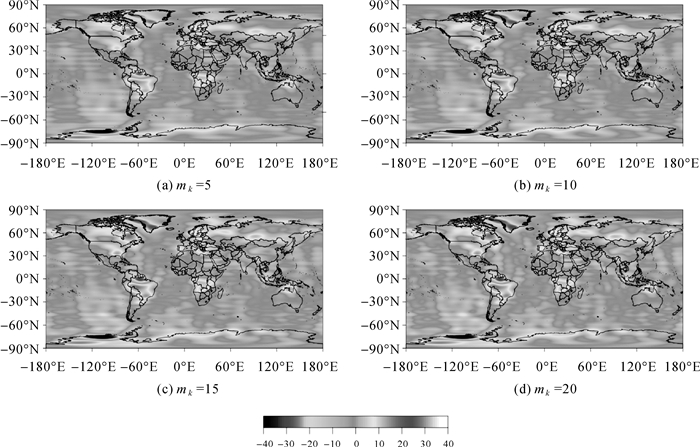
3 各向异性组合滤波试验分析试验中时变重力场模型数据和预处理过程同1.7节。各向异性组合滤波分界次数mk分别取5、10、15和20,以2010年1月全球陆地水储量变化反演结果为例,所得结果如图 5所示。从图 5可以看出,4种情形下的各向异性组合滤波整体上均有效消除了条带噪声,但随着分界次数mk增大,各向异性组合滤波结果在海洋区域上逐渐呈现微弱条带噪声。
|
| 图 5 不同参数各向异性组合滤波结果 Fig. 5 Ground water storage variation inversion results using non-isotropic combination filtering in different parameters |
表 3为4种情形反演结果信噪比值统计。从表 3结果可知,当分界次数mk取5、10、15和20时,反演结果信噪比值分别为2.949、2.958、2.940和2.920。由表 2可知,各向异性高斯滤波、组合滤波4及RMS滤波反演结果信噪比值最大,分别为2.934、2.836和2.778。对比表 2和表 3结果可知,当分界次数mk分别取5、10和15时,本文所提各向异性组合滤波结果信噪比大于单一使用各向异性高斯滤波或RMS滤波结果信噪比,且分界次数mk=10时,组合滤波结果信噪比值达到最大;与传统的两步法组合滤波结果相比,本文提出的组合滤波提高了反演信噪比值。以上结果表明:本文提出的各向异性组合滤波优于传统两步法组合滤波,并可通过选取合理的分界次数提高反演结果信噪比。
| 各向异性组合滤波 | 信噪比值 |
| mk=5 | 2.949 |
| mk=10 | 2.958 |
| mk=15 | 2.940 |
| mk=20 | 2.920 |
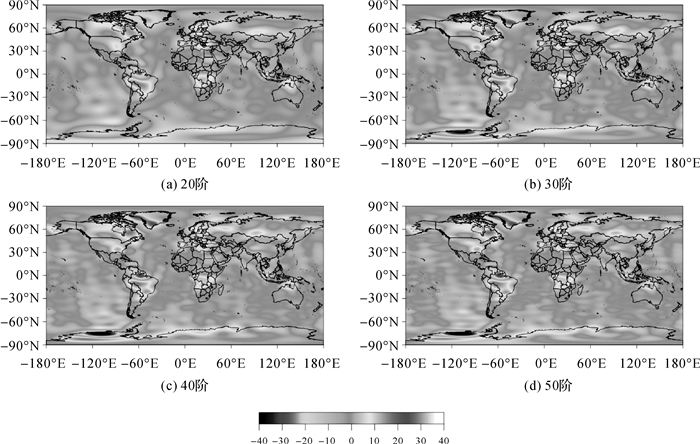
高斯滤波、维纳滤波及扇形滤波等方法通过降低时变重力场模型高阶次项系数权重从而达到去条带噪声效果,其实质是以牺牲模型的空间分辨率为代价换取空间平滑效果[13]。本文提出的组合滤波方法,由于是对RMS滤波和各向异性高斯滤波的滤波系数进行组合,本质上也是通过降低高阶次项系数权重从而达到去条带噪声效果,因此对模型数据的空间分辨率也存在一定程度的牺牲。而模型空间分辨率与模型阶数相关,阶数越大数据的空间分辨率相应越大。下面对采用不同阶数模型的组合滤波结果进行初步分析,试验所用模型数据和预处理过程同1.7节,其中时变重力场模型分别截断20、30、40、50阶使用,解算时采用本文所提组合滤波方法,分界次数取15,仍以2010年1月全球陆地水储量变化反演结果为例,所得结果如图 6所示。
|
| 图 6 采用不同阶模型的各向异性组合滤波结果 Fig. 6 Ground water storage variation inversion results using non-isotropic combination filtering in different degree of models |
从图 6结果可见,当模型阶数为20阶时,由于使用的模型阶数小,舍去了高阶次项中较多的有效信号,故滤波结果信号幅值相比其他情形较小;结合图 5结果,当阶数分别为30、40、50、60阶时,随着模型空间分辨率的变大,反演结果信号空间分布、幅值等未有显著变化。表 4为采用不同阶模型的反演结果信噪比值,从表 4结果可以看出,采用20阶模型时,反演结果信噪比值较小;阶数由30增大到50阶时,信噪比值相应增大;当模型阶数为60阶时,反演结果信噪比值与50阶模型结果信噪比值相比,略有减小。研究表明:时变重力场模型的低阶项(l < 20)主要是地幔以下地球重力场时变信号的体现,而高阶项(l> 30)则主要反映的是GRACE卫星数据的噪声信息,两者之间(20≤ l ≤30)则是信号和噪声的混合,体现了地表陆地水和海水等质量变化[23]。因此,当模型阶数为20阶时,由于舍去了较多有效信号,故反演结果信噪比值小;当阶数由30增大到50阶时,所用模型数据包含了更多的有效信号,故反演结果信噪比值也相应增大;当阶数为60阶时,由于模型高阶次项主要是噪声,且噪声随阶数增大而迅速增大,故反演结果信噪比值略有减小。综合上述结果和分析可知,本文所提组合滤波方法较好压制了高阶次项噪声,随着所用模型数据空间分辨率的增大,反演结果空间细节信息基本一致,受模型噪声影响较小,反演结果信噪比变化较小。
| 模型阶数 | 信噪比值 |
| 20 | 2.757 |
| 30 | 2.860 |
| 40 | 2.921 |
| 50 | 2.947 |
| 60 | 2.940 |
4 结论
滤波作为球谐系数法的核心环节,不同滤波方法和滤波参数的选取对反演结果具有重要影响。本文以信噪比最大为准则,通过试验确定了几种常用滤波方法的最优滤波参数,在此基础上提出了一种各向异性组合滤波方法,通过试验验证了所提方法的有效性,并对所提组合滤波方法滤波参数的最优选取进行了初步分析。主要结论如下:
(1) 在信噪比最大准则条件下,高斯滤波最优半径为500 km,各向异性高斯滤波最优半径为r0=200 km、r1=500 km,扇形滤波最优半径为400 km,RMS滤波最优参数为a=2、b=1.8;维纳滤波结果略优于高斯滤波(r=500 km)结果,与扇形滤波(r=400 km)去条带效果相当;单一滤波方法中,各向异性高斯滤波(r0=200 km、r1=500 km)和RMS滤波(a=2、b=1.8)的反演结果信噪比值最大。
(2) 本文提出的各向异性组合滤波方法,相比传统两步法组合滤波,仅需一步滤波处理,计算更为简单;该方法根据球谐系数误差特性,结合了各向异性高斯滤波和RMS滤波的特点,保留了更多低次项信号并压制了高次项噪声,能够有效消除南北条带噪声,相比单一滤波和传统两步法组合滤波方法,提高了反演结果信噪比,保留了更多有效真实信号。
由于国内外对GRACE卫星时变重力场模型数据滤波效果的评判尚无公认准则,仅采用信噪比评判滤波效果还不够全面。而滤波的同时往往也会造成信号泄露等问题,因此滤波方法选择和滤波参数选取应当在真实信号衰减和噪声减小之间作出平衡。后续,关于条带噪声产生机理、球谐系数误差特性、信噪比与泄露误差间关系、滤波效果评判准则等问题还需作进一步的研究。
致谢: 感谢德国洪堡学者陈秋杰博士、中国科学院测量与地球物理研究所冯伟副研究员、武汉大学测绘遥感重点实验室杨帆博士对本文提出的宝贵建议。
| [1] |
宁津生, 王正涛, 超能芳.
国际新一代卫星重力探测计划研究现状与进展[J]. 武汉大学学报(信息科学版), 2016, 41(1): 1–8.
NING Jinsheng, WANG Zhengtao, CHAO Nengfang. Research status and progress in international next-generation satellite gravity measurement missions[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 1–8. |
| [2] |
冯伟.区域陆地水与海平面变化的卫星重力监测研究[D].武汉: 中国科学院测量与地球物理研究所, 2013. FENG Wei. Regional terrestrial water storage and sea level variations inferred from satellite gravimetry[D]. Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2013. http://d.wanfangdata.com.cn/Thesis/Y2432132 |
| [3] |
邹正波, 罗志才, 吴海波, 等.
日本Mw9.0地震前GRACE卫星重力变化[J]. 测绘学报, 2012, 41(2): 171–176.
ZOU Zhengbo, LUO Zhicai, WU Haibo, et al. Gravity changes observed by GRACE before the Japan Mw9.0 earthquake[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 171–176. |
| [4] |
卢飞, 游为, 范东明, 等.
由GRACE RL05数据反演近10年中国大陆水储量及海水质量变化[J]. 测绘学报, 2015, 44(2): 160–167.
LU Fei, YOU Wei, FAN Dongming, et al. Chinese continental water storage and ocean water mass variations analysis in recent ten years based on GEACE RL05 data[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 160–167. DOI:10.11947/j.AGCS.2015.20130753 |
| [5] |
文汉江, 黄振威, 王友雷, 等.
青藏高原及其周边地区水储量变化的独立成分分析[J]. 测绘学报, 2016, 45(1): 9–15.
WEN Hanjiang, HUANG Zhenwei, WANG Youlei, et al. Independent component analysis of water storage changes interpretation over Tibetan plateau and its surrounding areas[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 9–15. DOI:10.11947/j.AGCS.2016.20140447 |
| [6] | SEO K W, WILSON C R, FAMIGLIETTI J S, et al. Terrestrial water mass load changes from gravity recovery and climate experiment (GRACE)[J]. Water Resources Research, 2006, 42(5): W05417. |
| [7] | WAHR J, MOLENAAR M, BRYAN F. Time variability of the earth's gravity field:hydrological and oceanic effects and their possible detection using GRACE[J]. Journal of Geophysical Research:Solid Earth, 1998, 103(B12): 30205–30229. DOI:10.1029/98JB02844 |
| [8] | ZHANG Zizhan, CHAO B F, LU Yang, et al. An effective filtering for GRACE time-variable gravity:fan filter[J]. Geophysical Research Letters, 2009, 36(17): L17311. DOI:10.1029/2009GL039459 |
| [9] | SASGEN I, MARTINEC Z, FLEMING K. Wiener optimal combination and evaluation of the gravity recovery and climate experiment (GRACE) gravity fields over Antarctica[J]. Journal of Geophysical Research:Solid Earth, 2007, 112(B4): B04401. |
| [10] | CHEN J L, WILSON C R, SEO K W. Optimized smoothing of gravity recovery and climate experiment (GRACE) time-variable gravity observations[J]. Journal of Geophysical Research:Solid Earth, 2006, 111(B6): B06408. |
| [11] | DUAN X J, GUO J Y, SHUM C K, et al. On the Postprocessing removal of correlated errors in GRACE temporal gravity field solutions[J]. Journal of Geodesy, 2009, 83(11): 1095–1106. DOI:10.1007/s00190-009-0327-0 |
| [12] | CHAMBERS D P. Evaluation of new GRACE time-variable gravity data over the ocean[J]. Geophysical Research Letters, 2006, 33(17): L17603. DOI:10.1029/2006GL027296 |
| [13] |
詹金刚, 王勇, 郝晓光.
GRACE时变重力位系数误差的改进去相关算法[J]. 测绘学报, 2011, 40(4): 442–446, 453.
ZHAN Jingang, WANG Yong, HAO Xiaoguang. Improved method for removal of correlated errors in GRACE data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 442–446, 453. |
| [14] | BELDA S, GARCÍA-GARCÍA D, FERRÁNDIZ J M. On the decorrelation filtering of RL05 GRACE data for global applications[J]. Geophysical Journal International, 2015, 200(1): 173–184. DOI:10.1093/gji/ggu386 |
| [15] |
超能芳, 王正涛, 孙健.
各向异性组合滤波法反演陆地水储量变化[J]. 测绘学报, 2015, 44(2): 174–182.
CHAO Nengfang, WANG Zhengtao, SUN Jian. The inversion of terrestrial water storage changes by non-isotropic combination filter[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 174–182. DOI:10.11947/j.AGCS.2015.20130719 |
| [16] |
詹金刚, 王勇, 史红岭, 等.
应用平滑先验信息方法移除GRACE数据中相关误差[J]. 地球物理学报, 2015, 58(4): 1134–1144.
ZHAN Jingang, WANG Yong, SHI Hongling, et al. Removing correlative errors in GRACE data by the smoothness priors method[J]. Chinese Journal of Geophysic, 2015, 58(4): 1134–1144. |
| [17] |
郗慧, 张子占, 陆洋, 等.
利用GRACE监测全球海水质量变化时滤波处理的影响分析[J]. 大地测量与地球动力学, 2016, 36(5): 380–385.
XI Hui, ZHANG Zizhan, LU Yang, et al. The performances of different filtering methods on ocean mass change estimated from GRACE[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 380–385. |
| [18] |
王星星, 李斐, 郝卫峰, 等.
GRACE RL05反演南极冰盖质量变化方法比较[J]. 武汉大学学报(信息科学版), 2016, 41(11): 1450–1457.
WANG Xingxing, LI Fei, HAO Weifeng, et al. Comparison of several filters in the rates of antarctic ice sheet mass change based on GRACE RL05 data[J]. Geomatics and Information Science of Wuhan University, 2016, 41(11): 1450–1457. |
| [19] | JEKELI C. Alternative methods to smooth the earth's gravity field[R]. Columbus: Department of Geodesy and Science and Surveying, Ohio State University, 1981. |
| [20] | HAN S C, SHUM C K, JEKELI C, et al. Non-isotropic filtering of GRACE temporal gravity for geophysical signal enhancement[J]. Geophysical Journal International, 2005, 163(1): 18–25. DOI:10.1111/gji.2005.163.issue-1 |
| [21] |
许才军, 龚正.
GRACE时变重力数据的后处理方法研究进展[J]. 武汉大学学报(信息科学版), 2016, 41(4): 503–510.
XU Caijun, GONG Zheng. Review of the post-processing methods on GRACE time varied gravity data[J]. Geomatics and Information Science of Wuhan University, 2016, 41(4): 503–510. |
| [22] | SWENSON S, WAHR J. Post-processing removal of correlated errors in GRACE Data[J]. Geophysical Research Letters, 2006, 33(8): L08402. |
| [23] | SASGEN I, MARTINEC Z, FLEMING K. Wiener optimal filtering of GRACE data[J]. Studia Geophysica et Geodaetica, 2006, 50(4): 499–508. DOI:10.1007/s11200-006-0031-y |


