2. 中国洛阳电子装备试验中心, 河南 洛阳 471000
2. Luoyang Electronic Equipment Test Center of China, Luoyang 471000, China
利用精密单点定位(precise point positioning, PPP)进行时频传递精度高,传递精度可以达到亚纳秒量级。与双向卫星时间频率传递方法(two way satellite time and frequency transfer, TWSTFT)相比,PPP时频传递不受卫星转发器限制,操作简便灵活,国际计量局(bureau international des poids et mesures, BIPM)将PPP作为时频传递的重要手段,并与国际GNSS服务组织(International GNSS Services, IGS)合作开展TAI-PPP工程,旨在利用PPP技术计算维持国际原子时(temps atomique international, TAI)[1-2]。目前针对PPP授时与时频传递的研究取得了许多卓有成效的成果。文献[3—5]采用无电离层组合、非组合观测值进行钟差解算,时间传递精度达到0.1~0.2 ns。文献[6]主要分析系统性偏差对PPP授时精度的影响,证明在授时和时间传递过程中,需要对差分码偏差进行修正。文献[7—10]根据授时型接收机外置原子钟的物理特性,以原子钟物理模型的先验信息作为钟差参数约束条件,授时精度与算法收敛速度均有所改善。现阶段对PPP授时与时频传递的研究多采用传统PPP方法,研究人员在此基础上开始探索PPP整周模糊度固定解技术(integer PPP, IPPP)在时频领域的应用。文献[11]将GNSS共视法与整数相位钟法相结合,提出一种基于站间单差模糊度固定的时频传递方法。文献[12]对整数相位钟法的时频传递方法进行研究,证明IPPP频率传递的短期稳定度和长期稳定度均比传统PPP有不同程度提升。
目前整数相位钟法的钟差计算存在以下问题:①在用户端,整数相位钟法观测方程的模糊度与钟差参数线性相关,其固定策略可能导致钟差结果包含与窄巷波长相关的系统性偏差;②在服务端,整数相位钟法所使用的相位钟产品包含类似的系统性偏差,该偏差在参数估计时可能被钟差参数吸收。以上问题严重影响IPPP钟差计算与时间传递性能。针对上述问题,本文采取多种方法改进整数相位钟法的模糊度固定策略、精化参数估计模型,并对改进方法的模糊度固定性能、时间传递与频率传递性能进行分析。
1 整数相位钟法基本原理 1.1 观测值组合模型整数相位钟法采用无电离层(ionosphere-free, IF)观测值组合进行参数估计,经过相对论效应、相位缠绕等误差改正后的伪距和载波组合模型为[13-14]
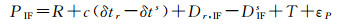 (1)
(1)
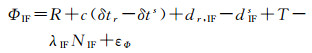 (2)
(2)
式中,上标s表示卫星;下标r表示接收机;下标P表示伪距;下标Φ表示载波相位;P表示伪距观测值,单位为米(m);Φ表示载波观测值,单位为米(m);R表示接收机天线到卫星天线相位中心的几何距离,单位为米(m);δt表示本地测站钟差,单位为秒(s);c表示真空中光速;d表示包括载波初始相位偏差的相位延迟误差,单位为米(m);D表示伪距延迟误差,单位为米(m);T表示对流层延迟误差,单位为米(m);λ表示信号波长,单位为米(m);N表示载波相位整周模糊度,单位为周;ε表示包括多径效应在内的其他未建模误差噪声,单位为米(m)。
整数相位钟法对相位和伪距观测方程的钟差进行区分[15],使用CNES-CLS分析中心的GRG(Groupe De Recherche De Geodesie Spatiale)相位钟产品估计相位方程钟差(简称相位钟),使用IGS最终产品估计伪距方程钟差(简称伪距钟),其中相位钟和伪距钟为真实钟差与相应的硬件延迟的组合,因此观测方程可表示为
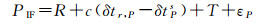 (3)
(3)
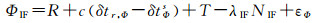 (4)
(4)
传统整数相位钟法固定非差模糊度。在用户端,整数相位钟法使用GRG宽巷小数周偏差产品,根据Melbourne-Wubbena(MW)组合固定宽巷模糊度,MW组合观测值AMW与宽巷模糊度NWL的关系为
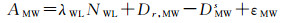 (5)
(5)
式中,Dr, MW、DMWs表示接收机与卫星的MW宽巷小数周偏差,单位为米(m)。由于宽巷波长较长,宽巷模糊度可以采取直接取整的方法固定。然后将式(4)中无电离层模糊度改写为宽巷与窄巷模糊度组合的形式,得到
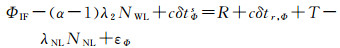 (6)
(6)
式中,α表示无电离层组合系数,它与频率f1、f2的关系满足α=f12/(f12-f22);NNL表示窄巷模糊度,单位为周;λNL表示窄巷波长,单位为米(m)。整数相位钟法对两类钟差参数严格区分,伪距钟所包含的硬件延迟没有被引入相位方程,因此模糊度参数具备较好的整数特性。但式(6)中钟差与模糊度线性相关,用户需要将某个窄巷模糊度设为任意基准值[15],然后才能够固定剩余模糊度并求解其他参数。
在服务端,钟差与模糊度参数线性相关问题仍然存在,同样需要任意固定一个基准模糊度,然后采用Bootstrap方法计算剩余模糊度。为保证相位钟在数值上接近伪距钟,CNES-CLS通常会在相位钟添加一定整周窄巷波长,以确保相位钟与相应的伪距钟差值不超过半个窄巷波长[16],即
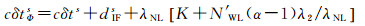 (7)
(7)
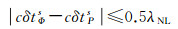 (8)
(8)
式中,K表示自由整数;N′WL表示可能存在的宽巷模糊度固定错误。根据宽巷与窄巷模糊度的关系可知,1周宽巷模糊度的错误可等效为(α-1)λ2/λNL周(约3.5周)的窄巷模糊度错误。事实上,由式(8)可知,0.5周的窄巷偏差很难区分,而且相位钟产品为以窄巷波长取模运算的离散值,因此两种钟差产品之间的系统性偏差必然存在。
2 利用整数相位钟法进行时频传递存在的问题本文通过GRG相位钟产品与IGS最终产品的双差试验验证上述分析。设dtIGSi和dtGRGi分别表示同时刻IGS最终产品的卫星钟差和GRG产品的卫星钟差,其中, 上标i表示卫星PRN编号。首先选择一颗参考星,并与其他所有卫星钟差做一次单差,得
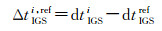 (9)
(9)
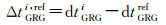 (10)
(10)
然后计算式(9)和式(10)的双差结果,得到
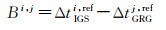 (11)
(11)
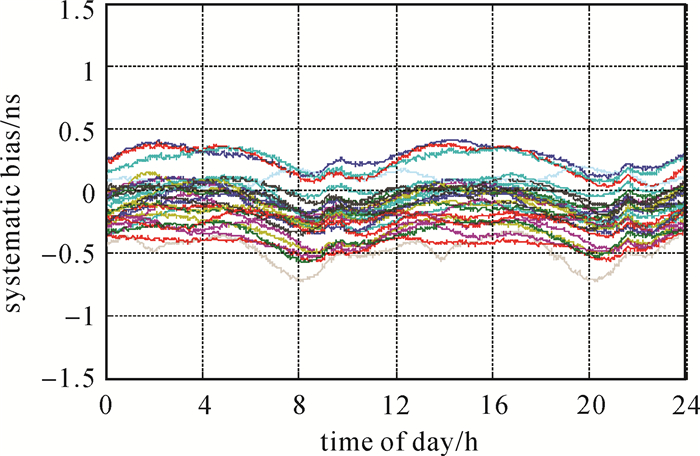
虽然IGS最终产品和GRG产品采用不同时间尺度,但双差处理可以消除时间尺度对系统性偏差分析的影响。从图 1可以看出,相对于同一参考星,两种产品的双差结果存在明显系统性偏差,偏差介于-0.5~+0.5 ns。该偏差表现出明显的离散化特征,这与相位钟以窄巷波长取模运算的离散取值策略有关,并且偏差项表现出与卫星轨道周期相似的周期性。该项偏差对IPPP时频传递的影响主要有以下几个方面:
|
| 图 1 不同卫星IGS最终产品卫星钟差与GRG相位钟产品卫星钟差的双差结果 Fig. 1 The double difference between IGS satellite clock offsets and the GRG satellite clock offsets for different satellites |
(1) 如果用户采用与服务端相同的模糊度固定策略,同样需要将某个窄巷模糊度任意固定为基准值,以确保相位钟和模糊度参数能够直接分离。此时接收机相位钟差具有和式(7)相似的形式
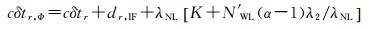 (12)
(12)
在时频传递时,由于各个测站参数估计的独立性,上述系统性偏差问题在传递过程中会发生积累,造成不超过1个窄巷波长的系统性偏差。
(2) 在用户端参数估计时,传统整数相位钟法将测站钟差建模为历元间独立的高斯白噪声,这种建模策略会导致GRG相位钟产品所包含的系统性偏差被测站钟差吸收,同样会影响IPPP时间传递精度。本文通过3组时间传递试验,计算GRG产品传递结果与IGS最终产品传递结果的差值。
如图 2所示,传递结果分别存在约0.1 ns(BRUX-DARW)、0.27 ns(CRO1-GODE)、0.33 ns(HOLB-VILL)的系统性偏差。试验结果证明,系统偏差在时间传递过程中会造成误差积累,不同传递结果中均存在一定的系统性偏差。该偏差大小无法准确估计,因此会影响IPPP时间传递性能。此外,文献[16]表明,单天内的非差模糊度小数周偏差可能超出1周,由于钟差与模糊度参数相关性,超出部分同样会被钟差吸收,影响时频传递精度。
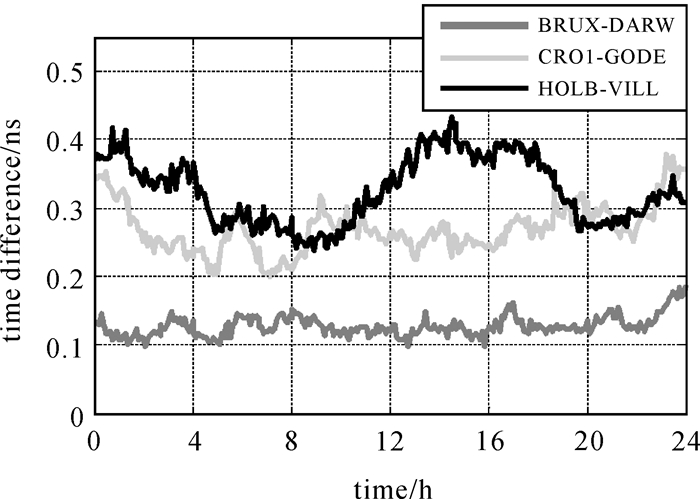
|
| 图 2 GRG产品时间传递结果与IGS最终产品差值 Fig. 2 The difference of time transfer results between GRG products and the IGS final products |
3 改进整数相位钟法 3.1 星间单差模糊度固定方法及质量控制策略
针对模糊度与钟差参数的线性相关问题,本文将伪距方程的钟差强约束为相位钟差,即伪距和载波方程均使用GRG相位钟产品,用户不需要设置模糊度的任意基准值,所有模糊度和钟差参数均可以直接估计准确得到。改进算法的观测值组合模型为
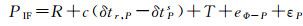 (13)
(13)
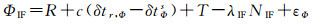 (14)
(14)
式中,eΦ-P表示伪距钟与相位钟的差值。将伪距钟差强约束为相位钟差,伪距方程中会增加一项eΦ-P。该项偏差小于1个窄巷波长,由于伪距的权远小于相位,eΦ-P的量级与伪距观测噪声、多径等误差项相比是可以容忍的,在参数估计过程中该项偏差会被伪距残差吸收[16]。
针对非差窄巷模糊度的不稳定问题,本文采用固定星间单差模糊度的方法,然后构建虚拟单差方程,以单差模糊度固定解为约束,计算其他参数的固定解[17]。具体固定方法为:
首先,固定单差宽巷模糊度。采用GRG宽巷小数周偏差产品,根据MW组合固定宽巷模糊度,为确保模糊度固定准确,对式(5)做星间单差,剔除接收机端宽巷偏差,则卫星p与卫星q单差模糊度为
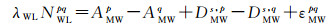 (15)
(15)
其次,固定单差窄巷模糊度。对收敛较好的非差无电离层模糊度浮点解做星间单差,消除接收端硬件延迟的影响,得到单差窄巷模糊度初始解
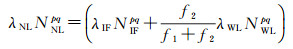 (16)
(16)
本文采用最小二乘模糊度降相关平差法(LAMBDA)搜索并固定单差窄巷模糊度。最后固定无电离层模糊度,并以固定模糊度为约束条件计算其他参数的固定解。本文采用扩展卡尔曼滤波进行参数估计,在估计过程中,对流层参数建模为随机游走,位置参数由于采用静态模式而建模为常数,模糊度参数建模为常数[13]。
由于钟差与模糊度参数相关,模糊度错误固定会直接影响时频传递的准确度和稳定度,因此IPPP定时计算需要执行比定位计算更严格的质量控制策略[18-20]。模糊度固定质量控制策略流程见图 3。

|
| 图 3 模糊度固定质量控制策略 Fig. 3 The flow chart of IPPP quality control strategy |
(1) 模糊度浮点解阶段:首先进行传统PPP计算,当卡尔曼滤波的位置方差平方根Q3D小于0.05 m时[21],模糊度收敛精度较高,转入IPPP计算。
(2) 固定宽巷模糊度阶段:剔除高度角低于16°的卫星观测数据(避免质量较差观测数据影响模糊度固定,阈值可视观测环境情况调整),并对MW组合观测值进行历元间平滑,确保模糊度准确固定。采用宽巷模糊度取整后剩余偏差小于0.25周和模糊度Bootstrapping检核成功率大于0.999 9两项条件作为固定成功判据。在单差基准星的选择上,本文参考文献[20, 22]的做法,构建所有可能的卫星对组成星间单差,并固定通过检验的模糊度参数。
(3) 固定窄巷模糊度阶段:以取整后剩余偏差小于0.25周和LAMBDA算法结果通过ratio-test作为窄巷模糊度固定成功判据。
(4) 参数更新阶段:当连续多个历元通过以上检验且前后固定一致时,认为固定结果趋于稳定,此时将传统PPP估计参数更新为IPPP参数;为防止模糊度固定错误,在状态更新前进行Q3D检验,若固定解Q3D大于传统PPP的Q3D,模糊度存在固定错误的可能,则该历元以传统PPP结果为准。
3.2 扩展原子钟模型传统白噪声钟差模型会导致钟差参数吸收来自GRG相位钟产品的系统性偏差等未建模误差,鉴于现阶段大多数时频传递测站配有高性能原子钟,本文利用原子钟建模的方法精化接收机钟差模型,将钟差、钟速参数加入卡尔曼滤波参数估计,避免GRG卫星钟差中的窄巷偏差被测站钟差吸收。仅考虑钟差模型的简化卡尔曼滤波观测方程与状态方程为
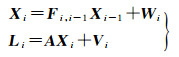 (17)
(17)
式中,Xi表示钟差、钟速二维状态向量;Wi表示过程噪声;Li表示观测量;Vi表示观测噪声;A=[1 0]表示观测方程系数矩阵;Fi, i-1表示状态转移矩阵。设相邻历元时间间隔为Δt,则有
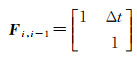 (18)
(18)
原子钟噪声包括调频随机噪声与调相随机噪声两大部分。其中相位测量噪声较小,并且不随时间积累,因此噪声协方差矩阵主要考虑调频噪声随时间积累产生的相位噪声,卡尔曼滤波过程噪声协方差矩阵与幂律谱系数h的关系为[23]
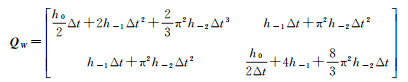 (19)
(19)
式中,h0、h-1、h-2分别表示调频白噪声、调频闪变噪声、调频随机游走噪声的幂律谱系数。幂律谱系数可以通过阿伦偏差(Allan deviation, ADEV)分段拟合得到[24],设平滑时间为τ,相应阿伦偏差表示为
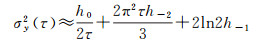 (20)
(20)
本文采用文献[10]的方法对原子钟模型初始化,原子钟模型初始值要求不包含明显系统性偏差,因此从GRG相位钟产品得到的测站钟差初值无法用于初始化。鉴于GRG相位钟产品溯源到GPST[25],本文根据前一天IGS最终产品给出一种可行的初始值确定方法
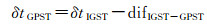 (21)
(21)
式中,δtGPST表示溯源到GPST时间尺度下的测站钟差;δtIGST表示溯源到IGST时间尺度下的同测站钟差;difIGST-GPST表示两种时间尺度的时间差值,该差值可以从IGS最终产品得到。
4 算例分析 4.1 改进整数相位钟法模糊度固定性能分析本文利用原子钟本身物理特性精化钟差参数的随机模型,避免了来自GRG相位钟产品的系统性偏差影响测站钟差计算。由于钟差与模糊度的相关性,该系统性偏差会转而被模糊度参数吸收,为检验改进整数相位钟法的模糊度固定性能,本文选择2016-08-02共7个原子钟测站的双频观测数据,数据采样率30 s,卫星截止高度角为10°,伪距和载波相位权比为1:100,使用GRG精密轨道钟差以及卫星宽巷偏差产品,采用原子钟模型与白噪声钟差模型两种方案,对两种方案的单差模糊度、模糊度固定成功率以及窄巷残差统计信息进行比较分析。
为更加清晰直观地表现两种方案中模糊度参数的变化情况,本文截取了BRUX站当天某时段内的单差窄巷模糊度。由图 4可见,两种方案中模糊度参数变化与弧段分布情况几乎相同,但部分弧段会有1周的偏差,其中变化明显的弧段已在图中标注。这主要是因为精化接收机钟差模型后,由于钟差与模糊度的相关性,原本会被钟差参数吸收的GRG产品系统偏差转而被模糊度参数吸收,但该偏差项幅度小于1个窄巷波长,对模糊度取值的影响很小,并且经过星间单差处理后,大部分偏差会被消除,因此只有部分弧段的模糊度参数出现1周变化。
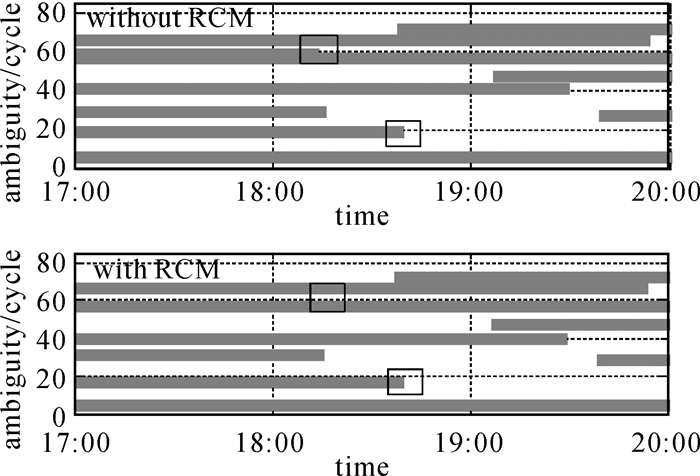
|
| 图 4 星间单差窄巷模糊度参数 Fig. 4 The single-difference narrow-lane ambiguity parameters between satellites |
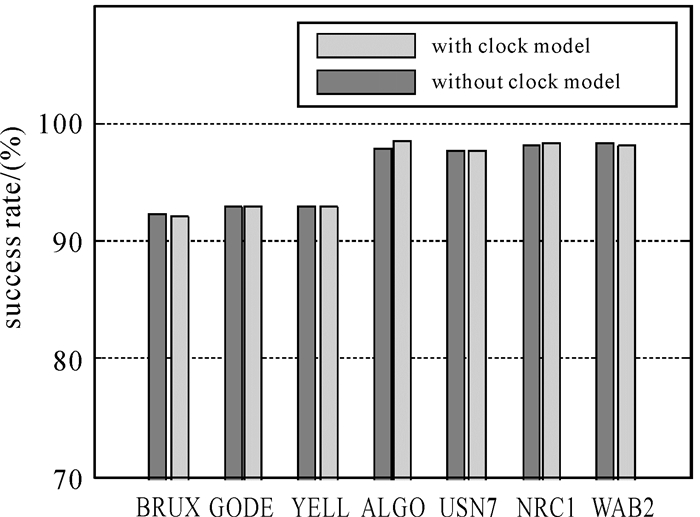
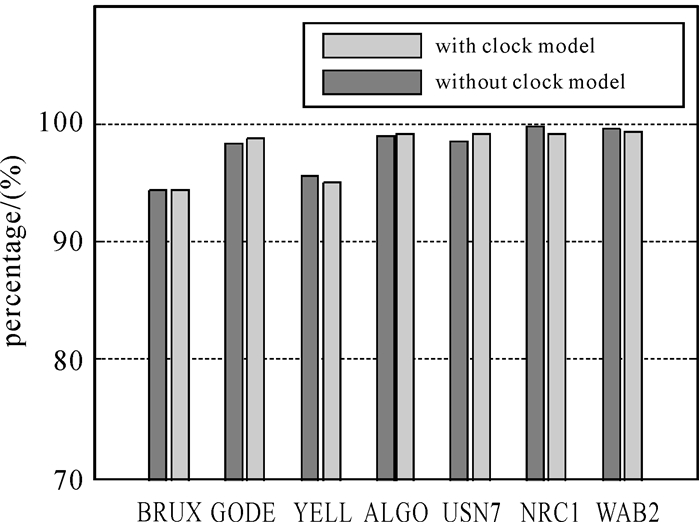
图 5、图 6分别表示模糊度固定的ratio-test检验成功率与小于0.15周窄巷残差所占比率。通过比较分析模糊度分布、模糊度固定成功率以及窄巷残差统计信息证明,两种方案的模糊度固定结果差异很小。虽然原子钟模型会使模糊度吸收来自GRG产品的系统性偏差,但一方面,星间单差方法可以消除大部分被模糊度吸收的偏差项;另一方面,由图 1可知,该系统性偏差相对稳定,原子钟模型对模糊度固定的影响只是使模糊度参数增加一比较稳定的偏差项。因此,使用原子钟模型精化钟差参数并不会影响模糊度固定性能。
|
| 图 5 Ratio-test模糊度检验成功率 Fig. 5 The success rate of ratio-test for ambiguity validation |
|
| 图 6 小于0.15周窄巷残差所占百分比 Fig. 6 The percentage of narrow-lane ambiguity residuals within 0.15 cycles |
4.2 改进整数相位钟法频率传递性能分析
为分析利用改进整数相位钟法进行频率传递的稳定度,本文选择6个原子钟测站2016-01-05—2016-01-08共4 d的双频观测数据,进行4组频率传递试验:GODE-YELL、GODE-BRUX、WTZR-NRC1、BRUX-OPMT,数据采样率30 s,采用修正阿伦偏差(modified Allan deviation, MDEV)作为评价指标,分析改进算法的频率稳定度。
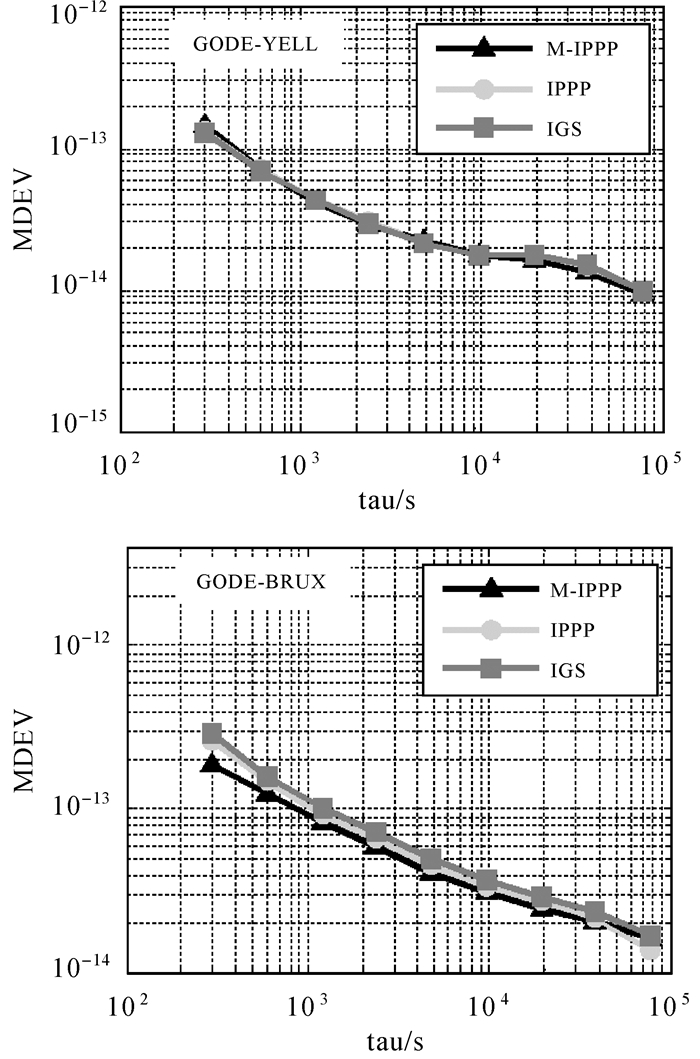
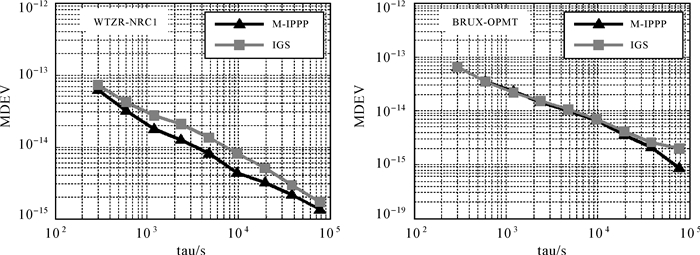
上述测站中,BRUX、GODE、YELL为IGS与CNES-CLS并置测站。在图 7的频率传递试验中,改进算法传递结果的频率稳定度与传统整数相位钟法稳定度一致,在大部分平滑时间内,改进算法的稳定度性能优于基于传统PPP的IGS最终产品。图 8所示测站为IGS与BIPM并置站,两组试验的频率传递的稳定度水平明显优于图 7所示频率传递结果,并且在部分平滑时间内,改进算法的频率稳定度达到甚至优于IGS最终产品的传递结果。经计算,改进整数相位钟法频率传递试验的单天稳定度平均为1.1×10-15/d。
|
| 图 7 改进整数相位钟算法与IGS最终产品和GRG产品修正阿伦偏差比较 Fig. 7 The modified Allan deviation of modified integer phase clock method compared with IGS final products and GRG products |
|
| 图 8 改进整数相位钟算法与IGS最终产品修正阿伦偏差比较 Fig. 8 The Modified Allan Deviation of modified integer phase clock method compared with IGS final products |
4.3 改进整数相位钟法时间传递性能分析
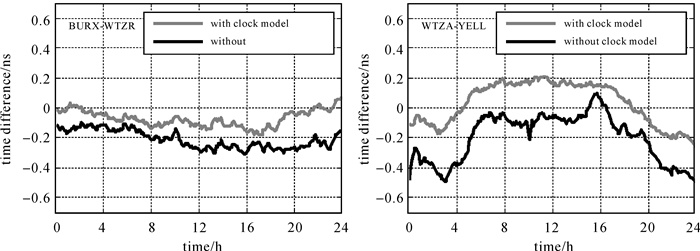
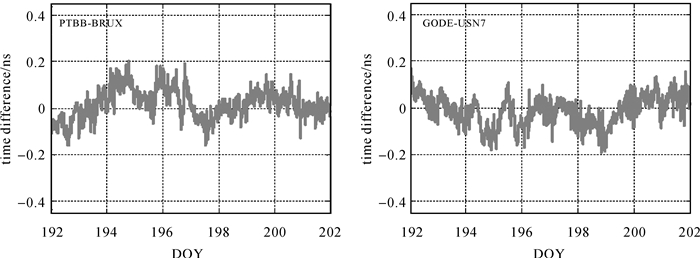
为检验改进整数相位钟法时间传递性能,本文首先选择2016-01-05的双频观测数据,进行2组时间传递试验:WTZA-YELL、BRUX-WTZR,分别采用原子钟模型与白噪声钟差模型两种时间传递方案,比较两种方案的时间传递结果与IGS参考值的差值序列,然后选择2016-07-10至2016-07-19(年积日2016-192至2016-201)10 d的双频观测数据,进行2组时间传递试验:PTBB-BRUX、GODE-USN7,分析采用原子钟模型改进算法的时间传递性能。
如图 9所示,白噪声钟差模型方案存在0.2~0.3 ns的系统性偏差,而使用原子钟模型约束钟差参数后,BRUX-WTZR、WTZA-YELL的IPPP时间传递精度约为0.09、0.14 ns,传递结果中的系统性偏差消失,并且剔除未建模误差对钟差计算的影响后,传递结果更加平滑。图 10的时间传递结果分别为PTBB-BRUX(0.07 ns)、GODE-USN7(0.08 ns),时间传递结果同样不存在系统性偏差,传递精度优于0.1 ns,证明改进算法在时间传递上的优异性能。以上试验结果表明,为保证IPPP时间传递精度,一方面需要改进原有的用户端模糊度固定方法,另一方面还需要避免来自GRG产品的系统偏差影响用户钟差计算。
|
| 图 9 单天M-IPPP时间传递结果与IGS产品参考值差值 Fig. 9 The difference between M-IPPP time transfer results and IGS products for one day |
|
| 图 10 10 d M-IPPP时间传递结果与IGS产品参考值差值 Fig. 10 The difference between M-IPPP time transfer results and IGS products for ten days |
5 结论
本文分析了整数相位钟法在钟差计算与时频传递中存在的问题,提出一种基于星间单差模糊度固定与原子钟精化模型的改进整数相位钟法,分析了改进算法的模糊度固定和时频传递性能。经检验,改进算法能够有效消除IPPP时频传递结果中的系统性偏差,提高IPPP时间传递精度,算例结果表明,4组时间传递试验的传递精度优于0.2 ns,频率传递试验的天稳定度平均为1.1×10-15/d。本文方法充分利用原子钟测站钟差在历元间的相关性,可适用于所有原子钟测站,但对于数据长时间间断等钟差间断情况,需要在参数估计前对数据完整性进行检核,并且在间断处重新滤波计算。
| [1] | RAY J, SENIOR K. IGS/BIPM pilot project:GPS carrier phase for time/frequency transfer and timescale formation[J]. Metrologia, 2003, 40(4): 205. DOI:10.1088/0026-1394/40/4/501 |
| [2] | PETIT G, HARMEGNIES A, MERCIER F, et al. The time stability of PPP links for TAI[C]//Proceedings of 2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum. San Francisco, CA: IEEE, 2011. |
| [3] |
陈宪冬.
基于大地型时频传递接收机的精密时间传递算法研究[J]. 武汉大学学报(信息科学版), 2008, 33(3): 245–248.
CHEN Xiandong. Precision time transfer methods based on geodetic time and frequency transfer receivers[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3): 245–248. |
| [4] |
闫伟, 袁运斌, 欧吉坤, 等.
非组合精密单点定位算法精密授时的可行性研究[J]. 武汉大学学报(信息科学版), 2011, 36(6): 648–651.
YAN Wei, YUAN Yunbin, OU Jikun, et al. Feasibility of precise timing with uncombined PPP[J]. Geomatics and Information Science of Wuhan University, 2011, 36(6): 648–651. |
| [5] |
张小红, 蔡诗响, 李星星, 等.
利用GPS精密单点定位进行时间传递精度分析[J]. 武汉大学学报(信息科学版), 2010, 35(3): 274–278.
ZHANG Xiaohong, CAI Shixiang, LI Xingxing, et al. Accuracy analysis of time and frequency transfer based on precise point positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 274–278. |
| [6] |
于合理, 郝金明, 田英国, 等.
GNSS单站授时系统性偏差分析[J]. 大地测量与地球动力学, 2017, 37(1): 30–34.
YU Heli, HAO Jinming, TIAN Yingguo, et al. Analysis of systematic bias of single station time service[J]. Journal of Geodesy and Geodynamics, 2017, 37(1): 30–34. |
| [7] | WANG Kan, ROTHACHER M. Stochastic modeling of high-stability ground clocks in GPS analysis[J]. Journal of Geodesy, 2013, 87(5): 427–437. DOI:10.1007/s00190-013-0616-5 |
| [8] | WEINBACH U, SCHÖN S. GNSS receiver clock modeling when using high-precision oscillators and its impact on PPP[J]. Advances in Space Research, 2011, 47(2): 229–238. DOI:10.1016/j.asr.2010.06.031 |
| [9] |
张小红, 陈兴汉, 郭斐.
高性能原子钟钟差建模及其在精密单点定位中的应用[J]. 测绘学报, 2015, 44(4): 392–398.
ZHANG Xiaohong, CHEN Xinghan, GUO Fei. High-performance atomic clock modeling and its application in precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 392–398. |
| [10] |
于合理, 郝金明, 刘伟平, 等.
附加原子钟物理模型的PPP时间传递算法[J]. 测绘学报, 2016, 45(11): 1285–1292.
YU Heli, HAO Jinming, LIU Weiping, et al. A time transfer algorithm of precise point positioning with additional atomic clock physical model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1285–1292. DOI:10.11947/j.AGCS.2016.20160217 |
| [11] | DELPORTE J, MERCIER F, LAURICHESSE D, et al. Fixing integer ambiguities for GPS carrier phase time transfer[C]//Proceedings of 2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum. Geneva, Switzerland: IEEE, 2007: 927-932. |
| [12] | PETIT G, KANJ A, LOYER S, et al. 1×10-16 frequency transfer by GPS PPP with integer ambiguity resolution[J]. Metrologia, 2015, 52(2): 301–309. DOI:10.1088/0026-1394/52/2/301 |
| [13] | KOUBA J, HÉROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12–28. DOI:10.1007/PL00012883 |
| [14] | LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J]. Navigation, 2009, 56(2): 135–149. DOI:10.1002/navi.2009.56.issue-2 |
| [15] | SHI Junbo, GAO Yang. A comparison of three PPP integer ambiguity resolution methods[J]. GPS Solutions, 2014, 18(4): 519–528. DOI:10.1007/s10291-013-0348-2 |
| [16] | MONTENBRUCK O, HACKEL S, JÄGGI A. Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations[J]. Journal of Geodesy, 2018, 92(7): 711–726. DOI:10.1007/s00190-017-1090-2 |
| [17] |
李彦杰, 杨元喜, 何海波.
附加约束条件对GNSS/INS组合导航结果的影响分析[J]. 武汉大学学报(信息科学版), 2017, 42(9): 1249–1255.
LI Yanjie, YANG Yuanxi, HE Haibo. Effects analysis of constraints on GNSS/INS integrated navigation[J]. Geomatics and Information Science of Wuhan University, 2017, 42(9): 1249–1255. |
| [18] | LI Tao, WANG Jinling, LAURICHESSE D. Modeling and quality control for reliable precise point positioning integer ambiguity resolution with GNSS modernization[J]. GPS Solutions, 2014, 18(3): 429–442. DOI:10.1007/s10291-013-0342-8 |
| [19] |
潘宗鹏, 柴洪洲, 刘军, 等.
基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1210–1218.
PAN Zongpeng, CHAI Hongzhou, LIU Jun, et al. GPS partial ambiguity resolution method for zero-difference precise point positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1210–1218. DOI:10.11947/j.AGCS.2015.20150056 |
| [20] |
刘帅, 孙付平, 郝万亮, 等.
整数相位钟法精密单点定位模糊度固定模型及效果分析[J]. 测绘学报, 2014, 43(12): 1230–1237.
LIU Shuai, SUN Fuping, HAO Wanliang, et al. Modeling and effects analysis of PPP ambiguity fixing based on integer phase clock method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1230–1237. DOI:10.13485/j.cnki.11-2089.2014.0195 |
| [21] | LOYER S, PEROSANZ F, MERCIER F, et al. Zero-difference GPS ambiguity resolution at CNES-CLS IGS analysis center[J]. Journal of Geodesy, 2012, 86(11): 991–1003. DOI:10.1007/s00190-012-0559-2 |
| [22] | PARKINS A. Increasing GNSS RTK availability with a new single-epoch batch partial ambiguity resolution algorithm[J]. GPS Solutions, 2011, 15(4): 391–402. DOI:10.1007/s10291-010-0198-0 |
| [23] | CHAN Fangcheng, JOERGER M, PERVAN B. Stochastic modeling of atomic receiver clock for high integrity GPS navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 1749–1764. DOI:10.1109/TAES.2014.120402 |
| [24] | YANG Yang, YUE Xiaokui, YUAN Jianping, et al. Enhancing the kinematic precise orbit determination of low earth orbiters using GPS receiver clock modelling[J]. Advances in Space Research, 2014, 54(9): 1901–1912. DOI:10.1016/j.asr.2014.07.016 |
| [25] | AC Coordinator, NOAA NGS.[IGSREPORT-24139] Wk 1875 IGS final orbits[EB/OL].[2016-01-04]. https://lists.igs.org/pipermail/igsreport/2016-January/024158.html. |


