天文定位是以已知准确空间位置的天体为基准,通过特定仪器观测天体得到高度角和方位角信息,再根据后方交汇的原理解算确定测量点的天文经纬度等位置信息的一种技术。它具有独立自主,不易受干扰的特性,因此被广泛应用在大地天文测量、航海、航空和航天等领域[1-2]。传统大地天文测量中采用的恒星天顶距法、恒星中天法、双星等高法和多星等高法[3-4]等测定经纬度的方法,其基本原理都是根据天体的高度角或者天顶距确定测量点的经纬度,称为高度角法或天顶距法。在航海领域,利用六分仪和天文钟进行舰船天文导航的高度差法[5]也属于天顶距法的范畴。
随着观测仪器以及计算机技术的进步,基于天顶距法的天文测量技术有了较大的发展。在海基方面,已实现了通过电子六分仪或大视场光学敏感器自动观测恒星进行定位导航的技术[6-8];在陆基方面,文献[9]提出利用TDM5000高精度全站仪和天宝4000 DL-GPS接收机组合进行天文定位和定向;文献[10]建立的基于电子经纬仪的天文测量系统则引入了自动寻星的技术。此外,随着图像处理技术的成熟,通过天文图像处理进行天文定位已成为新的趋势[11-12],进一步提高了天文观测数据的获取效率。天文观测数据处理的基本原理是最小二乘法,针对日益增加的观测数据,加权最小二乘[13]和抗差估计[14]的方法也被用于抑制粗差的影响并限制利用误差偏大的观测值。在这些方法中,算法基础都是天顶距法定位模型。该模型中观测恒星的数量和分布与天文定位精度之间存在密切的关系,即可以通过确定最优的选星方案,用最少的观测量和计算量达到特定的天文定位精度。
目前传统天顶距法的选星条件只是针对已知纬度求解经度或者已知经度求解纬度的情况,无法说明恒星的选择对同时解算天文经纬度的影响。本文借鉴卫星导航中的几何精度衰减因子(geometric dilution of precision, GDOP)[15]的概念,研究了天顶距法中恒星的数量及其分布对天文定位精度的影响,分别通过仿真数据和实测数据进行分析验证。结果表明,GDOP能够用来描述恒星的分布对定位结果影响的优劣,选择等高的方位角均匀分布的恒星进行解算能达到最优的定位结果。
1 天顶距法定位模型天顶距法即采用恒星的天顶距观测量进行天文定位解算,将天球坐标系作为基准建立相应的天顶距法定位模型。如图 1所示,P为北天极,Z为测站天顶,σ为观测的天体,N表示过北天极P和天体σ的大圆弧与赤道的交点,M表示过天顶Z和天体σ的大圆弧与地平圈的交点。
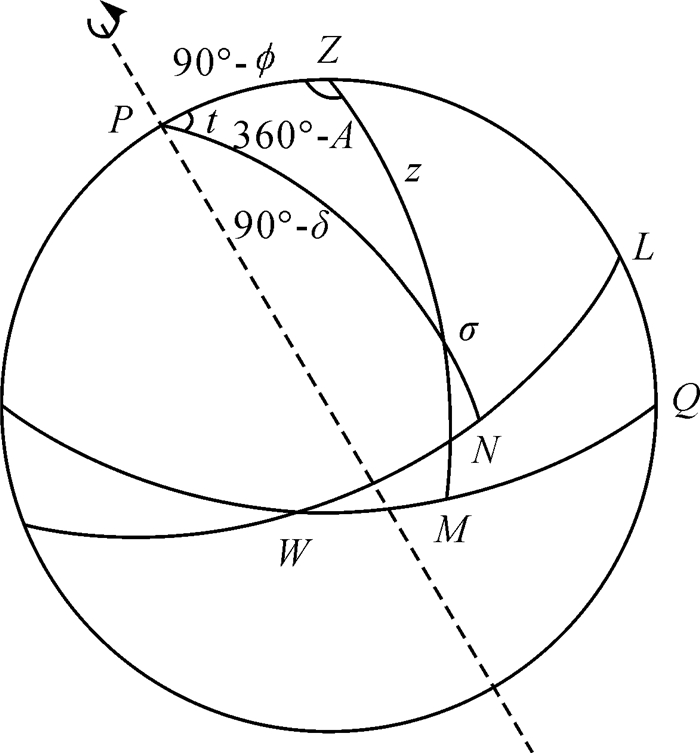
|
| 图 1 天文定位三角 Fig. 1 Astronomical triangle for positioning |
根据定义可得
 (1)
(1)
式中,φ表示测站的天文纬度;δ表示恒星的赤纬;z表示恒星的天顶距;t是时角,其与观测瞬间格林尼治真恒星时S,恒星的赤经α和测站的天文经度λ有如下关系
 (2)
(2)
天体的赤经α、赤纬δ可通过查询星表并进行恒星视位置计算得到,天体的天顶距z则通过相应的仪器观测得到,观测瞬间格林尼治真恒星时S可以由观测瞬间的UTC时刻T化算得到。根据球面三角的边余弦公式可得天顶距法的观测方程[14]
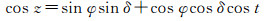 (3)
(3)
在采用光学观测手段时,恒星的天顶距存在大气折射误差[16]。由于大气成分的复杂以及高动态性,大气折射误差无法完全改正,因此将改正之后的残余误差Δz作为未知参数与测站的天文经纬度一同解算。此时观测方程为
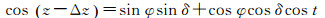 (4)
(4)
若对n个恒星进行观测,假设测站的初值为(φ0, λ0),对观测方程式(4)进行线性化,得到误差方程
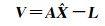 (5)
(5)
式中,V为n维的残差向量;A为n×3的系数阵;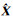
 (6)
(6)
式中
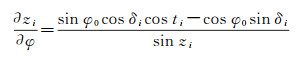 (7)
(7)
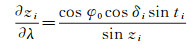 (8)
(8)
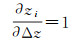 (9)
(9)
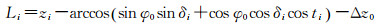 (10)
(10)
采用经典的最小二乘法解算,可得估计参数
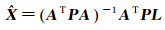 (11)
(11)
式中,P为观测值的权阵,表示数据相对可信赖程度的数值。假设在观测期间,测站对各个恒星的天顶距观测量zi互不相关且等权,则其权阵可认为是单位阵。对式(11)进行迭代解算即可得到测站的天文经纬度以及大气折射误差改正残余。
2 GDOP最小值的推导及应用通过协方差阵的运算可以得到误差传播的规律[17]。误差方程的系数阵A与恒星的具体分布紧密相关,以下通过对A阵进行变换讨论定位精度与恒星的分布的关系。
通过球面三角公式[10]对误差方程的系数阵A进行化简,最终误差方程式(5)可以表示为
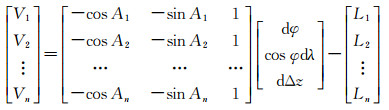 (12)
(12)
记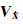
 (13)
(13)
式中,V表示天顶距的观测残差,假设在观测期间,测站对各个天体的天顶距观测量zi互不相关,经过大气折射改正之后的误差是零均值且具有相同的方差σz2。当各恒星独立等精度观测时,权阵P为单位阵,则定位误差的协方差阵为
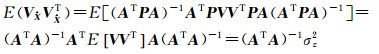 (14)
(14)
可见(ATA)-1是将测站测角误差转换到天文位置误差的变换因子矩阵。根据卫星导航中GDOP的定义[18-19]
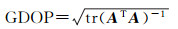 (15)
(15)
将本文中的GDOP表示为天顶距法天文定位中的精度因子,体现天顶距法天文解算时恒星的几何分布对最终的定位误差的影响程度。则最后的解算结果误差可以表示为
 (16)
(16)
由于参数cos φ仅与测站天文纬度有关,因此当测站固定时可认为是常数,则经度定位误差Vλ2最小等价于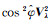
下面求解GDOP的最小值。法方程的系数阵ATA为
 (17)
(17)
假设矩阵ATA的3个特征值为λ1, λ2, λ3,则根据矩阵的迹的定义可得[20-22]
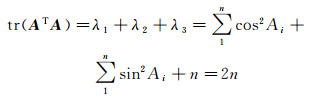 (18)
(18)
此时GDOP可以表示为
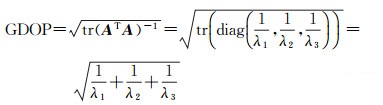 (19)
(19)
根据矩阵ATA的特征,其第3行第3列的元素总是n,而其他两个对角线元素具有相似性,可以通过矩阵论中的盖尔斯高林(Gerschgorin)圆盘定理[20, 23]说明前两个特征值的值域相同。下面对ATA做正交变换,有VTATAV=Γ且VTV=I,记ATA为G,则矩阵G和Γ酉等价
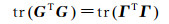 (20)
(20)
所以有
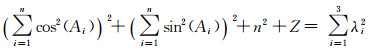 (21)
(21)
式中
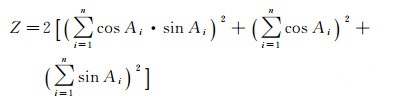 (22)
(22)
显然
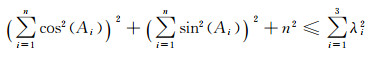 (23)
(23)
通过不等式化简(23)可得
 (24)
(24)
此时GDOP可以表示为
 (25)
(25)
经计算,当λ1=λ2=n/2且λ3=n时,GDOP取到最小值

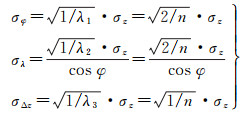 (26)
(26)
当单颗恒星的天顶距观测误差为0.5″时,理论上选取6颗方位角均匀分布的恒星进行解算纬度的精度能达到一等天文测量的要求[24](mφ=0.3″),而经度的解算精度与具体的测站纬度有关,纬度为60°时选取23颗方位角均匀分布的恒星进行解算能使经度的精度达到一等天文测量的要求(mλ=0.02 s),且随着纬度的增大,需要更多的观测恒星以满足特定的精度要求。
当恒星按照方位角均匀分布时的GDOP达到理论最小值,其只与恒星的个数有关,并随着恒星个数的增加,GDOP的理论最小值不断减小。具体变化规律如图 2所示。
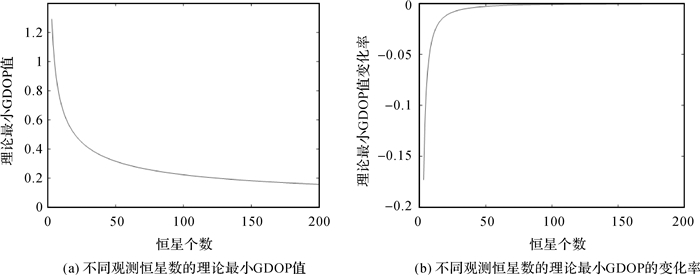
|
| 图 2 理论最小GDOP值与恒星个数的关系 Fig. 2 The relationship between the theoretical minimum of GDOP and the number of stars |
图 2(a)的横轴为恒星个数,纵轴为理论最小GDOP;图 2(b)的横轴为恒星个数,纵轴为理论最小GDOP的变化率。可见GDOP减小的速度随着恒星个数的增加而减小,当恒星个数增加到108(24)颗时,定位误差的减小量小于0.001×测量误差/每颗(0.01×测量误差/每颗)。且当恒星数大于5颗的时候,最优的分布GDOP小于1,表明最终的定位误差在数值上小于测角误差。
3 仿真算例与分析 3.1 仿真数据将单位球面作为天球坐标系的参考面,在天球上设置均匀分布的恒星,即等间隔选取赤经赤纬,通过坐标转换将恒星的赤经赤纬转换为当地地平坐标系下的方位角和天顶距,取地平面以上的恒星作为仿真星表。其在各自坐标系中的分布如图 3所示,其中仿真的恒星时时刻为0时,测站天文经纬度为(113°,34°)。
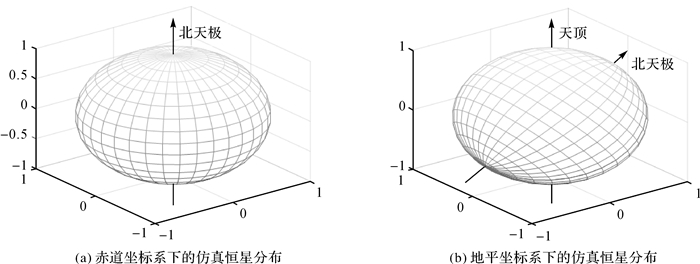
|
| 图 3 仿真星表分布 Fig. 3 Simulation catalog distribution diagram |
图 3(a)中纵向和横向的弧线分别表示等间隔的赤经圈和赤纬圈,其交点即为仿真恒星在赤道坐标系上的位置。经过坐标旋转后转换至当地地平坐标系下,如图 3(b)所示。
得到仿真星表后,按照方位角尽量均匀分布的原则(天顶距随机分布),依次选取3~100颗恒星进行5000次的蒙特卡洛仿真试验,每次仿真在天顶距上加上方差为5″的随机偶然误差以及2″的系统误差,通过最小二乘解算对最终定位结果进行分析。
图 4(a)是当观测的恒星的方位角均匀分布时,不同恒星个数下的仿真结果。可得结论:①由于仿真中方位角的误差只涉及数值计算过程中的舍入误差,对于GDOP的影响很小,因此在恒星方位角均匀分布时仿真GDOP的变化曲线与理论最小GDOP的几乎重合。随着恒星数量的增加,GDOP不断减小,与理论推断相符;②将图 4(a)中定位误差随恒星数量增加的变化趋势与GDOP的变化趋势进行对比可知,在天顶距测量误差一定的前提下,定位误差随恒星个数增加的变化趋势与GDOP的变化趋势基本一致,即GDOP的大小能用于表示天文定位精度的优劣;③图 4(a)中天顶距大气折射改正残余误差为1.95″~2.05″,与初始设置的2″系统误差接近,无明显偏差;④图 4(b)表示当观测的恒星数为100颗且方位角均匀分布时,每次仿真解算后的纬度和经度误差,总体无系统误差。根据定位模型以及GDOP取到最小值的条件,φ的中误差与cos φ·λ的中误差相等,即解算得到的纬度中误差会小于经度中误差,且测站越靠近赤道经纬度定位精度的差异越小。
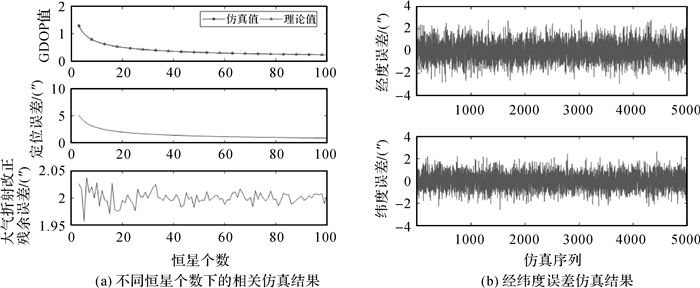
|
| 图 4 天顶距法天文定位仿真 Fig. 4 Simulation for altitude method in astronomical positioning |
3.2 仿真算例
以下通过仿真试验分别讨论天顶距与方位角的分布对定位精度的影响。
图 5表示在天顶距不变的条件下,采用20颗不同方位角分布的恒星的定位结果,包括GDOP值、定位误差及系统误差。可得结论:①当恒星方位角均匀分布时,解算所得GDOP为0.500 1,接近理论最小值0.5,相应的定位误差也取到最小值1.97″,当恒星方位角随机分布时,解算所得GDOP以及定位误差都明显大于方位角均匀分布时的,同时从图中可以看出GDOP与定位误差的变化趋势基本一致,即在观测误差一定时,可以采用GDOP的大小判断定位误差的大小;②当恒星方位角随机分布时,系统误差的解算结果为1.96″~2.05″,与真值2″接近,可认为天顶距存在固定的系统误差时,恒星方位角的不同分布对系统误差的解算影响较小。
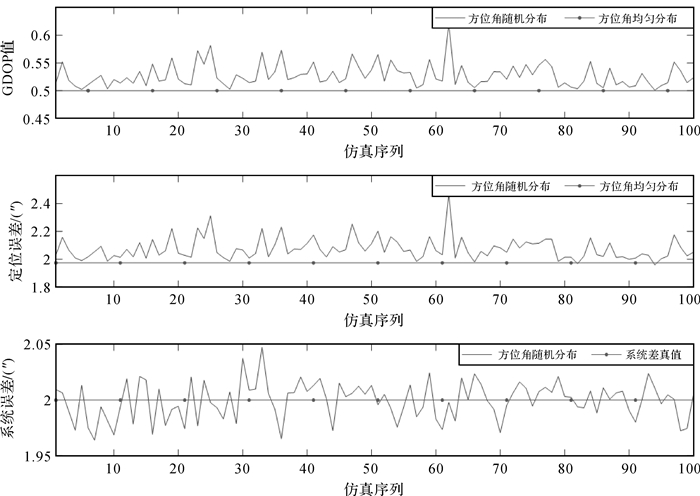
|
| 图 5 恒星天顶距为45°±0.5°且方位角不同分布时的定位仿真结果 Fig. 5 The simulation positioning results of stars in different distribution of azimuth and 45°±0.5° zenith distance |
图 6表示在方位角均匀分布的条件下,采用20颗不同天顶距分布的恒星的定位结果。可得结论:①当恒星天顶距随机分布时,解算所得GDOP的均值约为0.5,标准差为1.9×10-7,相应的定位误差为1.93″~2.03″,可认为天顶距固定时的解算结果基本一致,即当方位角呈均匀分布时,恒星天顶距的不同对定位结果的影响可以忽略,此外,文献[25]的研究表明在同等的观测误差下,天顶距法的定位精度与天顶距的具体取值无关,与本文结论一致;②当恒星天顶距随机分布时,系统误差的解算结果为1.96″~2.05″,与真值2″接近,可认为天顶距存在固定的系统误差时,恒星天顶距的不同分布对系统误差的解算影响较小。

|
| 图 6 恒星方位角均匀分布且天顶距随机时的定位仿真结果 Fig. 6 The simulation positioning results of stars with uniform azimuth distribution and random zenith distance |
4 试验验证
在实际观测中大气折射与天顶距的大小有强相关性,根据基本的大气折射修正模型[16, 26],恒星的天顶距越大,光线折射程度越大,并且由于大气折射会随着温度、气压的变化而不同,模型的误差也不尽相同。通常天顶距越大,模型推算的结果误差越大。因此严格意义上说,不同天顶距的恒星的大气折射改正残余不同。实际观测中用等高的方位角均匀分布的恒星进行天顶距法天文定位时与上文推导的计算模型最为接近。
2018年9月3日,在郑州某天文点用TS50全站仪观测天顶距为40°以及50°的恒星各30颗,该全站仪的标称测角精度为0.5″。按照方位角均匀分布的原则选取天顶距为40°的不同个数的恒星进行定位解算,结果如图 7所示。
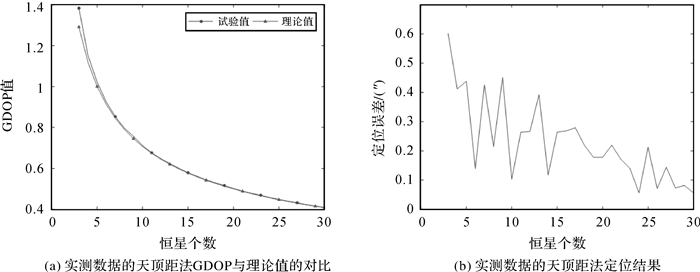
|
| 图 7 实测数据的天顶距法定位结果 Fig. 7 Altitude method of astronomical positioning in measured data |
由于实际观测的恒星无法严格按照方位角均匀分布进行选取,因此实际观测解算的GDOP一般大于理论最小值。最终定位精度存在波动,一方面是由于真实的GDOP与理论值的差异,另一方面是由于不同时段观测的不同的恒星的观测精度不尽相同。但随着观测恒星个数的增加,定位误差总体是呈逐渐下降的趋势。
分别选择天顶距为40°以及50°的不同方位角分布的20颗恒星进行解算,结果如图 8及表 1所示。

|
| 图 8 恒星天顶距分别为40°和50°且方位角不同分布时的定位试验结果 Fig. 8 The experimental positioning results of stars in different distribution of azimuth with zenith distance in 40° and 50° respectively |
| 恒星分布 | GDOP值 | 定位误差/(″) | 系统误差/(″) |
| 天顶距40°、方位角均匀分布 | 0.501 6 | 0.18 | 5.32 |
| 天顶距50°、方位角均匀分布 | 0.501 5 | 0.20 | 11.03 |
| 天顶距40°、方位角随机分布 | 0.500 7~0.574 4 | 0.11~0.61 | 4.61~6.14 |
| 天顶距50°、方位角随机分布 | 0.502 1~0.592 2 | 0.12~0.58 | 9.83~12.44 |
图 8(a)和图 8(b)分别表示在30颗天顶距为40°和50°的恒星中选取20颗不同方位角分布的恒星的定位结果。结合表 1中列出的部分统计结果可得结论:①当恒星方位角均匀分布时,试验所得GDOP与理论GDOP最小值0.5接近,小于恒星方位角随机分布时的解算结果;②当恒星方位角随机分布时,采用两种不同天顶距的恒星定位误差都存在小部分稍小于0.18″,这是实际观测时每颗星的观测精度不等造成的。整体而言采用方位角均匀分布的恒星能够得到最小的定位误差。
为验证不同天顶距对定位结果的影响,在尽量满足方位角均匀分布的条件下,从两种不同天顶距的恒星中各随机选取10颗进行的定位解算,结果如图 9及表 2所示。
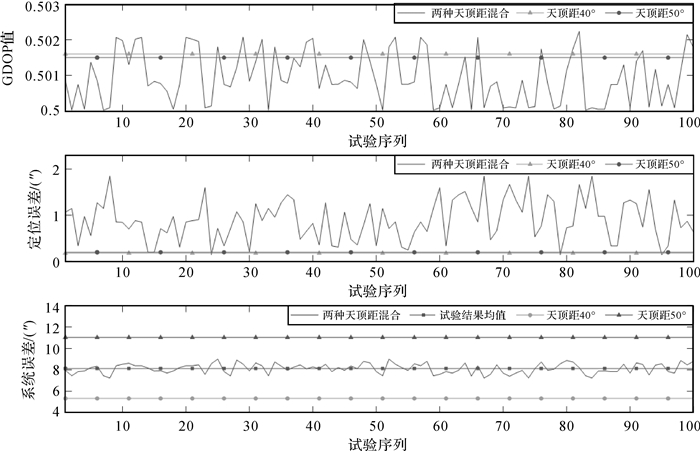
|
| 图 9 随机选取方位角均匀分布,天顶距为40°和50°的恒星各10颗定位解算结果 Fig. 9 The experimental positioning results of each 10 stars in random of 40° and 50° zenith distance and uniform azimuth respectively |
| 恒星分布 | GDOP值 | 定位误差/(″) | 系统误差/(″) |
| 方位角均匀分布,天顶距为40°和50°的恒星各10颗 | 0.500 0~0.503 0 | 0.18~1.77 | 7.24~9.01 |
图 9表示在方位角均匀分布的条件下,从天顶距为40°和50°的恒星中各随机选取10颗一同进行定位解算的结果。表 2中已列出相关的统计信息。与表 1进行对比可得:①GDOP稳定在0.5~0.503,与理论值0.5接近。整体小于方位角随机分布时的GDOP值,显然方位角的不同分布对GDOP的影响大于天顶距的不同分布对GDOP的影响,与理论推导结果基本符合。②当采用两种天顶距时的定位误差明显大于采用单一的天顶距时的,原因在于不同天顶距的大气折射改正残差不一致。③采用天顶距40°的恒星进行解算后得到的系统误差为5.512 9″,即大气折射改正残差约,同理天顶距50°的恒星的大气折射改正残差约为11.452 6″,而采用两种天顶距的恒星进行解算后得到的系统差为7.24″~9.01″,在定位模型中无相应的实际意义。
5 结论本文借鉴卫星导航中GDOP的定义,推导了天顶距法中GDOP的表达式,从数学上证明了天顶距法中GDOP取得最小值的条件并经过仿真实验以及实测试验验证。结果表明在测量精度一定时,GDOP与定位误差呈正相关,即可以用GDOP的大小表述定位精度的优劣。GDOP本身与恒星的几何分布以及数目有关,采用方位角均匀分布的恒星进行解算能得到GDOP最小值,为高效处理天文观测数据提供了理论依据。考虑到不同高度的恒星天顶距大气折射改正残差不同,在实际测量中应尽量采用等天顶距且方位角均匀分布的恒星。
| [1] |
王安国.
导航战背景下的天文导航技术——天文导航技术的历史、现状及其发展趋势[J]. 天文学进展, 2001, 19(2): 326–330.
WANG Anguo. Celestial navigation technique in the background of navigation war-the history, present situation and developing tendency of celestial navigation technique[J]. Progress in Astronomy, 2001, 19(2): 326–330. DOI:10.3969/j.issn.1000-8349.2001.02.055 |
| [2] |
王安国.
现代天文导航及其关键技术[J]. 电子学报, 2007, 35(12): 2347–2353.
WANG Anguo. Modern celestial navigation and the key techniques[J]. Journal of Electronics, 2007, 35(12): 2347–2353. DOI:10.3321/j.issn:0372-2112.2007.12.023 |
| [3] |
牛国华, 郑晓龙, 李雪瑞, 等.
大地天文测量[M]. 北京: 国防工业出版社, 2016: 126-127.
NIU Guohua, ZHENG Xiaolong, LI Xuerui, et al. Astronomical geodesy[M]. Beijing: National Defence Industry Press, 2016: 126-127. |
| [4] |
张捍卫, 许泽厚, 王爱生.
天文经纬度和天文方位角测定的基本原理[J]. 测绘科学, 2006, 31(4): 157–160.
ZHANG Hanwei, XU Zehou, WANG Aisheng. The basic principle of mensurating astronomical longitude, latitude and azimuth angle[J]. Science of Surveying and Mapping, 2006, 31(4): 157–160. DOI:10.3771/j.issn.1009-2307.2006.04.057 |
| [5] |
房建成, 宁晓琳.
天文导航原理及应用[M]. 北京: 北京航空航天大学出版社, 2006: 69-70.
FANG Jiancheng, NING Xiaolin. Principle and application of celestial navigation[M]. Beijing: Beihang University Press, 2006: 69-70. |
| [6] | VULFOVICH B, FOGILEV V. New ideas for celestial navigation in the third millennium[J]. Journal of Navigation, 2010, 63(2): 373–378. DOI:10.1017/S0373463309990348 |
| [7] | KAPLAN G H. New technology for celestial navigation[C]//Proceedings of Nautical Almanac Office Sesquicentennial Symposium. Washington, D.C.: U.S. Naval Observatory, 1999: 239-254. |
| [8] | BRACE T M, RAPIDS G. Method and system for spectral image celestial navigation: US NO: 2011/0077863 A1[P]. 2011-03-31. |
| [9] | BALODIMOS D D, KORAKITIS R, LAMBROU E, et al. Fast and accurate determination of astronomical coordinates Φ, Λ and azimuth, using a total station and GPS receiver[J]. Survey Review, 2003, 37(290): 269–275. DOI:10.1179/sre.2003.37.290.269 |
| [10] |
张超.基于电子经纬仪的天文测量系统及应用研究[D].郑州: 信息工程大学, 2009: 39-48. ZHANG Chao. System-level development and application research on astronomic surveying system base on electronic theodolites[D]. Zhengzhou: Information Engineering University, 2009: 39-48. http://cdmd.cnki.com.cn/Article/CDMD-90008-1011270858.htm |
| [11] |
赵亮.基于天文摄影测量的定位定向模型研究[D].西安: 西安科技大学, 2018: 2-3. ZHAO Liang. Research on positioning orientation model based on astronomical photogrammetry[D]. Xi'an: Xi'an University of Science and Technology, 2018: 2-3. |
| [12] |
孙剑明.基于星图识别的舰船天文导航关键技术研究[D].哈尔滨: 哈尔滨工程大学, 2013: 4-7. SUN Jianming. The key technology research on ships' celestial navigation based on star pattern recognition[D]. Harbin: Harbin Engineering University, 2013: 4-7. http://d.wanfangdata.com.cn/Thesis_D430786.aspx |
| [13] |
孙荣煜, 赵长印, 侯永刚.加权最小二乘在精密天文定位中的应用[C]//第四届中国卫星导航学术年会论文集-S3精密定轨与精密定位.武汉: 中国卫星导航学术年会组委会, 2013. SUN Rongyu, ZHAO Changyin, HOU Yonggang. Using weighted least square method for high precision astronomical calibration[C]//Proceedings of the 4th China Satellite Navigation Conference. Beijing: the Organizing Committee of China Satellite Navigation Conference, 2013. |
| [14] |
李崇辉, 郑勇, 张超, 等.
一种无需精密整平的抗差天文定位方法[J]. 测绘学报, 2013, 42(6): 810–816.
LI Chonghui, ZHENG Yong, ZHANG Chao, et al. A robust celestial positioning method without precise leveling[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 810–816. |
| [15] |
万丽华, 魏二虎.
导航系统定位精度和DOP的仿真研究[J]. 测绘地理信息, 2013, 38(4): 64–67.
WAN Lihua, WEI Erhu. Simulation study on positioning accuracy of satellite navigation and GDOP[J]. Journal of Geomatics, 2013, 38(4): 64–67. |
| [16] |
陈少杰, 郑勇, 詹银虎, 等.
天文大气折射改正模型比较分析[J]. 全球定位系统, 2017, 42(6): 61–65.
CHEN Shaojie, ZHENG Yong, ZHAN Yinhu, et al. Comparison and analysis of astronomical refraction correction model[J]. GNSS World of China, 2017, 42(6): 61–65. |
| [17] |
隋立芬, 宋力杰, 柴洪洲.
误差理论与测量平差基础[M]. 北京: 测绘出版社, 2010: 45-47.
SUI Lifen, SONG Lijie, CHAI Hongzhou. Error theory and foundation of surveying adjustment[M]. Beijing: Surveying and Mapping Press, 2010: 45-47. |
| [18] |
赵琳, 丁继成, 马雪飞.
卫星导航原理及应用[M]. 西安: 西北工业大学出版社, 2011: 126-127.
ZHAO Lin, DING Jicheng, MA Xuefei. Principle and application of satellite navigation[M]. Xi'an: Northwestern Polytechnical University Press, 2011: 126-127. |
| [19] |
李征航, 黄劲松.
GPS测量与数据处理[M]. 3版. 湖北: 武汉大学出版社, 2016: 182-188.
LI Zhenghang, HUANG Jinsong. GPS surveying and data processing[M]. 3rd ed. Hubei: Wuhan University Press, 2016: 182-188. |
| [20] |
李建文, 李作虎, 周巍, 等.
卫星导航中几何精度衰减因子最小值分析及应用[J]. 测绘学报, 2011, 40(S1): 85–88.
LI Jianwen, LI Zuohu, ZHOU Wei, et al. Study on the minimum of GDOP in satellite navigation and its applications[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 85–88. |
| [21] | YARLAGADDA R, ALI I, AL-DHAHIR N, et al. GPS GDOP metric[J]. IEE Proceedings:Radar, Sonar and Navigation, 2000, 147(5): 259–264. DOI:10.1049/ip-rsn:20000554 |
| [22] |
盛琥, 杨景曙, 曾芳玲.
伪距定位中的GDOP最小值[J]. 火力与指挥控制, 2009, 34(5): 22–24.
SHENG Hu, YANG Jingshu, ZENG Fangling. The minimum value of GDOP in pseudo-range positioning[J]. Fire Control & Command Control, 2009, 34(5): 22–24. DOI:10.3969/j.issn.1002-0640.2009.05.006 |
| [23] |
卜长江, 罗跃生.
矩阵论[M]. 哈尔滨: 哈尔滨工程大学出版社, 2003: 89-90.
BO Changjiang, LUO Yuesheng. Theory of matrices[M]. Harbin: Harbin Engineering University Press, 2003: 89-90. |
| [24] |
中华人民共和国国家质量监督检验检疫总局. GB/T 17943-2000大地天文测量规范[S].北京: 中国标准出版社, 2004. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. GB/T 17943-2000 Specifications for the geodetic astronomy[S]. Beijing: China Standards Publishing House, 2004. |
| [25] |
赵慧, 熊志, 王丽娜, 等.
基于恒星几何构型分布的天文定位误差建模及误差特性分析[J]. 兵工学报, 2015, 36(5): 813–822.
ZHAO Hui, XIONG Zhi, WANG Lina, et al. Modeling of celestial positioning error and analysis of error characteristics based on distribution of guide stars[J]. Acta Armamentarii, 2015, 36(5): 813–822. DOI:10.3969/j.issn.1000-1093.2015.05.008 |
| [26] |
张捍卫, 栾军, 雷伟伟.
大气折射的原理性公式[J]. 地球物理学进展, 2014, 29(2): 616–619.
ZHANG Hanwei, LUAN Jun, LEI Weiwei. A principle formula of atmospheric refraction[J]. Progress in Geophysics, 2014, 29(2): 616–619. |



