2. 常州市测绘院, 江苏 常州 213002
2. Changzhou Institute of Surveying and Mapping, Changzhou 213002, China
相比于传统地面测量,航空测量不受测区的地域限制,可以快速完成大范围区域内的测量任务,目前已经被广泛应用[1-3]。在航空测量场景下,基线距离在几公里到数百公里范围内变化,随着基线距离增加基准站与流动站各项参数之间的相关性减小,尤其是电离层参数与模糊度难以快速分离,导致传统动态相对定位的固定率下降,定位精度降低[4-6]。网络RTK(real-time kinematic, RTK)技术虽然可以通过参考网播发的改正数消除大气残余误差[7-11],但由于其需要多个基准站进行区域改正数的计算,在海上、沙漠等特殊区域应用难度较大。因此,研究单基站中长基线动态相对定位方法在航空测量领域具有重要意义。
1989年,文献[12-13]针对长基线动态相对定位问题提出了考虑大气误差的中长基线定位算法,但是该方法需要消除或估计大气参数,因而需要一定的收敛时间。1997年,文献[14]讨论了电离层延迟先验权重不同对模糊度固定的影响。文献[15-16]表明电离层等大气误差在时间上具有很强的相关性,并且提出了有效的电离层预测模型。文献[17]和[18]分别加入由参考网得到的电离层先验信息约束,实现了中长基线的单历元固定。2008年,文献[19]使用UWM-IPM模型对电离层误差进行预测,在中长基线静态实验中取得了厘米级定位精度。2017年,文献[20]分析了双差电离层延迟在空间域和时间域上的变化特性,使得BDS长基线相对定位精度达到1~2 cm。文献[21]在2010年使用非组合模型对模糊度参数施加强约束提高了静态长基线的固定率,但该方法容易受到周跳及信号失锁的影响,实际使用中仍存在风险。在中长基线相对定位中使用大气增强信息进行约束是目前普遍采用的方案,但是大气先验信息通常需要通过外部手段获取。而在航空测量场景中,机场内一般布设有基准站,飞机从机场起飞到测区,基线长从数百米变化到数百公里,具有由短到长的变化特点,利用短基线下固定的模糊度,可以推算出大气信息,大气信息通过实时建模预报可传递至长基线,等价于大气增强信息约束下的动态相对定位。
本文提出了一种适用于航空测量场景下,基线长度由短到长变化的动态相对定位方法。使用长基线机载数据分析了电离层延迟特性,讨论建模窗口长度和预测时长对电离层建模预测的影响。之后使用一组GNSS实测机载数据,使用无电离层组合模型、电离层加权模型及本文方法进行解算,比较3种方法的定位精度和模糊度固定效果。最后讨论了实际作业中不同实施条件对定位结果的影响。
1 基线短到长变化的动态相对定位方法航空测量场景下,飞机通常从基站附近出发然后进行大范围作业,基线长度具有由短到长的变化特点。在不同的基线长度下,大气误差对动态相对定位的影响也有所不同,根据距离长短可以将动态相对定位模型划分为:①小于10 km称为短基线模型;②大于10 km小于100 km称为中基线模型;③大于100 km称为长基线模型。飞机在执行测量任务时,可以充分利用基线长度的变化信息,利用短基线场景下的结果对电离层延迟精确建模,通过预报削弱电离层延迟误差对长基线相对定位模型的影响,最终获得全时段的高精度定位结果。
由原始观测值通过站星差分可以导出单颗卫星的相对定位通用模型为
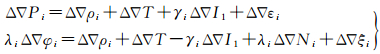 (1)
(1)
式中,△▽表示双差算子;i表示载波频率;P、$φ$表示伪距和载波相位观测值;λi表示频率i上信号的波长;γi表示第i个频率与第1个频率平方的比值;ρ表示卫星与接收机之间的距离;T表示对流层延迟;I1表示某个系统第1个频率上的电离层延迟;ε和ξ分别表示伪距和相位观测值的噪声。
当飞机与基准站之间的距离很短时,式(1)中双差对流层延迟和双差电离层延迟可以忽略不计,此时待估参数仅有位置参数和模糊度参数,方程简化为如下形式
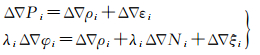 (2)
(2)
式(2)即为短基线相对定位模型,此时结合相位和伪距观测值便可以快速正确固定模糊度。随着飞机作业范围增大,基线长度逐渐增加,式(1)中的大气残余误差无法通过差分的方式消除,从而影响模糊度固定成功率,使得动态相对定位精度和可靠性不如短基线场景。其中电离层延迟与模糊度参数具有很强的相关性,是影响中/长基线动态定位精度的主要因素,为了削弱电离层延迟误差,一般采用无电离层组合方式消去电离层低阶项的影响[12](以下简称方案A),或者采用传统电离层加权模型,在非差非组合方程中把电离层延迟作为待估参数[22],将电离层参数建模为随机游走模型,采用文献[23]的方案,其初始方差根据基线长度给定(以下简称方案B),计算公式为
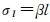 (3)
(3)
式中,l代表基线长度;β取1 mm/km。
本文提出的方法将电离层延迟作为待估参数,随机建模为白噪声。基于电离层参数的色散性质[24],利用准确的整数模糊度和相位观测值由电离层残差组合(geometry-free, GF可以计算该历元双差电离层延迟
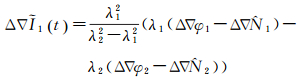 (4)
(4)
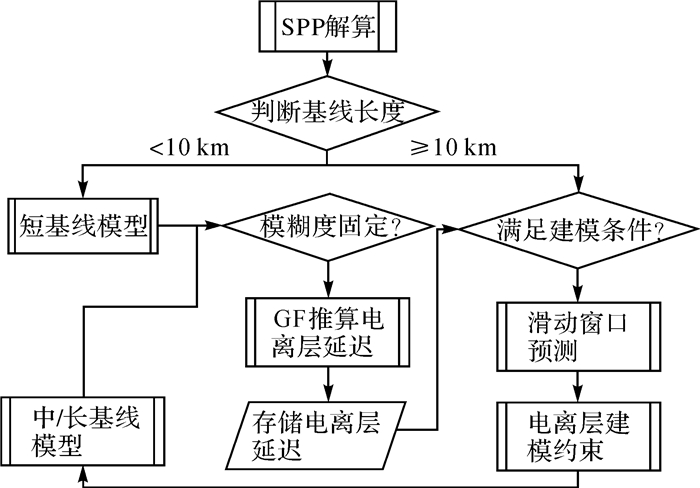
对得到的双差电离层延迟量进行滑动窗口预测,并将预报值作为虚拟观测值代入后续滤波的观测方程中,施加合适约束后使电离层参数和模糊度参数快速分离,进而成功固定整数模糊度,获得高精度定位结果(以下简称方案C),整个方法的流程如图 1所示。3种方案的相关参数设置如表 1所示。
|
| 图 1 算法流程 Fig. 1 Algorithm flowchart |
| 解算方案 | 数学模型 | 参数估计策略 | ||
| 位置参数 | 电离层延迟 | 对流层延迟 | ||
| A | 无电离层组合 | 白噪声估计 | 组合消去 | 模型改正+参数估计 |
| B | 非差非组合 | 白噪声估计 | 随机游走估计 | 模型改正+参数估计 |
| C | 非差非组合 | 白噪声估计 | 白噪声估计 | 模型改正+参数估计 |
2 电离层建模方案
通过电离层建模约束,将短基线场景下得到的高精度结果传递到后续历元是本文方法的关键,因此需要对影响电离层预报精度的因素进行细致分析,进而确定最优的电离层建模方案。使用长基线动态机载数据,数据采样率为1 Hz,采集时间约为3 h。对机载数据进行动态相对定位解算,利用固定后的模糊度按照式(4)推导出双差电离层延迟量。
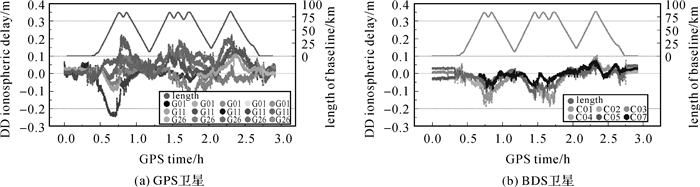
图 2显示了提取到的GPS和BDS双差电离层延迟序列和流动站与基站之间的距离变化。整体上双差电离层延迟大部分在正负1 dm的范围内缓慢变化,前后历元具有明显的相关性。在长基线场景下,电离层延迟量绝对值和基线长度有相似的变化趋势,从图中可以看出随着基线长度的增加,各个卫星的电离层延迟绝对值逐渐增大,个别GPS卫星的变化明显,其数值甚至超过2 dm。比较GPS卫星和BDS卫星的结果可以看出,BDS卫星的双差电离层延迟量更加平稳,整体变化小于2 dm,绝大部分在1 dm左右。造成这种结果的原因是由于该组数据观测到的BDS卫星大部分是GEO和IGSO卫星,而GEO和IGSO卫星的轨道高度高于MEO卫星,其运行速度较慢,历元间的相关性更强[25]。
|
| 图 2 导出的双差电离层延迟和基线长度变化 Fig. 2 Double-differenced (DD) ionospheric delay from GF combination for GPS (left) and BDS (right) |
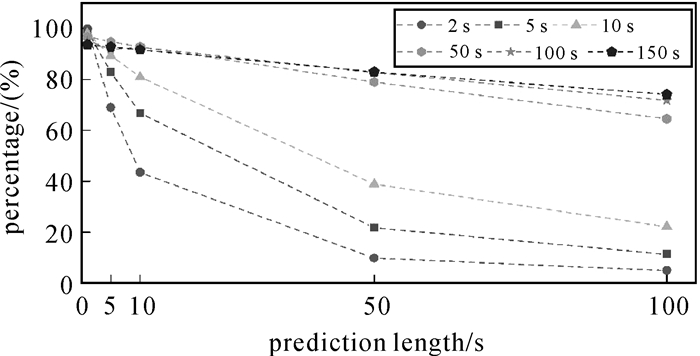
使用滑动窗口方法进行预报,建模窗口长度和预测时间是影响电离层预报精度的两个主要因素。分别以2 s、5 s、10 s、50 s、100 s、150 s不同窗口长度进行建模,再分别进行不同时长的预测,比较预报值与原始电离层延迟序列之差,统计预测误差在2 cm以内的比例,将该比例值作为预测精度指标,结果如图 3所示。
|
| 图 3 不同长度数据建模进行不同时长预测的误差序列 Fig. 3 The percentage of precise ionospheric predications with different length of predicated time by using different length of sliding window |
当预测时长小于5 s,窗口长度越小预报精度越高,但不同窗口长度的预测结果差异不大。随着预测时间增加,各组预报误差逐渐增大。进行长时间预测时,窗口长度越长预测精度越高。建模数据长度超过50 s时,在预测时长为100 s的情况下仍然有70%以上的预报值与原始值之差小于2 cm。当窗口长度大于100 s,此时随着预测时长的增加,窗口长度增大对精度的提升效果不明显。
在航空测量场景中,既要保证电离层实时预报的准确性,又要保证整个定位系统的可靠性,因此电离层建模的数据量需要根据当前历元的观测情况进行选取。当该历元观测环境良好,有多颗卫星被连续固定时可以采用10 s窗口长度的数据进行建模,电离层预报值的先验精度为2 cm。当出现信号中断或者模糊度频繁发生周跳时,采用120 s窗口长度进行建模,并根据外推时间长短放大电离层预报值的先验标准差。为了消除卫星在低高度角或复杂环境下可能出现的异常值所带来的影响,建模预报时以3倍样本数据的方差为阈值对异常值进行剔除。当剔除的数据量超过50%则认为该卫星本历元的电离层预报值不可用。
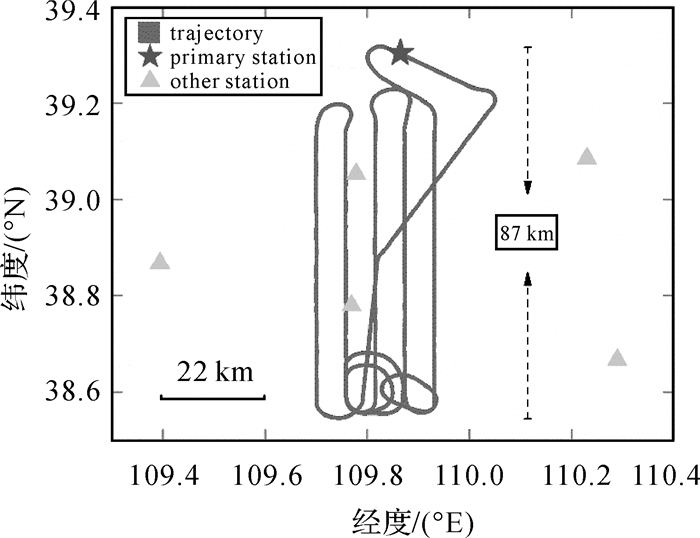
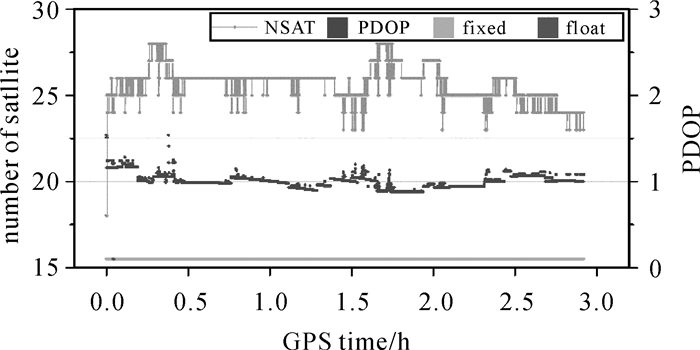
3 算法验证与结果分析采用一组实测机载数据对算法进行验证。机载数据采集于毛乌素地区,采样率为1 Hz,数据有效时长约为3 h,其中前25 min飞机与机场基准站的距离小于10 km,之后的基线长度在20~87 km范围内变化。飞机搭载GNSS多频接收机,可以接收GPS/GLONASS/BDS三系统观测数据,机场架设有一个基准站,测区内布设其他5个基准站(本文提出的方法仅以机场基站作为相对定位中的基准站),飞机轨迹如图 4所示。以商业软件IE多基站网解后处理结果作为飞机轨迹的参考真值。机载数据的可观测卫星数,PDOP值以及参考真值的模糊度固定情况如图 5所示,整体上数据的观测条件良好。本文采用多历元模糊度解算方法,利用LAMBDA方法进行模糊度固定,且固定后的模糊度不向后续历元传递,其中GLONASS卫星不参与固定。
|
| 图 4 飞机飞行轨迹 Fig. 4 Aircraft trajectory |
|
| 图 5 机载数据的观测卫星数、PDOP值及参考值的模糊度固定情况 Fig. 5 Number of observable satellites, PDOP and the status of double-differenced ambiguity for reference in the airborne experiment |
3.1 3种中/长基线动态相对定位方法比较
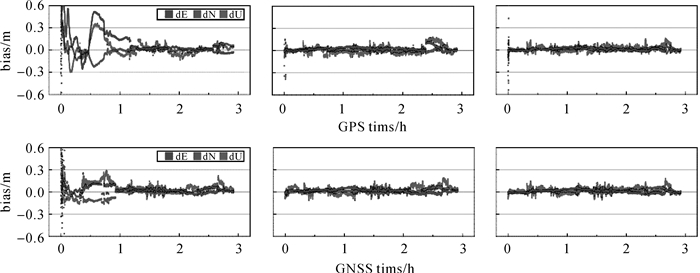
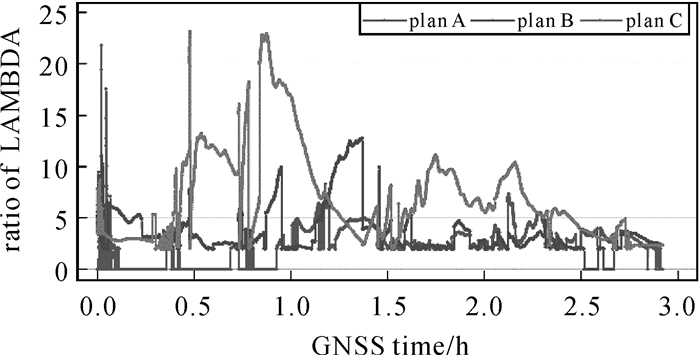
使用A、B、C 3种方案对实测数据进行解算,分别使用单独GPS数据和GPS/GLONASS/BDS多系统数据,将位置结果分别与参考真值比较,得到位置误差序列如图 6所示。图 7、图 8给出了多系统情况下3种方案解算过程中每个历元固定的卫星数目及ratio值(ratio值等于0代表本历元没有得到固定解),表 2统计了3组解算结果的位置误差均方根值(root mean square, RMS)及模糊度固定率。模糊度固定定义为某个历元固定的卫星数目大于4颗,且ratio值大于2。
|
| 图 6 多系统和单系统机载数据误差序列图(从上到下依次为:单GPS系统、GPS/GNLONASS/BDS三系统从左到右依次为:方案A、方案B、方案C) Fig. 6 Error sequence with airborne data for only-GPS (top) and multi-GNSS (bottom). left is the results of plan A, middle is results of the plan B, right is results of the plan C, respectively |

|
| 图 7 多系统3种解算方法固定的卫星数目序列图 Fig. 7 Number of ambiguity-fixed satellites with three strategies |
|
| 图 8 多系统3种解算方法ratio值序列图 Fig. 8 Ratio value with three strategies |
| 所用系统 | 解算方案 | 固定率/(%) | 位置误差/m | ||
| 东向 | 北向 | 天向 | |||
| GPS | A | 65.70 | 0.185 | 0.092 | 0.221 |
| B | 87.37 | 0.034 | 0.024 | 0.055 | |
| C | 99.85 | 0.024 | 0.024 | 0.044 | |
| GPS\GLON-ASS\BDS | A | 74.17 | 0.075 | 0.090 | 0.161 |
| B | 95.81 | 0.028 | 0.025 | 0.053 | |
| C | 99.99 | 0.021 | 0.020 | 0.040 | |
从图 6中可以看出方案A的位置误差序列存在明显的初始化过程,初始化阶段的位置精度仅在分米级,即使前25 min基线长度小于10 km, 也无法进行准确的模糊度固定。而其他两种方案在基线长度较短时由式(3)计算得到的电离层参数先验精度小于1 cm,此时的相对定位模型等价于短基线模型,因此可以快速将模糊度固定,固定率高于99%,并获得厘米级的定位精度。表 2的结果表明,仅有GPS系统数据的情况下,3种方案的固定率分别为65.70%、87.37%、99.85%,方案A在数据解算的前一个小时内处于参数初始化阶段,模糊度不能准确固定,初始化完成后也存在固定错误的情况,表明该方案的可靠性较低。方案B相比于方案A模糊度固定率和定位精度均有提高,但仍然存在模糊度固定错误的情况,固定率也不及短基线相对定位水平。而方案C的模糊度固定率接近100%,相比于其他两种方案模糊度固定率提高了52.0%和14.3%,且没有出现固定错误的情况,位置误差序列也稳定在厘米级,定位效果与短基线相对定位水平相当。在多系统情况下,3种方案的固定率相比于单GPS系统均有提高,分别为74.17%、95.81%、99.99%,方案C的固定率仍优于其他两种方案。另外结果表明仅使用单GPS系统,方案C的固定率即可以达到99%以上。
为了进一步说明本文方法对模糊度固定的贡献,以多系统解算结果为例,分别比较3种方案的固定卫星数和ratio值。结果表明方案C固定的卫星数目均在8颗以上,整个时段的固定数目比较稳定,ratio值在绝大部分历元明显高于其他两种方案,说明其模糊度固定结果更加可靠。而一旦模糊度固定正确,便可以利用相位观测值获得高精度定位结果,统计结果表明多系统情况下方案C平面和高程的位置精度可以达到3 cm和4 cm以内,位置误差随时间的变化比较平稳。单GPS系统下方案A、B的定位精度较差,而方案C的三维位置误差为(0.024, 0.024, 0.044) m,与多系统情况下的位置精度相当。相较于其他两种方案,3个方向的位置精度在单系统情况下分别改善72%、78%、75%,在多系统情况下分别改善了25%、20%、25%。以上结果表明航空测量场景下,方案C可以改善模糊度固定,定位结果优于传统长基线动态相对定位方法。
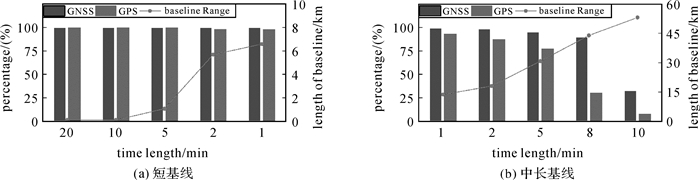
3.2 方案实施条件分析本文算法需要先依赖短基线场景获得可靠的电离层层残差估值结果,再通过电离层建模预测对中长基线场景下的解算进行约束,因此在实际使用中,必须考虑测量载体在短基线场景下的时长以及测量载体出发时的基线长度对定位结果的影响。使用同一组机载数据,分别使用GPS/GLONASS/BDS和单独GPS数据解算,设置不同的起算时间,使飞机位于短基线场景的时长逐渐减小,同时解算起点与基准站距离逐渐增加,统计整个时段的固定率,结果如图 9所示。
|
| 图 9 不同实施方案对模糊度固定率的影响 Fig. 9 The effect of different implementation schemes for the ambiguity fixing rate |
从图中可以看出飞机所处短基线场景的时长大于5 min时,全时段固定率一直保持在99%以上,且多系统固定率与单GPS的解算水平相当。当短基线数据时长继续减少时,多系统固定率仍然比较高,但是单GPS系统的结果有所下降。
随着短基线数据持续减少,初始时刻的基线长度由于飞机运动持续增加,流动站与基准站大气误差的相关性逐渐降低,此时的情形需要一定的初始化时间才能完成模糊度固定。当首历元基线长度接近20 km时,单GPS固定率已经明显下降,当起算时刻的基线长度约为40 km时,单系统的固定率低于30%。相比之下,使用多系统解算的固定率衰减速度明显变慢,首历元基线长度在40 km时,固定率仍然达到了90%左右,这说明使用多系统数据联合计算能够提高模糊度固定率,进而提高电离层预报精度。综上,该方案仅需要几分钟的短基线时长便可以实现连续高精度的定位结果,实际应用中不会增加额外的成本和时间消耗。在搭载有多系统接收机时,可以进一步放宽方案实施要求,扩大基准站的覆盖范围。
4 总结本文从航空测量场景出发,把测量载体与基准站之间的距离由近到远的实际情况作为先验信息,利用短基线模式下解得的双差整数模糊度通过GF组合导出准确的双差电离层延迟,然后对延迟量进行建模和预测并作为虚拟观测值辅助后续历元解算,最终在长基线场景下获得连续的高精度定位结果。使用长基线机载数据分析了提取到的电离层延迟量特性,并给出了带有质量控制的电离层建模方案。之后对实测中长基线机载数据的解算结果表明:与无电离层组合模型和传统电离层加权模型相比,本文提出的方法可以有效改善模糊度的固定效果,模糊度固定率在单GPS系统观测的情况下接近100%,全时段每个历元卫星固定数目和ratio值也高于传统无电离层组合和电离层加权方案,即使是在长基线情况下,仍然可以取得与短基线情形相当的模糊度解算效果。从定位精度上看,利用该方法,水平方向上的统计精度能达到2~4 cm,高程方向在5 cm以内。采用本文方法在实际使用中仅需要几分钟时长(采样率1 Hz)的短基线数据,不会额外消耗作业成本和时间,并且使用多系统GNSS接收机的情况下可以扩大测量载体起始时刻距离基准站的距离,提高了本方案的可操作性。
接下来,将会进一步研究地面测量场景下的中长基线定位方法,结合低成本惯性元器件,进一步研究复杂城市环境下的单基站动态组合导航算法。
| [1] |
张小红, 刘经南, FORSBERGR, 等.
基于精密单点定位技术的航空测量应用实践[J]. 武汉大学学报(信息科学版), 2006, 31(1): 19–22, 46.
ZHANG Xiaohong, LIU Jingnan, FORSBERG R, et al. Application of precise point positioning in airborne survey[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 19–22, 46. |
| [2] |
孙中苗, 翟振和, 肖云.
渤海湾航空重力及其在海域大地水准面精化中的应用[J]. 测绘学报, 2014, 43(11): 1101–1108.
SUN Zhongmiao, ZHAI Zhenhe, XIAO Yun. Airborne gravimetry in bo hai Bay and its role on the refining of the regional marine geoid[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1101–1108. DOI:10.13485/j.cnki.11-2089.2014.0174 |
| [3] |
宁津生, 黄谟涛, 欧阳永忠, 等.
海空重力测量技术进展[J]. 海洋测绘, 2014, 34(3): 67–72, 76.
NING Jinsheng, HUANG Motao, OUYANG Yongzhong, et al. Development of marine and airborne gravity measurement technologies[J]. Hydrographic Surveying and Charting, 2014, 34(3): 67–72, 76. DOI:10.3969/j.issn.1671-3044.2014.03.018 |
| [4] | LEICK A. GPS satellite surveying[M]. 3rd ed. Hoboken, NJ: John Wiley, 2004: 181-182. |
| [5] | ODIJK D. Weighting ionospheric corrections to improve fast GPS positioning over medium distances[C]//Proceedings of International Technical Meeting of Satellite Division of US Institute Navigation. Salt Lake City, USA: ION, 2000: 1113-1123. |
| [6] | WIELGOSZ P, KASHANI I, GREJNER-BRZEZINSKA D. Analysis of long-range network RTK during a severe ionospheric storm[J]. Journal of Geodesy, 2005, 79(9): 524–531. DOI:10.1007/s00190-005-0003-y |
| [7] | WÜBBENA G, BAGGE A, SEEBER G, et al. Reducing distance dependent errors for real-time precise DGPS applications by establishing reference station networks[C]//Proceedings of the 9th International Technical Meeting of the Satellite Division of the US Institute of Navigation. Kansas City, USA: ION, 1996: 1845-1852. |
| [8] |
高星伟, 陈锐志, 赵春梅.
网络RTK算法研究与实验[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1350–1353.
GAO Xingwei, CHEN Ruizhi, ZHAO Chunmei. A network RTK algorithm and its test[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1350–1353. |
| [9] | LI Bofeng, SHEN Yunzhong, FENG Yanming, et al. GNSS ambiguity resolution with controllable failure rate for long baseline network RTK[J]. Journal of Geodesy, 2014, 88(2): 99–112. DOI:10.1007/s00190-013-0670-z |
| [10] | RIZOS C. Network RTK research and implementation:a geodetic perspective[J]. Journal of Global Positioning Systems, 2002, 1(2): 144–150. DOI:10.5081/jgps |
| [11] | WANNINGER L. Virtual reference stations for centimeter-level kinematic positioning[C]//Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, Oregon: ION, 2002. |
| [12] | BLEWITT G. Carrier phase ambiguity resolution for the global positioning system applied to geodetic baselines up to 2000 km[J]. Journal of Geophysical Research:Solid Earth, 1989, 94(B8): 10187–10203. DOI:10.1029/JB094iB08p10187 |
| [13] | DONG Danan, BOCK Y. Global positioning system network analysis with phase ambiguity resolution applied to crustal deformation studies in California[J]. Journal of Geophysical Research:Solid Earth, 1989, 94(B4): 3949–3966. DOI:10.1029/JB094iB04p03949 |
| [14] | TEUNISSEN P J G. The geometry-free GPS ambiguity search space with a weighted ionosphere[J]. Journal of Geodesy, 1997, 71(6): 370–383. DOI:10.1007/s001900050105 |
| [15] | DAI Liwen, WANG Jinling, RIZOS C, et al. Predicting atmospheric biases for real-time ambiguity resolution in GPS/GLONASS reference station networks[J]. Journal of Geodesy, 2003, 76(11-12): 617–628. DOI:10.1007/s00190-002-0286-1 |
| [16] | CHEN H Y, RIZOS C, HAN S. An instantaneous ambiguity resolution procedure suitable for medium-scale GPS reference station networks[J]. Survey Review, 2004, 37(291): 396–410. DOI:10.1179/sre.2004.37.291.396 |
| [17] | KASHANI I, GREJNER-BRZEZINSKA D, WIELGOSZ P. Towards instantaneous network-based RTK GPS over 100 km distance[C]//Proceedings of the 60th Annual Meeting of the Institute of Navigation. Dayton, OH: ION, 2004: 679-686. |
| [18] | HU G, ABBEY D A, CASTLEDEN N, et al. An approach for instantaneous ambiguity resolution for medium-to long-range multiple reference station networks[J]. GPS Solutions, 2005, 9(1): 1–11. DOI:10.1007/s10291-004-0120-8 |
| [19] | WIELGOSZ P, KRANKOWSKI A, SIERADZKI R, et al. Application of predictive regional ionosphere model to medium range RTK positioning[J]. Acta Geophysica, 2008, 56(4): 1147–1161. DOI:10.2478/s11600-008-0059-1 |
| [20] | TU Rui, LU Cuixian, ZHANG Pengfei, et al. The study of BDS RTK algorithm based on zero-combined observations and ionosphere constraints[J]. Advances in Space Research, 2019, 63(9): 2687–2695. DOI:10.1016/j.asr.2017.07.023 |
| [21] | TAKASU T, YASUDA A. Kalman-filter-based integer ambiguity resolution strategy for long-baseline RTK with ionosphere and troposphere estimation[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR, USA: ION, 2010: 161-171. |
| [22] | TEUNISSEN P J G. An optimality property of the integer least-squares estimator[J]. Journal of Geodesy, 1999, 73(11): 587–593. DOI:10.1007/s001900050269 |
| [23] | LI Bofeng, VERHAGEN S, TEUNISSEN P J G. Robustness of GNSS integer ambiguity resolution in the presence of atmospheric biases[J]. GPS Solutions, 2014, 18(2): 283–296. DOI:10.1007/s10291-013-0329-5 |
| [24] | KLOBUCHAR J A. Ionospheric effects on GPS[M]//SPILKER J J JR, AXELRAD P, PARKINSON B W, et al. Global Positioning System: Theory and Applications. Washington, DC: The American Institute of Aeronautics and Astronautics, 1996: 485-515. |
| [25] | YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system[J]. Science China Earth Sciences, 2014, 57(1): 144–152. DOI:10.1007/s11430-013-4769-0 |


