2. 天津市地理空间信息技术工程中心, 天津 300387
2. Tianjin Engineering Center for Geospatial Information Technology, Tianjin 300387, China
电磁波在穿过地球大气层时,由于受大气折射影响其传播路径会发生延迟。其中延迟的电离层部分可由双频技术基本消除,而中性大气部分则成为了无线电空间大地测量技术的主要误差源。由于对流层占中性大气的主要部分并包含绝大部分的水汽,故中性大气延迟又被称为对流层延迟。研究高精度的对流层延迟估计方法对于提高空间大地测量技术的精度具有重要的意义。
目前常用的对流层延迟估计方法主要有3类,一是模型改正法,该方法主要通过构建对流层天顶延迟模型及投影函数,在计算得到对流层天顶延迟的基础上,将其投影到倾斜方向从而获得整个传播路径上的对流层延迟。此类模型主要有基于实测气象参数的Hopfiled、Saastamoinen等模型[1-2],基于标准大气模型参数的UNB系列、EGNOS等模型以及基于数值再分析资料的TropGrid1-2、GPT1-2、GPT2w、IGGtrop1-2等系列模型[3-13]。然而由于水汽变化的复杂与剧烈,湿延迟难以精确估计,模型的估计精度较低,目前标称精度最高的GPT2w也仅为3.6 cm。二是直接校准法,该方法是直接利用水汽辐射计或探空仪获取湿延迟,而干延迟计算仍采用模型估计法。比之纯模型估计法,该方法具有更高的精度,但由于仪器设备昂贵,时空分辨率低,易受气候条件影响难以得到广泛应用。三是参数估计法,它是在GNSS数据处理过程中,将对流层延迟作为待估参数,利用方程直接求解。该方法精度最高,可达毫米级,但受限于GNSS观测站的分布,无法获得任意位置的对流层延迟估计,尤其是在海洋区域。而随着近十几年大气数值模式的成熟发展,出现了一种基于大气数值模型获取对流层延迟的新方法,该方法获得的对流层延迟具有高时空分辨率、高精度的特点,是对上述3种传统方法的有效补充。
国际上,早在2001年文献[14]对利用HIRLAM大气数值模式获取的对流层天顶延迟进行了精度评估,结果表明其精度可达1.7 cm。之后,众多国外学者开展了针对不同大气数值模式获取对流层天顶延迟方法及其精度的评价研究,但由于研究区域的局限性,不同学者间获得的精度有一定的差异(1.2~3.3 cm)[15-20]。而在国内目前尚处于初步研究阶段,多侧重于利用全球数值模式的再分析资料计算ZTD[21-22],其获取的ZTD时空分辨率较低(多为6 h,1°×1°),而对于如何利用大气数值模式获取高时空分辨率ZTD的方法研究则尚未见诸报道。本文就如何利用中小尺度大气数值模式WRF(weather research and forecasting model)计算ZTD展开研究,提出了一种融合WRF模式的对流层天顶延迟计算方法,并与GPT2w和UNB3m等模型进行了比较。验证结果表明,该方法获得的ZTD不仅时空分辨率高,精度更是可达9.3 mm,相对于GPT2w和UNB3m模型的34.6 mm和49.6 mm,精度分别提高了约3.5倍和5倍,可满足GNSS、VLBI、SLR等空间大地测量技术的高精度对流层延迟改正需求。
1 WRF模式及其数据结构 1.1 WRF模式介绍WRF模式是由美国国家大气研究中心(National Center for Atmospheric Research, NCAR)等多个组织部门联合研发的下一代中尺度数值预报模式(该模式可在http://www2.mmm.ucar.edu/wrf/users/注册后免费获取)。WRF模式具有良好的动力框架,丰富的各种参数化方案,先进的数据同化系统和强大的嵌套能力。其水平格网精度可至米到几公里,垂直层数和时间输出间隔均可按需设置,根据初始边界条件的不同既可用于真实大气模拟,也能进行气象预报。WRF模式的输出参数有140多项,其中包含了与大气折射率密切相关的气压(P)、温度(T)、以及水汽混合比(QVAPOR),将其用于对流层延迟计算,可有效弥补现有方法在时空分辨率及预报精度上的不足。
初始场数据是WRF模式运行的必备条件,本文主要选择由美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)提供的FNL和GFS两类数据作为初始场边界条件(以上两类数据的获取地址为:https://rda.ucar.edu/datasets/)。其中FNL为再分析资料(其时空分辨率为6 h、1°×1°)。它是将卫星气象资料、探空资料以及地面实测气象资料等各类资料同化后的数据,因此具有一定的时延性,无法实时获取。GFS为全球预报场资料(其时空分辨率为3 h、1°×1°),每6 h更新一次,最长预报时间可达384 h。
1.2 数据结构分析WRF模式的输出数据(WRFout)是一个三维空间矩阵,在垂直方向上采用σ坐标系,其定义如下
 (1)
(1)
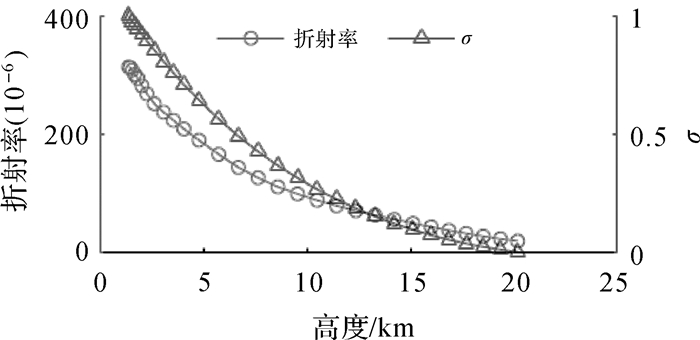
式中,ptop为顶层气压;ps为地表气压;p为σ值所对应层的气压,σ值取为[0, 1],随着高度的增加其值逐渐变小。需要说明的是各层间距不同,层距随着高度的增加而增大,使得σ值与大气折射率的分布较为相似,如图 1所示,这在一定程度上减少了直接采用WRF输出层计算ZTD所带来的积分误差。在水平方向采用的网格是Arakawa C网格,以格点交错的方式表示气象数据,在此本文将WRF输入参数所设行列参数值表示的点称为网格点,而WRFout数据中行列值表示的点称为计算点。如图 2所示,i、j、k分别表示行列层值,其中计算点则位于相邻8个网格点所组成的长方体中心。因此在提取各层相关气象参数计算折射率时,获得的折射率为计算层折射率,而各计算层的高度则为与之相邻两网格层高度之差,这对于后续正确采用直接积分法计算ZTD尤为重要。
|
| 图 1 σ值与折射率的垂直廓线 Fig. 1 The vertical profile of σ and refractive index |

|
| 图 2 WRFout数据结构 Fig. 2 Data structure of WRFout |
2 融合WRF模式的ZTD计算方法 2.1 算法参数设置
由上述WRFout数据的结构分析可知,WRFout数据是以某一参考坐标为中心,具有时间序列的三维气象场网格。为了避免因气象场格点与站点不重合所带来的插值误差,选择站点坐标作为中心参考坐标。同时顾及算法的时效性,采用单层模式,在空间上设置网格宽度为10×10 km,网格数为30×30水平范围,垂直层为30层,以1 h为输出时间分辨率,选择模式默认的参数化方案进行逐天解算。
2.2 高度改正与数据插值由于IGS提供的站点坐标的高度为大地高,而模式输出的高度为位势高度,为了使两者高度相统一,本文基于1′×1′的EGM2008重力场模型,将IGS站点的大地高改正到位势高。同时,由于WRF模式在进行地形插值时,易受原始地形精度及插值误差的影响,WRF模拟的位势高度与实际站点位势高度往往不一致,还需要将在WRF位势高度下的气象数据,插值到IGS站点高度上。对于水汽气象参数采用线性插值,温度采用温度递减率-6.5 K/km进行修正,气压修正则采用压高公式
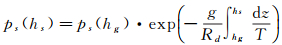 (2)
(2)
式中,hs、hg分别为站点与格点高度;ps(hs)、ps(hg)分别表示站点与格点高度上的表面气压;Rd=287.054Jkg-1K-1为干气气体常数;g为重力参数,其计算公式如下
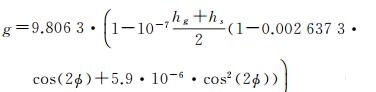 (3)
(3)
式中,ϕ为站点纬度。
2.3 ZTD计算ZTD可分为干延迟ZHD与湿延迟ZWD两部分。由于模拟气象数据廓线高度为20 km,而中性大气的高度一般为60 km,因此需要对ZHD进行分层计算,在20 km以下部分采用直接积分法计算干延迟值,其具体公式如下
 (4)
(4)
式中,ZHDunder表示20 km以下部分干延迟;k为最大层数;Δz为相邻网格层的高度差;Nd, i为第i计算层干折射率,根据Rǖeger等给出的最佳平均系数模型[23],其表达式为
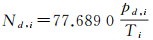 (5)
(5)
对于20 km以上部干延迟分则直接采用Saastamoinen模型进行计算,具体公式如下
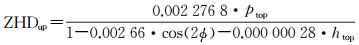 (6)
(6)
式中,ptop、htop为顶层大气压和高度;ϕ为站点纬度。
由于水汽大部分处于大气层16 km以下,因此湿延迟可直接积分得到
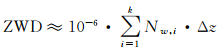 (7)
(7)
式中,ZWD表示湿延迟;k为最大层数;Δz为相邻网格层的高度差;Nw, i为第i计算层湿折射率,表达式为
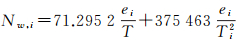 (8)
(8)
综上所述,天顶总延迟则可由下式计算得到
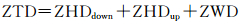 (9)
(9)
由于WRF模式的运行环境为Linux系统,因此本文在Linux环境下,采用C语言及bash脚本实现了对流层天顶延迟估计算法,其中bash主要负责WRF模式的参数设置与命令运行。算法的输入参数主要包括站点坐标、格网宽度及初始边界条件等。首先依据输入参数生成bash脚本代码并执行,由WRF模式模拟得到三维气象场数据。然后进行高程异常纠正与气象参数插值。最后采用直接积分与模型改正相结合的方式,分别计算ZHD与ZWD,输出总的天顶延迟值。根据初始边界条件的不同,本算法计算的总延迟值可分为ZTD再分析值和ZTD预报值,具体流程可见图 3。

|
| 图 3 本文算法的实现流程 Fig. 3 The flow chart of the algorithm |
3 算法有效性检验 3.1 算法时间分辨率分析
为了了解本文算法小时级分辨率的可靠性,采用日内异常值(日内异常值=每小时值-日平均值)对其展开分析。取全球不同纬度的3个IGS站点,BJFS[39.6°N,115.9°E],MAL2[-3.0°N,40.2°E],MOBS[-37.8°N,145.0°E],分别计算本文算法ZTD与IGS ZTD的日内异常值,从而获得各站全年的异常值分布(可见图 4),并统计得到各站两类异常值的相关性(可见表 1)。从图 4及表 1可以看到,本文算法ZTD与IGS ZTD异常值的全年分布整体较为相似,在BJFS与MOBS站,二者极值均出现在夏半年且在时间分布上较为一致,整体相关性分别达到了78.9%和87.4%。而在Mal2站二者极值全年均匀分布,一致性比之上述两站较低,相关性为65.8%,这主要是由于Mal2站地处赤道附近季节变化不明显,同时长年水汽充沛且变化剧烈导致湿延迟难以精确估计。总体上本文算法ZTD值不仅体现了日内ZTD变化趋势,且与IGS ZTD内日异常值具有较高的相似性,这表明了本文算法的小时级ZTD分辨率是真实可靠的。
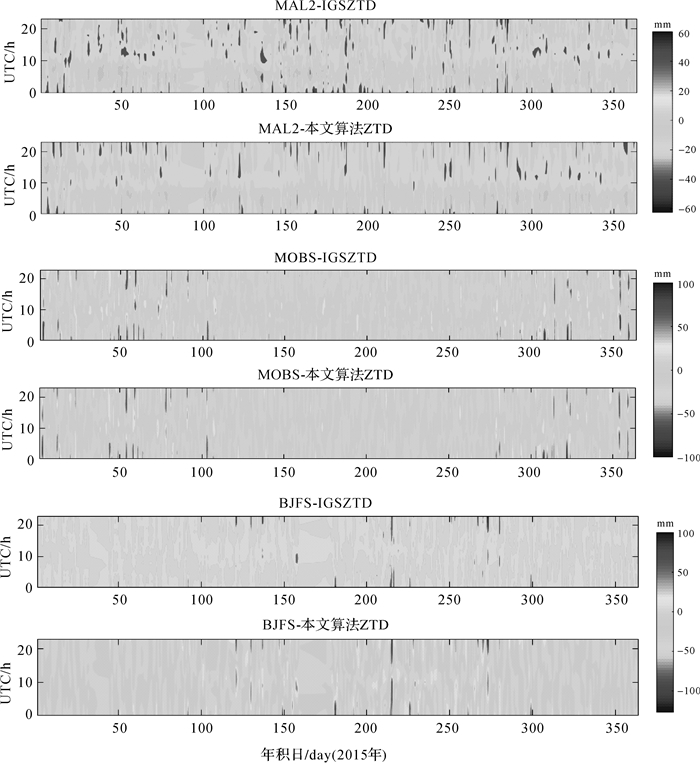
|
| 图 4 BJFS、MAL2、MOBS 3站的全年异常值分布 Fig. 4 Annual distribution of daily abnormal values at BJFS, MAL2 and MOBS |
| 台站 | 相关性/(%) |
| BJFS | 78.9 |
| MAL2 | 65.8 |
| MOBS | 87.4 |
3.2 算法精度评价
本文算法估算的ZTD分为再分析值和预报值,需要分别对两者精度进行验证。为了检验再分析值精度,选择2015年每站数据量超过180 d共292个IGS站的ZTD数据作为参考值,统计分析了ZTD再分析值的偏差bias与均方根误差RMS。图 5描述了本文算法平均bias与RMS值在292个IGS站的分布情况。从图 5中可以看到
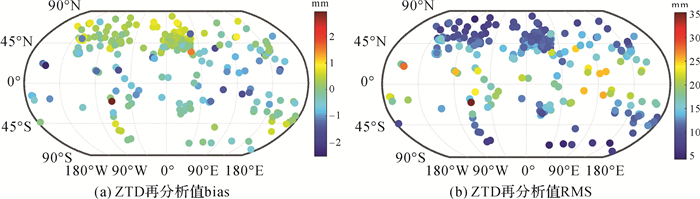
|
| 图 5 2015年292个站点上本文算法的bias和RMS分布 Fig. 5 Distribution of bias and RMS on 292 sites in 2015 |
本文算法具有以下特征:本文算法ZTD与IGS ZTD的符合程度很高,平均bias为-1.2 mm,平均RMS为13.6 mm;偏差值多集中在-10~10 mm之间,在纬度-45°~45°之间多为负偏,其他区域多为正偏;偏差值绝对值与RMS值的全球分布情况类似,均以赤道为中心向两极递减。这说明在中低纬地区本文算法ZTD估计整体偏低,这可能是由于该地区主要为热带及温带气候,气象条件更为复杂,而WRF模型的不同参数化方案对区域气候特征较为敏感,但本文针对全球区域统一采用了默认的参数化方案,并未考虑区域气候的差异性,因此对于局地区域的ZTD估算,应选择与之相适应的参数化方案可望进一步提高本算法的改正精度。
针对本文算法中存在的个别异常值,如图 5中标示出的IQQE与MKEA两个站,二者的bias、RMS分别为29.3 mm、35.2 mm和-25.2 mm、27.6 mm。首先分析两站的区域地形特征发现两站均处于地形复杂区,高差最大可达4000多米,这使得WRF模型在内插地形高度时存在较大误差,两站的插值高度与实际高度分别相差370 m和750 m。而地形数据是影响WRF模拟精度的因素之一,这种较大的地形误差势必会直接影响模拟精度。为此,本文对WRF模型的地形插值模块进行了修正,直接读取SRTM 30 m DEM数据进行数值模拟。表 2为MKEA与IQQE站地形修正前后估算ZTD精度的对比。从表中可以看到,经过修正后两站的ZTD估计精度提高近20%。但两站仍存在一定的整体偏差,考虑到初始场数据质量是影响WRF模拟精度主要因素,进一步分析了邻近两个站点的FNL格点数据,通过与测站附近探空资料或地面实测资料对比,可以发现气压、温度及水汽压均存在明显的偏差,且直接由FNL格点数据计算的ZTD与IGS ZTD同样存在较大的偏差,这表明较大的bias主要源自低质量的初始场数据。可见,对异常区域的的初始场数据进行资料同化可进一步提高算法的改正精度。
| 站名 | 地形改正前/mm | 地形改正后/mm | 精度提高率/(%) | |||||
| RMS | bias | RMS | bias | RMS | bias | |||
| MKEA | 27.6 | -25.2 | 22.3 | -18.5 | 19 | 27 | ||
| IQQE | 35.2 | 29.3 | 27.9 | 20.4 | 21 | 30 | ||
为了进一步验证本文算法的可靠性,将其与GPT2w和UNB3m模型进行对比分析。由于以上两种模型的时间分辨率仅为天,而本文算法为小时,为了统一时间分辨率,取日平均值进行比较。同样以2015年292个IGS站ZTD数据作为参考值,分别统计本文算法、GPT2w以及UNB3m模型的bias、RMS及相关系数,统计结果可见表 3及图 6。
| 方法 | 平均RMS/mm | 平均bias/mm | 平均相关性/(%) |
| 本文算法 | 9.3[2.929.4] | -1.2[-25.129.3] | 98.6[81.899.8] |
| GPT2w | 34.6[18.566.5] | -2.2[-25.423.9] | 66.4[19.090.1] |
| UNB3m | 49.6[20.7120.7] | 9.7[-46.7114.7] | 58.4[088.8] |
| 方括号内表示对应值的分布范围 | |||

|
| 图 6 3种ZTD计算方法的RMS与相关系数分布 Fig. 6 RMS and correlation coefficient distribution of three methods |
表 3显示了本文算法的全球改正精度为亚厘米级,平均bias为-1.2 mm,RMS为9.3 mm,相关系数为98.6%;本文算法的平均bias绝对值均小于GPT2w和UNB3m模型,且相关性均大于GPT2w和UNB3m模型;本文算法的平均RMS比之GPT2w的34.6 mm以及UNB3m的49.6 mm精度分别提高了约3.5倍和5倍;同时相比于小时级ZTD,两者RMS仅相差4.3 mm,这也进一步证实了本文算法计算小时级ZTD值的可靠性。图 6给出了本文算法、GPT2w和UNB3m 3个改正方法的RMS和相关系数的泰勒图。图上显示本文算法的RMS多集中在0~20 mm之间,相关系数在95%~100%之间(可见图 6(a)),其RMS和相关系数的集中度均高于GPT2w和UNB3m模型;UNB3m模型出现了较多的零相关甚至个别负相关的站点(可见图 6(c)),且这些站点多集中在纬度-15°~15°之间,这主要是由于UNB3m模型的气象参数在南北纬小于15°地区为常量,未考虑ZTD的季节变化;而GPT2w模型采用网格化方式对气象参数进行建模,考虑了气象参数的年和半年变化特征,时空分辨率比UNB3m模型有所提升,但无法表达气象参数在更小时间尺度上的变化特征,导致其相关性分布较为离散处于19.0%~90.1%之间(可见图 6(b))。通过以上3项指标的比较可以看到本文算法比GPT2w和UNB3m模型在精度及时空分辨率上均具有明显的优势。
为了更好地描述本算法的误差分布规律,分别按照纬度与高度统计了本算法、GPT2w和UNB3m模型的RMS。图 7显示了3类RMS在纬度方向上的分布情况,从整体看在绝大多数站点上本文算法的RMS值均低于GPT2w和UNB3m模型且改正精度最为稳定;在趋势上本文算法与GPT2w的分布趋势较为一致,呈现以赤道为中心南北对称的特征;UNB3m模型在南半球高纬度地区模拟精度明显低于北半球,这主要是由于球对性假设所导致的,这同文献[24]、文献[25]的结果类似。图 8和表 4是3类RMS值随高程的统计结果,从上述图表中可以看到GPT2w与UNB3m随着高度的增加精度逐渐提高;而本文算法在高度低于2000 m区间精度较为稳定,但在高于2000 m区间随着高度的增加精度呈现出降低的趋势,这也再次说明了在地形复杂区域必须考虑WRF地形插值误差对改正精度的影响。
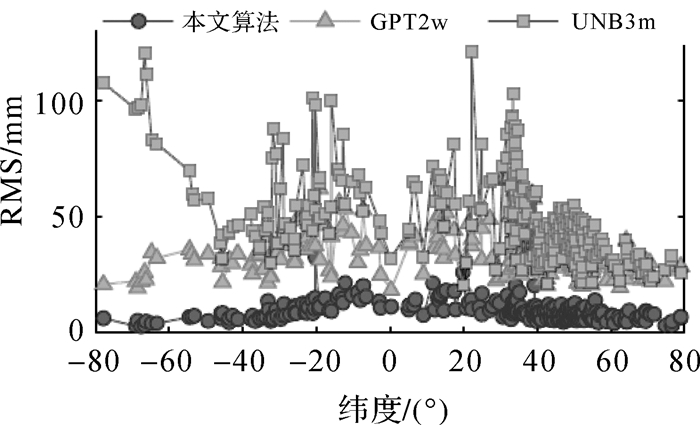
|
| 图 7 3种计算方法精度随纬度的变化情况 Fig. 7 RMS of three methods with respect to latitude variation |
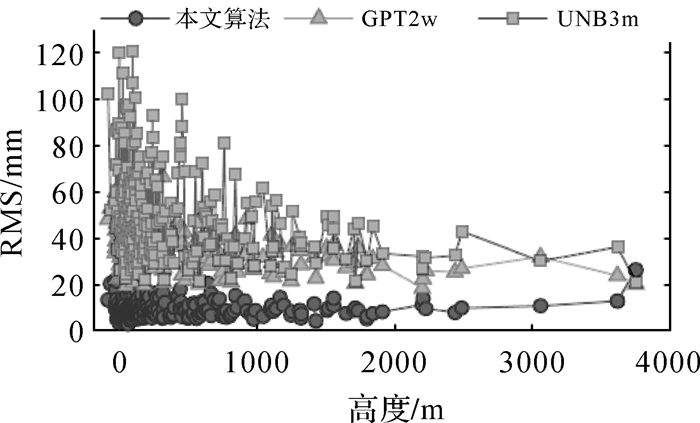
|
| 图 8 3种计算方法精度随高度的变化情况 Fig. 8 RMS of three methods with respect to height variation |
| 高度/m | 站数 | 本文算法 | GPT2w | UNB3m |
| < 500 | 217 | 9.2 | 36.0 | 52.6 |
| 500~1000 | 39 | 9.3 | 31.8 | 43.6 |
| 1000~1500 | 15 | 8.7 | 30.8 | 40.1 |
| 1500~2000 | 13 | 9.0 | 29.9 | 39.0 |
| >2000 | 8 | 12.8 | 24.4 | 31.7 |
对于本文算法的预报精度验证,选择了349个IGS站2018年第289~292天(96 h)的ZTD数据作为参考值,统计分析了ZTD预报值的偏差bias与均方根误差RMS。图 9显示了本文算法逐小时bias与RMS分布情况,本文算法平均bias为-14.5 mm,平均RMS为25.8 mm;RMS随预报长度的增加呈现阶梯式增长,其增长过程大致分为0~30、31~76及77~96 3个时段,各时段平均RMS分别为22 mm、26.2 mm及30.4 mm,整体变化范围为18.5~33.1 mm。这说明本文算法预报值虽整体偏低但仍具有较高的精度,在30 h的预报长度内,比GPT2w和UNB3m模型的全年日均精度分别高出12.6 mm和27.6 mm。
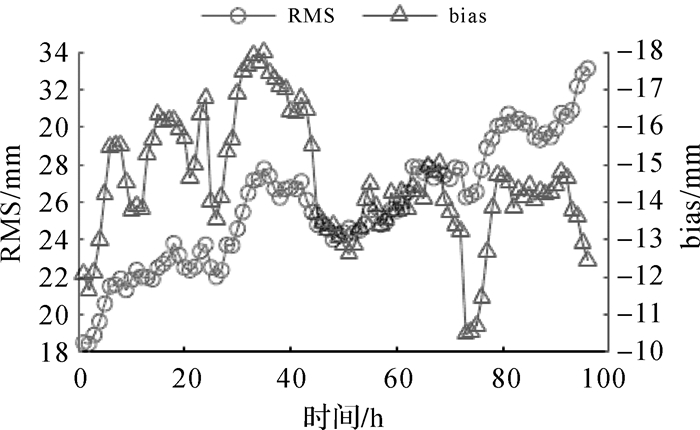
|
| 图 9 本文算法96 h内预报值的精度变化 Fig. 9 Accuracy variation of the algorithm in 96-hour forecast period |
4 结论
中尺度大气数值模式-WRF模式以其完全可压缩、非静力学的特点,可有效地模拟中小尺度下各大气参数的时空分布特征。本文在剖析WRF模拟机理的基础上,提出了一种融合WRF模式的对流层天顶延迟算法。该算法与传统的模型估计法相比,不仅在精度有着明显的提高,在时空分辨率上也是更加精细和稳定;所需数据源均可公开免费获取,比之直接校准法所需的昂贵仪器,更易推广应用;虽然在精度上仍不如参数估计法,但其不受测站限制,可计算全球任意地区高精度、高时空分辨率的对流层天顶延迟值,可弥补参数估计法在海洋区域难以应用的不足。同时本算法输出的三维气象场数据可直接用于计算对流层延迟的水平梯度,更可采用射线追踪方法获得可靠的对流层倾斜延迟,比现有方法具有更多的实际应用价值。本文算法既可用于空间测量技术的大气延迟后处理改正及相关科学研究,也可用于实时卫星导航定位,是对现有对流层延迟改正技术的有效补充。然而也看到,本文算法也存在一定的不足,在复杂气候条件和高海拔地区,计算的ZTD存在一定的整体性偏差,需要从优化参数化方案、下垫面数据修正及初始场资料同化等方面展开进一步研究以提高改正精度,并将其应用到GNSS、VLBI及InSAR等空间大地测量等领域。
| [1] | HOPFIELD H S. Two-quartic tropospheric refractivity profile for correcting satellite data[J]. Journal of Geophysical Research, 1969, 74(18): 4487–4499. DOI:10.1029/JC074i018p04487 |
| [2] | SAASTAMOINEN J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites[M]. HENRIKSEN S W, MANCINI A, CHOVITZ B H. The Use of Artificial Satellites for Geodesy. Washington, DC: American Geophysical Union, 1972: 247-251. |
| [3] | LEANDRO R F, SANTOS M C, LANGLEY R B. UNB neutral atmosphere models: development and performance[C]//Proceedings of the National Technical Meeting of the Institute of Navigation. Monterey, California: Institute of Navigation, 2006: 564-573. |
| [4] | PENNA N, DODSON A, WU Chen. Assessment of EGNOS tropospheric correction model[J]. The Journal of Navigation, 2001, 54(1): 37–55. DOI:10.1017/S0373463300001107 |
| [5] | KRUEGER E, SCHVLER T, ARBESSER-RASTBURG B. The standard tropospheric correction model for the European satellite navigation system Galileo[C]//Proceedings of the XXVⅢth General Assembly of the International Union of Radio Science. New Delhi, India: URSI, 2005. |
| [6] | SCHÜVLER T. The TropGrid2 standard tropospheric correction model[J]. GPS Solutions, 2014, 18(1): 123–131. DOI:10.1007/s10291-013-0316-x |
| [7] | BOEHM J, HEINKELMANN R, SCHUH H. Short Note:a global model of pressure and temperature for geodetic applications[J]. Journal of Geodesy, 2007, 81(10): 679–683. DOI:10.1007/s00190-007-0135-3 |
| [8] | LAGLER K, SCHINDELEGGER M, BÖHM J, et al. GPT2:empirical slant delay model for radio space geodetic techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069–1073. DOI:10.1002/grl.50288 |
| [9] | BÖHM J, MÖLLER G, SCHINDELEGGER M, et al. Development of an improved empirical model for slant delays in the troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433–441. DOI:10.1007/s10291-014-0403-7 |
| [10] |
姚宜斌, 张顺, 孔建.
GNSS空间环境学研究进展和展望[J]. 测绘学报, 2017, 46(10): 1408–1420.
YAO Yibin, ZHANG Shun, KONG Jian. Research progress and prospect of GNSS space environment science[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1408–1420. DOI:10.11947/j.AGCS.2017.20170333 |
| [11] | SCHVLER T. The TropGrid2 standard tropospheric correction model[J]. GPS Solutions, 2014, 18(1): 123–131. DOI:10.1007/s10291-013-0316-x |
| [12] | LI Wei, YUAN Yunbin, OU Jikun, et al. New versions of the BDS/GNSS zenith tropospheric delay model IGGtrop[J]. Journal of Geodesy, 2015, 89(1): 73–80. DOI:10.1007/s00190-014-0761-5 |
| [13] |
姚宜斌, 胡羽丰, 余琛.
一种改进的全球对流层天顶延迟模型[J]. 测绘学报, 2015, 44(3): 242–249.
YAO Yibin, HU Yufeng, YU Chen. An improved global zenith tropospheric delay model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 242–249. DOI:10.11947/j.AGCS.2015.20140089 |
| [14] | VEDEL H, MOGENSEN K S, HUANG X Y. Calculation of zenith delays from meteorological data comparison of NWP model, radiosonde and GPS delays[J]. Physics and Chemistry of the Earth, Part A:Solid Earth and Geodesy, 2001, 26(6-8): 497–502. DOI:10.1016/S1464-1895(01)00091-6 |
| [15] | BEHREND D, HAAS R, PINO D, et al. MM5 derived ZWDs compared to observational results from VLBI, GPS and WVR[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2002, 27(4-5): 301–308. DOI:10.1016/S1474-7065(02)00004-9 |
| [16] | SNAJDROVA K, BOEHM J, WILLIS P, et al. Multi-technique comparison of tropospheric zenith delays derived during the CONT02 campaign[J]. Journal of Geodesy, 2006, 79(10-11): 613–623. DOI:10.1007/s00190-005-0010-z |
| [17] | TEKE K, BÖHM J, NILSSON T, et al. Multi-technique comparison of troposphere zenith delays and gradients during CONT08[J]. Journal of Geodesy, 2011, 85(7): 395–413. DOI:10.1007/s00190-010-0434-y |
| [18] | TEKE K, NILSSON T, BÖHM J, et al. Troposphere delays from space geodetic techniques, water vapor radiometers, and numerical weather models over a series of continuous VLBI campaigns[J]. Journal of Geodesy, 2013, 87(10-12): 981–1001. DOI:10.1007/s00190-013-0662-z |
| [19] | WILGAN K, ROHM W, BOSY J. Multi-observation meteorological and GNSS data comparison with Numerical Weather Prediction model[J]. Atmospheric Research, 2015, 156: 29–42. DOI:10.1016/j.atmosres.2014.12.011 |
| [20] | WILGAN K, HURTER F, GEIGER A, et al. Tropospheric refractivity and zenith path delays from least-squares collocation of meteorological and GNSS data[J]. Journal of Geodesy, 2017, 91(2): 117–134. DOI:10.1007/s00190-016-0942-5 |
| [21] | CHEN Qinming, SONG Shuli, HEISE S, et al. Assessment of ZTD derived from ECMWF/NCEP data with GPS ZTD over China[J]. GPS Solutions, 2011, 15(4): 415–425. DOI:10.1007/s10291-010-0200-x |
| [22] |
黄瑾芳, 楼益栋, 张卫星, 等.
再分析资料计算中国区域对流层延迟精度[J]. 测绘科学, 2018, 43(5): 13–17.
HUANG Jinfang, LOU Yidong, ZHANG Weixing, et al. The assessment of ZTD calculated from reanalysis over China[J]. Science of Surveying and Mapping, 2018, 43(5): 13–17. |
| [23] | RÜEGER J M. Refractive index formulae for radio waves[J]. Washington, DC, USA:FIG XXⅡ International Congress, 2002. |
| [24] | LI Wei, YUAN Yunbin, OU Jikun, et al. A new global zenith tropospheric delay model IGGtrop for GNSS applications[J]. Chinese Science Bulletin, 2012, 57(17): 2132–2139. DOI:10.1007/s11434-012-5010-9 |
| [25] |
姚宜斌, 张豹, 严凤, 等.
两种精化的对流层延迟改正模型[J]. 地球物理学报, 2015, 58(5): 1492–1501.
YAO Yibin, ZHANG Bao, YAN Feng, et al. Two new sophisticated models for tropospheric delay corrections[J]. Chinese Journal of Geophysics, 2015, 58(5): 1492–1501. |


