2. 中国科学院大学, 北京 100049;
3. 南京邮电大学, 江苏 南京 210023
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Nanjing University of Posts and Telecommunications, Nanjing 210023, China
地球是一个高度动态的行星,在多个时间及空间尺度上表现出复杂的运动状态。其中,板块运动及板内形变、固体潮和冰川均衡调整是典型的固体地球宏观尺度运动现象,研究它们对于认识地球演化历史具有重要意义。当前,地球动力学理论和大地测量观测是研究固体地球宏观运动现象动力学机制及其演化过程的主要手段[1]。利用星载合成孔径雷达干涉测量(synthetic aperture radar interferometry, InSAR)的干涉相位信息可精确测量地表地形及其微小变化,使获取大范围、高精度地表形变图像成为可能[2-3],但是受限于卫星观测范围,一次只能同时覆盖百公里尺度的地区,难以对上千千米尺度的固体地球运动进行连续、稳定观测。
将月球作为一个对地观测平台, 在月球上布设合成孔径雷达(synthetic aperture radar, SAR)对地球进行大范围、持续、长期观测是一种全新的设想,月基合成孔径雷达系统与机载、星载平台等原理一致,都是通过雷达与目标相对运动合成孔径,虽然其系统设计更加复杂,但相比现有机载、星载对地观测平台而言,优势十分显著,包括:更大测绘幅宽、长期稳定的平台、灵活的观测周期、更丰富的观测模式以及可实现在轨维护和更新等[4-8],另外,月基SAR主要靠地球运动合成孔径,理论上具备更长合成孔径积分时间,因此,可望获取与星载合成孔径雷达相同甚至更高空间分辨率的SAR图像[9-10]。相比于星载SAR系统,月基SAR系统的设计与实施也存在挑战,受月球天平动等影响,月基SAR在空间的姿态不断变化,在月基SAR成像时,也需不断调整月基SAR在空间的指向。综合分析月基SAR系统特征,文献[11]考虑了月基SAR超长传输距离、月球半径、天体章动和平动因素带来的影响,给出了完整月基SAR回波仿真及成像结果,验证了月基SAR的可行性;文献[12]考虑了地-月同步运动,提出了一种更精确的月基SAR信号模型,并进行信号仿真,进一步验证月基SAR的可行性。月基SAR成像几何及特征是月基InSAR观测几何、干涉参数计算的基础,月基SAR成像技术的发展,为月基InSAR的发展及未来实现长期、高精度、超大范围测量固体地球形变参数提供了可能。
月基SAR重复轨道干涉测量是月基InSAR观测中的一种观测模式。目前,国内外只有为数不多的月基重复轨道干涉测量研究。文献[13]通过地-月相对运动特征的研究,表明月基SAR有望实现间隔一天的重复轨道干涉测量;文献[9]从简化的月基SAR观测几何出发,通过月球高度角变化引起的空间几何去相干,初步计算并分析月基重轨InSAR的时间基线,结果表明月基SAR在部分观测时间有望实现时间基线为1 d,1恒星月及其整数倍的重复轨道干涉测量,并且,随着月球高度角的减小,以及波长增加,越有利于实现重轨干涉测量,但文中并未给出月基重轨InSAR空间基线的计算方法;文献[14-15]利用相邻航迹对应的地心张角差计算垂直基线,通过极限基线约束,对隔日重轨干涉测量的观测范围进行分析,结果表明:当雷达波长越长,月球赤纬越大时,越有利于月基重轨InSAR的实施。以上研究主要通过空间几何去相干分析,表明月基SAR具有重复轨道干涉测量能力,但缺少对月基重轨InSAR时-空基线特征的深入研究。主要表现为:①月基SAR重访观测时需要考虑地-月同步运动,因此,月基SAR的重返时间并不为一整天,而是略大于一天;②重访观测时月球地心张角差不能完全代替两次观测的入射角差;③月基SAR位于月球表面,不能用月心位置代替雷达位置。
时-空基线是月基重轨InSAR能否实现大范围、高精度的对地观测的两个关键参数。月基重轨InSAR时-空基线的计算需要精确的月球轨道位置及姿态信息,须建立明确的坐标转换关系。本文在前人研究的基础上,通过分析地-月相对运动特征,建立月基重轨InSAR观测几何,改进了时-空基线计算方法,并利用DE430月球星历数据模拟分析月基重轨InSAR时-空基线的分布特征,为今后月基InSAR观测系统的参数设计提供参考。
1 月基重轨InSAR观测几何 1.1 地-月相对运动月基重轨InSAR是由地-月之间的相对运动实现对地观测,因此地-月间相对运动特征是研究月基重轨InSAR测量的基础。月球相对地球的运动特征可由月球星下点(地-月质心连线与地球椭球面的交点)轨迹描述。本文采用NASA/JPL DE430精密月球星历(见>2.1.1)分析地-月相对运动特征。
月球公转周期约为27.3 d(1恒星月),是地球自转周期的近30倍。图 1给出了2016年1月1日至1月30日每日UTC 0点(共30个)月球星下点的位置。随着地-月相对运动,月球赤经每天向东移动约12°,月球赤纬则在20°S-20°N变化,且变化速率不均,在赤道附近较快,一天内变化最大约5°。因此,地球自转一周,月球的空间位置变化较小,在一天内,月球星下点轨迹近似与纬线平行。

|
| 图 1 月球星下点位置分布(2016年1月) Fig. 1 The distribution of sub-lunar points in January 2016 |
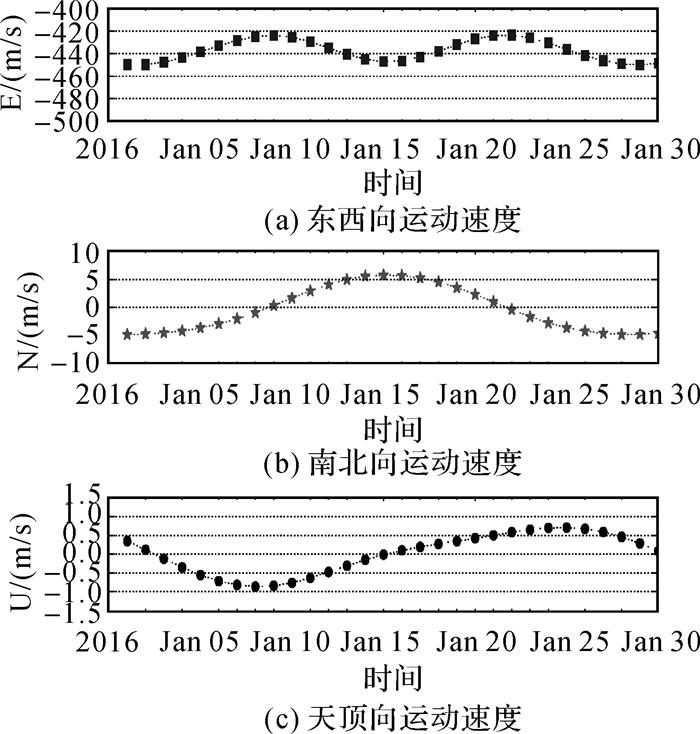
图 2给出了图 1中星下点对应的瞬时相对运动速度,用地表站心坐标系描述。东西向速度分量由地球自转和月球公转共同引起,前者是主要部分,平均值为-440 m/s(东为正);南北向分量由于月球公转时,白道-赤道(用白-赤交角描述)不重合所致。白-赤交角变化范围在18.3°~28.6°,且呈现18.6年的周期[16]。因此导致南北向分量在-6 m/s~6 m/s变化(北为正);天顶向分量由地-月距离变化引起,在-0.8 m/s~0.8 m/s变化(远离地球为正),且速率最小。
|
| 图 2 月球星下点在东西向、南北向和天顶向速度 Fig. 2 The east-west, north-south and zenith velocity of sub-lunar points |
由以上分析可知,月基SAR的合成孔径主要由地-月相对运动的东西向分量产生,月基SAR相对运动轨道近似平行于纬圈;南北向速度分量使月基SAR观测同一位置时,入射角发生改变,形成重复轨道干涉测量的空间基线(见图 3);天顶向速度分量意味着地-月距离时刻在变化,故用地-月平均距离计算空间基线存在误差,应采用星历数据进行分析。
|
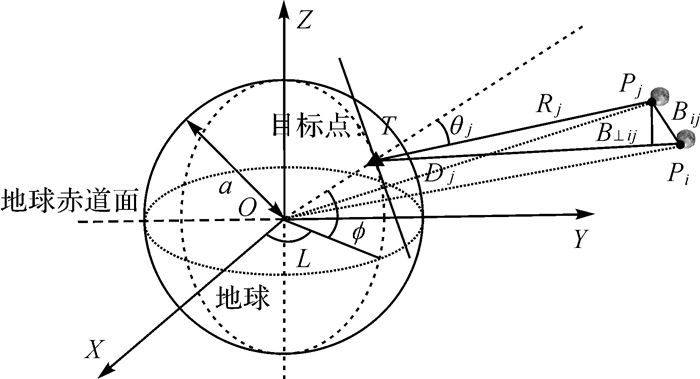
| 图 3 月基SAR重复轨道干涉测量观测几何 Fig. 3 The observation geometry of lunar-based repeat-track SAR interferometry |
1.2 观测几何
本文根据地-月相对运动特征,建立了月基重轨InSAR观测几何模型。如图 3所示,其中,O-XYZ为地心-地固坐标系;T为目标点;L与ϕ分别为目标点的经度与地心纬度;Pi与Pj为第i次与第j次观测同一经线L时月基SAR空间位置;Dj为第j次重访观测雷达距地心距离;Rj为第j次观测时雷达至观测目标的距离;θj为第j次观测目标T的入射角。为方便计算月基重轨InSAR时-空基线,本文对该模型进行了简化,具体如下:
(1) 假定地球为球体,半径为a(6378 km),这个假设所造成的成像误差在系统性能分析时可以忽略,但在精确成像模型中需要补偿[6, 17]。
(2) 假定月球为球体,半径为aM(1737 km)。
(3) 假定雷达位于月球表面(0°,0°)位置,且实时指向地心,但在月基SAR精确成像时,需根据月球姿态变化及天平动影响实时调整月基SAR天线的指向[18-19]。
(4) 月基SAR通过目标运动合成孔径,在一个合成孔径时间内,月球被认为近似“静止”状态[6, 9-10]。
使用月基重轨InSAR观测几何,在正侧视成像条件下,可认为两次观测的视线方向与地球的子午圈共面时形成重复轨道干涉,此时,两次观测的月基雷达经过同一经线,月基SAR两次重访观测同一目标的时间间隔Δt可表示为
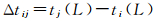 (1)
(1)
两次重访对应的垂直基线B⊥为
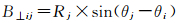 (2)
(2)
式中,ti(L)与tj(L)表示第i次与第j次重访同一经线L的时刻;θi为第i次观测目标T的入射角。
2 月基重轨InSAR时-空基线计算方法 2.1 数据使用及坐标转换 2.1.1 DE430月球星历数据本文选用高精度月球星历NASA/JPL DE430[20]计算月基SAR的重访时间和空间基线(见式(1)、式(2))。DE430星历数据继承了DE421及其前身DE405,并拟合了月球激光测距和最新的月球重力场数据,以切比雪夫多项式系数的形式记录了太阳系行星及月球在国际天球参考系统(international celestial reference system, ICRS)和太阳系质心动力学时(barycentric dynamical time, TDB)下的空间位置及其速度信息。在ICRS中,其坐标原点为太阳质心,XY平面为J2000.0历元下的平赤道,X轴指向J2000.0历元下的平赤道与平黄道的交点,Z轴垂直于XY平面,XYZ构成右手坐标系,而TDB是一种定义在太阳系质心的时间系统。为获得观测几何下的时-空基线,需要统一时空坐标系统,本文把时间系统统一到协调世界时(coordinated universal time, UTC),空间坐标系统一到地心-地固坐标系。
2.1.2 时间系统定义及转换在利用星历数据获取月基SAR某一时刻的空间位置时,须将UTC转换为TDB。其转换流程如图 4所示,其中,TAI(international atomic time)为国际原子时,TT(terrestrial time)为地球时,是在地表面建立的时间标准,TAI与TT为连续的时间系统。

|
| 图 4 时间系统转换 Fig. 4 Time coordinate transformation |
根据图 4,首先应通过跳秒将UTC转换为TAI,TT与TAI只差32.184 s,TDB与TT的转换关系已在文献[20-21]给出,本文不再赘述。
2.1.3 地-月坐标系统定义及转换由月基重轨InSAR观测几何可知,计算月基SAR重访同一经线的时间间隔以及相应的空间基线长度,需要已知月基SAR在大地坐标系中的位置。由于地球、月球、传感器一般处于不同的坐标系中,所以要获得月基SAR在大地坐标系中的位置,需要通过坐标转换实现。通常,该过程可通过以下6种坐标系(如图 5所示,P点为雷达在月表的位置)之间的互相转换得到[17, 19, 22-25],6种坐标系的具体定义如下:

|
| 图 5 坐标系统转换 Fig. 5 Illustration of coordinate systems transformation |
(1) 月面坐标系(selenographic coordinate system, SCS)。月面坐标系与大地坐标系类似,月球表面某点P的坐标可用(λm, $φ$m, Hm)。其中,λm为经度,由起始子午面起算,向东为正,称东经(0°~180°);向西为负,称西经(0°~180°)。$φ$m为纬度,由月球赤道起算,向北为正,称北纬(0°~90°);向南为负,称南纬(0°~90°)。Hm为P点与月心的连线至月表的距离,在月球表面安置雷达,Hm为0。
(2) 月心-月固坐标系(moon-centered moon-fixed coordinate system, MCMF)。坐标原点位于月球质心,Z轴指向月球北极,X轴指向月球本初子午线与月球赤道的交点,Y轴垂直于XOZ平面,构成右手坐标系。MCMF有两种形式,分为主轴坐标系(principal axes coordinate system, PA)和平地球/平旋转坐标系(mean-earth/mean-rotation coordinate system, MER)。PA的坐标轴为月球的3个主惯性轴,常用于月球动力学研究;MER中Z轴指向月球平极,本初子午线(0°经线)定义为平均地球方向,可用于MCMF与SCS的转换。由于月球非完全同步自转椭球,因此,这两个坐标系并非完全一致,在月表的差异可达1 km[24],MER可由PA通过3个旋转矩阵得到[20]
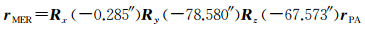 (3)
(3)
其中,Rx、Ry、Rz为3个坐标轴的旋转矩阵,分别为
 (4)
(4)
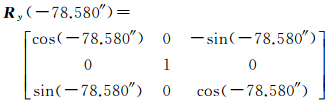 (5)
(5)
 (6)
(6)
(3) 月心惯性坐标系(inertial selenocentric coordinate system, MCI)。坐标原点位于月球质心,3个坐标轴与ICRS平行。
(4) 地心惯性坐标系(the earth-centered inertial coordinate system, ECI)。坐标原点位于地球质心,3个坐标轴与MCI平行,可由MCI平移得到,用来描述月球在轨位置。
(5) 地心-地固坐标系(the earth-centered earth-fixed coordinate system, ECEF)。坐标原点位于地球质心,Z轴从地心指向协议地球极(CPT),X轴由地心指向格林尼治平均子午面与CPT赤道的交点,Y轴与XOZ平面垂直构成右手坐标系。
(6) 大地坐标系(geodetic coordinate system, GCS),是ECEF的另一种表达方式,用(LP, ϕP, HP)表示,LP为P点与本初子午线的夹角,ϕP为P点与地心连线与赤道面的夹角,HP为P点与地心连线到地球面的距离。
为获得月基SAR在ECEF中的坐标,需进行一系列的坐标转换。首先,P点在MCMF中的坐标(Xm, Ym, Zm)可由月面坐标转换得到
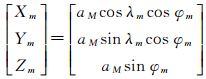 (7)
(7)
其次,P点在ECEF中的坐标(XP, YP, ZP)可通过MCMF经转换得到
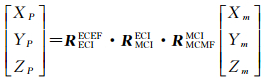 (8)
(8)
式中,RMCMFMCI为MCMF到MCI的转换矩阵,根据文献[20],该过程可由3个欧拉角(Φm, θm, ψm)旋转得到;RMCIECI为MCI到ECI的转换矩阵,可通过平移得到,平移量为月球轨道在ECEF中的位置;RECIECEF为ECI到ECEF的转换矩阵,根据文献[17, 26-27],该过程可由岁差、章动、地球旋转和极移所引起的旋转矩阵(P(t), N(t), Θ(t), Π(t))得到。3个转换矩阵可分别表示为
 (9)
(9)
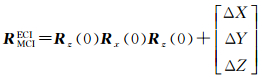 (10)
(10)
 (11)
(11)
最后,P点在GCS中的坐标(LP, ϕP, HP)可表示为
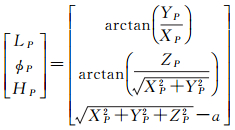 (12)
(12)
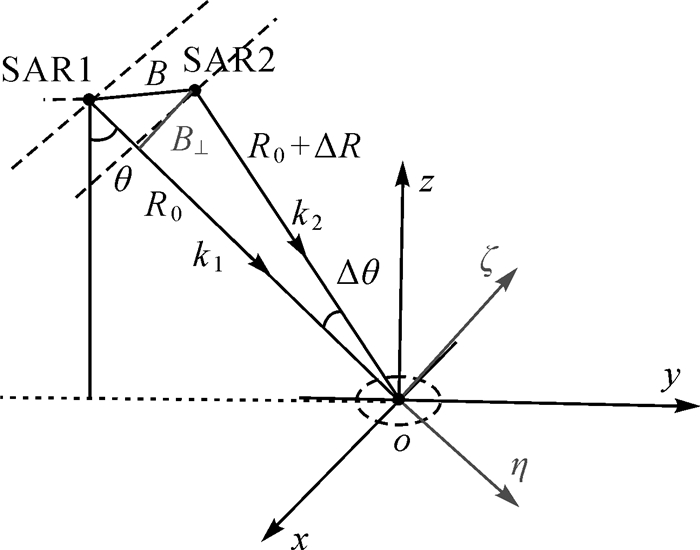
根据月基重轨InSAR观测几何,在不同的观测时间,月基SAR分别以不同的入射角对同一地物进行观测,如图 6所示(SAR1和SAR2分别为初始观测与重访观测雷达的位置,x为方位向,y为地距向,z垂直于xoy平面,构成右手坐标系,η为雷达视线向,δ在yoz平面,且垂直于η方向),根据干涉测量基本原理,两幅SAR影像的相干系数可表示
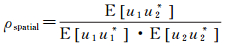 (13)
(13)
|
| 图 6 空间基线去相干 Fig. 6 Illustration of spatial baseline decorrelation |
式中,ρspatial为相干系数;u1和u2分别为初始观测与重访观测对应的SAR影像的分辨单元;u*为取共轭;E[·]为求数学期望。
此分辨单元,回波函数为雷达信号与地面反射系数的卷积,可表示为
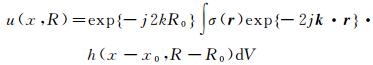 (14)
(14)
式中,x为方位向坐标;y为地距向坐标;R为雷达至目标的距离;(x0, R0)为零多普勒时刻雷达的位置;r为地面散射单元向量;k为波束向量;σ(·)为后向散射系数;h(·)为脉冲响应函数
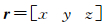 (15)
(15)
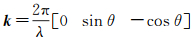 (16)
(16)
 (17)
(17)
不考虑轨道不平行、地面坡度引起的去相干以及两次观测时间不同产生的时间去相干,两幅SAR影像的相干系数可表示为
 (18)
(18)
式中,ΔR为两次观测的距离差。
 (19)
(19)
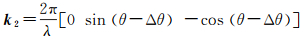 (20)
(20)
 (21)
(21)
将o-yz坐标系变换到o-ηξ坐标系
 (22)
(22)
把式(22)代入式(18),并转换到频率域,可得
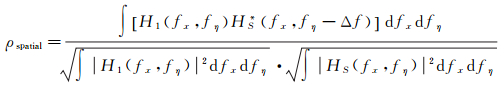 (23)
(23)
式中,Δf为两次观测入射角不一致产生的距离向频谱偏移,可表示为
 (24)
(24)
已有研究[9, 28-30]表明,在重复轨道干涉测量中,使用相同的波数值大小(k1=k2),当两次观测的入射角大于特定的阈值时,两次测量的结果不具备相干性。如L波段的Seasat卫星为0.32°,C波段的European Remote Sensing Satellite, ERS卫星为0.07°,因此,Δf可近似表示为
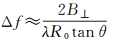 (25)
(25)
由两次观测入射角不一致产生的相干系数与雷达发射带宽有关,假设雷达带宽为BD,当两次雷达信号产生的频谱偏移大于雷达带宽时,两次测量的结果不具备相干性,此时,对应的最长基线为极限基线
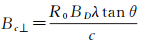 (26)
(26)
月基SAR在不同入射角下观测同一地物的相干系数与低轨卫星SAR,地基对金星观测SAR[31]以及地球同步轨道卫星SAR[32]等结论一致,可用垂直基线长度和极限基线表示
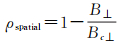 (27)
(27)
月基重轨InSAR存在约束条件:重访观测时,垂直基线应小于极限基线。文献[31]在对金星InSAR观测的研究中,为保证形变测量的灵敏度,建议垂直基线应小于1/4极限基线,因此,本文选择基线条件更加严格的1/4极限基线作为空间基线约束,即有效空间基线。
表 1给出4个典型雷达波段(X-band、C-band、S-band、L-band),入射角为20°~60°,发射带宽固定为:100 MHz[6, 9-10, 14-15]以及不考虑地表坡度影响的情况下对应的1/4极限基线长度, 单位为km。
| 波长/cm | 入射角/(°) | ||||
| 20 | 30 | 40 | 50 | 60 | |
| λϕX=3.12 | 360 | 570 | 830 | 1177 | 1711 |
| λϕC=5.66 | 652 | 1035 | 1504 | 2136 | 3104 |
| λϕS=10.0 | 1152 | 1828 | 2657 | 3773 | 5485 |
| λϕL=23.5 | 2708 | 4296 | 6244 | 8868 | 12 889 |
由表 1可知,一方面,长波雷达对应的空间极限基线较长;另一方面,极限基线随入射角的变化较大,随着入射角的增大InSAR极限基线的长度迅速增大,极限基线长度最大值可为最小值的4.8倍,根据文献[15],极限基线会影响月基重轨InSAR观测幅宽,随着极限基线的增大,月基重轨InSAR观测幅宽缩小,在月基重轨InSAR对地观测时,应综合考虑极限基线长度与观测幅宽。
2.3 时-空基线计算本文约定月基重轨InSAR的时间基线为两次相干影像获取的时间间隔,因此,计算月基重轨InSAR的时-空基线需要计算月基SAR的重访时间与对应的空间基线。
根据建立的重轨InSAR空间观测几何以及空间基线约束条件,笔者给出了利用月球星历数据计算时-空基线的具体过程(图 7),主要包括以下4个步骤:①数据输入,主要包括雷达在月表的位置、月球星历数据DE430和用于坐标转换的地球定向参数(earth orientation parameters, EOP),以及初始观测时间,并将UTC转换为TDB。②重访时间计算。③空间基线计算。④时-空基线判断,计算每次重访观测对应的观测时刻,以及对应的空间基线长度,并通过极限基线约束,判断该重访时间是否为月基重轨InSAR的时间基线。

|
| 图 7 时-空基线计算流程 Fig. 7 The calculation of spatio-temporal baseline |
2.3.1 时间基线
在重访观测中,本文使用1/4极限基线作为垂直基线约束,计算月基重轨InSAR时间基线。假设月基SAR初次观测某一目标的时刻为t0,此时,月基SAR在ECEF中的空间位置为(XP0, YP0, ZP0),月基SAR的经度为
 (28)
(28)
根据初始经度LP0计算出月基SAR的重返时刻t1, t2, …, tn,以及月基SAR重访观测的空间位置(XP1, YP1, ZP1),(XP2, YP2, ZP2),…, (XPn, YPn, ZPn)。
此时,可通过2.3.2计算出月基SAR第n次重访观测同一目标时的空间基线,通过极限基线判断该重访次数是否为月基重轨InSAR的时间基线。
2.3.2 空间基线式(2)给出了垂直基线计算公式。一方面,根据余弦定理,雷达至目标的观测距离RTP可表示为
 (29)
(29)
式中,a与ϕ是已知值,分别为地球半径和目标点的地心纬度;DOP与ϕP分别为雷达至地心的距离和雷达的地心纬度,可通过雷达在ECEF中位置得到
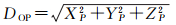 (30)
(30)
 (31)
(31)
另一方面,月基SAR观测目标点的入射角可由正弦定理得到
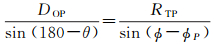 (32)
(32)
最后,根据月基SAR初始观测时刻t0,可计算出第n次重访观测对应的垂直基线
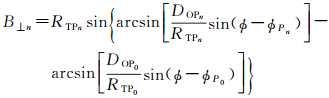 (33)
(33)
根据月基重轨InSAR观测几何,月基SAR的最短重访周期近似于地球自转一周所需的时间(约24.8 h),因此,在某一固定的观测位置,月基SAR在一个恒星月周期可实现多次重访观测,形成多个重访观测和空间基线的组合,每次初始观测在1恒星月至少有26次重访观测。
由地-月相对运动可知,月基重轨InSAR的垂直基线主要由南北向速度产生,随着观测时间的变化,月球空间位置会在南北半球变化(如图 1所示),且月球南北向速度也会产生变化,当月球靠近赤道时,南北向速度较快,而当月球远离赤道时,南北向速度降低,因此,月基SAR初始观测时间(位置)不同,可能会引起垂直基线的变化,为分析不同观测时间垂直基线特征,本文以图 1中的观测时刻作为初始观测来分析空间基线变化特征。
图 8给出了2016年每日UTC 0点为初始观测时间,每次初始观测具有27次重访观测,对应的垂直基线变化特征,图中每一列代表在给定初始观测时间下,垂直基线随重访次数的变化,即重复观测同一目标27次,每一次重复观测相对于初始观测的垂直基线变化;每一行代表在给定重访次数条件下,垂直基线随初始观测时间的变化,即月球在不同的位置以相同的重访次数观测不同的目标时,对应的垂直基线变化。

|
| 图 8 月基重轨InSAR空间基线分布 Fig. 8 The distribution of spatial baseline of lunar based SAR repeat-track interferometry |
可以看出,月基重轨InSAR的垂直基线会随访次数产生较大变化,最大可达250 000 km,此外,随着初始观测时间(月球空间位置)的变化,垂直基线长度呈现近1恒星月周期性变化特征。白-赤交角的存在、月球南北向速度变化、月球非圆形轨道等是导致月基重轨InSAR的垂直基线产生较大变化的主要原因。
3.1.2 时间基线为实现干涉测量,月基重轨InSAR构成的所有观测组合须满足极限基线的约束。极限基线的数值越大,满足约束的观测组合越多,反之则越少。但是,极限基线长度会影响月基重轨InSAR的观测幅宽,分别使用X,C,S和L波段,当极限基线分别为830、1504、2657、6244 km时,月基重轨InSAR至少可保证40°~60°的入射角范围,在地表的观测幅宽至少约为2200 km;当极限基线分别为360、652、1152、2708 km时,月基重轨InSAR至少可保证20°~60°的入射角范围,在地表的观测幅宽至少约为4400 km。
笔者分析了4种典型雷达波段(X, C, S和L)时间基线的分布。在权衡有效观测幅宽与观测组合个数的情况下,本文分别选用830、1504、2657、6244 km作为空间基线约束进行分析。由于不同的起始观测时间会导致最短重访周期存在细微差异,因此,采用重访次数来分析时间基线的特征。图 9给出了图 8对应不同波段的时间基线分布。每年可形成9855个干涉组合,分别约60个(X波段)、124个(C波段)、225个(S波段)、515个(L波段)观测组合满足空间基线约束。可以看出,不同波段时间基线的分布特征类似,都与初始观测时间和重访周期有关;随着雷达波段的增长,越有利于月基重轨InSAR观测。但在给定一定的初始观测时刻,只能在特定的时间基线上实现对地月基InSAR观测。如使用L波段,当初始观测时间为2016年1月7日时,只有第3次和第27次重访时才能进行月基InSAR测量;同时,不同的初始观测时间,可进行月基InSAR观测的次数存在较大不同。如当初始观测时间为1号时,只可进行1次月基InSAR观测,而10号则能进行4次观测。因此,在制定观测计划时,可根据需求及初始观测时间选择合适的时间基线开展对地观测。

|
| 图 9 不同波段时间基线分布 Fig. 9 The distribution of temporal baselines of various wavelengths |
3.2 时间基线与初始观测时间对干涉组合的影响
为分析不同时间基线与不同初始观测时间对干涉组合的影响,本文适当延长时间基线长度,假定初始观测时间为2016年1月-4月(即2016年前120天),每日UTC 0点为初始观测时间,相对于某一固定初始观测时间,月基重轨InSAR每年可重访观测同一目标约353次(重访时间最长约一年),并以830、1504、2657、6244 km作为4种波段(X, C, S和L)的极限基线(在空间基线约束下,4种波段分别共有398、684、1176、2551个干涉组合),对时间基线与初始观测时间展开分析。
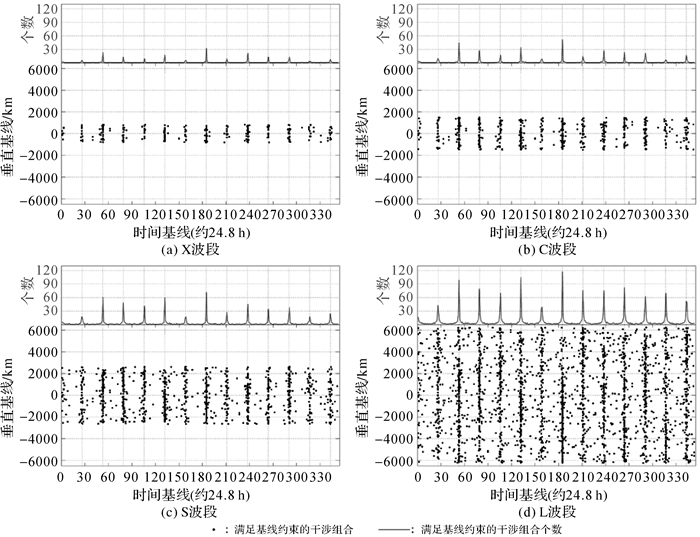
3.2.1 时间基线分析图 10给出了4种波段不同时间基线条件下,垂直基线长度分布以及满足基线约束的观测组合个数。分析可知,4种波段时-空基线分布特征相似,但长波雷达可有效增加干涉组合个数;月基重轨InSAR空间基线分布随时间基线的变化具有明显的周期性变化特征,当时间基线接近1恒星月及其整数倍时,满足基线约束的干涉组合个数最多,4种波段分别占比55%(X波段),56%(C波段),53%(S波段)和50%(L波段),而随着时间基线远离1恒星月及其整数倍时,满足基线约束的干涉组合个数迅速降低。
|
| 图 10 不同波段时-空基线分布 Fig. 10 The distribution of spatio-temporal baseline with different radar bands |
另外,在不同的恒星月附近,满足基线约束的干涉组合个数也存在一定的差异,其中主要原因为最短重访周期不为一整天,而是约24.8 h,随着重访时间靠近1恒星月时(即26和27个重访周期),时间基线分别约为26.9 d和27.9 d,此时相对于月球测初始观测位置偏移了0.4 d和0.6 d,随着重访时间靠近第2个恒星月时(即第52次和第53次重访观测时),此时相对于月球测初始观测位置偏移了0.75 d和0.25 d,此时,时间基线为53个重访周期对应的干涉组个数要大于时间基线为26个重访周期对应的干涉组合个数。
3.2.2 初始观测时间分析图 11给出了4种波段月球赤纬以及满足基线约束的干涉组合个数随初始观测时间的变化。从图中可知,随着观测时间的变化,月球赤纬和满足基线约束的干涉组合个数都呈现周期性变化,变化周期为1恒星月。使用L波段雷达,当月球接近赤道面时,满足基线约束的干涉组合个数最少,每次初始观测约有10个满足基线约束的干涉组合;当月球的赤纬升高时,满足基线约束的干涉组合个数增加,月球赤纬接近最大值时,每次初始观测可对应约45个满足基线约束的干涉组合。主要原因是,随着月球的赤纬的升高,月球南北向速度降低,小于极限基线的干涉组合个数增多。

|
| 图 11 不同波段满足基线约束的干涉组合个数和月球赤纬随初始观测时间的变化 Fig. 11 The number of interferometric combinations and the Moon's declination various with initial observation time at different radar bands |
表 2给出了4种波段,满足基线约束的干涉组合个数与月球赤纬的关系。可以看出,当月球的赤纬低于5°时,满足基线约束的干涉组合个数占比较低,4种波段分别占比8%、7%、9%和10%,月球赤纬在5°~10°区间时,满足基线约束的干涉组合个数占比与月球的赤纬低于5°时接近。随着月球赤纬的升高,满足基线约束的干涉组合个数增长速度越来越快;当月球赤纬大于10°时,4种波段满足基线约束的干涉组合个数分别占比83%、83%、81%和80%。随着初始观测时间的变化,时间基线个数也会不同,因此,在月球不同轨道位置处具有不同的重访观测能力。
| 波段 | 月球赤纬/(°) | 0-5 | 5-10 | 10-15 | >15 |
| X-band | 满足基线约束的干涉组合个数 | 31 | 37 | 84 | 246 |
| 占比/(%) | 8 | 9 | 21 | 62 | |
| C-band | 满足基线约束的干涉组合个个数 | 51 | 68 | 141 | 424 |
| 占比/(%) | 7 | 10 | 21 | 62 | |
| S-band | 满足基线约束的干涉组合个数 | 110 | 112 | 222 | 732 |
| 占比/(%) | 9 | 10 | 19 | 62 | |
| L-band | 满足基线约束的干涉组合个数 | 252 | 246 | 473 | 1580 |
| 占比/(%) | 10 | 10 | 18 | 62 |
4 结论
根据地-月相对运动特征,考虑雷达安置位置和地月同步运动等因素的情况下,建立了月基重轨InSAR观测几何模型。在此基础上,利用月基重轨InSAR时-空基线计算方法和高精度月球星历数据DE430,深入分析月基重轨InSAR时-空基线分布特征。研究结果表明:
(1) 本文考虑空间基线去相干、形变测量灵敏度以及观测幅宽等约束条件,针对4种波段(X, C, S, L)的极限基线展开分析,在100 MHz带宽条件下,月基重轨InSAR极限基线分别为830、1504、2657、6244 km,并以此作为空间基线的约束条件。
(2) 月基SAR重访观测同一目标的最短时间约为24.8 h(1.035 d),每恒星月约有27次重访观测。在空间基线约束下,月基重轨InSAR的时间基线与初始观测时间和波长有关。
(3) 受月球南北向速度影响,月基重轨InSAR的空间基线受初始观测时间和重访周期的影响会产生周期性变化,变化周期为1恒星月,且空间基线变化范围较大,月基重轨InSAR一年可形成约9855个干涉组合,对于X、C、S、L波段雷达,分别有60、124、225、515个干涉组合满足空间基线约束。
(4) 在空间基线约束下,不同时间基线可形成的干涉组合个数不同,当时间基线接近1恒星月及其整数倍时,约占总干涉组合个数的50%,随着时间基线远离1恒星月及其整数倍,干涉组合个数迅速降低;不同初始观测时刻月球赤纬可形成的干涉组合个数不同,当初始观测时刻月球赤纬大于10°时,约占总干涉组合个数的80%,随着月球靠近赤道,干涉组合个数迅速降低。
月基重轨InSAR平台设计以及数据获取计划应充分考虑载波波长、观测幅宽、初始观测时间和重访周期等。本文研究可以为面向宏观地球科学现象观测的月基SAR/InSAR测模式设计、观测频段选择、平台选址以及应用等提供借鉴和参考作用。但本文使用固定极限基线对空间基线进行约束,后续工作将考虑入射角对时-空基线的影响。
| [1] |
许才军, 申文斌, 晁定波.
地球物理大地测量学原理与方法[M]. 武汉: 武汉大学出版社, 2006.
XU Caijun, SHEN Wenbin, CHAO Dingbo. Geophysical geodesy principles and methods[M]. Wuhan: Wuhan University Press, 2006. |
| [2] |
张红, 王超, 吴涛, 等.
基于相干目标的DInSAR方法研究[M]. 北京: 科学出版社, 2009.
ZHANG Hong, WANG Chao, WU Tao, et al. D-InSAR method based on coherent target[M]. Beijing: Science Press, 2009. |
| [3] |
朱建军, 李志伟, 胡俊.
InSAR变形监测方法与研究进展[J]. 测绘学报, 2017, 46(10): 1717–1733.
ZHU Jianjun, LI Zhiwei, HU Jun. Research progress and methods of InSAR for deformation monitoring[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1717–1733. DOI:10.11947/j.AGCS.2017.20170350 |
| [4] | RAMSEY M. ESS findings: lunar science planning and workshop overview[C]//Proceedings of NASA Advisory Council Workshop on Science Associated with the Lunar Exploration Architecture. Arizona: NASA, 2007. |
| [5] | SARABANDI K. Lunar-based large baseline synthetic aperture radar interferometry of earth[C]//Proceedings of NASA Advisory Council Workshop on Science Associated with the Lunar Exploration Architecture. Arizona: NASA, 2007. |
| [6] |
郭华东, 丁翼星, 刘广, 等.
面向全球变化探测的月基成像雷达概念研究[J]. 中国科学:地球科学, 2013, 43(11): 1760–1769.
GUO Huadong, DING Yixing, LIU Guang, et al. Conceptual study of lunar-based SAR for global change monitoring[J]. Science China Earth Sciences, 2013, 43(11): 1760–1769. |
| [7] |
丁翼星, 郭华东, 刘广.
面向全球变化探测的月基对地观测覆盖性能分析[J]. 湖南大学学报(自然科学版), 2014, 41(10): 96–102.
DING Yixing, GUO Huadong, LIU Guang. Coverage performance analysis of earth observation from lunar base for global change detection[J]. Journal of Hunan University (Natural Sciences), 2014, 41(10): 96–102. |
| [8] | DING Yixing, GUO Huadong, LIU Guang. Potential applications of the moon based synthetic aperture radar for earth observation[C]//Proceeding of 2013 IEEE International Geoscience and Remote Sensing Symposium. Melbourne, Australia: IEEE, 2013: 1767-1769. |
| [9] | FORNARO G, FRANCESCHETTI G, LOMBARDINI F, et al. Potentials and limitations of Moon-borne SAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(7): 3009–3019. DOI:10.1109/TGRS.2010.2041463 |
| [10] | MOCCIA A, RENGA A. Synthetic aperture radar for Earth observation from a lunar base:Performance and potential applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 1034–1051. DOI:10.1109/TAES.2010.5545172 |
| [11] |
谷昕炜, 陈杰, 杨威, 等.
月基SAR仿真成像研究[J]. 无线电工程, 2018, 48(2): 88–91.
GU Xinwei, CHEN Jie, YANG Wei, et al. Research on echo simulation and imaging of lunar-based SAR[J]. Radio Engineering, 2018, 48(2): 88–91. DOI:10.3969/j.issn.1003-3106.2018.02.02 |
| [12] | XU Zhen, CHEN Kunshan. On signal modeling of moon-based synthetic aperture radar (SAR) imaging of earth[J]. Remote Sensing, 2018, 10(3): 486. DOI:10.3390/rs10030486 |
| [13] | RENGA A, MOCCIA A. Preliminary analysis of a Moon-based interferometric SAR system for very high resolution Earth remote sensing[C]//Proceedings of the 9th ILEWG International Conference on Exploration and Utilization of the Moon. Sorrento, Italy: Lunar Explorers Society, 2007: 22-26. |
| [14] | DING Y X, GUO H D, LIU G, et al. The analysis of moonborne cross track synthetic aperture radar interferometry for global environment change monitoring[J]. IOP Conference Series:Earth and Environmental Science. IOP Publishing, 2014, 17(1): 012278. |
| [15] |
丁翼星.月基对地观测合成孔径雷达与全球变化应用研究[D].北京: 中国科学院大学, 2014. DING Yixing. Moonborne earth observation synthetic aperture radar and its application in global change[D]. Beijing: Institute of Electronics, CAS, 2014. |
| [16] | WILLIAMS J G, BOGGS D H. DE421 lunar orbit, physical librations, and surface coordinates[C]//Proceedings of the 16th International Workshop on Laser Ranging. Poznań: Jet Propulsion Laboratory, 2008. |
| [17] | YE Hanlin, GUO Huadong, LIU Guang, et al. Observation scope and spatial coverage analysis for earth observation from a Moon-based platform[J]. International Journal of Remote Sensing, 2017, 39(18): 5809–5833. |
| [18] | YE Hanlin, GUO Huadong, LIU Guang, et al. Observation duration analysis for Earth surface features from a Moon-based platform[J]. Advances in Space Research, 2018, 62(2): 274–287. DOI:10.1016/j.asr.2018.04.029 |
| [19] |
丁翼星, 郭华东, 刘广.
基于JPL星历的月基SAR多普勒参数估算方法[J]. 北京航空航天大学学报, 2015, 41(1): 71–76.
DING Yixing, GUO Huadong, LIU Guang. Method to estimate the Doppler parameters of Moon-borne SAR using JPL ephemeris[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1): 71–76. DOI:10.3969/j.issn.1005-4561.2015.01.031 |
| [20] | FOLKNER W M, WILLIAMS J G, BOGGS D H, et al. The planetary and lunar ephemerides DE430 and DE431[C]//Proceedings of the Interplanetary Network Progress Report 42-196.[S.l.]: IPN, 2014: 1-81. |
| [21] |
金文敬.
太阳系行星和月球历表的发展[J]. 天文学进展, 2015, 33(1): 103–121.
JIN Wenjing. Development of planetary and lunar ephemeris in the solar system[J]. Progress in Astronomy, 2015, 33(1): 103–121. DOI:10.3969/j.issn.1000-8349.2015.01.06 |
| [22] | LIESKE J H. Precession matrix based on IAU/1976/system of astronomical constants[J]. Astronomy and Astrophysics, 1979, 73(3): 282–284. |
| [23] | SEIDELMANN P K, ABALAKIN V K, BURSA M, et al. Report of the IAU/IAG working group on cartographic coordinates and rotational elements of the planets and satellites:2000[J]. Celestial Mechanics and Dynamical Astronomy, 2002, 82(1): 83–111. DOI:10.1023/A:1013939327465 |
| [24] | GSFC. A standardized lunar coordinate system for the lunar reconnaissance orbiter[R]. LRO Project White Paper.[S.l.]: NASA, 2008. |
| [25] | REN Yuanzhen, GUO Huadong, LIU Guang, et al. Simulation study of geometric characteristics and coverage for moon-based earth observation in the electro-optical region[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(6): 2431–2440. DOI:10.1109/JSTARS.2017.2711061 |
| [26] | PETIT G, LUZUM B J. IERS conventions (2010)[R]. IERS Technical Note 36. Frankfurt am Main: IERS, 2010. |
| [27] | MCCARTHY D D, PETIT G. IERS CONVENTIONS (2003)[R] IERS Technical Note no. 32. Frankfurt am Main: IERS, 2004. |
| [28] | ZEBKER H A, VILLASENOR J. Decorrelation in interferometric radar echoes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(5): 950–959. DOI:10.1109/36.175330 |
| [29] | GATELLI F, GUAMIERI A M, PARIZZI F, et al. The wavenumber shift in SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4): 855–865. DOI:10.1109/36.298013 |
| [30] | HANSSEN R F. Radar interferometry:data interpretation and error analysis[M]. Dordrecht: Springer Science & Business Media, 2001. |
| [31] | MEYER F J, SANDWELL D T. SAR interferometry at Venus for topography and change detection[J]. Planetary and Space Science, 2012, 73(1): 130–144. DOI:10.1016/j.pss.2012.10.006 |
| [32] | HU Cheng, LI Yuanhao, DONG Xichao, et al. Optimal data acquisition and height retrieval in repeat-track geosynchronous SAR interferometry[J]. Remote Sensing, 2015, 7(10): 13367–13389. DOI:10.3390/rs71013367 |



