2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054;
4. 北京卫星导航中心, 北京 100094
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
4. Beijing Satellite Navigation Center, Beijing 100094, China
高精度电离层建模及预报是电离层研究中的重要课题[1-6]。大气分子在太阳紫外线、X射线等辐射下电离,产生自由电子和正负离子,形成电离层区域,对穿越其中的电磁波信号会产生反射、折射、散射和吸收等效应,对远程通信、卫星导航、航空航天、地震监测、天气预报等具有重要影响。电离层效应是卫星导航系统最严重的误差源之一,高精度的电离层延迟信息对提高单频用户的时延修正精度和双频/多频用户精密定位的收敛速度均具有重要作用[1]。1998年国际GNSS服务组织(International GNSS Service,IGS)意识到GPS是监测电离层活动的重要技术手段,决定提供电离层服务,目前国内外已有许多机构提供电离层服务[7-8]。
高精度电离层总电子含量(total electron content, TEC)建模及预报的核心是基于有限个电离层穿刺点(ionospheric pierce point,IPP)的电离层TEC,内插或外推区域内任意点电离层TEC[2]。传统插值算法可分为准确插值和光滑插值两类,其中,克吕金(Kriging)插值、反距离加权法等属于准确插值,球冠模型、低阶球谐模型、多项式模型、三角函数模型等属于光滑插值[9-17]。一般地,当观测量密集且分布均匀时,采用准确插值,反之,采用光滑插值。Kriging插值方法是南非金矿地质学家Krige提出、法国学者Matheron完善的一种空间插值方法。它以区域化变量为基础,以变异函数为工具,主要用于研究空间上既有随机性又有结构性的自然现象,已广泛应用于矿产、海洋、地质、土壤、气象、水文等领域。国内外许多学者采用Kriging插值方法对电离层TEC开展大量研究,认为该方法考虑电离层的时空相关性,电离层插值精度明显优于其他模型[9-17]。文献[5]利用中国及周边地区GPS实测电离层TEC数据,Kriging插值精度为0.5~2.5 TECU(total electron content unit);文献[6]基于中国陆态网GPS数据的多种电离层TEC建模对比,表明Kriging方法明显优于球谐模型和多项式模型,且边缘效应不明显;文献[14]分析了我国中纬度地区,Kriging插值内符合精度为2.19 TECU,优于就近插值法和多项式回归方法,且数据稀少时仍能得到较好的插值效果;文献[16]采用青岛地区CORS站实测电离层TEC插值,表明Kriging插值精度优于反距离加权方法、多元回归法和多项式插值法,且在数据分布不均匀时仍能得到较高的插值精度。但是,在电离层插值中,已有研究存在以下问题:①由于环境因素、人为因素、仪器异常等导致观测量中不可避免地存在着粗差,进而影响电离层插值的精度,兼顾精度和效率,需要实现自动化粗差剔除;②目前Kriging插值方法仅在有限区域试验,在全球范围的适应性需进一步论证。
本文讨论Kriging插值的粗差剔除和全球电离层插值精度。通过分析变异函数,构造电离层TEC粗差剔除统计量,自动化检测和剔除粗差,实现高精度电离层插值。然后,采用全球电离层GIM(global ionosphere maps)产品和单站双频提取电离层TEC,进行插值试验,分析Kriging全球插值精度。
1 Kriging插值原理 1.1 区域化变量区域化变量是Kriging插值方法的基础,电离层TEC可以看作一种满足Kriging插值条件的区域化变量[13]。设Z(x)为区域化变量,x是用经纬度表述的电离层穿刺点坐标x=(lon, lat),区域内一系列采样点x1,x2,…,xn的观测值为Z(x1),Z(x2),…,Z(xn),满足Kriging插值使用条件,则区域内某一点x0的估计值(x0)可以用下式计算
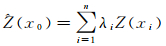 (1)
(1)
式中,λi为加权系数,即Kriging系数。
由于薄层电离层TEC为二维产品,文献[10-12]引入电离层距离实现利用Kriging电离层区域重构。已知穿刺点xi(loni,lati)和xj(lonj,latj),两点间电离层距离为dij
 (2)
(2)
式中,sf为尺度因子,经验值为0.2,用来调节电离层TEC与经度lon、纬度lat的空间相关性差异。
1.2 变异函数变异函数是Kriging插值的工具,是用于描述采样点之间、采样点与插值点之间空间关系的函数模型。定义为任意两点xi和xj的观测值之差的半方差,记为γ(xi, xj)[18],则
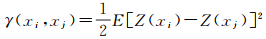 (3)
(3)
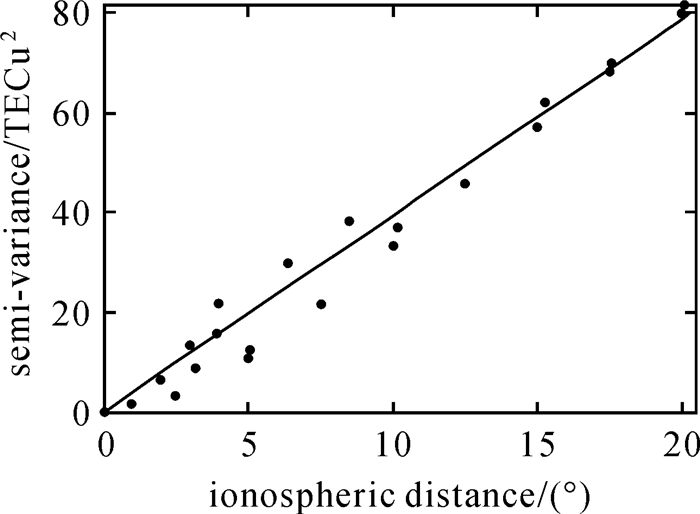
变异函数一般利用样本计算观测值之差的半方差,然后选择合适模型拟合得到,常用的拟合模型有线性模型、指数模型、高斯模型和球面模型等[19-22]。文献[19]研究了Kriging插值变异函数选取的理论模型,通过对多种模型分析,认为采用线性模型、指数模型、球面模型拟合变异函数的插值效果相当。文献[20-22]采用线性模型,实现了高精度的电离层插值。按照下文中最大20°×20°的插值范围,dij的取值范围为0~20.4°,半方差γ(xi, xj)的取值为0~87.2 TECU2,可以认为3种模型拟合差异不大,同时,距离待插值点越近,半方差越小,认为模型是变异函数是经过原点。为此,本文选用过原点的线性模型,见式(4),采用2014年1月1日GIM数据拟合验证,拟合残差RMS约为3.1 TECU,达到较好的拟合效果(见图 1)。
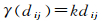 (4)
(4)
|
| 图 1 变异函数拟合结果 Fig. 1 Variation function fitting results |
1.3 解算方法
在线性无偏、最优估计条件下,得到电离层TEC插值的Kriging方程组[18]
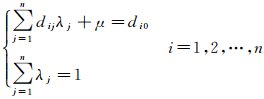 (5)
(5)
式中,μ为拉格朗日乘数因子;di0为插值点与观测值间距离。
求解式(5)获得加权系数λi,则区域内点x0(lon0, lat0)的电离层TEC估计值
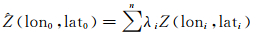 (6)
(6)
本节从Kriging插值变异函数入手,构造粗差剔除统计量,实现电离层粗差的自动化检测和剔除。分析γ(dij)定义不难发现,电离层TEC变异函数只与两个点之间的“电离层距离”有关,与观测值无关,当插值样本中存在粗差时,势必会影响最后的插值结果。
为实现自动化粗差剔除,构造粗差剔除统计量。定义中γ(xi, xj)是两个观测值之间的半方差,与γ(dij)存在比例关系,因此,先构造粗差剔除统计量K,公式为
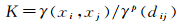 (7)
(7)
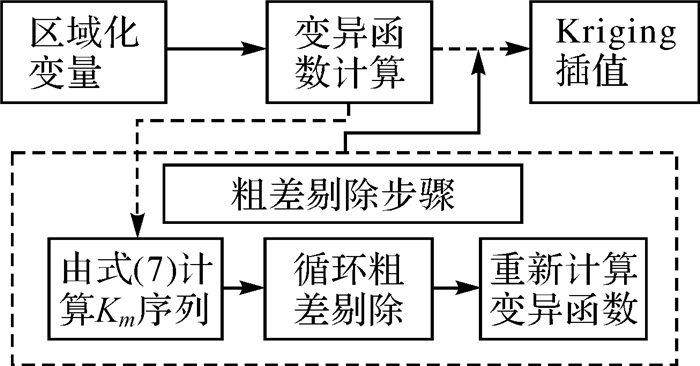
统计量K可以理解为单位电离层距离空间变异值,p是两者之间的幂次关系,本文取值2,粗差剔除过程如图 2所示。假设有n个插值观测量,计算任一点与区域内其他观测值的统计量序列K1,K2,…,Km(m=Cn2)。以序列的中位数为阈值,当某一点与所有其他点统计量序列K1,K2,…,Kn-1中有(n-1)/2个值超出阈值,则剔除该观测值,多次循环直至所有粗差被识别。最后,采用“干净”观测值解算Kriging方程组,实现自动高精度插值。
|
| 图 2 考虑粗差剔除的Kriging流程 Fig. 2 Kriging interpolation process by considering eliminating gross error |
2.2 精度分析
该粗差剔除统计量是基于任意两个观测值计算的“单位电离层距离空间变异值”序列,粗差剔除阈值是序列中位数。理论上认为,观测值足够时,具备“多点”粗差剔除能力。
为了分析粗差剔除统计量的有效性并评估Kriging插值精度,设计了两个指标,分别是插值残差error和残差均方根误差RMS,计算公式如下
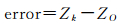 (8)
(8)
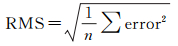 (9)
(9)
式中,Zk为Kriging插值结果;ZO为待插值点的已知值;n表示参与统计的插值点个数。
3 试验分析 3.1 试验数据及方案文献[23]对IGS发布的1998年以来所有GIM产品的评估,认为目前GIM产品的精度为2.5~3.5 TECU。本文选择太阳活动高年2014年的GIM产品作为试验样本[24]。
生成粗差试验样本时,GIM产品本身就是球谐模型的插值产品,是全球性、高精度的格网产品,认为没有粗差。本文采用2014年1月1日UTC 7 h北半球GIM数据,选取经度0°~360°、纬度10°~70°为试验区域,划分为15°×20°格网,共选取92个格网点作为待插值点(未知点)。每个待插值点插值时,以周围10°×15°或20°×20°范围格网点作为插值样本(观测值)。考虑实际数据中粗差分布的随机性,试验过程由计算机随机分配一个观测值分别加入5、10和15 TECU粗差,共制作了92×3×2=368组粗差样本。
插值区域决定了采样点的分布、数量,最终影响插值精度。文献[25]分析GNSS监测站单站IPP的覆盖范围约为30°×30°。本文选择10°×15°进行插值分析,再选择20°×20°的插值范围进行验证,如图 3所示。

|
| 图 3 插值区域 Fig. 3 The interpolation area |
试验包括粗差剔除统计量验证和全球插值精度分析。
(1) 粗差剔除统计量验证。采用制作的粗差样本,设计以下3种策略,验证算法效果:
策略S1:无粗差GIM产品的Kriging插值。
策略S2:有粗差GIM产品的Kriging插值。
策略S3:应用粗差剔除统计量的有粗差GIM产品Kriging插值。
(2) 全球插值精度分析。考虑太阳活动和季节变化,选用2014年“两分两至”日UTC 7 h的GIM产品进行分析,即是春分日DOY080、夏至日DOY172、秋分日DOY266及冬至日DOY356,代表春夏秋冬四季,进行插值试验,分析全球插值精度。
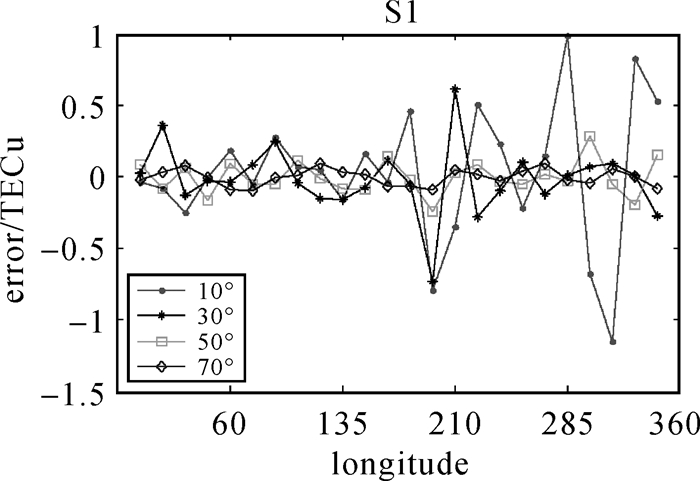
3.2 粗差剔除统计量验证 3.2.1 10°×15°插值试验图 4和表 1给出了策略S1中插值精度与地理经纬度的关系。显然,当观测值无粗差时,Kriging插值精度随纬度的增加而提高。在低纬度地区(10°)插值精度最差,个别点残差error超过1.0 TECU,在中高纬度地区则小于0.5 TECU;纬度10°、30°、50°和70°上所有待插值点插值残差error均方根误差RMS分别为0.47 TECU、0.24 TECU、0.12 TECU和0.06 TECU。
|
| 图 4 无粗差时Kriging插值残差error序列 Fig. 4 The interpolation residual sequence of Kriging without gross error |
| TECU | |||||||
| 纬度/(°) | S1 | 5 TECU粗差 | 10 TECU粗差 | 15 TECU粗差 | |||
| S2 | S3 | S2 | S3 | S2 | S3 | ||
| 10 | 0.47 | 0.53 | 0.49 | 1.17 | 0.75 | 0.80 | 0.24 |
| 30 | 0.24 | 0.57 | 0.50 | 1.07 | 0.67 | 1.46 | 0.26 |
| 50 | 0.12 | 0.58 | 0.43 | 0.99 | 0.06 | 1.43 | 0.07 |
| 70 | 0.06 | 0.60 | 0.07 | 1.51 | 0.05 | 1.35 | 0.05 |
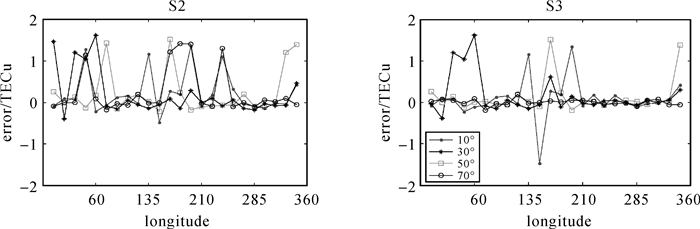
图 5-图 7和表 1对比给出了分别加入5、10和15 TECU粗差后,策略S2和S3的插值精度。可以看出:
|
| 图 5 加入5 TECU粗差的插值残差error序列对比 Fig. 5 Comparison of interpolation residual sequence by adding 5 TECU gross error |
|
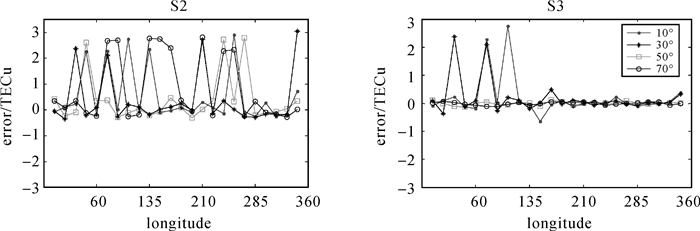
| 图 6 加入10 TECU粗差的插值残差error序列对比 Fig. 6 Comparison of interpolation residual sequence by adding 10 TECU gross error |
|
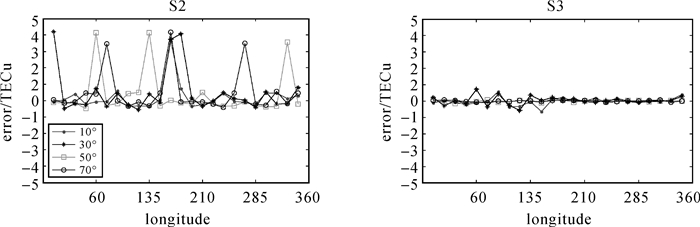
| 图 7 加入15 TECU粗差的插值残差error序列对比 Fig. 7 Comparison of interpolation residual sequence by adding 15 TECU gross error |
(1) 对于Kriging插值,分别加入5、10和15 TECU粗差后,Kriging插值残差error明显变大,分别达到2.0、3.0和4.0 TECU。
(2) 应用粗差剔除算法后,Kriging插值残差明显减小,分别加入5、10和15 TECU粗差后,在低纬度地区,个别点粗差剔除不理想,但Kriging插值残差error小于2.0 TECU,中高纬度地区,粗差均被有效剔除,Kriging插值残差error好于0.5 TECU;不同纬度上所有待插值点插值残差error均方根误差RMS小于1.0 TECU。
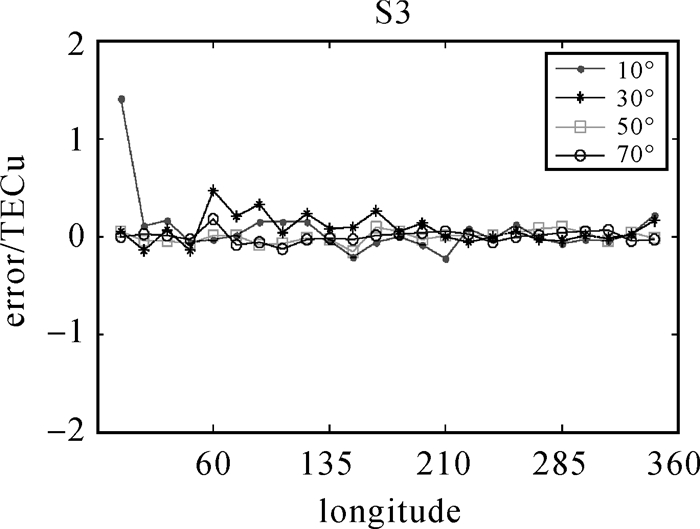
3.2.2 20°×20°插值试验图 8-图 10和表 2给出了采用20°×20°插值区域,分析统计量K的粗差剔除能力。
|
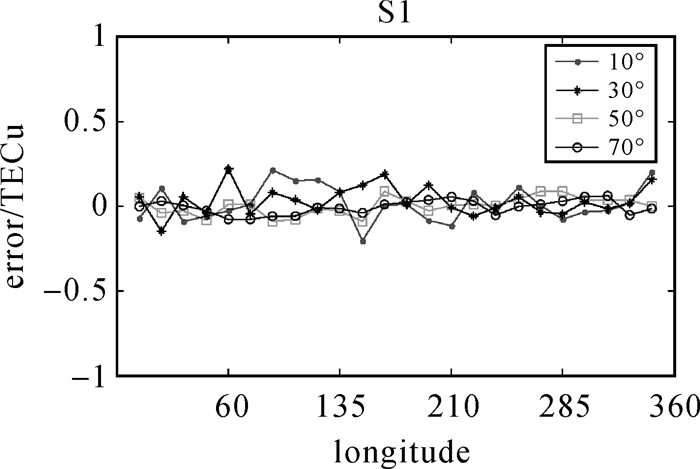
| 图 8 无粗差Kriging插值残差error序列 Fig. 8 The interpolation residual sequence of Kriging without gross error |
|
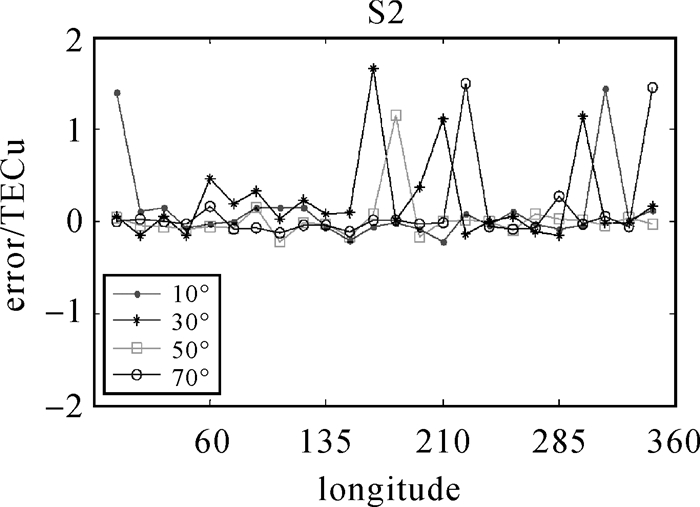
| 图 9 有粗差Kriging插值残差error序列 Fig. 9 The interpolation residual sequence of Kriging with gross error |
|
| 图 10 考虑粗差剔除Kriging插值残差error序列图 Fig. 10 The interpolation residual sequence of Kriging by eliminating gross error |
| TECU | |||
| 纬度/(°) | S1 | S2 | S3 |
| 10 | 0.10 | 0.43 | 0.31 |
| 30 | 0.09 | 0.50 | 0.16 |
| 50 | 0.05 | 0.25 | 0.06 |
| 0 | 0.04 | 0.44 | 0.06 |
(1) 数据无粗差时,如图 8所示,Kriging插值残差error优于0.5 TECU,明显好于图 3中10°×15°插值结果。
(2) 加入5 TECU粗差后,Kriging插值残差error如图 9所示,优于图 4中10°×15°插值结果,考虑粗差剔除统计量的Kriging插值残差error如图 10所示,粗差剔除效果更加明显。
观测量增多后,5 TECU的粗差对插值点的影响明显变小,3种方案不同纬度上所有待插值点插值残差error均方根误差RMS相当,均好于采用10°×15°插值区域的插值效果。
3.2.3 对比分析综上试验,可以得出:
(1) 粗差剔除效率与粗差值大小相关。插值区域为10°×15°,单个观测值加入5.0 TECU粗差,低纬度格网点插值残差error为0~2.0 TECU,与样本精度相当。这是因为该插值区域内,可用观测值有20个,假设各观测值对插值点的影响相当,即Kriging系数值相当,则Kriging系数约为0.05,粗差值对插值点的影响仅为0.25 TECU,对低纬度格网点影响非常小,但对于电离层TEC相对平静的高纬度格网点,0.25 TECU仍然是较大的误差,所以粗差剔除统计量可以识别和剔除粗差。当粗差为15 TECU,假设Kriging系数相当,粗差对插值点的影响达到了0.75 TECU,无论是对低纬度格网点还是中高纬度格网点,这都是较大的误差,能够有效识别并剔除。
(2) 粗差剔除能力与观测值数量相关。假设加入粗差值仍为5 TECU,采用20°×20°插值区域,观测值增多,有44个格网点,相比10°×15°插值区域,观测值数量增加了1倍,从插值残差error结果看,不同纬度上所有插值点残差的RMS相当,均好于插值区域为10°×15°时的插值结果。因为,观测值越多,单个观测值误差对插值点影响越小。
(3) 本文设计的粗差剔除统计量能有效保证插值结果不被粗差数据污染,使插值精度与样本精度匹配。建议在观测量数据充足时,采用更大范围(如20°×20°插值区域)的观测值进行插值。
3.3 全球插值精度分析Kriging插值方法在全球范围内适用性是本文重点之一,鉴于GIM产品的全球性,选择作为试验样本。本文选用2014年“两分两至”日UTC 7 h GIM产品,采用Kriging算法进行插值,插值区域为20°×20°,插值结果如图 11-图 14所示。

|
| 图 11 DOY080 Kriging插值残差error序列图 Fig. 11 The interpolation residual sequence of Kriging for DOY080 |
|
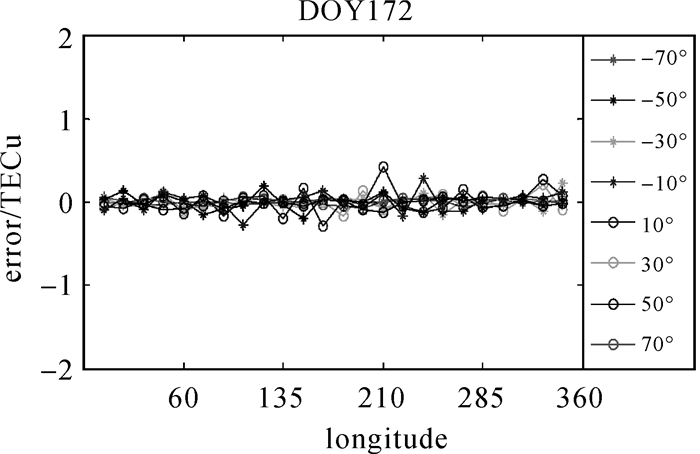
| 图 12 DOY172 Kriging插值残差error序列图 Fig. 12 The interpolation residual sequence of Kriging for DOY172 |
|
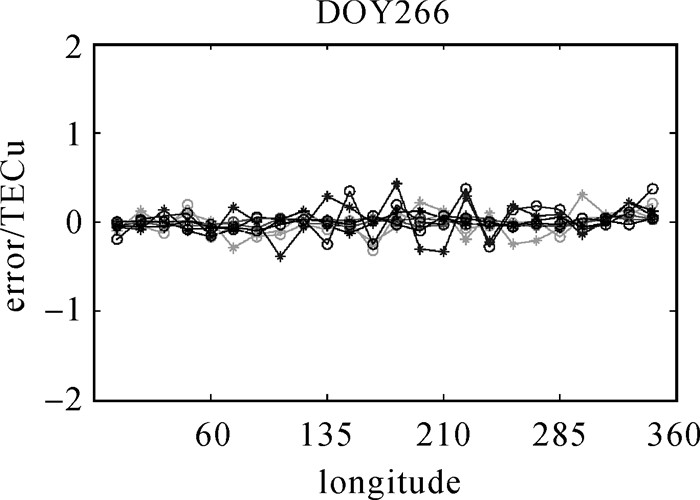
| 图 13 DOY266 Kriging插值残差error序列图 Fig. 13 The interpolation residual sequence of Kriging for DOY266 |
|
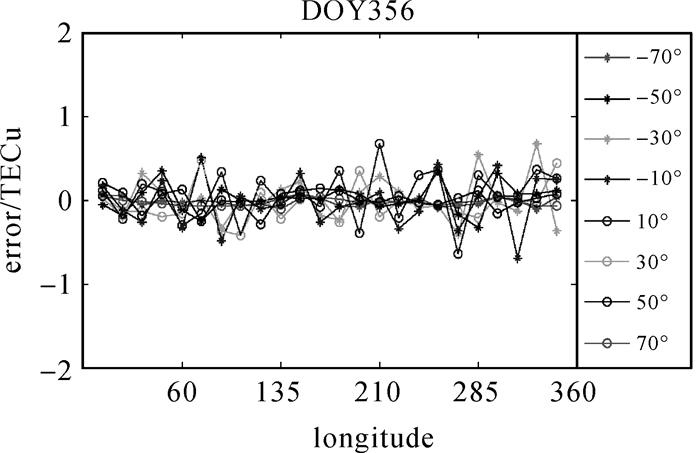
| 图 14 DOY356 Kriging插值残差error序列图 Fig. 14 The interpolation residual sequence of Kriging for DOY356 |
(1) 不同经纬度、不同时间,Kriging插值残差error约1.0~2.0 TECU,与GIM产品精度相当。
(2) 春分日、秋分日和冬至日插值点残差error略大于夏至日。
(3) 低纬度地区插值残差error大于高纬度地区,在纬度±10°区域插值残差error最大。
(4) 白天(经度15°~240°)插值残差error大于夜间。
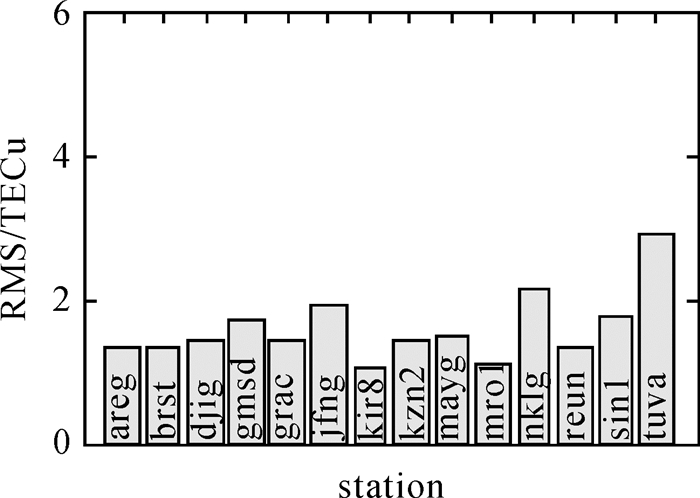
鉴于Kriging样本是分布均匀的规则格网点,取值范围具有特殊性,本文从全球选择19个MGEX测站(部分测站缺失),选用2014年“两分两至”日数据,按照300 s采样率,以其中一个卫星穿刺点为待插值点(“未知点”),其他卫星穿刺点为插值样本(“观测值”),比较已知值和插值结果的残差error。遍历所有历元、所有卫星,每个测站每天统计一组RMS,插值结果如图 15-图 18所示。

|
| 图 15 DOY080 Kriging单站插值RMS Fig. 15 RMS of single station Kriging interpolation for DOY080 |
|
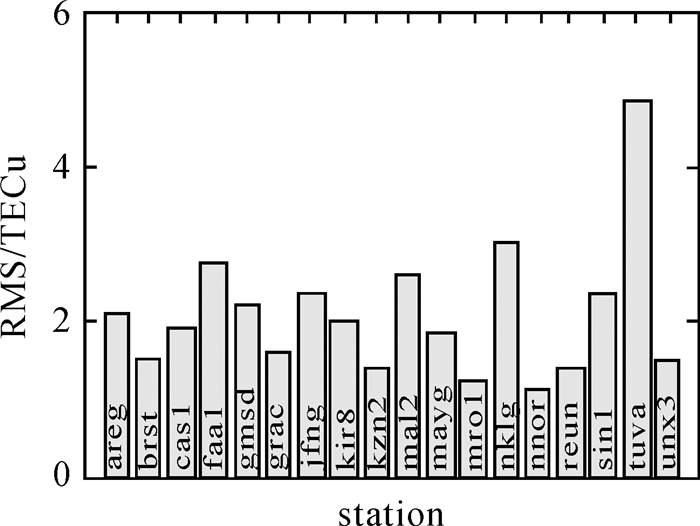
| 图 16 DOY172 Kriging单站插值RMS Fig. 16 RMS of single station Kriging interpolation for DOY172 |
|
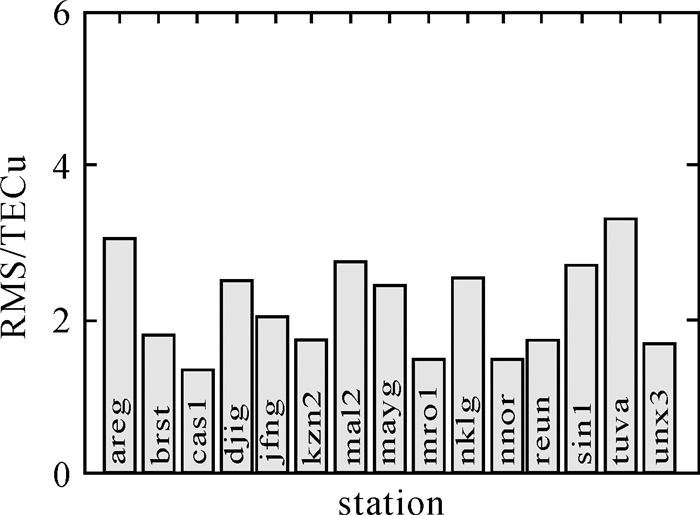
| 图 17 DOY266 Kriging单站插值RMS Fig. 17 RMS of single station Kriging interpolation for DOY266 |
|
| 图 18 DOY356 Kriging单站插值RMS Fig. 18 RMS of single station Kriging interpolation for DOY356 |
(1) 单站Kriging插值的RMS一般为1.04~4.82 TECU,精度略差于GIM产品插值结果。
(2) tuva测站插值结果较差,可能与测站DCB精度或当地电离层活动有关,不考虑该站时,单站Kriging插值的RMS一般为1.04~ 3.62 TECU。
(3) 春分日、秋分日和冬至日单站Kriging插值的RMS略大于夏至日。
(4) 低纬度区域测站插值精度略差于中、高纬度区域。
4 总结电离层是卫星导航系统最严重的误差源之一,高精度的电离层延迟信息不仅可以支撑服务区内单频用户导航定位需要,还有助于提高双频/多频用户精密定位的收敛速度。本文对Kriging方法在电离层TEC插值应用中亟待解决的两个问题进行研究。初步结果如下:
(1) 考虑粗差剔除的高精度Kriging插值问题。构造了粗差剔除统计量,分析该统计量的粗差剔除能力。结果表明,本文构造的统计量粗差剔除能力取决于粗差值与样本精度相对值,以及观测量的数量。该统计量能有效剔除较大粗差,保证插值结果不被粗差数据污染,使插值精度与样本精度匹配。
(2) Kriging插值方法的全球电离层TEC插值精度问题。利用太阳活动高年“两分冬至”日(代表春夏秋冬)GIM产品,采用Kriging插值。结果表明,基于本文试验样本,在太阳活动高年,不同纬度区域、不同时间,Kriging插值精度RMS约为1.0~5.0 TECU。
| [1] |
袁运斌, 霍星亮, 张宝成.
近年来我国GNSS电离层延迟精确建模及修正研究进展[J]. 测绘学报, 2017, 46(10): 1364–1378.
YUAN Yunbin, HUO Xingliang, ZHANG Baocheng. Research progress of precise models and correction for GNSS ionospheric delay in China over recent years[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1364–1378. DOI:10.11947/j.AGCS.2017.20170349 |
| [2] | SCHAER S. Mapping and predicting the earth's ionosphere using the global positioning system[D]. Bern: The University of Bern, 1999. |
| [3] | BHUYAN P K, BORAH R R. TEC derived from GPS network in india and comparison with the IRI[J]. Advances in Space Research, 2007, 39(5): 830–840. DOI:10.1016/j.asr.2006.12.042 |
| [4] |
张小红, 任晓东, 吴风波, 等.
自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报, 2014, 43(2): 118–124.
ZHANG Xiaohong, REN Xiaodong, WU Fengbo, et al. Short-term TEC prediction of ionosphere based on ARIMA model[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 118–124. |
| [5] |
王建平.中国及周边地区电离层TEC短期预报方法研究[D].西安: 西安电子科技大学, 2008. WANG Jianping. Study of the short-term forecasting of the ionospheric TEC in China and its surrounding area[D]. Xi'an: Xidian University, 2008. |
| [6] |
黄玲, 章红平, 徐培亮, 等.
中国区域VTEC模型Kriging算法研究[J]. 武汉大学学报(信息科学版), 2016, 41(6): 729–737.
HUANG Ling, ZHANG Hongping, XU Peiliang, et al. VTEC modeling with Kriging algorithm over China area[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 729–737. |
| [7] | MANNUCCI A J, WILSON B D, EDWARDS C D. Global maps of ionospheric total electron using the IGS GPS network[J]. EOS Trans, 1992, 73(43Sup.): 127–132. |
| [8] | MANNUCCI A J, WILSON B D, YUANG D N, et al. A global mapping technique for GPS-derived ionospheric total electron content measurements[J]. Radio Science, 1998, 33(3): 565–582. DOI:10.1029/97RS02707 |
| [9] | SAMARDJIEV T, BRADLEY P A, CANDER L R, et al. Ionospheric mapping by computer contouring techniques[J]. Electronics Letters, 1993, 29(20): 1794–1795. DOI:10.1049/el:19931194 |
| [10] | STANISKAWSKA I, JUCHNIKOWSKI G, CANDER L R. Kriging method for instantaneous mapping at low and equatorial latitudes[J]. Advances in Space Research, 1996, 18(6): 217–220. DOI:10.1016/0273-1177(95)00927-2 |
| [11] | STANISLAWSKA I, JUCHNIKOWSKI G, HANBABA R, et al. Cost 251 recommended instantaneous mapping model of ionospheric characteristics-PLES[J]. Physics and Chemistry of the Earth, Part C:Solar, Terrestrial & Planetary Science, 2000, 25(4): 291–294. |
| [12] | STANISLAWSKA I, JUCHNIKOWSKI G, CANDER L R, et al. The Kriging method of TEC instantaneous mapping[J]. Advances in Space Research, 2002, 29(6): 945–948. DOI:10.1016/S0273-1177(02)00050-9 |
| [13] | ANSARI K, PANDA S K, CORUMLUOGLU O. Mathematical modelling of ionospheric TEC from Turkish permanent GNSS network (TPGN) observables during 2009-2017 and predictability of NeQuick and Kriging models[J]. Astrophysics and Space Science, 2018, 363: 42. DOI:10.1007/s10509-018-3261-x |
| [14] |
毛田, 万卫星, 孙凌峰.
用Kriging方法构建中纬度区域电离层TEC地图[J]. 空间科学学报, 2007, 27(4): 279–285.
MAO Tian, WAN Weixing, SUN Lingfeng. Central and northern China TEC map using the Kriging method[J]. Chinese Journal of Space Science, 2007, 27(4): 279–285. DOI:10.3969/j.issn.0254-6124.2007.04.003 |
| [15] | ORU'S R, HERNÁNDEZ-PAJARES M, JUAN J M, et al. Improvement of global ionospheric VTEC maps by using Kriging interpolation technique[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2005, 67(16): 1598–1609. DOI:10.1016/j.jastp.2005.07.017 |
| [16] |
王建立, 韩晓冬, 王家胜, 等.
区域格网电离层建模空间插值方法研究[J]. 全球定位系统, 2015, 40(1): 65–68.
WANG Jianli, HAN Xiaodong, WANG Jiasheng, et al. Analysis of spatial interpolation methods in regional grid ionospheric model[J]. GNSS World of China, 2015, 40(1): 65–68. |
| [17] |
翁利斌, 方涵先, 杨升高, 等.
基于IRI背景场的单站电离层TEC地图重构技术[J]. 空间科学学报, 2011, 31(4): 453–458.
WENG Libin, FANG Hanxian, YANG Shenggao, et al. Technique of reconstructing ionospheric TEC map with the data of single station based on the background field by using IRI[J]. Chinese Journal of Space Science, 2011, 31(4): 453–458. |
| [18] |
沈云中, 陶本藻.
实用测量数据处理方法[M]. 2版. 北京: 测绘出版社, 2012.
SHEN Yunzhong, TAO Benzao. Practical methods for surveying data processing[M]. 2nd ed. Beijing: Surveying and Mapping Press, 2012. |
| [19] |
曾怀恩, 黄声享.
基于Kriging方法的空间数据插值研究[J]. 测绘工程, 2007, 16(5): 5–8, 13.
ZENG Huaien, HUANG Shengxiang. Research on spatial data interpolation based on Kriging interpolation[J]. Engineering of Surveying and Mapping, 2007, 16(5): 5–8, 13. DOI:10.3969/j.issn.1006-7949.2007.05.002 |
| [20] |
崔书珍, 周金国, 李天和, 等.
基于重庆CORS网的电离层VTEC插值研究[J]. 测绘科学技术学报, 2016, 33(2): 116–120.
CUI Shuzhen, ZHOU Jinguo, LI Tianhe, et al. Research on ionospheric VTEC interpolation algorithm based on Chongqing CORS network[J]. Journal of Geomatics Science and Technology, 2016, 33(2): 116–120. |
| [21] |
陈春, 宋磊, 班盼盼, 等.
中国地区电离层foF2的重构方法研究[J]. 电波科学学报, 2014, 29(2): 303–309.
CHEN Chun, SONG Lei, BAN Panpan, et al. A study on the reconstruction of foF2 in China region[J]. Chinese Journal of Radio Science, 2014, 29(2): 303–309. |
| [22] |
崔书珍, 周金国.
克里金插值法内插IGS电离层图精度分析[J]. 全球定位系统, 2016, 41(4): 43–47.
CUI Shuzhen, ZHOU Jinguo. Analyse the interpolation accuracy of IGS ionospheric maps using the Kriging interpolation method[J]. GNSS World of China, 2016, 41(4): 43–47. |
| [23] |
李子申, 王宁波, 李敏, 等.
国际GNSS服务组织全球电离层TEC格网精度评估与分析[J]. 地球物理学报, 2017, 60(10): 3718–3729.
LI Zishen, WANG Ningbo, LI Min, et al. Evaluation and analysis of the global ionospheric TEC map in the frame of international GNSS services[J]. Chinese Journal of Geophysics, 2017, 60(10): 3718–3729. DOI:10.6038/cjg20171003 |
| [24] |
赵海山, 杨力, 徐世依.
太阳活动高低年电离层TEC变化特性分析[J]. 导航定位学报, 2017, 5(1): 24–30.
ZHAO Haishan, YANG Li, XU Shiyi. Analysis of ionospheric TEC variation characteristics in solar activity years[J]. Journal of Navigation and Positioning, 2017, 5(1): 24–30. |
| [25] |
冯来平, 朱永兴.
北斗区域卫星导航系统电离层建模精度分析[J]. 海洋测绘, 2016, 36(5): 47–50.
FENG Laiping, ZHU Yongxing. Precision analysis of regional ionosphere model based on Beidou navigation satellite system[J]. Hydrographic Surveying and Charting, 2016, 36(5): 47–50. DOI:10.3969/j.issn.1671-3044.2016.05.012 |



