2. 北京卫星导航中心, 北京 100094;
3. 地理信息工程国家重点实验室, 陕西 西安 710054;
4. 西安测绘研究所, 陕西 西安 710054;
5. 中国科学院上海天文台, 上海 200030
2. Beijing Satellite Navigation Center, Beijing 100094, China;
3. National Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
4. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
5. Shanghai Astronomical Observatory, Shanghai 200030, China
北斗三号全球卫星导航系统将于2020年提供全球服务,届时北斗三号将有30颗在轨卫星。其中,3颗GEO卫星分别位于80°E、110.5°E和140°E;3颗IGSO卫星轨道倾角为55°;24颗MEO卫星平均分布在3个轨道面,每个轨道面8颗卫星,不同轨道面之间升交点赤经相差120°[1-3]。截至2018年12月底,北斗三号已经完成了19颗卫星的发射任务(其中18颗MEO卫星处于在轨服务状态,1颗GEO卫星处于在轨测试状态),并开始向全球用户提供基本服务。
高精度的卫星轨道产品是卫星导航系统提供高性能定位导航授时服务的前提[4-5]。由于北斗卫星导航系统只能在中国境内布设监测站,当MEO卫星运行到境外时,监测站星地跟踪监视中断,极大地制约了北斗卫星轨道的精度[6-9]。
20世纪80年代,美国学者率先提出了基于星间链路的自主导航,以降低GPS系统对地面设施的依赖[10]。1997年,首次搭载了UHF波段星间链路载荷的GPS BLOCK IIR卫星发射,并成功进行一系列自主导航试验[11-14]。鉴于GPS的成功经验,GLONASS、Galileo也相继提出了各自的星间链路发展规划[15-17]。
北斗三号卫星进行了一系列的技术升级[3-4, 18],搭载了Ka波段星间链路载荷,实现了卫星与卫星之间的高精度测距与通信,不但能够在地面运控系统发生故障时切换成自主导航模式,也可以与地面监测站一起进行联合定轨,提高卫星轨道精度。星间链路也可以解决境外卫星广播星历无法及时上注的难题,实现广播星历境内上注、空中分发和整网更新,对缩短卫星星历数据龄期具有重要意义[19-23]。
本文利用国内12个监测站对基本系统的18颗北斗三号组网卫星开展了区域站定轨和区域站+星间链路联合定轨试验,分析了星间链路测量噪声与测距精度,并对比了两种定轨模式的模型和策略,最后对两种定轨模式的重叠弧段轨道误差、轨道预报精度和SLR检核精度进行了分析。
1 星间链路测量噪声与测距精度分析北斗系统星间链路采用时空分多址体制,在轨卫星根据地面规划在不同时刻与不同卫星建链,每次建链时长为3 s,其中前1.5 s是正向测距及通信,后1.5 s是反向测距及通信[24]。根据文献[25]的算法可以将两个相邻时刻的正反向测距值归算至同一时刻。归算后的正反向测距值相加即为卫星相对距离可用于卫星轨道确定,两个测距值相减则为卫星相对钟差,如式(1)所示。可以看出,相对钟差δTAB消除了卫星相对距离,仅与卫星相对钟差、星间链路设备收发时延、未模型化的系统误差以及测量噪声有关
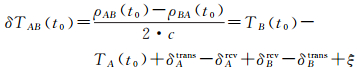 (1)
(1)
式中,t0是归算时刻;δTAB为卫星A与卫星B的相对钟差;ρAB和ρBA为正反向测距值;TA和TB为卫星钟面时;δAtrans、δArcv、δBrcv和δBtrans为星间链路设备的接收和发射时延;ξ为随机噪声等误差项;c为光速。
观测噪声是指观测值中的高频随机抖动白噪声,无趋势性变化。通常认为,星间链路设备收发时延在短时间内不发生变化。对1 h弧段的δTAB进行二次多项式拟合得到的残差,消除了卫星相对钟差、星间链路设备收发时延,以及其他未知系统误差的常数项和慢变项,可用于分析星间链路的观测噪声水平。
测距精度受观测噪声影响的同时,还会受到未知系统误差常数项和慢变项的影响。因此,对24 h弧段的δTAB进行二次多项式拟合得到的残差削弱了卫星相对钟差、星间链路设备收发时延的影响,仅剩余未模型化的系统误差和测量噪声,可用于分析星间链路的测距精度。
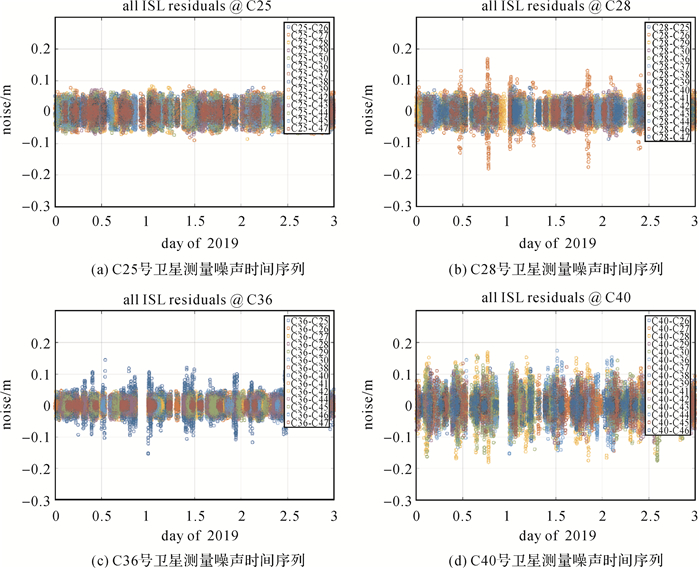
选取2019年1月1日—2019年1月3日的星间链路相对钟差数据,分析星间链路的测量噪声和测距精度。为了保证星间链路测距值的归算精度,认为只有3 s以内完成双向测距,才能进行正反向测距值配对,进而得到卫星之间的相对距离和相对钟差,否则仅有单向测距值时,通常视为无效数据。随着BDS-3组网卫星的陆续发射及星间链路状态的逐步稳定,在18星状态下,每天所有星间链路的双向测距值数据总量约为57万个,数据有效率约为85%,每天可以获得约25万个有效的相对距离和相对钟差数据。图 1给出了以1 h为步长进行多项式拟合后得到的测量噪声时间序列,其中,图(a)、(b)、(c)和(d)分别表示C25、C28、C36和C40号卫星,由于篇幅的限制,只展示其中4颗卫星,其他卫星情况与其类似。横轴表示数据对应的年积日,时长为3 d,纵轴为测量噪声大小,不同颜色代表不同的链路。可以发现,各颗卫星的测量噪声时间序列比较稳定,没有随时间产生明显变化。大部分测量噪声小于5 cm,但是各颗卫星与C40号卫星之间星间链路观测噪声都比较大,从图 1(d)可以看出,C40号卫星整体噪声水平相比其他卫星略高。
|
| 图 1 C25、C28、C36和C40号卫星的测量噪声时间序列 Fig. 1 The time series of C25、C28、C36 and C40 measurement noise |
表 1为星间链路测量噪声及测距精度统计结果。可以发现,C25—C30、C44、C45号卫星测量噪声RMS约为3.2 cm,C36—C43、C46、C47号卫星的测量噪声RMS约为2.3 cm,各颗卫星的平均噪声水平为2.9 cm。需要注意的是,C40号卫星的测量噪声RMS约为5.5 cm,明显高于其他卫星。各条链路以24 h为步长拟合得到的星间链路测距精度基本一致,约为4.4 cm。该精度水平优于伪距测量值,但是低于载波相位测量值。
| cm | |||||
| SCID | 测量噪声RMS | 测距精度RMS | SCID | 测量噪声RMS | 测距精度RMS |
| 25 | 3.04 | 4.48 | 39 | 2.35 | 4.44 |
| 26 | 3.04 | 3.54 | 40 | 5.58 | 7.13 |
| 27 | 3.40 | 4.44 | 41 | 2.02 | 3.71 |
| 28 | 3.97 | 4.52 | 42 | 2.16 | 4.15 |
| 29 | 3.02 | 4.09 | 43 | 2.26 | 3.83 |
| 30 | 2.88 | 4.12 | 44 | 3.01 | 4.45 |
| 36 | 2.51 | 4.16 | 45 | 3.05 | 4.32 |
| 37 | 2.45 | 3.55 | 46 | 2.36 | 3.93 |
| 38 | 2.38 | 4.61 | 47 | 2.41 | 4.25 |
2 定轨模型及策略
为了分析星间链路对北斗三号卫星轨道精度的提升,将定轨试验分为两组:区域站定轨和区域站+星间链路定轨。参与定轨的卫星包括北斗二号所有卫星以及北斗三号基本系统18颗MEO卫星,测站包括中国境内12个监测站。考虑到测站数量少且分布不合理,将定轨弧长设置为3 d。表 2给出了定轨所采用的模型及策略,地面监测站观测数据为L波段B1I和B3I的伪距和相位消电离层组合,采样间隔为30 s,星间链路观测数据为Ka波段伪距归算值,采样间隔为3 s。测站坐标约束为ITRF2008坐标值,卫星和接收机的相位中心改正设置为先验值,忽略PCV改正。模糊度采用浮点解,光压模型采用BERNESE ECOM5参数模型,EOP参数约束至IERS C04模型。
| 参数 | 模型 |
| 弧长/d | 3 |
| 采样间隔/s | L:30 Ka:3 |
| 观测量 | L: B1I&B3I LC+PC Ka:伪距归算值 |
| 站坐标 | 地固系ITRF 2008 |
| 卫星和接收机相位中心改正 | 先验PCO,不考虑PCV |
| 对流层延迟 | L: Saastamoinen模型+GMF模型改正Ka:不考虑 |
| 电离层延迟 | L:消电离层组合消除一阶电离层延迟Ka:小于3 cm,利用Klobuchar模型改正 |
| 模糊度 | 浮点解 |
| 重力场模型 | EGM2008 12×12 |
| 岁差章动模型 | IAU2000R06 |
| 潮汐模型 | L:海洋+大气+固体潮+极潮Ka:不考虑 |
| N体引力 | JPL DE405计算日月及其他行星 |
| 光压模型 | BERNESE ECOM5参数模型 |
| EOP参数 | 约束到IERS C04模型 |
监测站L波段伪距和相位观测数据与星间链路Ka波段伪距观测数据的误差改正方法有所不同:监测站观测数据利用Saastamoinen模型改正+GMF模型参数估计改正对流层延迟,而星间链路观测数据不受对流层影响;监测站观测数据采用双频组合消除一阶电离层延迟,忽略高阶项影响,星间链路观测数据电离层延迟小于3 cm,可利用Klobuchar模型改正;监测站观测数据还需考虑海洋潮、大气潮、固体潮和极潮的影响,而星间链路观测数据则不受潮汐的影响。
3 定轨试验结果及分析选取2019年1月1日至2019年1月14日共14 d的观测数据进行定轨,定轨弧长为3 d,相邻两个弧段时间相差1 d。下面对重叠弧段误差、轨道预报精度以及SLR检核精度进行统计,对比分析区域站定轨和区域站+星间链路定轨的结果。
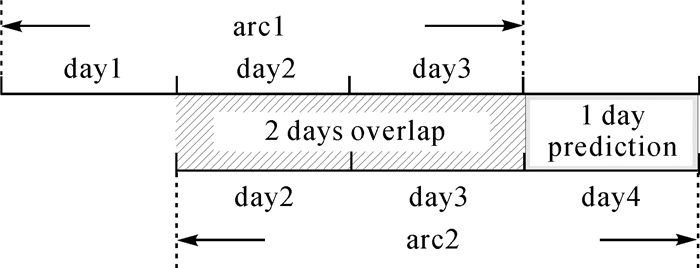
3.1 重叠弧段误差试验的定轨弧长为3 d,arc1采用day1—day3的观测数据定轨,arc2采用day2—day4的观测数据,两个弧段独立计算各自的轨道参数如图 2所示。
|
| 图 2 重叠弧段精度检原理 Fig. 2 The principle of overlapping orbit comparisons |
卫星真实运动轨迹只有一条,在理想情况下,两个弧段重叠部分的轨道估计结果应该完全相同。通过引入重叠弧段轨道互差RMS来评价两条轨道重叠部分在径向、迹向、法向以及三维位置上的差异,可以反映定轨结果的精度和稳定性。
各重叠弧段的平均误差如图 3所示,其中,图 3(a)为仅区域监测站的定轨结果,图 3(b)为区域监测站+星间链路的定轨结果。横轴为卫星的SCID号,纵轴为重叠弧段轨道误差,其中黑色、红色、蓝色和绿色分别为径向、切向、法向和位置误差。表 3为重叠弧段误差统计结果,可以看出:

|
| 图 3 重叠弧段轨道精度 Fig. 3 The precision of overlapping orbit difference |
| cm | |||||||||
| SCID | RS | RS & ISL | |||||||
| radial | along | cross | 3D | radial | along | cross | 3D | ||
| 25 | 12.79 | 63.43 | 39.05 | 75.58 | 1.88 | 9.49 | 11.55 | 15.07 | |
| 26 | 11.94 | 46.80 | 23.84 | 53.86 | 1.51 | 9.38 | 11.96 | 15.27 | |
| 27 | 12.92 | 47.92 | 23.50 | 54.91 | 1.92 | 12.73 | 10.04 | 16.32 | |
| 28 | 14.08 | 57.16 | 25.53 | 64.16 | 1.75 | 11.94 | 9.60 | 15.42 | |
| 29 | 11.60 | 47.43 | 19.72 | 52.66 | 1.64 | 12.36 | 9.43 | 15.64 | |
| 30 | 11.33 | 43.87 | 21.38 | 50.10 | 1.82 | 12.10 | 9.50 | 15.49 | |
| 36 | 16.87 | 85.32 | 37.62 | 94.76 | 1.65 | 10.72 | 11.05 | 15.48 | |
| 37 | 16.87 | 73.82 | 32.19 | 82.28 | 1.51 | 9.97 | 10.68 | 14.69 | |
| 38 | 10.83 | 52.30 | 33.66 | 63.13 | 1.35 | 10.66 | 11.10 | 15.45 | |
| 39 | 13.81 | 56.79 | 32.78 | 67.01 | 1.59 | 10.90 | 11.31 | 15.79 | |
| 40 | 11.56 | 51.51 | 31.52 | 61.49 | 1.31 | 9.39 | 10.86 | 14.42 | |
| 41 | 12.21 | 54.61 | 35.52 | 66.28 | 1.23 | 9.12 | 11.38 | 14.63 | |
| 42 | 14.67 | 60.08 | 33.21 | 70.20 | 1.23 | 10.58 | 10.77 | 15.15 | |
| 43 | 17.48 | 87.26 | 35.05 | 95.65 | 1.11 | 10.94 | 11.28 | 15.75 | |
| 44 | 16.31 | 63.31 | 23.19 | 69.37 | 2.44 | 16.46 | 9.30 | 19.06 | |
| 45 | 13.24 | 52.96 | 22.37 | 59.00 | 1.75 | 12.49 | 9.03 | 15.51 | |
| 46 | 13.23 | 51.33 | 26.69 | 59.35 | 0.98 | 8.48 | 11.37 | 14.22 | |
| 47 | 12.75 | 54.87 | 31.36 | 64.47 | 1.25 | 10.12 | 11.77 | 15.58 | |
| 平均 | 13.58 | 58.38 | 29.34 | 66.73 | 1.55 | 10.99 | 10.67 | 15.39 | |
(1) 仅采用区域站定轨时,各颗卫星重叠弧段误差相当,径向误差RMS为13.6 cm,切向为58.4 cm,法向为29.3 cm,位置误差为66.7 cm。
(2) 加入星间链路以后,径向、切向、法向和位置重叠弧段误差下降至1.6、11.0、10.7和15.4 cm,精度分别提升了88.2%、81.2%、63.5%和76.9%。
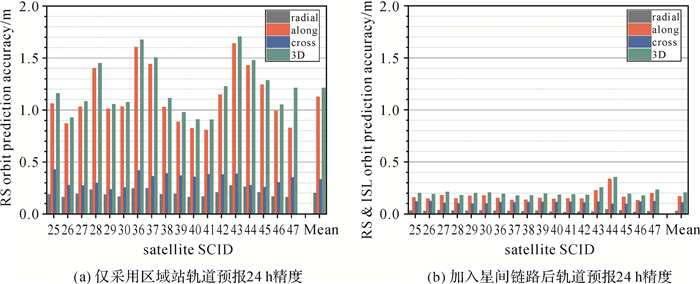
3.2 轨道预报精度地面控制系统利用卫星轨道参数估计值积分得到预报轨道,拟合成易于计算的广播星历,上注至导航卫星,通过卫星播发给用户使用,因此,轨道预报精度直接影响着用户的定位精度。如图 2所示,将arc1得到的轨道进行24 h预报,可以与arc2中的day4实测轨道形成重叠弧段,进而得到预报轨道径向、迹向、法向以及三维位置精度。对上文计算得到的卫星轨道进行预报,统计区域站定轨和区域站+星间链路定轨两种不同方法轨道预报24 h的精度,具体结果如图 4所示。其中,图 4(a)为仅区域监测站的轨道预报结果,图 4(b)为区域监测站+星间链路的轨道预报结果。
|
| 图 4 预报24 h轨道精度 Fig. 4 The accuracy of 24 hour orbit prediction |
表 4给出了预报24 h轨道精度的统计结果,可以看出:
| cm | |||||||||
| SCID | RS | RS & ISL | |||||||
| radial | along | cross | 3D | radial | along | cross | 3D | ||
| 25 | 18.68 | 105.95 | 42.54 | 115.69 | 3.04 | 15.62 | 11.77 | 19.79 | |
| 26 | 15.87 | 86.75 | 27.46 | 92.36 | 2.59 | 14.32 | 12.04 | 18.88 | |
| 27 | 19.21 | 102.95 | 27.06 | 108.17 | 3.33 | 17.83 | 10.31 | 20.86 | |
| 28 | 23.06 | 139.91 | 29.45 | 144.82 | 2.97 | 14.57 | 9.84 | 17.84 | |
| 29 | 18.57 | 100.95 | 23.46 | 105.29 | 2.85 | 17.12 | 9.76 | 19.91 | |
| 30 | 16.41 | 103.07 | 25.22 | 107.37 | 3.20 | 17.53 | 9.78 | 20.32 | |
| 36 | 24.31 | 160.21 | 41.56 | 167.29 | 2.80 | 15.03 | 11.21 | 18.96 | |
| 37 | 24.61 | 143.86 | 35.95 | 150.31 | 2.59 | 13.25 | 10.91 | 17.36 | |
| 38 | 18.59 | 102.70 | 38.71 | 111.32 | 2.37 | 13.42 | 11.15 | 17.61 | |
| 39 | 19.24 | 88.41 | 36.79 | 97.67 | 2.78 | 15.09 | 11.45 | 19.15 | |
| 40 | 15.97 | 82.06 | 35.45 | 90.81 | 1.91 | 14.21 | 11.13 | 18.15 | |
| 41 | 16.76 | 80.52 | 37.96 | 90.58 | 1.59 | 14.52 | 11.38 | 18.51 | |
| 42 | 20.69 | 114.57 | 37.60 | 122.34 | 1.93 | 14.28 | 10.76 | 17.99 | |
| 43 | 27.28 | 193.74 | 38.34 | 199.37 | 1.91 | 22.33 | 11.53 | 25.21 | |
| 44 | 26.09 | 142.63 | 27.56 | 147.59 | 4.23 | 33.43 | 9.51 | 35.01 | |
| 45 | 20.62 | 124.15 | 25.54 | 128.41 | 3.10 | 16.15 | 9.38 | 18.93 | |
| 46 | 16.75 | 98.96 | 30.26 | 104.83 | 1.66 | 12.95 | 11.54 | 17.42 | |
| 47 | 16.02 | 82.63 | 35.02 | 91.17 | 2.24 | 19.64 | 11.87 | 23.06 | |
| 平均 | 19.93 | 114.11 | 33.11 | 120.48 | 2.62 | 16.74 | 10.85 | 20.28 | |
(1) 仅采用区域测站轨道预报24 h,径向精度(RMS)为19.9 cm,切向为114.1 cm,法向为33.1 cm,位置精度为120.5 cm。
(2) 加入星间链路以后,径向、切向、法向和位置精度分别提升至2.6、16.7、10.9和20.3 cm,分别提升了86.9%、85.4%、67.1%和83.2%。
3.3 SLR精度检核SLR精度检核是通过激光测距得到的地面站到卫星激光反射器距离检核卫星轨道的径向精度。计算时,已知激光检核站的高精度坐标和轨道估计结果,可以计算出星地距离,加上相位中心、地球自转潮汐等改正后与实际观测值相减得到的O-C值就是卫星轨道的径向误差,作为一种独立检核卫星轨道径向外符合精度的手段。
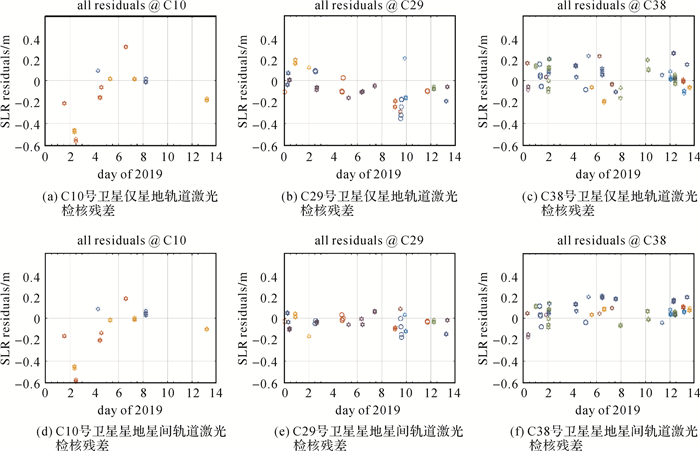
从2018年8月开始,国际激光服务组织(International Laser Ranging Service,ILRS)已经开始安排C29、C30、C37和C38共4颗北斗三号卫星的观测任务,可以利用激光观测数据检核北斗三号卫星轨道外符合精度。激光检核的时段为2019年1月1日—2019年1月14日,共14 d。用于检核的激光地面站共11个,其中亚太地区5个,欧洲5个,美国1个。为了进行精度对比,对北斗二号C01、C08和C10这3颗卫星也进行了分析,结果如图 5所示,统计结果见表 5。
|
| 图 5 激光检核误差时间序列 Fig. 5 The time series of SLR validation residuals |
| cm | ||||||||||
| SCID | 仅星地 | 星地+星间 | 数据量 | |||||||
| 最大 | 最小 | 平均 | RMS | 最大 | 最小 | 平均 | RMS | |||
| C01 | 71.05 | -50.77 | -3.27 | 43.61 | 65.47 | -48.33 | -2.51 | 41.07 | 14 | |
| C08 | -8.27 | -36.06 | -23.70 | 27.22 | 8.52 | -10.57 | -2.60 | 9.01 | 11 | |
| C10 | 31.19 | -56.75 | -13.45 | 26.75 | 18.10 | -59.04 | -14.16 | 26.11 | 32 | |
| C29 | 20.41 | -35.43 | -7.47 | 14.34 | 8.58 | -17.91 | -3.98 | 7.52 | 74 | |
| C30 | 22.94 | -40.86 | -8.35 | 15.07 | 8.52 | -17.63 | -2.56 | 5.99 | 63 | |
| C37 | 23.80 | -20.13 | 3.13 | 13.70 | 19.44 | -12.75 | 4.85 | 9.65 | 70 | |
| C38 | 25.44 | -20.81 | 3.53 | 11.89 | 20.63 | -17.81 | 6.50 | 10.30 | 102 | |
图 5(a)、(b)、(c)分别为C10、C29、C38的仅星地定轨激光检核结果;图 5(d)、(e)、(f)则为星地星间联合定轨激光检核结果。其中,不同颜色及不同的符号表示不同激光地面站的数据。
结果表明:
(1) 对于3颗北斗二号卫星来说,两种定轨方法径向精度均为25~50 cm,加入星间链路对北斗二号卫星影响不大。
(2) 对于4颗北斗三号卫星来说,加入星间链路之前,激光检核残差RMS为13.8 cm,加入星间链路后,激光检核残差RMS降低为8.4 cm,精度提升了39.7%。
4 结论北斗三号卫星的星间测量噪声约为2.9 cm,测距精度约为4.4 cm;仅采用区域测站定轨时,卫星重叠弧段位置误差为66.7 cm,加入星间链路后降低至15.4 cm,精度提高了76.9%;仅采用区域测站轨道预报24 h的位置误差为114.1 cm,加入星间链路以后,降低至20.3 cm,提升了83.2%;加入星间链路后,北斗三号组网星轨道激光检核RMS为8.4 cm,明显优于北斗二号。
北斗三号通过加入星间链路,有效地提高了区域监测站定轨精度,降低了轨道测定对于地面监测站的依赖。可以预见,随着北斗三号卫星的继续发射和星间链路观测数据的增加,北斗三号的轨道精度会得到进一步提升。而且依托于星间链路,北斗三号实现了广播星历境内上注、空中分发和整网更新,使卫星播发的广播星历始终都保持最新,缩短了轨道预报时间,进一步提升了广播轨道的精度,限于篇幅,本文未作详细讨论。星间链路对于北斗卫星导航系统的作用,不仅仅是实现了自主导航,提高了定轨精度,它对于卫星钟差精度的提高、境外卫星状态监视与控制以及卫星自主完好性监测都具有重要意义,其潜能还有待进一步挖掘。
| [1] |
杨元喜.
北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6.
YANG Yuanxi. Progress, contribution and challenges of compass/BeiDou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] |
杨元喜.
综合PNT体系及其关键技术[J]. 测绘学报, 2016, 40(5): 505–510.
YANG Yuanxi. Concepts of comprehensive PNT and related key technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 40(5): 505–510. DOI:10.11947/j.AGCS.2016.20160127 |
| [3] | YANG Yuanxi, XU Yangyin, LI Jinlong, et al. Progress and performance evaluation of BeiDou global navigation satellite system:data analysis based on BDS-3 demonstration system[J]. Science China Earth Sciences, 2018, 61(5): 614–624. DOI:10.1007/s11430-017-9186-9 |
| [4] | CHEN Jinping, HU Xiaogong, TANG Chengpan, et al. Orbit dertermination and time synchronization for new-generation BeiDou satellites:preliminary results[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2016, 46(11): 119502. |
| [5] |
陈康慷, 徐天河, 杨玉国, 等.
iGMAS GNSS钟差产品综合与评估[J]. 测绘学报, 2016, 45(S2): 46–53.
CHEN Kangkang, XU Tianhe, YANG Yuguo, et al. Combination and assessment of GNSS clock products from iGMAS analysis centers[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 46–53. DOI:10.11947/j.AGCS.2016.F025 |
| [6] |
杨元喜, 李金龙, 王爱兵, 等.
北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 57(1): 144–152.
YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system[J]. Science China Earth Sciences, 2014, 57(1): 144–152. |
| [7] | GUO Rui, HU Xiaogong, TANG Bo, et al. Precise orbit determination for geostationary satellites with multiple tracking techniques[J]. Chinese Science Bulletin, 2010, 55(8): 687–692. DOI:10.1007/s11434-010-0074-x |
| [8] | ZHOU Shanshi, HU Xiaogong, WU Bin. Orbit determination and prediction accuracy analysis for a regional tracking network[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(6): 1130–1138. DOI:10.1007/s11433-010-4020-3 |
| [9] |
郭睿, 陈金平, 朱陵凤, 等.
北斗卫星超短弧运动学定轨方法优化与试验分析[J]. 测绘学报, 2017, 46(4): 411–420.
GUO Rui, CHEN Jinping, ZHU Lingfeng, et al. Kinematic orbit determination method optimization and test analysis for BDS satellites with short-arc tracking data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 411–420. DOI:10.11947/j.AGCS.2017.20160361 |
| [10] | ANANDA M P, BEMSTEIN H, CUNNINGHAM K E, et al. Global positioning system (GPS) autonomous navigation[C]//Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences. Las Vegas, Nevada: IEEE, 1990: 497-508. |
| [11] | RAJAN J A. Highlights of GPS Ⅱ-R autonomous navigation[C]//Proceedings of the ION 58th Annual Meeting of the Institute of Navigation and CIGTF 21st Guidance Test Symposium. Albuquerque, NM: ION, 2002. |
| [12] | MERRIGAN M J, SWIFT E R. Expected improvement in NIMA precise orbit and clock estimates due to adding crosslink ranging data[R]. Dahlgren, Virginia: PN, 1999. |
| [13] | ABUSALI P A M, TAPLEY B D, SCHUTZ B E. Autonomous navigation of global positioning system satellites using cross-link measurements[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 321–327. DOI:10.2514/2.4238 |
| [14] | FISHER S C, GHASSEMI K. GPS ⅡF-the next generation[J]. Proceedings of the IEEE, 1999, 87(1): 24–47. DOI:10.1109/5.736340 |
| [15] | REVNIVYKH S G. GLONASS status and modernization[C]//Proceedings of ION GNSS 2011. Nashville, TN: ION, 2011: 3931-3949. |
| [16] | POLISCHUK G M, REVNIVYKH S G. Status and development of GLONASS[J]. Acta Astronautica, 2008, 54(11-12): 949–955. |
| [17] | FERNÁNDEZ F A. Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data[J]. Advances in Space Research, 2011, 47(5): 786–801. DOI:10.1016/j.asr.2010.10.002 |
| [18] | WU Ziqian, ZHOU Shanshi, HU Xiaogong, et al. Performance of the BDS3 experimental satellite passive hydrogen maser[J]. GPS Solutions, 2018, 22(2): 43. DOI:10.1007/s10291-018-0706-1 |
| [19] |
宋小勇, 毛悦, 冯来平, 等.
BD卫星星间链路定轨结果及分析[J]. 测绘学报, 2017, 46(5): 547–553.
SONG Xiaoyong, MAO Yue, FENG Laiping, et al. The preliminary result and analysis for BD orbit determination with inter-satellite link data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 547–553. DOI:10.11947/j.AGCS.2017.20160203 |
| [20] | XU Hongliang, WANG Jinling, ZHAN Xingqun. Autonomous broadcast ephemeris improvement for GNSS using inter-satellite ranging measurements[J]. Advances in Space Research, 2012, 49(6): 1034–1044. DOI:10.1016/j.asr.2012.01.001 |
| [21] | WANG Haihong, XIE Jun, ZHUANG Jianlou, et al. Performance analysis and progress of inter-satellite-link of Beidou system[C]//Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, Oregon: ION, 2017. |
| [22] | REN Xia, YANG Yuanxi, ZHU Jun, et al. Orbit determination of the next-generation Beidou satellites with intersatellite link measurements and a priori orbit constraints[J]. Advances in Space Research, 2017, 60(10): 2155–2165. DOI:10.1016/j.asr.2017.08.024 |
| [23] | ZHAO Qile, WANG Chen, GUO Jing, et al. Precise orbit and clock determination for BeiDou-3 experimental satellites with yaw attitude analysis[J]. GPS Solutions, 2017, 22(1): 4. DOI:10.1007/s10291-017-0673-y |
| [24] | YANG Daoning, YANG Jun, LI Gang, et al. Globalization highlight:orbit determination using BeiDou inter-satellite ranging measurements[J]. GPS Solutions, 2017, 21(3): 1395–1404. DOI:10.1007/s10291-017-0626-5 |
| [25] | TANG Chengpan, HU Xiaogong, ZHOU Shanshi, et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements[J]. Journal of Geodesy, 2018, 92(10): 1155–1169. DOI:10.1007/s00190-018-1113-7 |


