2. 中国科学院大学天文与空间科学学院, 北京 100049;
3. 上海市空间导航与定位技术重点实验室, 上海 200030;
4. 同济大学测绘与地理信息学院, 上海 200092;
5. 北京卫星导航中心, 北京 100094;
6. 战略支援部队信息工程大学, 河南 郑州 450001
2. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 100049, China;
3. Shanghai Key Laboratory of Space Navigation and Positioning Techniques, Shanghai 200030, China;
4. College of Surveying and Geo-Informatics, Tong ji University, Shanghai 200092, China;
5. Beijing Satellite Navigation Center, Beijing 100094, China;
6. Information Engineering University, Zhengzhou 450001, China
北斗卫星导航系统在设计阶段就综合考虑了基本服务(legacy PNT)和星基增强服务(SBAS)的一体化,其中,基本服务为用户免费提供基本导航信息,星基增强服务通过GEO卫星仅向用户广播广域差分和完好性等信息[1-4]。从2017年1月开始,北斗星基增强系统播发了4类参数[5],包括:①实时轨道改正数;②实时钟差改正数;③电离层格网改正数;④分区综合改正数。其中实时轨道和钟差改正数综合了CNMC(code noise and multipath correction)平滑的伪距以及历元间差分的载波相位观测值[6], 格网电离层改正数服务于单频用户[7]。分区综合改正是在以上改正数的基础上,北斗系统播发的特有的改正信息,其包含了指定区域卫星轨道、卫星钟差、测站钟差、对流层延迟及模糊度的综合误差[8-9],已有测试表明,综合使用北斗系统播发的以上四类广播参数,双频用户实时动态精密单点定位PPP(precise point positioning)平均在7 min内收敛至1 m,收敛后平面精度优于0.1 m,高程精度优于0.2 m[8]。针对单频用户,其动态定位三维误差平均20 min能收敛至0.8 m,收敛后的定位精度在水平方向优于0.3 m,高程方向优于0.5 m[10]。总体而言,当北斗用户距离分区中心1000 km范围内时,上述北斗星基增强参数将能提供实时分米级定位服务。
在北斗系统进行广域差分定位性能的大量大范围测试评估中,发现以上服务性能存在不稳定的情况。其中一个重要影响因素为卫星播发的分区改正数存在中断的情况。此外,根据北斗广域差分系统分区综合改正数的使用原则“用户采用系统播发的距离自身最近分区的综合改正数”,动态用户在使用过程中,存在最近分区切换的情况。以上两种情况下,要保证实时广域差分定位连续的高精度服务性能,需要对用户使用的分区改正数进行分区切换,也就是将采用的分区综合改正数从原有分区切换至邻近分区。本文针对这一问题提出了一种连续定位的精密算法。
1 北斗广域四重差分改正数北斗广域四重差分改正数包括实时轨道改正数、实时钟差改正数、电离层格网改正数及分区综合改正数[6, 8]。其中卫星轨道改正参数是利用地面观测站网的观测数据,实时对卫星轨道预报的误差进行解算,用于实时修正基本导航电文中的卫星轨道;t0时刻其模型如下
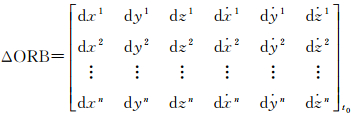 (1)
(1)
式中,n为北斗卫星的颗数;dx、dy、dz、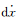
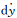
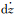
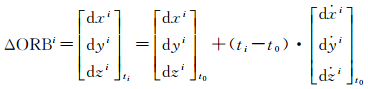 (2)
(2)
卫星钟差改正数是利用地面观测站网的观测数据,在轨道改正数的基础上,实时对卫星钟差预报的误差进行解算,用于实时修正基本导航电文中的卫星钟差参数;t0时刻其模型如下
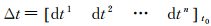 (3)
(3)
在有效作用时间t0时刻至ti时刻内,卫星i的钟差改正数保持不变,由下式计算
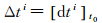 (4)
(4)
格网电离层改正数适用于实时电离层延迟的修正,t0时刻的其模型可表示为
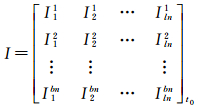 (5)
(5)
式中,Ilnbn为穿刺点格网上的垂直电离层延迟,其中格网区域按照经纬度一定间隔的定义,划分为经度方向[1,ln],纬度方向[1,bn]个区间。在有效作用时间t0时刻至ti时刻内,电离层改正数为穿刺点(b, l)处的电离层延迟可采用相邻4个格网点上电离层延迟的双线性插值获得[11]。
在进行了高精度的轨道修正、钟差修正及电离层修正、以及对流层经验模型修正的基础上,一定区域内测站观测的剩余误差部分较平稳。分区综合改正参数利用各个分区内的观测站的观测数据,综合获取设计区域内伪距以及载波相位的综合改正数[8]。t0时刻载波相位分区综合改正参数模型如下
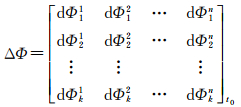 (6)
(6)
式中,n为北斗卫星的颗数;k为分区的个数;每行代表一个分区,不同的列代表每个分区内不同卫星的分区综合改正数。在有效作用时间t0时刻至ti时刻内,每个分区内每颗卫星的分区综合改正数保持不变。卫星i第k分区的分区综合改正数可由下式计算
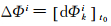 (7)
(7)
当用户接收到北斗卫星播发的广域四重差分星基增强参数后,可采用精密单点定位PPP模型进行实时定位[12]。应用广域四重差分改正数,测站s对卫星i的双频观测用户的观测模型为
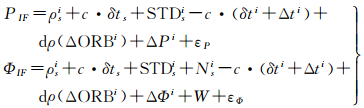 (8)
(8)
式中,PIF、ΦIF分别为双频无电离层组合伪距和载波相位观测值;ρsi为卫星至接收机的几何距离;c为光速;δts为测站钟差参数;STDsi为斜路径对流层延迟改正;δti为广播星历中的卫星钟差;Δti为实时钟差改正数;dρ为轨道改正数转换到视向观测方向的距离改正;ΔPi、ΔΦi分别为伪距、相位观测值的分区综合改正数,其中由于播发资源的限制,目前北斗系统没有播发伪距分区综合改正数;W为相位缠绕改正;εP、εΦ为剩余误差,包含多路径、噪声等误差。在以上PPP观测模型中,所采用的卫星轨道以及钟差由用户接收到的广播星历参数计算;广域四重差分参数直接对观测值进行修正,并且参数通过北斗卫星广播,用户无须增加额外接口。为减弱伪距观测噪声对定位收敛的影响,可对伪距采用实时载波相位平滑[13]。
对于单频用户,为降低电离层误差对定位的影响,精密单点定位可采用UofC模型[14]。应用广域四重差分改正数,以B1频点为例,测站s对卫星i单频用户观测模型为
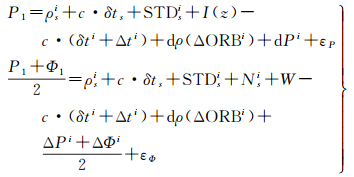 (9)
(9)
式中,P1、Φ1分别为B1频点伪距和载波相位观测值;I(z)为根据格网电离层模型计算得到的天底角为z电离层斜路径延迟改正,其他参数定义同式(8)。
3 广域四重差分参数PPP应用面临的问题利用广域四重差分改正数进行PPP定位应用时,卫星轨道和钟差改正数适用于北斗所有服务区域;格网电离层模型按照测站卫星连线的空间分布进行格网的双线性内插;分区综合改正数改正效果最优的分区通常为中心位置距离用户概略位置最近的分区。实际应用中,由于系统数据限制等原因,目前系统播发的单个分区综合改正数尚存在不连续的情况;同时动态用户在使用过程中还存在从一个服务分区进入到另一个服务分区的情况。以上情况下,为保证用户定位的高精度和连续性,要求用户使用的分区改正数由原分区切换至新分区。
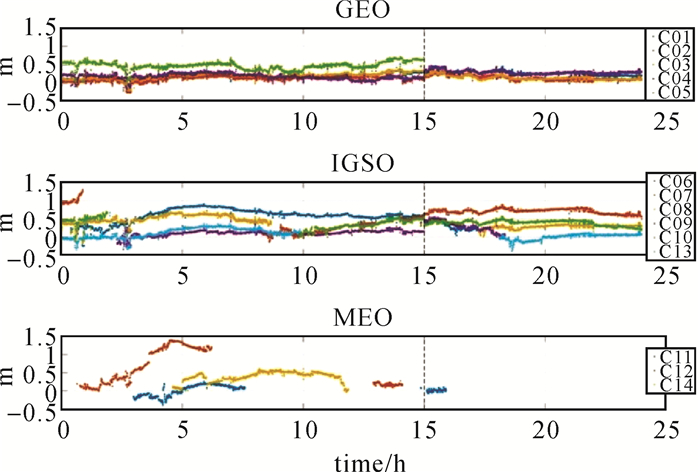
图 1为2018年10月25日北斗系统播发的相邻分区01和04的载波相位分区综合改正数的时序图。其中0~15 h显示的是01分区的分区综合改正数,15~24 h为04分区综合改正数。可以看出,在15:00由01分区切换至04分区后,各颗卫星的相位分区综合改正数产生明显跳变。
|
| 图 1 分区01与04的相位分区综合改正数 Fig. 1 Carrier phase zone corrections of zone 01 and 04 |
针对以上分区切换情况,目前北斗广域差分用户使用说明并没有给出解决方法。在以上情况下,如果01分区在15点开始中断了参数播发,按照传统PPP算法,通常可采用3种策略:
(1) 由于无高精度分区改正数输入,无法进行高精度定位;
(2) 对01分区综合改正数进行外推预报;
(3) 直接采用卫星播发的邻近04分区的分区综合改正数。
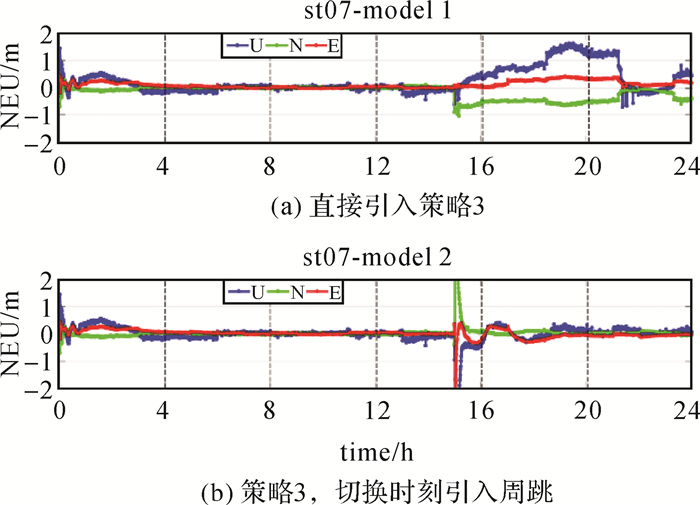
采用第1种策略无法获得高精度定位结果;而采用第2种策略,取决于分区综合改正数中断的时间,预报时间超过3 min,其性能将迅速降低。按照第3种策略,图 2为st07测站双频动态PPP的单天坐标时间序列,在15:00进行分区切换,切换前后分别采用01和04分区的综合改正数。图 2(a)采用策略3进行处理,可以看出,切换后各个方向的定位误差迅速增大且不再收敛,尤其高程方向出现多次剧烈的定位跳变。在使用策略3时, 分区切换引起的分区综合改正数跳变,也可以视为用户对所有卫星的观测产生了周跳,从而可在切换时刻引入周跳重新固定所有卫星的模糊度,图 2(b)显示了在这种处理方式下的定位序列。可以看到,切换分区后用户需要十几分钟的收敛时间才能达到分米级精度,影响了实时动态定位的连续性与可靠性。
|
| 图 2 测站st07基于北斗广域四重差分改正数的PPP动态定位结果 Fig. 2 Daily kinematic coordinate estimates using SBAS PPP based on zone corrections for station st01 |
4 分区切换北斗广域差分精密单点定位算法
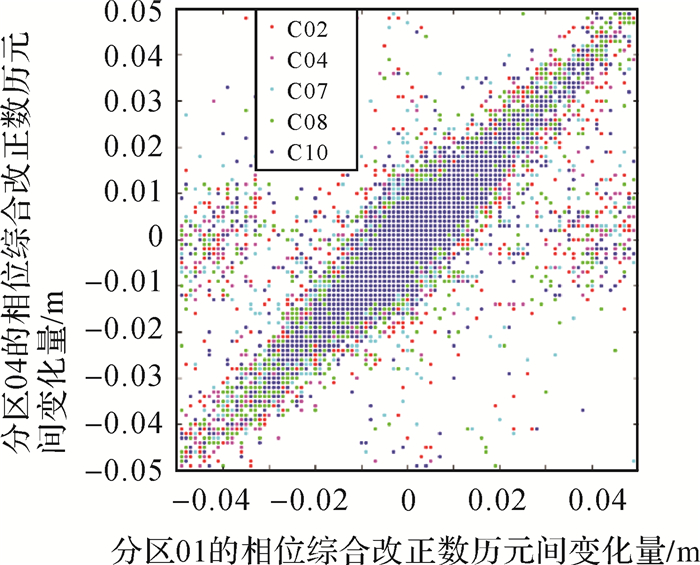
根据分区相位综合改正数的计算原理[8],载波相位分区综合改正数包含了每颗卫星的初始模糊度的偏差以及环境剩余误差,并且每个分区对应同一颗卫星的偏差并不相同。因此,当进行分区切换后,载波相位分区综合改正数的跳变值(分区偏差)实质上包含了两个部分:①两个分区由于所处区域环境误差不同,造成的分区改正的差异;②相邻分区间每颗卫星模糊度初值间差异的影响。将以上相邻两个分区上所有共视卫星的相位综合改正数历元间变化量进行比较,图 3显示了2018年10月25日分区01和分区04上2颗GEO(C02、C04)和3颗IGSO(C07、C08、C10)卫星的相关序列图。可以看出,相邻两个分区的相位综合改正数历元间变化量呈现较高的线性相关,平均相关系数达到0.86。对这两个分区该天所有公共卫星进行统计,其平均相关系数为0.73。
|
| 图 3 分区01和04的载波相位综合改正数历元间变化量 Fig. 3 Epoch difference of carrier phase zone corrections for the zone 01 and 04 |
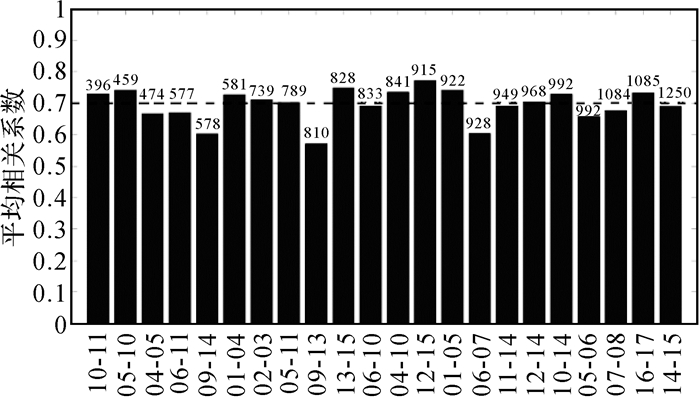
利用2018年10月25日至10月27日共3 d的相位综合改正数数据(采样率36 s),统计所有相邻分区相位综合改正数历元间变化量的相关性。相邻分区的选取原则为:两分区中心间距离不超过1300 km。需要说明的是,第18分区在测试期间未提供产品,故仅评估01至17分区。图 4显示了22组相邻分区中所有卫星的相位综合改正数历元间变化量的平均相关系数,其中横坐标为配对分区的编号(例:分区01与04为“01-04”),按照相邻分区距离递增的顺序标注, 距离值(单位:km)标注在柱状图顶部。可以看到,所有相邻分区间相位综合改正数历元间变化量均呈现较强相关特性,平均达到了0.70(见图 4中虚线),也即相邻分区间相位综合改正数历元间变化量的统计差异约为其误差的30%。考虑到经过分区综合改正后的北斗系统空间信号约为0.2 m[5],从而,该差异引起的误差大约为6 cm左右。
|
| 图 4 相邻分区载波相位综合改正数历元间变化量的相关性统计 Fig. 4 Epoch difference correlation of carrier zone corrections for 22 pairs of adjacent zones |
基于以上相邻分区的相位综合改正数历元间变化量高度相关的特性,在进行分区切换之后,可将新分区卫星i的相位综合改正数历元间变化量叠加在旧分区的相位综合改正数上,逐历元计算出一个“伪”载波相位综合改正数ΔΦi,其公式如下
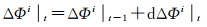 (10)
(10)
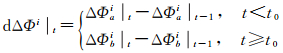 (11)
(11)
式中,dΔΦi为卫星i在前后相邻历元相位综合改正数的变化量;a表示切换前的分区;b表示切换后的分区;t0为切换分区的历元。通过该算法,切换分区后,由于dΔΦi在新旧分区之间差异仅为数厘米,从而防止了载波相位综合改正数的大幅跳变,实现载波相位分区综合改正数的连续一致。
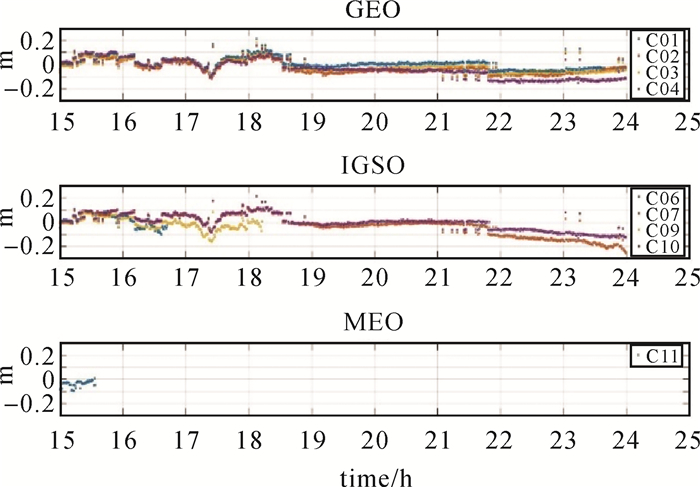
应用以上变换,图 5显示了以上卫星分区综合改正数从分区01切换到分区04后,由分区04计算的“伪”载波相位分区综合改正数与分区01实际的载波相位分区综合改正数差值情况,经统计,两者差值的RMS为0.062 m(与前文分析一致),能够满足系统分米级定位的需求。需要说明的是,对于切换历元两个分区的非共视卫星(C05、C08、C12、C13、C14)无须进行相位分区综合改正数的归算,在后续定位中对其模糊度进行初始化即可。此外,当不发生分区切换时,dΔΦi与原分区的相位综合改正数完全相同,因此,该算法也适用于不切换分区的情况。
|
| 图 5 “伪”相位分区综合改正数与原分区实际相位分区综合改正数的差异 Fig. 5 Difference between pseudo-zone corrections and original zone corrections |
5 新算法的测试分析 5.1 数据处理策略
对以上基于北斗广域四重差分参数的PPP定位算法进行静态测站及动态测站定位测试。静态测站定位测试中,选取了位于中国境内东南西北及中部的7个北斗观测站2018年3月14日至3月23日10 d的观测数据;动态测试采用了2017年7月12日在新疆某地山区车载实时动态试验数据。静态和动态测站的数据处理均采用了卡尔曼滤波进行逐历元参数估计;待估参数包括:测站坐标、接收机钟差及各颗卫星在连续观测弧段内的模糊度信息等。双频定位中电离层延迟采用无电离层组合消除一阶项误差;单频定位中,电离层采用格网电离层模型进行修正;对流层延迟干分量和湿分量初值采用GPT2w模型改正[15],值得注意的是,由于分区综合改正数中已包含对流层延迟的残余误差,故不再对其残余误差进行估计[16]。卫星轨道和钟差采用北斗广播星历,无须对卫星端的PCO(phase center offset)/PCV(phase center variation)进行改正。具体的数据处理策略见表 1,表中P为权重;e为卫星高度角。
| 参数 | 处理策略 |
| 北斗广域四重差分PPP定位 | |
| 观测量 | BDS伪距+载波相位 |
| 信号 | B1+B2(双频)/B1(单频) |
| 截止高度角 | 10° |
| 先验约束 | 伪距1 m;载波相位0.01 m |
| 观测值权重 | 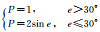 |
| 卫星轨道、钟差 | 广播星历 |
| 星基增强参数 | 卫星钟差;轨道改正数;格网电离层改正数;分区综合改正数 |
| 对流层延迟 | GPT2w+SAAS+VMF1 |
| 固体潮、海潮、相对论、地球自转 | IERS2010[17] |
| 相位缠绕 | 模型改正 |
| 测站坐标 | 估计,先验约束10 km |
| 接收机钟差 | 估计,先验约束1 ms |
| 模糊度 | 估计,浮点解 |
本文定义基于分区综合改正数的北斗广域四重差分原有PPP算法为算法1(model 1),基于本文分区切换的北斗广域四重差分PPP新算法为算法2(model 2)。按照上述数据处理策略,分别采用北斗静态站数据和车载动态数据进行实时动态定位,以对新算法(model 2)进行分析验证。
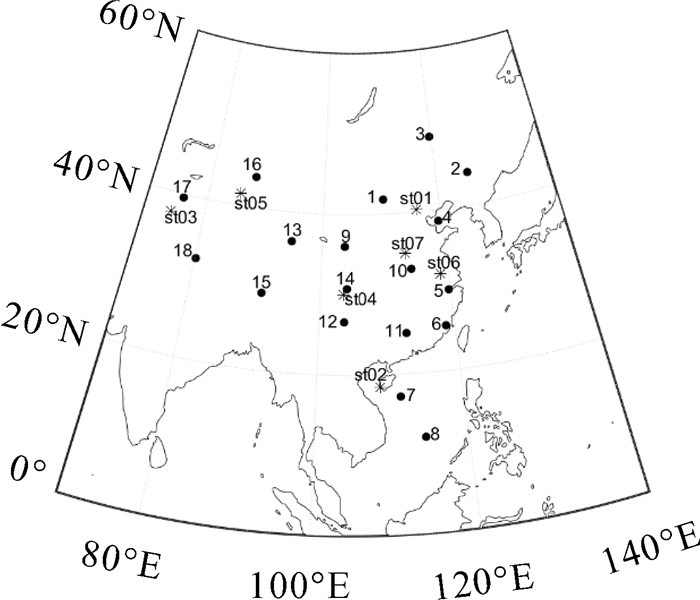
5.2 BDS静态站数据测试静态测站(雪花形)及分区中心(实心圆点)的分布如图 6所示,各个测站坐标已精确测定,位置精度优于2 cm。表 2为测站与分区的对应情况,其中zone1表示测站所处分区,zone2表示测站邻近分区,选取原则是分区综合改正数的应用范围尽量不超过1000 km。
|
| 图 6 北斗静态测站与分区中心分布 Fig. 6 Static sites distribution and center of BDS zones |
| site | zone1 | zone2 | 相邻分区中心之间距离/km |
| st01 | 01 | 04 | 581 |
| st02 | 07 | 06 | 928 |
| st03 | 17 | 16 | 1085 |
| st04 | 14 | 09 | 578 |
| st05 | 16 | 17 | 1085 |
| st06 | 05 | 11 | 790 |
| st07 | 10 | 01 | 637 |
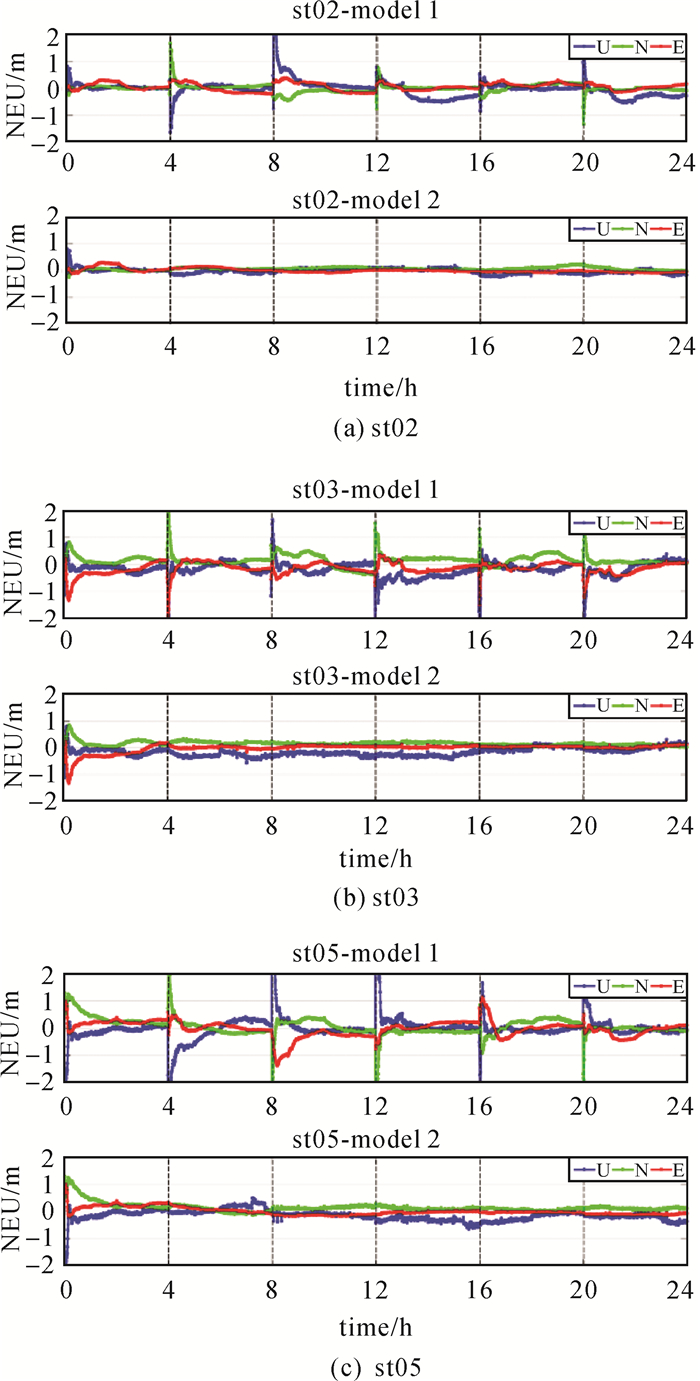
图 7为2018年3月16日测站st02、st03、st05双频动态PPP定位的结果(采样率30 s),每幅图的上子图表示算法1,下子图表示算法2。处理过程中人为进行分区的切换,切换时刻如图中黑色虚线所示,其中00:00至04:00采用zone1分区,此后每隔4 h在zone1和zone2间来回切换。可以看出,每个测站在分区切换前均能快速收敛至1 m,并达到分米级精度,说明分区综合改正数可以较好地消除各种未模型化的残余误差,实现北斗高精度定位。当发生分区切换时,算法1的定位结果在南北(N)、东西(E)、高程(U)方向上均出现明显跳变,原因是算法1在切换时刻重新固定了所有卫星的模糊度,需要重新收敛。算法2对载波相位分区综合改正数进行实时归算,使切换后的分区与原分区的相位综合改正数保持了较好的一致性,从而保证了实时动态定位的连续性。
|
| 图 7 测站(a)st02,(b)st03,(c)st05基于算法1和算法2的动态定位单天解 Fig. 7 Daily kinematic coordinate estimates using model 1 and model 2 for the stations (a)st02, (b)st03, (c)st05 |
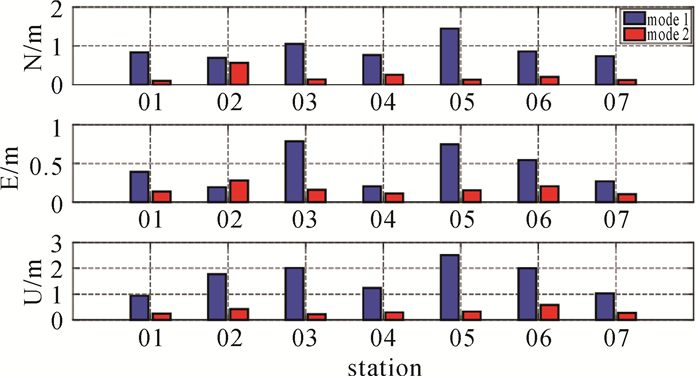
基于分区综合改正数的双频动态PPP平均收敛时间通常不超过10 min[8, 13],将分区切换时刻起连续10个历元(5 min)的定位误差(N、E、U方向)的RMS作为精度指标,比较两种算法的性能。统计7个测站10 d(1 d切换5次)的定位结果,如图 8所示,可以看出算法2相对于算法1,所有测站的定位精度在水平方向,特别是高程方向都得到了显著提高,其中算法2在定位的南北和东西方向误差不超过0.3 m,高程方向优于0.5 m。表 3统计了所有测站的三维定位误差RMS,从中可以看到算法2在分区切换后10个历元的整体平均定位精度为0.45 m,满足分米级定位要求, 采用新算法在分区切换时未发生定位跳变,可有效保证实时动态定位的连续性。
|
| 图 8 各个测站切换分区后两种算法的定位误差统计 Fig. 8 Coordinate precision of SBAS PPP models for all stations in north, east and up component |
| m | ||
| site | 3D RMS | |
| mode 1 | mode 2 | |
| 01 | 1.36 | 0.29 |
| 02 | 2.00 | 0.80 |
| 03 | 2.44 | 0.30 |
| 04 | 1.55 | 0.41 |
| 05 | 3.06 | 0.39 |
| 06 | 2.29 | 0.66 |
| 07 | 1.33 | 0.31 |
| mean | 2.00 | 0.45 |
5.3 动态车载数据测试
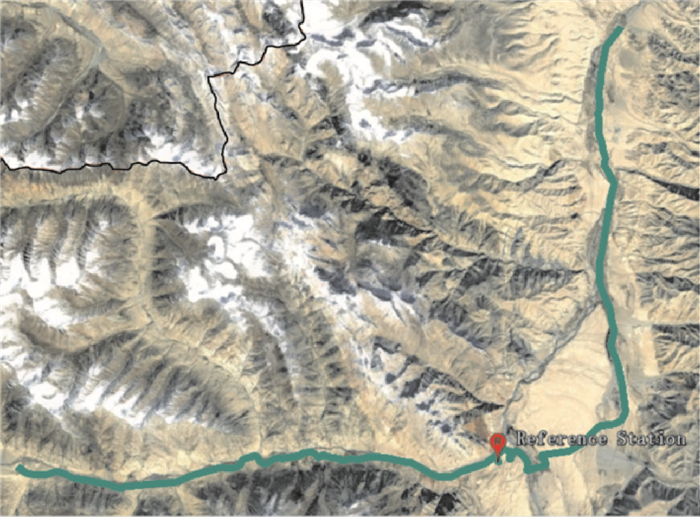
为验证新算法在实际实时动态定位中的性能,进一步开展了车载实时定位测试。图 9为2017年7月12日在新疆某地山区进行车载实时动态定位试验的路线图,测试时长约2 h(当天10:35至12:30)。图中三角标志为设置的基准站,使用司南M300接收机采集GPS/GLONASS/BDS三系统观测数据,基准点坐标采用GPS PPP静态单天解;车载测试采用司南T300接收机采集GPS/GLONASS/BDS三系统观测数据,行驶路线最远点距离基准站约30 km,车载轨迹基准坐标采用GPS/GLONASS双系统差分定位解,截止高度角为10°,模糊度固定阈值设置为2,固定率为84.1%。
|
| 图 9 车载动态定位测试路线 Fig. 9 Real-time on-road tracks |
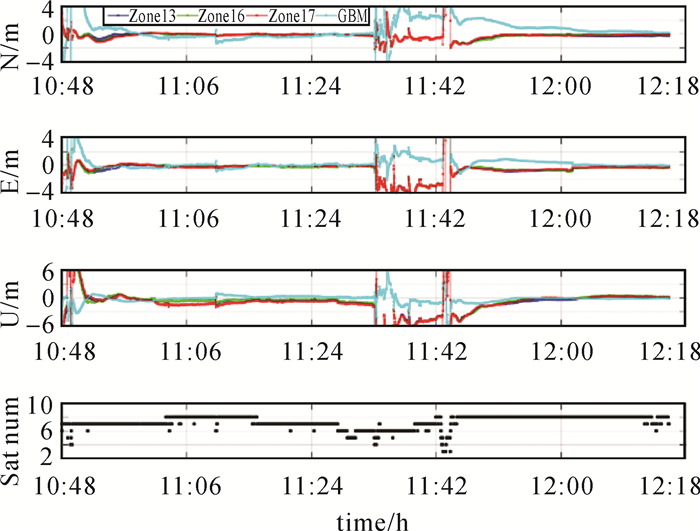
图 10为当天10:48至12:18采用北斗广域四重差分改正数的车载双频实时PPP动态定位结果与RTK解算结果的差值。其中Zone13、Zone16、Zone17分别表示采用13、16、17分区综合改正数的BDS星基增强PPP定位结果,13和17分区均为测试地点的邻近分区,GBM表示采用GFZ分析中心提供的北斗事后精密产品的BDS PPP定位结果。可以看出,在定位收敛后,基于GBM精密产品的PPP定位精度在高程方向上略好于基于分区综合改正数的PPP定位,而在平面方向上精度不如北斗实时播发的广域四重差分改正数的结果。采用不同分区的综合改正数,其水平方向的定位误差曲线基本一致,精度优于0.5 m;高程方向上,17分区的定位精度略差于13和16分区,原因是车载测试地点距离17分区中心较远,达到1000 km左右,信号传播路径上各种共性误差的相关性降低,影响了分区综合改正的效果。值得注意的是,在11:33至11:48期间,由于车载接收机信号受到部分遮挡,可观测卫星数骤降至3~4颗(见图 10中第4幅子图),导致出现定位多次重收敛现象。
|
| 4幅子图分别为坐标在南北,东西,高程的误差以及可见卫星个数;不同颜色代表采用不同输入数据 图 10 基于北斗广域实时四重差分改正数及GBM精密产品PPP车载动态定位结果与RTK的差值 Fig. 10 Kinematic coordinate differences between SBAS PPP and RTK |
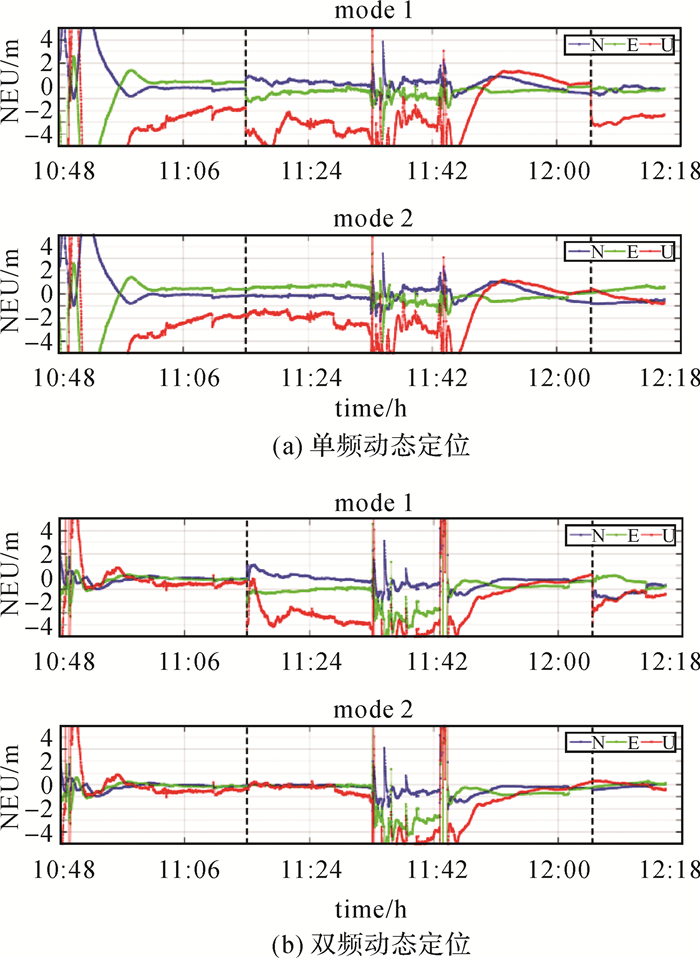
对以上的车载数据进行分区切换试验。人为对使用的分区进行切换,图 11为基于分区切换的BDS星基增强PPP定位结果,切换时刻在11:15和12:05(图中虚线所示),其中11:15由Zone16切换至Zone13, 12:05由Zone13切换至Zone16。图 11(a)中显示了单频动态定位与RTK解算结果的差值。图中显示,基于分区综合改正数单频平面坐标13 min左右能够收敛到1 m以内,在竖线切换时刻,现有算法(mode1 1)产生了最大为5 m的跳变。图 11(b)为双频动态定位与RTK解算结果的差值。图中显示,基于分区综合改正数双频平面坐标3 min左右能够收敛到1 m以内,高程需要5 min左右收敛到1 m以内,在竖线切换时刻,现有算法(mode 1)造成了定位的重新收敛。采用本文分区切换算法(mode 2),单频和双频的定位结果都保持连续无跳变,定位精度与切换前基本一致。
|
| 图 11 车载动态下,不同分区综合数互相切换的星基增强单、双频PPP结果与RTK的差值 Fig. 11 Kinematic coordinate differences between SBAS PPP and RTK |
6 结论
本文介绍了北斗广域四重差分改正数及其使用方法,并对分区切换引起相位综合改正数跳变的原因进行详细阐述,指出原有BDS星基增强PPP算法在分区切换定位中存在较大偏差,无法保证实时动态定位的连续性。
根据相邻分区的相位综合改正数历元间变化量高度相关这一特性,提出了一种基于分区切换的BDS星基增强PPP算法,利用北斗测站静态数据和车载动态数据对新算法进行了评估验证。结果表明采用新算法静态测站的水平和高程定位误差分别不超过0.3 m和0.5 m,平均三维定位精度优于0.5 m;车载实时动态定位中,单双频定位3个方向的误差曲线均保持平稳且无跳变,与切换前的定位精度保持一致,证明了新算法的有效性与正确性。以上算法对于北斗广域差分服务在分米级精度上的推广和应用具有较好的应用效果。此外,北斗系统广域差分定位产生跳变的根本原因是系统端参数的缺失,将本文提出的方法应用于系统的建设,有助于解决系统端参数的跳变问题。
| [1] |
杨元喜.
弹性PNT基本框架[J]. 测绘学报, 2018, 47(7): 893–898.
YANG Yuanxi. Resilient PNT concept frame[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 893–898. |
| [2] |
杨元喜.
北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6.
YANG Yuanxi. Progress, contribution and challenges of compass/BeiDou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [3] |
杨元喜, 李金龙, 王爱兵, 等.
北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72–81.
YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system[J]. Science China:Earth Sciences, 2014, 44(1): 72–81. |
| [4] |
杨元喜, 李金龙, 徐君毅, 等.
中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1734–1740.
YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the compass satellite navigation system to global PNT users[J]. Chinese Science Bulletin, 2011, 56(21): 1734–1740. |
| [5] |
周建华.北斗导航与广域差分的性能提升及实验验证[C]//第八届中国卫星导航学术年会.上海: [s.n.], 2017. ZHOU Jianhua. BDSSIS performance improvement for legacy PNT and differential service[C]//Proceedings of China Satellite Navigation Conference (CSNC) 2017. Shanghai: [s.n.], 2017. |
| [6] |
陈俊平, 杨赛男, 周建华, 等.
综合伪距相位观测的北斗导航系统广域差分模型[J]. 测绘学报, 2017, 46(5): 537–546.
CHEN Junping, YANG Sainan, ZHOU Jianhua, et al. A pseudo-range and phase combined SBAS differential correction model[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 537–546. |
| [7] | WU Xiaoli, HU Xiaogong, WANG Gang, et al. Evaluation of compass ionospheric model in GNSS positioning[J]. Advances in Space Research, 2013, 51(6): 959–968. DOI:10.1016/j.asr.2012.09.039 |
| [8] |
陈俊平, 张益泽, 周建华, 等.
分区综合改正:服务于北斗分米级星基增强系统的差分改正模型[J]. 测绘学报, 2018, 47(9): 1161–1170.
CHEN Junping, ZHANG Yize, ZHOU Jianhua, et al. Zone correction:a SBAS differential correction model for BDS decimeter-level positioning[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(9): 1161–1170. DOI:10.11947/j.AGCS.2018.20170156 |
| [9] | CHEN Junping, ZHANG Yize, YANG Sainan, et al. A new approach for satellite based GNSS augmentation system: from sub-meter to better than 0.2 meter era[C]//Proceedings of the ION 2015 Pacific PNT Meeting. Honolulu, Hawaii: [s.n.], 2015. |
| [10] |
张益泽, 陈俊平, 杨赛男, 等.
北斗广域差分分区综合改正数定位性能分析[J]. 武汉大学学报(信息科学版), 2019, 44(2): 159–165.
ZHANG Yize, CHEN Junping, YANG Sainan, et al. Analysis of PPP performance based on BDS comprehensive zone corrections[J]. Geomatics and Information Science of Wuhan University, 2019, 44(2): 159–165. |
| [11] | WU Xiaoli, ZHOU Jianhua, TANG Bo, et al. Evaluation of Compass ionospheric grid[J]. GPS Solutions, 2014, 18(4): 639–649. DOI:10.1007/s10291-014-0394-4 |
| [12] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005–5017. DOI:10.1029/96JB03860 |
| [13] |
陈俊平, 胡一帆, 张益泽, 等.
北斗星基增强系统性能提升初步评估[J]. 同济大学学报(自然科学版), 2017, 45(7): 1075–1082.
CHEN Junping, HU Yifan, ZHANG Yize, et al. Preliminary evaluation of performance of BeiDou satellite-based augmentation system[J]. Journal of Tongji University (Natural Science), 2017, 45(7): 1075–1082. |
| [14] | GAO Yang, SHEN Xiaobing. A new method for carrier-phase-based precise point positioning[J]. Journal of Navigation, 2002, 49(2): 109–116. DOI:10.1002/navi.2002.49.issue-2 |
| [15] | SAASTAMOINEN J. Atmospheric correction for the troposphere and stratosphere in radio ranging Satellites[C]//proceedings of The Use of Artificial Satellites for Geodesy. Washington D C: [s.n.], 1972. |
| [16] | ZHANG Yize, CHEN Junping, YANG Sainan, et al. Initial assessment of BDS zone correction[C]//SUN J, LIU J, YANG Y, et al. China Satellite Navigation Conference (CSNC) 2017 Proceedings: Volume Ⅱ. CSNC 2017. Lecture Notes in Electrical Engineering. Singapore: Springer, 2017. |
| [17] | PETIT G, LUZUM B. IERS Conventions(2010)[M]. Frankfurt am Main: Verlag des Bundesamtsfür Kartographie und Geodäsie, 2010. |



