规则格网数字高程模型以一系列的规则格网单元高程值对地形表面进行模拟和模式化表达,其数据结构简单、计算处理方便的特性使其成为地形分析的重要数据来源[1]。作为数字流域、水文分析以及土壤侵蚀分析等领域的关键技术[2-3],基于DEM的谷地线自动提取已成为GIS应用分析研究的热点问题。常用的谷地线提取采用流水模拟法,以水流路径算法描述地表物质在格网单元中由高处向低处的传输和流动[4],其提取结果依赖于相邻格网之间的高程差以及邻域关系[5-6],表现为格网单元之间的连线。基于规则格网DEM谷地线提取受格网的几何形态、空间剖分和网格布局影响较大。传统规则格网DEM结构中,四边形格网的边邻域与角邻域之间存在1: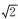
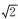
作为构建DEM的规则格网单元应满足形状单一、无缝拼接、编码规范、层次性强以及易于与地理空间转换等特性,有关研究发现正三角形、正四边形以及正六边形可作为规则格网单元对地形曲面进行剖分。其中,三角形不具有可平移性,即构建过程中会产生格网单元方向的变化,该特性加大了后续的计算和分析的难度[12]。正四边形通过阵列结构表达适合计算机处理、存储、计算,因此,基于正四边形规则格网DEM(以下简称为四边形DEM)数据已成为一种通用的DEM数据标准。然而,正四边形存在边邻域和对角邻域两种不同邻域关系(在距离度量上表现为1与2的差别),使其作为DEM格网单元在两方向上对于地形表达具有差异性[13]。正六边形则具有更一致的邻接性,即6个邻域单元均与中心格网以边邻接,且与中心格网的距离相同,该特性使六边形在处理最近邻域、移动路径等邻域处理问题中具有一定的优势[14-15]。在面积相同情况下,六边形更接近于圆形,其格网结构更紧凑,研究表明[17]六边形作为栅格数据结构中的栅格单元表现更优越,同四边形结构相比,在相同数据量下,具有较高的数据精度。此外,六边形具有更高阶的对称性,即六边形更具各向同性,在空间场建模中越来越得到重用。将六边形优势应用于DEM的流向分析,文献[18-19]认为六边形可在一定程度上减小流向算法对于格网方向的依赖性,且在重采样后的低分辨率下保持原分辨率的流向能力更好。然而,六边形优势对于谷地线提取结果存在的影响未可知。
针对该问题,本文探讨了六边形DEM构建以及谷地线自动提取在六边形DEM格网结构上的实现,并以等高线数据分别建立四边形DEM和六边形DEM,采用多分辨率分析方法,以谷地线数量、长度和形状3个特征指标对2种DEM所提取的结果进行讨论,以此评价DEM网格几何形态对于谷地线提取的影响。
1 六边形格网DEM建立 1.1 六边形格网结构格网结构是DEM表达真实地理空间的数字格网空间基础,为了满足DEM应用分析,六边形格网结构的建立应包括:①建立适合计算机存储与处理,易于与矢量坐标实现对接的格网坐标系;②建立格网之间的邻域关系。
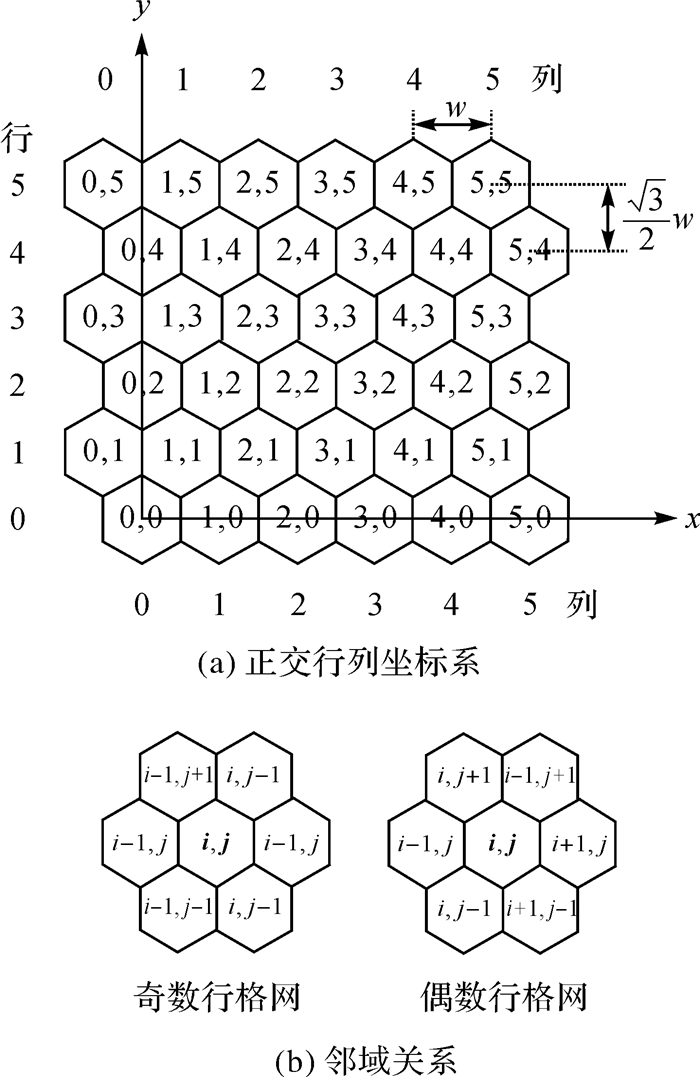
正六边形格网坐标系包括正交行列坐标系、极坐标系、三斜轴坐标系以及Gosper曲线坐标系[15-16]。其中正交行列坐标系是标记六边形格网单元最简单的方式,其思想与四边形格网结构类似,即用行列号直接对格网单元进行编码,该坐标系与笛卡儿坐标系兼容,便于计算机存储与组织,易于实现从格网坐标到地理坐标的转换。本文基于“奇数行左偏移”的正交行列坐标系构建六边形格网结构,如图 1所示,以(i, j)为对格网坐标进行编码,其中i和j分别为格网单元所在的列、行数,(0, 0)格网中心点为坐标系原点,该结构中行与行之间呈“之”字形错位。
|
| 图 1 六边形格网结构 Fig. 1 Hexagon gridded structure |
基于“点栅格”的观点,DEM格网单元的属性以及格网之间的计算与分析均以对应的网格中心点代替,则获取格网结构中每个网格中心点的地理坐标值是六边形格网结构应用于DEM的关键一步。根据图 1所建立的格网坐标系,六边形格网单元水平方向宽度为w,行列两方向上格网间隔比值为1: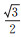
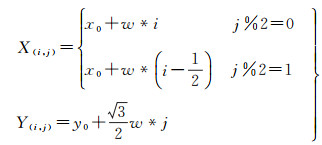 (1)
(1)
式中,X(i, j)和Y(i, j)为格网坐标为(i, j)网格中心点的地理坐标;x0为格网坐标原点所对应的地理横坐标;y0为格网坐标原点所对应的地理纵坐标。
6邻域关系是六边形格网结构应用于DEM分析中邻域处理的基本关系。然而,行之间的错位使奇数行格网和偶数行格网的6邻域格网坐标编码规律存在差异,如图 1(b)标红邻域,偶数行格网中该邻域的列号均比奇数行格网大1,以此编码规律便可构建格网之间的邻域关系。
1.2 规则格网DEM构建为保证六边形DEM和四边形DEM在建立过程中误差来源的一致性,本文利用等高线构建规则格网DEM[20]。
(1) 在二维平面上,对研究区域进行格网划分(格网大小取决于DEM应用要求),构建格网单元之间的邻域关系,建立格网结构。为保证2种DEM高程点采样密度相同,本文以面积定义分辨率,则相同面积下,六边形格网单元水平方向格网宽度(w)与四边形格网单元边长(l)的比值为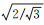
(2) 根据格网坐标与地理坐标之间的对应关系,获取格网结构中每个格网单元中心点对应的地理坐标,以便后续格网高程值的内插计算。
(3) 利用等高线构建TIN数据结构,建立六边形格网中心点与TIN三角形的对应关系(图 2),对于每个格网中心点,获取其所在TIN结构中的三角形,基于三角形的线性内插法计算格网中心点的高程值。
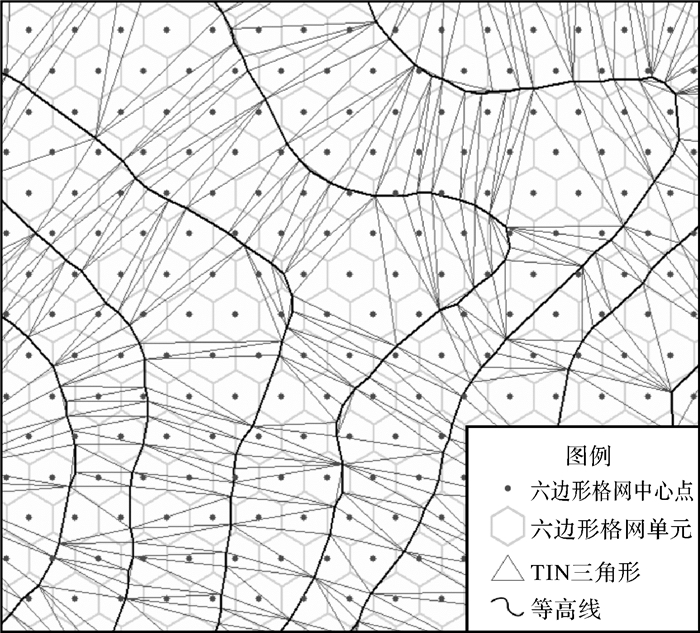
|
| 图 2 六边形格网中心点与TIN三角形对应 Fig. 2 Correspondence between central points of hexagons and triangles of TIN |
2 基于六边形DEM的谷地线提取
谷地线提取的原理[7]源于地表径流的自然特性,即水流沿斜坡最陡方向,通过比较邻域格网的高程值计算各格网点水流方向,基于水流方向计算汇合到每一个格网的地表径流量,通过设定流量阈值,提取大于该阈值的格网即可获得相应的谷地线起始位置以及谷地线网络。简而言之,谷地线自动提取过程包括:填洼处理、水流方向计算、水流累积量计算及流量阈值确定,最后根据流向追踪提取谷地线。其中填洼处理、水流方向计算及平地区域水流方向确定决定了后续步骤的计算,为谷地线提取的关键问题,为此,国内外提出了众多算法[21-23],然而算法的实现均基于四边形DEM格网结构以及邻域关系,未对六边形DEM格网结构下算法实现的可行性进行讨论。因此,本文基于W&L算法、单流向算法分别讨论在六边形格网DEM结构中填洼处理、流向计算的实现,并为平地区域设计流向计算方法。
2.1 填洼处理W & L算法是高效率填洼算法之一[24]。通过模拟洪水淹没自然地形的过程,即水平面从最低点逐渐抬升至淹没整个地表,栅格单元从外围向内部逐个被淹没,该算法以DEM的边缘最低点作为出水口点,通过与邻域格网点高程值进行比较,以确定每个格网单元流向出水口的最小高程值为溢水高程值,并将格网单元高程值提升至溢水高程值,其实质就是从潜在出口向内部进行逆向邻域搜索完成整个填洼过程。其实现过程是在溢水高程值的基础上,利用最小代价搜索,以优先队列数据结构完成填洼。
该算法应用到六边形DEM格网结构中原理相同,而最大的不同之处在于由出水口向内部搜索时对于格网单元由8方向到6方向的邻域处理变化,具体实现步骤为:
(1) 将六边形DEM数据的边缘格网高程值设置为溢出高程值,并压入最小优先队列,将相应格网标记为“1”。
(2) 获取最小优先队列中队首元素以及对应的格网单元c,根据最小邻域单元查找6邻域格网中所有未被标记的格网,并利用下式计算邻域格网的溢出高程值
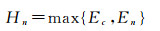 (2)
(2)
式中,Hn为第n个邻域格网的溢出高程值;Ec和En分别为格网单元c以及第n个邻域格网的原始高程值。
(3) 从最小优先队列中删除格网单元c对应的溢出高程值,将步骤(2)中未被标记的邻域格网溢出高程值压入最小优先队列,并将其标注为已处理。
(4) 重复步骤(2)、(3),直至最小优先队列为空,填平结束。
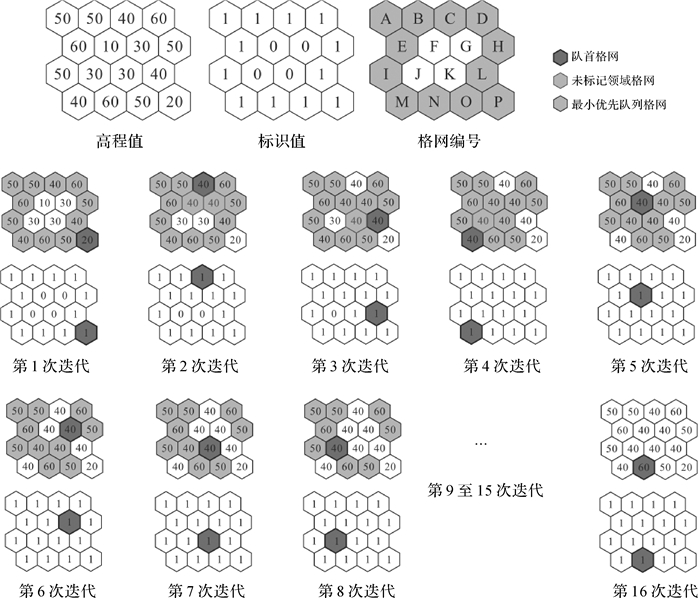
图 3为算法示意图,第2次迭代中,C为队首元素所对应的格网单元,通过查找可知其邻域单元中F和G未被标记,根据计算公式可得F和G的溢出高程均为40,将F和G压入最小优先队列,删除C,即完成了F和G格网的填洼。同理,格网K和J分别在第3、4次迭代中被填平,直至第16次迭代,整个区域完成填洼过程。根据上述算法实现步骤,W & L算法原理应用到六边形格网结构中的邻域关系,也可为六边形DEM实现填洼处理。
|
| 图 3 六边形DEM格网结构下W & L填洼算法流程 Fig. 3 W & L depression filling algorithm based on hexagon gridded structure |
2.2 D6算法
类比于四边形DEM中应用最为广泛的单流向算法—D8算法[7],本文提出D6算法以计算六边形DEM中格网的流向。该算法基于最大坡降法,可定义为:对于任何一个六边形格网c,在其相邻六个格网点中选择满足高程落差值最大的邻域格网点作为其流向(即水流的流出方向)。其具体计算步骤包括:
(1) 格网水流方向编码。根据六边形格网结构中邻域关系,规定水流从中心格网流向正东方向格网为初始方向,逆时针对该6个邻域单元流向编码为1,2,…,6,该编码也为邻域格网顺序编号。
(2) 邻域格网坡降计算。根据式(3),分别计算中心格网高程值与其6个邻域格网的高程值差值分别作为其邻域格网坡降值
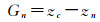 (3)
(3)
式中,Gn为中心格网在编号为n的邻域格网方向上的坡降值;zc和zn分别为中心格网和编号为n的邻域格网的高程值。
(3) 水流方向确定。根据(2)中的计算结果,令中心格网水流流向具有最大坡降值的邻域格网。
D8算法与D6算法的本质区别在于邻域处理。一方面邻域距离度量不同,相比于D8算法在距离度量上所表现的1: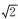
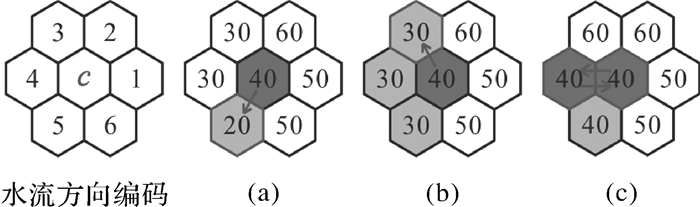
经过填洼处理,D6算法流向计算结果分为3种情况:①仅有一个具有最大坡降值的邻域格网,如图 4(a),该情况下水流方向值唯一;②多个具有最大坡降值大于0的邻域格网,如图 4(b),该情况下可按编码顺序将水流方向指向第一个邻域格网;③多个具有最大坡降值等于0的邻域格网,如图 4(c),该情况下为平地格网,若按照情况②进行处理,易出现“流向互指”现象,影响后续计算,需对平地格网进行特殊计算。
|
| 图 4 D6算法 Fig. 4 D6 algorithm |
对于无流向值平地格网,通过六邻域搜索寻找流向出水口的路径,并由该路径逆序计算平地格网流向值,具体方法为:
(1) 基于D6算法确定非平地格网单元流向值,将平地格网单元存入待处理数组中。
(2) 对待处理数组中每个平地格网作如下处理:
步骤1,按顺序查找6邻域中高程值与中心格网相等的邻域格网,若存在已有流向值且流向不指向中心格网的邻域格网,则将中心格网的流向指向该邻域,并删除该格网。
步骤2,若不存在步骤1中的邻域格网,则依次以无流向值的邻域格网为中心格网,执行步骤1。
步骤3,重复步骤2,直至待处理数组为空,平地区域水流方向计算结束。
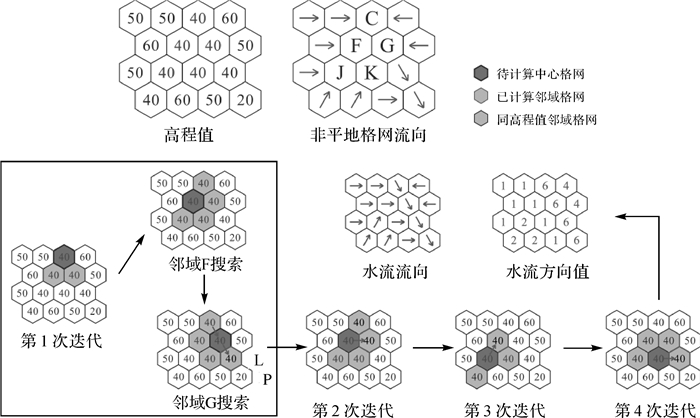
图 5中的平地区域是由2.1节中W & L算法填洼处理后所形成,其中格网C、F、G、J和K为平地格网。以格网C流向计算为例,其邻域格网中不存在已有流向值且流向不指向中心格网的邻域格网,因此按顺序对其无流向值的邻域格网F和G遍历,第1次F邻域搜索中未找到流向出水口的路径,第2次G邻域搜索中查找到格网L为出水口P的相邻格网,则路径为C→G→L→P,逆序对G和C流向进行计算,结果均为6。同理,计算格网F、J和K流向分别为1、2和1。由计算结果可知,该方法可有效避免平地区域流向结果“互指”现象。
|
| 图 5 平地格网水流计算 Fig. 5 Flow direction calculation for flat area grids |
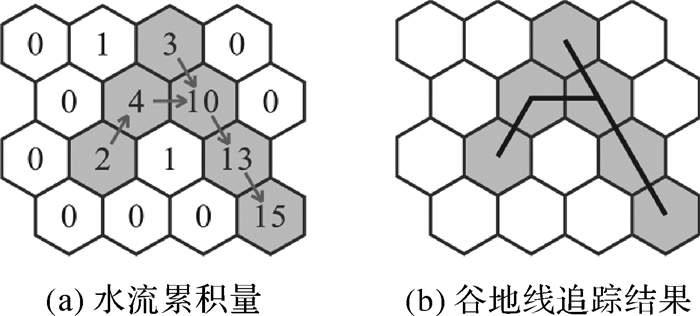
基于六边形格网的邻域处理,结合W & L填洼算法、D6算法以及平地区域流向的计算为基于六边形DEM谷地线的提取提供明确的水流方向,如图 6,后续水流累计量计算依赖于流向结果完成,提取累积量大于2的格网单元,并按照对应格网的流向线作拓扑连通组织,完成谷地线的追踪提取。
|
| 图 6 谷地线提取 Fig. 6 Extraction of valley lines |
3 试验与分析 3.1 规则格网DEM建立结果
本文试验区域为四川省德阳市西北部龙门山脉中段,该区域地势西北高东南低,谷地发育明显。试验数据为国家测绘部门标准化生产的1:5万DLG等高线数据,其等高距为10 m,最高高程为4400 m,最低高程为1000 m,以此数据分别构建九种分辨率的四边形DEM和六边形DEM数据,相同分辨率下四边形DEM和六边形DEM水平方向格网宽度比值约为0.93,见表 1。
| m | |||||
| 分辨 率 | 水平方向格网宽度 | 格网点高程中误差 | |||
| 四边形 | 六边形 | 四边形 | 六边形 | ||
| 1 | 23.25 | 25 | 9.33 | 9.37 | |
| 2 | 46.5 | 50 | 11.29 | 10.55 | |
| 3 | 93 | 100 | 20.06 | 18.39 | |
| 4 | 139.5 | 150 | 31.49 | 35.34 | |
| 5 | 186 | 200 | 49.96 | 46.37 | |
| 6 | 232.5 | 250 | 65.50 | 61.57 | |
| 7 | 279 | 300 | 74.77 | 70.91 | |
| 8 | 325.5 | 350 | 89.43 | 76.48 | |
| 9 | 372 | 400 | 96.01 | 80.56 | |
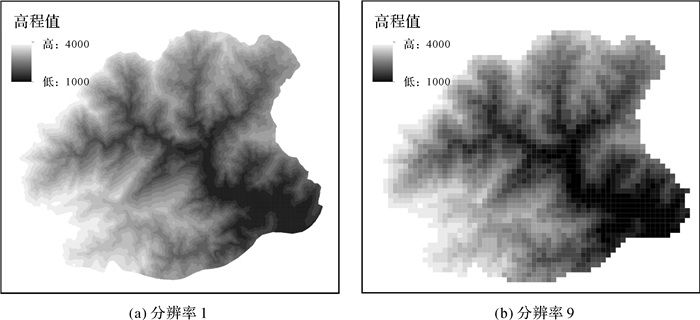
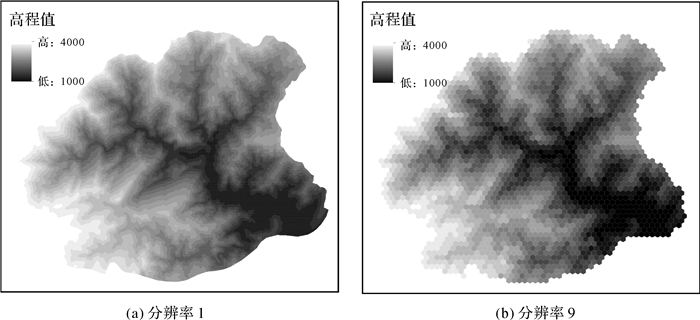
如图 7和图 8,高分辨率下,基于六边形格网结构和四边形格网结构所构建的DEM对地形可视化效果差异不大,而在低分辨率下,不同高程值格网之间的界线以及区域边界在六边形DEM中表现更为明显、平滑,地形变化更直观。
|
| 图 7 四边形DEM构建结果 Fig. 7 The results of square gridded DEM generation |
|
| 图 8 六边形DEM构建结果 Fig. 8 The results of hexagon gridded DEM generation |
为保证后续谷地线提取结果的可信性,本文采用检查点法[25],随机选取研究区域内和边缘的42个地貌特征点作为检测点,以格网点高程中误差对所建立的六边形DEM和四边形DEM数据精度分别进行评定,其公式为
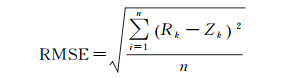
式中,RMSE为DEM高程中误差;Zk(k=1, 2, …, n)为检测点高程值;Rk为DEM内插所得对应检测点高程值。
由表 1结果可知,本文基于等高线所建立的2种DEM在分辨率1的高程中误差分别为9.33 m和9.37 m,分辨率2的高程中误差为11.29 m和10.55 m。根据我国1:5万DEM精度标准中对于高山地区域25 m格网间隔DEM的中误差限差为19 m的要求[25],以本文方法所建立的四边形格网DEM在格网间隔为25 m时,精度在9.33 m至11.29 m之间,与该分辨率对应的六边形DEM的格网宽度约为27 m,精度在9.37 m至10.55 m之间,均符合高程中误差限差19 m的要求。此外,随着分辨率降低,所构建的六边形DEM精度损失程度整体上小于四边形DEM,尤其在分辨率8和9时,其精度损失程度远低于四边形DEM。
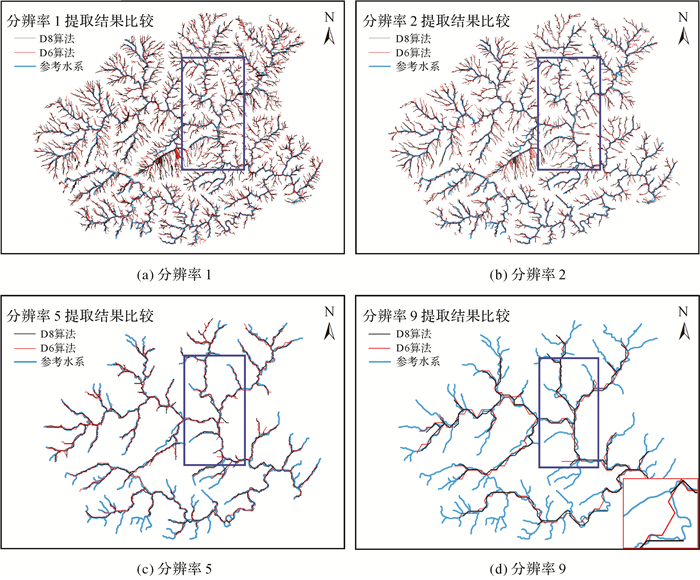
3.2 谷地线提取结果对比分析根据3.1节中构建的四边形DEM和六边形DEM,按照谷地线提取步骤,基于D8算法和D6算法,以25为累积流量阈值分别提取不同分辨率下的谷地线网络。如表 2所示,相同分辨率下,六边形DEM所提取的谷地线长度均大于四边形DEM提取结果,但谷地线数量差异并不大。以1:5万DLG水系数据作为参考水系,将提取结果分别与参考水系进行对比可知,分辨率1时,两种DEM所提取的谷地线主干大致相同,但在地形起伏较小区域均易出现“平行谷地线”,如图 9中绿框区域,但两者邻域之间的角度不同使该区域谷地线的流向存在差异,六边形DEM谷地线流向与正东方向所成夹角多呈30°,而四边形DEM则呈45°或90°。
| 分辨率 | 谷地线长度/m | 谷地线数量 | 误差带宽度/m | |||||
| 四边形 | 六边形 | 四边形 | 六边形 | 四边形 | 六边形 | |||
| 1 | 1 294 465 | 1 308 312 | 5 751 | 5 696 | 45.96 | 45.65 | ||
| 2 | 861 452 | 895 300 | 3 133 | 3 091 | 37.96 | 31.39 | ||
| 3 | 393 932 | 408 200 | 705 | 708 | 29.88 | 29.99 | ||
| 4 | 261 516 | 270 150 | 305 | 295 | 33.19 | 30.95 | ||
| 5 | 194 883 | 205 000 | 172 | 173 | 36.28 | 35.28 | ||
| 6 | 150 789 | 163 500 | 104 | 92 | 41.82 | 39.46 | ||
| 7 | 128 380 | 134 400 | 71 | 69 | 50.74 | 47.53 | ||
| 8 | 111 788 | 118 300 | 54 | 54 | 55.30 | 51.91 | ||
| 9 | 97 647 | 105 600 | 44 | 38 | 59.87 | 58.11 | ||
|
| 图 9 不同分辨率下谷地线提取结果对比 Fig. 9 The results of extracted valley lines under different resolutions |
随着分辨率减小,两种DEM下所提取的谷地线长度和数量均随之减少,分支丢失,形状逐渐被简化,但两者提取结果差异变大。低分辨率,六边形DEM在保持谷地线形状弯曲特征上效果更好,四边形DEM下提取的谷地线形状简化程度明显,尤其是对于纵向支流的提取,如图 9中蓝框区域。为了更直观的对比该区域中不同分辨率下两者提取结果的简化程度,将提取结果进行放大显示,由图 10和图 11可知,分辨率2,两者结果形状简化均不明显,数量和长度简化较为明显,四边形DEM所提取的谷地线在分辨率5时趋于平直,分辨率9,被简化为直线,反观六边形DEM提取结果仍保持一定的弯曲度。此外,分辨率9时,基于四边形DEM的谷地线提取结果在图 9(d)中红色区域中出现断裂的情况,而六边形DEM提取结果仍保持水流线之间相互连接关系。

|
| 图 10 D8算法谷地线提取结果局部放大图 Fig. 10 Enlarged results of extracted valley lines with D8 algorithm |

|
| 图 11 D6算法谷地线提取结果局部放大图 Fig. 11 Enlarged results of extracted valley lines with D6 algorithm |
为了定量化对比2种DEM所提取谷地线形状特征,本文以误差带宽度表示各分辨率下谷地线提取结果偏离参考水系的程度
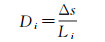 (5)
(5)
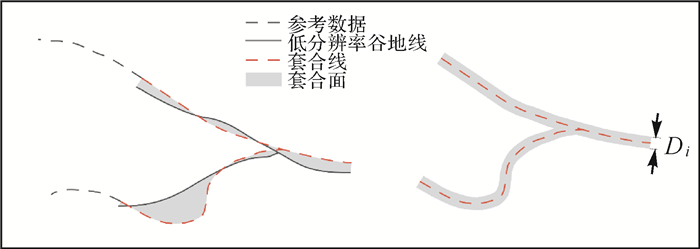
式中,Di为分辨率i下误差带宽度;Δs为套合面面积;Li为分辨率i下参考数据套合线长度。Di值越小,所提取谷地线形状特征与参考水系吻合程度越高。由表 2误差带宽度结果可知,随着分辨率减小,四边形DEM和六边形DEM所提取的谷地线误差带宽度呈现出先减小后增大的趋势,均在分辨率3时出现最小值,分别为29.88 m和29.99 m,即该分辨率下两者提取结果与参考水系最为吻合。分辨率4-9,两种DEM所提取的谷地线与参考水系形成的误差带宽度随分辨率减小而增大,吻合程度降低,但误差带宽度在六边形DEM中均低于四边形DEM,分别低了6.75%、2.76%、5.64%、6.33%、6.13%及2.94%,这表明,中、低分辨率下六边形DEM提取结果与参考水系吻合程度较高,在保持形状特征方面优于四边形DEM,较大程度的保持了弯曲特征。
|
| 图 12 误差带 Fig. 12 Error band |
4 结论
本文从DEM结构角度,采用多分辨率分析方法,探讨格网几何形态对于谷地线提取的影响。鉴于六边形具有邻域一致性、各向同性、紧凑性、采样率高等优点,本文以六边形为基本格网单元构建DEM,并基于六邻域处理单元,对六边形DEM谷地线提取过程中填洼、流向计算以及平地区域流向确定三个关键步骤进行讨论实现,从而实现谷地线在六边形DEM中的提取。试验结果表明:在DEM构建方面,六边形格网结构可保持更高的数据精度;在谷地线提取方面,六边形格网结构的优势表现为对于谷地线形状的保持,随着分辨率减小,六边形DEM所提取的谷地线与实测数据吻合程度高,弯曲特征继承性强。因此,在相同数据存储量条件下,六边形DEM数据精度更高,且其提取的谷地线网络的形状特征更为精细。
然而,本文集中于讨论四边形与六边形在谷地线提取的差异,未考虑到提取算法的优化,仍采用单流向D6算法,其提取结果仍无法避免“平行谷地线”,使其与真实谷地线不符,对此,后续研究还需结合多流向算法或利用真实谷地线网络对DEM进行修正从而改善“平行谷地线”现象。此外,从应用角度,进一步的研究包括将六边形DEM谷地线应用在后续流域划分、汇流面积计算等水文参数的提取中。
| [1] | AI Tinghua, LI Jingzhong. A DEM generalization by minor valley branch detection and grid filling[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(2): 198–207. DOI:10.1016/j.isprsjprs.2009.11.001 |
| [2] | GOPINATH G, SWETHA T V, ASHITHA M K. Automated extraction of watershed boundary and drainage network from SRTM and comparison with Survey of India toposheet[J]. Arabian Journal of Geosciences, 2014, 7(7): 2625–2632. DOI:10.1007/s12517-013-0919-0 |
| [3] | DIETRICH W E, WILSON C J, MONTGOMERY D R, et al. Analysis of erosion thresholds, channel networks, and landscape morphology using a digital terrain model[J]. Journal of Geology, 1993, 101(2): 259–278. DOI:10.1086/648220 |
| [4] | DESMET P J J, GOVERS G. Comparison of routing algorithms for digital elevation models and their implications for predicting ephemeral gullies[J]. International Journal of Geographical Information Systems, 1996, 10(3): 311–331. DOI:10.1080/02693799608902081 |
| [5] | VAZE J, TENG Jin, SPENCER G. Impact of DEM accuracy and resolution on topographic indices[J]. Environmental Modelling & Software, 2010, 25(10): 1086–1098. |
| [6] | HODGSON M E. What cell size dose the computed slope/aspect angle represent?[J]. Journal of Photogrammetric Engineering and Remote Sensing, 1995, 61(5): 513–517. |
| [7] | O'CALLAGHAN J F, MARK D M. The extraction of drainage networks from digital elevation data[J]. Computer Vision, Graphics, and Image Processing, 1984, 28(3): 323–344. DOI:10.1016/S0734-189X(84)80011-0 |
| [8] |
刘学军.基于规则格网数字高程模型解译算法误差分析与评价[D].武汉: 武汉大学, 2002. LIU Xuejun. On the accuracy of the algorithms for interpreting grid-based digital terrain model[D]. Wuhan: Wuhan University, 2002. http://d.wanfangdata.com.cn/Thesis_Y698879.aspx |
| [9] | WOODROW K, LINDSAY J B, BERG A A. Evaluating DEM conditioning techniques, elevation source data, and grid resolution for field-scale hydrological parameter extraction[J]. Journal of Hydrology, 2016, 540: 1022–1029. DOI:10.1016/j.jhydrol.2016.07.018 |
| [10] | TAN M L, FICKLIN D L, DIXON B, et al. Impacts of DEM resolution, source, and resampling technique on SWAT-simulated streamflow[J]. Applied Geography, 2015, 63: 357–368. DOI:10.1016/j.apgeog.2015.07.014 |
| [11] | AGUILAR F J, AGVERA F, AGUILAR M A, et al. Effects of terrain morphology, sampling density, and interpolation methods on grid DEM accuracy[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(7): 805–816. |
| [12] | RAPOSO P. Scale-specific automated line simplification by vertex clustering on a hexagonal tessellation[J]. Cartography and Geographic Information Science, 2013, 40(5): 427–443. DOI:10.1080/15230406.2013.803707 |
| [13] |
汤国安, 赵牡丹, 曹菡.
DEM地形描述误差空间结构分析[J]. 西北大学学报(自然科学版), 2000, 30(4): 349–352.
TANG Guoan, ZHAO Mudan, CAO Han. An investigation of the spatial structure of DEM errors[J]. Journal of Northwest University (Natural Science Edition), 2000, 30(4): 349–352. |
| [14] | WANG Jue, KWAN M P. Hexagon-based adaptive crystal growth voronoi diagrams based on weighted planes for service area delimitation[J]. ISPRS International Journal of Geo-Information, 2018, 7(7): 257. DOI:10.3390/ijgi7070257 |
| [15] | BIRCH C P D, OOM S P, BEECHAM J A. Rectangular and hexagonal grids used for observation, experiment and simulation in ecology[J]. Ecological Modelling, 2007, 206(3-4): 347–359. DOI:10.1016/j.ecolmodel.2007.03.041 |
| [16] |
信睿, 艾廷华, 何亚坤.
Gosper地图的非空间层次数据隐喻表达与分析[J]. 测绘学报, 2017, 46(12): 2006–2015.
XIN Rui, AI Tinghua, HE Yakun. Visualisation and analysis of non-spatial hierarchical data of Gosper map[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(12): 2006–2015. DOI:10.11947/j.AGCS.2017.20160596 |
| [17] |
林辉, 彭长辉.
地理信息系统中栅格单元大小和形状的选择[J]. 遥感信息, 2001(1): 21–23.
LIN Hui, PENG Changhui. The role of raster pixel size and shape in geographic information system[J]. Remote Sensing Information, 2001(1): 21–23. DOI:10.3969/j.issn.1000-3177.2001.01.005 |
| [18] | HYVÄLUOMA J. Reducing the grid orientation dependence of flow routing on square-grid digital elevation models[J]. International Journal of Geographical Information Science, 2017, 31(11): 2272–2285. DOI:10.1080/13658816.2017.1358365 |
| [19] | DE SOUSA L, NERY F, SOUSA R, et al. Assessing the accuracy of hexagonal versus square tilled grids in preserving DEM surface flow directions[C]//Proceedings of the 7th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences. Lisboa: Instituto Geográphico Português Lisbon, 2006: 191-200. |
| [20] | LI Z L, ZHU Q, GOLD C. Digital terrain modeling:principles and methodology[M]. Boca Raton: CRC, 2005. |
| [21] | MARTZ L W, GARBRECHT J. Numerical definition of drainage network and subcatchment areas from Digital Elevation Models[J]. Computers & Geosciences, 1992, 18(6): 747–761. |
| [22] | MARTZ L W, GARBRECHT J. Automated recognition of valley lines and drainage networks from grid digital elevation models:a review and a new method-comment[J]. Journal of Hydrology, 1995, 167(1-4): 393–396. DOI:10.1016/0022-1694(94)02619-M |
| [23] |
俞伟斌.基于DEM的数字流域时空特征及提取研究[D].杭州: 浙江大学, 2014. YU Weibin. Research on spatial and temporal features of digital basins and algorithms for features extraction based on raster DEMs[D]. Hangzhou: Zhejiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014359318.htm |
| [24] | WANG L, LIU H. An efficient method for identifying and filling surface depressions in digital elevation models for hydrologic analysis and modelling[J]. International Journal of Geographical Information Science, 2006, 20(2): 193–213. |
| [25] |
汤国安, 刘学军, 闾国年.
数字高程模型及地学分析的原理与方法[M]. 北京: 科学出版社, 2005.
TANG Guoan, LIU Xuejun, LÜ Guonian. Principle and method of DEM and geoscience analysis[M]. Beijing: Science Press, 2005. |



