2. 郑州轻工业大学计算机与通信工程学院, 河南 郑州 450001;
3. 61512部队, 北京 100088
2. School of Computer and Communication Engineering, Zhengzhou University of Light Industry, Zhengzhou 450001, China;
3. 61512 Troops, Beijing 100088, China
双/多变量制图(bivariate/multivariate mapping)是指能够同时表示两种或两种以上地理现象的制图方法[1]。目前的双/多变量制图方法主要分为两类:
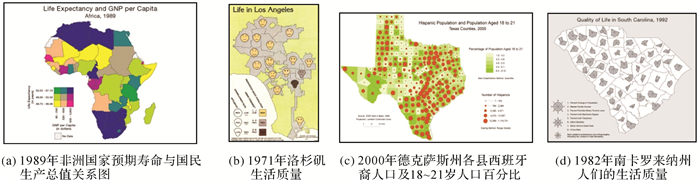
(1) 在专题地图表示方法如等值区域法、分区统计图表法等方法的基础之上,运用多种视觉变量的组合或地图符号的扩展的方法,从而达到表示两种或者多种地理现象的目的。具体方法[2-4]包括使用不同色相的二维编码(图 1(a))、Chemoff脸谱符号(图 1(b))、不同尺寸符号和明度组合(图 1(c))以及星形/雪花符号(图 1(d))等表达双/多变量。
|
| 图 1 基于专题地图表示方法的双/多变量制图方法示例 Fig. 1 Examples of traditional bivariate/multivariate cartographic methods |
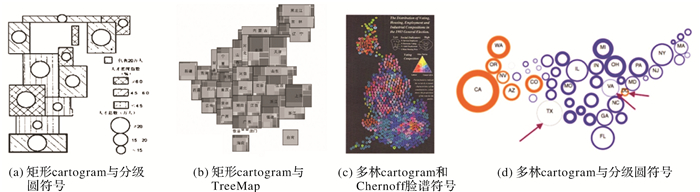
(2) 基于面域拓扑图(area cartogram)表达双/多变量。Cartogram是一种以地理对象面积或距离来表示其属性特征的图形表达方法,分为面cartogram和线cartogram。目前cartogram有拓扑地图、统计地图、示意地图、属性地图或变形地图等多种中文释义,但这些中文释义往往只强调了cartogram的某一方面[5],因此本文以下仍沿用英文cartogram这一术语。面cartogram主要包括4种类型[5-11]:简单连续面cartogram(如矩形cartogram)、简单离散面cartogram(如多林cartogram)、复杂离散面cartogram和复杂连续面cartogram。目前关于cartogram双/多变量制图主要是基于矩形cartogram和多林cartogram这类简单图形的面cartogram,在此基础上通过符号扩展实现双/多变量的表达。具体方法包括矩形cartogram和纹理、形状视觉变量相结合[12](图 2(a));矩形cartogram与TreeMap相结合[13-15](图 2(b));多林cartogram与Chemoff脸谱符号相结合[16](图 2(c));多林cartogram基础上通过对圆形符号的扩展[17](图 2(d))。
|
| 图 2 基于面cartogram表达双/多变量制图方法示例 Fig. 2 Examples of bivariate/multivariate cartographic methods based on area cartogram |
虽然面cartogram中地理区域形状扭曲变形,但其本身面积已经表达了第1个变量,就为更多变量的表达以及不同变量空间分布规律的对比提供了更多可能。然而,目前基于面cartogram的双/多变量制图还存在以下两个问题:
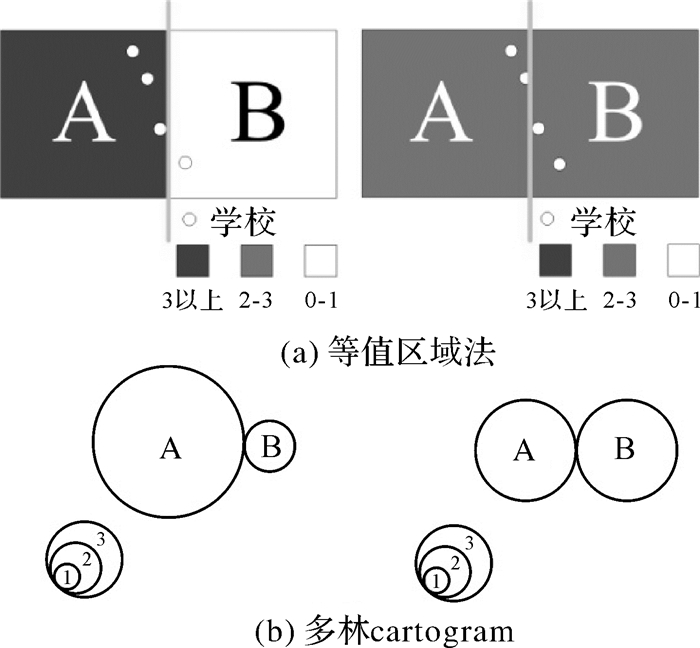
(1) 难以表达相邻区域之间的基本状况。目前基于面cartogram的双/多变量制图方法一般是以行政区域为单元进行变量统计,这样能够很好地反映各个独立乃至整体区域的基本情况。但由于没有考虑地理现象在区域中的位置,很难反映区域与区域之间,尤其是相邻区域之间的基本情况。如图 3所示,无论是使用等值区域法或者多林cartogram的表示方法,区域单元线的略微偏移都会造成两种迥然不同的结果。而且这两种表示方法都无法反映两个区域边界地区学校密集、其他地区学校稀疏的地理分布特征。
|
| 图 3 学校分布案例 Fig. 3 The example of school distribution |
(2) 不利于不同类型地理现象空间分布规律和差异特征的表达。由于矩形cartogram和多林cartogram难以保证整个区域的连续性,虽然圆形和矩形本身形状简单,面积易于估计和对比且易于分割,适合不同指标量化信息的传递,但难以有效表达不同地理现象的分布特征。
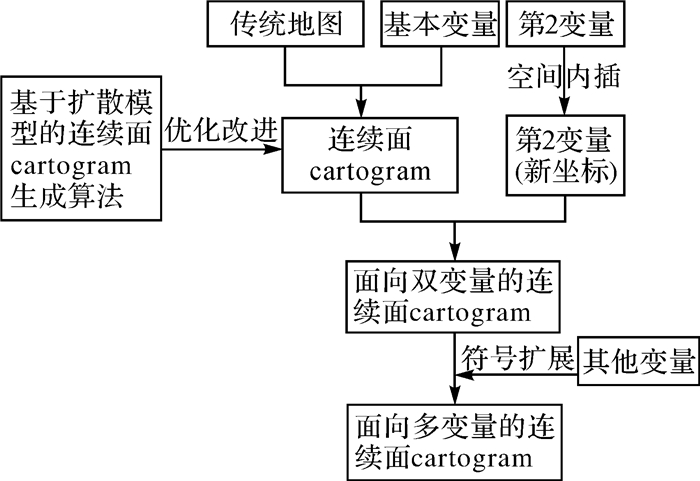
连续面cartogram通过变形来调整地理单元大小的同时保持整个区域的连续性,更能表现区域边界处的地理要素分布状况,同时也适用于表达不同地理现象的分布。因此,本文将连续面cartogram应用于双/多变量的制图表达中,首先对基于扩散模型的连续面cartogram生成算法进行优化实现,然后提出基于连续面cartogram的双/多变量表达方法,最后通过两个案例分别实现双、多变量表达。研究方法的整体思路具体如图 4所示,大致可分为两个步骤:
|
| 图 4 面向双/多变量的连续面cartogram可视化方法的整体思路 Fig. 4 The general idea of visualization method of a continuous area cartogram for two or multiple variables |
(1) 选择基本变量并根据该变量值完成原地图到连续面cartogram的转换。在该转换过程中,本文选择最为经典的基于扩散模型的连续面cartogram生成算法,并在具体实现中进行部分优化改进,一定程度上提升了算法的效率。
(2) 双/多变量在连续面cartogram中的表达。第2变量(如学校分布)通过空间内插,重新计算其在连续面cartogram的位置,并与连续面cartogram进行叠加,从而实现面向双变量的连续面cartogram可视化;其他变量(如学校能够招收的学生数量及学生类型等),则通过扩展符号实现面向多变量的连续面cartogram可视化方法。
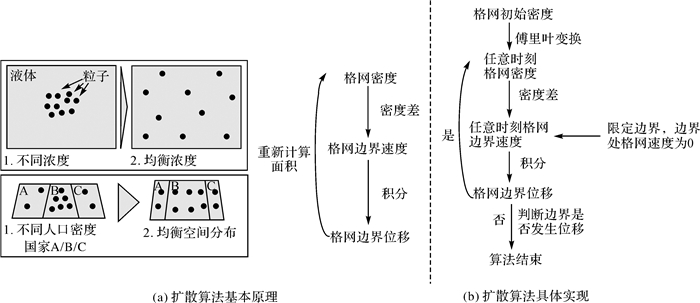
1 基于扩散模型的连续面cartogram生成算法的优化实现 1.1 扩散算法的基本原理和实现基于扩散模型的连续面cartogram生成算法来源于物理学中的扩散模型思想,模拟了液体从高密度向低密度扩散至密度均衡状态的过程。在该转换中,以人口密度地图为例,允许人口从高密度地区流向低密度地区,最终改变地理区域的形状使得每个区域密度均衡,即首先通过格网密度计算每个格网边界上的扩散速度,然后再将扩散速度进行积分从而求解格网边界的位移,从而得到了变形后的格网,再次求解格网密度,直至格网密度均衡,整个算法结束。由于该算法有效且快速,同时保留了区域间的连续性,在易读性和地理准确性方面非常突出,此外在图形扭曲度上保持了一定的灵活度,用户可以在密度均衡程度和图形扭曲程度之间作出调整,因此是应用最为广泛的连续面cartogram生成算法[18-22]。该算法的基本思想和原理直观明了,但在具体实现过程中,需要解决以下两个基本问题:
(1) 面cartogram的边界问题。在实际的面cartogram生成过程中,如果对面cartogram的边界不作限制,人口数据会无限制地从高密度地区流入到低密度地区,直至完全稀释趋近于0;
(2) 任意时刻格网密度的求解问题。格网密度一直随时间动态变化,且与位置、速度是相互作用的,因此难以求解任意时刻任意格网的密度。
文献[18]中采用边界条件[23]和傅里叶变换较好地解决了上述问题,并指出如果选定的边界范围足够大于研究区域,那么不同类型的边界条件对面cartogram变形的影响非常小。从算法实现和逻辑合理性上综合考虑,采用了第2类边界条件(诺依曼边界条件[24])来限定扩散模型,即使用一个“墙”作为面cartogram的边界,并认为在边界“墙”处不存在数据的流动,速度为0。具体算法流程如下:
(1) 计算格网初始密度;
(2) 通过傅里叶变换(在诺依曼边界条件下的傅里叶变换实际上是离散余弦变换)得到任意时刻的格网密度;
(3) 通过邻近格网的密度差计算出该时刻格网边界速度,由于限定了边界条件,因此边界处的格网边界速度为0;
(4) 通过积分得出格网边界位移;
(5) 判断所有格网边界位移是否发生变化,没有变化则整个算法结束,否则回到步骤(2)。
扩散算法的基本原理及其实现如图 5所示。
|
| 图 5 基于扩散模型的等密度cartogram算法基本原理和实现 Fig. 5 Basic principles and implementation of diffusion-based cartogram |
1.2 扩散算法的优化
上述扩散算法在实现细节上仍存在以下两个问题:
(1) 格网密度差异问题。当格网密度为0或者邻接格网密度差异很大的时候,很可能会使得算法迭代多次都无法达到密度均衡的要求,从而导致算法失败;
(2) 积分循环次数过长问题。理论上只有时间趋近于无穷,才会生成等密度cartogram,同时为了确保积分的准确性,时间步长会设置的非常小,从而导致循环次数过长,运行效率低下。
本文提出通过格网密度补偿和积分步长逐步试探的方法来解决上述两个问题。
针对问题(1)本文将人口的数值做一个整体的正向偏移,具体偏移方法如式(1)所示
 (1)
(1)
偏移系数可以依据实际情况而定。这样既可以避免零值出现,也可以一定程度减小邻接格网密度差异。
针对问题(2)本文提出了一种积分步长逐步试探法,能够有效缩短循环次数,提高运行效率。在计算机中进行积分运算,工程上通常采用最为广泛的高精度单步算法-四阶龙格-库塔法[25],即已知时刻tn的位置rn,下一个时间间隔h的rn+1公式(2)如下
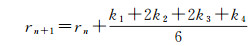 (2)
(2)
式中
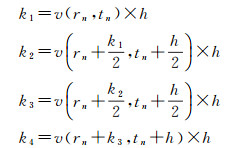
积分步长逐步试探法的核心思想是首先按照单步步长h进行积分,通过rn计算出rn+1,再依据rn+1计算出rn+2。同时也采用双步步长2h积分计算出r′n+2。如果格网前后积分的位移不再发生变化或者是位移小于某一给定阈值φ,即rn=rn+2=r′n+2 or |r′n+2-rn| < φ∧|rn+2-rn| < φ则整个程序结束。如果rn+2,r′n+2还存在位移误差,根据位移误差的大小计算时间步长比率。如式(3)所示
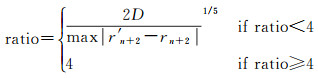 (3)
(3)
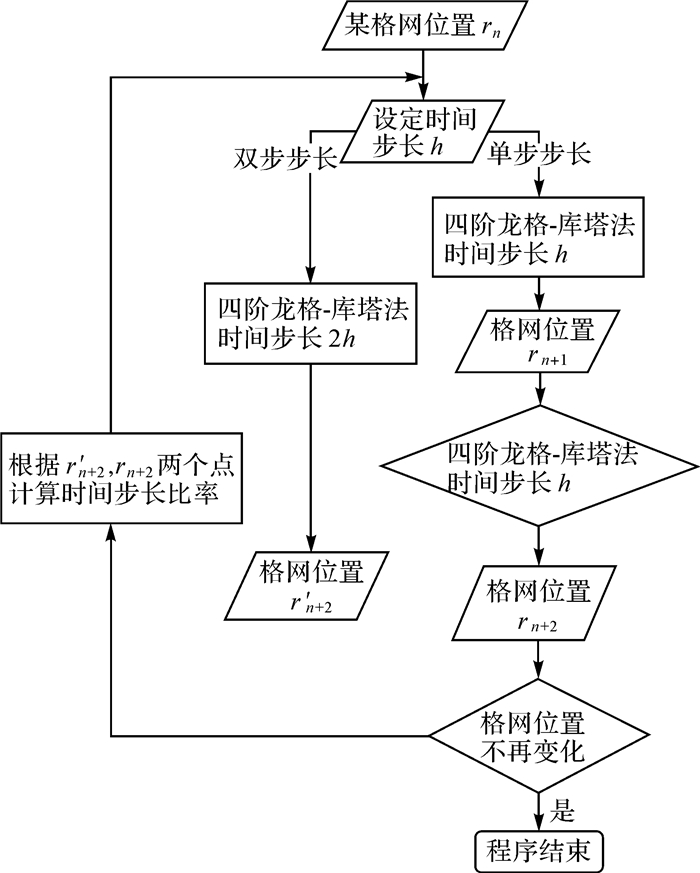
式中,D为常量。为确保积分的准确性,本文限定了时间步长比率最大为4,如果依据式(3)计算出来的步长比率大于4,则步长按照4倍进行扩展,如果计算出来的步长比率小于4,则按照计算出来的步长比率进行扩展。算法流程如图 6所示,直至前后积分位移不再产生变化,算法结束。
|
| 图 6 积分步长逐步试探法流程 Fig. 6 Integral step size step-by-step trial method |
1.3 扩散算法的算例实现
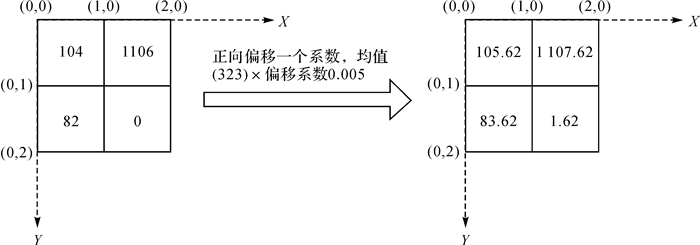
以一个1 km×1 km的四格网为例,格网中的人口数如图 7所示,以左上角点为原点,建立二维平面直角坐标系,首先将人口数值依据式(1)做一个整体的正向偏移,该算例中将偏移系数设置为0.005,对格网进行了整体密度补偿,并创建格网坐标,如图 7所示。
|
| 图 7 格网数值的总体正向偏移 Fig. 7 Overall forward offset of grid values |
根据初始密度,可以计算出每个格网在水平方向和垂直方向的速度,如图 8所示。对于每个格网节点而言,数据从该格网节点所对应的左下方格网流入为正,流出为负。
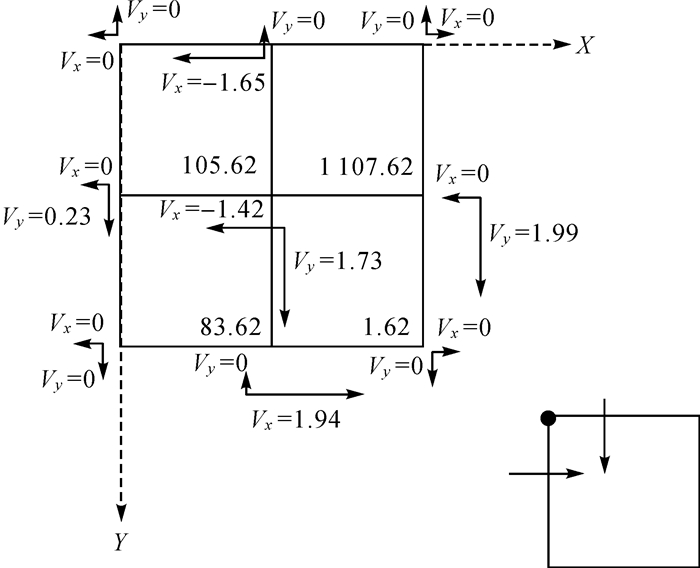
|
| 图 8 依据初始密度计算水平和垂直方向的速度 Fig. 8 Calculate horizontal and vertical speeds based on initial density |
取初始时间步长为0.002 s,按照积分步长逐步试探法,每次循环按照两种方法计算下一个时刻格网点的位移rn+2与r′n+2,两者进行比较求得格网点中位移最大的误差,依据式(3)计算出时间步长比率,经过实践,认为D取值为0.01可以取得较好的效果。如表 1所示,在近180 s内,仅经历了11次循环迭代,计算结果就得到了快速收敛,各格网点不再位移,呈现了稳态。
| 序号 | 时间/s | 步长 | 位移 误差 | 计算步 长比率 | 实际步 长比率 |
| 1 | 0 | 0.002 | 6×10-12 | 80.37 | 4 |
| 2 | 0.002 | 0.008 | 4.05×10-9 | 21.81 | 4 |
| 3 | 0.01 | 0.032 | 1.09×10-6 | 7.12 | 4 |
| 4 | 0.042 | 0.128 | 4.783×10-5 | 3.34 | 3.34 |
| 5 | 0.17 | 0.428 | 1.371×10-4 | 2.71 | 2.71 |
| 6 | 0.598 | 1.159 | 1.426×10-4 | 2.69 | 2.69 |
| 7 | 1.757 | 3.116 | 1.469×10-4 | 2.67 | 2.67 |
| 8 | 4.874 | 8.326 | 3.265×10-7 | 9.07 | 4 |
| 9 | 13.200 | 33.304 | 1.611×10-15 | 415.68 | 4 |
| 10 | 46.504 | 133.217 | 0 | - | - |
| 11 | 179.721 | - | - | - | - |
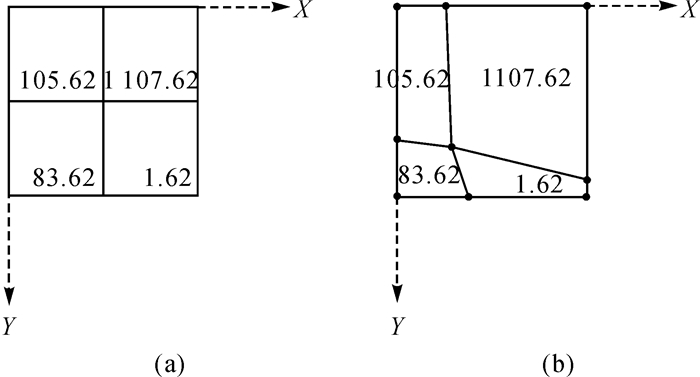
原始格网和变换后格网的结果对比如图 9所示。
|
| 图 9 原始格网和变换后格网对比图 Fig. 9 The comparison of original grid and transformed grid |
2 基于连续面cartogram的双/多变量表达方法 2.1 双/多变量在连续面cartogram中的表达
双/多变量在连续面cartogram中的表达方法主要有两种:
(1) 面cartogram+点图(dot map):可以将空间内插后的第2变量的地理位置以点图的形式叠加在面cartogram上,从而实现面向双变量的面cartogram可视化。因此空间内插是该表达方法的关键技术,将在2.2节详细讨论。
(2) 面cartogram+符号扩展:符号扩展的核心思想是灵活使用多种基本视觉变量,使得能够表达两种或者两种以上的变量。通常在表示各种统计数据时,可以采用点状符号的扩展,即点状符号实际上是一个具有一定面积的二维平面,该平面的总面积表示事物的总量,用各分量占总量的百分比表示其内部构成。圆、环和扇面是最容易进行分割的图形,也是人们应用最多的符号之一。将这些扩展的点状符号叠加在面cartogram上,从而实现面向多变量的面cartogram可视化。
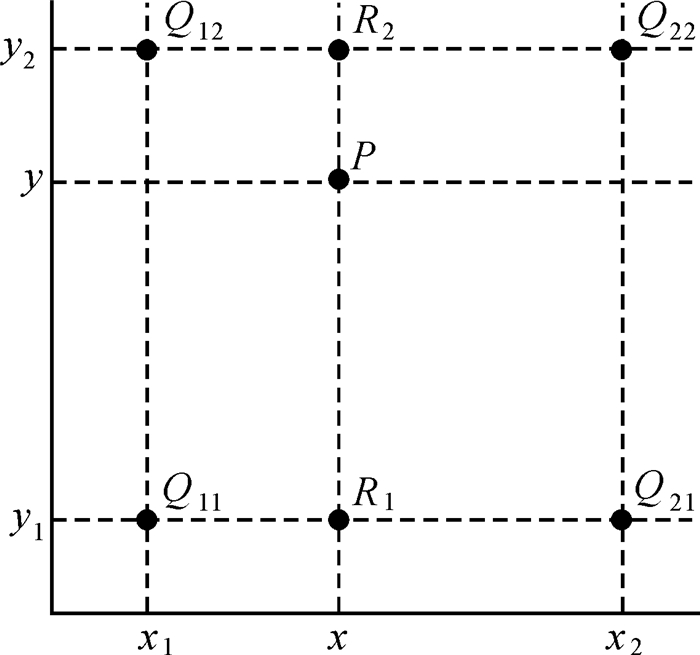
2.2 基于连续面cartogram的空间内插本文采用基于格网的双线性插值方法来解决基于连续面cartogram的空间内插,即在水平和垂直两个方向上分别进行一次线性插值。如图 10所示,已知格网上的4个点分别在原地图和面cartogram上的坐标。Q11、Q12、Q21和Q22表示4个点在地图上的坐标,f(Q11)、f(Q12)、f(Q21)、f(Q22)表示4个点在面cartogram上的坐标。内插格网中任意点P在面cartogram上的坐标f(P)。
|
| 图 10 二次线性内插原理 Fig. 10 The principle of quadratic linear interpolation |
首先在水平方向上进行一次线性内插得到R1和R2两个点,插值公式如下
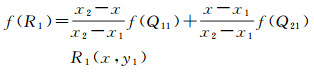 (4)
(4)
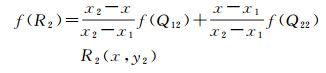 (5)
(5)
然后在垂直方向上进行一次线性内插,得到最终的结果P点,插值公式如下
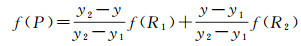 (6)
(6)
双线性插值与插值先后顺序是无关的,无论先是从水平方向还是垂直方向上所得结果都相同。如果将4个已知点Q11、Q12、Q21和Q22作归一化处理,将其分别简化为坐标(0,0)、(0,1)、(1,0)和(1,1),则上述公式还可以进一步简化为
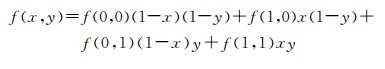 (7)
(7)
本文中基础变量选用人口统计数据。由于国内人口统计数据多按照省、市、自治区等行政区划进行统计,人口按照格网进行统计的数据集比较少,精度也不太高,部分精度高的数据也较难以获得。因此本文选用欧盟人口格网统计数据作为cartogram转换的基础数据。该数据集有两个版本,最新版本数据为2016年,采用的是投影坐标系(ETRS89/LAEA),格网精度为1 km。
在试验区域的选取上,考虑到便于实地查看和验证,选取了两个类型不同的德国南部城市,慕尼黑和奥格斯堡。慕尼黑是德国巴伐利亚州的首府,总面积达310 km2,2016年城市人口为146万,是德国南部第一大城市,全德国第三大城市,仅次于柏林和汉堡。奥格斯堡位于德国南部巴伐利亚州西南,距离慕尼黑60多千米。人口截至2015年不足30万人,面积146 km2。
通过编写爬虫程序从Google地图上获取了慕尼黑、奥格斯堡市的银行、ATM、学校幼儿园等不同类型基础设施的兴趣点数据作为试验中的第2变量。奥格斯堡的幼儿看护数据主要来自Google地图以及奥格斯堡官方发布的奥格斯堡的幼儿看护(Kinderbetreuung in Augsburg,http://kinderbetreuung.augsburg.de/)本文对格斯堡市政府的全市幼儿园名册进行了数字化,获取了幼儿园的位置数据以及各幼儿园不同年龄段能够接收的幼儿数量信息作为试验研究的第3、第4变量。
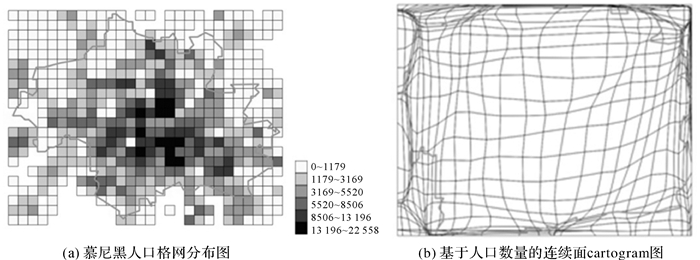
3.2 基于连续面cartogram的双变量表达案例:以慕尼黑城区为例 3.2.1 可视化结果按照统一的欧盟人口格网划分,横轴方向28个格网,纵轴方向22个格网即可完全覆盖慕尼黑城区,每平方千米格网人口从0到2万多不等,图 11分别是慕尼黑人口格网分布图和根据人口数量生成的连续面cartogram。
|
| 图 11 慕尼黑人口格网分布图和基于人口数量的连续面cartogram图 Fig. 11 Population grid map of Munich and population grid cartogram of Munich |
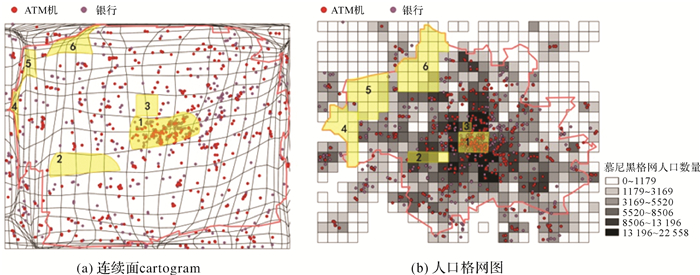
通过编写爬虫程序,从Google地图上获取了慕尼黑兴趣点数据23 216条,以银行(995条)和ATM机(454条)为例经过空间内插,分别叠加到基于人口数量的连续面cartogram图上,其中红的圆色点表示ATM机,紫的圆色点表示银行,将它们分别叠加在地图和连续面cartogram图上,如图 12所示。
|
| 图 12 ATM和银行分别叠加在连续面cartogram和人口格网图 Fig. 12 The distribution of ATMs and banks in population grid cartogram and in population grid map |
3.2.2 实例分析
通过两幅图对比并结合在Google Earth上观察和实地走访,得到如下分析结论:
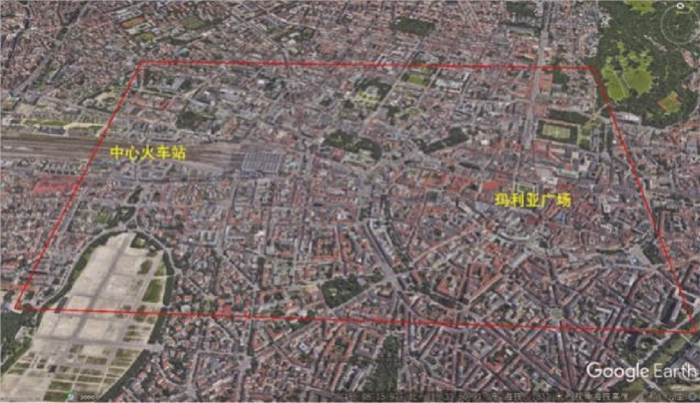
(1) 在图 12(b)中能够发现,在人口稠密的中心城区ATM机和银行分布较为密集,但是在连续面cartogram上还能够进一步发现,中心城区的1号区域比它周边人口更为稠密区域的ATM机和银行分布更多。通过在Google Earth上观察以及实地走访,1号区域正是从慕尼黑中心火车站通往玛丽亚广场的步行街地段,是慕尼黑重要的商业和旅游区域, 如图 13所示,因此也就不难解释为什么人口密度小于周边区域,但是ATM机和银行却更多的原因。
|
| 图 13 Google Earth上观察到的1号区域 Fig. 13 Area 1 on Google Earth |
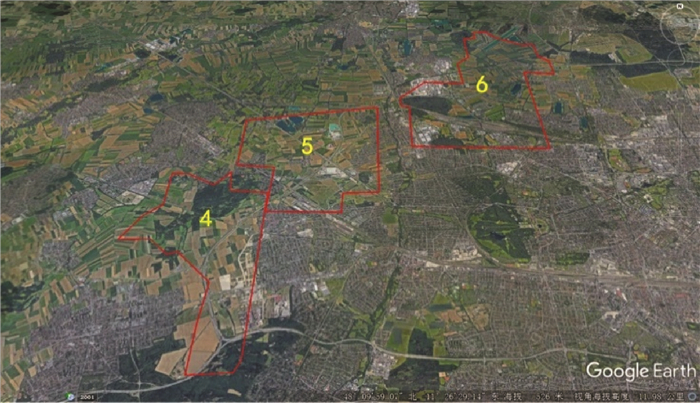
(2) 在图 12(b)中易于发现,4号、5号和6号区域上存在较大的“洞”,即在这3个区域中几乎没有ATM机和银行,虽然根据图例能够判断这些区域人口较为稀少,但是无法确切获知具体数量,因为对应的人口数量是一定范围的(0-1179)。而在连续面cartogram上,这3个区域已经急剧缩小,并未产生明显的“洞”,因此并不引人注意。通过在Google Earth上观察以及实地走访,如图 14所示,这3个区域均存在非常广袤的农田,人口稀疏,因此ATM机和银行数量较少。
|
| 图 14 Google Earth上观察到的4号、5号和6号区域 Fig. 14 Area 4, 5 and 6 on Google Earth |
(3) 而在图 12(b)中难以发现到2号和3号区域上存在的“洞”,而在连续面cartogram上则非常明显,这两个区域人口都较为稠密,但是缺少ATM机和银行的分布。
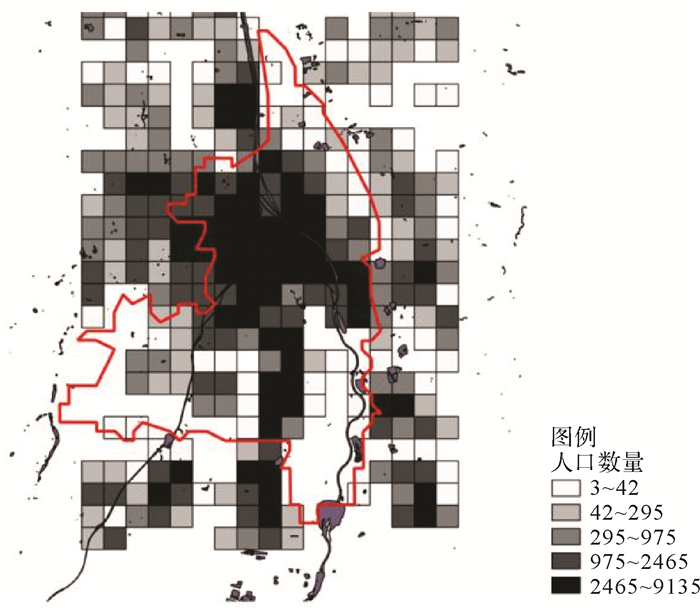
3.3 基于连续面cartogram的多变量表达案例:以奥格斯堡城区为例 3.3.1 可视化结果按照统一的欧盟人口格网划分,横轴方向17个格网,纵轴方向25个格网即可完全覆盖奥格斯堡城区,如图 15所示。
|
| 图 15 奥格斯堡每平方千米人口分布图 Fig. 15 Population grid map of Augsburg |
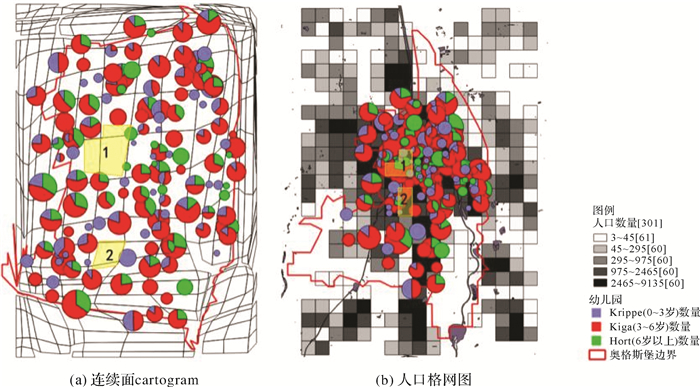
在奥格斯堡幼儿看护按照年龄可以划分为0~3岁(Krippe),3~6岁(Kiga)学龄前儿童看护,以及6岁以上(Hort)学龄儿童看护。图 16是幼儿看护地可接收不同年龄段的儿童数量在连续面cartogram和人口格网图的分布情况。
|
| 图 16 幼儿看护地可接收不同年龄段儿童数量在连续面cartogram和人口格网图的分布情况 Fig. 16 Child care locations which include the number of children of different ages in population grid cartogram and in population grid map |
3.3.2 实例分析
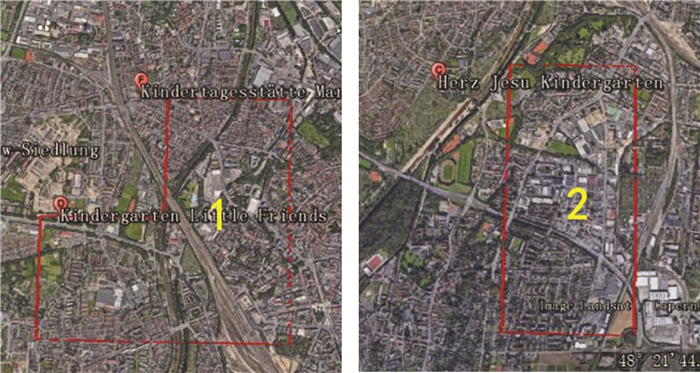
由于要表现幼儿看护地可接收的幼儿数量,需要使用到一定尺寸的分级圆符号,而不是单纯的点符号。因此在人口格网图中难以发现奥格斯堡的幼儿看护地有什么分布不均衡的地方,但是在连续面cartogram上可以看到在中心城区(1号区域)和中心城区下方(2号区域)出现了明显的“洞”,如图 17所示。通过实地走访和Google Earth可以验证上述两个区域确实没有幼儿看护地,邻近的也是在区域周边。
|
| 图 17 Google Earth上观察到的1号和2号区域 Fig. 17 Area 1 and 2 on Google Earth |
3.4 算法评价和分析
上述两个案例中,由于均采用密度补偿,因此试验区域都没有出现因密度差异较大而无法收敛的情况,且慕尼黑的边界整体变形非常光滑。但由于奥格斯堡西南边存在大量的森林(森林自然公园),人口极其稀少,即使进行了密度补偿,仍然边界出现一些急剧变形,这一点难以避免,如果对稀少人口进一步进行密度补偿,则会影响cartogram本身的准确性。
此外,上述两个案例由于都采用积分步长逐步试探法,因此都在迭代20次左右就达到收敛。从表 2中可以看出,按照初始步长0.002 s开始循环,整个慕尼黑地区的连续面cartogram生成需要经历20 712 s才能收敛,如果不采用积分步长逐步试探法,则需要循环10 356 000次才能收敛,采用积分步长逐步试探法循环迭代19次就达到收敛。整个奥格斯堡地区的连续面cartogram生成经历18 001.925 s,如果不采用积分步长逐步试探法,则需要循环9 000 963次才能收敛,采用积分步长逐步试探法循环迭代了24次就达到收敛。从表 2中还能发现其收敛速度和地区大小并没有相对关系,可能会同区域的人口分布存在一定关系,这一点还需要后续进一步验证和研究。
| 序号 | 慕尼黑区域 (28×32格网, 单位km) | 奥格斯堡区域 (17×25格网, 单位km) | ||
| 时间/s | 步长/s | 时间/s | 步长/s | |
| 1 | 0 | 0.002 | 0 | 0.002 |
| 2 | 0.002 | 0.008 | 0.002 | 0.008 |
| 3 | 0.01 | 0.032 | 0.01 | 0.032 |
| 4 | 0.042 | 0.085 | 0.042 | 0.02 |
| 5 | 0.127 | 0.091 | 0.062 | 0.014 |
| 6 | 0.218 | 0.280 | 0.076 | 0.031 |
| 7 | 0.498 | 0.744 | 0.107 | 0.037 |
| 8 | 1.242 | 1.527 | 0.144 | 0.024 |
| 9 | 2.769 | 3.137 | 0.168 | 0.017 |
| 10 | 5.906 | 7.036 | 0.185 | 0.069 |
| 11 | 12.942 | 16.707 | 0.254 | 0.208 |
| 12 | 29.649 | 36.253 | 0.462 | 0.467 |
| 13 | 65.902 | 77.128 | 0.929 | 1.089 |
| 14 | 143.030 | 158.885 | 2.018 | 2.407 |
| 15 | 301.905 | 384.097 | 4.425 | 5.489 |
| 16 | 686.012 | 953.619 | 9.914 | 12.182 |
| 17 | 1 639.631 | 3 814.476 | 22.096 | 24.242 |
| 18 | 5 454.107 | 15 257.903 | 46.338 | 53.843 |
| 19 | 20 712.010 | - | 100.181 | 112.89 |
| 20 | - | - | 213.071 | 296.514 |
| 21 | - | - | 509.585 | 832.968 |
| 22 | - | - | 1 342.553 | 3 331.875 |
| 23 | - | - | 4 674.428 | 13 327.498 |
| 24 | - | - | 18 001.926 | - |
4 结语
本文主要有两点贡献:①通过密度补偿和积分步长逐步试探法改进和优化基于扩散模型的等密度算法,有效缩短积分循环次数,提高了算法效率;②将连续面cartogram应用到双/多变量的制图表达中,并通过试验对比发现,面向双/多变量的连续面cartogram更能有效地发现不同变量空间分布差异明显的区域,并且更容易察觉出变量之间差异的层次感,同时弱化差异不明显的地方,有效引导人的视觉注意力,这为进一步分析内部成因提供基础,也能够为城市规划、政策制定等提供辅助参考决策。
| [1] | ELMER M E. Symbol considerations for bivariate thematic mapping[D]. Madison: University of Wisconsin-Madison, 2012. |
| [2] | CHERNOFF H. The use of faces to represent points in k-dimensional space graphically[J]. Journal of the American Statistical Association, 1973, 68(342): 361–368. DOI:10.1080/01621459.1973.10482434 |
| [3] | LEONOWICZ A. Two-variable Choropleth maps as a useful tool for visualization of geographical relationship[J]. Geografija, 2006, 42(1): 33–37. |
| [4] |
曾兴国, 杜清运, 任福.
一种采用Mashup的网络地图多变量制图方法[J]. 武汉大学学报(信息科学版), 2015, 40(9): 1215–1219.
ZENG Xingguo, DU Qingyun, REN Fu. A web multi-variate mapping method based on Mashup[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1215–1219. |
| [5] |
王丽娜, 江南, 李响, 等.
Cartogram表示方法研究综述[J]. 计算机辅助设计与图形学学报, 2017, 29(3): 393–405.
WANG Lina, JIANG Nan, LI Xiang, et al. A survey of cartogram[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(3): 393–405. DOI:10.3969/j.issn.1003-9775.2017.03.001 |
| [6] |
艾廷华.
适宜空间认知结果表达的地图形式[J]. 遥感学报, 2008, 12(2): 347–354.
AI Tinghua. Maps adaptable to represent spatial cognition[J]. Journal of Remote Sensing, 2008, 12(2): 347–354. |
| [7] | HENNIG B D. Rediscovering the world: gridded cartograms of human and physical space[D]. Sheffield: University of Sheffield, 2011. http://core.ac.uk/display/1145770 |
| [8] | DORLING D. Area cartograms: their use and creation[C]//Concepts and Techniques in Modern Geography. Norwich: University of East Anglia, 1996. |
| [9] | TOBLER W. Thirty five years of computer cartograms[J]. Annals of the Association of American Geographers, 2004, 94(1): 58–73. DOI:10.1111/j.1467-8306.2004.09401004.x |
| [10] | SPECKMANN B, KREVELD M V, FLORISSON S. A linear programming approach to rectangular cartograms[M]//RIEDL A, KAINZ W, ELMES G A. Progress in Spatial Data Handling. Berlin, Heidelberg: Springer, 2006: 529-546. |
| [11] | KEIM D A, PANSE C, NORTH S C. Medial-axis-based cartograms[J]. IEEE Computer Graphics and Applications, 2005, 25(3): 60–68. |
| [12] |
张军海, 胡文亮, 韩宪生.
拓扑图传递量化信息的方法[J]. 地图, 2001(1): 3–6.
ZHANG Junhai, HU Wenliang, HAN Xiansheng. Method for representing quantitative information in topological map[J]. Cartography, 2001(1): 3–6. |
| [13] |
艾廷华, 周梦杰, 陈亚婕.
专题地图属性信息的LOD表达与TreeMap可视化[J]. 测绘学报, 2013, 42(3): 453–460.
AI Tinghua, ZHOU Mengjie, CHEN Yajie. The LOD representation and TreeMap visualization of attribute information in thematic mapping[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 453–460. |
| [14] | SLINGSBY A, DYKES J, WOOD J. Rectangular hierarchical cartograms for socio-economic data[J]. Journal of Maps, 2010, 6(1): 330–345. DOI:10.4113/jom.2010.1090 |
| [15] | BUCHIN K, EPPSTEIN D, LÖFFLER M, et al. Adjacency-preserving Spatial TreeMaps[M]//DEHNE F, IACONO J, SACK J R. Algorithms and Data Structures. Berlin, Heidelberg: Springer, 2011(6844): 159-170. |
| [16] | HUGH H. Multivariate mapping[EB/OL]. (2016-11-08)[2019-03-15]. http://www.geotechcenter.org/uploads/2/4/8/8/24886299/16_multivariate_mapping_s12.ppt. |
| [17] | NUSRAT S, ALAM M J, SCHEIDEGGER C, et al. Cartogram visualization for bivariate geo-statistical data[J]. IEEE Transactions on Visualization and Computer Graphics, 2018, 24(10): 2675–2688. DOI:10.1109/TVCG.2945 |
| [18] | GASTNER M T, NEWMAN M E J. Diffusion-based method for producing density-equalizing maps[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(20): 7499–7504. DOI:10.1073/pnas.0400280101 |
| [19] |
张珣, 钟耳顺, 张小虎, 等.
一种尺度效应指数修正的格网数据示意地图制图算法[J]. 武汉大学学报(信息科学版), 2015, 40(8): 1100–1104.
ZHANG Xun, ZHONG Ershun, ZHANG Xiaohu, et al. A modified algorithm to construct gridded area cartograms by scale effect index[J]. Geomatics and Information Science of Wuhan University, 2015, 40(8): 1100–1104. |
| [20] | OYANA T J, RUSHOMESA R I, BHATT L M. Using diffusion-based cartograms for visual representation and exploratory analysis of plausible study hypotheses:the small and big belly effect[J]. Journal of Spatial Science, 2011, 56(1): 103–120. DOI:10.1080/14498596.2010.521976 |
| [21] |
陈谊, 赵云芳, 杜晓敏.
变形统计地图构建方法综述[J]. 系统仿真学报, 2016, 28(9): 1970–1978.
CHEN Yi, ZHAO Yunfang, DU Xiaomin. Overview of cartogram algorithm[J]. Journal of System Simulation, 2016, 28(9): 1970–1978. |
| [22] | LI Ziqiang, ARYANA S. Diffusion-based cartogram on spheres[J]. Cartography and Geographic Information Science, 2017, 45(5): 464–475. |
| [23] | ZAITSEV V F, POLYANIN A D. Handbook of exact solutions for ordinary differential equations[M]. 2nd ed. Boca Raton: CRC Press, 2002. |
| [24] | CHENG A H D, CHENG D T. Heritage and early history of the boundary element method[J]. Engineering Analysis with Boundary Elements, 2005, 29(3): 268–302. DOI:10.1016/j.enganabound.2004.12.001 |
| [25] | SVLI E, MAYERS D F. An introduction to numerical analysis[M]. Cambridge: Cambridge University Press, 2003. |



