2. 自然资源部国土卫星遥感应用中心, 北京 100048
2. Land Satellite Remote Sensing Application Center, MNR, Beijing 100048, China
合成孔径雷达干涉(interferometric synthetic aperture radar, InSAR)技术具有全天时、全天候、高精度等优势[1-2],在地形测绘中具有良好的应用前景。然而,高精度DEM的获取,一方面取决于InSAR平台指标的设计,包括载荷设计和姿轨控制等,另一方面则取决于几何及干涉参数的检校工作[3]。几何检校通过校准获取的几何参数来提升SAR影像的几何定位精度,而干涉测量检校技术是通过校准获取的干涉参数来提升干涉结果的高程精度,二者共同决定了全球DEM的精度水平[4]。几何检校技术一般以距离-多普勒(Range-Doppler, R-D)模型为基础解算方位向时间延迟和距离向时间延迟参数[5]。ALOS_PALSAR卫星使用几何检校方法后,条带模式的几何定位精度达9.7 m[6];Radarsat-2卫星利用角反射器进行几何检校后,获得了5.74 m的平面定位精度[7];TerraSAR-X利用角反射器完成了系列卫星的高精度几何检校,实现了0.3 m的平面定位结果[8-9];2018年,文献[10]针对TerraSAR-X/TanDEM-X影像和GF-3影像进行了几何检校,检校后的TerraSAR-X/TanDEM-X影像几何定位精度优于3 m,GF-3影像几何定位精度优于7.5 m。因此,几何检校方法已经在工程和科研上取得了成功应用。干涉测量检校技术较为复杂,国内外已开展了大量研究工作,提出了很多干涉测量检校方法。1999年,文献[11]分析了影响干涉测高的系统参数,并对误差源进行了敏感度分析,在平地几何关系下推导出基于敏感度方程的机载干涉测量检校方法;2001年,文献[12]在此基础上,推导出斜视下基于干涉敏感度方程的机载干涉测量检校方法,通过仿真数据证明了不同敏感度矩阵条件数对干涉测量检校产生不同的影响,但是没有针对定标器布放问题进行研究;2003年,文献[13]针对干涉敏感度方程的推导引入了三维重建模型,并提出一种使敏感度矩阵条件数最小化的定标器布放算法;2010年,文献[14]提出一种考虑干涉相位偏置、基线长度和基线水平角参数的机载干涉定标模型,但是未考虑控制点的平面信息;文献[15]在此基础上提出利用控制点三维信息的机载双天线SAR干涉定标方法,验证了定标后DEM的平面精度和高程精度,但是并没有独立解算每一项干涉参数的修正量;2011年,文献[16]基于三维重建模型的基础上,提出了一种分布式卫星SAR干涉测高模型,通过仿真数据针对基线矢量和相位误差特性进行了分析;2014年,文献[17]提出了星载InSAR立体基线的检校方法,通过仿真数据表明该方法能完成高精度基线矢量检校,但是缺少试验数据的支撑;2016年,文献[18]利用TanDEM-X数据验证了基于InSAR三维重建模型、敏感度方程的干涉测量检校方法,证明了星载InSAR干涉测量检校方法的通用性。现阶段,商业软件GAMMA在反演InSAR高程时只利用控制点的高程信息完成了对干涉参数的精估计,没有考虑平面精度。另外,软件中并未独立分解干涉误差源,没有达到高精度的干涉测量检校要求。到目前为止,从机载干涉测量检校模型发展到星载中,尽管已经开展大量研究工作,但是在干涉过程中,多数参数的误差具有极强的耦合性,联合解算却无法进行准确的区分,从而导致干涉参数修正量不够精确。本文针对这一问题,提出利用参数独立分解的干涉测量检校方法,在保证几何定位精度的前提下,通过4对TanDEM-X/TerraSAR-X数据处理验证了星载SAR干涉测量检校方法的正确性。
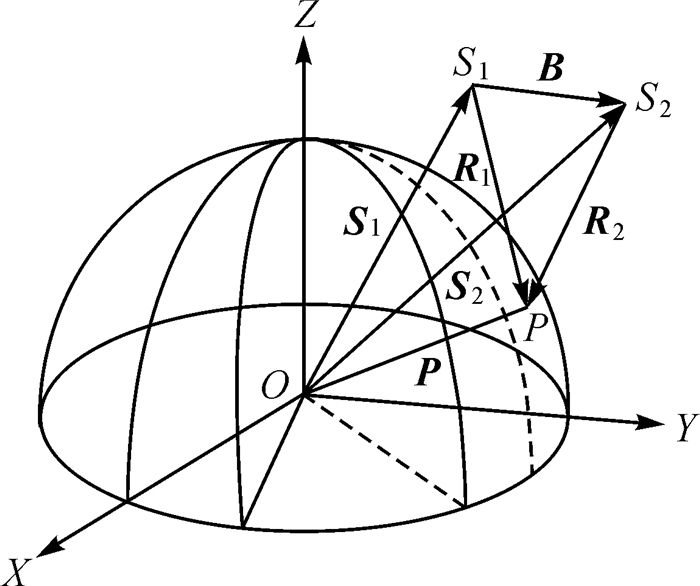
1 InSAR三维重建模型InSAR三维重建模型基本原理是通过联立距离方程、多普勒方程和干涉相位方程获取地面目标点的三维坐标。图 1所示为地心坐标系下InSAR测量的几何关系,其中S1、S2为主辅天线相位中心位置矢量,R1、R2表示主辅天线相位中心到地面点的位置矢量,R1、R2分别为主辅天线相位中心到地面点P的距离,P为地面目标点位置矢量,v为速度矢量,B为基线矢量,fdop为多普勒频率,λ为雷达波长,φ为绝对干涉相位,ϕ为缠绕干涉相位,k为整周期数,Q为天线收发模式,Q=1表示“一发双收”模式,Q=2表示“乒乓”模式。
|
| 图 1 星载InSAR在地形测绘中的几何关系 Fig. 1 Geometric relationship of InSAR in topographic mapping |
本文研究主要集中于星载InSAR交轨干涉测量(cross track interferometry, XTI)模式[13],则三维重建几何关系表示为
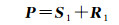 (1)
(1)
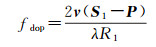 (2)
(2)
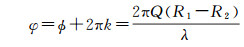 (3)
(3)
根据干涉SAR的几何关系,目标点坐标在地心空间直角坐标系下表示为
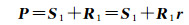 (4)
(4)
式中,R1为视向量;r为单位视向量。根据式(4)可知,对目标点坐标的求解一般采用视向量分解法[13],即将视向量转换为对单位视向量的求解。单位视向量需要在移动坐标系VPQ中分解为V、P和Q 3个坐标轴方向[15, 18]。VPQ坐标系是以主天线相位中心为坐标原点,速度矢量方向为V轴,速度和基线叉乘方向为Q轴,V轴、P轴和Q轴满足右手坐标系关系。rv、rp和rq分别表示单位视向量r在V轴、P轴和Q轴上的分量,即
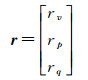 (5)
(5)
视向量分解法将视向量从移动坐标系向地心空间直角坐标系转换,从而获取目标点的三维坐标[19]。
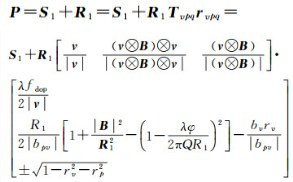 (6)
(6)
式中,Tvpq是将视向量转换为地心空间直角坐标系的变换矩阵;bv为基线在速度方向的分量;bpv为基线在垂直于速度方向的分量。
由三维重建模型表达式可知,影响干涉SAR测高精度的主要因素有:主星位置、主星速度、主星斜距、多普勒频率、干涉相位误差、基线矢量误差等。主星位置、主星速度、主星斜距、多普勒频率等参数在几何检校中校正,以提升SAR影像的平面精度[20-21]。而干涉相位误差和基线矢量误差采用本文提出的干涉测量检校方法进行校正,以提升干涉结果的高程精度,最终获取高精度的DEM产品。
2 干涉敏感度分析本文在保证几何检校精度的前提下,本文针对干涉相位和基线矢量参数引起的误差进行敏感度分析,即定量分析干涉参数的变化对高程误差的影响,同时为后续试验部分提供理论参考。
2.1 干涉相位误差敏感度分析干涉相位误差一般由随机误差、系统误差和绝对相位偏差组成。其中随机误差是由InSAR系统各项相干源造成,对应的相位呈随机分布特性,在本文中不参与检校;系统误差成分主要由硬件设备随工作温度变化的剩余漂移相位造成[22-23],呈缓慢特性,在本文中不参与检校;绝对相位偏差是指绝对干涉相位与解缠相位和平地相位之间相差的固定常数,因此,干涉相位误差的主要成分为绝对相位偏差。干涉相位误差Δφ引起的DEM高程误差Δh为
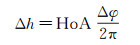 (7)
(7)
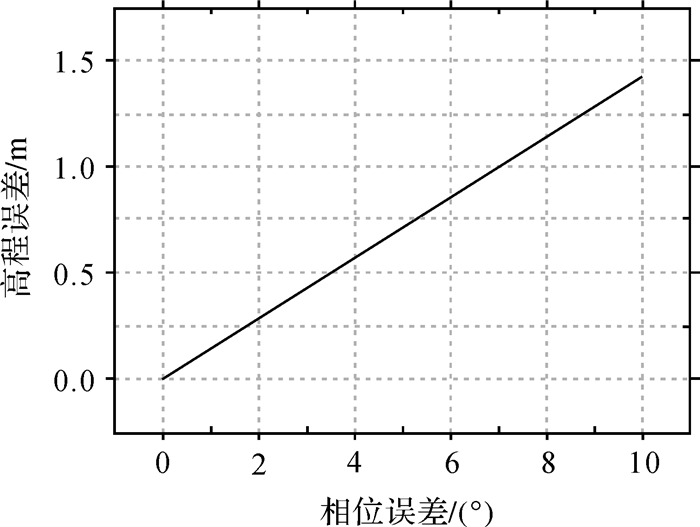
式中,HoA为高程模糊度。TanDEM-X采用了两期的HoA设置,第1期为40~55 m,第2期为35 m,即2π相位变化引的HoA在35~55 m之间[3, 24]。在HoA=35 m的情况下,10°的相位误差引入高程误差约为0.97 m,在HoA=55 m的情况下,10°的相位误差引入高程误差约为1.54 m。因此,约10°的相位误差引起的高程误差变化范围在0.97~1.54 m之间。设定干涉相位误差范围为[0°,10°],结合三维重建模型表达式评定其对高程测量结果的影响,如图 2所示,10°相位误差引起高程误差约为1.42 m,随着干涉相位误差的增加,高程测量误差呈线性递增的趋势。如果要进行1:50 000比例尺地形图测绘,那么丘陵地的高程精度需要达到5 m,相位误差的影响已经约占28.4%,因此,干涉相位误差是InSAR地形测绘中的重要误差因子。
|
| 图 2 干涉相位误差敏感度分析 Fig. 2 Sensitivity analysis of interferometric phase |
2.2 基线误差敏感度分析
在星载InSAR地形测绘中,基线矢量直接影响着高程模糊度、高程误差的传递系数等诸多因素。基线是一个三维矢量,为了更方便的表达基线参数,一般采用TCN坐标系,以主天线相位中心为坐标原点,N轴由主天线相位中心指向地心,N轴与速度矢量叉乘方向为C轴正方向,T、C、N三轴构成右手坐标关系[18]。本文将基线矢量分解为TCN坐标系下的基线初值和与时间相关的基线速率,考虑到交轨干涉过程中,所有的计算都是投影到主影像的零多普勒平面中进行的,因此沿轨基线恒为零,即Bt=0[25]。
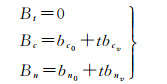 (8)
(8)
式中,Bt、Bc和Bn分别表示TCN坐标系的基线分量;bc0和bcv表示基线Bc在C方向分解的基线初值和基线速率;bn0和bnv表示基线Bn在N方向分解的基线初值和基线速率。由于三维重建模型是在地心空间直角坐标系表示InSAR的几何关系,因此,本文需要将基线由TCN坐标系转换为地心空间直角坐标系,即
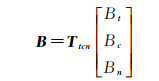 (9)
(9)
式中,Ttcn为TCN与空间直角坐标系之间的变换矩阵。由于基线误差对DEM高程精度影响较为复杂,本文在TCN坐标系下分析基线分量bc0、bcv、bn0和bnv对高程精度的影响,在地心空间直角坐标系下分析基线长度B对高程精度的影响。
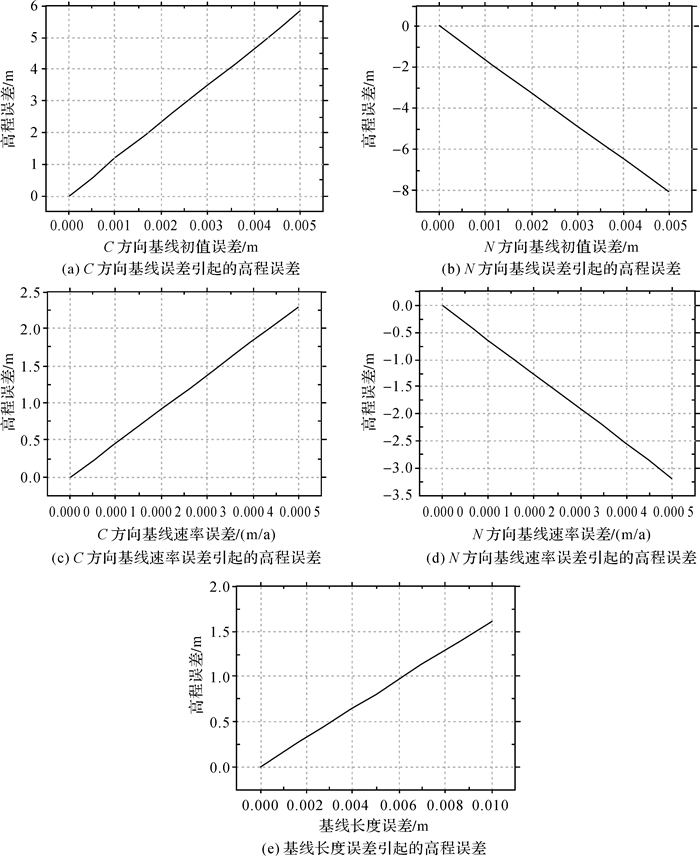
若对C、N方向基线初值添加1 mm误差,如图 3(a)、(b)所示,C方向引起1.2 m的高程误差,N方向引起-1.6 m的高程误差;若对C、N方向基线速率添加0.1 mm/s误差,如图 3(c)、(d)所示,C方向引起0.5 m高程误差,N方向-0.6 m的高程误差。可以看出,数毫米级的基线初值误差可引起米级的高程误差,数亚毫米级的基线速率误差可引起米级的高程误差。此外,与基线初值误差相比,基线速率误差对高程测量精度影响更为敏感,与C方向基线矢量误差相比,N方向对高程测量精度影响更为敏感。
|
| 图 3 基线误差敏感度分析 Fig. 3 Sensitivity analysis of baseline errors |
若对基线长度添加1 cm误差,如图 3(e)所示,则引入高程误差约为1.61 m。如果要进行1:50 000比例尺地形图测绘,那么丘陵地的高程精度需要达到5 m,基线误差的影响已经约占32%,综上所述,基线矢量是InSAR地形测绘中一个重要的误差因子。
3 InSAR干涉测量检校模型本文方法基于干涉相位误差与基线矢量误差到高程误差的不同传递特性进行建模。通过敏感度分析可知,干涉相位引入的高程误差为1.42 m,基线在方位向和距离向引入高程误差为1.61 m,由此可见,干涉相位误差和基线矢量误差对地形测绘的影响不可忽视。因此,本文提出一种利用参数独立分解的干涉测量检校方法。首先解算干涉相位误差,随后解算基线矢量误差。为了保证两种干涉参数的解算方法完全独立,本文采用计算绝对干涉相位与解缠相位和平地相位之间固定偏差的方法,来获取干涉相位误差。首先根据地面控制点来求取每一个点的绝对干涉相位,然后依据该局部绝对干涉相位对解缠相位和平地相位进行补偿,最后求取整景相位数据应该补偿的固定偏差,即可获取每一景影像的干涉相位误差。
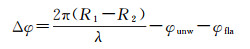 (10)
(10)
式中,R1、R2表示主辅影像的斜距;φunw为解缠相位;φfla为滤波前的平地相位;Δφ为干涉相位误差。
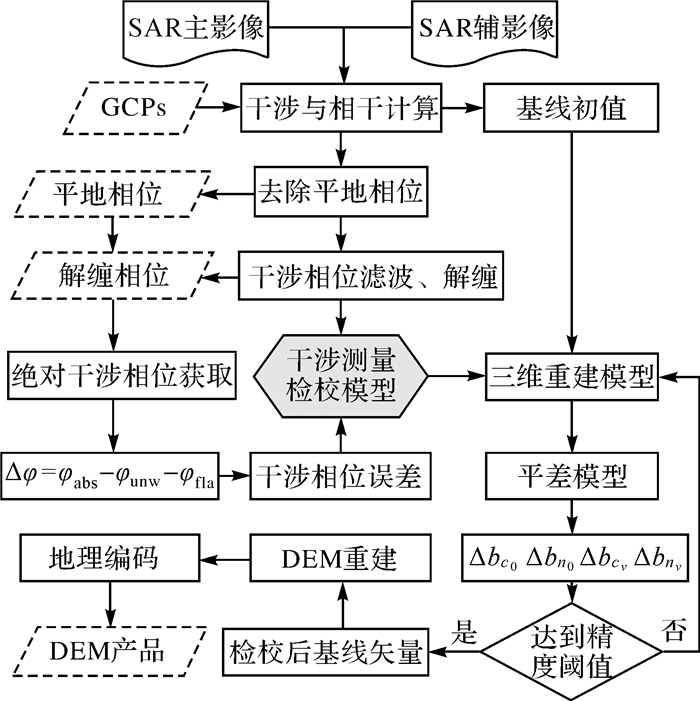
对基线矢量参数进行干涉测量检校时,首先从InSAR三维重建模表达式出发,然后建立敏感度方程,最后采用平差模型基于最小二乘法准则解算干涉参数的修正量。为了提高解算精度,本文采用迭代方式,将迭代前后坐标差值的均方根定义为检校精度,当检校精度小于指定阈值(本文取ε=0.05)时,则迭代收敛,最终获取高精度的干涉参数,从而保证生成高精度DEM产品,干涉测量检校流程如图 4所示。
|
| 图 4 干涉测量检校流程 Fig. 4 Flow chart of interferometric calibration |
利用三维重建模型表达式在地心空间直角坐标系推导出3个坐标轴方向的三维重建方程,形式如下[19]
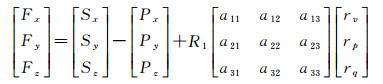 (11)
(11)
式中,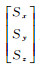
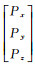

根据三维重建方程对基线矢量计算偏导数,建立干涉敏感度方程,形式如下
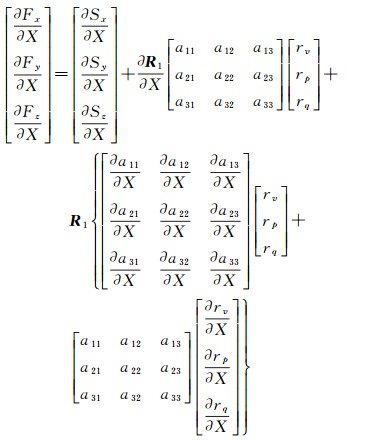 (12)
(12)
建立误差方程式
 (13)
(13)
式中,Δbc0、Δbcv分别表示C方向基线初值修正量、基线速率修正量;Δbn0、Δbnv分别表示N方向基线初值修正量、基线速率修正量。观测值误差为[(Fx1)…(Fzn)]T=[P0x1-Px1…P0zn-Pzn]T,其中[P0xi P0yi P0zi]表示控制点的三维重建坐标,[Pxi Pyi Pzi]表示已知控制点的三维坐标,观测值真值[Fx1…Fzn]T=0。
在干涉测量检校过程中,由于不同观测条件下,观测值的精度往往不同,因而误差也不同,不同控制点位置的数据质量也不同。由于相干性系数是评价SAR影像质量的重要标准,因此对控制点的相干性系数定权[22],会在后续研究中考虑其他定权方法。此时目标函数为
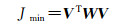 (14)
(14)
式中,W是对角权阵
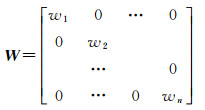 (15)
(15)
式中,wi(i=1, 2, …, n)为每个控制点的相干性系数。
给定干涉参数的初值X0,解算干涉参数的修正量,得
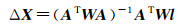 (16)
(16)
从而得到检校后的干涉参数
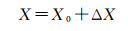 (17)
(17)
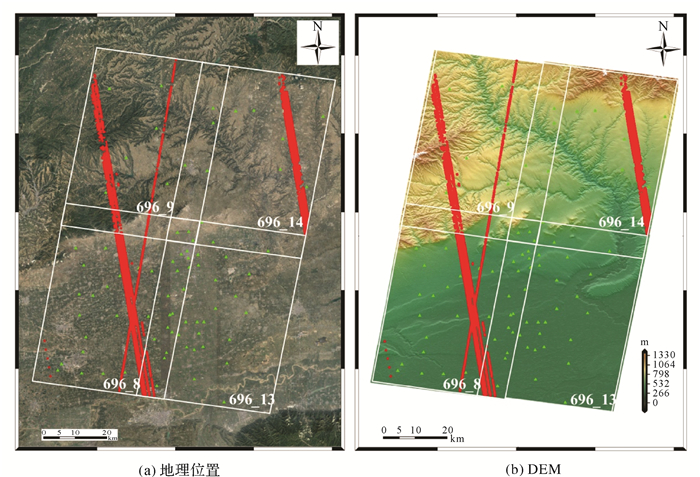
试验数据中心区域位于陕西渭南市,中心经纬度为109°34′25″E、35°01′48″N,东西向范围约达63 km,南北向范围约达108 km。区域内兼有平地和山地,海拔156~1338 m,其地理位置如图 5(a)所示。选取了83个地面控制点,通过采用SF-3050星站差分GNSS接收机实测,坐标系为大地坐标系,平面测量误差为15 cm,可满足1:25 000比例尺地形图测绘精度要求;高程测量误差为20 cm,引入的干涉相位误差小于1.12°,可用于进行高精度测量检校。本文选取的地面控制点主要分布在SAR影像中具有明显成像特征的区域,如道路交叉口、房屋拐角点等[26],详细点位分布如图 5中绿色三角形所示。本文在使用ICESat激光测高数据前进行了数据筛选[18, 27],将一些受云层、树木、建筑物等遮挡引起高程误差达到几十米甚至到几百米的数据剔除,最终共选择激光点7480个,详细点位分布如图 5中红色圆点所示,图 5(b)为检校后DEM结果。
|
| 图 5 试验区域地理位置及DEM的分布图 Fig. 5 Geographical location and DEM distribution map of study area |
试验数据为4对TanDEM-X/TerraSAR-X干涉数据,如图 5中白色线框所示,获取时间为2013年9月3日与2013年9月25日。选择90 m格网分辨率SRTM作为外部DEM数据。试验影像基本参数如表 1所示。
| 影像 编号 | 成像时间 | TCN方向基线 初值/m | TCN方向基线 速率/(m/s) |
| 696_8 | 2013-09-03 | 0,233.724 8,-51.834 4 | 0,0.196 9,0.289 6 |
| 696_9 | 2013-09-03 | 0,232.339 0,-53.860 0 | 0,0.199 0,0.289 1 |
| 696_13 | 2013-09-25 | 0,184.718 9,-94.254 0 | 0,0.166 4,0.269 6 |
| 696_14 | 2013-09-25 | 0,183.548 5,-96.138 6 | 0,0.168 0,0.268 8 |
4.2 结果与分析
在保证几何精度的条件下,应用三维重建模型解算控制点高程,与已知控制点高程进行精度评价,如表 2所示。
| 影像编号 | 影像类型 | 高程精度/m |
| 696_8 | 检校景 | 20.016 |
| 696_9 | 检校景 | 21.591 |
| 696_13 | 检校景 | 9.444 |
| 696_14 | 检校景 | 8.925 |
由表 2可知,不同轨道干涉图结果的高程精度存在较大差异。例如同轨696_13、696_14的高程精度低于9.44 m,而另一同轨696_8、696_9的高程精度低于21.59 m。高程存在较大误差的原因在于,首先,由于地形的限制,导致控制点本身精度降低;其次,存在几何检校的残余误差,导致在干涉测量检校中引入几何误差。
考虑到对基线误差解算会引入干涉相位误差,再对干涉相位误差解算反而增加高程误差。本文首先对干涉相位进行检校,将每一景影像的干涉相位误差分解后,根据三维重建模型解算控制点高程,与已知控制点高程进行精度评价,结果如表 3所示。
| 影像编号 | 影像类型 | 干涉相位误差/(°) | 高程精度/m |
| 696_8 | 检校景 | -120.768 | 2.057 |
| 696_9 | 检校景 | -127.059 | 2.848 |
| 696_13 | 检校景 | -50.099 | 2.726 |
| 696_14 | 检校景 | -52.105 | 2.312 |
由图 2干涉相位误差敏感度线性关系可知,以影像696_8为例,当干涉相位误差增加120.768°时,则引起约17.20 m的高程误差敏感度。本试验中,120.768°的相位误差引起高程误差变化量是17.96 m,与敏感度分析结果基本一致。由表 3可知,通过对干涉相位误差检校后,所有干涉结果的高程精度均优于2.85 m。在此基础上,对基线矢量展开检校,精度评价结果如表 4所示。
| 影像 编号 | 影像 类型 | 基线误差修正量 | 高程精 度/m | |||
| Δbc0 /m | Δbn0 /m | Δbcv /(m/s) | Δbnv /(m/s) | |||
| 696_8 | 检校景 | 0.059 7 | -0.047 3 | -0.009 2 | 0.007 2 | 1.469 |
| 696_13 | 检校景 | -0.055 2 | 0.042 0 | 0.005 7 | -0.004 3 | 2.535 |
本文将基线矢量分解为TCN方向的基线初值和基线速率,其共同影响干涉结果的高程精度。以影像696_8为例,C、N方向基线初值误差为0.059 7 m、-0.047 3 m,基线速率误差为-0.009 2 m/s、0.007 2 m/s。由式(18)计算得到沿方位向时间变化的基线误差在[0.029,0.122]之间,基于检校前后的高程精度,发现基线误差引起高程误差为19.16 m。根据图 3(e)基线误差敏感度线性关系,将基线误差增加到0.122 m时,高程误差已经达到19.63 m,与检校结果基本一致。通过表 4可以看出,对基线矢量检校后,所有干涉结果的高程精度均优于2.54 m。综上所述,干涉测量检校技术可提高干涉结果的高程精度。
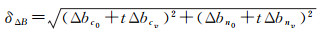 (18)
(18)
为了验证同轨影像之间检校参数的适用性,本文进行检校补偿验证。分别将影像696_8、696_13检校结果补偿于同轨影像696_9、696_14,最终对验证景数据进行精度评价,如表 5所示。
| 影像编号 | 影像类型 | 干涉参数修正量 | 高程精度 /m | ||||
| Δφ/(°) | Δbc0/m | Δbn0/m | Δbcv/(m/s) | Δbnv/(m/s) | |||
| 696_9 | 验证景 | -120.768 | 0.059 7 | -0.047 3 | -0.009 2 | 0.007 2 | 1.649 |
| 696_14 | 验证景 | -50.099 | -0.055 2 | 0.042 0 | 0.005 7 | -0.004 3 | 2.230 |
由表 5可知,利用检校参数对验证景补偿后,无控制点的干涉结果高程精度均优于2.23 m,满足山地地区1:25 000地形图测绘要求。
本文通过提出了利用参数独立分解的干涉测量检校方法,分解了星载InSAR系统中的主要误差源,同时这些因素也是引起DEM产品误差的主要来源。本文选用冰、云和陆地高程卫星(Ice, Cloud, and land Elevation Satellite, ICESat)[27-28]数据分别对未检校和检校后DEM的绝对高程精度进行了评估。如表 6所示,影像696_8和696_13位于平地地区,高程精度提升到1.21 m;影像696_9和696_14位于山地地区,高程精度提升到3.11 m,其满足了我国1:25 000比例尺平地地区1.5 m、山地地区4 m的测绘精度。
| 影像编号 | 未检校 | 检校后 |
| 696_8 | 8.055 | 0.594 |
| 696_9 | 10.774 | 3.108 |
| 696_13 | 10.184 | 1.205 |
| 696_14 | 9.344 | 1.869 |
综上所述,本文提出的干涉检校方法均可以提高DEM产品精度。但是检校后平地地区获取DEM产品的精度始终优于山地地区,这主要是因为山地地形起伏较大,且植被茂盛,相干性较差,对干涉结果产生一定的影响,从而导致该区域的高程误差较大,误差分布比较离散。
5 结论目前,随着国产SAR卫星的陆续发射,迫切需要对星载SAR干涉测量检校技术深入研究,提高国产星载SAR系统获取高精度DEM的能力。由于国内外InSAR干涉测量检校工作一般从机载工作开始研究,以此作为平台逐步将干涉检校技术扩展到星载平台。本文针对传统干涉测量检校模型中存在参数耦合性过强的问题,提出了一种利用参数独立分解的星载SAR干涉测量检校方法,采用两种独立检校算法分别对相位误差和基线矢量误差进行校正,通过获取4对TanDEM-X/TerraSAR-X干涉数据开展干涉测量检校试验。结果表明,对于该试验数据,干涉测量检校后干涉结果的高程精度均优于2.54 m。通过ICESat数据分别对未检校、检校后的DEM产品精度进行评估,检校后平地地区DEM产品的绝对高程精度优于1.21 m,山地地区DEM产品的绝对高程精度优于3.11 m。由此可见,本文提出的干涉测量检校方法能提高DEM产品精度,证明本文的方法是有效可行的。本文工作仍存在一些问题有待深入研究,例如未对控制点选取的数量以及分布情况进行探讨,特别是如何减少检校点的数量,实现稀少检校点的干涉测量检校等。另外,由于缺少高精度角反射器,本文未能对卫星在轨检校问题进行验证,后续研究工作将主要针对这两方面开展。
致谢: 感谢由德国宇航中心提供TerraSAR-X、TanDEM-X数据,美国航空航天局提供ICESat数据。
| [1] |
刘国祥, 丁晓利, 陈永奇, 等.
极具潜力的空间对地观测新技术——合成孔径雷达干涉[J]. 地球科学进展, 2000, 15(6): 734–740.
LIU Guoxiang, DING Xiaoli, CHEN Yongqi, et al. New and potential technology for observation of earth from space:synthetic aperture radar interferometry[J]. Advance in Earth Sciences, 2000, 15(6): 734–740. DOI:10.3321/j.issn:1001-8166.2000.06.020 |
| [2] |
刘国祥, 丁晓利, 李志林, 等.
使用InSAR建立DEM的试验研究[J]. 测绘学报, 2001, 30(4): 336–342.
LIU Guoxiang, DING Xiaoli, LI Zhilin, et al. Experimental investigation on DEM generation through InSAR[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 336–342. DOI:10.3321/j.issn:1001-1595.2001.04.012 |
| [3] | GONZÁLEZ J H, BACHMANN M, KRIEGER G, et al. Development of the TanDEM-X calibration concept:analysis of systematic errors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 716–726. DOI:10.1109/TGRS.2009.2034980 |
| [4] |
唐新明, 李涛, 高小明, 等.
雷达卫星自动成图的精密干涉测量关键技术[J]. 测绘学报, 2018, 47(6): 730–740.
TANG Xinming, LI Tao, GAO Xiaoming, et al. Research on key technologies of precise InSAR surveying and mapping application using automatic SAR imaging[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(6): 730–740. DOI:10.11947/j.AGCS.2018.20170621 |
| [5] | CURLANDER J C, MCDONOUGH R N. Synthetic aperture radar:systems and signal processing[M]. New York, NY: John Wiley & Sons, 1991. |
| [6] | SHIMADA M, ISOGUCHI O, TADONO T, et al. PALSAR radiometric and geometric calibration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(12): 3915–3932. DOI:10.1109/TGRS.2009.2023909 |
| [7] | ZHOU Xiao, ZENG Qiming, JIAO Jian, et al. Field calibration and validation of radarsat-2[C]//Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS. Melbourne: IEEE, 2014: 4451-4454. |
| [8] | CONG Xiaoying, BALSS U, EINEDER M, et al. Imaging geodesy-centimeter-level ranging accuracy with TerraSAR-X:an update[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 948–952. DOI:10.1109/LGRS.2012.2187042 |
| [9] | EINEDER M, MINET C, STEIGENBERGER P, et al. Imaging geodesy-toward centimeter-level ranging accuracy with terrasar-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 661–671. DOI:10.1109/TGRS.2010.2060264 |
| [10] |
吕冠南, 唐新明, 艾波, 等.
稀少控制的多平台星载SAR联合几何定标方法[J]. 测绘学报, 2018, 47(7): 986–995.
LÜ Guannan, TANG Xinming, AI Bo, et al. Hybrid geometric calibration method for multi-platform spaceborne SAR image with sparse GCPs[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 986–995. DOI:10.11947/j.AGCS.2018.20170283 |
| [11] | ZINK M, GEUDTNER D. Calibration of the interferometric X-SAR system on SRTM[C]//Proceedings of IEEE 1999 International Geoscience and Remote Sensing Symposium. Hamburg: IEEE, 1999. |
| [12] | MALLORQUI J J, BARA M, BROQUETAS A. Calibration requirements for airborne SAR interferometry[C]//Proceedings of SPIE 4173, SAR Image Analysis, Modeling, and Techniques Ⅲ. Barcelona, Spain: SPIE, 2000: 267-278. |
| [13] |
王彦平.机载干涉SAR定标模型与算法研究[D].北京: 中国科学院电子学研究所, 2003. WANG Yanping. Studies on calibration model and algorithm for airborne interferoemtric SAR[D]. Beijing: Institute of Electrics, Chinese Academy of Sciences, 2003. http://d.wanfangdata.com.cn/Thesis/Y646668 |
| [14] |
靳国旺, 张薇, 向茂生, 等.
一种机载双天线InSAR系统干涉参数定标新方法[J]. 测绘学报, 2010, 39(1): 76–81.
JIN Guowang, ZHANG Wei, XIANG Maosheng, et al. A new calibration algorithm of interferometric parameters for dual-antenna airborne InSAR systems[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 76–81. |
| [15] |
张薇, 向茂生, 吴一戎.
利用控制点三维信息标定机载双天线干涉SAR参数[J]. 测绘学报, 2010, 39(4): 370–377.
ZHANG Wei, XIANG Maosheng, WU Yirong. Using control points' 3D information to calibrate the interferometric parameters of dual-antenna airborne inSAR systems[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 370–377. |
| [16] |
胡继伟, 洪峻.
基于三维重建的分布式卫星SAR干涉测高模型及误差分析[J]. 中国科学院研究生院学报, 2011, 28(4): 489–497.
HU Jiwei, HONG Jun. Systematic model and errors analysis for distributed satellites SAR system based on three-dimensional reconstruction model[J]. Journal of Graduate University of Chinese Academy of Sciences, 2011, 28(4): 489–497. |
| [17] |
陈刚, 汤晓涛, 钱方明.
星载InSAR立体基线定标方法[J]. 武汉大学学报(信息科学版), 2014, 39(1): 37–41.
CHEN Gang, TANG Xiaotao, QIAN Fangming. A three-dimensional baseline calibration method of spaceborne InSAR[J]. Geomatics and Information Science of Wuhan University, 2014, 39(1): 37–41. |
| [18] |
吴丹芹.机载/星载InSAR定标模型与方法[D].成都: 西南交通大学, 2017. WU Danqin. Modeling and methodology for airborne and spaceborne InSAR calibration[D]. Chengdu: Southwest Jiaotong University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10613-1017129572.htm |
| [19] |
花奋奋.多基线干涉SAR高程反演研究[D].徐州: 中国矿业大学, 2015. HUA Fenfen. Elevation inversion through multi-baseline InSAR[D]. Xuzhou: China University of Mining and Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10290-1016705731.htm |
| [20] |
丁赤飚, 刘佳音, 雷斌, 等.
高分三号SAR卫星系统级几何定位精度初探[J]. 雷达学报, 2017, 6(1): 11–16.
DING Chibiao, LIU Jiayin, LEI Bin, et al. Preliminary exploration of systematic geolocation accuracy of GF-3 SAR satellite system[J]. Journal of Radars, 2017, 6(1): 11–16. |
| [21] |
陈继伟, 曾琪明, 焦健, 等.
利用轨道参数修正的无控制点星载SAR图像几何校正方法[J]. 测绘学报, 2016, 45(12): 1434–1440.
CHEN Jiwei, ZENG Qiming, JIAO Jian, et al. Spaceborne SAR image geometric rectification method without ground control points using orbit parameters modulation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1434–1440. DOI:10.11947/j.AGCS.2016.20160182 |
| [22] |
王青松, 黄海风, 董臻.
星载干涉合成孔径雷达——高效高精度处理技术[M]. 北京: 科学出版社, 2012.
WANG Qingsong, HUANG Haifeng, DONG Zhen. High-effciency and high-precision processing techniques of spaceborne interferometric synthetic aperture radar[M]. Beijing: Science Press, 2012. |
| [23] |
张永俊.星载分布式InSAR系统的误差分析与DEM精度提高方法研究[D].长沙: 国防科学技术大学, 2011. ZHANG Yongjun. Study on error analysis and DEM precision improvement methods of spaceborne distributed InSAR[D]. Changsha: National University of Defense Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-90002-1012020155.htm |
| [24] | ROSSI C, GONZALEZ F R, FRITZ T, et al. TanDEM-X calibrated raw DEM generation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012(73): 12–20. |
| [25] | KRIEGER G, MOREIRA A, FIEDLER H, et al. TanDEM-X:a satellite formation for high-resolution SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3317–3341. DOI:10.1109/TGRS.2007.900693 |
| [26] |
汪韬阳, 张过, 李德仁, 等.
资源三号测绘卫星影像平面和立体区域网平差比较[J]. 测绘学报, 2014, 43(4): 389–395, 403.
WANG Taoyang, ZHANG Guo, LI Deren, et al. Comparison between plane and stereo block adjustment for ZY-3 satellite images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 389–395, 403. DOI:10.13485/j.cnki.11-2089.2014.0058 |
| [27] | GRUBER A, WESSEL B, HUBER M, et al. Operational TanDEM-X DEM calibration and first validation results[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012(73): 39–49. |
| [28] | GAO Xiaoming, LIU Yaolin, LI Tao. High precision DEM generation algorithm based on inSAR multi-look iteration[J]. Remote Sensing, 2017, 9(7): 741. DOI:10.3390/rs9070741 |



