2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013;
3. 西南交通大学地球科学与环境工程学院, 四川 成都 611756;
4. 东华理工大学水资源与环境工程学院, 江西 南昌 330013
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, Nanchang 330013, China;
3. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China;
4. School of Water Resources & Environmental Engineering, East China University of Technology, Nanchang 330013, China
低空无人机因具有机动灵活、快速高效、受环境条件制约小等优势,近年来以其作为平台的垂直和倾斜摄影测量方式广泛运用于土地资源调查、城市规划、灾害监测等方面[1-2]。
相比传统航空航天摄影,低空摄影存在平台姿态不稳定、影像重叠度不规则等问题[2],因此,传统的摄影测量方法难以满足低空影像处理的需要。其中,影像的外方位元素高精度高效地解算是关键技术之一,近年来许多研究人员针对这一关键技术展开了广泛而深入的研究,最具代表性的方法是利用计算机视觉中运动恢复结构(structure from motion, SfM)[3]来恢复影像的位置与姿态参数。SfM算法可通过具有重叠的影像恢复相机的外方位元素,无须任何辅助信息即可重建三维场景,与传统摄影测量比较,对摄影相机、影像重叠规则性等要求低,且具有自动化程度高和通用性好等优势,被广泛应用到低空摄影测量数据处理中[4-9]。
在计算机视觉中,SfM算法通常是利用两两匹配遍历全局影像关联影像,n幅影像匹配时间复杂度为o(n2),其三维重建效率低下,不适用于低空摄影测量数据处理需要,低空无人机GPS/IMU信息常被用于辅助SfM算法三维重建[10-13]。文献[6]利用低空无人机飞控记录数据构建影像拓扑关系,缩小关联影像搜索范围来提高SfM算法中匹配效率。然而,基于成本、风险等原因,低空无人机通常不搭载高精度的POS设备,直接采用记录的GPS/IMU数据作为外方位元素初值参与光束法区域网平差会给三维重建结果带来明显的系统误差[13],因此,影像外方位元素全局一致性初值仍需其他算法来准确解算。文献[7]采用增量式SfM算法进行低空摄影测量数据处理,取得了与高精度POS辅助光束法平差基本相当的精度。但增量式SfM算法为避免累积误差的快速增大,在增加新的影像过程中,需经多次光束法平差迭代优化物方点和相机内、外方位元素,平差耗时随影像数增多呈指数级增加[13],从而制约了SfM算法在低空摄影测量数据处理效率的进一步提高。此外,增量式SfM算法依赖于初始像对选取,且仅依靠单一的匹配点数最多或关联节点数最多为依据遍历影像难以锁定最佳的候选影像,以及近平面的地形物方点三维坐标解算结果可能不稳定,这些问题都将影响三维重建精度。由此可见,利用GPS/IMU数据或多次平差的传统增量式SfM算法限制了外方位元素全局一致性全自动快速高精度解算。
在低空摄影测量外方位元素解算过程中,影像姿态求解是核心的环节,也是制约SfM算法精度和效率的主要因素之一。旋转平均是用于解算影像全局一致性姿态参数最常用的算法[14-15]。最初,文献[14]利用奇异值分解和最小二乘解算出全局一致性四元数形式的旋转矩阵,在相对旋转估计无粗差的理想情况下,这些算法能获得高精度的旋转相机旋转矩阵。然而,基于影像间匹配点估计相对旋转矩阵,由于匹配点数量、质量及分布情况等导致相对旋转矩阵解算不可避免地存在粗差[9]。针对这一问题,相应的改进算法也被提出,具有代表性的有利用半定松弛算法削弱粗差的全局运动估计[16]、利用迭代特征向量法剔除外点[17],引入李代数进行线性化旋转平均迭代剔除粗差[9, 15]。这些方法虽能在一定程度上剔除粗差和提高旋转平均计算效率,但局限于减小最小二乘旋转平均全局优化中的粗差影响,在旋转矩阵初值的确定过程中未有类似增量式SfM的平差优化过程。因此,全局影像旋转矩阵初值可能存在较大的累积误差,而初值的好坏影响到全局平差优化的迭代收敛效率和最终的平差精度[18-19]。特别是飞行不稳定的轻小型无人机平台易造成相机姿态角变化大,若旋转与平移矩阵初值未被准确解算可能造成平差优化迭代不收敛。
针对上述问题,本文顾及旋转矩阵初值确定,旨在构建适用于低空无人机平台摄影测量三维重建方法,提出一种耦合单-多旋转平均迭代优化的低空影像SfM三维重建方法,以匹配点数、关联节点数等多因素构建最优增量决策函数,利用顾及粗差的单旋转平均(single rotation averaging, SRA)增量方式添加立体模型,兼顾多旋转平均(multiple rotation averaging, MRA)自适应迭代优化旋转矩阵,最后利用光束法区域网平差统一优化整个网络,得到精确的物方点、影像旋转与平移矩阵。
1 耦合单-多旋转平均的SfM算法 1.1 增量式SfMSfM算法的核心在于通过特征匹配得到关联重叠影像之间的同名点,以最小化特征点的重投影误差来精确求解相机内外方位元素与物方点三维坐标的最大似然估计[7]。在计算机视觉中,三维物方点与二维平面点映射关系可由投影变换表示为
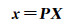 (1)
(1)
式中,图像点齐次坐标x=[x y 1]T;物方点坐标X=[X Y Z 1]T;投影矩阵P=K[R t],其中,K为相机内参数矩阵; R、t为表示相机的旋转与平移矩阵。利用自动匹配得到的同名点与影像关联来解算相邻影像间相对的旋转与平移矩阵,以三维物方点在影像上重投影误差最小为目标求解投影矩阵与物方点的最大似然估计。其目标函数为[7]
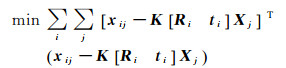 (2)
(2)
式中,Xj为待求的第j个物方点;xij为Xj对应在影像i上的已知坐标。
当前,增量式SfM是低空摄影测量数据处理中通常采用的方法[7]。在增量式SfM中,首先需要选取两个初始立体像对构建初始局部坐标系。通常选择足够多同名点和多度重叠的像对作为初始像对,但若选择的像对是近平面的地形,解算的物方点存在不稳定性。而且,增量式SfM通常依靠单一的匹配点数最多或关联节点数最多为依据遍历所有影像和光束法循环平差迭代优化,其缺点在于随着影像数增多平差耗时急剧增加。
针对增量式SfM方法存在的问题,全局SfM方法也被提出,用于大范围场景重建[15]。其关键在于采用旋转与平移平均算法来获得全局一致性的旋转与平移矩阵再进行一次光束法平差优化整个网络。然而,全局旋转与平移平均算法和光束法平差不同的是无须依赖三维物方点来参与平差和剔除粗差点,而是基于影像几何图与相对定向关系,通过最小二乘迭代求解最优的全局旋转与平移参数,因此对相对定向中存在的粗差较为敏感[7, 15]。
1.2 本文方法针对增量式和全局SfM方法存在的问题并兼顾两者的优势,本文提出一种耦合单-多旋转平均迭代优化方法。以增量式方法添加影像,但添加影像的局部构网平差过程并不采用光束法平差,避免因多次光束法平差造成增量式SfM方法效率低的问题。在局部构网时,为避免在物方点未参与平差而对噪声的稳健性不强、易受粗差干扰的问题,采用局部旋转平均对添加的影像进行平差,以缓解相对定向旋转矩阵中粗差带来的影响。
此外,优化初始化模型确定和影像增量添加方法,并在影像添加过程中判别已添加的影像集误差矩阵是否超限,来进一步削弱粗差的影响,从而实现低空影像SfM快速高精度三维重建。
本文方法流程见图 1,主要思路与步骤:①构建局部参考坐标系,以基准影像对优选函数来确定初始化模型,并以其中一影像的像空间坐标系作为基准构建局部参考坐标系;②构建正置扩展树,采用增量决策函数添加强关联影像;③根据基于四元数与旋转向量的单旋转平均公式(10)和随机采样一致性算法(random sample consensus, RANSAC)计算各影像的像空间坐标系相对于局部参考坐标系的旋转矩阵,并以选权迭代最小二乘法进行优化;④根据影像集Simg旋转矩阵误差为依据,自适应确定是否进行多旋转平均优化,进而抑制累积误差传递,并利用加权最小二乘计算平移矩阵;⑤在完成所有影像添加过程后,通过前方交会计算物方点三维坐标,采用绝对定向与光束法平差优化物方点、旋转与平移矩阵,得到地面坐标系下的三维重建结果。

|
| 图 1 本文方法流程 Fig. 1 Workflow of the proposed method |
1.2.1 局部参考坐标系构建
首先,为避免穷举匹配,利用低空摄影平台飞控记录的GPS/IMU数据搜索重叠影像。影像特征匹配利用基于SIFT与亚像素Harris结合的算法获取同名点[2],采用严密相对定向方法解算立体像对相对定向参数[20],并构建关联网络无向图G
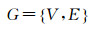 (3)
(3)
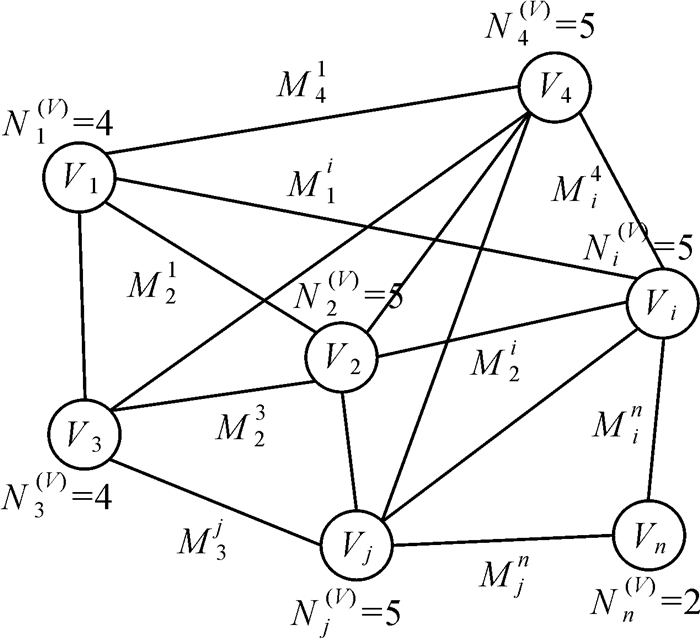
式中,V表示影像节点,连接边(i, j)∈E表示影像i与j的相对定向关系。具体见图 2示例,V1、V2、V3、V4、Vi、Vj、Vn表示影像节点。
|
| 图 2 关联网络无向图 Fig. 2 Example of undirected graph of correlated network |
其次,顾及同名点数量及其分布、关联图连通分量、累积误差最短传播路径等,综合同名点数M、关联节点个数N(V)、匹配点离散度D(STD)、单应矩阵估计中误差H为依据来确定初始像对(l, r),构建基准影像对ref优选函数
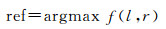 (4)
(4)
 (5)
(5)
式中,nimgs是影像数;l、r为影像节点索引;Mlr、Hlr分别为像对(l, r)的同名点数与其估计的单应矩阵误差;Hlr大小表征了物方点的起伏程度;Nl(V)表示与影像节点索引l关联的节点个数;Dl(std)是影像l中匹配点坐标的标准差以表征匹配点分布的离散度。此外,式(5)前3部分定义为影像增量决策函数。
在构建局部参考系(像空间辅助坐标系)后,以增量的形式(增量决策函数值最大为依据)添加剩余影像到影像集Simg中,扩充多旋转平均影像关联有向图(图 3),采用SRA计算各影像的像空间坐标系相对于局部参考系的旋转矩阵,并根据影像集Simg旋转矩阵误差是否超限来自适应进行MRA优化。图 3是图 2中影像节点在SRA与MRA结合的遍历过程:Vi→V2→V4→Vj→V3→V1→Vn,即在确定基准影像节点Vi后,在SRA(图 3(a)),待添加的影像在①—⑥中分别为V2、V4、Vj、V3、V1、Vn,以Simg旋转矩阵误差是否超限来确定是否进行①—⑥各步MRA(图 3(b))优化。

|
| 图 3 单-多旋转平均遍历 Fig. 3 Traverse images using single-multiple rotation averaging |
1.2.2 单旋转平均
若影像的像空间坐标系相对于局部参考系loc的已知旋转矩阵为R(loc),影像j的像空间坐标系相对于局部参考系的未知旋转矩阵Rj(loc)可通过立体像对(i, j)的相对定向旋转矩阵Rji和式(6)来计算
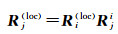 (6)
(6)
式中,Rj(loc)可通过引入原始相机坐标系(像空间坐标系)与局部参考系的两组共轭单位向量的平行约束[21-23]用3个沿着坐标系x、y、z轴的合成单位向量表示为
 (7)
(7)
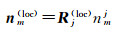 (8)
(8)
式中,nmi、nmj分别为影像i、j所在像空间坐标系的单位向量表示;Rij=(Rji)-1;nm(loc)是局部参考系loc的单位向量表示。
假定在参考坐标系与待添加的影像之间存在p个立体像对,故存在3p个共轭单位向量构建3p个等式。采用最小二乘法求解未知旋转矩阵Rj(loc),其表达式为[24]
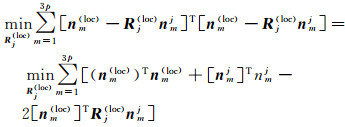 (9)
(9)
式中,[nm(loc)]Tnm(loc)、[nmj]Tnmj分别是单位向量nm(loc)和nmj真值为1的模,且向量Rj(loc)nmj和nm(loc)同向,故[nm(loc))TRj(loc)nmj为正值。易知式(9)最小化可归结为[nm(loc)]TRj(loc)nmj的最大化(见式(10)),并转化为点积计算。
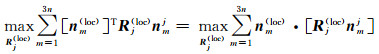 (10)
(10)
式中,·表示点积;nm(loc)、nmj为已知单位向量;Rj(loc)为未知旋转矩阵。然后,Rj(loc)nmj可转化为四元数乘法运算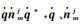

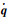
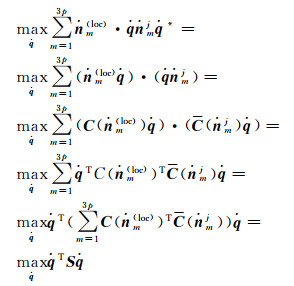 (11)
(11)
式中,C与C是由基于四元数乘法转换为基于矩阵乘法的4×4矩阵;S是以nmj和nm(loc)为所有共轭矢量对构建的4×4矩阵。
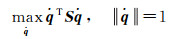 (12)
(12)
式中,在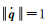
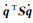
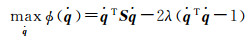 (13)
(13)
 (14)
(14)
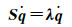 (15)
(15)
式中,λ为矩阵S的特征值;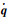
根据最小二乘选权迭代优化原理[25],将式(9)由min VTV改化为min VTWV。旋转矩阵R(loc)j0的改正数
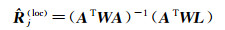 (16)
(16)
式中,A是系数矩阵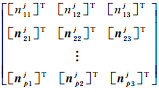
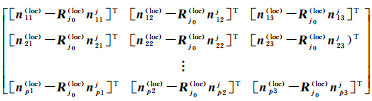
平移矩阵可由式(17)求解
 (17)
(17)
式中,tj(loc)为影像在参考系loc中3×1的平移矩阵;si为尺度因子。
1.2.3 多旋转平均迭代优化本文与传统单旋转平均不同关键在于添加影像后,初值优选与局部坐标系内影像影像集Simg优化思路见图 3。在关联图中,旋转矩阵计算采用正置树结构,然后,采用选权迭代多旋转平均自适应优化影像集Simg中的旋转矩阵。多旋转平均算法中,基于四元数旋转矩阵转换表达式为
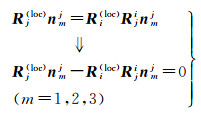 (18)
(18)
式中,nmj、Rjinmj表示影像i与j在相机坐标系中的共轭单位向量矩阵。传统的MRA中,通过SVD算法来解算在局部参考坐标系loc中两个未知矩阵Ri(loc)、Rj(loc)[26]。而本文中这两个旋转矩阵初值可由前述SRA中获得,并构建全局类似式(16)的选权迭代最小二乘法,并引入Huber函数约束粗差[9],优化影像集Simg中所有影像的旋转矩阵。
多旋转平均中,像对(i, j)平移向量变换关系为
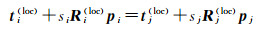 (19)
(19)
式中,pi、pj分别是两同名点坐标[xi yi -fi]T、[xj yj -fj]T;si、sj是两比例因子。结合式(17)、(19)构建最小二乘误差方程解算全局一致性平移矩阵。
1.2.4 区域网平差与三维重建在完成添加关联影像到影像集Simg和解算全局一致性旋转与平移矩阵后,利用地面控制点进行绝对定向和计算地面坐标系下的物方点坐标。然后,采用自检校光束法区域网平差对内、外方位元素和物方点云坐标进行整体统一优化。本文以最优化恢复影像姿态与位置为主旨,添加影像过程中规避物方点参与平差运算来提高SfM效率。
2 试验与分析 2.1 试验数据为验证本文方法在多飞行平台多地形地物环境下低空摄影测量数据处理方面的可行性、精度与效率,采用固定翼与DJI S1000+旋翼两种飞行平台及其搭载的两种相机分别获取的316幅(8条不规则航带)与126幅影像(2条航带)进行试验。飞行平台信息与相机参数见表 1、表 2,影像在进行空三处理前都经过了畸变差改正。试验区包括两个区域:①江西省上饶市尊桥乡,包含丘陵、平原等地形,以及建筑物、道路、河流、农田、村镇等地物,部分影像见图 4(a);②美国西拉法叶市郊区,主要包含玉米地,部分影像见图 4(b)。
| 飞行平台 | 固定翼无人机 | 旋翼无人机 |
| 相机 | Nikon D810 | Sony Alpha 7R |
| 影像大小 | 7360×4912 | 7360×4912 |
| 航摄时间 | 2016年7月 | 2017年8月 |
| 相对航高/m | 500 | 50 |
| 地面分辨率/cm | 10 | 0.7 |
| 参数 | 检校值 | |
| Nikon | Sony | |
| 像主点x0/mm | 0.130 9 | 0.220 2 |
| 像主点y0/mm | -0.022 5 | 0.018 4 |
| 焦距f/mm | 24.640 6 | 35.813 3 |
| 像元大小/um | 4.88 | 4.9 |
| 径向畸变κ1 | 1.481 72e-009 | 1.385 4e-010 |
| 径向畸变κ2 | -2.967 78e-017 | -8.951 66e-018 |
| 偏心畸变p1 | 2.003 1e-008 | 1.943 61e-007 |
| 偏心畸变p2 | -4.092 4e-008 | 2.573 67e-007 |

|
| 图 4 影像集部分影像 Fig. 4 Parts of images sets |
2.2 对比试验
同时,为便于比较分析,采用增量式单旋转平均(Incremental)[7]、基于全局旋转平均(Global)、基于李代数迭代选权旋转平均方法[9, 15](IRLS)、本文方法进行试验。固定翼与旋翼无人机影像(即尊桥与西拉法叶影像)外方位元素中误差见表 3、表 4。可见本文方法相对于其他3种方法能获得精度更好的外方位元素。固定翼无人机影像中global与IRLS结果较为接近,Incremental相对最差,而表 4中Global方法明显比其他3种方法精度更低。
| 参数 | Incremental | Global | IRLS | 本文方法 |
| ϕ/(°) | 1.03 | 0.89 | 0.84 | 0.72 |
| ω/(°) | 1.26 | 0.93 | 0.97 | 0.59 |
| k/(°) | 1.52 | 0.77 | 0.63 | 0.46 |
| Xo/(%) | 6.23 | 4.38 | 3.66 | 3.25 |
| Yo/(%) | 8.64 | 3.71 | 4.28 | 3.79 |
| Zo/(%) | 7.87 | 3.84 | 3.65 | 3.21 |
| 参数 | Incremental | Global | RLARA | 本文方法 |
| ϕ/(°) | 1.45 | 4.74 | 0.88 | 0.74 |
| ω/(°) | 1.03 | 2.89 | 0.79 | 0.53 |
| k/(°) | 1.35 | 8.82 | 0.87 | 0.49 |
| Xo/(%) | 7.27 | 7.13 | 3.72 | 3.04 |
| Yo/(%) | 5.98 | 8.54 | 4.71 | 3.52 |
| Zo/(%) | 8.53 | 10.64 | 3.15 | 3.42 |
| 注:表中平移向量[Xo Yo Zo]误差根据基线归一化的百分比表示。 | ||||
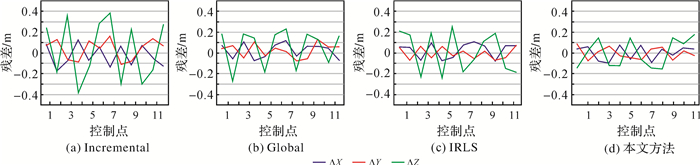
在固定翼与旋翼飞行平台试验区域,分别采集了15个和9个地面控制点进行绝对定向,以及分别采集了12个地面控制点用于检核,其中,西拉法叶试验区布设了地面标识点。4种方法的检查点残差中误差见表 5、表 6,检查点物方残差见图 5、图 6。尊桥影像中,本文方法检查点平面残差均小于0.1 m,高程中误差约为0.13 m;西拉法叶影像中,本文方法检查点平面与高程中误差分别接近0.01 m、0.02 m。由图 4(a)可知,固定翼无人机平台所摄区域纹理相对于旋翼无人机所摄区域更为丰富,图 4(b)重复纹理较多,可能存在匹配点少、分布不均匀以及匹配粗差等,导致Global方法精度明显比其他3种方法低。
| m | ||||
| Incremental | Global | IRLS | 本文方法 | |
| X | 0.103 9 | 0.072 7 | 0.074 0 | 0.064 5 |
| Y | 0.100 6 | 0.068 1 | 0.054 6 | 0.053 3 |
| Z | 0.283 9 | 0.182 8 | 0.192 1 | 0.130 2 |
| m | ||||
| Incremental | Global | IRLS | 本文方法 | |
| X | 0.020 4 | 0.075 4 | 0.021 1 | 0.011 9 |
| Y | 0.022 3 | 0.084 6 | 0.020 2 | 0.010 7 |
| Z | 0.051 2 | 0.096 7 | 0.032 5 | 0.020 8 |
|
| 图 5 尊桥影像检查点物方残差 Fig. 5 Residual error of check points in object space of Zunqiao images |

|
| 图 6 西拉法叶影像检查点物方残差 Fig. 6 Residual error of check points in object space of West Lafayette images |
4种方法在多视匹配得到相同的匹配点集后,通过前方交会解算物方点三维坐标,并经光束法平差和以重投影误差大于两个像素或3倍中误差为约束条件来剔除粗差点,得到重建点云见图 7、图 8,本文方法获得的三维点云明显比其他3种方法更为密集。在尊桥影像中,本文方法可得到171 941个三维点,而Incremental法、Global法、IRLS法分别得到77 338、96 451、137 902个点;在西拉法叶影像中,本文方法可得到63 294个三维点,而Incremental法、Global法、IRLS法分别得到42 352、29 676、47 470个点。采用本文方法解算的旋转与平移参数精度最高,重投影误差相对较小,因而能恢复出更多的三维点。

|
| 图 7 尊桥影像4种方法重建点云对比 Fig. 7 Comparison of reconstructed points cloud by four methods with Zunqiao images |

|
| 图 8 西拉法叶影像4种方法DSM对比 Fig. 8 Comparison of reconstructed points cloud by four methods with West Lafayette images |
本文主要针对SfM中全局一致性旋转与平移矩阵的高精度快速解算展开研究。为便于比较分析,4种方法在特征提取、特征匹配阶段采用同样的方法和结果,在同一硬件条件下,运动恢复结构的耗时情况见表 7所示。Incremental方法在添加新的影像时进行多次光束法平差迭代优化三维点坐标与影像内、外方位元素,平差计算随影像数增多而不断扩大,运动恢复结构耗时最长;Global方法因仅进行了一次全局一致性旋转平均优化,耗时最短;IRLS与本文方法在旋转平均过程中未有三维点云参与平差,效率也较高,且随着影像数增多,效率提升更为显著,但因多次旋转平均优化导致效率比Global方法稍逊。
| min | ||
| 方法 | 尊桥 | 西拉法叶 |
| Incremental | 257.26 | 91.03 |
| Global | 28.49 | 12.14 |
| IRLS | 34.12 | 15.28 |
| 本文方法 | 30.96 | 11.82 |
结合外方位元素中误差、检查点物方残差与中误差、运动恢复结构效率统计和数字地表模型视觉效果对比,权衡精度与效率可知,本文方法相对于Incremental、Global、IRLS 3种方法在低空影像运动恢复结构更具优势。
3 结论针对SfM算法用于低空摄影测量存在初始框架构建不尽合理、影像增量决策单一、迭代优化对粗差敏感等问题,本文从初始参考系着手,构建影像增量多因素决策函数添加强关联影像,利用四元数支持下无须物方参与平差的多旋转平均选权迭代自适应优化获取全局一致性旋转与平移矩阵,从而剔除粗差和抑制累积误差传递。通过固定翼与旋翼无人机影像试验表明,得益于增量候选影像优选与外方位元素自适应优化方法,本文方法相对于传统增量式SfM算法、全局优化、IRLS能获得更高的成果精度,且相比传统增量式SfM算法效率提高了8倍以上、接近全局优化方法效率,验证了本文方法不仅适用于固定翼无人机平台的高精度高效低空摄影测量数据处理,也适用于轻小型无人机平台影像处理。
| [1] |
李德仁, 李明.
无人机遥感系统的研究进展与应用前景[J]. 武汉大学学报(信息科学版), 2014, 39(5): 505–513, 540.
LI Deren, LI Ming. Research advance and application prospect of unmanned aerial vehicle remote sensing system[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 505–513, 540. |
| [2] |
何海清.低空摄影测量航带重构及数据处理方法研究[D].武汉: 武汉大学, 2013. HE Haiqing. The study of strips reconstruction oriented data processing methodology in low-altitude photogrammetry[D]. Wuhan: Wuhan University, 2013. |
| [3] | SNAVELY N, SEITZ S M, SZELISKI R. Modeling the world from internet photo collections[J]. International Journal of Computer Vision, 2008, 80(2): 189–210. DOI:10.1007/s11263-007-0107-3 |
| [4] |
沈永林, 刘军, 吴立新, 等.
基于无人机影像和飞控数据的灾场重建方法研究[J]. 地理与地理信息科学, 2011, 27(6): 13–17.
SHEN Yonglin, LIU Jun, WU Lixin, et al. Reconstruction of disaster scene from UAV images and flight-control data[J]. Geography and Geo-Information Science, 2011, 27(6): 13–17. |
| [5] | ROSNELL T, HONKAVAARA E. Point cloud generation from aerial image data acquired by a quadrocopter type micro unmanned aerial vehicle and a digital still camera[J]. Sensors, 2012, 12(1): 453–480. DOI:10.3390/s120100453 |
| [6] |
许志华, 吴立新, 刘军, 等.
顾及影像拓扑的SfM算法改进及其在灾场三维重建中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(5): 599–606.
XU Zhihua, WU Lixin, LIU Jun, et al. Modification of SfM algorithm referring to image topology and its application in 3-dimension reconstruction of disaster area[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 599–606. |
| [7] |
薛武, 张永生, 赵玲, 等.
增量式SfM与POS辅助光束法平差精度比较[J]. 测绘学报, 2017, 46(2): 198–207.
XUE Wu, ZHANG Yongsheng, ZHAO Ling, et al. Comparison of the accuracy of incremental SfM with POS-aided bundle adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 198–207. DOI:10.11947/j.AGCS.2017.20160274 |
| [8] |
吴子敬, 邓非.
SfM的倾斜航空影像空中三角测量[J]. 测绘科学, 2017, 42(11): 97–101.
WU Zijing, DENG Fei. Aerial triangulation of oblique aerial images based on SfM[J]. Science of Surveying and Mapping, 2017, 42(11): 97–101. |
| [9] |
李劲澎, 姜挺, 龚志辉, 等.
稳健李代数旋转平均用于GPS辅助无人机影像三维重建[J]. 光学精密工程, 2017, 25(6): 1607–1618.
LI Jinpeng, JIANG Ting, GONG Zhihui, et al. GPS-supported 3D reconstruction of UAV images based on robust lie-algebraic rotation averaging[J]. Optics and Precision Engineering, 2017, 25(6): 1607–1618. |
| [10] | IRSCHARA A, HOPPE C, BISCHOF H, et al. Efficient structure from motion with weak position and orientation priors[C]//Proceedings of IEEE CVPR 2011 WORKSHOPS. Colorado: IEEE, 2011: 21-28. |
| [11] |
郭复胜, 高伟.
基于辅助信息的无人机图像批处理三维重建方法[J]. 自动化学报, 2013, 39(6): 834–845.
GUO Fusheng, GAO Wei. Batch reconstruction from UAV images with prior information[J]. Acta Automatica Sinica, 2013, 39(6): 834–845. |
| [12] |
曹雪峰, 王庆贺, 谢理想.
融合低精度GPS/IMU参数的无人机影像批处理三维重建方法[J]. 系统仿真学报, 2015, 27(10): 2409–2421.
CAO Xuefeng, WANG Qinghe, XIE Lixiang. Batched 3D reconstruction of UAV images fused low precision position and orientation parameters[J]. Journal of System Simulation, 2015, 27(10): 2409–2421. |
| [13] |
李劲澎, 姜挺, 肖达, 等.
基于关系图的无人机影像三维重建[J]. 光学 精密工程, 2016, 24(6): 1501–1509.
LI Jinpeng, JIANG Ting, XIAO Da, et al. On diagram-based three-dimensional reconstruction of UAV image[J]. Optics and Precision Engineering, 2016, 24(6): 1501–1509. |
| [14] | GOVINDU V M. Combining two-view constraints for motion estimation[C]//Proceedings of 2001 IEEE Computer Conference on Computer Vision and Pattern Recognition (CVPR). Kauai: IEEE, 2001, 218-225. |
| [15] | CHATTERJEE A, GOVINDU V M. Efficient and robust large-scale rotation averaging[C]//Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 521-528. |
| [16] | ARIE-NACHIMSON M, KOVALSKY S Z, KEMELMACHER-SHLIZERMAN I, et al. Global motion estimation from point matches[C]//Proceedings of 2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission. Zurich: IEEE, 2012: 81-88. |
| [17] | OZYESIL O, SINGER A, BASRI R. Stable camera motion estimation using convex programming[J]. SIAM Journal on Imaging Science, 2015, 8(2): 1220–1262. DOI:10.1137/140977576 |
| [18] |
盛庆红, 柳建锋, 虞梦昕, 等.
对偶四元数近景影像空中三角测量法[J]. 测绘学报, 2015, 44(5): 503–509.
SHENG Qinghong, LIU Jianfeng, YU Mengxin, et al. Aerial triangulation close-range images with dual quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 503–509. |
| [19] | CUI Hainan, GAO Xiang, SHEN Shuhan, et al. HSfM: Hybrid structure-from-motion[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017: 1212-1221. |
| [20] |
何海清, 程朋根, 王晋.
低空立体像对的严密相对定向[J]. 遥感信息, 2014, 29(6): 11–15.
HE Haiqing, CHENG Penggen, WANG Jin. Rigorous relative orientation of low-altitude stereo images[J]. Remote Sensing Information, 2014, 29(6): 11–15. DOI:10.3969/j.issn.1000-3177.2014.06.003 |
| [21] | HORN B K P. Close-form solution of absolute orientation using unit quaternions[J]. Journal of the Optical Society of America A, 1987, 4(4): 629–642. DOI:10.1364/JOSAA.4.000629 |
| [22] | GUAN Yunlan, ZHANG Hongjun. Initial registration for point clouds based on linear features[C]//Proceedings of the 4th International Symposium on Knowledge Acquisition and Modeling. Washington, DC: IEEE, 2011: 474-477. |
| [23] | HE Fangning. 3D Reconstruction from passive sensors[D]. West Lafayette: Purdue University, 2017. |
| [24] | HE Fangning, HABIB A. A closed-form solution for coarse registration of point clouds using linear features[J]. Journal of Surveying Engineering, 2016, 142(3): 04016006. DOI:10.1061/(ASCE)SU.1943-5428.0000174 |
| [25] |
李德仁, 袁修孝.
误差处理与可靠性理论[M]. 2版. 武汉: 武汉大学出版社, 2012.
LI Deren, YUAN Xiuxiao. Error processing and reliability theory[M]. 2nd ed. Wuhan: Wuhan University Press, 2012. |
| [26] | MARTINEC D, PAJDLA T. Robust rotation and translation estimation in multiview reconstruction[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis: IEEE, 2007: 1-8. |


