空间关系是指若干地理实体及实体间相互作用的关系,主要包括拓扑、距离、方向关系及一些其他类型的空间特征。作为空间关系中重要的组成部分,复杂对象间的拓扑关系及其描述是地理信息科学的一个基础研究问题,对完善空间关系理论体系、空间推理、人工智能等具有重要意义[1]。
拓扑数据模型和数据结构的出现很大程度上是受到不准确的几何计算结果和有限的数字系统的影响,拓扑模型出现的最初动机是人们对认知合理的定性空间模型的需求。现阶段对空间拓扑关系的研究主要集中在线面拓扑关系与面面拓扑关系。在线面空间关系方面,文献[2]基于线面空间关系提出了元拓扑概念,总结出线面复合关系的集成表达模型;文献[3]提出了一种基于节点度的线面细分拓扑关系描述与计算方法,在定义线/面单元交线并分析其特点的基础上, 引入节点度来区分线/面单元交线细分类型。在面与面空间关系方面,区域连接演算(RCC)[4-5]是空间关系的一个重要形式。另一个相似的形式是Egenhofer[6-9]的9交模型9IM, 其使用九交矩阵分析了各种带洞面之间的拓扑关系。Tryfona和Egenhofer在将有多个面的区分解为简单区的基础上来处理拓扑关系;文献[10]在此研究基础上增加了两个带洞面目标之间的拓扑关系;文献[11]在9交模型9IM的基础上提出了一种25交模型25IM, 根据点集拓扑理论在排除不符合逻辑的拓扑关系后对8种基本拓扑关系进行描述,更详细地表达空间面拓扑关系;文献[12]提出了空间面目标间拓扑关系区分的层次表达方法,针对空间区之间的交与差、空间区边界间的交与差运算以及简单面与带洞面的外部间的交运算描述了简单面和带洞面间的23种层次拓扑关系;文献[13]提出了分层方向关系矩阵模型,将方向关系分解为外部方向关系矩阵,MBR外部方向关系矩阵和目标整体方向关系矩阵3个层面。
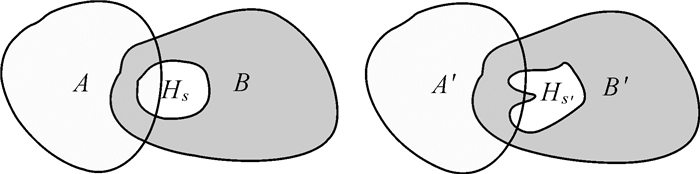
尽管现阶段对拓扑关系的研究取得了丰硕成果[14-19],但现有模型对复杂的面实体边界间可能发生的复杂交互的描述能力仍然不足[20-25]。如带洞面间或带洞面与由多个部分组合成的多区实体之间,它们的拓扑关系实际上不一样,而现有的拓扑关系描述模型可能会得到拓扑等价的结果。如图 1所示,A、A′是简单面,B、B′是带洞面,而HB、HB′分别是B和B′中的洞。现有模型对图 1中的空间关系进行描述,将会得到两者空间关系完全一致的结论。若从人的空间认知角度出发,其中的差别则很明显,原因在于(HB, A)的交集与(HB′, A)的不同。故对于存在着复杂边界交互的空间实体,已有模型对其拓扑关系的描述仍然存在改进空间。因此本文顾及复杂面实体的拓扑相交细节,利用元拓扑关系组合来对复杂面实体的拓扑关系进行精细化表达。
|
| 图 1 复杂空间对象的拓扑关系 Fig. 1 Topological relations of complex spatial object |
1 复杂面实体及其拓扑关系
从应用的观点出发,空间应用处理复杂的空间实体更多,而不是当前空间数据库系统、空间查询语言和GIS中常见的简单点、线和面。现实中的空间对象可能有若干组成部分,不同组成部分间可能会互相重叠,且面中可能有洞。Vasardani提出的带洞面的定性模型主要由5个互不相同的部分组成,如图 2所示,B°是B的内部;B-1是B所围绕着的内部区域,同时也填充了B中的洞;B-0是B的外部区域;∂1B是B的内部边界,分隔B0与B-1;∂0B是B的外部边界,分隔B0与B-0,如图 2所示。

|
| 图 2 带洞面的定性模型 Fig. 2 Qualitative model of the surface with hole |
复杂空间对象可通过复合空间对象模型进行构建,其主要思想是对简单对象进行几何组合生成,如合并和求差。例如:对于面A和B,若A和B相离,则(A∪B)构成有两个子区的多区(图 3(a)),在A包含B的限制条件下,结构(A-B)形成一个带洞面(图 3(b)),对于A包含B,而C与A, B相离的情况,结构(A-B)∪C形成有2个子面的多面,其中一个子面为带洞面(图 3(c)),在A包含B,B包含C的条件下,结构(A-B)∪C形成一个子面落在另一个子面洞内的多面(图 3(d))。

|
| 图 3 复杂空间对象的构成 Fig. 3 Component of complex spatial object |
如图 3中的复杂空间对象,虽然可以用Vasardani定性模型等方法对其进行描述,但对其拓扑关系的精细化表达仍存在一定不足。例如,图 4(a)和(b)中A和C所形成的复杂面通过Vasardani定性模型描述都是(A-B)∪C,但二者的拓扑关系有着明显的不同。

|
| 图 4 复杂面拓扑关系 Fig. 4 Topological relation of complex planar |
2 复杂面实体的元拓扑边界交集描述 2.1 线面实体间拓扑关系
实体(包括直线、曲线等)间的拓扑关系可以有多种,实体间边界的交点可以有多个,故线实体间的拓扑关系又可细分多种。若考虑线元素集合的有序性和基本拓扑关系组合的任意性,顺序与组合方式不同,拓扑关系则不同。线实体间的拓扑关系可以非常简单,也可以非常复杂,为便于区分,可进行如下定义:
定义1:将线实体之间相交次数为0或1的拓扑关系称为简单拓扑关系。
定义2:将线实体之间相交次数大于1的拓扑关系称为复合拓扑关系。
复杂拓扑关系可由简单拓扑关系进行组合形成。
定义3:若线L1与线L2的交集为空(不相交),则将其拓扑关系定义为相离。
定义4:线L1与线L2,当线L1与线L2的交集不为空时,作线L1与线L2交集的领域ε,则ε与线L1及线L2存在交点,依据交点数目可定义以下线L1与L2的拓扑关系:
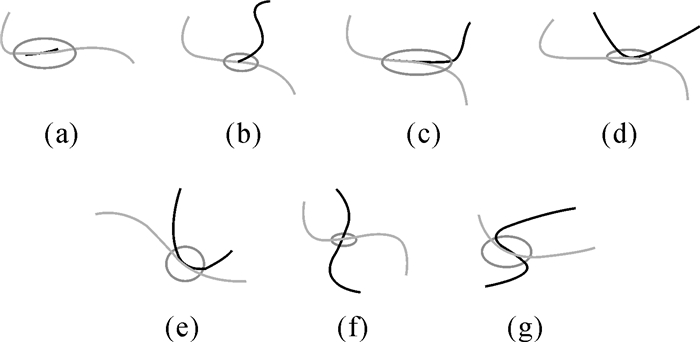
定义4.1:若交点为2,则将其拓扑关系定义为包含或重合,如图 5(a)所示;
|
| 图 5 拓扑关系示意图 Fig. 5 Schematic diagram of topological relations |
定义4.2:若交点为3,则将其拓扑关系定义为相接,如图 5(b)、(c)所示;
定义4.3:若交点为4,有两种情况:①按顺时针或逆时针方向,若ε穿越L1和L2的顺序为交替进行,则将其拓扑关系定义为相交,如图 5(f)、(g)所示;②按顺时针或逆时针方向,若ε穿越L1或L2连续两次,则将其拓扑关系定义为相切,如图 5(d)、(e)所示。
简而言之,在线实体间的拓扑关系中,当两个线实体发生接触时,每条线的两个端点在同一侧,则为相切关系;若线的两个端点跨越了接触部,则为相交关系;若线的一个端点位于接触部,一个端点不位于接触部,则为相接关系。
另外,在线与线发生接触的情况下,根据线线之间交集的维数,相接有0维相接(0, M)(图 5(b))和1维相接(1, M)(图 5(c)),相切有0维相切(0, T)(图 5(d))和1维相切(1, T)(图 5(e)),相交有0维相交(0, C)(图 5(f))和1维相交(1, C)(图 5(g)),包含(重合)只有1维(图 5(a))。
2.2 元拓扑关系只有线与线之间发生接触时才有可能产生复合线拓扑关系,相离则不能构成复合线关系。而在发生接触的简单线关系中,包含重合可看成是一条线,因此包含重合也不能构成复合线关系。因此,线与线之间的复合拓扑关系只能由相接、相切和相交关系组成。由此,可以定义元拓扑关系。
定义5:将能够组成线复合关系的、最小不可分的线简单拓扑关系称为线元拓扑关系。易得,线元拓扑关系有3类6种,即0维相交(C0)、1维相交(C1)、0维相切T0、1维相切T1、0维相接(M0)和1维相接(M1)。元拓扑关系具有如下特点:
概括性。概括性是指元拓扑关系必须概括所有复合关系的基本特征。即任意一个复合关系都可以由若干元拓扑关系按照一定的排序,经过有限次组合而成。元拓扑关系作为基本组成元素存在,必须能概括复合关系的所有特征。
“基本”不可分性。“基本”不可分性,是指一般情况下,元拓扑关系就是组成复合拓扑关系的最小单元,不可再分。但元拓扑关系又不可过于具体,否则会导致过多的繁琐工作。元拓扑关系必须在保证概括性的前提下,保证其不可分性。
2.3 元拓扑关系的方位描述在线与线发生接触时,若把其中一条线看成是一个面的边界部分,则线线关系转变成线面关系。而线与面发生接触时,线可能在面的外部,也可能在面的内部,这就涉及线与面的内外方位问题。
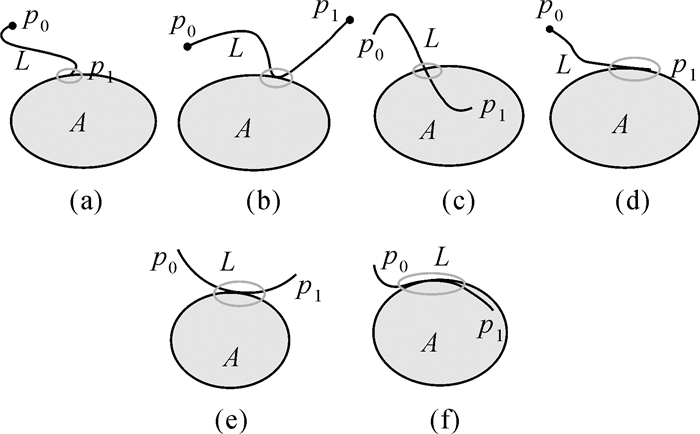
对于每个元拓扑关系来说,设线的两个端点为p0和p1,以p0为起始点,沿着L向p1前进,记下L与ε的第1个交点,若此交点在面A的内部,则记为in;在面A的外部,则记为out。当然,也可以以p1为起点进行描述。纳入方位关系以后,分别以p0和p1为起点,线面关系会有3类6种。
图 6(a)(out, M0), (out, M0);(b)(out, T0), (out, T0);(c)(out, C0), (in, C0);(d)(out, M1), (out, M1);(e)(out, T1), (out, T1);(f)(out, C1), (in, C1)。
|
| 图 6 元拓扑关系 Fig. 6 Basic topological relations |
记∂A为面A的边界,R(L, A)表示面A和线L的关系
R(L, A)<=>R(L, ∂A)=(Orie, MetaR)
其中
Orie={in, out},MetaR={M1, T1, C1, M0, T0, C0}
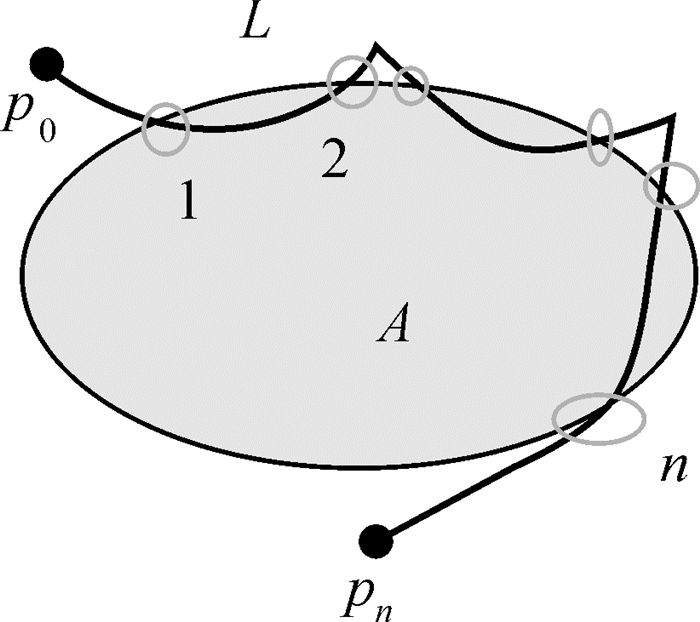
2.4 元关系的连接 2.4.1 元关系的连接顺序元拓扑关系的类型、内外方向的定义对元拓扑关系本身进行了描述,但元拓扑关系之间的连接关系则需要连接顺序和连接方向来进行约束。设线L与面A边界之间有n个元拓扑关(如图 7所示),线的两个端点分别为p0、pn, p0为起点,每个交点依次被编号,以面A的边界∂A为参考,从第1个元拓扑关系起,按顺时针方向跟踪,记下每个元拓扑关系的编号,直到最后一个元拓扑关系为止,则有
|
| 图 7 连接顺序 Fig. 7 Connecting order |
Order(L, A)=(k1, k2, k3, …, kn), n≥2
将上式纳入到元拓扑关系的连接中,有
R(L, A)<=>R(L, ∂A)=(Order, Orie, MetaR)
其中
Order={1, 2, 3, …, n},Orie={in, out},MetaR={M1, T1, C1, M0, T0, C0}
2.4.2 元关系的连接方向在线L与面A边界相交的n个元拓扑关系中,第i个元拓扑关系的连接方向是从i个元拓扑关系到第i+1个元拓扑关系之间的连接线对应于面边界投影线的方向,如图 8所示,第1个元拓扑关系的连接方向是顺时针(clockwise),图中顺时针箭头所示,第2个元拓扑关系的连接方向是逆时针(anticlockwise),图中逆时针箭头所示,最后一个元拓扑关系没有方向。

|
| 图 8 连接方向 Fig. 8 Connecting direction |
进一步纳入元拓扑关系的连接中,有
R(L, A)<=>R(L, ∂A)=(Order, Orie1, Orie2, MetaR)
其中
Order={1, 2, 3, …, n}, Orie1={in, out}, Orie2={c, a}, MetaR={M1, T1, C1, M0, T0, C0}
2.5 线面空间关系集成表达模型的约束性线面空间关系集成表达模型有3个约束条件,分别是元拓扑关系的排序,元拓扑关系的形式,元拓扑关系的连接方式。元拓扑关系的排序是指每个元拓扑关系的访问次序,例若按顺时针来进行访问,第2个元拓扑关系不一定紧随第1个元拓扑关系之后,访问次序可根据元拓扑关系编号的排列顺序确定。元拓扑关系的形式可依据元拓扑关系的内外方向(Orie1),元拓扑关系的类型(MetaR)来确定。元拓扑关系的连接方式是指元关系的连接方向,可通过Orie2的值来判断。如图 9所示,沿顺时针方向,将拓扑关系的描述式写成矩阵的形式,则有

|
| 图 9 拓扑关系示例 Fig. 9 Example of topological relations |
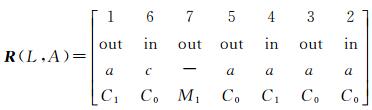
矩阵的第1行表示元拓扑关系的编号,其排列顺序就是元拓扑关系的排序;矩阵的第2行和第4行则表示元拓扑关系的形式,第3行代表元拓扑关系的连接方式,其中第7个元拓扑关系处于最后,所以连接方式为空。
2.6 复杂面边界间拓扑关系描述面与面拓扑相交,归根结底为面边界之间的相交,故面实体的边界交集问题可以通过对线实体之间的交集改进解决。
2.6.1 简单面边界拓扑关系描述现用上述的元拓扑关系来描述不含洞的简单面实体间的拓扑关系。
定义6:沿顺时针方向遍历面对象R的边界∂R时存在n个交集Inter∂R,每个交集可用相接(M),相切(T)和相交(C)来描述,描述子如下
Inter∂R={Intersection1, Intersection2, …, Intersectionn}
式中,Intersectionn=S(Order, Orie1, Orie2, MetaR),S表示与R有交集的面。
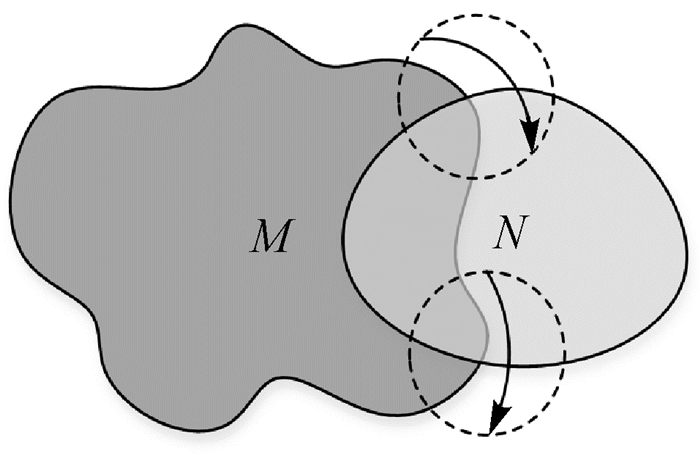
在图 10中,面M和面N的边界相交,对边界∂M进行顺时针遍历时会得到两个C0交集,即交集中没有边界重叠。在边界相交部分,第1个交集中N的边界从外由内穿入M中,第2个交集N的边界从内到外穿出M,因此完整的交集表达式可表示为
|
| 图 10 拓扑关系示例 Fig. 10 Example of topological relations |
Inter∂M:{N(1, out, c, C0), N(2, in, -, C0)}
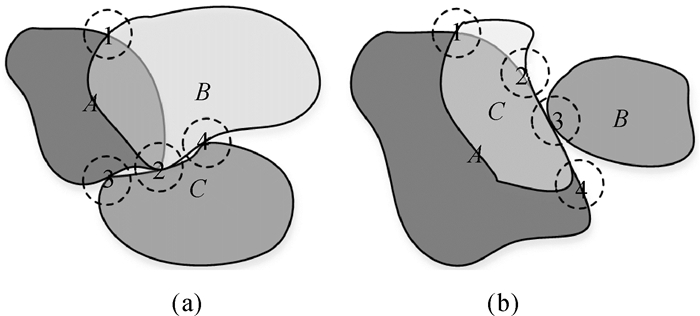
有时多条边界线会在一个点上交汇(图 11(a)中的交集2)或边界交集中同时存在1维相交和0维相切(图 11(b)中的交集3),如上图所示。从图 11(a)可得到如下3条交集表达式,其中边界的遍历都以顺时针的方向从区域外部开始。
|
| 图 11 拓扑关系示例 Fig. 11 Example of topological relations |
Inter∂A={B(1, out, c, C0), B(2, in, -, C0), C(3, out, c, T0), C(4, out, -, T0)}
Inter∂B={C(1, out, c, T0), C(2, out, -, T0), A(3, out, a, C0), A(4, in, -, C0)}
Inter∂C={A(1, out, a, T0), A(2, out, -, T0), B(3, out, c, T0), B(4, out, -, T0)}
图 11(b)中A和C在2、3、4的交集为1维相交,B和C以及B和A在3处的交集为0维相切,因此边界交集可表达为
Inter∂A={C(1, in, c, C0), C(2, out, -, C1), B(3, out, -, T0)}
Inter∂B={C(1, out, -, T0), A(2, out, -, T0)}
Inter∂C={B(1, out, -, T0), A(2, in, c, C1), A(3, out, -, C0)}
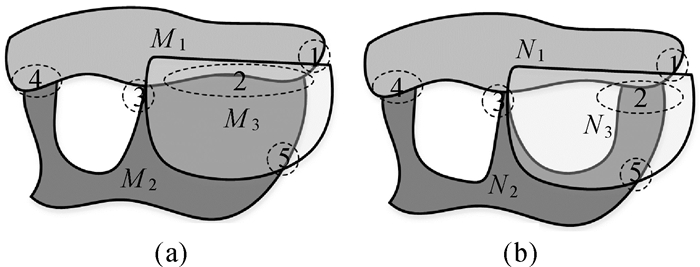
2.6.2 重叠面积描述图 12(a)中,面M1和M2相接,且它们之间形成一个外部分区,面M3分别与面M1和M2交叠,图 12(b)中N1和N2相接,它们间存在两个外部分区,面N3分别与面N1和N2交叠。首先利用上述的元拓扑关系对两个实体组合中的关系进行描述。
|
| 图 12 拓扑关系事例 Fig. 12 Example of topological relations |
Inter∂M1={M2(1, out, c, T1)M2(2, out, -, T1)M3(3, out, c, C0)M3(4, in, -, C0)}
Inter∂M2={M1(1, out, a, T1)M1(2, out, -, T1)M3(3, out, a, C0)M3(4, in, -, C0)}
Inter∂M3={M1(1, out, a, C0)M1(2, in, -, C0)M2(3, out, a, C0)M2(4, in, -, C0)}
Inter∂N1={N2(1, out, c, T1)N2(2, out, c, T0)N2(3, out, -, T1)N3(4, out, c, C0)N3(5, in, -, C0)}
Inter∂N2={N1(1, out, c, T1)N1(2, out, c, T0)N1(3, out, -, T1)N3(4, out, a, C0)N3(5, in, -, C0)}
Inter∂N3={N1(1, out, a, C0)N1(2, in, -, C0)N2(3, out, a, C0)N2(4, in, -, C0)}
在图 12中,(M2, M3)和(N2, N3)间的边界交集有着十分相似的表达式,但是它们有着不同的拓扑形态。故此元拓扑关系虽然可以描述面实体,但是仍不能精确地区别部分复杂面关系。
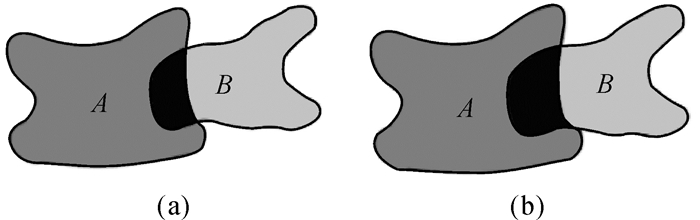
在图 13中(a)(b)的元拓扑关系及其表达式完全相同,但是用眼睛来判断二者的空间对象关系却不一样, 原因在于图 13(a)中A和B重叠部分比图 13(b)中的少。故只用元拓扑关系来描述,不能完全区分开复杂面的关系;引入重叠部分的面积进行辅助描述,则可进一步区分复杂面的关系。现引入重叠面积的概念,图 13中阴影部分的面积可记为Area则Area=area(A∩B)。
|
| 图 13 重叠面积示例 Fig. 13 Example of topological area |
在元拓扑关系中,相接和相切的重叠面积可记为∅,于是面实体间的描述子可进一步记为
Inter∂R={Intersection1, Intersection2, …, Intersectionn, Area1, Area2, …, Aream}
其中Intersectionn=S(Order, Orie1, Orie2, MetaR)。
此时图 12中的拓扑关系可进一步表示成如下:
Inter∂M1={M2(1, out, c, T1)M2(2, out, -, T1)M3(3, out, c, C0)M3(4, in, -, C0), area(M1∩M3)}
Inter∂M2={M1(1, out, a, T1)M1(2, out, -, T1)M3(3, out, a, C0)M3(4, in, -, C0), area(M2∩M3)}
Inter∂M3={M1(1, out, a, C0)M1(2, in, -, C0)M2(3, out, a, C0)M2(4, in, -, C0), area(M3∩M1), area(M3∩M2)}
Inter∂N1={N2(1, out, c, T1)N2(2, out, c, T0)N2(3, out, -, T1)N3(4, out, c, C0)N3(5, in, -, C0), area(N1∩N3)}
Inter∂N2={N1(1, out, c, T1)N1(2, out, c, T0)N1(3, out, -, T1)N3(4, out, a, C0)N3(5, in, -, C0), area(N2∩N3)}
Inter∂N3={N1(1, out, a, C0)N1(2, in, -, C0)N2(3, out, a, C0)N2(4, in, -, C0), area(N3∩N1), area(N3∩N2)}
在上述表达式中,(M2, M3)和(N2, N3)的表达式十分相似,但它们的重叠面积却不相同,因此可以精确地区别出不同的复杂面拓扑关系。
2.6.3 带洞面边界拓扑关系描述以上是对非洞简单面边界拓扑关系的讨论,现在引入重叠面积辅助描述的简单面元拓扑关系表达模型的基础上讨论含洞的复杂面边界拓扑关系表达模型。
当洞中不含面时,先以定义6遍历并描述对象R的外边界∂R。再沿顺时针方向遍历对象R的内边界∂R′,会存在n个交集Inter∂R′, 每个交集可用相接(M),相切(T)和相交(C)来描述,描述如下
Inter∂R′={Intersection1, Intersection2, …, Intersectionn, -R′}
其中, Intersectionn=S(Order, Orie, MetaR),S表示与R的洞R′有交集的面; -R′代表S与洞R′的重叠面积,但由于R′是洞故将重叠面积置为-R′。
当洞中含有面时,为了在表达式中明确的体现出此关系,可以遍历内边界时将洞中面和洞的关系加入到内边界所对应的表达式中。描述如下
Inter∂R′={Intersection1, Intersection2, …, Intersectionn, -R′, R′⊇/=I}
其中, R′为带洞面的内边界,-R′为相交面与洞的重叠面积,I为洞中所包含的面,R′⊇I代表面I完全被洞R′包含但没有完全重合,R′=I代表面I与R′完全重合。
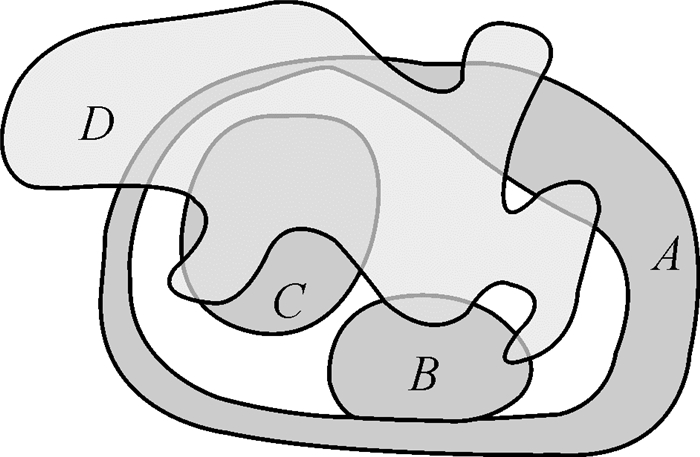
现以图 14、图 15为例进行说明:两图中面A的洞内分别存在与A完全相离的面B和与A相切的面B;面D同时与这3个面相交,但在边界细节处的拓扑关系存在不同。若使用九交模型,方向矩阵或其他拓扑描述方法来描述,将会得到两个空间组合拓扑关系相同的结论,且实体间的方位关系一致,使得难以分辨两个组合间的差别。使用扩展(重叠面积辅助描述)的元拓扑定义可对两个实体组合间的拓扑关系进行辨认。

|
| 图 14 面实体组合 Fig. 14 Combination of plane entities |
|
| 图 15 面实体组合 Fig. 15 Combination of plane entities |
由上述的扩展元拓扑关系的定义可以得到图 14的拓扑关系表达式,如下
Inter∂A={D(1, out, c, C0)D(2, in, -, C0)area(A∩D)}
Inter∂A′={D(1, out, a, C0)D(2, in, -, C0)B(3, out, -, T1), -, -, A′⊇B, A′⊇C}
Inter∂B={D(1, out, a, C0)D(2, in, -, C0)A′(3, in, -, T1)area(B∩D, -, B⊆A′)}
Inter∂D={A(1, out, a, C0)A(2, in, -, C0)A′(3, out, a, C0)A′(4, in, -, C0)B(5, out, a, C0)B(6, in, -, C0)C(7, out, c, C0)C(8, in, -, C0)area(D∩A), -, area(D∩B)area(D∩C)}
由上述的扩展元拓扑关系的定义可以得到图 15的拓扑关系表达式,如下
Inter∂A={D(1, out, c, C0)D(2, in, a, C0)D(3, out, c, C0)D(4, in, -, C0)area(A∩D)}
Inter∂A={D(1, out, c, C0)D(2, in, a, C0)D(3, out, c, C0)D(4, in, -, C0)B(5, out, -, T1)-, -, A′⊇B, A′⊇C}
Inter∂B={D(1, out, a, C0)D(2, in, c, C0)D(3, out, a, C0)D(4, in, -, C0)A′(5, in, -, T1)area(B∩D), -, B⊆A′}
Inter∂C={D(1, out, c, C0)D(2, in, a, C0)D(3, out, c, C0)D(4, in, -, C0)area(C∩D), C⊆A′}
Inter∂D={A(1, out, c, C0)A(2, in, c, C0)A(3, out, a, C0)A(4, in, -, C0)B(5, out, a, C0)B(6, in, a, C0)B(7, out, a, C0)B(8, in, -, C0)C(9, out, c, C0)C(10, in, c, C0)C(11, out, c, C0)C(12, in, -, C0)A′(13, out, a, C0)A′(14, in, c, C0)A′(15, out, a, C0)A′(16, in, -, C0)area(D∩A)area(D∩B)area(D∩C)-}
分别比较上述图 14和图 15的拓扑关系表达式,可以看出图 14和图 15的Inter∂A, Inter∂A′, Inter∂B, Inter∂C, Inter∂D都有明显的差异,故文中提出的扩展元拓扑关系可以很好地区分出复杂面实体边界的拓扑关系。且每一个表达式都可用矩阵表示。现将图 15中的拓扑关系表达式转化为矩阵形式,如下
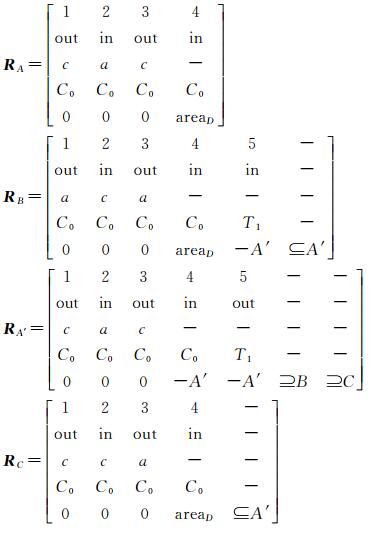

上述矩阵中,每一列代表一个元拓扑关系,其中矩阵的第5行代表重叠面积;矩阵RA、RA′、RB、RC、RD是图 14中的面实体组合的拓扑关系矩阵。
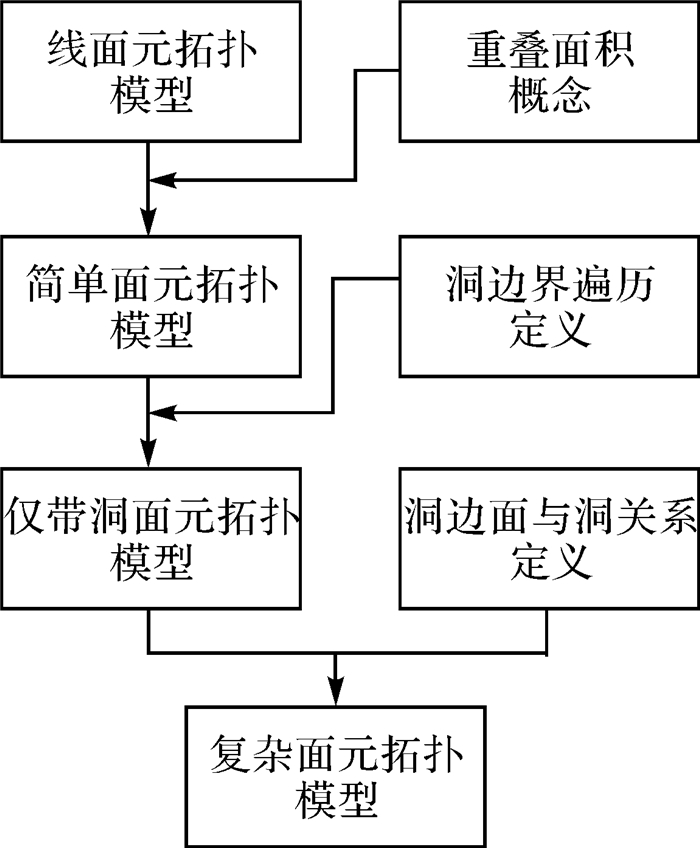
3 复杂面实体的拓扑关系精细化表达如图 16所示,文中从线面元拓扑关系模型出发,通过引入重叠面积,洞边界遍历定义和洞中面与洞关系定义扩展线面拓扑关系模型,完成对复杂面实体的拓扑关系精细化表达。
|
| 图 16 概念流程图 Fig. 16 Flow diagram of concept |
3.1 基础程序算法
基于以上所引入的概念和定义,现可将复杂面实体的拓扑关系精细化表达方式总结并设计出相应的算法并实现。基本算法如下:
组合表达算法
//初始调用INOUT: R->{r1, r2, …, rn}(复杂面实体集合);
n(复杂面实体个数);
OUTPUT:M->{m1, m2, m3…}(关系矩阵集合);
COMBINED-EXPRESSION(R, N, M):
foreach r∈R do //遍历每个复杂面实体
foreach b∈r do //遍历复杂面实体中的内外边界
If b==out then //如果b是外边界
foreach p∈b do //顺时针遍历改边界上的交点
assert p==out/in //判断该点的进出
assert p==c/a //判断该点与下一点之间的方向
assert p==C0/C1/T0/T1 //判断该点的相交方式
If p==lastone then //如果p是当前边界的最后一个交点
assert r∩r′==∅ or r∩r′!=∅ //判断b所在的实体r是否与其他实体是否有面积相交
assert r∈r′ or r∉r′ //判断b所在的实体是否被包含在其他实体内
If b==in then //如果b是外边界
foreach p∈b do //逆时针遍历改边界上的交点
assert p==out/in //判断该点的进出
assert p==c/a //判断该点与下一点之间的方向
assert p==C0/C1/T0/T1 //判断该点的相交方式
If p==lastone then //如果p是当前边界的最后一个交点
assert r∩r′==∅ or r∩r′!=∅ //判断b所在的实体r是否与其他
//实体是否有面积相交
assert r′∈r or r′ ∉r //判断b所在的实体是否包含在其他实体
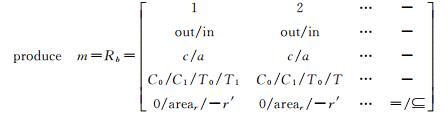
//生成该边界的组合关系矩阵表达式
produce M={m1, m2, m3…} //生成关系矩阵表达式
return M
3.2 数据类型分析与归纳通过归纳分析,元拓扑表达关系描述面与面相交时可以分为三大类,五小类的基础相交情况,而更为复杂的面与面相交的拓扑情况均可由5种基础相交的情况叠加生成。三大类分别是简单面(不含洞)与简单面(不含洞)相交,简单面(不含洞)与含洞面相交,含洞面与含洞面相交;其中含洞面可分为仅含洞的面和洞中有面的面;而洞中有面的面依据洞中面和面的关系又可分为洞中面边界与洞边界完全重合,部分重合,不重合3种情况。通过将线面之间相交的元拓扑关系扩展到5类面面基础相交情况中,便可以将元拓扑关系扩展到复杂面边界间的拓扑关系之中,如图 17所示。

|
| 图 17 复杂面相交情况分解图 Fig. 17 Decomposition diagram of complex planar objects |
3.3 模拟数据验证
为验证算法能否有效的通过精细化组合表达模型区分复杂面实体拓扑关系的不同,可在3.2节5种基础相交情况上通过比较每种基础相交情况简单交互和复杂交互模型,比较该算法所生成的元拓扑关矩阵的差异。算法所生成的5种基础相交情况的元拓扑关系矩阵如下表 1。
| 类型 | 复杂面拓扑关系图 | 扩展元拓扑关系矩阵 |
| 带洞面相交(洞中含面且与洞重合) | 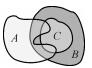 |
 |
| 带洞面相交(洞中面与洞相切) | 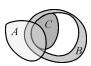 |
 |
 |
 |
|
| 带洞面相交(洞中面与洞相离) | 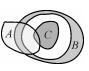 |
 |
| 带洞面相交(洞中面与洞相离) |  |
 |
通过比较表 1中的每种拓扑关系的矩阵表达式,可以看出即使在相同的基础相交情况下简单交互与复杂交互模型的矩阵表达式之间也存在明显的差异,因此可以通过每种拓扑关系的扩展元拓扑关系表达式来更好辨别大体相似但细节处不同的复杂面实体之间的拓扑关系,做到精细化表达。综上所述,本文所提出的引出重叠面积辅助描述的元拓扑关系可以很好地区别复杂面实体边界拓扑关系。
4 总结与展望本文对包含着复杂边界交集的面之间的拓扑关系进行了分析,探讨了使用元拓扑关系对此类面对象进行拓扑关系描述时所存在的限制,针对限制提出了使用边界交集元拓扑表达式对细节进行呈现,沿顺时针方向记录对象间的各个边界交集,并使用0维或1维,相交或相接的方式对边界交集的不同形式进行区分。为了消除具有相同边界交集表达式但拓扑关系不同而造成的模糊性,引入了重叠面积的概念,并与元拓扑关系结合对空间区组合间的拓扑关系进行描述。
在实际应用中,除了面对象外,还包括了点、多点、线、多线以及由点、线、区组合形成的复杂空间对象,因此未来的研究工作:①需要对以上用来描述空间面实体的方法在点、线上进行扩展,以实现对二维空间中任意对象的处理;②提取空间场景中的定性不变量,如方向和距离等,用此类定性概念加强对空间对象拓扑关系的描述;③将对空间对象间拓扑关系的描述扩展到拥有大量空间实体的场景中,以实现对空间场景拓扑关系的描述。
| [1] |
陈占龙, 冯齐奇, 吴信才.
复合面状对象拓扑关系的表达模型[J]. 测绘学报, 2015, 44(4): 438–444, 452.
CHEN Zhanlong, FENG Qiqi, WU Xincai. Representation model of topological relations between complex planar objects[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 438–444, 452. DOI:10.11947/j.AGCS.2015.20130708 |
| [2] |
曹亚妮, 吴芳华, 王立军, 等.
基于元拓扑关系的线面空间关系集成表达模型[J]. 武汉大学学报(信息科学版), 2016, 41(1): 123–130.
CAO Yani, WU Fanghua, WANG Lijun, et al. The integrated representation model of line-region spatial relations based on meta-relations[J]. Geomatics And Information Science of WuHan University, 2016, 41(1): 123–130. |
| [3] |
周晓光, 陈斐, 陈军.
引入结点度的线/面拓扑关系细分方法与应用[J]. 测绘学报, 2015, 44(4): 445–452.
ZHOU Xiaoguang, CHEN Fei, CHEN Jun. A node-degree based line/polygon topological relationship refinement model and its application[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 445–452. DOI:10.11947/j.AGCS.2015.20140138 |
| [4] | FRANKLIN W R. Cartographic errors symptomatic of underlying algebra problems[C]//Proceedings of the International Symposium on Spatial Data Handling. Zurich, Switzerland: [s.n.], 1984: 190-208. |
| [5] | RANDELL D, CUI Z, COHN A. A spatial logic based on regions and connection[C]//Proceedings of the 3rd International Conference on Knowledge Representation and Reasoning. Cambridge, MA: [s.n.], 1992: 165-176. |
| [6] | EGENHOFER M J, CLEMENTINI E, DI FELICE P. Topological relations between regions with holes[J]. International Journal of Geographical Information Systems, 1994, 8(2): 128–142. |
| [7] | EGENHOFER M J, VASARDANI M. Spatial reasoning with a hole[C]//Proceedings of the 8th International Conference on Spatial Information Theory. Melbourne, Australia: Springer. 2007: 303-320. |
| [8] | KODRATOFF Y, LEMERLE-LOISEL R. Learning complex structural descriptions from examples[J]. Computer Vision, Graphics, and Image Processing, 1984, 27(3): 266–290. DOI:10.1016/0734-189X(84)90032-X |
| [9] | EGENHOFER M J. Deriving the composition of binary topological relations[J]. Journal of Visual Languages & Computing, 1994, 5(2): 133–149. |
| [10] |
刘波, 李大军, 邹时, 等.
带孔洞面域间的拓扑关系的组合推理[J]. 测绘学报, 2011, 40(2): 262–267.
LIU Bo, LI Dajun, ZOU Shi, et al. Combinational reasoning of topological relations between regions with holes[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 262–267. |
| [11] |
沈敬伟, 周廷刚, 朱晓波.
面向带洞面状对象间的拓扑关系描述模型[J]. 测绘学报, 2016, 45(6): 722–730.
SHEN Jingwei, ZHOU Tinggang, ZHU Xiaobo. Topological relation representation model between regions with holes[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 722–730. DOI:10.11947/j.AGCS.2016.20150352 |
| [12] |
邓敏, 李志林, 李光强.
简单面目标与带孔洞面目标间拓扑关系的层次表达方法[J]. 测绘学报, 2008, 37(3): 330–337.
DENG Min, LI Zhilin, LI Guangqiang. A hierarchical approach to topological relations between a simple area and an area with holes[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 330–337. DOI:10.3321/j.issn:1001-1595.2008.03.011 |
| [13] |
唐雪华, 秦昆, 孟令奎.
基于拓扑参考的定性方向关系矩阵描述模型[J]. 测绘学报, 2014, 43(4): 396–403.
TANG Xuehua, QIN kung, MENG Lingkui. A qualitative matrix model of direction-relation based on topological refer-ence[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 396–403. DOI:10.13485/j.cnki.11-2089.2014.0059 |
| [14] |
吴华意, 刘波, 李大军, 等.
空间对象拓扑关系研究综述[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1269–1276.
WU Huayi, LIU Bo, LI Dajun, et al. Topological relations of spatial objects:a review[J]. Geomatics And Information Science of Wuhan University, 2014, 39(11): 1269–1276. |
| [15] | RODRÍGUEZ M A, EGENHOFER M J, BLASER A D. Query pre-processing of topological constraints: comparing a composition-based with neighborhood-based approach[C]//Proceedings of the 8th International Symposium on Advances in Spatial and Temporal Databases. Santorini Island, Greece: Springer, 2003: 362-379. |
| [16] |
吴长彬, 闾国年.
空间拓扑关系若干问题研究现状的评析[J]. 地球信息科学学报, 2010, 12(4): 524–531.
WU Changbin, LÜ Guonian. Spatial topological relationships:an overview and analysis[J]. Geo-Information Science, 2010, 12(4): 524–531. |
| [17] |
郭庆胜, 杜晓初, 刘浩.
空间拓扑关系定量描述与抽象方法研究[J]. 测绘学报, 2005, 34(2): 123–128.
GUO Qingsheng, DU Xiaochu, LIU Hao. Research on quantitative representation and abstraction of spatial topological relation between two regions[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 123–128. DOI:10.3321/j.issn:1001-1595.2005.02.006 |
| [18] |
郭庆胜, 刘小利, 陈宇箭.
线与线之间的空间拓扑关系组合推理[J]. 武汉大学学报(信息科学版), 2006, 31(1): 39–42.
GUO Qingsheng, LIU Xiaoli, CHEN Yujian. Combinational reasoning of topological spatial relations between two lines[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 39–42. |
| [19] |
吴长彬, 闾国年.
复杂线-线对象的拓扑关系描述与计算方法[J]. 地球信息科学学报, 2014, 16(6): 839–845.
WU Changbin, LÜ Guonian. Representation and Calculation method of topological relationships for complex line objects[J]. Journal of Geo-Information Science, 2014, 16(6): 839–845. |
| [20] | GALTON A. Modes of overlap[J]. Journal of Visual Languages & Computing, 1998, 9(1): 61–79. |
| [21] | CLEMENTINI E, DI FELICE P. Topological invariants for lines[J]. IEEE Transactions on Knowledge and Data Engineering, 1998, 10(1): 38–54. DOI:10.1109/69.667085 |
| [22] | EGENHOFER M J, FRANZOSA R D. On the equivalence of topological relations[J]. International Journal of Geographical Information Systems, 1995, 9(2): 133–152. DOI:10.1080/02693799508902030 |
| [23] | AKTOUF Z, BERTRAND G, PERROTON L. A three-dimensional holes closing algorithm[J]. Pattern Recognition Letters, 2002, 23(5): 523–531. DOI:10.1016/S0167-8655(01)00152-0 |
| [24] | EGENHOFER M J. A reference system for topological relations between compound spatial objects[C]//Proceedings of the 28th International Conference on Conceptual Modeling. Gramado, Brazil: Springer, 2009: 307-316. |
| [25] | EGENHOFER M J, VASARDANI M. Spatial reasoning with a hole[C]//Proceedings of the 8th International Conference on Spatial Information Theory. Melbourne, Australia: Springer, 2007: 303-320. |


