2. 中南大学地球科学与信息物理学院, 湖南 长沙 410083;
3. 中南林业科技大学土木工程学院, 湖南 长沙 410004
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
3. School of Civil Engineering, Central South University of Forestry and Technology, Changsha 410004, China
不确定性是一种广义的误差,它包含可度量的数值误差和无法用数值度量的误差。不确定性不再是一个具体数值,它在一定的实数区间内变动,或者仅是一个模糊数。抑制不确定性的影响,现有的平差理论还存在局限性。最近有许多学者研究了一种新的不确定性假设“未知但有界(unknown-but-bound,UBB)噪声”在测量数据处理中的应用[1-3]。由于UBB噪声不需要太多的先验条件,只要求噪声满足有界假设,这一点在实际测量中容易得到保证。如果能够找到由所有与观测数据、模型结构和噪声的有界假设相容的参数组成的集合[4-7],那么,此集合中的任何元素都可以成为参数解,此集合一般被称为参数的可行集(feasible solution set)。在一定的条件下,随着样本容量增大,成员集所包含的范围逐渐缩小,最后成员集最终收敛于系统的真实参数[8]。这种基于有界不确定性噪声(UBB噪声)的参数估计方法称为集员估计(set membership estimation)方法[4, 9-13]。2005年Mathematical and Computer Modeling of Dynamical Systems杂志出了一期专刊介绍集员估计理论与方法的研究成果[14]。Schweppe(1968)是早期研究椭球集员估计算法的学者。他采用椭球近似描述状态可行集[15]。文献[16]首先提出基于UBB噪声的参数的集员估计方法,其集合的Chebyshev中心可作为参数真实值的一个点估计。文献[17]又进一步改善了其算法,将椭球引入参数可行集的近似描述中来,提出了椭球集员估计算法。最近几年,椭球集员估计算法得到了迅速的发展[18-20]。用椭球集合来描述不确定性,实际上就是测量平差中用误差椭圆来描述点位误差的扩展,目前测量数据处理中,已有一些针对于椭圆和区间集合的简单算法[21-23]。用一个集合来描述不确定性,然后再用集合的特征(如体积),来度量不确定性是对误差概念的一种较好的扩展。本文将在椭球集合描述不确定性的基础上建立一个新的不确定性平差模型。通过定界集合的运算,以两个集合的交集来研究不确定度的传递过程。基于椭球集合特征矩阵的迹最小化建立最小不确定度平差准则,并寻找在此准则下的最优解。
1 有界椭球不确定性平差模型平差模型为
 (1)
(1)
式中,A为m×n(m≥n)维设计矩阵,且列满秩;L为n维观测向量;X=[x1 x2 … xn]T为n维参数向量;e为m维有界观测噪声,其有界性用范数形式来描述,如||e||≤γ,也可用区间来描述,如e∈[el, eu],这些描述方法,都可以统一用一个椭球集合来表示
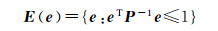 (2)
(2)
式中,P为n阶正定矩阵。它是椭球的特征矩阵,用来刻画椭球的形状特征,类似于e的协方差阵描述e的特征。有许多学者研究了矩阵P的构造[24-25]。在几何上,椭球的扁平程度以及椭球的体积是由椭球的特征矩阵来确定的。由于本文研究的不确定性是一种有界约束(椭球约束),这个有界性是通过矩阵P来刻画的,它相当于e的协方差阵来刻画e的特征一样。
若L=AX是相容方程组,取X0使得L=AX0。当L=AX不相容时,取X0=XLS=(ATA)-1ATL,这时,L≈AX0,利用式(1)有
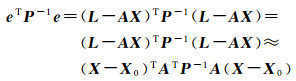
e的有界不确定性也可以近似地表示为
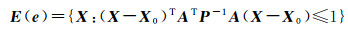 (3)
(3)
若X带有椭球约束先验信息,X的可行空间可以用下面的椭球集合来表示
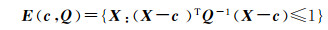 (4)
(4)
式中,c是椭球的中心;Q是椭球的特征矩阵,用来刻画椭球的形状特征。对于下面的平差模型
 (5)
(5)
称式(5)为带有椭球不确定性的平差模型。利用式(3),式(5)的约束条件可以写成
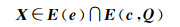
故式(5)也可以表示为
 (6)
(6)
E=E(e)∩E(c, Q)是参数向量的可行解集。
2 带有椭球不确定性约束的集员估计首先,建立一个不确定性椭球最小化的准则来确定式(6)的集员估计解。设E(z1, P1)和E(z2, P2)为两个椭球,它们分别定义为
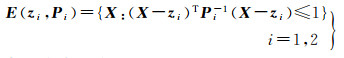
它们的交定义为
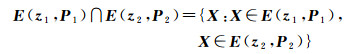 (7)
(7)
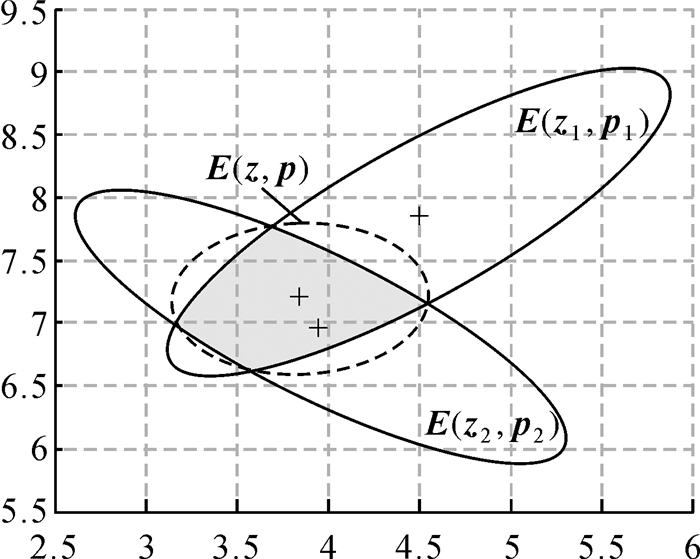
显然,两个椭球的交集不一定是一个椭球,它可以用一个外包椭球来近似[19],如图 1所示。设其外包椭球族为E(z, P),有
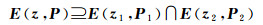 (8)
(8)
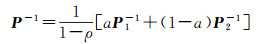 (9)
(9)
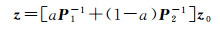 (10)
(10)
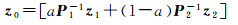 (11)
(11)
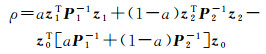 (12)
(12)
|
| 图 1 两个椭球交的最小外包椭球 Fig. 1 The minimum circumscribed ellipsoid with two ellipsoid intersections |
式中,0 < a < 1。上面的交的运算式(8)—式(12)的推导可以参考文献[26]。通过优化系数a,可以得到最小迹或最小体积外包椭球[19, 26]。如图 1,现在假设式(6)的可行解集E=E(e)∩E(c, Q)的外包椭球为
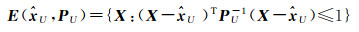
由式(9)与式(10),有
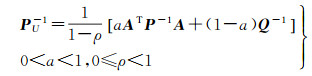 (13)
(13)
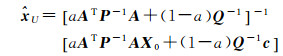 (14)
(14)
由文献[16]可知,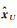
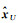
利用(F-CG-1D)-1=F-1+F-1C(G-DF-1C)-1DF-1,式(13)和式(14)可以化为

利用上面PU的计算,可以得到
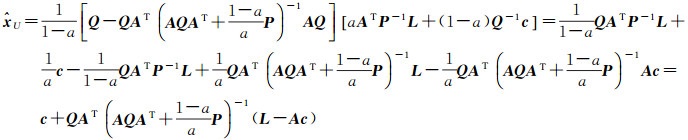
令
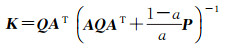 (15)
(15)
有
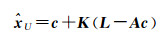 (16)
(16)
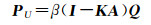 (17)
(17)
式中,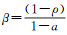
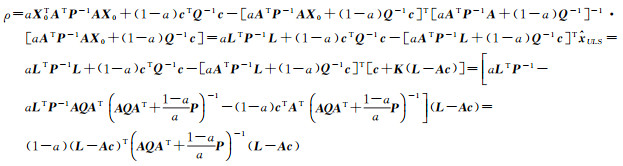
因此
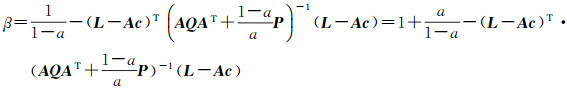 (18)
(18)
不同的a可以得到不同的测量更新椭球。为了保证椭球交的外包椭球的最小性,可以通过优化系数a,得到最小迹外包椭球。
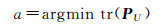 (19)
(19)
许多文献给出了式(19)中a的计算方法,但通常较为复杂,本文方法是直接搜索。因为,0 < a < 1,0≤ρ < 1,可知a必须使得
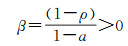 (20)
(20)
由式(13)可知,PU是一个正定矩阵,因此a还必须满足
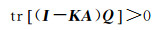 (21)
(21)
a在满足式(20)和式(21)的条件下,直接利用搜索算法(a从0开始到1止,通过增量Δa,逐步搜索得到使tr(PU)达到最小的a)求出a的值,从而求出参数估计值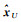
算例1 为了便于画出椭圆进行分析说明,特设计如下的平差模型
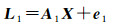 (22)
(22)
式中,X的真值为[4 7]T
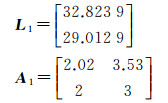
误差向量e1的不确定性和参数向量X的椭圆约束信息分别定义如下
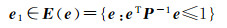 (23)
(23)
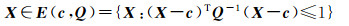 (24)
(24)
式中
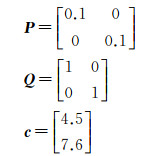
计算采用Matlab的随机函数生成的满足式(23)的随机数,e1=[0.033 90.012 9]T,利用式(19)算得:a=0.059 2,利用式(16)和式(17)计算得到

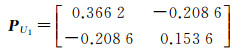
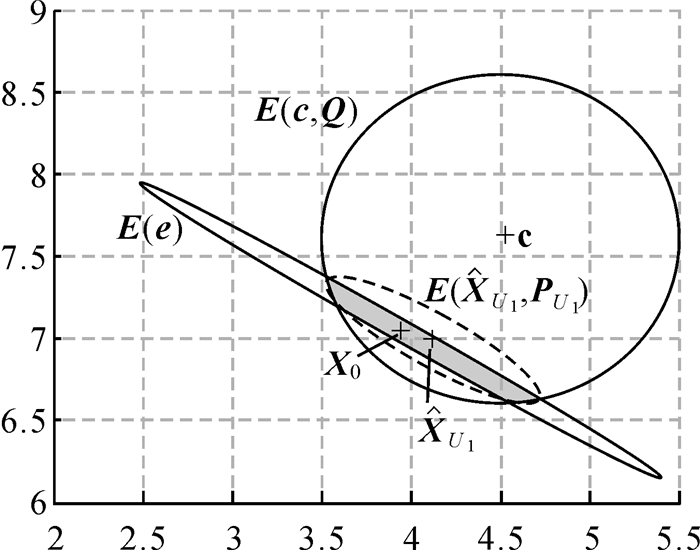
图 2给出了3个相应的不确定性椭圆,其中,E(e)通过(3)变换以后的椭圆{X:(X-X0)TATP-1A(X-X0)T≤1},其中X0=A1-1L1=[3.943 87.041 7]T,E(c, Q)为约束椭圆。这两个椭圆的交集中的每一个点都可以作为参数估计的解,交集的最小迹外包椭球为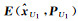

|
| 图 2 算例1中的误差椭圆,X的约束椭圆及解的不确定性椭圆 Fig. 2 Error ellipse, constrained ellipse of X and the uncertainty ellipse of solution in example 1 |
算例2 在算例1中,为了验算病态模型下算法的效率,取
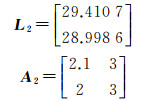
此算例中,A2的病态性相较于算例1有了适当的增加(为了图形的效果,没有进行更大的增加,对于较严重的病态情形,参见算例3)。计算中采用Matlab的随机函数生成的满足式(23)的随机数,e2=[0.021 60.039 3]T,利用式(19)算得:a=0.057 0,利用式(16)和式(17)计算得到
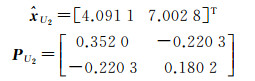
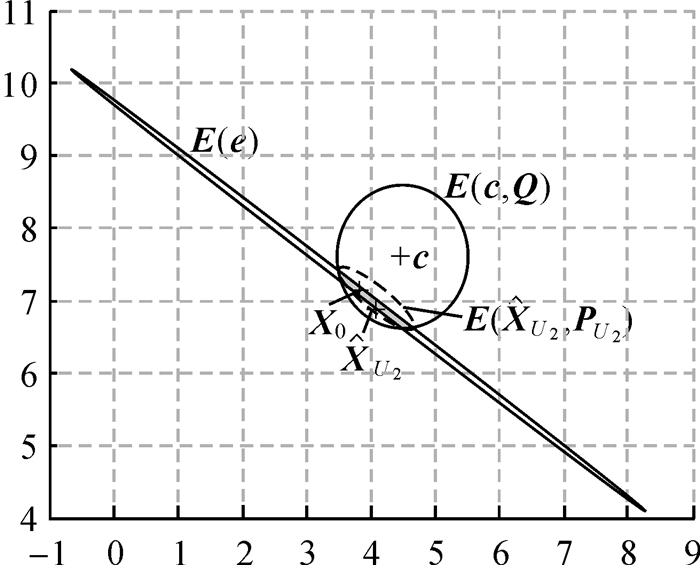
图 3给出了3个相应的不确定性椭圆,其中,E(e)通过式(3)变换以后的椭圆{X:(X-X0)TATP-1A(X-X0)T≤1},这里X0=A2-1L2=[3.823 07.131 1]T,E(c, Q)为约束椭圆。由于椭圆变换中牵涉到了逆矩阵运算,使得变换后的矩阵形状有了较大的变化。交集的最小迹外包椭球为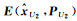

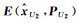
|
| 图 3 算例2中的误差椭圆,X的约束椭圆及解的不确定性椭圆 Fig. 3 Error ellipse, constrained ellipse of X and the uncertainty ellipse of solution in example 2 |
算例3 设有一测边网,P1、P2为已知点,其坐标分别为(48 580.285 m, 600 500.496 m)和(48 570.013 m, 60 555.845 m)。为了便于分析比较,算例中的点P3、P4、P5、P6的真实坐标假设为已知(表 1),边长的观测值是利用真实坐标计算,再加上误差得到的,观测边长视为同精度(表 2)。
| 点名 | 真实坐标 | 近似坐标 | |||||||
| P3 | P4 | P5 | P6 | P3 | P4 | P5 | P6 | ||
| x/m | 53 743.151 | 48 681.398 | 43 767.234 | 40 843.239 | 53 743.674 | 48 680.496 | 43 768.794 | 40 840.905 | |
| y/m | 61 003.810 | 55 018.270 | 57 968.590 | 64 867.876 | 61 006.568 | 55 018.806 | 57 966.087 | 64 870.541 | |
| 边号 | 观测边长/m |
| 1 | 45.075 |
| 2 | 5 222.056 |
| 3 | 5 187.391 |
| 4 | 7 838.867 |
| 5 | 5 483.162 |
| 6 | 5 731.756 |
| 7 | 5 438.383 |
| 8 | 7 493.316 |
| 9 | 8 884.603 |
| 10 | 8 839.687 |
为了便于分析,假设由前期的观测得到了P3、P4、P5、P6的近似坐标(表 1),以及它们相应的点位精度。相对于近似坐标的改正数构成的未知向量为X=[x3 y3 x4 y4 x5 y5 x6 y6]T,可以得到相应的平差模型的系数矩阵A和观测向量L。由于已知点P2的坐标非常靠近P1点,导致算法中的系数矩阵病态。
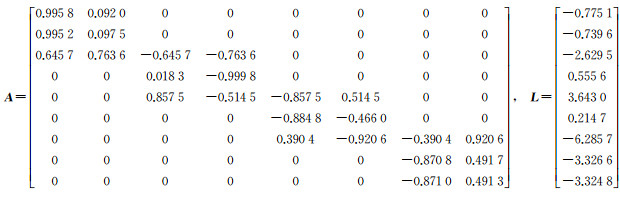
相应的平差模型为
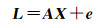 (25)
(25)
误差向量e的不确定性和参数向量X的椭圆约束信息分别定义如下
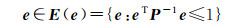 (26)
(26)
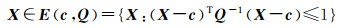 (27)
(27)
式中
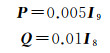

由于在平差算法中没有直接解算带有椭球约束的平差方法,在数学上通常是拉格朗日函数求极值的方法,转化成岭估计方法。如文献[25],将带椭球约束的线性模型估计写成

其拉格朗日函数为
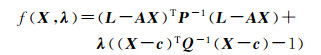
求得椭球约束下的广义岭估计

文献[25]给出了其岭参数的计算方法,但同时说明“当设计阵病态时,使用这种类似于两步估计的做法应该格外小心,理论上已经表明此时不宜采用广义最小二乘估计”。因此,在本算例中,采用通常的岭参数计算方法求出岭估计再与本文的方法进行比较。
利用式(19)求得a=0.052 8,利用式(16)和式(17)可以得到


综上,对实例解算有如下说明与分析:
(1) 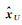
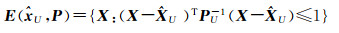
来进行计算。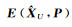

(2) 从加权混合估计的角度来看,因为计算得到a=0.052 8,说明参数约束先验信息式(27)在参数估计中的作用更大。这也正好说明当模型出现病态时,利用参数先验信息可以改善其病态性。
(3) 令
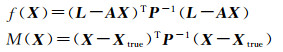
式中,Xtrue是参数的真值。从表 3可以看出,最小二乘算法的目标函数值是最小的。但因为系数矩阵病态,使得得到的最小二乘解严重偏离了真值,因此M(X)值是最大的。本文给出的算法中,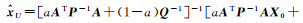

| 真值 | 最小二乘方法 | 截断奇异值法 | 岭估计法(L曲线法) | 本文算法 | |
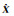 |
-0.523 0 | -1.347 3 | -0.535 0 | -0.552 7 | -0.510 7 |
| -2.758 0 | 6.162 5 | -2.372 9 | -2.263 9 | -2.677 4 | |
| 0.902 0 | 10.443 9 | 1.358 5 | 1.382 6 | 1.034 0 | |
| -0.536 0 | -0.364 5 | -0.530 7 | -0.497 5 | -0.540 6 | |
| -1.560 0 | 2.869 2 | -1.331 3 | -1.328 4 | -1.480 0 | |
| 2.503 0 | -5.908 4 | 2.067 1 | 2.080 8 | 2.368 2 | |
| 2.334 0 | -5.331 9 | 1.907 1 | 1.935 5 | 2.184 4 | |
| -2.665 0 | -16.214 1 | -3.387 3 | -3.328 9 | -2.907 2 | |
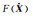 |
0.004 3 | 1.686 1×10-5 | 0.001 2 | 0.004 4 | 0.306 8 |
| m | 0 | 504.044 1 | 1.303 2 | 1.308 9 | 0.129 7 |
(4) 本文算法中不确定度的最小化是通过求椭球最小特征矩阵的迹来实现的,也可以通过最小化的椭球体积(对应的是特征矩阵的行列式最小),相关的算法可参看文献[8]。
(5) 算法中,a=0.052 8是一个近拟值。a从0开始,通过增量Δa=0.000 1,逐步搜索得到使tr(PU)达到最小的a。
(6) 对于病态模型的其他算法,如表 3中的截断奇异值算法和岭估计算法,它们是利用数学原理来处理病态系数矩阵,不能有效地利用先验信息,计算的结果不如本文的算法。更重要的是,本文算法不仅能给出参数估计的值,而且还能对参数估计的不确定度进行估计。
5 结束语不论是观测过程,还是未知参数本身,都存在不确定性噪声的干扰。然而,不确定性噪声非常复杂,难以确切了解诸如噪声的分布或均值和方差等统计特性。本文在椭球集合描述不确定性的基础上建立一个新的不确定性平差模型,以两个集合的交集来研究不确定度的传递。基于椭球集合特征矩阵的迹最小化建立最小不确定度平差准则,得到了在最优准则下的最优解。它与文献[27]提出的加权混合估计在形式上是一致的,都是对先验信息的利用。a的确定方法可以看作加权混合估计的权的一种新的确定方法。不确定性因素会以不确定度的形式反映在测绘数据中,其统计特性难以准确获得,需要在平差解算的同时,尽量使不确定度达到最小。不同于误差用数值来描述和度量不确定性,本文尝试用一个椭球来描述不确定性,然后用椭球特征矩阵的迹来度量不确定性的大小,这是对于不确定性描述与度量的一种尝试。
| [1] |
葛旭明, 伍吉仓.
误差限的病态总体最小二乘解算[J]. 测绘学报, 2013, 42(2): 196–202.
GE Xuming, WU Jicang. A regularization method to ill-posed total least squares with error limits[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 196–202. |
| [2] |
宋迎春, 谢雪梅, 陈晓林.
不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135–141.
SONG Yingchun, XIE Xuemei, CHEN Xiaolin. Adjustment criterion and algorithm in adjustment model with uncertain[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135–141. DOI:10.11947/j.AGCS.2015.20130213 |
| [3] |
王志忠, 陈丹华, 宋迎春.
具有不确定性平差算法[J]. 测绘学报, 2017, 46(7): 334–340.
WANG Zhizhong, CHEN Danhua, SONG Yingchun. An algorithm in adjustment model with uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 334–340. DOI:10.11947/j.AGCS.2017.20160522 |
| [4] | ELDAR Y C, BECK A, TEBOULLE M. A minimax Chebyshev estimator for bounded error estimation[J]. IEEE Transactions on Signal Processing, 2008, 56(4): 1388–1397. DOI:10.1109/TSP.2007.908945 |
| [5] | GARULLI A, VICINO A, ZAPPA G. Optimal induced-norm and set membership state smoothing and filtering for linear systems with bounded disturbances[J]. Automatica, 1999, 35(5): 767–776. DOI:10.1016/S0005-1098(98)00212-X |
| [6] | GARULLI A, VICINO A, ZAPPA G. Conditional central algorithms for worst case set-membership identification and filtering[J]. IEEE Transactions on Automatic Control, 2000, 45(1): 14–23. DOI:10.1109/9.827352 |
| [7] | BAI Erwei, FU Minyue, TEMPO R, et al. Convergence results of the analytic center estimator[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 569–572. DOI:10.1109/9.847746 |
| [8] |
梁礼明, 钟敏.
集员辨识理论发展及算法综述[J]. 自动化技术与应用, 2007, 26(11): 7–9, 18.
LIANG Liming, ZHONG Min. A survey of the set membership identification[J]. Techniques of Automation and Applications, 2007, 26(11): 7–9, 18. DOI:10.3969/j.issn.1003-7241.2007.11.003 |
| [9] | ALAMO T, BRAVO J M, REDONDO M J, et al. A set-membership state estimation algorithm based on DC programming[J]. Automatica, 2008, 44(1): 216–224. DOI:10.1016/j.automatica.2007.05.008 |
| [10] | BRAVO J M, ALAMO T, REDONDO M J, et al. An algorithm for bounded-error identification of nonlinear systems based on DC functions[J]. Automatica, 2008, 44(2): 437–444. DOI:10.1016/j.automatica.2007.05.026 |
| [11] | WALTER É, KIEFFER M. Guaranteed nonlinear parameter estimation in knowledge-based models[J]. Journal of Computational and Applied Mathematics, 2007, 199(2): 277–285. DOI:10.1016/j.cam.2005.07.039 |
| [12] | OTANEZ P G, CAMPBELL M E. Bounded switched linear estimator for smooth nonlinear systems[J]. IEEE Transactions on Control Systems Technology, 2007, 15(2): 358–368. DOI:10.1109/TCST.2006.886436 |
| [13] | JOACHIM D, DELLER J R. Multiweight optimization in optimal bounding ellipsoid algorithms[J]. IEEE Transactions on Signal Processing, 2006, 54(2): 679–690. DOI:10.1109/TSP.2005.861893 |
| [14] | CHERNOUSKO F, POLYAK B. Special issue on the set membership modelling of uncertainties in dynamical systems[J]. Mathematical and Computer Modelling of Dynamical Systems, 2005, 11(2): 123–124. DOI:10.1080/13873950500067296 |
| [15] | SCHWEPPE F C. Recursive state estimation:unknown but bounded errors and system inputs[J]. IEEE Transactions on Automatic Control, 1968, 13(1): 22–28. DOI:10.1109/TAC.1968.1098790 |
| [16] | FOGEL E. System identification via membership set constraints with energy constrained noise[J]. IEEE Transactions on Automatic Control, 1979, 24(5): 752–758. DOI:10.1109/TAC.1979.1102164 |
| [17] | FOGEL E, HUANG Y F. On the value of information in system identification-bounded noise case[J]. Automatica, 1982, 18(2): 229–238. DOI:10.1016/0005-1098(82)90110-8 |
| [18] |
梁礼明, 吴莉, 李钟侠.
一种改进型椭球外定界集员辨识算法[J]. 自动化技术与应用, 2009, 28(11): 11–13, 50.
LIANG Liming, WU Li, LI Zhongxia. An improved set-membership identification algorithm based on ellipsoid outside[J]. Techniques of Automation and Applications, 2009, 28(11): 11–13, 50. DOI:10.3969/j.issn.1003-7241.2009.11.003 |
| [19] |
黄一, 陈宗基, 魏晨.
最小迹扩展集员估计[J]. 中国科学:信息科学, 2010, 40(4): 526–538.
HUANG Yi, CHEN Zongji, WEI Chen. Least trace extended set-membership filter[J]. Scientia Sinica Informationis Sciences, 2010, 40(4): 526–538. |
| [20] |
周波, 戴先中.
自适应噪声定界的改进集员辨识算法[J]. 控制理论与应用, 2012, 29(2): 167–171.
ZHOU Bo, DAI Xianzhong. Improved set-membership identification algorithm with adaptive noise bounding[J]. Control Theory & Applications, 2012, 29(2): 167–171. |
| [21] |
刘大杰, 华慧.
GIS位置不确定性模型的进一步探讨[J]. 测绘学报, 1998, 27(1): 45–49.
LIU Dajie, HUA Hui. The more discussion to the modeling uncertainty of line primitives in GIS[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(1): 45–49. DOI:10.3321/j.issn:1001-1595.1998.01.007 |
| [22] |
范爱民, 郭达志.
误差熵不确定带模型[J]. 测绘学报, 2001, 30(1): 48–53.
FAN Aimin, GUO Dazhi. The uncertainty band model of error entropy[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 48–53. DOI:10.3321/j.issn:1001-1595.2001.01.010 |
| [23] |
蓝悦明, 陶本藻.
以点位误差描述线元位置不确定性的误差带方法[J]. 测绘学报, 2004, 33(4): 289–292.
LAN Yueming, TAO Benzao. End points accuracy based error band method for determination of a line segment position uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(4): 289–292. DOI:10.3321/j.issn:1001-1595.2004.04.002 |
| [24] |
孙先仿, 范跃祖, 宁文如.
有界误差模型的一种结构辨识方法[J]. 自动化学报, 1999, 25(2): 242–246.
SUN Xianfang, FAN Yuezu, NING Wenru. A structure identification method for bounded-error models[J]. ActaAutomatica Sinica, 1999, 25(2): 242–246. |
| [25] |
杨婷, 杨虎.
椭球约束与广义岭型估计[J]. 应用概率统计, 2003, 19(3): 232–236.
YANG Ting, YANG Hu. Ellipsoidal restriction and generalized ridge estimation[J]. Chinese Journal of Applied Probability and Statistics, 2003, 19(3): 232–236. DOI:10.3969/j.issn.1001-4268.2003.03.002 |
| [26] | DURIEU C, WALTER É, POLYAK B. Multi-input multi-output ellipsoidal state bounding[J]. Journal of Optimization Theory and Applications, 2001, 111(2): 273–303. DOI:10.1023/A:1011978200643 |
| [27] | SCHAFFRIN B, TOUTENBURG H. Weighted mixed regression[J]. Zeitschrift für Angewandte Mathematik und Mechanik, 1990, 70(6): T735–T738. |



