2. 西安测绘研究所, 陕西 西安 710054;
3. 信息工程大学地理空间信息学院, 河南 郑州 450001
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
3. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China
Stokes/Hotine积分是计算(似)大地水准面的理论工具[1-6]。Stokes/Hotine积分理论上需要全球积分,但由于全球重力数据难以获取,且全球积分计算量较大,因此实际计算通常使用移去恢复技术,此时边值解算仅需进行近区Stokes/Hotine积分。为了减弱远区影响、提高(似)大地水准面的解算精度,出现了众多核函数的修正方法。核函数修正方法可分为确定性修正与随机性修正两类。确定性修正理论包括有Meissl方法[7]、Molodensky方法、Sjöberg方法[8]、Wong和Gore方法等[9-10],随机性修正需将模型重力数据和实测重力数据的误差阶方差作为先验信息,而实测数据的误差阶方差信息很难获取,限制了随机性修正方法的应用[11]。
使用移去恢复技术时需选定一个模型重力场作为参考场,因此Stokes/Hotine积分中包含了实测重力和模型重力两类重力数据。重力测量、水准测量、地形归算[12-13]、格网化[14]等使Stokes/Hotine积分中的实测重力数据存在一定的长波误差[15],而重力场模型的长波精度较高(satellite-only卫星重力场模型的前20阶已达到非常高的精度[16-17]),因此Stokes/Hotine积分时,应选择对实测重力数据具有高通滤波属性的积分核函数。截断核函数(the spheroidal kernel,由标准核函数除去一定阶数的Legendre多项式得到)是一种非常有效的高通滤波器[18],可有效地避免实测重力数据的长波误差传播到(似)大地水准面中,因此在基于移去恢复的边值解算中应用较为广泛。但模型重力数据的累积误差随着模型阶数的增加而增大,而实测重力数据的中高频误差相对较小,因此为了获得高精度的(似)大地水准面不宜过滤过多频段的实测重力信息。
传统积分核函数的研究主要为了减小远区截断误差,但在移去恢复模式下,积分核对边值解算精度的影响方式发生了转变:在高频波段(大于模型重力场截止阶数的频率波段),核函数决定了高频远区截断误差的大小以及谱泄露的程度;在低频波段(小于模型重力场截止阶数的频率波段),核函数决定了实测与模型两类重力数据对低阶高程异常/大地水准面高的贡献率。因此,在移去恢复模式中核函数的研究应分高频和低频两个频段展开。
Stokes积分核与Hotine积分核[19-21]具有相似的频谱特性,Stokes核函数理论可方便地应用于Hotine积分核,反之亦然。根据Stokes-Helmert理论方法构建的加拿大重力大地水准面CGG2010[22]使用了高低阶均修正的截断Stokes核函数。本文以Hotine积分核为例在其基础上提出了更加高效的低阶修正的截断核函数,不仅包括余弦低阶修正核函数,还构造了一种线型低阶修正核函数。本文首先对扩展Hotine核函数展开频谱分析,然后根据Hotine-Helmert理论方法使用不同的Hotine核函数解算了试验区的似大地水准面,以验证不同Hotine核函数的应用效果。
1 Hotine截断核函数在移去恢复模式下,使用传统截断Hotine核函数计算高程异常(高程异常为似大地水准面到参考椭球面的距离)的算法公式为
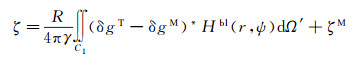 (1)
(1)
式中,ζ为高程异常;ζM为模型高程异常;C1为Hotine的近区积分范围;R为地球平均半径;r为计算点的地心向径;γ为地面点的正常重力;ψ为流动点与计算点间的球心角距;δgT为地面重力扰动;δgM为模型重力扰动;*表示向下延拓过程[23-26],通过向下延拓可将地面重力值转化为边界面重力值;Hbl(r, ψ)为扩展形式的Hotine截断核函数,为方便表述下文省略“扩展”。
目前广泛使用的Hotine截断核函数有两种。一种是高低阶均截断的核函数
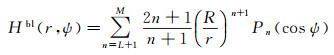 (2)
(2)
式中,L为低阶截断频率(阶数);M为由地形分辨率决定的高阶截断频率;Pn(cos ψ)为Legendre函数。另一种为仅低阶截断的核函数
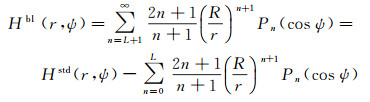 (3)
(3)
式中,Hstd为标准形式的Hotine积分核
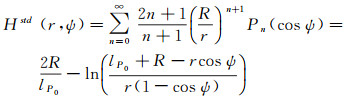 (4)
(4)
式中, 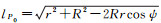
修正的截断核函数是通过对传统截断核函数增加修正因子得到的,即
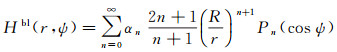 (5)
(5)
式中, αn为修正因子,也可称为平滑因子。
2.1 高低阶均修正文献[22]提出了余弦函数构建的高低阶均修正的截断核函数,其修正因子为
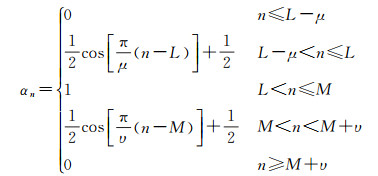 (6)
(6)
式中,μ为低阶修正带宽;υ为高阶修正带宽,修正带宽表示修正的阶数区间。从式(6)可以看出该修正因子在L-μ阶到L阶的频率波段从0逐渐增大至1,在M阶到M+υ阶的频率波段由1逐渐减少至0。当修正区间(L-μ, L)和(M, M+υ)的各阶修正因子均取0时,高低阶均修正的截断核函数转化为式(2)所示的传统高低阶均截断的核函数。
由于边值解算采用的重力数据、地形数据均为离散的网格数据,因而需对Hotine积分进行离散化。当对中央网格(计算点地心向径穿过的网格)进行离散化时,通常将中央网格近似为圆形区域。采用高低阶均修正的Hotine截断核函数时,通过推导可得出中央网格重力扰动对高程异常贡献ζ0的近似公式为
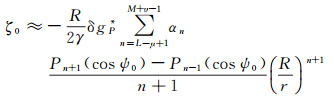 (7)
(7)
式中,ψ0为中央网格的圆形近似区域的半径,ψ0的大小可通过实际中央网格区域与圆形近似区域面积相等的原则确定,即πψ02=ΔλΔφcos φ(Δλ、Δφ分别为中央网格在经度、纬度方向增量的正值,φ为计算点的纬度);δgP*为中央网格重力扰动在边界面上的取值(下标P表示计算点)。
2.2 低阶修正本文在高低阶均修正的截断核函数的基础上提出了仅低阶修正的截断核函数,两种修正核函数的差别在于修正因子的不同。低阶修正的截断核函数的修正因子αn为
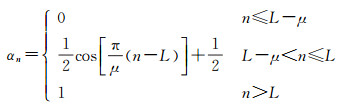 (8)
(8)
从式(8)可看出,低阶修正核函数的修正因子在L-μ阶到L阶的频率区间由0逐步增大至1。当低阶修正频率区间(L-μ, L)的各阶修正因子均取0时,低阶修正核函数转化为传统仅低阶截断的核函数。式(8)所示的低阶修正核函数的修正因子是由余弦函数构造的。本文进一步提出一种线型低阶修正的核函数,其修正因子为
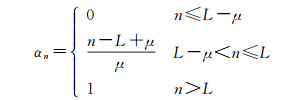 (9)
(9)
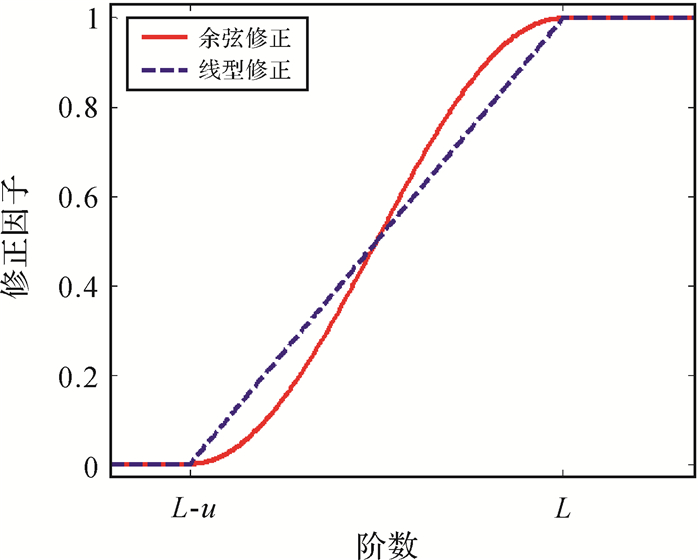
式(9)所示的线型低阶修正核函数的修正因子同样具有在L-μ阶至L阶的频段由0逐步增大至1的特点。图 1为两种低阶修正核函数的修正因子的取值。
|
| 图 1 两种修正因子的取值 Fig. 1 Values of the two modification factors |
由图 1可知,对于余弦修正核函数,修正因子在修正初始频段和修正末尾频段变化相对较慢,而在修正的中间频段变化相对较快;对于线型低阶修正核函数,修正因子在修正频段保持固定的变化速度。修正因子的类型及参数设置与实测重力数据和模型重力数据的相对精度有关。当使用低阶修正的Hotine截断核函数时,通过推导可得出中央网格重力扰动对高程异常贡献ζ0为
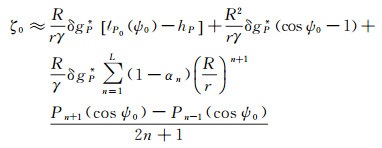 (10)
(10)
式中,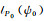
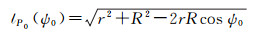
在移去恢复模式下,Hotine积分仅需近区积分。根据勒让德函数的球面积分算法和Molodensky截断理论,近区Hotine积分可表示为如下谱形式
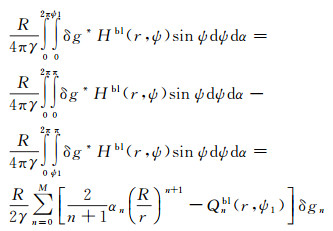 (11)
(11)
式中,δgn为n阶重力扰动;ψ1为近区积分半径;Qnbl(r, ψ1)为Molodensky截断系数
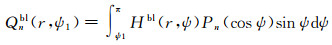 (12)
(12)
式(11)、式(12)不仅适用于修正形式的Hotine截断核函数,对于传统Hotine截断核函数也是适用的,此时αn只有0和1两种取值(传统Hotine截断核函数为修正Hotine截断核函数的特例)。根据式(11)所示的谱表示方法可对式(1)进行如下改化
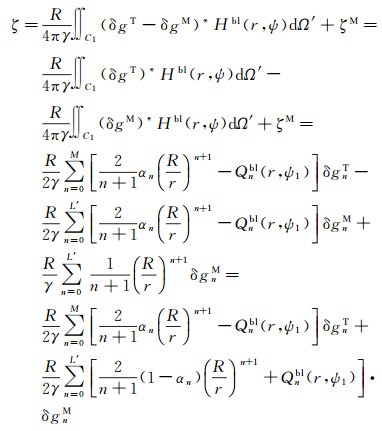 (13)
(13)
式中,δgnT、δgnM分别表示边界面上的n阶实测、模型重力扰动;L′为移去恢复的模型最高阶数。式(13)即为移去恢复模式下Hotine积分的谱分解式。从式(13)可看出在移去恢复模式下Hotine核函数在低、高频段对求解的高程异常的影响方式不同:
(1) 在0~L′的低频波段,高程异常来自于实测和模型两类重力数据的贡献。实测和模型重力数据的n阶系数分别为2/(n+1)·αn(R/r)n+1-Qnbl、2/(n+1)·(1-αn)(R/r)n+1+Qnbl(忽略公共系数R/(2γ)),两系数之和为2/(n+1)·(R/r)n+1。两系数与其和的比值αn-(n+1)/2·(r/R)n+1Qnbl、1-αn+(n+1)/2·(r/R)n+1Qnbl表征了实测和模型数据对n阶高程异常的贡献率。在0~L′的低频波段,实测和模型重力数据对高程异常的贡献率之和总为1。对于不同的Hotine核函数,αn、Qnbl不同,因而实测和模型重力数据对高程异常的贡献率也不同。在将重力扰动转化为高程异常的过程(即Hotine积分)中,实测和模型数据的低阶误差也以各自的“贡献率”(也可称为“转化率”)传播到高程异常中。由于实测和模型重力数据的各阶误差不同,因此不同Hotine核函数计算的低阶高程异常不同。
(2) 在L′+1~M的高频波段,高程异常仅来自于实测数据的贡献,又由于Hotine积分为非全球积分,因此高阶高程异常的误差一方面来自实测重力数据本身存在的高频误差,另一方面来自于非全球Hotine积分产生的远区截断误差。在高频波段,实测数据对高程异常的各阶贡献率为αn-(n+1)/2·(r/R)n+1Qnbl。由于不同的Hotine核函数的αn、Qnbl不同,因此不同Hotine核函数计算的高阶高程异常也是不同的。
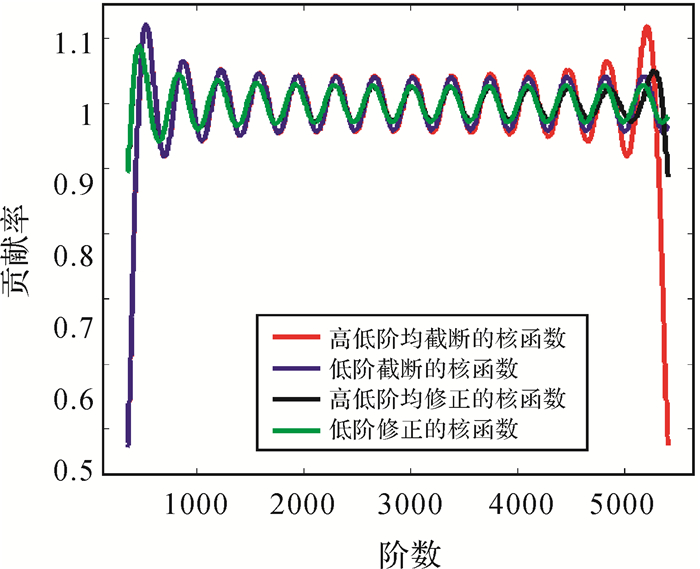
4 试验与分析 4.1 频谱分析根据上文分析,在移去恢复模式下核函数在高、低频波段对高程异常的影响方式不同,因此对核函数的频谱分析应分高、低频两个波段进行。本节频谱分析过程中将计算点高程设为1000 m,Hotine积分半径设为1°,低、高阶截断频率(阶数)分别取为360、5400。图 2为使用不同的Hotine核函数时实测重力数据对高程异常的高阶贡献率,其中修正因子采用余弦函数形式,低、高阶修正带宽均为180阶。
|
| 图 2 实测数据的高阶贡献率 Fig. 2 High-degree contribution rates of the measured data |
根据图 2,在高频波段的初始频段,高低阶均截断与低阶截断的Hotine核函数对高程异常的高阶贡献率差异很小,而高低阶均修正与仅低阶修正的Hotine核函数的高阶贡献率的差异也非常小。贡献率越接近1,重力数据越能够有效地传播到解算的高程异常中。图 2中传统截断核函数在高频波段的初始频段贡献率较低,说明传统截断核函数存在较严重的谱泄露现象。修正的截断核函数能够有效地控制谱泄露现象,提高了实测数据在高频波段初始频段的贡献率。在高阶截断频率附近,几种核函数中高低阶均截断的核函数存在比较明显的谱泄露现象。图 3为使用不同的Hotine核函数时模型和实测数据对高程异常的低阶贡献率。
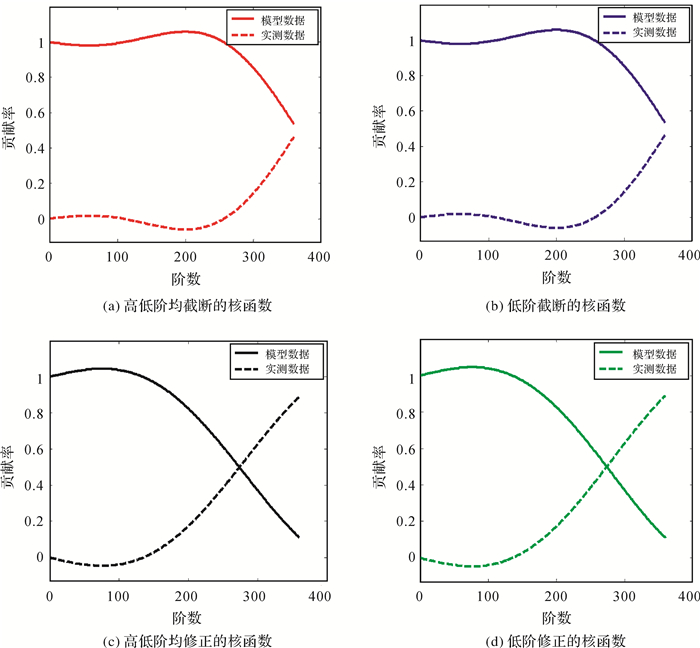
|
| 图 3 模型和实测数据的低阶贡献率 Fig. 3 Low-degree contribution rates of the measured data and model data |
从图 3可以看出,在低频波段,两种截断Hotine核函数的低阶贡献率差异很小,两种修正Hotine核函数的低阶贡献率差异也很小。在低频波段的初始频段,使用截断和修正形式的核函数时模型数据的贡献率均接近1,说明在低频波段的初始频段高程异常主要来自模型数据的贡献。在修正频段(L-μ~L,此处为180~360),使用修正核函数时实测数据对高程异常的贡献多于使用传统截断核函数时实测数据对高程异常的贡献。
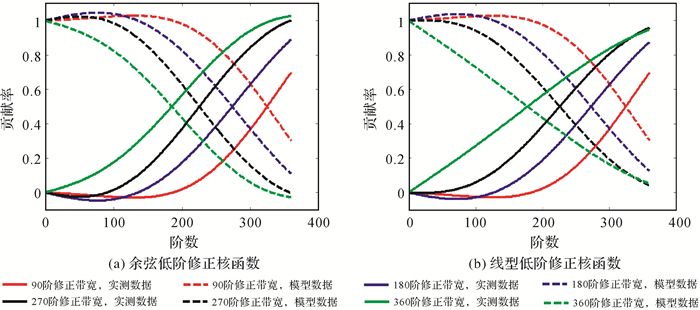
下面分析不同修正带宽下实测和模型数据对高程异常的贡献率的变化,使用的核函数分别为余弦低阶修正和线型低阶修正的Hotine截断核函数。图 4所示为不同修正带宽下实测数据的高阶贡献率。
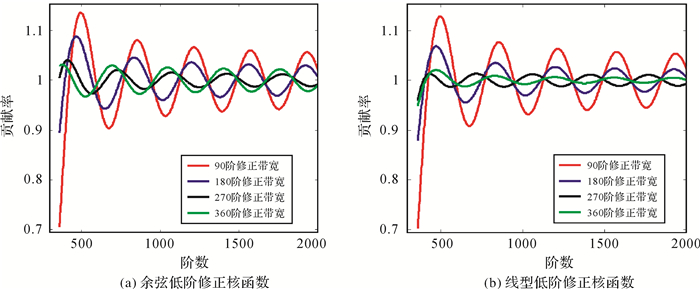
|
| 图 4 不同修正带宽下实测数据的高阶贡献率 Fig. 4 High-degree contribution rates of the measured data using different modification bandwidths |
由图 4可知,在高频波段的初始频段,对于两种(余弦与线型)低阶修正的Hotine核函数,低阶修正带宽为90阶时实测重力数据的贡献率均明显小于修正带宽为180、270、360阶时的贡献率,说明90阶修正带宽下两种低阶修正核函数对谱泄露现象的改善程度不及180、270、360阶修正带宽下修正核函数对谱泄露的改善程度。图 4中,使用余弦与线型低阶修正核函数时实测重力数据的高阶贡献率相差不大,但当修正带宽为360阶时,使用线型低阶修正核函数时实测重力数据的高阶贡献率更接近1,说明此时线型低阶修正核函数稍优于余弦低阶修正核函数。图 5所示为不同修正带宽下模型和实测重力数据的低阶贡献率。
|
| 图 5 不同修正带宽下实测和模型数据的低阶贡献率 Fig. 5 Low-degree contribution rates of the measured data and model data using different modification bandwidths |
从图 5可以看出,使用两种低阶修正核函数时实测与模型重力数据对低阶高程异常的贡献率相差不大。在未修正的频率区间(0~L-μ),低阶高程异常的贡献主要来自于模型重力扰动;在修正的频率区间(L-μ~L),实测重力扰动的贡献逐渐增大,而模型重力扰动的贡献逐渐减少。从图 5中还可看出,修正带宽越大,模型重力数据的贡献越少而实测重力数据的贡献越多,因此可通过调整修正带宽控制实测和模型重力数据对低阶高程异常贡献的权重。
4.2 应用试验为了说明不同Hotine核函数的应用效果,针对不同形式的Hotine核函数解算似大地水准面进行了试验。似大地水准面的区域范围为108°E—114°E,28°N—32°N,该区域海拔最高2700 m,平均607 m。本试验收集了105.5°E—116.5°E,25.5°N—34.5°N范围内的70 822个地面离散重力点,剔除粗差后,将剩余的70 379个实测重力点作为边值解算的基础重力数据。本试验边值解算采用基于移去恢复的Hotine-Helmert理论方法[27],其中地形直接、间接影响采用文献[28]给出的算法公式。试验区共有68个GPS水准点,利用试验区GPS水准点对截断至360阶和2190阶的EIGEN-6C4、EGM2008重力场模型分别进行精度检核,其结果统计于表 1。
| m | ||||||
| 重力场模型 | 截断阶数 | 最小值 | 最大值 | 平均值 | 均方差 | 标准差 |
| EIGEN-6C4 | 360 | -1.027 | 0.869 | 0.102 | 0.298 | 0.282 |
| 2190 | -0.109 | 0.300 | 0.106 | 0.132 | 0.078 | |
| EGM2008 | 360 | -1.649 | 0.350 | -0.304 | 0.422 | 0.295 |
| 2190 | -0.703 | -0.115 | -0.300 | 0.318 | 0.106 | |
表 1中,截断到360和2190阶的EIGEN-6C4模型精度(标准差)分别为±28.2 cm与±7.8 cm,而截断到360和2190阶的EGM2008模型精度分别为±29.5 cm与±10.6 cm,由此可看出试验区EIGEN-6C4模型精度优于EGM2008模型。
下面首先利用两种截断(高低阶均截断、低阶截断)Hotine核函数计算似大地水准面,为了提高计算速度,本试验采用2′×2′的格网分辨率。表 2统计了解算的重力似大地水准面的精度与Hotine积分所需时间,其中Hotine积分半径为1°,高阶截断阶数取5400阶(根据Nyquist采样定律可知2′×2′分辨率格网对应5400阶的高阶截断频率),低阶截断阶数取360,参考模型取EIGEN-6C4模型的前360阶。
| 核函数 | 最小值 /m |
最大值 /m |
平均值 /m |
均方差 /m |
标准差 /m |
耗时 /min |
| 高低阶均截断 | -0.058 | 0.427 | 0.126 | 0.152 | 0.086 | 150.0 |
| 低阶截断 | -0.058 | 0.426 | 0.126 | 0.152 | 0.087 | 10.5 |
从表 2可以看出,两种传统截断核函数计算的似大地水准面精度基本没有差别,但图 2中两种传统截断核函数在高阶截断频率附近差异较大,这反映了高程异常对高频信息不敏感的频谱特性。根据表 2,在解算精度一致的前提下,使用低阶截断核函数时Hotine积分所需的计算时间较高低阶均截断的核函数明显缩短,因此对于两种截断核函数,低阶截断的核函数比高低阶均截断的核函数更适于边值解算。
表 3比较了两种修正(高低阶均修正、低阶修正)Hotine核函数在边值解算精度与计算时间上的差别,其中低阶修正带宽取180阶,高阶修正带宽分别取180、540阶,修正核函数采用余弦修正形式,其他参数设置与表 2相同。
| 核函数 | 高阶修正带宽 /阶 |
最小值 /m |
最大值 /m |
平均值 /m |
均方差 /m |
标准差 /m |
耗时 /min |
| 高低阶均修正 | 180 | 0.008 | 0.408 | 0.150 | 0.166 | 0.072 | 156.7 |
| 540 | 0.008 | 0.408 | 0.150 | 0.166 | 0.072 | 166.8 | |
| 低阶修正 | — | 0.008 | 0.407 | 0.150 | 0.166 | 0.072 | 12.3 |
从表 3可得出,当低阶修正带宽一定时,两种修正核函数解算的似大地水准面的精度基本相同。另外还可看出,高阶修正带宽对似大地水准面的精度的影响非常小。由于低阶修正核函数较高低阶均修正核函数大大缩短了计算时间,而二者的计算精度相同,因此低阶修正的核函数比高低阶均修正的核函数更适于边值解算。此外,对比表 2、表 3可看出,低阶修正核函数计算的似大地水准面精度优于低阶截断核函数的计算精度,二者在计算效率方面的差别也不大,因此低阶修正的截断核函数的应用效果优于其他核函数。
为了说明低阶修正带宽对边值解算精度的影响,表 4统计了使用不同的低阶修正带宽时求解的重力似大地水准面的精度,其中低阶修正核函数采用余弦修正形式,地形分辨率为1.5′×1.5′,Hotine积分半径为1°,同样以EIGEN-6C4重力场模型的前360阶作为参考模型。
| 低阶修正带宽/阶 | 最小值 /m |
最大值 /m |
平均值 /m |
均方差 /m |
标准差 /m |
| 0(未修正) | -0.069 | 0.349 | 0.123 | 0.147 | 0.082 |
| 90 | -0.036 | 0.333 | 0.131 | 0.148 | 0.071 |
| 180 | -0.007 | 0.309 | 0.143 | 0.157 | 0.066 |
| 270 | 0.005 | 0.262 | 0.141 | 0.153 | 0.059 |
| 360 | -0.022 | 0.194 | 0.104 | 0.115 | 0.048 |
低阶修正带宽取0时低阶修正核函数实际即为传统的低阶截断核函数。从表 4可知,低阶修正带宽对似大地水准面的精度具有较大的影响。在本文试验区360阶低阶修正带宽解算的似大地水准面精度最高(±4.8 cm),而传统截断核函数计算的似大地水准面精度仅为±8.2 cm。似大地水准面精度的提高一方面是由于低阶修正核函数有效地控制了传统截断核函数存在的谱泄露问题,另一方面是由于低阶修正核函数增大了实测重力数据在低阶修正频段对高程异常的贡献。
表 5统计了不同低阶修正带宽下线型低阶修正Hotine核函数计算的重力似大地水准面精度,其参数设置同表 4。
| 低阶修正带宽/阶 | 最小值 /m |
最大值 /m |
平均值 /m |
均方差 /m |
标准差 /m |
| 90 | -0.036 | 0.333 | 0.131 | 0.149 | 0.071 |
| 180 | -0.010 | 0.306 | 0.142 | 0.156 | 0.065 |
| 270 | -0.006 | 0.246 | 0.130 | 0.141 | 0.056 |
| 360 | -0.070 | 0.158 | 0.073 | 0.087 | 0.048 |
比较表 4、表 5可知,在相同的低阶修正带宽下,线型低阶修正与余弦低阶修正核函数计算的似大地水准面精度基本一致。将表 4、表 5的结果与表 2进行比较可以看出低阶修正核函数的应用效果较好。
由于不同重力场模型的精度不同,而修正带宽起到调整模型和实测重力数据在高程异常中贡献的比重的作用,因此使用不同的参考模型时适宜的低阶修正带宽也存在差异。为此,表 6统计了以EIGEN-6C4模型与EGM2008模型的前360阶作为参考模型时不同低阶截断阶数下适宜的低阶修正带宽(即使用该低阶修正带宽时边值解算精度相对较高)及相应的似大地水准面精度,其中核函数采用余弦低阶修正核函数。
| 重力场模型 | 低阶截断阶数 /阶 |
适宜的低阶修正带宽 /阶 |
最小值 /m |
最大值 /m |
平均值 /m |
均方差 /m |
标准差 /m |
| EIGEN-6C4模型 | 360 | 360 | -0.022 | 0.194 | 0.104 | 0.115 | 0.048 |
| 240 | 240 | -0.107 | 0.181 | 0.060 | 0.079 | 0.051 | |
| 120 | 0 | -0.077 | 0.255 | 0.091 | 0.105 | 0.053 | |
| EGM2008模型 | 360 | 360 | -0.604 | -0.092 | -0.304 | 0.314 | 0.081 |
| 240 | 240 | -0.646 | -0.144 | -0.349 | 0.356 | 0.071 | |
| 120 | 60 | -0.687 | -0.189 | -0.383 | 0.390 | 0.074 |
表 6中,当以EIGEN-6C4模型的前360阶作为参考模型时,低阶截断阶数与低阶修正带宽均取360解算的似大地水准面精度最高(±4.8 cm),而当低阶截断阶数取120时,核函数不进行修正时边值解算精度相对较高。当以EGM2008模型的前360阶作为参考模型时,低阶截断阶数与低阶修正带宽均取240解算的似大地水准面精度最高(±7.1 cm),但不及以EIGEN-6C4模型的前360阶作为参考模型的边值解算精度。
表 7统计了采用2190阶的EIGEN-6C4模型与EGM2008模型作为参考模型时,不同低阶截断阶数下适宜的低阶修正带宽及相应的似大地水准面精度。
| 重力场模型 | 低阶截断阶数 /阶 |
适宜的低阶修正带宽 /阶 |
最小值 /m |
最大值 /m |
平均值 /m |
均方差 /m |
标准差 /m |
| EIGEN-6C4模型 | 2190 | 360 | -0.110 | 0.324 | 0.127 | 0.152 | 0.084 |
| 360 | 360 | -0.016 | 0.191 | 0.104 | 0.114 | 0.047 | |
| 240 | 240 | -0.090 | 0.155 | 0.061 | 0.077 | 0.047 | |
| 120 | 0 | -0.042 | 0.204 | 0.091 | 0.101 | 0.045 | |
| EGM2008模型 | 2190 | 360 | -0.646 | -0.049 | -0.279 | 0.300 | 0.113 |
| 360 | 360 | -0.604 | -0.092 | -0.304 | 0.314 | 0.081 | |
| 240 | 240 | -0.629 | -0.170 | -0.348 | 0.354 | 0.068 | |
| 120 | 60 | -0.687 | -0.189 | -0.383 | 0.390 | 0.074 |
表 7中,当以2190阶的EIGEN-6C4模型与EGM2008模型作为参考模型时,低阶截断阶数取2190阶计算的似大地水准面精度并不理想。根据上文频谱分析可知,当低阶截断阶数取2190阶时解算的高程异常主要来自于模型数据的贡献,因此不能有效地利用实测数据的信息。当2190阶EIGEN-6C4模型作为参考场时边值解算精度(最高达±4.5 cm)优于2190阶EGM2008模型作为参考场时边值解算精度(最高达±6.8 cm)。对比表 6可以看出,以2190阶EIGEN-6C4模型作为参考模型较以360阶EIGEN-6C4模型作为参考模型求解的似大地水准面的精度提高不明显(分别为±4.5 cm与±4.8 cm),这反映了远区高程异常的高频(361~2190阶频段)信息非常少。
5 结论利用基于移去恢复技术的Stokes-Helmert边值理论或Hotine-Helmert边值理论求解(似)大地水准面时,截断形式的Stokes/Hotine核函数是一种有效的高通滤波器。但传统的截断核函数存在谱泄露现象,影响了(似)大地水准面的解算精度,因此本文引入并进一步发展了一种低阶修正的截断核函数。本文的创新点与结论主要有:
(1) 在余弦函数构造的高低阶均修正的核函数的基础上提出了余弦低阶修正核函数,进一步提出了线型低阶修正核函数,并给出了使用高低阶均修正核函数与低阶修正核函数时Hotine积分的中央区算法。
(2) 对移去恢复模式下核函数在解算似大地水准面中的作用进行了频谱分析,说明了在移去恢复模式下核函数研究的内容及内涵已发生转变:在高频波段,核函数影响着高频远区截断误差的大小以及谱泄露的程度,但在低频波段,核函数决定了实测重力数据与模型重力数据对高程异常的贡献率。通过对不同核函数的频谱分析得出,修正核函数能够有效地控制谱泄露现象,并且增大了实测数据在修正频段对高程异常的贡献率。余弦低阶修正与线型低阶修正核函数的频谱特性比较接近。
(3) 试验结果表明,采用相同的低阶修正带宽时,线型和余弦低阶修正的核函数计算的似大地水准面精度与高低阶均修正的核函数的计算精度一致,均优于传统截断核函数计算的似大地水准面精度。在计算效率上,低阶修正的核函数明显优于高低阶均修正的核函数。
(4) 通过本文的试验可看出,在基于Helmert第二压缩法的边值问题中低阶修正的截断核函数能够有效地改善边值解算的精度,具体应用时应结合参考模型精度、试验区实测重力数据精度、模型截止阶数等因素确定适宜的低阶截断阶数以及低阶修正带宽。
本文的研究是对文献[29]提出的厘米级精度要求下重新研究核函数的改进和构造截断函数问题进行的理论探索与实践,在Stokes-Helmert/Hotine-Helmert边值理论的研究和应用方面具有一定的参考价值。
| [1] |
管泽霖, 管铮, 黄谟涛, 等.
局部重力场逼近理论和方法[M]. 北京: 测绘出版社, 1997.
GUAN Zelin, GUAN Zheng, HUANG Motao, et al. Theory and method of regional gravity field approximation[M]. Beijing: Surveying and Mapping Press, 1997. |
| [2] | MARTINEC Z. Boundary-value problems for gravimetric determination of a precise geoid[M]. Berlin: Springer, 1998. |
| [3] |
李建成.
最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J]. 测绘学报, 2012, 41(5): 651–660, 669.
LI Jiancheng. The recent Chinese terrestrial digital height datum model:gravimetric quasi-geoid CNGG2011[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 651–660, 669. |
| [4] |
荣敏. Stokes-Helmert方法确定大地水准面的理论与实践[D].郑州: 信息工程大学, 2015. RONG Min. Stokes-Helmert method for geoid determination[D]. Zhengzhou: Information Engineering University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-90005-1016058463.htm |
| [5] |
马健. Hotine-Helmert边值问题确定似大地水准面的理论与方法[D].郑州: 信息工程大学, 2018. MA Jian. Theory and methods of the Hotine-Helmert boundary value problem for the determination of the quasi-geoid[D]. Zhengzhou: Information Engineering University, 2018. |
| [6] |
邓标, 洪绍明, 宋雷.
区域厘米级似大地水准面的精化[J]. 大地测量与地球动力学, 2009, 29(3): 125–127.
DENG Biao, HONG Shaoming, SONG Lei. Refining of centimeter-precise local quasi-geoid[J]. Journal of Geodesy and Geodynamics, 2009, 29(3): 125–127. |
| [7] |
荣敏, 周巍, 任红飞.
Meissel-Stokes核函数应用于区域大地水准面分析[J]. 测绘工程, 2015, 24(9): 5–10.
RONG Min, ZHOU Wei, REN Hongfei. Meissel-Stokes function used in the regional geoid determination[J]. Engineering of Surveying and Mapping, 2015, 24(9): 5–10. DOI:10.3969/j.issn.1006-7949.2015.09.002 |
| [8] | SJÖBERG L E, HUNEGNAW A. Some modifications of Stokes' formula that account for truncation and potential coefficient errors[J]. Journal of Geodesy, 2000, 74(2): 232–238. DOI:10.1007/s001900050281 |
| [9] | WONG L, GORE R. Accuracy of geoid heights from modified Stokes kernels[J]. Geophysical Journal International, 1969, 18(1): 81–91. DOI:10.1111/gji.1969.18.issue-1 |
| [10] | FEATHERSTONE W E, EVANS J D, OLLIVER J G. A Meissl-modified Vaníček and Kleusberg kernel to reduce the truncation error in gravimetric geoid computations[J]. Journal of Geodesy, 1998, 72(3): 154–160. DOI:10.1007/s001900050157 |
| [11] | FEATHERSTONE W E. Band-limited kernel modifications for regional geoid determination based on dedicated satellite gravity field missions[M]//TZIAVOS I N. Gravity and Geoid. Thessaloniki: [s.n.], 2003: 341-346. |
| [12] |
王伟, 李姗姗, 马彪, 等.
基于均衡理论构建区域平均空间重力异常方法研究[J]. 大地测量与地球动力学, 2013, 33(4): 146–150.
WANG Wei, LI Shanshan, MA Biao, et al. A method for establishing mean free-air gravity anomaly based on isostatic theory[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 146–150. |
| [13] |
马健, 魏子卿, 武丽丽, 等.
有限范围的重力层间改正算法[J]. 测绘学报, 2017, 46(1): 26–33.
MA Jian, WEI Ziqing, WU Lili, et al. The Bouguer correction algorithm for gravity with limited range[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(1): 26–33. DOI:10.11947/j.AGCS.2017.20160173 |
| [14] |
孙文, 吴晓平, 王庆宾, 等.
高精度重力数据格网化方法比较[J]. 大地测量与地球动力学, 2015, 35(2): 342–345.
SUN Wen, WU Xiaoping, WANG Qingbin, et al. Comparison and analysis of high-precision gravity data gridding methods[J]. Journal of Geodesy and Geodynamics, 2015, 35(2): 342–345. |
| [15] |
李姗姗, 曲政豪.
重力数据误差对大地水准面模型建立的影响[J]. 大地测量与地球动力学, 2016, 36(10): 847–850, 869.
LI Shanshan, QU Zhenghao. Effect of error of gravity data on geoid determination[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 847–850, 869. |
| [16] | VANÍČEK P, KLEUSBERG A. The Canadian geoid-Stokesian approach[J]. Manuscripta Geodaetica, 1987, 12(2): 86–98. |
| [17] | FEATHERSTONE W E, KIRBY J F, KEARSLEY A H W, et al. The AUSGeoid98 geoid model of Australia:data treatment, computations and comparisons with GPS-levelling data[J]. Journal of Geodesy, 2001, 75(5-6): 313–330. DOI:10.1007/s001900100177 |
| [18] | VANÍČEK P, FEATHERSTONE W E. Performance of three types of Stokes's kernel in the combined solution for the geoid[J]. Journal of Geodesy, 1998, 72(12): 684–697. |
| [19] |
李建成, 晁定波.
利用Poisson积分推导Hotine函数及Hotine公式应用问题[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 55–57.
LI Jiancheng, CHAO Dingbo. Derivation of Hotine function using Poisson integral and application of Hotine formula[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 55–57. |
| [20] | FEATHERSTONE W E. Deterministic, Stochastic, hybrid and band-limited modifications of Hotine's integral[J]. Journal of Geodesy, 2013, 87(5): 487–500. DOI:10.1007/s00190-013-0612-9 |
| [21] |
程芦颖.
不同扰动位泛函间的积分变换广义核函数[J]. 测绘学报, 2013, 42(2): 203–210.
CHENG Luying. General kernel functions based on integral transformation among different disturbing potential elements[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 203–210. |
| [22] | HUANG J L, VÉRONNEAU M. Canadian gravimetric geoid model 2010[J]. Journal of Geodesy, 2013, 87(8): 771–790. DOI:10.1007/s00190-013-0645-0 |
| [23] |
刘敏, 黄谟涛, 欧阳永忠, 等.
顾及地形效应的重力向下延拓模型分析与检验[J]. 测绘学报, 2016, 45(5): 521–530.
LIU Min, HUANG Motao, OUYANG Yongzhong, et al. Test and analysis of downward continuation models for airborne gravity data with regard to the effect of topographic height[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 521–530. DOI:10.11947/j.AGCS.2016.20150453 |
| [24] |
翟振和, 王兴涛, 李迎春.
解析延拓高阶解的推导方法与比较分析[J]. 武汉大学学报(信息科学版), 2015, 40(1): 134–138.
ZHAI Zhenhe, WANG Xingtao, LI Yingchun. Solution and comparison of high order term of analytical continuation[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 134–138. |
| [25] | WEI Ziqing. High-order radial derivatives of harmonic function and gravity anomaly[J]. Journal of Physical Science and Application, 2014, 4(7): 454–467. |
| [26] |
马健, 魏子卿, 任红飞, 等.
顾及远区影响的向下延拓实用算法[J]. 地球物理学进展, 2018, 33(2): 498–502.
MA Jian, WEI Ziqing, REN Hongfei, et al. Practical algorithm of the downward continuation considering the far-zone effect[J]. Progress in Geophysics, 2018, 33(2): 498–502. |
| [27] |
马健, 魏子卿, 任红飞.
确定似大地水准面的Hotine-Helmert边值解算模型[J]. 测绘学报, 2019, 48(2): 153–160.
MA Jian, WEI Ziqing, REN Hongfei. Hotine-Helmert boundary-value calculation model for quasi-geoid determination[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(2): 153–160. DOI:10.11947/j.AGCS.2019.20170594 |
| [28] |
马健, 魏子卿.
近区地形直接与间接影响的棱柱模型算法[J]. 测绘学报, 2018, 47(11): 1429–1436.
MA Jian, WEI Ziqing. Prism algorithms for the near-zone direct and indirect topographic effects[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(11): 1429–1436. DOI:10.11947/j.AGCS.2018.20170369 |
| [29] |
李建成.
我国现代高程测定关键技术若干问题的研究及进展[J]. 武汉大学学报(信息科学版), 2007, 32(11): 980–987.
LI Jiancheng. Study and progress in theories and crucial techniques of modern height measurement in China[J]. Geomatics and Information Science of Wuhan University, 2007, 32(11): 980–987. |


