海岸线作为海图上一类重要的要素,其自动综合的研究一直受到人们的关注。与普通线要素化简不同,海岸线化简需要顾及“扩陆缩海”等特定原则,因此普通的线要素化简算法并不适用于海岸线化简[1-2]。
当前海岸线化简方法主要有双向缓冲区方法[3-8]和指标化简方法[9-22]两类。双向缓冲区方法利用其缩小或填平凹部的特性实现海岸线化简,但由于其基于固定半径的滚动圆进行变换,在一些瓶颈区域容易出现“潟湖沙嘴封死”、“岛礁上岸”、“海岸线相交”现象(如图 1(a)、图 1(b)、图 1(c)所示,其中粗线条表示化简后的海岸线,较细的线条表示原始海岸线);指标化简方法通常是采用弯曲识别方法(单调段识别方法[9-13]或Delaunay三角网法[14-22])对弯曲进行识别,并以海岸线弯曲的高度(最大垂距)、深度、面积、宽度及骨架线长度等作为化简的指标,对弯曲进行取舍以达到化简的目的,这类方法可避免上述“潟湖沙嘴封死”、“岛礁上岸”的现象。但由于其针对单一海岸线进行处理,在弯曲进行取舍时,对其与附近海岸线之间的空间关系考虑不足,仍避免不了“海岸线相交”现象(如图 1(d)所示),且上述两类方法对于一些不同海岸线之间相对较为狭窄的海峡区域(如图 1(e)所示),当比例尺缩小以后,不能有效处理邻近距离较小的问题,容易出现“海岸线相接”的视觉性错误。

|
| 图 1 常见海岸线化简图理性问题 Fig. 1 The diagrammatic sketch of frequent faults |
考虑到当前海岸线化简方法基本只考虑单一线要素,未顾及其与周围海岸线之间的空间邻近关系,在海岸线较为密集的复杂海区容易出现图理性错误,本文提出一种顾及空间邻近关系的多条海岸线协同化简方法。
1 基于层次化三角网分区的多海岸线协同化简 1.1 现有方法问题产生根源及解决思路从现有方法的缺陷来看,主要是不能有效顾及化简海岸线与周围海岸线之间的空间邻近关系。Delaunay三角网作为空间分析的重要工具,已被证明具有探测要素间空间邻近关系的潜能[23-25],且已有文献将Delaunay三角网用于海岸线化简,但这些方法均只对某单一海岸线单独构网并对其进行化简,并未顾及海岸线之间的空间邻近关系,这样易出现海岸线相交的图理性错误,如图 2(a)所示,对海岸线L1上的数据点构建约束Delaunay三角网,取其海部三角形,并将其中的黄色多边形w1所包含海岸线弧段视为弯曲,根据三角形可视判别条件(根据三角形是否位于视觉缓冲区内[16]或该三角形区域宽度是否大于阈值[22]),将其中红色线条所示区域的三角形进行删除,在这一过程中并未对海岸线L1与L2的邻近关系进行考虑和处理,从而导致了海岸线相交的图理性错误,如图 2(b)所示。为了有效处理好海岸线之间的空间邻近关系,本文将多条海岸线上的点同时参与构网,并将可能产生图理性错误的区域自动识别出来。如图 2(c)所示,根据三角形所邻近的海岸线数目,可将其分为单一海岸线三角形(如三角形T1,该三角形的顶点A、B、C均为海岸线上L1的点)、非单一海岸线三角形(如三角形T2,该三角形的顶点D为海岸线L1上的点,顶点E、F为海岸线L2上的点),并将非单一海岸线三角形均设置为不可删除的三角形,那么当再次利用视觉约束条件对海岸线进行化简时,则只会对图中的单一海岸线三角形(图 2(c)中黄色多边形区域所示三角形)进行化简,不会出现图 2(b)所示的海岸线相交的错误。

|
| 图 2 本文方法与现有方法过程比对 Fig. 2 Comparison between the method and the literature method |
为了将这一思想应用于多海岸线的协同化简,本文首先利用约束Delaunay三角网对能否化简的区域进行划分和标识;然后,利用二叉树构建层次关系模型,对各区域实体进行有序的组织;最后,有序地对可化简的标识区域进行渐进式化简,并对局部狭窄区域进行自适应夸大,从而实现多海岸线的协同化简,其主要流程如图 3所示。

|
| 图 3 基于层次化三角网分区的多条海岸线协同化简方法 Fig. 3 Multiple coastline collaborative simplification methods based on hierarchical triangulation |
1.2 约束Delaunay三角网构建
本文首先采用文献[24]所述方法对海岸线的数据点进行加密处理,之后构建约束Delaunay三角网,并根据重心点坐标提取位于海部的三角形。对于一种相对较为特殊的情形,如图 4所示,根据文中所述三角形划分方法,可将这一区域的三角形分为单一海岸线三角形(图中褐色多边形A、B所含三角形,绿色多边形D所含三角形, 紫色多边形E所含三角形)和非单一海岸线三角形(图中黄色多边形C所含三角形)。根据之前的分析,只针对单一海岸线三角形区域进行化简,但对于如图 4所示区域而言,若对单一海岸线三角形区域D、E删除,而其中的非单一海岸线三角形区域C进行保留,则会出现不合理的“内陆湖”现象。所以在上述区域中,真正可化简的区域仅有A、B。通过上述分析,可以知道,对于相对较为复杂的区域而言,真正可化简的区域为弯曲支路上不含岛屿的弯曲(即在该弯曲支路上不存在岛屿,如图中区域B)和支路末端的单一海岸线三角形区域(如图中区域A)。为对这一区域进行有效识别并进行化简操作,就必须对这些三角形所组成的各区域进行系统组织,并有序建立各区域之间的层次关系。

|
| 图 4 多海岸线约束Delaunay三角网 Fig. 4 Multiple coastline Delaunay triangle network diagram |
借鉴文献[24]所述三角形分类方法,再将其分为Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类三角形,以用于层次模型的构建。如图 4所示,将这些Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类三角形分别填充为红色、白色、蓝色、黄色。其中Ⅰ类三角形主要分布在峡湾末端,也称为源头三角形;Ⅲ类三角形主要分布在岔路口;Ⅳ类三角形主要分布在岸线的边界处,称为边界三角形;而Ⅱ类三角形则主要是对上述这些三角形进行连接。
需要说明的是,为便于之后化简,本文将未闭合的单一海岸线,与海图图廓一起形成闭合的陆地多边形。
为了便于后续处理过程中对岸线自身弯曲以及多海岸线之间关系的表达,对三角形建立如下数据结构:
struct TRIANGLE
{
int ID; //三角形序号
int Type; //三角形类型
int NumberVertex[3]; //三角形顶点序号
int belong_to[3]; //三角形顶点所属海岸线编号
int neighbor[3]; //三角形的邻近三角形编号
point Gpt; //三角形重心点坐标
bool Mark; //标记,用于构建结构化层次关系模型,初始值为“假”
}
1.3 带悬挂节点的层次关系模型建立由上文的分析可知,约束Delaunay三角网可对其不可化简区域进行识别,但对一些复杂区域(图 4),单一海岸线三角形区域与非单一海岸线三角形区域相间、交错分布,可化简区域不易自动识别,因此,本文采用二叉树模型对这些区域进行系统组织,利用节点与节点之间的父子和兄弟关系表达区域之间邻近关系,以对其中的可化简区域进行识别。需要说明的是,在构建过程中,始终以左子节点为“主子节点”,即在两子节点产生冲突时,优先顾及左子节点。本文所述层次关系模型构建步骤如下:
(1) 获取标记为“假”的边界三角形作为二叉树的根三角形,将其放入当前根节点进行存储,并将该三角形标记设置为“真”,转步骤(2),若所有的边界三角形均标记为“真”,则模型构建完毕。
(2) 由当前节点的当前三角形出发,根据三角形之间的邻近关系搜索附近的三角形,若该邻近三角形为Ⅱ类三角形,则将该Ⅱ类三角形放入当前节点进行存储,并将其标记为“真”,之后继续寻找“新标记”三角形附近的三角形,直到该邻近三角形为Ⅰ类三角形、已标记为“真”的三角形、Ⅲ类三角形、边界三角形时停止,若为Ⅰ类三角形、已标记为“真”的三角形时,则转步骤(3),若为Ⅲ类三角形、边界三角形,则转步骤(4)。
(3) 由该当前节点向上层节点回溯遍历,寻找是否存在未设置的节点。首先寻找当前节点的兄弟节点是否设置完毕,若未设置则将该节点设为当前节点转步骤(2),若设置完毕,则向上继续判断父节点的兄弟节点,逐渐向上层追溯,直到该二叉树的所有节点均设置完成后,转步骤(1)。
(4) 为当前节点设置子节点,并将步骤(2)中搜索到的Ⅲ类三角形或边界三角形放入当前节点和两子节点进行存储,将其中的左子节点设置为当前节点,转步骤(2)。
图 5(a)为约束Delaunay三角网构建示意图,利用上述步骤构建的二叉树如图 5(b)所示,其中值得注意的是,当前节点为m2→m3(这一符号表示该节点存储了从三角形m2到三角形m3的全部三角形)时,此时创建子节点,首先由左子节点进行扩展,到m4后,为节点m3→m4创建子节点m4→b3及m4→m3,此时节点m3→m4的所有子节点均设置完毕,准备判断其兄弟节点,但其兄弟节点的起始三角形m3的邻近三角形均已被标记为“真”,此时无法继续向其中添加新的三角形,因此该节点仅有一个三角形m3,本文将这种仅含有一个三角形的节点称为悬挂节点。图 6为两种特殊类型层次关系模型构建过程图,对于峡湾海岸中存在岛屿的情形,其层次模型构建时,仍以左子节点为主子节点,优先扩充左侧节点

|
| 图 5 多海岸线层次二叉树模型构建 Fig. 5 Multiple coastline binary tree model |

|
| 图 6 两种特殊类型的层次二叉树模型构建 Fig. 6 The construction of two special types of hierarchical binary tree model |
基于上述模型,可将多条海岸线分区域分层次系统存储,每一节点均为某一待处理的区域。对于上述二叉树模型,具有以下特点:
(1) 除悬挂节点外,层次二叉树中的每一节点均代表了图中某一待处理区域,且节点与区域一一对应,这些节点所表示的区域,相互独立,互不影响。
(2) 对于表达可化简区域的节点,其存储的最后一个三角形为Ⅰ类三角形,且该节点不存在子节点。
1.4 顾及空间邻近关系的多海岸线协同化简 1.4.1 基本过程步骤根据层次二叉树模型的特点可知,在层次关系模型中,节点与待处理区域一一对应,而可进行化简的区域则主要集中于层次树模型的末端海岸线自身弯曲部分,且这些节点的最后一个三角形为Ⅰ类三角形。本文首先利用这一特性将表达可化简区域节点进行识别并化简,之后对图中全体较为狭窄区域进行自适应夸大。其具体步骤如下:
(1) 输入海岸线数据,并根据文中所述方法构建结构化层次关系模型,获取集合Δend={node|(Typenode_endtri=1)∩(belong_tonode_endtri[0]=belong_tonode_endtri[1]=belong_tonode_endtri[2])}(其中,Typenode_endtri表示节点的末端三角形类型,belong_tonode_endtri表示节点末端三角形顶点所属海岸线编号,Δend描述的是所有末端三角形为Ⅰ类三角形且该三角形顶点属于同一海岸线的节点集合)。
(2) 遍历集合Δend,根据式(1)计算节点的面积
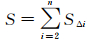 (1)
(1)
式中,SΔi表示节点中第i个三角形的面积,n表示该节点中三角形的数目;由于末端节点是从Ⅲ类三角形开始,到Ⅰ类三角形结束,但该Ⅲ类三角形不属于海岸线自身弯曲的一部分,因此该求和公式从第2个三角形开始,但该节点的第1个三角形为其他类型的三角形,那么上述求和公式从1开始。
若弯曲面积S < Sd,则认为其为锯齿状小弯曲,将该节点区域的所有三角形集合标记为“待删除”,反之则需考虑“部分删除”,将其中需要删除的三角形标记为“待删除”。
(3) 遍历集合Δend中所有节点三角形,判断是否存在标记为“待删除”的三角形,若有,将其中所有标记为“待删除”的三角形区域进行填充删除,更新海岸线数据,转步骤(1),反之,转步骤(4)。
(4) 遍历模型中全体节点,对其进行局部自适应夸大操作。
1.4.2 可化简弯曲部分删除对于那些面积相对较大,不足删除条件的节点,需要考虑部分删除操作。其具体过程为首先从节点的源头三角形(该节点的末端三角形)向上进行回溯,逐一获取其宽度Ltri,并进行判断Ltri < Ld,若是,则将该三角形标记为“待删除”,之后继续判断下一三角形,反之,部分删除结束。
本文将三角形的宽度作如下定义:如图 7所示,对于Ⅰ类三角形,将其与邻接三角形的公共边(p0p1)长度作为三角形的宽度,将Ⅱ类三角形中与海岸线重合的边和其相对顶点之间的最短距离作为该三角形的宽度(Δp3p4p5为支路节点上的Ⅱ类三角形,其中边p4p5为海岸线上的线段,将点p3到线段p4p5的最短距离[26]定义为该三角形的宽度),Ⅲ类三角形不予求取三角形宽度。Ld为宽度阈值。

|
| 图 7 部分删除操作 Fig. 7 Partial deletion operation diagram |
1.4.3 顾及空间关系的局部自适应夸大
为了对各节点区域中的部分较为狭窄区域进行夸大,针对单一节点,采用如下操作进行处理:
(1) 由节点数据提取节点三角形如图 8(b)所示,遍历节点中的三角形,获取各三角形宽度Ltri,并判断其中是否存在三角形满足Ltri < Ld;若是,转步骤(2);若不存在,则表明该节点不存在需要夸大区域,退出局部夸大操作。

|
| 图 8 局部自适应夸大过程 Fig. 8 Schematic diagram of local adaptive exaggeration process |
(2) 将该节点的所有三角形进行“合并”,得到节点多边形plydeal,遍历节点三角形,将则将其中满足条件(Ltri < Ld)的三角形(图 8(b)中的绿色三角形)区域,沿该三角形最短距离线的方向,向两侧拓宽(Ld-Ltri)/2(以其中的三角形T为例,若其最短距离线为p1p2,将节点多边形plydeal上的点p1沿p2p1方向移动(Ld-Ltri)/2,同时将节点多边形plydeal上的点p2和p3沿p1p2方向移动(Ld-Ltri)/2), 转步骤(3)。
(3) 根据拓宽后的节点多边形plydeal(如图 8(c)所示),将海岸线上较为狭窄的部分采用节点多边形边界进行替代(如图 8(d)所示),即得到最终夸大以后的海岸线(在这一过程,为防止夸大操作使得原有海岸线形态发生较大变化,作以下判断,若经夸大以后陆地变化区域(图 8(d)中的Δ1和Δ2)面积占原有陆地面积的比值大于1/4,则放弃这一海岸线的夸大操作)。
需要说明的是,本文虽主要针对海岸线要素进行化简,但若海岸线周围存在点状岛屿,也可将其视为一类特殊的海岸线进行存储,同样参与构网,并建立层次关系模型。这样做的优势在于,在之后的化简过程中,不会出现“点岛上岸”的错误,同时在局部夸大时,若该点状岛屿与海岸线距离较近,此时只夸大海岸线一侧,对点状岛屿不作处理。
2 试验与分析为对本文方法的有效性及适用性进行评估,本文将双向缓冲区方法以及文献[16]所提河口湾化简方法作为比对算法。参照文献[16]的研究,本文设置面积阈值Sd为0.003 2 cm2,设置曲线宽度为0.01 cm,根据人眼最小识别距离0.02 cm,将视觉宽度阈值Ld设为人眼最小识别距离与曲线线划宽度的和(0.03 cm)。对于综合结果的评估包括定性及定量两方面,试验海区包括潟湖海岸线和河口湾海岸线,其中潟湖海岸线取自海图编号16100,河口湾海岸线取自海图编号16700,原始比例尺为1:25万。双向缓冲区的宽度设置为0.015 cm,河口湾方法与本文方法的基本参数设置相同。利用C++以及动态库GDAL2.2.0编程实现,并利用ArcGIS进行结果显示,以完成本文试验。
需要说明的是,根据海图制图综合的一般原则,应当先选取,之后再进行岸线的化简,但由于本文的研究重点在于海岸线的化简,对于岛屿要素的选取不作为本文研究重点。考虑到实际应用,在本文的所有实验中,按分界尺度进行选取,即对于面积小于0.5 mm2的岛屿直接进行删除,对剩余的岸线进行化简。
2.1 定性评估分别将试验海图化简至1:50万、1:75万、1:100万、1:125万。潟湖海岸线在双向缓冲区、河口湾化简方法、本文方法的综合效果图分别展示如图 9、图 10、图 11所示,并对其中的局部细节部分进行放大显示。河口湾海岸线在上述3种方法下的综合效果图分别展示如图 12、图 13、图 14所示,并对局部细节进行放大显示。以下图像由于文章篇幅限制,均未按实际比例尺绘制,在图中,为方便对化简方法的化简效果进行展示,本文将化简前后的海岸线同时在文中进行绘出,蓝色线条为化简过后的海岸线,而黑色线条则为原始海岸线。

|
| 图 9 双向缓冲区化简效果 Fig. 9 Bidirectional buffer comprehensive rendering |

|
| 图 10 河口湾化简方法化简效果 Fig. 10 Comprehensive effect map of the comprehensive method of the estuary |

|
| 图 11 本文方法化简效果 Fig. 11 The comprehensive effect diagram of this method |

|
| 图 12 双向缓冲区方法化简效果 Fig. 12 Bidirectional buffer comprehensive rendering |

|
| 图 13 河口湾化简方法化简效果 Fig. 13 Comprehensive effect map of the comprehensive method of the estuary |

|
| 图 14 本文方法化简效果 Fig. 14 The comprehensive effect diagram of this method |
2.1.1 试验1:潟湖区域
对本试验海区而言,最主要的特征是潟湖海岸,对于这一区域的评估主要包括以下几个方面:
(1) 潟湖沙嘴是否予以保留,若不易识别时,是否予以适当夸大。
(2) 对于潟湖中相对较为尖锐且不可视的弯曲是否予以删除,且其曲线是否平滑。
(3) 对于其中不可合并的岛屿,当其距离较近时,是否予以适当夸大。
(4) 是否出现自相交、岸线相交等图理性错误。
对上述4个方面的综合效果情况统计如表 1所示。
| 化简方法 | A | B | C | D |
| 双向缓冲区方法 | 比例尺小于100万后,出现将沙嘴“堵住”的错误现象 | 对于其中不可视的弯曲进行了适当删除,且曲线平滑性较好 | 无夸大 | 比例尺为1:100万时,出现了“岛屿上岸”的错误,但无相交的错误 |
| 河口湾化简方法 | 保留,且在距离比较近时,予以适当夸大 | 对于部分特殊弯曲(图中圆圈1所示弯曲)未能进行有效综合,且曲线平滑性较差 | 无夸大 | 无图理性错误 |
| 本文方法 | 保留,且在距离比较近时,予以适当夸大 | 对于其中不可视的弯曲进行了适当删除,且曲线平滑性较好 | 适当夸大 | 无图理性错误 |
需要说明的是,在图中圆圈1所示区域的尖锐弯曲,文献[16]所述河口湾化简方法,在对弯曲进行识别时,需要其骨架线长度大于平均宽度的2倍,才被认为是条带状弯曲,并进行部分删除操作。而上述弯曲明显不能达到上述条件,因而被认为是普通弯曲,但该弯曲面积始终达不到删除的阈值,因而始终进行了保留,本文对这一处理进行了改进,对全体面积大于阈值的弯曲进行了部分删除操作,使之更符合化简的需求,从结果来看,本文方法取得了较好的效果。
2.1.2 试验2:河口湾区域本次试验区域为典型的河口湾海岸,对于这一区域的评估主要包含以下方面内容:
(1) 对图中较为尖锐且不可视的弯曲进行删除。
(2) 对于其中相对较为狭窄的区域是否予以适当夸大拓宽。
(3) 对于当出现不同岛屿以及岸线距离相近时,是否予以适当的夸大拓宽。
(4) 是否出现自相交或不同海岸线相交的现象。
对于上述几个方面的评估情况统计如表 2所示。
综上所述,双向缓冲区方法可以得到较为平滑的曲线,但由于其自身算法原理的限制,使得其在综合部分潟湖区域,以及出现狭长弯曲的河谷区域时,容易综合尺度过大,且没有夸大操作;而河口湾综合方法,主要用于解决单一河口湾海岸线的化简问题,在河口湾的化简效果较好,但对于部分不为条带状的弯曲,难以进行有效化简,其化简的曲线平滑性不够。综合来看,本文方法则取得较好的综合效果。
2.2 位置精度评估为了对各算法的综合效果进行更加科学性的定量评估,将文中所述不同方法综合结果的平均位置偏移量进行统计,其统计数据如表 3、表 4所示。由于位置偏移的数值一般十分微小,因此,在这里将其统一换算到实地距离(单位为cm),以方便比对。
| cm | ||||||||
| 比例尺 | 双向缓冲区 | 河口湾化简方法 | 本文化简方法 | |||||
| 正向 | 负向 | 正向 | 负向 | 正向 | 负向 | |||
| 1:50万 | 44.793 | 0.023 | 0.0 | 0.0 | 187.944 | 51.496 | ||
| 1:75万 | 159.157 | 0.037 | 18.069 | 0.0 | 210.353 3 | 93.574 | ||
| 1:100万 | 44 470.228 | 0.044 | 113.694 | 1.980 | 476.675 | 4.208 | ||
| 1:125万 | 44 480.438 | 0.056 | 113.694 | 14.087 | 610.071 | 10.758 | ||
| cm | ||||||||
| 比例尺 | 双向缓冲区 | 河口湾化简方法 | 本文化简方法 | |||||
| 正向 | 负向 | 正向 | 负向 | 正向 | 负向 | |||
| 1:50万 | 447.747 | 0.011 | 61.928 | 29.871 | 220.273 | 11.760 | ||
| 1:75万 | 1 623.742 | 0.021 | 284.025 | 49.791 | 916.836 | 75.490 | ||
| 1:100万 | 2 299.872 | 0.034 | 934.568 | 91.900 | 1 232.109 | 130.238 | ||
| 1:125万 | 2 839.793 | 0.048 | 2 172.785 | 34.432 | 2 578.581 | 214.726 | ||
由上述两表可以看出,双向缓冲区方法的正向位置偏移量较大,特别是在表 3中,在比例尺小于1:100万后,其位置偏移量超出其他2种方法两个数量级;本文方法与河口湾化简方法相比,其正向和负向偏移量都大于河口湾化简方法。
单独从表 3、表 4来看,本文方法相比于河口湾化简方法,其位置偏移量较大。出现这一现象的主要原因在于:一方面,对于正向偏移而言,其正向的位置精度主要体现在化简后海岸线在原始海岸线的基础上向海部方向的偏移量,在本文方法中,对全体弯曲的不可视部分进行了适当地部分删除操作,而河口湾方法则只针对其中的“条带状弯曲”进行了部分删除操作,从而显得本文方法的正向偏移较大;另一方面,负向偏移量主要体现在夸大方面,对于一些“瓶颈”区域或者不同海岸线相距较近区域,对于这一部分,一般需要制图作业员对其进行适当地夸大,从而防止出现视觉性错误,而河口湾方法不是一种顾及多条海岸线间协调关系的方法,因而对于不同海岸线相距较近的区域未进行处理,而本文方法则对这一部分进行了夸大操作,从而使得在精度评估时,本文方法负向偏移量较大。由于上述两方面的原因,从而显得本文的偏移量较大。但本文这样做的目的是使得化简结果更加贴近实际作业,提高化简质量,减少化简过程中出现的图理性错误。
3 结论通过分析、计算及试验比对,得出如下结论:
(1) 相比于双向缓冲区方法,本文方法在化简精度上有较大提高,且有效克服了其在瓶颈区域化简尺度过大的问题;相比于河口湾化简方法,对于一些面积较大且宽度变化较大的非条带状弯曲,本文方法化简效果更好。
(2) 相较于以上两种海岸线化简方法,本文充分顾及了复杂海区,多岛屿、多海岸线条件下的不同海岸线之间的空间邻近关系,有效解决了可能出现的图理性问题,海岸线的化简质量有了明显的提高。
当然,任何方法都有其适用范围,本文只是考虑了复杂海区,多岛屿、多海岸线条件下,各海岸线之间协调处理问题,但对于一些变化剧烈且存在大量河流支流的入海口区域自动综合,这里还未涉及,这些问题有待进一步研究。
| [1] |
王厚祥, 李进杰.
海图制图综合[M]. 北京: 测绘出版社, 1999.
WANG Houxiang, LI Jinjie. Generalization of nautical charts[M]. Beijing: Surveying and Mapping Press, 1999. |
| [2] |
国家质量技术监督局. GB 12320-1998中国航海图编绘规范[S].北京: 中国标准出版社, 1999. The State Bureau of Quality and Technical Supervision. GB 12320-1998 Specifications for Chinese nautical charts[S]. Beijing: China Standard Press, 1999. |
| [3] |
高王军, 彭认灿, 陈轶, 等.
双向缓冲区算法及其在海图线状要素综合中的应用研究[J]. 测绘科学, 2009, 34(2): 187–190.
GAO Wangjun, PENG Rencan, CHEN Yi, et al. The research of the double direction buffering algorithm and its application on the generalizing of chart linear feature[J]. Science of Surveying and Mapping, 2009, 34(2): 187–190. DOI:10.3771/j.issn.1009-2307.2009.02.063 |
| [4] |
王亮, 吴艳兰, 汤军, 等.
改进的双向缓冲海岸线综合方法研究[J]. 测绘科学, 2015, 40(1): 18–21, 13.
WANG Liang, WU Yanlan, TANG Jun, et al. A coastline generalization method for marine delimitation[J]. Science of Surveying and Mapping, 2015, 40(1): 18–21, 13. DOI:10.3969/j.issn.1673-6338.2015.01.004 |
| [5] | CHRISTENSEN A H J. Cartographic line generalization with waterlines and medial-axes[J]. Cartography and Geographic Information Science, 1999, 26(1): 19–32. DOI:10.1559/152304099782424893 |
| [6] |
董箭, 彭认灿, 张立华, 等.
顾及"保真性"原则的双向滚动球变换DDM多尺度表达算法[J]. 测绘学报, 2017, 46(6): 789–801.
DONG Jian, PENG Rencan, ZHANG Lihua, et al. Multi-scale representation of digital depth model based on double direction rolling ball transform according to the reality principle[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 789–801. DOI:10.11947/j.AGCS.2017.20160558 |
| [7] |
董箭, 彭认灿, 张立华, 等.
利用滚动圆变换的多波束测深数据滤波算法[J]. 武汉大学学报(信息科学版), 2016, 41(1): 86–92.
DONG Jian, PENG Rencan, ZHANG Lihua, et al. An algorithm of filtering noises in multi-beam data based on rolling circle transform[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 86–92. |
| [8] |
董箭, 彭认灿, 张立华, 等.
滚动球变换的数字水深模型多尺度表达[J]. 地球信息科学学报, 2012, 14(6): 704–711.
DONG Jian, PENG Rencan, ZHANG Lihua, et al. Multi-scale representation of digital depth model based on rolling ball transform[J]. Journal of Geo-information Science, 2012, 14(6): 704–711. |
| [9] |
陈惠荣, 彭认灿, 郑义东, 等.
以弯曲骨架线为化简指标的海岸线综合方法[J]. 武汉大学学报(信息科学版), 2011, 36(12): 1418–1422.
CHEN Huirong, PENG Rencan, ZHENG Yidong, et al. Coastline generalization based on skeleton line of curve bends[J]. Geomatics and Information Science of Wuhan University, 2011, 36(12): 1418–1422. |
| [10] |
刘欢, 谢三德, 王芳.
海岸线自动综合方法综述[J]. 测绘科学技术学报, 2010, 27(3): 225–228.
LIU Huan, XIE Sande, WANG Fang. Study on the method of automatic cartographic generalization of coastline[J]. Journal of Geomatics Science and Technology, 2010, 27(3): 225–228. DOI:10.3969/j.issn.1673-6338.2010.03.018 |
| [11] |
刘颖, 翟京生.
海岸线形态的表达与自动综合[J]. 测绘与空间地理信息, 2005, 28(4): 78–81.
LIU Ying, ZHAI Jingsheng. The research on pattern presentation and automatic generalization of coastlines[J]. Geomatics & Spatial Information Technology, 2005, 28(4): 78–81. DOI:10.3969/j.issn.1672-5867.2005.04.026 |
| [12] |
陈惠荣, 郑义东, 关海波, 等.
基于骨架线的Douglas-Peucker算法改进[J]. 海洋测绘, 2011, 31(5): 18–20.
CHEN Huirong, ZHENG Yidong, GUAN Haibo, et al. Improvement of Douglas-Peucker algorithm based on skeleton line[J]. Hydrographic Surveying and Charting, 2011, 31(5): 18–20. DOI:10.3969/j.issn.1671-3044.2011.05.006 |
| [13] | VISVALINGAM M, WHELAN J C. Implications of weighting metrics for line generalization with visvalingam's algorithm[J]. The Cartographic Journal, 2016, 53(3): 253–267. DOI:10.1080/00087041.2016.1149906 |
| [14] | AI Tinghua, ZHOU Qi, ZHANG Xiang, et al. A simplification of ria coastline with geomorphologic characteristics preserved[J]. Marine Geodesy, 2014, 37(2): 167–186. DOI:10.1080/01490419.2014.903215 |
| [15] |
黄亚锋, 艾廷华, 刘耀林, 等.
顾及地理特征保持的溺谷海岸线化简算法[J]. 测绘学报, 2013, 42(4): 595–601.
HUANG Yafeng, AI Tinghua, LIU Yaolin, et al. Geographic-feature oriented ria coastline simplification[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 595–601. |
| [16] |
杜佳威, 武芳, 李靖涵, 等.
一种河口湾海岸线渐进化简方法[J]. 测绘学报, 2018, 47(4): 547–556.
DU Jiawei, WU Fang, LI Jinghan, et al. A progressive simplification method for the estuary coastline[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(4): 547–556. DOI:10.11947/j.AGCS.2018.20170440 |
| [17] |
艾廷华, 郭仁忠, 陈晓东.
Delaunay三角网支持下的多边形化简与合并[J]. 中国图象图形学报, 2001, 6(7): 703–709.
AI Tinghua, GUO Renzhong, CHEN Xiaodong. Simplification and aggregation of polygon object supported by Delaunay triangulation structure[J]. Journal of Image and Graphics, 2001, 6(7): 703–709. DOI:10.3969/j.issn.1006-8961.2001.07.017 |
| [18] |
艾廷华, 郭仁忠, 刘耀林.
曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报, 2001, 30(4): 343–348.
AI Tinghua, GUO Renzhong, LIU Yaolin. A binary tree representation of curve hierarchical structure in depth[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 343–348. DOI:10.3321/j.issn:1001-1595.2001.04.013 |
| [19] | VAN DER POORTEN P M, JONES C B. Characterisation and generalisation of cartographic lines using Delaunay triangulation[J]. International Journal of Geographical Information Science, 2002, 16(8): 773–794. DOI:10.1080/13658810210149434 |
| [20] | ZHENG Xianwei, XIONG Hanjiang, GONG Jianya, et al. A robust channel network extraction method combining discrete curve evolution and the skeleton construction technique[J]. Advances in Water Resources, 2015(83): 17–27. |
| [21] |
翟仁建, 武芳, 朱丽, 等.
利用地理特征约束进行曲线化简[J]. 武汉大学学报(信息科学版), 2009, 34(9): 1021–1024, 1089.
ZHAI Renjian, WU Fang, ZHU Li, et al. Line simplification method based on geographic-feature constraint[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1021–1024, 1089. |
| [22] |
高朝.顾及地理特征的复杂形态湖泊地图综合研究[D].南京: 南京师范大学, 2016. GAO Zhao. Geographic-feature oriented map generalization of complex lake[D]. Nanjing: Nanjing Normal University, 2016. |
| [23] |
艾廷华, 郭仁忠.
支持地图综合的面状目标约束Delaunay三角网剖分[J]. 武汉测绘科技大学学报, 2000, 25(1): 35–41.
AI Tinghua, GUO Renzhong. A constrained Delaunay partitioning of areal objects to support map generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(1): 35–41. |
| [24] |
艾廷华, 郭仁忠.
基于约束Delaunay结构的街道中轴线提取及网络模型建立[J]. 测绘学报, 2000, 29(4): 348–354.
AI Tinghua, GUO Renzhong. Extracting center-lines and building street network based on constrained Delaunay triangulation[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(4): 348–354. DOI:10.3321/j.issn:1001-1595.2000.04.012 |
| [25] | SELVI H Z, BILDIRICI I O, YERCI M. Triangulation method for area-line geometry-type changes in map generalisation[J]. The Cartographic Journal, 2010, 47(2): 157–163. DOI:10.1179/000870409x12584524218965 |
| [26] |
李宁, 彭认灿, 张俊杰.
矢量海图上线状要素间最短距离求解与应用[J]. 测绘科学, 2010, 35(S1): 75–76, 194.
LI Ning, PENG Rencan, ZHANG Junjie. Research on arithmetic of the shortest distance between lines on vector digital chart[J]. Science of Surveying and Mapping, 2010, 35(S1): 75–76, 194. DOI:10.16251/j.cnki.1009-2307.2010.s1.027 |



