2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054;
4. 国防科技大学智能科学学院, 湖南 长沙 410073;
5. 国防大学联合作战学院, 河北 石家庄 050001
2. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. National University of Defense Technology, Changsha 410073, China;
5. National Defense University Joint Operations College, Shijiazhuang 050001, China
近年来,伴随着传感器与硬件平台性能的提升、计算机视觉与机器学习理论的发展、同时定位与建图(simultaneously localization and mapping,SLAM)与运动恢复结构(structure from motion,SFM)技术的迅速普及,地面移动测量系统(mobile mapping system,MMS)与无人驾驶车(autonomous vehicle,AV,或称自主驾驶车)两个行业已然走向了深层次的相互借鉴、融合与进步[1-6]。目前的两个平台的主要区别仅在于驾驶控制方式与应用目的的不同,平台安装的传感器件、采用的载体定位定姿、高精度地图建立等核心关键技术几乎是一致的[7-10]。从长期发展来看,MMS的未来必将是无人化、互联化甚至实时化的地面移动测量,而AV的发展也将走向实时高精度地图建立、自主决策控制、车联网云端导航等方向。在不远的将来,MMS与AV平台将可能融合成为一个集实时测图、上传云端实时建图、更新互联发布、实时导航的有机平台。
当前,多传感器融合获取载体精确的位置姿态仍是MMS与AV两个系统共同的基础核心关键问题[7-8, 10],其中视觉传感器的位置姿态确定离不开视觉里程计(visual odometry,VO)技术。VO技术作为视觉SLAM(visual-SLAM,VSLAM)的前端技术内容,近年来发展迅速。VO主要分为单目(monocular VO)与双目(stereo VO)两类,分别是指通过单目或双目相机作为输入估计载体自身运动位置姿态变化的过程[11]。单目VO由于只能恢复运动到一个尺度因子,而绝对尺度需要利用场景中目标大小、运动约束或集成其他传感器来确定,因此其序列图像定位定姿跟踪的稳定性较差。双目VO能够直接利用基线获得尺度、深度,因此其序列图像位姿估计精度和稳定性都显著优于单目[12]。但是,目前VO、VSLAM算法精度和稳健性与视觉、POS、LiDAR多传感器融合后的组合导航结果相比,精度约低一个数量级,稳健性也显著低于组合系统,主要用于低成本轻量化平台的位姿估计、组合系统的位姿初值获取以及与LiDAR融合实现环境地图生成。
目前VO的典型方法有基于特征法的ORB-SLAM[13]、基于半直接法的SVO[14],以及基于直接法(或称光流法)的多种方法。直接法依利用光流数量的多少还可分为稠密法(如REMODE[15]、DTAM[16])、半稠密法(如LSD-SLAM[17])、稀疏法(如DSO[18])等, 适用于不同计算平台和建图应用需求。其中稀疏法一般用于需要实时高效位姿估计的场合,大多数稀疏算法是将六自由度的位置姿态在同一重投影误差最小化过程中整体估计出来[19-20],或是以一定合理假设为前提限定载体部分姿态变化而后估计其他位姿参数,相比六自由度整体估计的方法计算效率更高但因载体姿态的限定而精度略有损失[21-22]。RotROCC法[23]提出首先抵消旋转分量,仅保留平移分量,实现平移分量解耦,然后利用解耦归一化重投影残差,实现仅利用平移分量进行位置变化估计中的外点剔除,从而实现载体位姿估计的优化,但其利用的模型存在近似,因此无法分离平移和深度误差,也就无法利用旋转分量进行姿态变化估计中的外点剔除。本文针对MMS和AV车辆平台下双目相机拍摄的图像序列中视觉里程计位姿估计优化问题,在RotROCC法的基础上,利用光流运动场模型中载体位姿与图像光流矢量间关系,不仅将光流矢量解耦为平移、旋转分量,并进一步解耦为3个平移分量、3个旋转分量和深度分量,充分推导分析了解耦后单个分量、组合分量误差对位姿估计的影响,分别利用仿真和真实数据试验,验证了不同模型下的误差分离方法。最后,结合组合分量的误差分离模型,针对双目VO序列位姿估计提出了解耦光流运动场的位姿优化算法,并在公开的KITTI数据集[24]中进行了多个序列真实数据验证。
1 光流运动场模型及解耦 1.1 光流运动场当相机与场景间有相对运动时,图像上亮度的运动变化就称为光流[25],因此,图像中光流的运动规律直接反映了与相机固联的载体的位置姿态变化,这一模型可以通过式(1)描述[26-27],下称光流运动场模型
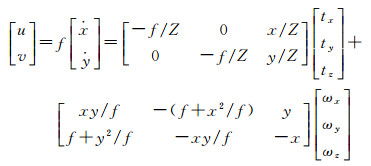 (1)
(1)
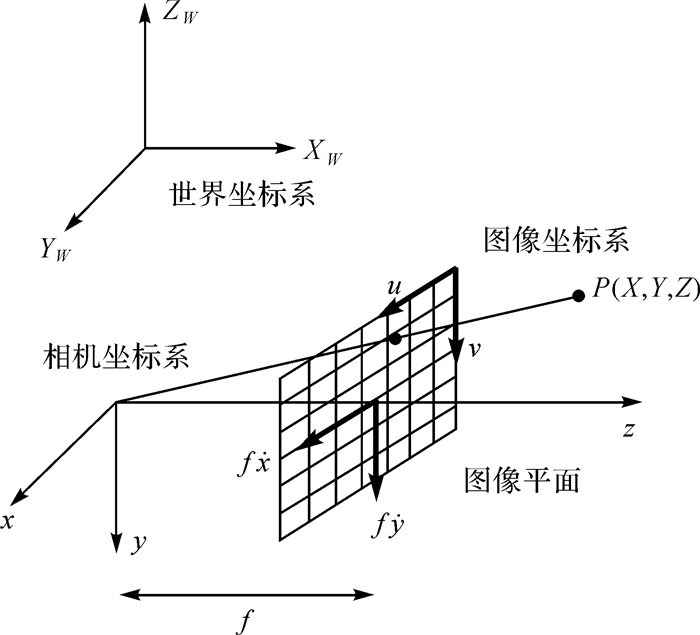
为方便计算,本文坐标系定义与KITTI数据集坐标系定义一致。式(1)中,物方点P(X, Y, Z)经小孔成像投影于归一化相机平面为(x, y),f为成像焦距。当场景与相机间发生相对运动时,(ẋ, ẏ)即为P点对应相机坐标系中点的速度, (u, v)为点P投影到图像的帧间像素坐标变化量,即光流矢量。因此,式(1)左、中部分描述了图像中的光流矢量;式(1)右部分描述了相机坐标系下投影点的运动与场景深度Z、相机沿世界坐标系三轴平移变化量t、相机绕世界坐标系三轴的旋转变化量ω之间的关系。式(1)等号右侧加号两边分别为光流的平移分量与旋转分量。从式(1)可见,光流场的平移分量体现出了场景深度Z及平移量t,光流场的旋转分量体现了旋转量ω的信息。变量的几何意义如图 1所示。
|
| 图 1 光流运动场投影模型图像平面 Fig. 1 Projection model of flow motion field |
1.2 解耦光流分量
图像中的光流运动场展现的是前后帧间载体六自由度的位置姿态变化速度。为了考察光流及解耦分量在不同相对运动场景下的变化规律,本文选取了KITTI数据集的两个典型场景给出不同载体运动状态下的光流场。如图 2左侧,是KITTI序列2第3、4帧间运动下的光流场,该场景以载体快速前向运动为主,旋转运动较小。与之对比,图 2右侧,是KITTI序列2第45、46帧间运动下光流场,该场景以载体低速转向为主,平移运动较小。图 2(a)左右光流场中的每个光流矢量均以蓝、绿点为起、终点,箭头指向光流场方向,邻帧间的变化量即为位姿变化速度。

|
| 图 2 两个典型场景的光流场及解耦光流分量 Fig. 2 Flow fields and decoupled flow components in 2 typical scenes |
将光流矢量解耦为旋转(rotational)角速度分量ω(即旋转分量)和平移(translational)速度分量t(即平移分量),如图 2(b)、(c),在左侧前向运动场景中,旋转分量光流较小且大小均一,平移分量光流大小不一随深度变化;在右侧旋转运动场景中,旋转分量光流较大且大小均一,平移光流大小不一随深度变化。可见,在不同相对运动状态下,光流场矢量受不同解耦分量影响差别显著。
将平移分量进一步解耦为载体沿世界坐标系三轴的3个位移分量,即t=[tx, ty, tz]T;将旋转分量进一步解耦为载体绕世界坐标系三轴的3个旋转角分量,即ω=[ωx, ωy, ωz]T,类似,在图中绘制出KITTI序列2第3、4帧间前向运动场景和序列2第45、46帧间旋转运动场景下解耦的六自由度分量光流,如图 2(d)-(i)所示。
从图 2(d)-(i)左右场景对比可见,左侧前向运动场景的3个旋转分量光流较小,右侧旋转运动场景的ωx, ωz分量光流较小,ωy分量光流较大;左右两场景中3个平移分量光流中tx、ty两个分量的光流均较小,tz分量光流大小随深度变化。可见,光流矢量受6个不同分量大小的影响也是显著不同的。
2 解耦光流运动场误差模型与仿真 2.1 解耦光流运动场误差模型1.2节中定性分析了不同光流分量的特点,本节通过模型推导分析各分量误差对模型估计的影响。由式(1)可知,不失一般性,可以令其中f=1,记为式(2)
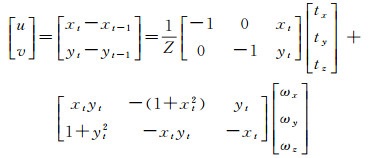 (2)
(2)
令ρ=1/Z,即逆深度,将式(2)右侧等号两边简写为
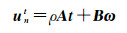 (3)
(3)
对光流运动场模型,可以通过令式(3)等号两边残差最小化实现对其中载体运动变量
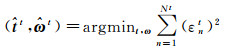 (4)
(4)
式中
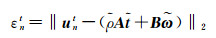 (5)
(5)
同时,令
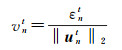 (6)
(6)
令εnt为最小二乘估计残差(least square error,LSE),vnt为归一化最小二乘估计残差(normalized LSE,NLSE)。
2.2 单变量误差模型与仿真 2.2.1 单变量误差模型下面考察单个位姿参数LSE及NLSE的数学形式,并作仿真比对:
(1) 若仅ωx参数存在误差,有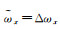
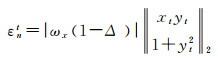 (7)
(7)
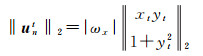 (8)
(8)
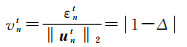 (9)
(9)
(2) 若仅ωy参数存在误差,有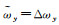
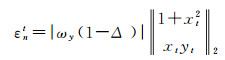 (10)
(10)
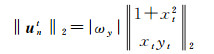 (11)
(11)
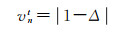 (12)
(12)
(3) 若仅ωz参数存在误差,有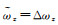
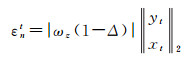 (13)
(13)
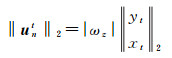 (14)
(14)
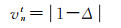 (15)
(15)
(4) 若仅tx参数存在误差,有
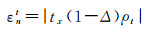 (16)
(16)
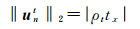 (17)
(17)
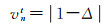 (18)
(18)
(5) 若仅ty参数存在误差,有
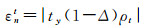 (19)
(19)
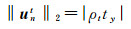 (20)
(20)
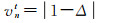 (21)
(21)
(6) 若仅tz参数存在误差,有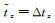
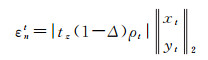 (22)
(22)
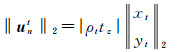 (23)
(23)
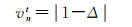 (24)
(24)
(7) 若仅Z参数存在误差,有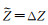
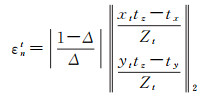 (25)
(25)
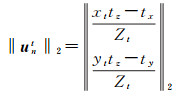 (26)
(26)
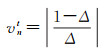 (27)
(27)
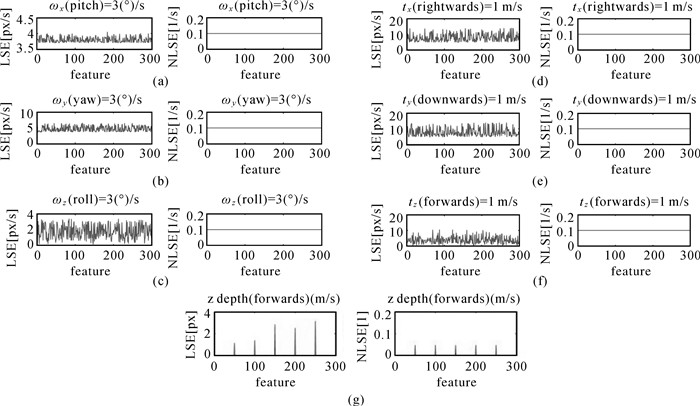
将2.2.1节中步骤(1)-(7)的单个位姿参数LSE及NLSE进行计算仿真,如图 3所示。仿真图像特征点对应光流个数为300个,仿真3个旋转角(速度)分量为3(°)/s,误差为10%,即0.3(°)/s,即|1-Δ|=0.1;3个平移(速度)分量为1 m/s,误差10%,即0.1 m/s,即|1-Δ|=0.1;深度分量仿真中,前向tz方向行驶速度为50 km/h, 帧率为10 Hz,另两方向的行驶速度为tx=0.1tz,ty=0.01tz。深度分量仅在特征光流为第50、100、150、200、250时存在,且误差为5%,即|(1-Δ)/Δ|=0.05。
|
| 图 3 单变量误差仿真 Fig. 3 Error simulation of single variable |
图 3中分别给出了7个变量包含误差时,一帧中300个特征的LSE与NLSE。
从图 3可见,单个变量的LSE会随着特征光流矢量所在图像坐标的不同而出现随机残差,将LSE归一化后,计算出单个变量的NLSE不再随特征光流所在坐标变化,而仅余下单个变量NLSE的残差,大小为|Δ-1|,即变量本身包含的误差,也就是说,最小二乘估计残差LSE中随特征点所在坐标产生的随机误差被很好地分离了。
2.3 组合误差模型与仿真 2.3.1 组合误差模型2.2节是单个位姿变量包含误差情况下,将其LSE中随机残差进行归一化分离的数学推导和仿真验证。在实际计算中,7个变量一般不会仅单个存在误差,需要分析推导多变量存在误差的情况下,随机残差的分离方法。考虑采用去耦合的方法分离位置或姿态分量部分随图像坐标产生的随机残差。考虑到式(5)、式(6),令
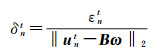 (28)
(28)
为解耦的归一化最小二乘残差(decoupled normalized least square error,DNLSE1),令
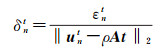 (29)
(29)
为DNLSE2。考察不同组合位置姿态参数包含误差条件下的DNLSE的数学形式:
(1) 若仅平移分量t存在误差, 即
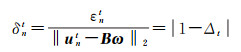 (30)
(30)
(2) 若仅旋转分量ω存在误差,即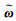
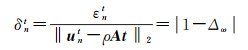 (31)
(31)
(3) 若仅深度Z存在误差,即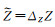
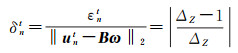 (32)
(32)
(4) 若平移分量和深度存在误差,即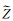
 (33)
(33)
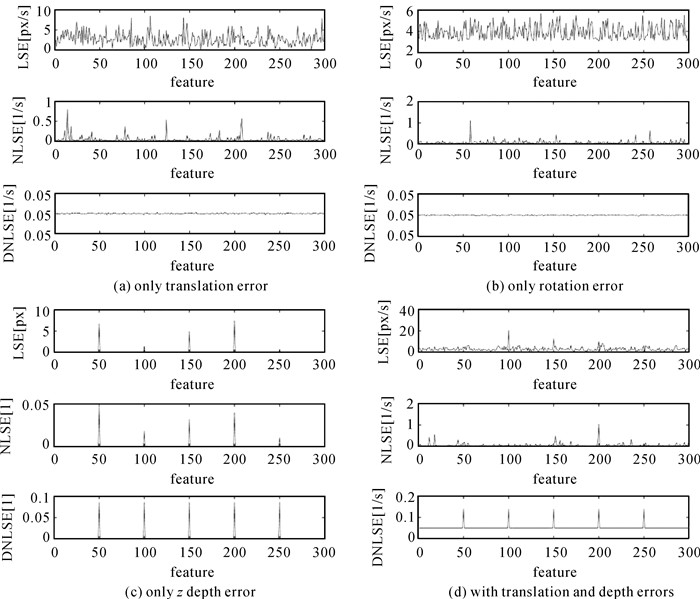
下面将组合位姿参数在2.3.1节中(1)-(4)不同情况下的LSE、NLSE、DNLSE进行了计算仿真,如图 4所示。仿真的图像特征点对应光流个数为300个,仿真的3个旋转角(速度)分量为ω=[1°, 5°, 0.5°]T,误差为5%,即|1-Δω|=0.05;3个平移(速度)分量的仿真中,前向tz方向行驶速度为50 km/h, 帧率为10 Hz,3个平移(速度)分量为t=[0.1tz, 0.01tz, tz]T,误差5%,即|1-Δt|=0.05;深度分量仅在特征点对应光流为第50、100、150、200、250时存在,误差为8%,|(1-ΔZ)/ΔZ|=0.08。
|
| 图 4 组合变量误差仿真 Fig. 4 Error simulation of combined variables |
从图 4可见,组合变量存在误差时,LSE随着特征光流矢量所在图像坐标的不同而出现随机残差;组合变量的NLSE能够分离大部分这些随机误差,但并不能完全分离;组合变量的DNLSE计算结果不再随特征光流所在坐标变化,而仅余下各组合变量本身的误差部分,这说明组合变量存在误差情况下,利用DNLSE模型时,最小二乘估计残差中随特征点所在坐标的部分残差能够被很好地分离。表 1将不同组合变量存在误差时可采用的DNLSE模型列出,“√”表示可分离的误差类型。误差种类不同时,DNLSE的计算式不同。利用DNLSE1模型能够在无旋转分量误差的条件下,较好地分离平移分量和深度误差中光流在图像坐标引入的随机残差部分;利用DNLSE2模型能够在无平移分量和深度误差的条件下,较好地分离旋转分量光流在图像坐标引入的随机残差部分。
| 平移误差 | 旋转误差 | 深度误差 | 所用模型 | |
| 1 | √ | DNLSE1 | ||
| 2 | √ | DNLSE2 | ||
| 3 | √ | DNLSE1 | ||
| 4 | √ | √ | DNLSE1 |
2.3.3 组合误差分离试验 2.3.3.1 仿真数据试验
将2.3.2节中情况(1)“仅平移分量存在误差,旋转分量与深度无误差,利用DNLSE1计算”的过程,即图 4第1组仿真,在本次试验中用图像光流场的误差条(ErrorBar)形式给出LSE和DNLSE计算结果的对比。如图 5(a),光流矢量起点的红色“工”形误差条的高度代表该光流矢量LSE残差大小,经过DNLSE1模型的误差分离,在图 5(b)中,光流矢量起点的绿色“工”形误差条高度明显降低,说明LSE中的残差被显著分离。

|
| 图 5 2.3.2节(1)计算结果对比 Fig. 5 Computation results comparison of (1) in section 2.3.2 |
2.3.3.2 真实数据试验
将2.3.2节表 1列出的(2)、(4)情况对真实数据进行误差分离计算过程试验,以期用尽量少的计算次数覆盖所有误差的分离。试验中对KITTI数据集序列2第3、4帧与序列2第45、46帧,分别用DNLSE1、DNLSE2模型进行计算,结果如图 6。图 6中(a)、(c)、(e)是序列2第3、4帧的高速前向运动场景,(b)、(d)、(f)是序列2第45、46帧的慢速旋转场景。图 6(a)、(b)给出了计算出的LSE模型误差,以红色误差条显示,图 6(c)、(d)是计算出的DNLSE1模型误差,以绿色误差条显示,图 6(e)、(f)是计算出的DNLSE2模型误差,以蓝色误差条显示。

|
| 图 6 两类场景真实数据组合误差分离试验 Fig. 6 Combined error separation experiments using data of two real scenes |
仔细对比图 6(a)、(c)的前向运动场景和图 6(b)、(d)的旋转运动场景,均可见图 6(c)、(d)的部分绿色误差条分别比图 6(a)、(b)的红色误差条反而高(如:图 6(a)、(b)黄色箭头和图 6(c)、(d)红色箭头对应的几个光流矢量误差条),这是DNLSE1显著分离LSE中的随机误差之后,暴露出了真实数据中存在着的一定旋转误差,即两场景下均有点DNLSE1>LSE,图 6中所有该情况的特征光流编号统计结果见表 2。类似,对比图 6(a)、(e)可以看到图 6(e)的部分蓝色误差条比图 6(a)的红色误差条反而高(如:图 6(a)蓝色箭头和图 6(e)红色箭头对应的光流矢量误差条),这是DNLSE2显著分离LSE中的随机误差之后,暴露出了真实数据中存在着的一定平移和深度误差,即前向运动场景下有点的DNLSE2>LSE,图 6中所有该情况的特征光流编号统计结果见表 2。但是对比图 6(b)和图 6(f),从中观察和试验统计结果都得到蓝色误差条比红色误差条高的数量为0,即旋转场景中无点DNLSE2>LSE,这说明DNLSE2显著分离LSE中的随机误差之后,由于场景中的平移分量很小,因此没有残余显著的平移和深度误差。
| 前向运动场景(图 6左) | 旋转运动场景(图 6右) | |
| DNLSE1>LSE 的特征光流编号 (绿色误差条) |
1、2、5、7、8、9、12、13、15、16、18、20、22、23、25、26、28、33、39、41、42、43、44、53、55、56、57、60、61、62、66、68、71、75、81、85、91、92、95、96、103、111、112、114、118、123、124、125、26、136、137、139、140、144、145、150、153、157、64、167、174(53个) | 53、96、118、133、204、208、220、289、296、325、327、337、339、373(14个) |
| DNLSE2>LSE的 特征光流编号 (蓝色误差条) |
15、24、30、31、32、34、35、45、56、68、73、80、83、89、91、97、98、110、113、115、116、119、128、134、137、140、142、144、146、149、155、158、161、162、170、171、173、176、180(33个) | 无 |
| 特征光流矢量总数/个 | 182 | 388 |
3 解耦光流运动场双目视觉里程计位姿优化算法
在完成了组合误差分离的真实数据试验后,本文针对真实车辆运行时利用序列图像进行载体位姿估计的问题设计实现了解耦光流运动场双目视觉里程计位姿优化算法,并利用KITTI集的多个序列进行了解算试验。本文采用了双目视觉里程计先进行载体位姿初值的估计,然后利用解耦光流运动场误差模型进行图像位置随机误差的分离,并对残留位姿误差作进一步优化,以使载体位姿的估计精确化。
3.1 双目视觉里程计初始化在双目视觉里程计初始估计的实现中,本文采用了文献[19]算法并对模板滤波作了改进,提升了计算效率(以下称Badino算法)。具体的初始化计算过程如下:对于第1帧,计算左图的Harris角点以固定特征点数(1024个),然后计算这1024个点的偏差量,将有效的偏差结果保存到特征矢量;对于第2帧,利用光流跟踪这1024个特征点,去掉跟踪失败的点后得到这些点新的像素坐标,同时再次计算Harris角点以补足至1024个点,同样计算这1024个点的偏差量,结果存入特征矢量。接下来,利用前后两帧的特征矢量计算位姿变化。首先选择在两帧中均计算出有效偏差的对应点对,将上一帧的三维点坐标进行帧间转移矩阵变换,得到当前帧的局部坐标,然后投影到当前图像中,与当前图像中的特征点位置进行比较,结果越小的越好。这一过程不断迭代,每次迭代后仅保留重投影误差较小的点对,抛弃误差较大的点对,并且每个点对的权重反比于投影误差。最后对结果进行卡尔曼滤波,滤波后的结果作为双目VO的估计初值。
3.2 解耦光流运动场的位姿优化算法在具备了双目VO估计的位姿初值和前后帧对应的初始特征内点集后,利用当前内点集的重投影误差最小化迭代估计旋转位置变化量[19-20],直至重投影误差小于一定阈值或迭代次数超限,接着对式(5)利用DNLSE1进行图像中光流位置引入的随机误差分离和显著旋转误差的外点去除。
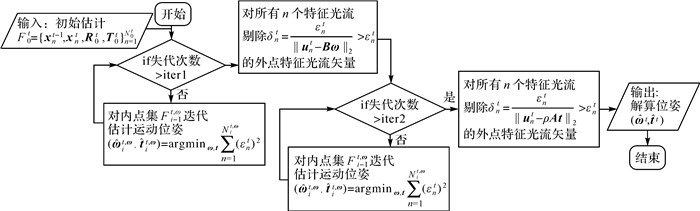
接着,固定前一轮估计出的旋转变化量,利用当前特征内点集的重投影误差最小化迭代估计位置变化量,直至重投影误差小于一定阈值或迭代次数超限,接着对式(5)利用DNLSE2进行图像中光流位置引入的随机误差分离和显著平移深度误差的外点去除。算法流程见图 7。
|
| 图 7 解耦光流运动场的位姿优化算法流程 Fig. 7 Pose estimation algorithm for optical flow-decoupled motion field model |
4 试验与分析
为验证本文算法的有效性和计算精度,利用KITTI数据集序列00、02分别进行了算法解算试验。试验平台为LenovoX240s(CPU酷睿i7-4510U,2.00 GHz×4核,内存8 GB)笔记本电脑,本文所有试验都在Ubuntu14.04系统下,利用Matlab2014b、MexOpenCV2.4、C++11语言混合编程实现。
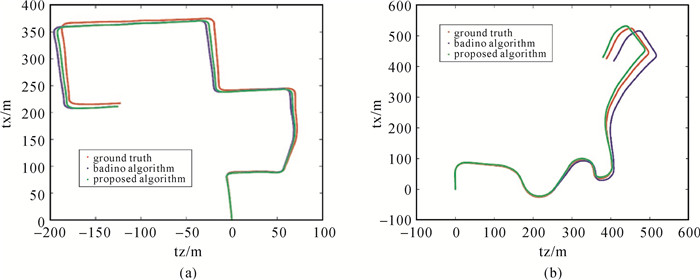
利用KITTI数据集的00序列和02序列的第0帧至第1200帧进行算法试验,绘制的二维轨迹如图 8。图 8给出的是位置分量t=[tx, ty, tz]T中的tx和tz分量,其中tz沿世界系Z轴指向载体前向运动方向,tx沿世界系X轴指向载体右侧横向运动方向,ty指向载体重力方向。图中红色轨迹为KITTI数据集给出的轨迹真值,蓝色轨迹为Badino算法的计算结果,绿色为本文提出的位姿优化算法进行计算的轨迹结果。
|
| 图 8 解算轨迹对比((a)序列00,(b)序列02) Fig. 8 Comparisons of calculated trajectories ((a) sequence 00, (b) sequence 02) |
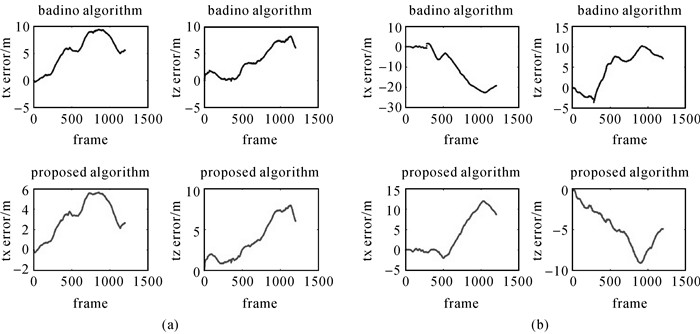
图 9为两种算法解算tx、tz方向的误差对比,具体统计结果见表 3。从统计结果可见,本文算法较好地分离了初始化计算结果中仍然存在的特征光流位置随机误差,以及平移、旋转、深度分量的残差,明显减少了Badino算法的累积误差。
|
| 图 9 解算误差对比((a)序列00,(b)序列02) Fig. 9 Comparisons of calculation errors ((a) sequence 00, (b) sequence 02) |
| 算法 类型 |
KITTI集序列00第0-1200帧 | KITTI集序列02第0-1200帧 | tx方向误差平均百分比/(%) | tz方向误差平均百分比/(%) | tx方向误差降低了53.6%;tz方向误差降低了15.4% | |||||||||
| tx误差 | tz误差 | tx误差 | tz误差 | |||||||||||
| 误差值/m | 百分比/(%) | 误差值/m | 百分比/(%) | 误差值/m | 百分比/(%) | 误差值/m | 百分比/(%) | |||||||
| Badino算法 | <10 | 4.56 | <9 | 2.79 | <25 | 4.93 | <11 | 1.16 | 4.75 | 2.2 | ||||
| 本文算法 | <6 | 2.16 | <8 | 2.77 | <13 | 2.24 | <9 | 1.16 | 2.2 | 1.9 | ||||
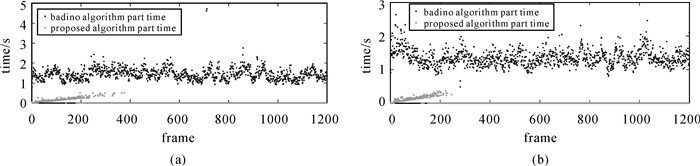
图 10统计对比了序列00与序列02每帧计算中利用Badino算法完成初始位姿估计部分所耗费时间和完成本文算法精度优化部分所耗时间。统计结果可见,本文提出算法部分的耗时相对初始化位姿估计部分耗时增加不多或几乎没有增加,计算效率与原算法基本相当,能够用于多种低功耗嵌入式计算场合。
|
| 图 10 计算耗时对比((a)序列00,(b)序列02) Fig. 10 Comparisons of calculation time ((a) Sequence 00, (b) Sequence 02) |
5 结论
本文利用图像中光流矢量与载体位置姿态变化速率之间的模型关系--光流运动场模型,将光流矢量解耦到对应的六自由度载体位姿变量,考察解耦后的光流矢量与单个、组合载体位姿变量误差之间的关系,推导出利用NLSE分离LSE中的光流矢量位置随机误差,利用DNLSE进一步分离组合变量下NLSE中的光流矢量位置随机误差,并利用仿真和真实数据进行了试验验证。在双目视觉里程计算中,利用本文提出的解耦光流运动场位姿优化算法,既能够分离光流矢量位置的随机误差,同时能够通过外点剔除减少DNLSE1和DNLSE2模型计算后残留的平移、深度、旋转角度残差。试验表明,算法将载体横向平移平均误差由4.75%降低至2.2%,误差平均降低了53.6%;将载体前向平移平均误差由2.2%降低至1.9%,误差平均降低了15.4%。算法在明显减少双目视觉里程计位置姿态估计中的累积误差的同时计算效率与原算法相当,适用于嵌入式低功耗实时位置姿态估计和组合导航系统的位姿初值获取。在计算量允许的条件下,还可接续进行SLAM图优化算法,预计能够进一步降低整体位置姿态估计误差。
| [1] |
高俊.
图到用时方恨少, 重绘河山待后生——《测绘学报》60年纪念与前瞻[J]. 测绘学报, 2017, 46(10): 1219–1225.
GAO Jun. The 60 anniversary and prospect of acta geodaetica et cartographica sinica[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1219–1225. DOI:10.11947/j.AGCS.2017.20170503 |
| [2] |
程传奇, 郝向阳, 李建胜, 等.
移动机器人视觉动态定位的稳健高斯混合模型[J]. 测绘学报, 2018, 47(11): 1446–1456.
CHENG Chuanqi, HAO Xiangyang, LI Jiansheng, et al. Robust Gaussian mixture model for mobile robots' vision-based kinematical localization[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(11): 1446–1456. DOI:10.11947/j.AGCS.2018.20170649 |
| [3] |
高翔, 张涛, 刘毅, 等.
视觉SLAM十四讲:从理论到实践[M]. 北京: 电子工业出版社, 2017.
GAO Xiang, ZHANG Tao, LIU Yi, et al. 14 lectures on visual SLAM:from theory to practice[M]. Beijing: Publishing House of Electronics Industry, 2017. |
| [4] |
周志华.
机器学习[M]. 北京: 清华大学出版社, 2016.
ZHOU Zhihua. Machine learning[M]. Beijing: Tsinghua University Press, 2016. |
| [5] | THRUN S, BURGARD W, FOX D. Probabilistic robotics[M]. Cambridge: The MIT Press, 2006. |
| [6] | HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision[M]. Cambridge: Cambridge University Press, 2004. |
| [7] |
张晓东.可量测影像与GPS/IMU融合高精度定位定姿方法研究[D].郑州: 信息工程大学, 2013. ZHANG Xiaodong. Research on high precision position and orientation method based on digital measurable image and GPS/IMU integration[D]. Zhengzhou: Information Engineering University, 2013. |
| [8] |
程传奇.非结构场景下移动机器人自主导航关键技术研究[D].郑州: 信息工程大学, 2018. CHENG Chuanqi. Research on the key technologies of autonomous navigation for mobile robots in unstructured environments[D]. Zhengzhou: Information Engineering University, 2018. |
| [9] |
陈驰, 杨必胜, 田茂, 等.
车载MMS激光点云与序列全景影像自动配准方法[J]. 测绘学报, 2018, 47(2): 215–224.
CHEN Chi, YANG Bisheng, TIAN Mao, et al. Automatic registration of vehicle-borne mobile mapping laser point cloud and sequent panoramas[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(2): 215–224. DOI:10.11947/j.AGCS.2018.20170520 |
| [10] |
魏崇阳.城市环境中基于三维特征点云的建图与定位技术研究[D].长沙: 国防科学技术大学, 2016. WEI Chongyang. 3D feature point clouds-based research on mapping and localization in urban environments[D]. Changsha: National University of Defense Technology, 2016. |
| [11] | NISTER D, NARODITSKY O, BERGEN J. Visual odometry[C]//Proceedings of 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC, USA: IEEE, 2004. |
| [12] | SCARAMUZZA D, FRAUNDORFER F. Visual odometry Part Ⅰ:the first 30 years and fundamentals[J]. IEEE Robotics and Automation Magazine, 2011, 18(4): 80–92. DOI:10.1109/MRA.2011.943233 |
| [13] | MUR-ARTAL R, MONTIEL J M M, TARDÓS J D. ORB-SLAM:a versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147–1163. DOI:10.1109/TRO.2015.2463671 |
| [14] | FORSTER C, ZHANG Zichao, GASSNER M, et al. SVO:semidirect visual odometry for monocular and multicamera systems[J]. IEEE Transactions on Robotics, 2017, 33(2): 249–265. |
| [15] | PIZZOLI M, FORSTER C, SCARAMUZZA D. REMODE: Probabilistic, monocular dense reconstruction in real time[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation. Hong Kong, China: IEEE, 2014: 2609-2616. |
| [16] | NEWCOMBE R A, LOVEGROVE S J, DAVISON A J. DTAM: dense tracking and mapping in real-time[C]//Proceedings of the 2011 International Conference on Computer Vision. Barcelona, Spain: IEEE, 2011: 2320-2327. |
| [17] | ENGEL J, SCHÖPS T, CREMERS D. LSD-SLAM: Large-scale direct monocular SLAM[C]//Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland: Springer, 2014: 834-849. |
| [18] | ENGEL J, KOLTUN V, CREMERS D. Direct sparse odometry[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 611–625. DOI:10.1109/TPAMI.2017.2658577 |
| [19] | BADINO H, KANADE T. A head-wearable short-baseline stereo system for the simultaneous estimation of structure and motion[C]//Proceedings of the IAPR Conference on Machine Vision Application. Nara, Japan, 2011: 185-189. |
| [20] | KITT B, GEIGER A, LATEGAHN H. Visual odometry based on stereo image sequences with RANSAC-based outlier rejection scheme[C]//Proceedings of 2010 IEEE Intelligent Vehicles Symposium. San Diego, CA, USA: IEEE, 2010. |
| [21] | STEIN G P, MANO O, SHASHUA A. A robust method for computing vehicle ego-motion[C]//Proceedings of the 2000 IEEE Intelligent Vehicles Symposium Dearborn, MI, USA: IEEE, 2000. |
| [22] | SCARAMUZZA D, FRAUNDORFER F, SIEGWART R. Real-time monocular visual odometry for on-road vehicles with 1-point RANSAC[C]//Proceedings of 2009 IEEE International Conference on Robotics and Automation. Kobe, Japan: IEEE, 2009. |
| [23] | BUCZKO M, WILLERT V. Flow-decoupled normalized reprojection error for visual odometry[C]//Proceedings of the 19th IEEE International Conference on Intelligent Transportation Systems. Rio de Janeiro, Brazil: IEEE, 2016: 1161-1167. |
| [24] | GEIGER A, LENZ P, URTASUN R. Are we ready for autonomous driving? The KITTI vision benchmark suite[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA: IEEE, 2012. |
| [25] |
章毓晋.
计算机视觉教程[M]. 北京: 人民邮电出版社, 2011.
ZHANG Yujin. A course of computer vision[M]. Beijing: Posts & Telecom Press, 2011. |
| [26] | MALIK J. Dynamic perspective[EB/OL].[2015-05-16]. http://www-inst.eecs.berkeley.edu/~cs280/sp15/lectures/4.pdf. |
| [27] | SABATINI S, CORNO M, FIORENTI S, et al. Vision-based pole-like obstacle detection and localization for urban mobile robots[C]//Proceedings of 2018 IEEE Conference on Intelligent Vehicles Symposium. Changshu, China: IEEE, 2018. |


