2. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
用遥感影像提取水体信息是水利行业解决洪涝灾害监测、水资源管理等需求的重要方式。SAR数据以其全天候、全天时的成像特点,适用于洪涝灾害信息的提取和监测[1],在水利遥感领域发挥着重要作用。作为我国自主研发的首颗分辨率高达1 m的C波段SAR卫星[2],GF-3的投入运行为水利遥感带来了更为广阔的发展前景。
经典的遥感影像水体提取方法包括阈值分割[3-4]、结合多种特征的分类器分割[5]、基于水平集理论的分割[1, 6]、基于能量函数的图像分割[7-9]等。当研究区域环境复杂时,水体提取过程常常出现虚警、漏警现象,导致水体提取结果精度不高。这种环境复杂性带来的精度问题,一定程度上源自像元分类的不确定性[10]。根据某些属性对像元分类时,可能存在将某些与水体像元散射特征或是光谱特征相似,但实际上不是水体的像元错分为水体的现象,使得像元分类结果存在不确定性;当数据的分辨率不高时,影像中某些像元反映的实际区域可能同时包含了多种地物,在分类上存在着不确定性。此外,在灰度值分割中阈值的选取同样会造成分类结果的不确定性。显然,二值水体分布图式的水体提取结果无法反映上述不确定性。
不同于传统的图像分割思路,水体分布概率估计[11]基于贝叶斯推断,根据SAR影像后向散射系数值计算水体的概率分布图。其最大的特点在于结果图上每一点取值范围不再是离散的{0, 1}集合,而是连续的[0, 1]区间,该值表示该点属于水体的概率。与常规水体提取方法得到二值水体分布图形式的结果不同,水体分布概率估计方法得到的是信息量更丰富的概率图,能够定量反映SAR影像中水体像元分类存在的不确定性。水体分布概率图充分描述了影像中水体像元的分布信息,可以用索引图的形式将水体概率值映射为不同颜色、进而直观表示水体像元的分布,也可以通过阈值分割退化为二值水体提取结果,还可以应用于水位估计[12-13]、水动力学模型校准[14-16]等场景。
水体分布先验概率是水体概率估计方法中的一个重要参数。在先验概率估计方面,现有的概率估计方法[11, 17]将先验概率默认置为0.5,这会使推导出的地物后向散射系数统计模型不够准确,降低概率估计结果的精度。针对先验概率估计不充分的问题,本文提出了改进的水体概率估计方法,借助k-means聚类分析分割影像的结果估计先验概率,并利用这一先验概率估计值优化了后向散射系数分布参数估计方法。本文试验以GF-3影像为数据源,结果表明改进的水体概率估计方法能够有效提升水体概率估计精度。
1 水体概率估计理论水体概率估计理论依赖于像元后向散射系数统计分布假设与贝叶斯推断。将研究区域所有像元组成的样本集合视作水体(W)和背景(W)两部分的非交并集[18],并用后向散射系数(σ0)描述其特征。记水体像元的后向散射系数分布概率密度函数为p(σ0|W),背景像元的后向散射系数分布概率密度函数为p(σ0|W),研究区域后向散射系数边际分布的概率密度函数为p(σ0),则
 (1)
(1)
式中,p(W)与p(W)分别表示水体与背景像元所占比例,p(W)+p(W)=1。即p(σ0)可视为两类像元的混合分布。
记Pprior=p(W),p(W)=1-Pprior,式(1)可写作
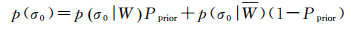 (2)
(2)
对于影像中的某个像元,希望根据其后向散射系数σ0判断其类别,即计算p(W|σ0)。根据条件概率公式,有
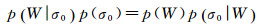 (3)
(3)
则p(W|σ0)可以写作
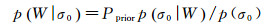 (4)
(4)
根据式(2)、式(4),为了得到p(W|σ0),需要分别估计Pprior、p(σ0|W)、p(σ0|W)。为此,下面对p(σ0|W)、p(σ0|W)作进一步的分布假设。
水体由于其镜面反射现象,在SAR影像中呈现为低后向散射系数的均匀区域,含有一定范围水体的SAR影像后向散射系数统计分布直方图h(σ0)常聚为大小两类,整体呈双峰状。这种山峰型走势恰好与Gauss分布的概率密度函数一致。事实上,已有的研究发现经过对数变换的SAR强度数据服从Gauss分布[19-20]。根据文献[11]在洪水概率估计(probabilistic flood mapping)中对水体、背景两类像元的Gauss分布假设,本文同样假设p(σ0|W)与p(σ0|W)均服从Gauss分布,即
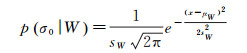 (5)
(5)
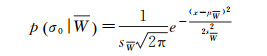 (6)
(6)
相应的,结合式(2),边际分布p(σ0)表现为含有两个簇的混合Gauss分布形式。理论上其概率密度函数恰好具有双峰曲线的形式,这与实际分析得到的直方图形态特征一致。
确定后向散射系数分布假设后,估计模型中的未知参数即可确定其统计特征,给定的σ0即可计算其属于水体的概率值p(W|σ0)。从上述水体概率估计的理论来看,本文方法的核心是参数估计,包括水体分布先验概率Pprior和后向散射系数分布参数(μW, sW, μW, sW)。本文从先验概率估计方法上着手改进。考虑到p(σ0)的混合Gauss分布形式,引入k-means聚类算法估计先验概率,并将其运用于分布参数估计方法中,优化参数估计方法。
2 方法设计 2.1 先验概率估计关于水体分布先验概率估计,在文献[11]的方法中,先验概率值默认设置为0.5,称为默认先验方法。其假设的情况是研究区域中水体、背景像元数相同的情况,然而该条件在大多数情况下远不成立。注意到含有水体的影像后向散射系数边际分布p(σ0)的混合Gauss分布模型形式,考虑采用k-means算法对各像元进行聚类分析,并用聚类的结果估计水体分布先验概率。
k-means算法以平方误差为标准,通过迭代对给定样本集寻找簇内样本相似度最高的簇划分,具体算法步骤不再赘述。根据p(σ0)的混合Gauss分布模型形式,结合统计分布直方图h(σ0)呈现出的双峰形态,研究区域所有像元的σ0组成的样本集合按取值大小聚集为两簇。并且根据水体像元后向散射系数普遍低于背景像元这一特点,可以直接判定聚类得到的低σ0簇为水体像元簇,高σ0簇为背景像元簇。得到聚类结果后,计算水体像元比例作为水体分布先验概率Pprior的估计值。此外,统计两簇样本的均值和标准差用于初始化后续参数估计中的迭代步骤。
2.2 σ0分布参数估计统计学上认为直方图是对概率密度函数的估计[21]。之前的推导已经得到了Pprior的估计值,接下来直接将理论概率密度函数p(σ0)叠加到实际分析研究区域影像数据得到的直方图h(σ0)之上进行曲线拟合,估计未知分布参数(μW, sW, μW, sW)。参数估计过程主要为:
(1) 计算研究区域影像后向散射系数统计分布直方图。统计分布直方图h(σ0)计算需要的参数为其每个条带的宽度,称为带宽。本次试验中带宽的计算公式为
 (7)
(7)
式中,n为统计样本个数;IQR为样本的四分位差。研究表明[21],由上式给出的带宽适用于Gauss分布样本数据。
(2) 叠加理论概率密度函数p(σ0)。直方图h(σ0)的取值是像元个数,概率密度函数p(σ0)取值是概率值,二者在曲线拟合之前需经过叠加[21]操作。具体方法为先对p(σ0)乘以系数A,再用Ap(σ0)对h(σ0)作曲线拟合,其中A表示直方图的面积(带宽×高度)。
(3) 非线性拟合。使用Levenberg-Marquardt算法进行非线性最小二乘拟合[11, 22],迭代计算分布参数。迭代初始化时,用聚类步骤中得到的水体、背景样本均值和标准差作为算法初值。
得到分布参数(μW, sW, μW, sW)的估计值后,代入式(4)即得到水体概率估计的结果式。给定某像元的后向散射系数σ0,由式(4)即可得到该像元属于水体的概率p(W|σ0)。
2.3 方法流程综上所述,本文方法的主要流程如图 1所示。由于引入了先验概率估计的步骤,理论上本文方法有两点优势:

|
| 图 1 本文方法流程 Fig. 1 Workflow of the algorithm |
(1) 精度更高。先用聚类估计先验概率、再用非线性拟合估计分布参数的流程会估计得到的使p(σ0)更贴合h(σ0),即更能贴合σ0分布的实际统计规律,理论上会获得更高的概率估计精度。
(2) 效率更高。在估计模型参数初始化值设置时,默认先验的方法采用人工设置经验初值,当初值选取不合适时可能会出现求解过程中迭代次数过多、甚至找不到局部最优解的情况。本文方法用聚类结果数据初始化模型参数,效率更高,同时也避免了因初值设置不当而可能出现的找不到最优解的情况。
3 试验结果 3.1 试验数据试验使用了GF-3 L2级产品,包含FSI、FSII、QPSI等3种成像模式,分别对应3、10与8 m分辨率。验证数据由研究区域的GF-1影像人工标注得来,影像的拍摄时间与试验用GF-3影像相距在15 d以内。在开始数据分析前对影像应用了窗口大小为5×5的Gamma滤波,研究表明[23-24]这一选择可以在尽可能地保持影像空间细节的情况下提高信噪比。
3.2 结果可靠性评价选取研究区域的GF-1影像,采用人工标注的方法,得到二值水体区域图作为真值,采用可靠性图(reliability diagram)[11, 25]的方式验证结果。将概率取值的[0, 1]区间均匀分割为N=10个小区间Ik,即
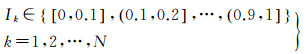 (8)
(8)
水体概率图上任意一个像元的值则属于上述10个小区间中的某一个。记取值在Ik的像元为集合Ωk,则Ik中每个像元属于水体的概率在Ik区间范围内。那么理论上Ωk中水体像元的比例在Ik区间范围内,取其中值记为Pk。同时,以二值水体区域图为真值参考,统计Ωk中水体像元的实际比例Pk,则可以用理论比例Pk与实际比例Pk的偏差对概率图的精度做定量评价,以判断本文方法所计算的水体概率值是否准确。以Pk和Pk(k=1, 2, …, N)为横纵坐标所作的图即是可靠性图。具体的,对于水体概率图和给定的二值水体区域图,有如下的可靠性度量[25-27]
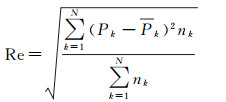 (9)
(9)
式中,nk为研究区域内取值在Ik上的像元数目。可靠性度量是以加权均方根误差的形式给出的,表示理论比例Pk与实际比例Pk的偏差程度。Re值越小,水体概率图精度越高。
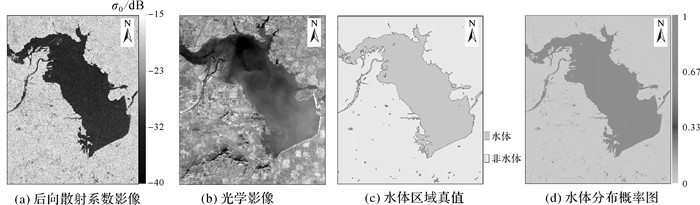
3.3 结合先验概率估计的水体概率估计方法试验结果以河北省鹿泉市黄壁庄水库周边区域和湖北省黄冈市龙感湖周边区域为例开展试验。这些区域内水体集中分布于水库库区或湖区及周边河道内,其他部分则均为典型的背景地物,成分简单且分布互不混淆,适用于初步测试本文方法的效果,试验结果如图 2、图 3和表 1。图 2(a)为河北鹿泉地区经辐射定标得到的GF-3后向散射系数影像。可以看出与非水地物相比,水体因其低σ0值而呈现为明显的暗色区域。图 2(b)为用作参考的GF-1影像,分辨率为8 m。图 2(c)为人工标注的水体区域真值图。图 2(d)为水体概率估计的结果,由颜色的深浅变化对应条件概率p(W|σ0)不同大小。结合图 2(c)和图 2(d)来看,概率估计有效提取出了水体区域。水库库区及其周边河道的水体条件概率取值很高(p(W|σ0>0.9),与周围地物区分明显。湖北黄冈地区试验结果与鹿泉地区情况相似,如图 3所示。
| 研究区域 | Pprior | μW | sW | μW | sW |
| 鹿泉 | 0.277 7 | -30.912 2 | 1.736 8 | -19.331 6 | 1.542 7 |
| 黄冈 | 0.402 3 | -28.341 6 | 1.329 3 | -17.640 0 | 1.425 0 |
|
| 图 2 鹿泉地区试验结果 Fig. 2 The experimental result in Luquan area |

|
| 图 3 黄冈地区试验结果 Fig. 3 The experimental result in Huanggang area |
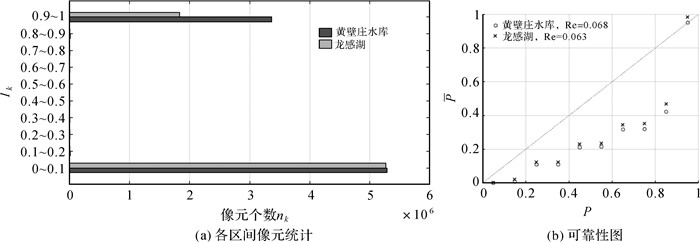
图 4(a)为两个区域试验的p(W|σ0)取值在I1到I10各个区间内像元数目的柱状图。从图上看,两个边缘区间I1和I10包含了绝大部分像元,表明影像中绝大部分区域都被可靠地区分为了水体或背景,而这一理想结果的产生得益于该地区简单的地物成分以及互不混淆的地物分布状态。图 4(b)为可靠性图,其中(Pk, Pk点均靠近于直线y=x,表明根据人工标注的验证数据,本文方法对像元属于水体的概率值的估计较为准确。
|
| 图 4 水体概率分析图 Fig. 4 Analysis of probabilistic water body map |
3.4 与默认先验方法的结果精度对比
对比试验研究区域地处湖北咸宁地区长江沿岸。该区域包含水田、沟渠、河道等零散细小水体以及大范围的滩涂、湿地等难以与水体区分的地物,可用于检验本文方法在复杂地物情况下的效果,数据及结果见图 5。同时,使用默认先验概率估计方法用作对照,对比分析的结果见图 6。

|
| 图 5 咸宁地区试验结果 Fig. 5 The experimental result in Xianning area |
|
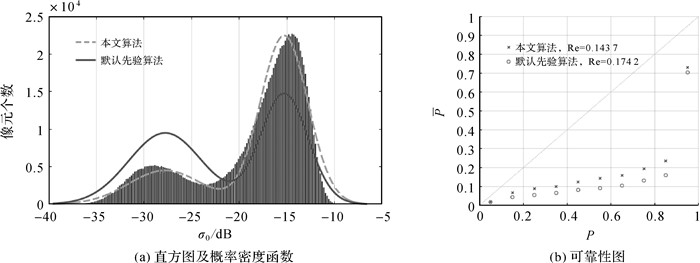
| 图 6 水体概率图分析 Fig. 6 Analysis of probabilistic water body map |
图 6(a)在σ0灰度直方图上同时叠加了本文方法估计出的σ0理论概率密度函数p1(σ0)与默认先验方法估计出的σ0理论概率密度函数p2(σ0)。从曲线形状上看,p1(σ0)与直方图高度相同、走势一致,契合度高,说明本文方法对σ0分布参数的估计基本反映出了真实规律;p2(σ0)曲线虽然也呈现出与直方图一致的双峰走势,但是对一个波峰峰值估计过高、对第二个波峰峰值估计过低,造成曲线整体与直方图的契合度偏低,未能刻画出σ0的分布规律。从参数估计结果上看,两种方法的估计值几乎是相同的,唯一的区别在于先验概率。根据式(2),当两个分布的参数(μW, μW, sW, sW)一致时,先验概率Pprior作为比例系数决定了理论σ0分布概率密度函数曲线p(σ0)的形状。因此当先验概率偏差较大时,其对概率估计结果的影响直观上就体现为直方图h(σ0)与叠加其上的p(σ0)曲线不匹配,本质上则是对研究区域地物后向散射系数σ0分布规律描述不够准确的表现。图 6(b)可靠性图从定量分析的角度描述了两种概率估计方法精度上的差异。从图上看,本文方法的Pk值在k=1, 2, …, 10处均高于默认先验方法得到的结果、对应的点(Pk, Pk)均更靠近直线y=x,这反映出不论σ0取值高低,即在各种地物状态条件下,本文方法对像元属于水体的概率值的估计均取得了更好的效果。采用可靠性度量Re的评价方式,本文方法较默认先验方法结果误差降低了17.6%。
3.5 先验概率对概率估计精度的影响前文的试验表明结合先验概率估计的水体概率估计较默认先验的估计方法在精度上的提升,并且推测这一结果差异与先验概率估计准确与否有关。对于先验概率对结果带来的影响,可以作进一步的解释。
从之前的研究区域中截取7个大小为200×200像元的子区域。这些子区域中水体面积所占区域总面积的比例各不相同,即各区域的水体分布先验概率各不相同。而在这些区域实施水体概率估计时,默认先验的方法统一将先验概率估计值置为0.5,这就造成了估计值与实际值的偏差,且各子区域偏差值各不相同。根据7个子区域的试验结果,尝试分析先验概率对结果带来的影响,试验结果见表 2及图 7。
| 研究区域 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 先验概率实际值 | 0.153 | 0.254 | 0.342 | 0.505 | 0.602 | 0.696 | 0.832 |
| 先验概率估计值(默认先验) | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 |
| 先验概率估计值(本文方法) | 0.163 | 0.323 | 0.391 | 0.557 | 0.681 | 0.711 | 0.831 |
| 默认先验Re1 | 0.201 3 | 0.102 1 | 0.105 9 | 0.075 5 | 0.070 0 | 0.071 6 | 0.096 3 |
| 本文方法Re2 | 0.142 1 | 0.089 5 | 0.089 9 | 0.075 5 | 0.076 0 | 0.064 1 | 0.065 8 |
| (Re1-Re2)/Re1 | 29.4% | 12.4% | 15.1% | 0 | -8.6% | 10.6% | 31.7% |
|
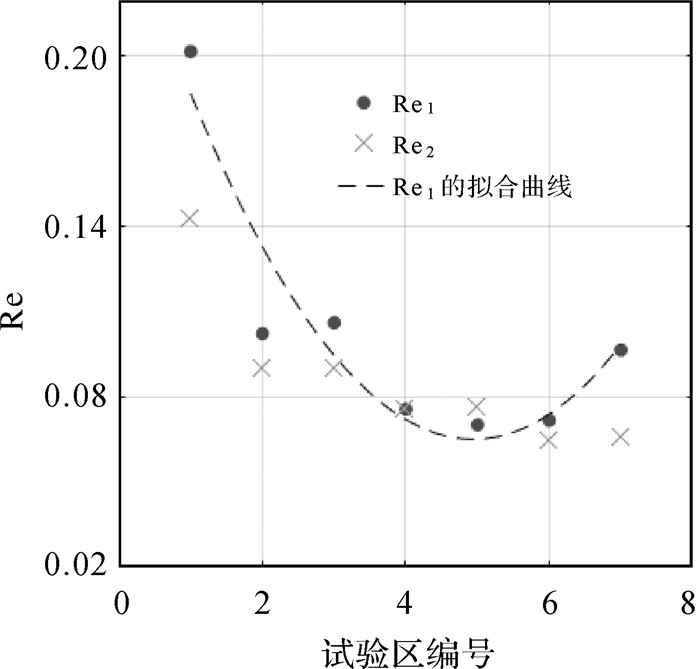
| 图 7 可靠性度量比较分析 Fig. 7 Comparison of reliability |
默认先验方法的Re值按1到7的顺序整体呈现先减小再增大的“U”形走势。这与默认先验概率值与各区域先验概率实际值偏差大小的变化规律一致。说明Re与先验概率偏差呈正相关,意味着准确的先验概率可以提升水体概率估计精度。
根据可靠性度量的减小比例,除去第5个区域的结果,在其他6个区域上本文方法精度均优于默认先验的方法,且精度提升比例按1到7的顺序也呈两端大中间小的“U”形走势。这一现象是合理的,根据表第2、4行,本文方法对先验概率的估计较为准确,相应的先验概率偏差值保持在较小的范围内,而默认先验方法的先验概率偏差值则会出现“U”形波动。这一结果也再次验证了水体概率估计精度与先验概率偏差呈正相关关系,结合先验概率估计的水体概率估计方法精度更高。
3.6 从概率图到二值图水体概率图可以通过阈值分割的方法退化为二值化水体分布图。考虑如下的划分准则:若像元属于水体的概率不小于属于背景的概率,即p(W|σ0)≥p(W|σ0)时,认为该像元为水体像元。因为p(W|σ0)+p(W|σ0)=1,上述准则即选取p(W|σ0)=0.5为决策面对水体概率图进行阈值划分。以一景江西南昌附近的鄱阳湖区域GF-3影像为例,其水体提取结果如图 8(a)。从图上看,水体提取结果与水体范围真值基本一致。其像元分类结果的混淆矩阵是

|
| 图 8 南昌地区试验结果 Fig. 8 The experimental result in Nanchang area |

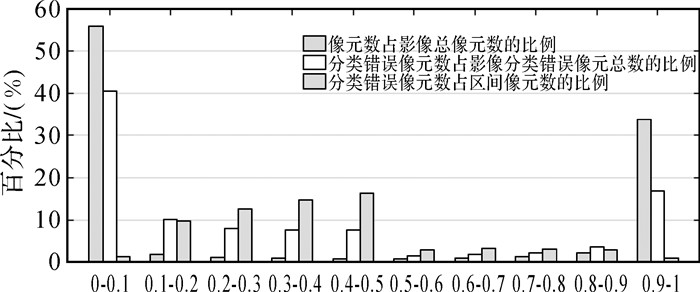
即97.51%的像元被正确分类。剩余2.49%分类错误像元在各概率区间的分布情况如表 3所示。结合图 9,分类错误像元在[0, 0.1]与[0.9, 1]区间占比较高,但这两个区间内像元所占像元总数比例也高,因此分类错误像元占区间像元总数的比例反而较低。与之相反的是,8个中间概率区间只含有影像10.3%的像元,分类错误部分却占了错误分类像元总数的57.5%,占各区间像元数目的比例也远远高于[0, 0.1]和[0.9, 1]两个区间。这说明具有中间概率值的像元更容易被错误分类。特别取出这部分像元(水体概率取值于0.1到0.9),如图 8(b),发现普遍位于水体边界地带。该类区域多为湿地、沼泽,常覆盖有浅层水面,呈现出与水体类似的低后向散射特征,易于出现虚警、漏警现象,仅依据后向散射系数无法准确分类此种地物。这是阈值划分方法不可避免的缺陷,取0.5作为水体概率的分割阈值恰好是一种折中的思路。
| 概率区间 | n/N | nerror/Nerror | nerror/N |
| 0.0~0.1 | 0.559 | 0.406 | 0.013 |
| 0.1~0.2 | 0.019 | 0.101 | 0.098 |
| 0.2~0.3 | 0.012 | 0.081 | 0.125 |
| 0.3~0.4 | 0.009 | 0.076 | 0.147 |
| 0.4~0.5 | 0.008 | 0.077 | 0.163 |
| 0.5~0.6 | 0.009 | 0.014 | 0.030 |
| 0.6~0.7 | 0.010 | 0.018 | 0.032 |
| 0.7~0.8 | 0.013 | 0.022 | 0.031 |
| 0.8~0.9 | 0.023 | 0.036 | 0.029 |
| 0.9~1.0 | 0.338 | 0.169 | 0.009 |
| 注:n为区间像元数;N为像元总数;nerror为区间分类错误像元数;Nerror为分类错误像元总数。 | |||
|
| 图 9 各概率区间像元分布 Fig. 9 The distribution of pixels in each interval |
对水体概率图做阈值划分本质上是对后向散射系数影像做阈值划分。本节所述的由水体概率图退化得到水体二值图的方法属于阈值法提取水体的范畴。选择水体概率取0.5时的后向散射系数值作为分割阈值,对应理论分布概率密度曲线上水体与背景两类像元两组密度函数曲线的交点处,也即直方图两峰值之间的“波谷”处,与一些阈值划分方法中通过寻找直方图“波谷”确定阈值的思路一致。不过与之不同的是,本节所述水体提取方法根据两类像元理论分布推导而来,在像元分布估计准确的前提下,阈值选取的效果必然是好的。与直接在直方图上寻找“波谷”的方法相比,该方法具有更强的理论基础,同时会减少直方图中噪声带来的误差。
4 结语本文针对水体概率估计中水体分布先验概率估计不充分的问题,使用k-means聚类估计先验概率并优化了后续的参数估计步骤,改进了水体概率估计方法。在水体概率估计方法中,先验概率估计的偏差会带来模型对地物后向散射系数分布规律描述的偏差,进而影响水体概率估计精度。本文方法由于对先验概率估计更充分,进而结果精度更高。此外,本文方法使用聚类结果数据初始化模型参数让参数迭代求解过程能够更快地收敛至最优值,同时也简化了人工迭代初值设置的步骤。此外,由于该方法使用的是单极化数据,因此同样适用于多时相或是多种极化方式的影像,具有很好的推广性。
需要指出的是,本文方法的推导建立在研究区域后向散射系数统计分布直方图呈双峰形这一前提条件上,根据水域与背景间后向散射系数的差异提出模型假设。但是这一条件未必总是成立,例如当影像中水体与背景像元中的一类数目远远大于另一类时,其后向散射系数分布会被一类像元主导;或是风浪导致的水体后向散射系数变高并与背景像元混淆,直方图也无法呈现双峰形走势,影响概率估计效果。对于此类问题及本文方法适用条件的定量描述,是今后研究工作的重点。在实际应用中,可以通过设置河流、湖泊等水体目标缓冲区等方式避免研究区域水体比例出现极端值的情况,保证概率估计的效果。
| [1] |
徐川, 华凤, 眭海刚, 等.
多尺度水平集SAR影像水体自动分割方法[J]. 武汉大学学报(信息科学版), 2014, 39(1): 27–31.
XU Chuan, HUA Feng, SUI Haigang, et al. Automatic water segmentation method in SAR images using multi-scale level Set[J]. Geomatics and Information Science of Wuhan University, 2014, 39(1): 27–31. |
| [2] |
张庆君.
高分三号卫星总体设计与关键技术[J]. 测绘学报, 2017, 46(3): 269–277.
ZHANG Qingjun. System design and key technologies of the GF-3 satellite[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 269–277. |
| [3] |
李景刚, 黄诗峰, 李纪人.
ENVISAT卫星先进合成孔径雷达数据水体提取研究——改进的最大类间方差阈值法[J]. 自然灾害学报, 2010, 19(3): 139–145.
LI Jinggang, HUANG Shifeng, LI Jiren. Research on extrac-tion of water body from envisat ASAR images:a modified otsu threshold method[J]. Journal of Natural Disasters, 2010, 19(3): 139–145. |
| [4] | OTSU N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62–66. DOI:10.1109/TSMC.1979.4310076 |
| [5] | LÜ Wentao, YU Qiuze, YU Wenxian. Water extraction in SAR images using GLCM and support vector machine[C]//IEEE 10th International Conference on Signal Processing Proceedings. Beijing, China: IEEE, 2010. |
| [6] | SILVEIRA M, HELENO S. Separation between water and land in SAR images using region-based level sets[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 471–475. DOI:10.1109/LGRS.2009.2017283 |
| [7] | KASS M, WITKIN A, TERZOPOULOS D. Snakes:active contour models[J]. International Journal of Computer Vision, 1988, 1(4): 321–331. |
| [8] |
孟令奎, 吕琪菲.
复杂水体边界提取的改进正交T-Snake模型[J]. 测绘学报, 2015, 44(6): 670–677.
MENG Lingkui, LÜ Qifei. Improved orthogonal T-snake model for complex water boundary extraction[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 670–677. DOI:10.11947/j.AGCS.2015.20140404 |
| [9] |
韩斌, 吴一全.
SAR图像河流分割的加权指数区域能量模型[J]. 测绘学报, 2017, 46(9): 1174–1181.
HAN Bin, WU Yiquan. Weighted exponential region energy model for river segmentation of SAR images[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1174–1181. DOI:10.11947/j.AGCS.2017.20170134 |
| [10] | GIUSTARINI L, VERNIEUWE H, VERWAEREN J, et al. Accounting for image uncertainty in SAR-based flood mapping[J]. International Journal of Applied Earth Observation and Geoinformation, 2015(34): 70–77. |
| [11] | GIUSTARINI L, HOSTACHE R, KAVETSKI D, et al. Probabilistic flood mapping using synthetic aperture radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 6958–6969. DOI:10.1109/TGRS.2016.2592951 |
| [12] | HOSTACHE R, MATGEN P, SCHUMANN G, et al. Water level estimation and reduction of hydraulic model calibration uncertainties using satellite SAR images of floods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(2): 431–441. DOI:10.1109/TGRS.2008.2008718 |
| [13] | SCHUMANN G, MATGEN P, PAPPENBERGER F. Conditioning water stages from satellite imagery on uncertain data points[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 810–813. DOI:10.1109/LGRS.2008.2005646 |
| [14] | DI BALDASSARRE G, SCHUMANN G, BATES P D. A technique for the calibration of hydraulic models using uncertain satellite observations of flood extent[J]. Journal of Hydrology, 2009, 367(3-4): 276–282. DOI:10.1016/j.jhydrol.2009.01.020 |
| [15] | MONTANARI M, HOSTACHE R, MATGEN P, et al. Calibration and sequential updating of a coupled hydrologic-hydraulic modelusing remote-sensing derived water stages[J]. Hydrology and Earth System Sciences, 2009, 13(3): 367–380. DOI:10.5194/hess-13-367-2009 |
| [16] | BEVEN K. A manifesto for the equifinality thesis[J]. Journal of Hydrology, 2006, 320(1-2): 18–36. DOI:10.1016/j.jhydrol.2005.07.007 |
| [17] | WESTERHOFF R S, WINSEMIUS H C, HUIZINGA H J, et al. Automated global water mapping based on wide-swath orbital synthetic-aperture radar[J]. Hydrology and Earth System Sciences, 2013, 17(2): 651–663. DOI:10.5194/hess-17-651-2013 |
| [18] | CHINI M, GIUSTARINI L, HOSTACHE R, et al. An automatic SAR-based flood mapping algorithm combining hierarchical tiling and change detection[C]//ESA Living Planet Symposium. Prague, Czech Republic: ESA, 2016. |
| [19] | ULABY F T, MOORE R K, FUNG A K. Microwave remote sensing, active and passive:Vol Ⅱ:radar remote sensing and surface scattering and emission theory[M]. [S.l.]: Artech House, 1982. |
| [20] | XIE Hua, PIERCE L E, ULABY F T. Statistical properties of logarithmically transformed speckle[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(3): 721–727. DOI:10.1109/TGRS.2002.1000333 |
| [21] | WILKS D S. Statistical methods in the atmospheric sciences[M]. Oxford: Academic Press, 2011: 34. |
| [22] | MARQUARDT D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431–441. |
| [23] | CHINI M, HOSTACHE R, GIUSTARINI L, et al. A hierarchical split-based approach for parametric thresholding of SAR images:flood inundation as a test case[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 6975–6988. DOI:10.1109/TGRS.2017.2737664 |
| [24] | SHI Zhenghao, FUNG K B. A comparison of digital speckle filters[C]//1994 IEEE International Geoscience and Remote Sensing Symposium. Pasadena, CA: IEEE. |
| [25] | HOSTACHE R, MATGEN P, MONTANARI A, et al. Propagation of uncertainties in coupled hydro-meteorological forecasting systems:a stochastic approach for the assessment of the total predictive uncertainty[J]. Atmospheric Research, 2011, 100(2-3): 263–274. DOI:10.1016/j.atmosres.2010.09.014 |
| [26] | HORRITT M S. A methodology for the validation of uncertain flood inundation models[J]. Journal of Hydrology, 2006, 326(1-4): 153–165. DOI:10.1016/j.jhydrol.2005.10.027 |
| [27] | BRÖCKER J, SMITH L A. Increasing the reliability of reliability diagrams[J]. Weather and Forecasting, 2007, 22(3): 651–661. DOI:10.1175/WAF993.1 |



