2. 甘肃省地理国情监测工程实验室, 甘肃 兰州 730070
2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China
利用三角高程代替水准建立高程控制网一直是测绘领域的一个难题。文献[1]将三角高程测量应用于变形监测,通过稳定点间的已知高差反求大气折光系数,再对监测点三角高程测量观测值进行球气差改正, 取得了良好的效果。文献[2]通过研究认为三角高程测量精度受大气折光的影响极大,方向不同、时段不同、植被不同会导致大气折光系数不同。文献[3-4]利用同时对向观测法精密三角高程代替精密水准,精度达到了二等水准的要求。文献[5-7]更是在长距离复杂气象条件下的跨海高程传递中,使用同时对向观测精密三角高程代替精密水准,精度也能够满足二等水准的标准。显然,同时对向观测法是目前精密三角高程代替精密水准的关键核心技术。
在高速铁路高程控制网的建设中,由于CPⅢ点非常密集,利用精密水准建立高程控制网是一项非常繁琐的工作。文献[8]结合我国的国情,提出了矩形法构网方法,在实践中得到广泛应用。文献[9]在矩形法的基础上又提出了外业效率更高的新矩形法、单程矩形法和双程矩形法。文献[10]为了提高外业施测效率,提出了Z形法,精度和效率都优于传统的矩形法。然而CPⅢ高程控制网建网最高效的方式却是充分利用平面控制网观测数据中的竖直角和斜距观测值,通过精密三角高程方式构网。由于CPⅢ点的特殊性,无法采用对向观测来削弱三角高程观测值中大气折光和地球曲率的影响。文献[11-12]基于中间差分法研究了高速铁路CPⅢ三角高程网构网与平差计算的方法,可消除大部分球气差影响。该成果作为一项自主创新技术,已被高速铁路工程测量规范采纳。文献[13-16]对这种方法进行了验证,试验表明绝大多数成果能够满足规范要求。而文献[17]在实践中发现差分法CPⅢ三角高程成果与精密水准成果的差值最高可达3 cm。
差分法一方面大大削弱了大气折光和地球曲率的影响,另一方面也产生了下列问题:
(1) 差分法平差模型的观测值是三测站6个三角高程观测值的线性组合,因此测量噪声远远大于非差观测值。
(2) 差分观测值不再是独立观测值,而是相关观测值。
(3) 当相邻两个目标与测站点不等距时,所形成的差分观测值中球气差影响残余量仍然比较大[15]。
(4) 差分法观测值超限时,参与差分的两原始三角高程观测值全部作废,造成数据的浪费,因此数据利用率不高。
本文利用非差三角高程观测值构建CPⅢ高程控制网平差模型,在观测方程中引入参数来吸收球气差影响,并通过统计检验对参数矩阵进行了优化。试验证明,这种方法数据利用率高、算法简单、解算精度更高。由于涉及斜距和竖直角两种类型的原始观测值,本文还对CPⅢ精密三角高程观测值严密定权方法进行了研究,并通过实测数据进行了验证。
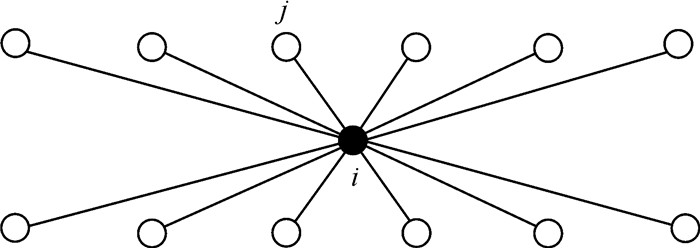
1 参数法CPⅢ精密三角高程平差模型图 1为CPⅢ平面控制网i测站观测示意图,其中实心圆圈、空心圆圈分别为测站点和CPⅢ点。对各目标进行观测,可获得方向观测值、斜距观测值和竖直角观测值,其中斜距观测值和竖直角观测值可形成三角高程观测值,用于构建CPⅢ精密三角高程控制网。因CPⅢ点采用强制对中装置安置棱镜,因此无法采用同时对向观测来消除大气折光和地球曲率对观测高差的影响。差分法则通过相邻两观测目标精密三角高程观测值之间进行差分来削弱大气折光和地球曲率对观测高差的影响,但这种方法具有一定的局限性,因此本文提出了参数法CPⅢ精密三角高程平差模型。
|
| 图 1 CPⅢ精密三角高程控制网i测站观测 Fig. 1 Schematic diagram of i station observation at CPⅢ precision trigonometric leveling network |
1.1 随机模型
设共有n个三角高程观测值,其中第i个为

式中,si为斜距;αi为竖直角。
对上式求微分得
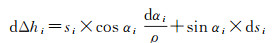
n个三角观测值可以写出n个如上的微分式,其矩阵形式为
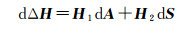
式中
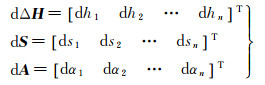


设全站仪竖直角先验中误差为mβ秒,距离先验中误差为(a+bppm×s)mm,观测r测回,则竖直角观测值中误差


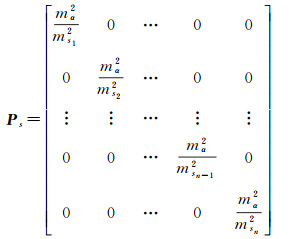
由协因数传播定律可得三角高程观测值权矩阵
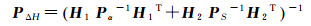
在测站点i对目标点j进行观测。设竖直角为αij,斜距为sij,且测站点i仪器中心最或然高程为yi,CPⅢ点j最或然高程为xj,测站点i所在位置在测量时刻球气差系数为kf,则可得j点与i点之间的高差观测值
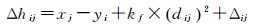 (1)
(1)
式中,Δhij=sij×sinαij;dij=sij×cosαij;Δij为观测误差。则可得误差方程
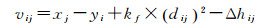 (2)
(2)
当j点为已知点,且其高程为Hj时,其误差方程为
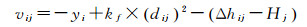 (3)
(3)
设共有n个三角高程观测值,待求CPⅢ点数为t,测站点数为u,引入球气差参数m个,且1≤m≤u,则可写出n个方程,待求参数个数为t+u+m,写出其矩阵形式如下
 (4)
(4)
式中


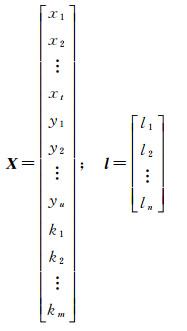

利用最小二乘法即可解算出待求参数X=(BTPΔHB)-1BTPΔHl(文献[18]),并对其进行精度评定。
1.3 球气差参数矩阵的优化在CPⅢ控制网外业数据采集时,如各测站间大气状况变化显著,则需要在每测站引入一个球气差参数;如果大气状况稳定,所有测站共用一个球气差参数即可。但更多的情况则是连续若干测站共用一个球气差参数,因此需要对球气差参数矩阵进行优化。
初始状态各测站共用一个球气差参数,然后逐测站尝试引入新的球气差参数,并通过F检验判断,如果单位权方差有显著变化,则接纳;反之则废弃。
设,在i测站引入新的球气差参数前,多余观测值为f1,残差值为V1;引入新参数后,多余观测值为f2,残差值为V2。设

令
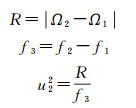
依据文献[19],R与Ω1随机独立,提出假设
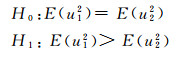
统计量为
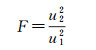
引入新参数后,重新平差计算。选定显著水平α,分子自由度为f3,分母自由度为f1,采用F检验法判断新模型单位权方差与原模型单位权方差是否有显著差异。由α查得Fα,f3,f1,如果F<Fα,f3,f1,则接受H0假设,表示单位权方差没有发生显著变化,也即当前测站和上一测站大气状况变化甚微,不需要引入新参数;反之则拒绝原假设,表明在该测站大气状况发生了显著变化,从该测站起后续所有测站都采用新的球气差参数。重复上述过程,直至所有测站检测完毕。
2 三角高程观测值严密定权文献[11]提出,精密三角高程观测值由斜距和竖直角两类原始观测值所得,因此,CPⅢ三角高程网的合理定权问题,是亟待解决的关键问题之一。本文采用最小范数二次无偏估计对精密三角高程观测值进行定权,并通过试验对定权效果进行验证和分析。
在高精度数据处理中,依据仪器标称精度定权的方法是不够精确的,因此需要采用严密定权方式。设δα2和δs2分别为竖直角和斜距的验后单位权方差,令T1=H1×H1T, T2=H2×H2T, T=T1+T2, 且

依据最小范数二次无偏估计[20]可得
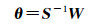
式中,θ=[δα2 δs2]T。
由此可得未知数协方差矩阵分别为M1和M2。

竖直角和斜距的权分别为

重新计算高差观测值权阵

再次利用P′ΔH'获取待求参数最优估计值并进行精度评定。
3 实例验证为了验证参数法CPⅢ精密三角高程控制网数据处理方法的可行性,开发相应数据处理程序,利用工程现场平面控制网观测数据中的斜距、竖直角观测值构建精密三角高程控制网。以线路水准基点(满足二等水准要求)为约束点[21]进行平差,将其解算结果与CPⅢ精密水准测量解算结果进行对比。依据文献[22],要求CPⅢ高程中误差小于1 mm,相邻两点间高差中误差小于0.5 mm;按照复测要求与水准测量结果比较,高程差值不超过3 mm,相邻点间高差的差值不超过2 mm。由于篇幅限制,本文只给出一段线路的中误差曲线,其余线路解算结果以表格形式给出。
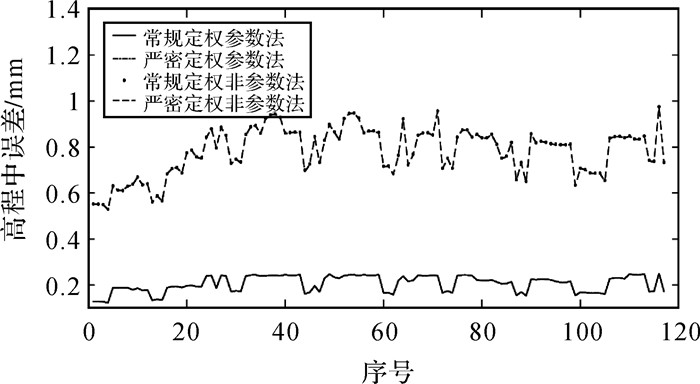
某段线路长4 km,利用CPⅢ平面控制测量观测数据中的斜距和竖直角构建精密三角高程控制网,平均每千米约束一个高程点,利用参数法进行解算,解算结果与精密水准测量结果进行比较。图 2、图 3分别为引入参数前后精密三角高程解算所得各点高程中误差曲线图与相邻点高差中误差曲线图。由图可知,引入参数前最大高程中误差为0.97 mm,最大相邻点高差中误差为1.15 mm,引入参数后降为0.25 mm与0.32 mm。由此可知,球气差参数的引入对最终解算结果精度的提升是非常明显的。引入球气差参数后,CPⅢ相邻两点高差中误差不超过0.5 mm,因此CPⅢ三角高程控制网测量结果满足规范要求。另外由图 2、图 3可知,采用严密定权前后解算精度未有明显变化。
|
| 图 2 参数法、非参数法高程中误差曲线 Fig. 2 Parametric and non-parametric elevation error curves |

|
| 图 3 参数法、非参数法相邻点高差中误差曲线 Fig. 3 The curve diagram of the middle error of the height difference of the adjacent points for the parameter method and no parameter method |
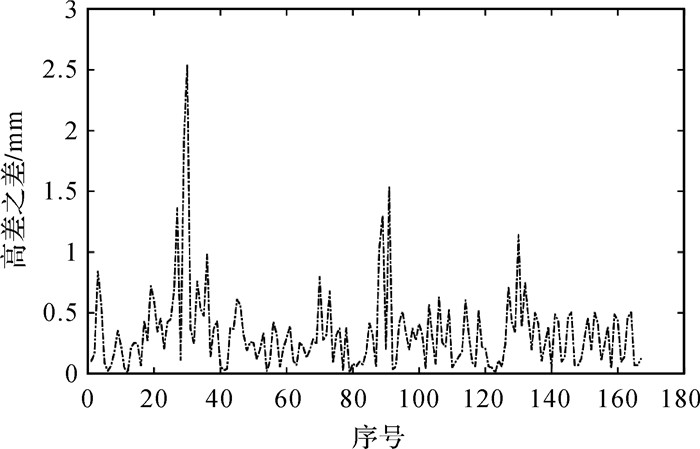
图 4、图 5分别为参数法所得各点高程值、相邻点的高差值与精密水准测量所得结果差值对比曲线。按照规范要求,两种方法所得高差互差不能超过2 mm,高程之差不能超过3 mm。由图可知,参数法所得高程值全部符合规范要求,高差观测值超限数为1。

|
| 图 4 参数法与精密水准测量所得高程估计值之差对比 Fig. 4 Schematic diagram of the comparison between the height estimate of the parameter method and the precision leveling survey |
|
| 图 5 参数法与精密水准测量所得高差估计值对比 Fig. 5 Schematic diagram of the comparison of height difference estimation between parameter method and precise leveling survey |
表 1为不同线路中参数法精密三角高程、差分法精密三角高程分别与精密水准测量结果差异的对比。由表 1可知,参数法高程估计值全部符合规范要求,高差观测值每条线路各有0~2个超限值;差分法有一条线路高程估计值出现了超限值,高差观测值每条线路各有1~5个超限值。
| 序 号 |
线路长度 /km |
约束 点数 /mm |
参数法 | 差分法 | |||||||||
| 高程差 异均值 /mm |
高程差 异最大 值/mm |
相邻点高 差差异均 值/mm |
相邻点高 差差异最 大值/mm |
超 限 数 |
高程差 异均值 /mm |
高程差 异最大 值/mm |
相邻点高 差差异均 值/mm |
相邻点高 差差异最 大值/mm |
超 限 数 |
||||
| 1 | 4 | 9 | 0.35 | 2.35 | 0.34 | 2.54 | 1 | 0.69 | 2.47 | 0.47 | 2.91 | 2 | |
| 2 | 5 | 11 | 0.27 | 1.65 | 0.27 | 1.88 | 0 | 0.34 | 2.60 | 0.31 | 2.09 | 1 | |
| 3 | 7 | 15 | 0.53 | 1.88 | 0.55 | 1.59 | 0 | 0.61 | 2.58 | 0.58 | 2.29 | 2 | |
| 4 | 10 | 21 | 0.75 | 2.21 | 0.68 | 1.99 | 0 | 1.43 | 3.63 | 0.81 | 2.42 | 2 | |
| 5 | 6 | 13 | 0.46 | 1.60 | 0.49 | 2.13 | 1 | 0.64 | 2.91 | 0.57 | 2.33 | 3 | |
| 6 | 6 | 13 | 0.55 | 1.77 | 0.49 | 2.13 | 1 | 0.67 | 1.89 | 0.59 | 2.02 | 2 | |
| 7 | 6 | 13 | 0.53 | 1.88 | 0.51 | 2.23 | 2 | 0.66 | 2.84 | 0.53 | 2.12 | 2 | |
| 8 | 6 | 13 | 0.44 | 1.85 | 0.53 | 1.86 | 0 | 0.52 | 2.08 | 0.57 | 3.05 | 5 | |
| 9 | 4 | 8 | 0.36 | 1.96 | 0.33 | 2.42 | 1 | 0.70 | 2.36 | 0.51 | 2.95 | 1 | |
| 10 | 5 | 10 | 0.58 | 2.22 | 0.56 | 1.86 | 0 | 0.59 | 2.31 | 0.57 | 2.24 | 1 | |
通过试验可得如下结论:
(1) 由试验可知,采用参数法消除精密三角高程测量中球气差的影响,可获得良好的效果,其解算精度明显优于差分法解算精度,而且随着约束点密度的降低,这种差异会更加明显。
(2) 严密定权前后,CPⅢ精密三角高程网解算结果未有显著变化。在进行CPⅢ控制测量时,线下工程已经完成,场地较为平坦,且目标点高于地面1 m左右且大致等高[23]。目标点距离仪器越近,竖直角绝对值越大。设水平距离最短为30 m,仪器横轴与目标点间高差最大为1.5 m,则竖直角绝对值最大不超过3°(现场实测数据中竖直角绝大多数小于1°)。假设测距误差为1 mm(实际更小),则其对三角高程测量值的影响仅仅为0.05 mm,这个影响甚至小于棱镜在高程方向的安装误差的限差(0.2 mm),因此可以忽略不计。由此可知,在CPⅢ精密三角高程测量中,测距误差可以忽略不计,不必进行严密定权,仅采用常规定权即可,试验数据也证明了这一点。
(3) 由图 2、图 3可以看出,通过精密三角高程测量数据解算所得CPⅢ点高程中误差以及相邻CPⅢ点间高差中误差均符合规范要求,但在图 5中,水准测量方法所得高差估计值和参数法精密三角高程所得同名高差估计值的差值出现超限的情况。
考虑到精密三角高程数据和精密水准数据在不同时期进行采集,且使用了不同的连接杆,初步判断由点位发生沉降或者连接杆未旋到位引起的,文献[24]表明了这种可能性的存在。表 1中也出现了类似的情况,这种情况还需要通过对现场超限点的核对来确认。
4 结束语本文研究了参数法CPⅢ精密三角高程数据处理模型,通过引入球气差参数来削弱大气折光和地球曲率的影响,避免了差分法带来的观测值之间的相关性等问题。试验证明,该模型解算精度优于差分法模型。
由于涉及两种类型的原始观测值,因此尝试采用最小范数二次无偏估计对CPⅢ精密三角高程观测值进行定权。但试验表明,控制网解算结果在严密定权前后未有显著变化。进一步分析可知,CPⅢ点竖直角绝对值不超过3°,测距误差对于精密三角高程观测值的影响可以忽略不计,因此严密定权效果不甚明显。
通过试验发现,适当增加约束点的个数,能有效提高CPⅢ精密三角高程控制网的精度,从而使CPⅢ点高程中误差以及相邻点高差中误差完全满足规范的要求。文献[22]要求每2 km布设一个线路水准基点,但通过试验对比发现,每千米约束1~2个点效果最佳。由于试验所用数据大部分来自已经完工的项目,因此采用了若干CPⅢ精密水准测量成果点作为约束点,在实际应用中需要按照二等水准的要求对线路水准基点进行加密。除此之外,在下一步研究中还需要解决以下问题:①CPⅢ精密三角高程控制网与精密水准测量成果对比通常会出现若干同名相邻点间高差差值超限情况,具体原因还需要结合现场情况进一步判断;②在CPⅢ精密三角高程测量中,系统误差除了球气差影响还有垂线偏差的影响[25],单向观测模式无法削弱垂线偏差的影响,垂线偏差影响到底有多大以及如何削弱,这是未来需要进一步研究的问题。
| [1] |
丘志宇, 卢松耀, 卢凌燕.
自动化变形监测的精密测距三角高程测量研究[J]. 测绘地理信息, 2017, 42(3): 106–109.
QIU Zhiyu, LU Songyao, LU Lingyan. Precise ranging trigonometric leveling based on automatic deformation monitoring[J]. Journal of Geomatics, 2017, 42(3): 106–109. |
| [2] |
白少云, 杨琦.
基于MS05AX测量机器人的精密三角高程误差来源与精度分析[J]. 测绘通报, 2015(2): 58–63.
BAI Shaoyun, YANG Qi. Analysis of errors and precision for precise triangulated height based on MS05AX measuring robots[J]. Bulletin of Surveying and Mapping, 2015(2): 58–63. DOI:10.13474/j.cnki.11-2246.2015.0042 |
| [3] |
邹进贵, 朱勇超, 徐亚明.
基于智能全站仪的机载精密三角高程测量系统设计与实现[J]. 测绘通报, 2014(3): 1–5.
ZOU Jingui, ZHU Yongchao, XU Yaming. Design and implement of onboard precise trigonometric leveling system based on intelligent total station[J]. Bulletin of Surveying and Mapping, 2014(3): 1–5. DOI:10.13474/j.cnki.11-2246.2014.0075 |
| [4] |
孔宁, 林鸿, 欧海平, 等.
基于自动照准全站仪的精密三角高程测量代替二等水准测量的研究与应用[J]. 测绘通报, 2016(2): 107–109.
KONG Ning, LIN Hong, OU Haiping, et al. Research and application of precise trigonometric leveling to replace second-order leveling based on intelligent total station[J]. Bulletin of Surveying and Mapping, 2016(2): 107–109. DOI:10.13474/j.cnki.11-2246.2016.0062 |
| [5] |
徐亚明, 施斌, 王代雄, 等.
改进的三角高程法在跨海高程传递中的应用[J]. 测绘通报, 2014(4): 65–67, 78.
XU Yaming, SHI Bin, WANG Daixiong, et al. An improved trigonometric leveling method for cross-sea elevation transfer[J]. Bulletin of Surveying and Mapping, 2014(4): 65–67, 78. DOI:10.13474/j.cnki.11-2246.2014.0126 |
| [6] |
吴迪军, 李剑坤, 何广源.
三角高程法超长距离跨海高程传递实验研究[J]. 测绘科学, 2017, 42(12): 195–200.
WU Dijun, LI Jiankun, HE Guangyuan. Study of extra-long distance sea-crossing elevation transference based on trigonometric levelling[J]. Science of Surveying and Mapping, 2017, 42(12): 195–200. |
| [7] |
郭子珍, 常建增, 余成磊.
不稳定条件下远距离高精度跨海水准测量方法探索及实施[J]. 测绘通报, 2016(4): 138–139.
GUO Zizhen, CHANG Jianzeng, YU Chenglei. Exploration and implementation of long distance and high accuracy cross sea quasi measurement under unstable conditions[J]. Bulletin of Surveying and Mapping, 2016(4): 138–139. |
| [8] |
李书亮, 刘成龙, 倪先桃, 等.
高速铁路CPⅢ高程控制网测量方法研究[J]. 测绘科学, 2011, 36(1): 45–47, 16.
LI Shuliang, LIU Chenglong, NI Xiantao, et al. Surveying method of CPⅢ vertical control network in high-speed railway[J]. Science of Surveying and Mapping, 2011, 36(1): 45–47, 16. |
| [9] |
刘定威, 范东明, 何思源, 等.
轨道高程控制网的优化设计[J]. 测绘科学, 2016, 41(9): 152–158.
LIU Dingwei, FAN Dongming, HE Siyuan, et al. Optimization design of CPⅢ elevation control network[J]. Science of Surveying and Mapping, 2016, 41(9): 152–158. |
| [10] |
李建平, 吕豆豆, 宗婷婷, 等.
轨道高程控制网优化设计及应用[J]. 测绘科学, 2014, 39(9): 117–120.
LI Jianping, LÜ Doudou, ZONG Tingting, et al. Design and application of CPⅢ elevation control net optimization[J]. Science of Surveying and Mapping, 2014, 39(9): 117–120. |
| [11] |
付建斌, 刘成龙, 卢建康, 等.
基于自由测站的高速铁路CPⅢ高程控制网建网方法研究[J]. 铁道工程学报, 2010(11): 32–37.
FU Jianbin, LIU Chenglong, LU Jiankang, et al. Study on the CPⅢ vertical control network establishing method of high-speed railway based on free-station[J]. Journal of Railway Engineering Society, 2010(11): 32–37. DOI:10.3969/j.issn.1006-2106.2010.11.008 |
| [12] |
刘成龙, 杨雪峰, 卢建康, 等.
高速铁路CPⅢ三角高程网构网与平差计算方法[J]. 西南交通大学学报, 2011, 46(3): 433–439.
LIU Chenglong, YANG Xuefeng, LU Jiankang, et al. Construction and adjustment method for CPⅢ trigonometric leveling network of high-speed railway[J]. Journal of Southwest Jiao Tong University, 2011, 46(3): 433–439. |
| [13] |
高山, 吴会军, 刘丹妮, 等.
基于精密三角高程的高寒地区高铁路基冻胀监测[J]. 铁道科学与工程学报, 2016, 13(12): 2360–2367.
GAO Shan, WU Huijun, LIU Danni, et al. The frost heaving monitoring of high-speed railway subgrade in cold regions based on precise trigonometric leveling[J]. Journal of Railway Science and Engineering, 2016, 13(12): 2360–2367. DOI:10.3969/j.issn.1672-7029.2016.12.007 |
| [14] |
方杨.
CPⅢ控制网自由测站三角高程测量数据处理与精度分析[J]. 铁道勘察, 2015(4): 21–23.
FANG Yang. Data process and accuracy analysis of CPⅢ trigonometric leveling[J]. Railway Investigation and Surveying, 2015(4): 21–23. DOI:10.3969/j.issn.1672-7479.2015.04.007 |
| [15] |
王子轩, 张明, 姚连璧.
地铁CPⅢ三角高程构网方法研究[J]. 工程勘察, 2016, 44(10): 52–56.
WANG Zixuan, ZHANG Ming, YAO Lianbi. Study on CPⅢ trigonometric leveling net in metro construction[J]. Geotechnical Investigation & Surveying, 2016, 44(10): 52–56. |
| [16] |
杨云洋.
一种新的CPⅢ三角高程测量数据处理方法研究[J]. 铁道勘察, 2016, 42(3): 1–3.
YANG Yunyang. The study of a new method for CPⅢ trigonometric elevation data processing[J]. Railway Investigation and Surveying, 2016, 42(3): 1–3. DOI:10.3969/j.issn.1672-7479.2016.03.001 |
| [17] |
王兵海.
高速铁路自由测站三角高程测量代替CPⅢ精密水准测量的适用性分析[J]. 铁道勘察, 2018, 44(4): 10–12.
WANG Binghai. Subtitution of applicability analysis of trigonometric heighting by free stationing CPⅢ precise leveling in high-speed railway[J]. Railway Investigation and Surveying, 2018, 44(4): 10–12. |
| [18] |
武汉大学测绘学院测量平差学科组.
误差理论与测量平差基础[M]. 3版. 武汉: 武汉大学出版社, 2014: 112-113.
SubjectGroup of Surveying Adjustment, School of Surveying and Mapping, Wuhan University. Error theory and foundation of surveying adjustment[M]. 3rd ed. Wuhan: Wuhan University Press, 2014: 112-113. |
| [19] |
陶本藻, 邱卫宁.
广义测量平差误差理论与测量平差[M]. 武汉: 武汉大学出版社, 2012: 158-160.
TAO Benzao, QIU Weining. Generalized surveying error theory and adjustment[M]. Wuhan: Wuhan University Press, 2012: 158-160. |
| [20] |
崔希璋, 於宗俦, 陶本藻, 等.
广义测量平差[M]. 2版. 武汉: 武汉大学出版社, 2009: 103-114.
CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized surveying adjustment[M]. 2nd ed. . Wuhan: Wuhan University Press, 2009: 103-114. |
| [21] |
李广云, 范百兴.
精密工程测量技术及其发展[J]. 测绘学报, 2017, 46(10): 1742–1751.
LI Guangyun, FAN Baixing. The development of precise engineering surveying technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1742–1751. DOI:10.11947/j.AGCS.2017.20170313 |
| [22] |
中华人民共和国铁道部.高速铁路工程测量规范: TB 10601-2009[S].北京: 中国铁道出版社, 2009. Ministry of Railways of the People's Republic of China. Specifications for engineering of high speed railway: TB 10601-2009[S]. Beijing: China Railway Publishing House, 2009. |
| [23] |
张正禄.
工程测量学[M]. 2版. 武汉: 武汉大学出版社, 2013: 242-243.
ZHANG Zhenglu. Engineering surveying[M]. 2nd ed. Wuhan: Wuhan University Press, 2013: 242-243. |
| [24] |
刘士旬.
徕卡全站仪和电子水准仪在高速铁路CPⅢ控制网复测中的应用[J]. 测绘通报, 2015(2): 133–135.
LIU Shixun. Application of Leica total station and electronic level in CPⅢ control network retest of high-speed railway[J]. Bulletin of Surveying and Mapping, 2015(2): 133–135. DOI:10.13474/j.cnki.11-2246.2015.0061 |
| [25] |
刘冠兰, 杨川, 崔国立.
高原地区精密三角高程测量实践[J]. 测绘地理信息, 2016, 41(5): 12–16.
LIU Guanlan, YANG Chuan, CUI Guoli. Practice of precise trigonometric leveling in plateau area[J]. Journal of Geomatics, 2016, 41(5): 12–16. |



