2. 中铁第一勘察设计院集团有限公司, 陕西 西安 710043;
3. 甘肃铁道综合工程勘察院有限公司, 甘肃 兰州 730000
2. China Railway First Survey and Design Institute Group Co. Ltd., Xi'an 710043, China;
3. The General Engineering Survey Institute of Railways of Gansu Co. Ltd., Lanzhou 730000, China
在大地测量和制图学中,除了大地纬度之外,还有6种常用的辅助纬度,它们都有着广泛的应用[1-3]。如等量纬度常用于墨卡托投影,地心纬度和归化纬度常用于椭球的几何学,等角纬度、等距离纬度和等面积纬度常用于双重投影[4-6]。在进行投影转换等分析计算时,经常用到它们与大地纬度间的解析展开式,众多国内外学者对此展开了研究[7]。地心纬度、归化纬度和大地纬度间正反解函数关系式较简洁,文献[8]利用拉格朗日共轭级数法严格得到了相应的无穷级数展开。而其余4种辅助纬度与大地纬度间关系式较复杂,除等量纬度、等角纬度与大地纬度间正解具有明显的函数关系式外,一般表现为第一偏心率的幂级数形式,或者大地纬度的三角级数形式。由于直接推导的计算量较大,文献[9—10]也只分别得到了展开至e′6、e8阶等量纬度关于大地纬度的反解展开式。文献[11]首次系统研究了辅助纬度与大地纬度间的展开式,并给出了至e8阶的正反展开式。由于计算机代数系统可以进行符号运算,一些较复杂的人工推导可以交由计算机完成。因此,借助Mathematica、Maxima等计算机代数软件,文献[12—13]及其他文献(http://geographiclib.sourceforge.net/html/auxlat.html; https://www.academia.edu/7580468/Funciones_de_Latitud)得到了更高阶的等角纬度、等距离纬度和等面积纬度关于大地纬度正反解展开式。然而,除了地心纬度和归化纬度,其他几种辅助纬度与大地纬度间的无穷展开仍然没有给出,上述文献致力于直接推导求解有限阶的辅助纬度展开式,也没有给出展开式系数的一般公式。虽然这类无穷展开表现为幂级数和三角函数组合的形式,但利用傅里叶级数方法仍然很难得到具体的无穷展开式。另外,由于等面积纬度与大地纬度间的关系式存在多层函数嵌套,也很难得到等面积纬度与大地纬度间的无穷展开式。由此,本文拟通过泰勒展开定理和拉格朗日反演定理,推导等量纬度、等角纬度和等距离纬度与大地纬度间的无穷展开式,并取CGCS2000参考椭球,对辅助纬度正反解展开式进行算例分析。
1 等量纬度展开式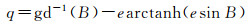 (1)
(1)
式中,e是椭球第一偏心率,为一个小参数,gd-1(x)=arctanh(sinx),为古德曼函数的反函数[15-16]。当大地纬度趋近于极点时,等量纬度趋向于无穷大。在进行数值计算时,为了避免舍入误差,gd-1(x)通常修正为gd-1(x)=arcsinh(tanx)。
根据反双曲函数的级数展开,等量纬度可展开成无穷级数
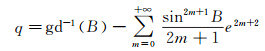 (2)
(2)
等量纬度与大地纬度的反解可通过等角纬度与大地纬度的反解展开式和等量纬度与等角纬度的闭合关系式而得到,但是等量纬度与大地纬度的反解也有直接关系式。为求得等量纬度与大地纬度的反解展开,应用拉格朗日反演定理[17],有
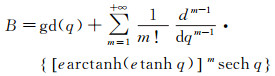 (3)
(3)
式中,gd(x)=arcsin(tanhx),为古德曼函数[15-16]。同样,为了避免舍入误差,取计算式gd(x)=arctan(sinhx)。
现在来求得一个有用的级数恒等式,利用组合函数和幂级数的性质[16],可得
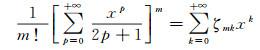 (4)
(4)
式中,系数ζmk用递推形式表示为
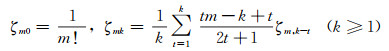 (5)
(5)
部分系数为
 (6)
(6)
令
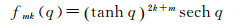 (7)
(7)
将式(7)和式(4)代入式(3)得
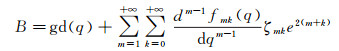 (8)
(8)
通过逐次微分运算,可以建立递推式
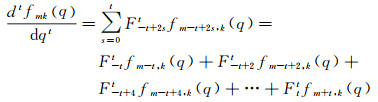 (9)
(9)
进一步可得系数递推式
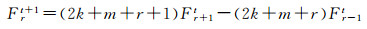 (10)
(10)
式中,初始值F00=1,0≤t≤m-1,r=-(t+1)+2r′,其中0≤r′≤t+1,-(t+1)≤r≤t+1。当|r|>t时,Frt=0,特别地
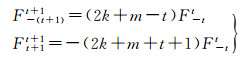 (11)
(11)
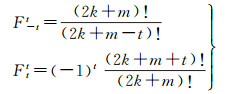 (12)
(12)
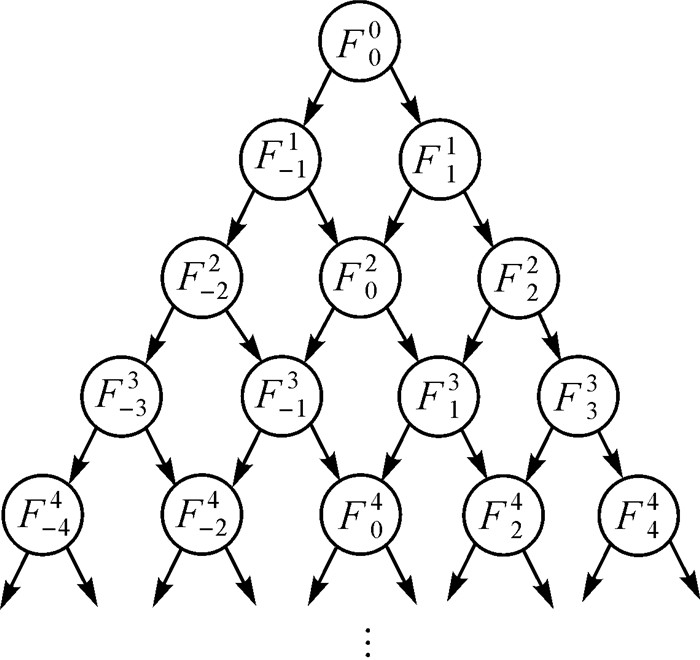
式(10)中的系数递推关系可用图解表示,如图 1所示。
|
| 图 1 Frt递推关系 Fig. 1 Recursion relations for Frt |
部分系数Frt为
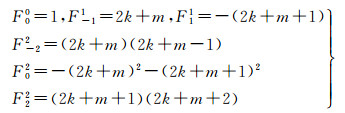 (13)
(13)
因此,有
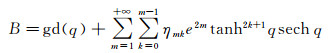 (14)
(14)
或者
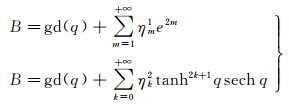 (15)
(15)
式中,系数
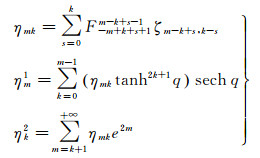 (16)
(16)
相对于式(10)、式(13)中系数Frt的m、k,式(16)中对应的为m-k+s、k-s。式(14)和式(15)即为等量纬度与大地纬度的反解展开式,给出了一般项系数的计算式,是一种一般式。实际应用中,为了避免舍入误差,一般展开到e12或者n6(n为第三扁率[14]),系数ηmk可用矩阵表示为(0≤k≤m-1)
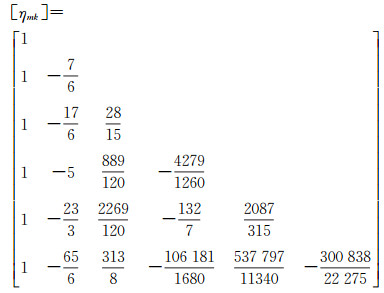 (17)
(17)
特别地,有ηm0=F-m+1m-1ζm0=1,因此
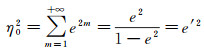 (18)
(18)
式中,e′为椭球第二偏心率。
n与e的关系式为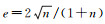
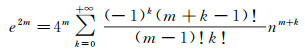 (19)
(19)
文献[9-10]分别给出了到e′6、e8阶等量纬度与大地纬度反解展开式的精度,文献[10]还讨论了反解展开式的精度。文献[18-20]也分别用数值方法、解析方法对大地纬度反解等量纬度作了一定的研究。利用第二偏心率与第一偏心率的关系式和恒等式sech2q=1-tanh2q,可验证文献[9—10]的结果分别与本文展开至e6、e8的结果一致。
2 等角纬度展开式 2.1 古德曼函数的泰勒展开根据泰勒展开定理,古德曼函数在有一增量Δ时,可表达为
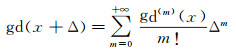 (20)
(20)
式中,gd(m)(x)为古德曼函数对自变量的m阶导数。
利用导数递推公式和数学归纳法,容易得到
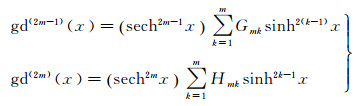 (21)
(21)
式中,系数G11=-H11=1,当k=0或k>m时Gmk=Hmk=0,其他情况可由下列递推公式计算
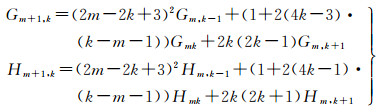 (22)
(22)
或者
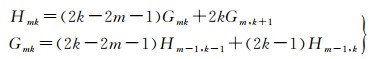 (23)
(23)
特别地,有
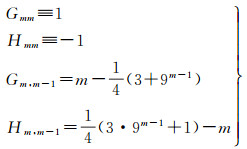 (24)
(24)
以及一些低阶系数
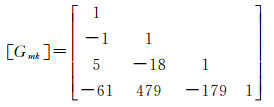 (25)
(25)
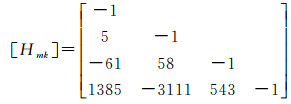 (26)
(26)
反正弦函数也有类似的泰勒展开,可用于求解等面积纬度的展开式。但由于等面积纬度与大地纬度的关系式存在多层函数嵌套,很难求得一个简洁的无穷展开式,需借助Mathematica或者Maxima软件来求解一定阶的级数展开式。
2.2 等角纬度的正解展开式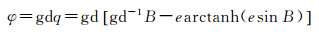 (27)
(27)
将式(2)、式(4)代入式(27),得
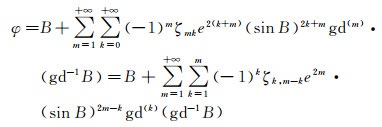 (28)
(28)
不难得到
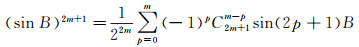 (29)
(29)
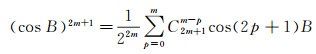 (30)
(30)
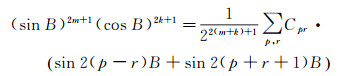 (31)
(31)
式中,Cpr=(-1)pC2m+1m-pC2k+1k-r,0≤p≤m,0≤r≤k。
取当且仅当m为奇数且l=(m+1)/2时δml=0,其余情况为δml=1,以及
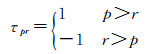 (32)
(32)
利用恒等式sinh(gd-1B)=tanB和cosh(gd-1B)=secB,连同式(20)、式(28)—式(31),可得
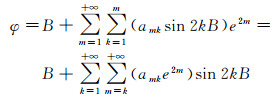 (33)
(33)
式中,系数
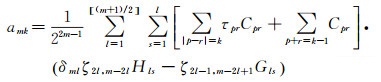 (34)
(34)
式中,相对于式(31)系数Cpr中的整数m、k,此处应用m+s-l-1、l-s替代;展开到e8阶的系数参考文献[11],展开到e10阶的系数和精度分析参考文献[13],本文计算结果均与其一致,并补充e12阶的系数
 (35)
(35)
将式(27)代入式(14),并利用恒等式tanhq=sinφ和sechq=cosφ,有
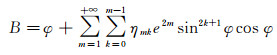 (36)
(36)
因此
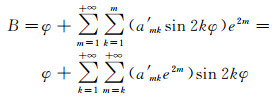 (37)
(37)
式中
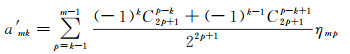 (38)
(38)
或者
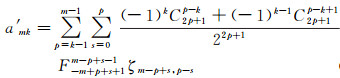 (39)
(39)
展开到e10阶的系数和精度分析仍然可以参考文献[13],本文计算结果与其一致,并补充e12阶的系数
 (40)
(40)
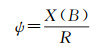 (41)
(41)
式中,X为子午线弧长,R为等距离半径,分别为(取椭球常半轴为单位长度)
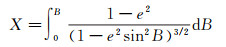 (42)
(42)
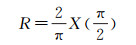 (43)
(43)
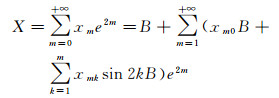 (44)
(44)
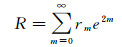 (45)
(45)
式中,系数x0=B, r0=1,
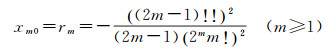 (46)
(46)
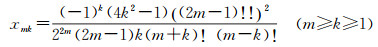 (47)
(47)
从式(44)、式(46)可以看出,子午线弧长X展开式关于大地纬度线性项的系数就是等距离半径R。因此,根据级数除法公式[16],有
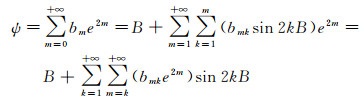 (48)
(48)
式中,系数
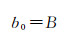 (49)
(49)
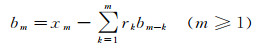 (50)
(50)
或者
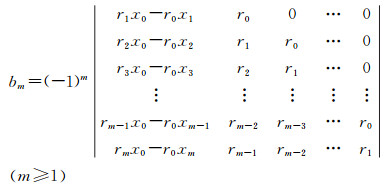 (51)
(51)
由于rk=xk0(k≥1),式(51)中行列式第一列rkx0-r0xk关于B的线性项rkx0-r0xk0B为0,对bm的计算没有影响,这也是显然的。因此,在计算bmk时,可以去除所有关于B线性项和正弦项sin2lB(l≠k),再通过行列式的逐次运算,可进一步得到
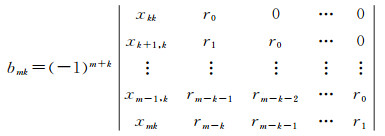 (52)
(52)
特别地
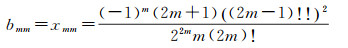 (53)
(53)
展开到e10阶的系数和精度分析参考文献[13],本文计算结果与其一致,并补充e12阶的系数
 (54)
(54)
对于等距离纬度关于大地纬度的反解展开式,可以根据正解公式,运用拉格朗日反演方法,或者直接建立常微分方程
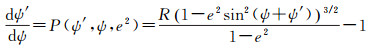 (55)
(55)
再根据小参数展开的庞加莱方法[23]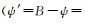
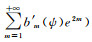
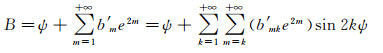 (56)
(56)
等距离纬度反解展开式的计算量很大,也很难得到比较简洁的递推公式,必须借助Mathematica或者Maxima软件计算得到一定阶的展开式。展开到e10阶的系数和精度分析可参考文献[13],本文补充e12阶的系数
 (57)
(57)
为了进一步验证本文辅助纬度与大地纬度间无穷展开式的正确性,可将本文方法(递推法)得到的高阶展开式与计算机代数系统直接推导(直接法)得到的结果进行比较。其中,在利用计算机代数系统直接推导正解展开式时是对原函数进行泰勒展开,而在反解时直接应用拉格朗日反演定理。显然,本文求解展开式系数的递推方法也可以利用计算机代数系统编程实现。为了节省程序运行时间,应用拉格朗日反演定理时应先把三角级数乘积化简成倍角形式再进行求导,而在递推求解等距离纬度正解展开式时,应用如下递推公式替代式(46)、式(47)
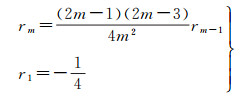 (58)
(58)
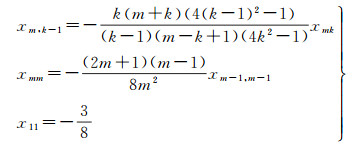 (59)
(59)
采用Mathematica(10.4版本)编写程序,结果表明,两种方法都可以较快速得到相应阶数的展开式,二者e0~e40阶展开结果均完全一样,这说明了本文方法的正确性。两种方法的程序运行时间见表 1,其中时间单位为s,取到小数点后3位。在编程求解等量纬度反解时,求解系数Frt是根据式(10)进行符号化递推的(m、k是字母变量),然后再代入式(16)计算得到反解系数。如果将求解系数Frt嵌入式(16)编程计算内部,那么m、k(实际为m-k+s、k-s)就是确定的整数,可以避免很多字母变量的符号化计算。根据式(38),等角纬度递推反解可以用等量纬度反解展开式系数求出,而直接推导等距离纬度正解时计算子午线弧长和等距离半径可以利用式(58)和式(59)。上述3种改进方法都可以大大缩短程序运行时间,改进后的程序运行时间见表 2。计算机配置为Intel Core i5-7300HQ CPU、16 GB内存,其中CPU主频2.5 GHz(睿频3.5 GHz),操作系统为Windows 10 64位。
| s | |||||
| 阶次 | 方法 | q反解 | φ正解 | φ反解 | ψ正解 |
| e10 | 直接法 | 0.407 | 0.234 | 0.125 | 2.469 |
| 递推法 | 0.000 | 0.016 | 0.016 | 0.000 | |
| e20 | 直接法 | 2.938 | 4.562 | 0.671 | 28.531 |
| 递推法 | 0.032 | 0.187 | 0.172 | 0.016 | |
| e30 | 直接法 | 6.610 | 90.797 | 2.344 | 81.921 |
| 递推法 | 0.594 | 1.484 | 5.095 | 0.235 | |
| e40 | 直接法 | 14.031 | 2 713.563 | 5.594 | 140.687 |
| 递推法 | 17.765 | 6.125 | 193.453 | 7.859 | |
| s | ||||
| 阶次 | e10 | e20 | e30 | e40 |
| q反解(递推法改进) | 0.000 | 0.063 | 0.312 | 1.157 |
| φ反解(递推法改进) | 0.000 | 0.016 | 0.031 | 0.062 |
| ψ正解(直接法改进) | 0.015 | 0.015 | 0.047 | 0.078 |
由表 1、表 2可以看出,求解等量纬度反解时,本文方法一般比直接法计算用时短,但超过e40阶时直接法可能更快一些,这是因为等量纬度解析式(1)并不复杂,但在改进程序后,本文方法计算速度远远优于直接法;求解等角纬度正解时,直接法计算用时远远大于本文方法,说明等角纬度进行直接泰勒展开并不是一种高效的运算,耗费了大量时间;求解等角纬度反解时,取e0~e20阶本文方法计算用时短,取更高阶时直接法用时短,这是因为直接法直接利用了正解展开式系数,经过改进后,本文方法计算用时大大缩短,小于直接法;求解等距离纬度正解时,直接法计算用时大于本文方法,但直接法在改进后用时缩短,也比本文方法更快,说明Mathematica内部对级数除法运算优化地较好。综合来说,进行具体系数运算时,本文方法不仅提供了一种递推计算方法,也加快了运算。但更重要的是,本文分析的是展开式及其系数的一般形式,这是直接法所无法比拟的。
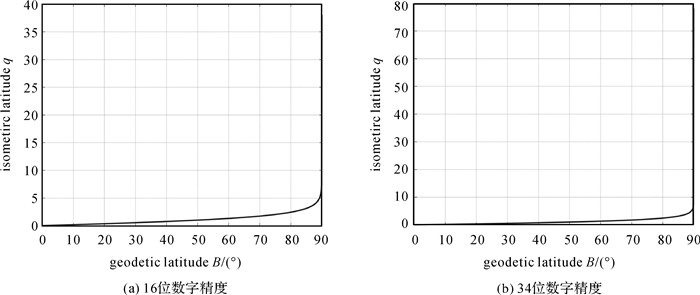
在进行数值分析时,可采用Fortran 90语言编写程序(用Intel Visual Fortran Composer XE 2013 SP1 Update 1编译),分别取双精度(16位)和四精度(34位)浮点数运算。本文利用Matlab软件将Fortran输出结果绘制成图,等量纬度随大地纬度变化的曲线如图 2所示。其中,大地纬度B∈(0, 90°),而B∈(-90°, 0)情况类似,取CGCS2000参考椭球,其扁率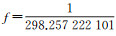
|
| 图 2 等量纬度随大地纬度B∈(0, 90°)变化的曲线 Fig. 2 Curve of the isometric latitude varying with the geodetic latitude B∈(0, 90°) |
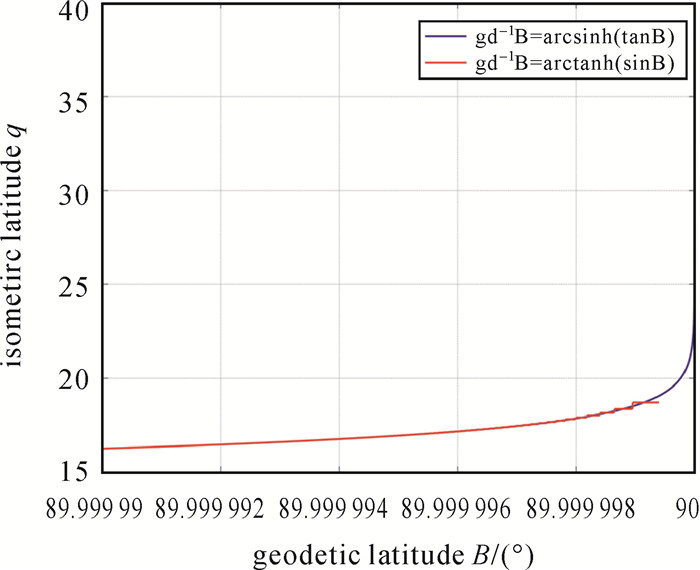
取大地纬度小区间B∈(89.999 99°, 90°),在古德曼反函数修正和未修正时等量纬度随大地纬度变化曲线如图 3所示(16位数字精度)。
|
| 图 3 等量纬度随大地纬度B∈(89.999 99°, 90°)变化的曲线 Fig. 3 Curve of the isometric latitude varying with the geodetic latitude B∈(89.999 99°, 90°) |
由图 2可看出,在B∈(0, 90°)时,等量纬度随大地纬度单调递增,在接近极点时,曲线斜率非常大。理论上在极点处等量纬度为无穷大,但进行数值计算时不可能处理无穷大量;16位和34位数字精度下所能计算的等量纬度最大值分别为qmax16=38.018 293 995 274 90,qmax34=78.115 872 564 187 653 490 898 757 927 628 82,可得其比值qmax34/qmax16≈2.05;因此,提高数字精度可有效增加等量纬度计算范围,显然,这也增加了数值计算精度。由图 3可以看出,由于舍入误差影响,在古德曼反函数未修正时(gd-1B=arctanh(sinB)),等量纬度随大地纬度变化曲线在趋近极点时成折线,在一定区间内不再变化;等量纬度计算范围减小,最大值仅为18.708 264 496 564 56,在B>89.999 999 396 289 99°时根本无法计算;而在古德曼反函数修正后,等量纬度函数曲线是正常、连续的;这些是基于16位数字精度运算情况下的,对34位数字精度情况也有类似结果。
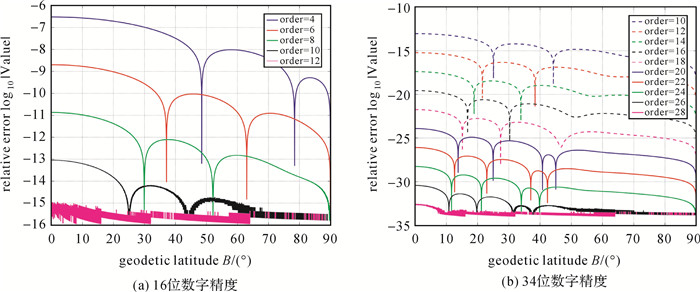
为了分析等量纬度反解精度,设有一大地纬度B,可由解析式(1)计算得到等量纬度,再利用反解式(14)得到另一大地纬度B′,因此B′-B就是反解理论值与实际值的误差。等量纬度反解相对误差(取对数log10(B′-B)/B)随大地纬度变化的曲线如图 4所示。
|
| 图 4 等量纬度反解误差随大地纬度变化的曲线 Fig. 4 Relative error of the inverse solution of the isometric latitude |
由图 4可以看出,等量纬度反解相对误差随展开式阶数逐渐减小,在16位数字精度下,取到e8阶时反解式相对误差最大绝对值约为1.34×10-11,取到e10阶时约为9.04×10-14,取到e12阶时约为1.14×10-15,已经接近数字精度,取更高阶时精度几乎不再增加(Fortran的16位机器精度约为2.22×10-16);而在34位数字精度下,取到e8、e10和e12阶时反解式最大相对误差约为1.34×10-11、9.00×10-14和6.03×10-16,比16位精度时略好,取到e28阶时接近数字精度(Fortran的34位机器精度约为1.93×10-34)。另外,等量纬度正解展开式取到e8、e10和e12时最大相对误差分别为5.49×10-13、3.34×10-15和5.44×10-16(16位精度时),比反解精度高,不过一般直接用定义的解析式直接计算等量纬度;其余辅助纬度与大地纬度之间展开式的相对误差情况类似,本文不再赘述,文献[4, 13]也有一定论述。在大地测量和制图学的实际应用中,取到e8或e10阶一般已经满足精度要求,而要求精度较高时,为了避免舍入误差,一般取到e12阶。
5 结论本文从无穷级数理论出发,详细推导了旋转椭球情况下等量纬度、等角纬度和等距离纬度关于大地纬度和参考椭球第一偏心率的无穷级数公式,主要表现为递推形式。计算结果表明,展开至e6、e8阶的等量纬度反解式与文献[9—10]等结果是一致的,展开至e10阶辅助纬度展开式也与文献[13]结果一致;借助Mathametica进一步检验了e0~e40阶展开式,并比较了本文方法与利用计算机代数系统直接推导展开式的程序运行时间,不仅说明本文方法是正确的,也可以加快展开式的求解运算;利用Fortran对辅助纬度正反解进行了数值分析,说明增加数字精度可以增加等量纬度计算范围,也略增了数值计算精度,若要避免16位、32位数字精度运算的舍入误差,展开式分别需要展开到e12阶、e28阶。本文严格推导的辅助纬度关于大地纬度的无穷展开公式,是一种一般形式,也是一种有效、快速的算法,对于完善制图学的数学体系具有重要参考意义。
| [1] | GRAFAREND E W, KRUMM F W. Map projections:cartographic information systems[M]. Berlin: Springer, 2006. |
| [2] |
杨启和.
测量和地图学中应用的六种纬度及其变换关系式[J]. 测绘科技通讯, 1995, 18(3): 14–19.
YANG Qihe. Six latitudes used in geodesy and cartology and their transformation relations[J]. Geomatics Technology and Equipment, 1995, 18(3): 14–19. |
| [3] |
陈成, 边少锋, 李厚朴.
一种解算椭球大地测量学反问题的方法及应用[J]. 海洋测绘, 2015, 35(6): 8–13.
CHEN Cheng, BIAN Shaofeng, LI Houpu. A method for solving inverse problems in ellipsoidal geodesy and its application[J]. Hydrographic Surveying and Charting, 2015, 35(6): 8–13. DOI:10.3969/j.issn.1671-3044.2015.06.002 |
| [4] | OSBORNE P. The mercator projections[M]. Edinburgh: Edinburgh University Press, 2008. |
| [5] |
方俊.
等面积纬度和等量纬度与地理纬度的关系[J]. 地理学报, 1957, 23(4): 379–388.
FANG Jun. Formulae and tables for conversion of the geographical latitude to the authalic and isometric latitudes[J]. Acta Geographica Sinica, 1957, 23(4): 379–388. |
| [6] | YANG Q H, SNYDER J P, TOBLER W R. Map projection transformation:principles and applications[M]. London: Taylor & Francis, 2000. |
| [7] |
李厚朴, 边少锋, 钟斌.
地理坐标系计算机代数精密分析理论[M]. 北京: 国防工业出版社, 2015.
LI Houpu, BIAN Shaofeng, ZHONG Bin. Precise analysis theory of geographic coordinate system by computer algebra[M]. Beijing: National Defend Industry Press, 2015. |
| [8] |
熊介.
椭球大地测量学[M]. 北京: 解放军出版社, 1988.
XIONG Jie. Ellipsoidal geodesy[M]. Beijing: The People's Liberation Army Press, 1988. |
| [9] |
华棠.
海图数学基础[M]. 北京: 海潮出版社, 1985.
HUA Tang. The mathematical basis of chart[M]. Beijing: Haichao Press, 1985. |
| [10] | DAY J W R. The formula for finding the ordinary latitude from the isometric latitude[J]. Survey Review, 1988, 29(230): 383–385. DOI:10.1179/sre.1988.29.230.383 |
| [11] | ADAMS O S. Latitude developments connected with geodesy and cartography with tables, including a table for lambert equal-area meridional projection[M]. Washington: U.S Coast and Geodetic Survey Special Publishing, 1921. |
| [12] |
边少锋, 纪兵.
等距离纬度等量纬度和等面积纬度展开式[J]. 测绘学报, 2007, 36(2): 218–223.
BIAN Shaofeng, JI Bing. The expansions of rectifying latitude, conformal latitude and authalic latitude[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 218–223. DOI:10.3321/j.issn:1001-1595.2007.02.018 |
| [13] | BIAN Shaofeng, LI Houpu. Mathematical analysis in cartography by means of computer algebra system[M]//BATEIRA C. Cartography-A Tool for Spatial Analysis. Croatia: InTech, 2012. |
| [14] | KAWASE K. A general formula for calculating meridian arc length and its application to coordinate conversion in the Gauss-Krüger projection[J]. Bulletin of the Geospatial Information Authority of Japan, 2011(59): 1–13. |
| [15] | PETERS J M H. The gudermannian[J]. The Mathematical Gazette, 1984, 68(445): 192–196. DOI:10.2307/3616342 |
| [16] | GRADSHTEYN I S, RYZHIK I M. Table of integrals, series, and products[M]. Amsterdam: Academic Press, 2015. |
| [17] |
王竹溪, 郭敦仁.
特殊函数概论[M]. 北京: 北京大学出版社, 2000.
WANG Zhuxi, GUO Dunren. Introduction to special function[M]. Beijing: Peking University Press, 2000. |
| [18] | LICHTENEGGER H. Transformation of geodetic and isometric latitude by numerical integration[J]. Survey Review, 1990, 30(236): 294–296. DOI:10.1179/003962678791486176 |
| [19] | BOWRING D R. New ideas on isometric latitude[J]. Survey Review, 1990, 30(236): 270–280. DOI:10.1179/003962678791486167 |
| [20] | KAYA A. An alternative formula for finding the geodetic latitude from the isometric latitude[J]. Survey Review, 1994, 32(253): 450–452. DOI:10.1179/sre.1994.32.253.450 |
| [21] | BERMEJO-SOLERA M, OTERO J. Simple and highly accurate formulas for the computation of transverse Mercator coordinates from longitude and isometric latitude[J]. Journal of Geodesy, 2009, 83(1): 1–12. DOI:10.1007/s00190-008-0224-y |
| [22] |
陈成.极区海图投影及其变换研究[D].武汉: 海军工程大学, 2015. CHEN Cheng. Research on polar nautical chart projections and their transformations[D]. Wuhan: Naval University of Engineering, 2015. |
| [23] | KUZMINA R P. Asymptotic methods for ordinary differential equations[M]. Dordrecht: Springer, 2000. |


