2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013;
3. 江西省数字国土重点实验室, 江西 南昌 330013
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASG, Nanchang 330013, China;
3. Key Laboratory for Digital Land and Resources of Jiangxi Province, Nanchang 330013, China
在测量数据处理中,Gauss-Markov模型是常用的平差模型,模型解算常用的方法为最小二乘方法。然而在某些实际情况中,Gauss-Markov模型系数矩阵A的元素可能由某些含有观测误差的观测值构成,此时经典的最小二乘平差方法不够严密。总体最小二乘[1-4]是同时顾及了观测向量与系数矩阵误差的平差方法,是变量误差(errors-in-variables,EIV)模型的严密估计方法。文献[5—7]研究了总体最小二乘的迭代算法;文献[8—14]研究了附有等式约束和不等式约束条件的总体最小二乘方法;文献[15]研究了提高计算效率的总体最小二乘方法。部分变量误差[16](partial error-in-variables,Partial EIV)模型是考虑了EIV模型系数矩阵中存在随机元素和非随机元素的情况,相比于EIV模型,Partial EIV模型更具有一般性和适用性,且在算法及应用中都得到了广泛的研究[17-25]。
由于EIV模型或Partial EIV模型受非线性的影响,总体最小二乘解算得到的参数估值及单位权方差估值是有偏的[26-27]。文献[28]分析了系数矩阵误差对EIV模型平差参数估值的影响。文献[29]基于泰勒公式展开的二次项,得到了非线性函数的偏差公式。文献[30]基于EIV模型,通过线性化处理得到了参数估值及参数估值一阶近似协方差阵。文献[27]对迭代的最后一步表达式进行线性化,得到了参数估值的一阶近似协方差阵。文献[16]根据非线性理论得到了参数估值偏差及一阶近似协方差阵。文献[31]通过迭代计算得到参数估值的协方差阵。文献[32]推导了多元总体最小二乘算法并得到了参数估值的一阶近似协方差阵。以上计算方法及通过协方差传播得到的参数估值方差只计算到一阶近似。文献[33]使用SUT(scaled unscented transformation)方法计算得到总体最小二乘参数估值的二阶近似协方差阵。文献[34]推导了总体最小二乘精度评定的二阶近似函数法,将参数估值精度提高至二阶,进一步完善了总体最小二乘精度评定理论。
方差分量估计[35-39]是针对随机模型不准确从而对权进行修正的验后估计方法,方差分量估计方法通过预平差得到的信息根据一定的原则对观测量的验前方差或协方差进行估计、重新定权。文献[40]分析了EIV模型的最小二乘方差分量估计。文献[41]引入权修正因子,推导了Partial EIV模型的Helmert方差分量估计。文献[42]得到了Partial EIV模型的非负最小二乘方差分量估计;然而以上总体最小二乘方差分量估计方法中并未考虑参数估值有偏性的影响。文献[43]推导了EIV模型的最小范数二次无偏估计,分析了由参数估值偏差引起的方差分量估值的偏差,推导了方差分量估值偏差的表达式。
基于上述分析,本文考虑总体最小二乘估计参数估值的偏差,进行偏差改正得到偏差改正后的参数估值,更新由参数估值引起变化的中间变量,将偏差改正与方差分量归为整体同时迭代计算,进行偏差改正后的方差分量估计及二阶精度评定。通过算例试验,将偏差改正后得到的结果与未进行偏差改正的结果进行对比分析,验证本文方法的可行性。
1 Partial EIV模型参数偏差及精度评定 1.1 Partial EIV模型解算针对EIV模型系数矩阵中存在固定元素及重复出现的随机元素,文献[16]将系数矩阵中的随机元素分离,提出了Partial EIV模型,其数学模型为
函数模型
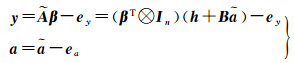 (1)
(1)
随机模型
 (2)
(2)
式中,Ã表示n×m系数矩阵真值,h是一个确定的nm×1常数向量,由Ã中非随机元素和零组成;B是一个给定的nm×t矩阵,t表示系数矩阵Ã中随机元素的个数;y表示n×1的观测向量;ey表示观测向量误差;a是系数矩阵Ã中随机元素组成的t×1列向量;ã表示其真值;ea表示a的随机误差;β表示待求参数,Qy表示观测量误差的协因数阵;Qa表示系数矩阵误差的协因数阵;σ02表示单位权方差;In表示n×n单位矩阵。
目前针对Partial EIV模型的解法较多,本文参考文献[19]的求解思路,构造拉格朗日条件极值函数
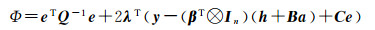 (3)
(3)
式中,λ为拉格朗日乘子;
对式(3)进行解算最终可得到参数估值的表达式为
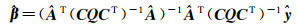 (4)
(4)
式中,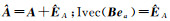

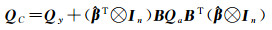 (5)
(5)
由于总体最小二乘方法顾及了系数矩阵误差,式(1)可以看作为非线性模型,Partial EIV模型解算得到的参数是有偏或近似无偏的[16]。将Partial EIV模型视为非线性模型得到
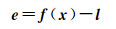 (6)
(6)
式中,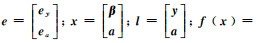
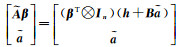
非线性模型的常用解算方法是将模型线性化,近似成线性模型进行平差解算,因此将式(6)在近似值x0处展开,令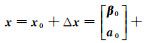

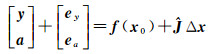 (7)
(7)
式中,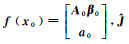
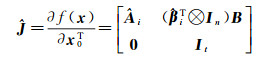 (8)
(8)
式中,
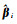
 (9)
(9)
式中,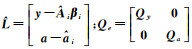
通过迭代计算最终得到参数估值为
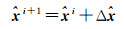 (10)
(10)
式(4)与式(10)是等价的,通过迭代计算都能得到相同的参数估值。
1.2 基于二阶导数的偏差计算及精度评定文献[16]针对Partial EIV模型的非线性推导了参数估值的偏差表达式及参数估值的一阶近似协方差阵。参数估值偏差表达式和协方差表达式分别为[16]
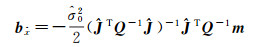 (11)
(11)
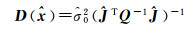 (12)
(12)
式中,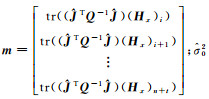
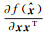
同理,式(4)通过协方差传播律可以得到参数估值的一阶近似协方差
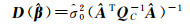 (13)
(13)
然而针对非线性模型,在线性化过程中难免会产生模型误差,由式(12)和式(13)得到的一阶近似协方差往往会高估参数估值的精度信息,为了更合理地对参数估值精度进行评定,文献[34]基于二阶导数推导了参数估值的二阶近似协方差;将非线性函数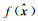
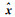
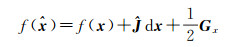 (14)
(14)
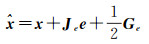 (15)
(15)
式中,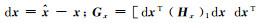
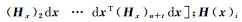
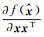
 (16)
(16)
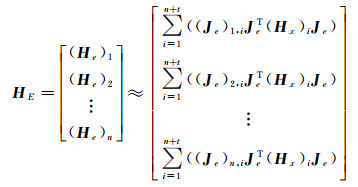 (17)
(17)
式(15)可以得到参数估值的偏差
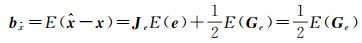 (18)
(18)
进而可以得到偏差改正后的参数估值
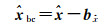 (19)
(19)
式中,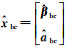
根据协方差传播可以得到参数估值
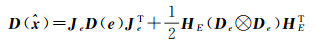 (20)
(20)
随机模型的验后估计又称方差分量估计,是针对平差前给定的随机模型不准确而提出的方法。方差分量估计的基本思想是先对各类观测值定初权,进行预平差,利用预平差后得到的信息,主要是各类观测值的改正数,并根据得到的观测值的改正数对各类观测值的验前方差和协方差进行估计,重新定权。
考虑式(2)随机模型形式为
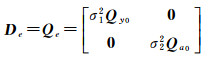 (21)
(21)
式中,σ12、σ22为方差分量,Qy0、Qa0为观测值初始协因数阵。则式(5)变为
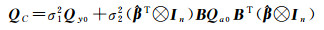 (22)
(22)
对总体最小二乘解算可以得到
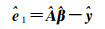 (23)
(23)
式中,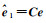
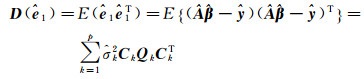 (24)
(24)
式中,p在本文中取值为2,Qk的形式为
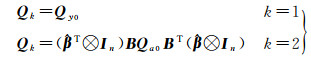 (25)
(25)
式中,k=1时,表示观测量y对应的初始协因数阵;k=2时,表示系数矩阵对应的初始协因数阵。
本文以最小二乘方差分量估计方法为例,文献[40]分析了总体最小二乘的最小二乘方差分量估计,将方差分量作为参数进行最小二乘平差解算得到
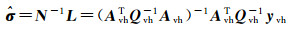 (26)
(26)
式中,vh表示取出对称矩阵的上三角元素按照一定的顺序排列成列向量。
文献[36]通过公式转换得到法矩阵N和列向量L的形式为
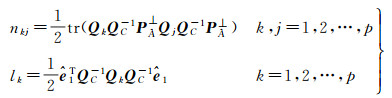 (27)
(27)
式中,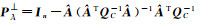
针对Partial EIV模型式(1),模型的总观测量个数为n+t,必要观测量个数为t+m,在平差计算时是将系数矩阵含有观测误差的数据作为参数进行解算;根据非线性解算理论,参数β与系数矩阵观测值a组成的向量x在进行式(10)的迭代计算时是存在偏差的,而参数估值影响观测值改正数,从而影响方差分量估计。将偏差改正后的参数估值代入方差分量估计中,即存在
 (28)
(28)
继而有
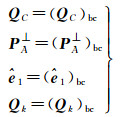 (29)
(29)
式中,下标bc表示偏差改正后对应的值。
将
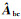
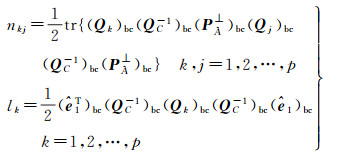 (30a)
(30a)
进而得到
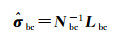 (30b)
(30b)
考虑到偏差改正后的方差分量估值、式(21)随机模型的形式及方差分量估计的表达式,参数估值偏差对方差分量估值有直接影响,继而影响式(13)或式(20)的精度评定。因此,在进行参数估值进度评定时,也应用到偏差改正后的分差分量估值,即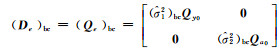
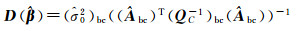 (31a)
(31a)
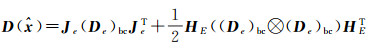 (31b)
(31b)
将参数估值偏差改正与方差分量估计作为一个整体进行迭代计算,其迭代流程见图 1。
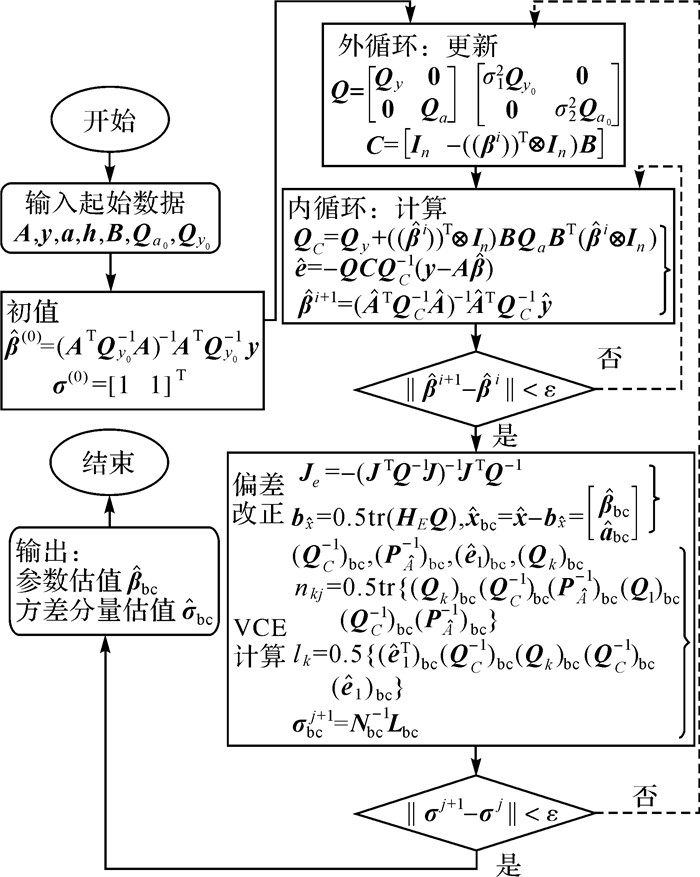
|
| 图 1 偏差改正方差分量估计迭代流程 Fig. 1 Flow chart of bias correction variance components estimation iteration |
3 算例与分析 3.1 算例1直线拟合
采用文献[18]的数据,直线拟合的模型为
 (32)
(32)
已知坐标观测值(xi, yi)和相应的权值(pxi, pyi),见表 1。
| 点号 | 观测数据 | 权值 | |||
| yi | xi | pyi | pxi | ||
| 1 | 5.9 | 0.0 | 1.0 | 1 000.0 | |
| 2 | 5.4 | 0.9 | 1.8 | 1 000.0 | |
| 3 | 4.4 | 1.8 | 4.0 | 500.0 | |
| 4 | 4.6 | 2.6 | 8.0 | 800.0 | |
| 5 | 3.5 | 3.3 | 20.0 | 200.0 | |
| 6 | 3.7 | 4.4 | 20.0 | 80.0 | |
| 7 | 2.8 | 5.2 | 70.0 | 60.0 | |
| 8 | 2.8 | 6.1 | 70.0 | 20.0 | |
| 9 | 2.4 | 6.5 | 100.0 | 1.8 | |
| 10 | 1.5 | 7.4 | 500.0 | 1.0 | |
考虑观测数据的个数,构造Partial EIV模型的向量h与矩阵B的形式为
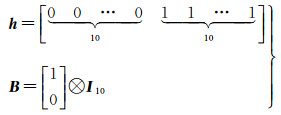 (33)
(33)
现分别使用最小二乘(LS)、总体最小二乘(TLS)、总体最小二乘的最小二乘方差分量估计方法[40](TLS-VCE)及本文方法(偏差改正的方差分量估计)计算,得到的参数估值、参数估值偏差及方差分量估值结果见表 2。
| 估值 | LS | TLS | TLS-VCE | 本文方法 | 参数估 值偏差 |
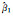
|
-0.610 813 | -0.480 533 | -0.489 907 | -0.488 458 | -0.002 910 |
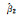
|
6.100 109 | 5.479 910 | 5.527 558 | 5.522 168 | 0.011 351 |
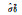
|
1.483 294 | — | — | — | |

|
— | — | 0.656 376 | 0.609 549 | — |
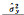
|
— | — | 1.821 311 | 1.832 322 | — |
从表 2可以看出,经过偏差改正后的方差分量估计得到的方差分量估值及参数估值都有所改变,这主要是由参数估值的偏差引起的,参数估值偏差越大,对结果的影响也越大。计算得到参数估值的标准差结果见表 3。
| 参数估值 标准差 |
LS | TLS | TLS-VCE | 本文方法 (一阶) |
本文方法 (二阶) |
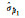
|
0.062 341 | 0.070 620 | 0.067 155 | 0.066 281 | 0.066 458 |
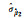
|
0.424 059 | 0.359 247 | 0.361 275 | 0.358 512 | 0.359 077 |
3.2 算例2二维仿射变换
根据文献[38—39]算例思想,在长宽为100 m的正方形区域内,沿纵横坐标方向每隔10 m选取一个点,共121个点,在正方形区域的所有点中均匀选取31个点作为公共点进行二维仿射变换。二维仿射变换模型可以表示为
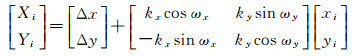 (34)
(34)
式中,Δx、Δy为平移参数;ωx、ωy为旋转参数;kx、ky为尺度参数;(xi,yi)、(Xi,Xi)分别为第i个公共点的原始坐标系及目标坐标系的坐标。
将式(34)改写成矩阵形式得到
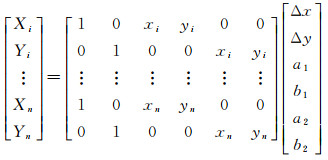 (35)
(35)
式中,a1=kxcosωx;b1=kysinωy;a2=-kxsinωx;b2=kycosωy,构造Partial EIV模型的向量h与矩阵B的形式为
 (36)
(36)
式中,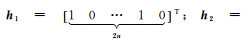
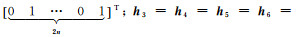
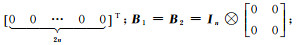
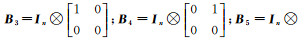

给定一组转换参数真值,Δx=Δy=0,ωx=100,ωy=110,kx=1.01,ky=1.02,假设目标坐标系坐标之间相互独立且等精度,原始坐标同一点中x、y坐标独立,不同点间坐标相关,对应协因数阵中非对角线元素为
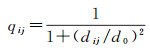 (37)
(37)
式中,qij为协因数阵中对应的元素值;dij为i、j点间的距离;d0为常数且取值为10 m。
现分别给原始坐标与目标坐标模拟均值为0,服从正态分布的随机误差。其中,原始坐标单位权中误差为1 cm,目标坐标单位权中误差为3 cm。分别使用最小二乘(LS)、总体最小二乘(TLS)、总体最小二乘的最小二乘方差分量估计[40](TLS-VCE)及本文方法计算,得到的参数估值、参数估值偏差及参数估值与真值的差值范数见表 4。
| 方案 | 
|
|
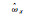
|
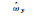
|
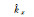
|

|
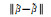
|
| LS | -0.010 507 | -0.000 285 | 10.001 318 | 11.006 626 | 1.010 133 | 1.019 889 | 0.012 493 |
| TLS | -0.009 630 | -0.001 896 | 10.000 999 | 11.007 636 | 1.010 113 | 1.019 922 | 0.012 476 |
| TLS-VCE | -0.010 196 | -0.000 477 | 10.001 274 | 11.006 858 | 1.010 127 | 1.019 899 | 0.012 364 |
| 本文方法 | -0.010 196 | -0.000 476 | 10.001 274 | 11.006 857 | 1.010 127 | 1.019 898 | 0.012 363 |
| 真值 | 0 | 0 | 10 | 11 | 1.01 | 1.02 | — |
| 偏差 | -3.96×10-7 | -2.75×10-7 | 7.04×10-9 | 8.85×10-10 | -1.7×10-9 | 7.27×10-9 | — |
从表 4可以看出,由于该算例中参数估值偏差较小,不同方法得到的参数估值相差较小,参数估值与真值的差值范数也较小,但方差分量估计方法可以得到与平差前给定的方差分量相近的估值;计算得到原始坐标与目标坐标的方差分量估值见表 5。
| 方差分量估值 | LS | TLS | TLS-VCE | 本文方法 | 真值 |
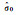
|
0.238 453 | 0.023 296 | — | — | — |
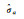
|
— | — | 0.029 946 89 | 0.029 946 90 | 0.03 |
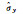
|
— | — | 0.011 421 52 | 0.011 421 49 | 0.01 |
从表 5可以看出,方差分量估计方法得到原始坐标的观测精度为2.994 689 cm,目标坐标的观测精度为1.142 152 cm,与平差前给定的3 cm和1 cm接近;而由于该算例中参数估值偏差较小,经过偏差改正后的方差分量估值与未经过偏差改正的相差较小,但都接近于验前给定的方差分量。
3.3 算例3四参数坐标转换在算例2中,由于观测量误差较小,在构造总体最小二乘平差模型时,系数矩阵误差很小,TLS与LS结果相差较小;文献[28]指出系数矩阵的信噪比达到一定量级时,参数估值的相对偏差很小,LS与TLS结果必然没有差别。考虑一个四参数坐标转换模型
 (38)
(38)
在该算例中模拟5个坐标点,转换参数真值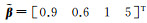
| 点号 | 原始坐标系 | 目标坐标系 | |||||||
| xi | Qxi | yi | Qyi | Xi | QXi | Yi | QYi | ||
| 1 | 1.156 9 | 1 | 2.314 4 | 3 | 0.674 8 | 1 | 7.992 7 | 2 | |
| 2 | 1.429 4 | 6 | 2.929 3 | 1 | 1.297 0 | 3 | 8.656 3 | 1 | |
| 3 | 2.359 8 | 1 | 2.987 3 | 3 | 1.642 9 | 5 | 9.421 9 | 4 | |
| 4 | 3.282 5 | 4 | 2.411 5 | 3 | 2.272 1 | 2 | 9.026 2 | 4 | |
| 5 | 2.430 1 | 6 | 1.310 6 | 5 | 2.927 7 | 2 | 7.933 6 | 1 | |
根据所提供坐标个数,得到向量h、B形式如下
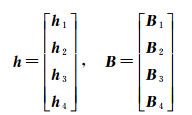 (39)
(39)
式中,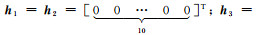
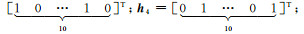
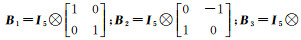

现分别使用最小二乘(LS)、总体最小二乘(TLS)、总体最小二乘的最小二乘方差分量估计[40](TLS-VCE)及本文方法计算,参数估值、参数估值偏差、参数估值与真值差值范数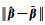
| 估值 | LS | TLS | TLS-VCE | 本文方法 | 真值 | 参数估值偏差 |
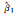
|
0.816 704 | 0.869 034 | 0.901 387 | 0.914 601 | 0.9 | -0.006 479 |

|
0.591 251 | 0.616 815 | 0.622 195 | 0.621 941 | 0.6 | 0.000 381 |
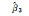
|
1.335 291 | 1.318 447 | 1.295 961 | 1.268 229 | 1 | 0.017 362 |
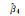
|
5.410 062 | 5.152 773 | 5.043 577 | 5.007 308 | 5 | 0.015 749 |
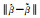
|
0.536 270 | 0.354 950 | 0.299 978 | 0.269 620 | — | — |
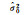
|
0.306 421 | 0.019 20 | — | — | — | — |
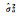
|
— | — | 0.025 638 | 0.026 188 | 0.025 | — |

|
— | — | 0.010 577 | 0.009 920 | 0.01 | — |
| 方案 | σβ1 | σβ2 | σβ3 | σβ4 |
| LS | 0.312 733 | 0.396 139 | 1.049 066 | 1.180 785 |
| TLS | 0.146 566 | 0.175 790 | 0.552 852 | 0.511 277 |
| TLS-VCE | 0.162 263 | 0.191 993 | 0.628 532 | 0.554 969 |
| 本文方法 (一阶) |
0.156 244 | 0.187 795 | 0.612 652 | 0.536 898 |
| 本文方法 (二阶) |
0.162 830 | 0.193 005 | 0.631 021 | 0.557 697 |
从表 7与表 8可以看出,方差分量估计方法可以得到与平差前相近的方差分量,对参数估值也有修正作用,而加入偏差改正后的方差分量估计方法得到的参数估值与真值的差值范数最小,数值为0.269 620,更接近于参数真值。
3.4 算例分析(1) 算例1中,方差分量估计方法可以得到不同类数据的方差分量估值,而考虑总体最小二乘参数估值的有偏性时,对参数估值进行偏差改正,将改正后的参数估值与方差分量估计结合成整体进行计算,可以得到修正后的参数估值与方差分量估值。方差分量估值影响参数估值的精度评定,从表 3的参数估值标准差可以看出,偏差改正后的参数估值标准差小于未偏差改正的参数估值标准差,而二阶方差在数值上要大于一阶,说明在非线性模型的精度评定时应尽可能考虑线性化过程中舍去的高次项信息。
(2) 算例2中,由于观测数据的量级与观测误差的量级差别较大,系数矩阵误差对平差结果的影响较小,相应地将平差模型作为非线性模型时,得到的参数估值偏差很小,量级为10-7,表 4所提供的参数估值结果都与LS结果相差较小;表 5中方差分量估计方法都可以得到接近于平差前给定的方差分量,说明了方差分量估计方法的有效性;而由于参数估值偏差较小的原因,经过偏差改正后得到的方差分量估值与未经过偏差改正得到的方差分量估值接近一致,这也说明偏差大小与数据初始精度及模型的非线性强度有关[44]。
(3) 算例3中,考虑观测数据量级较小且观测量的方差较大的四参数坐标转换模型,表 7中给出计算得到参数估值的偏差最大为0.017 362,参数的偏差百分比为1.34%,模型具有非线性形态且有必要考虑泰勒展开式的二阶项[44],表 7提供的参数估值与真值的差值范数中,经过偏差改正后的方差分量估计得到的参数估值最接近于真值,相比于不考虑偏差改正的方差分量估计方法,更说明了偏差改正的必要性;从表 8中的参数估值标准差可以看出,加入偏差改正后得到一阶近似标准差要比不加偏差改正的小,而考虑泰勒级数展开的二阶项时,二阶近似要大于一阶近似标准差,在线性化过程中忽略高次项时可能会舍去某些信息,而考虑了部分随机量的随机性的方法在理论上更加严密。
4 结束语非线性模型在线性近似过程中会带来模型误差,导致得到的最小二乘估计的参数估值是有偏的。本文考虑了Partial EIV模型参数估值的偏差并得到偏差改正后的参数估值,在方差分量估计中,参数估值对观测值改正数等有直接影响,进而影响方差分量估计的准确性。因此,本文将参数估计、偏差改正和方差分量估计作为整体进行迭代计算,将偏差改正后的参数估值代入方差分量估计中,从而获得更加可靠的方差分量估值与参数估值。根据不同的平差模型及数据结构,当系数矩阵误差与系数矩阵量级很大时,模型的非线性强度较低,参数估值的偏差必然很小,此时进行偏差改正得到的结果变化不大;当偏差较大时,进行偏差改正可以得到更好的结果;得到更加合理的方差分量估值对随机模型进行修正,从而获得更加合理的参数估值及精度信息,是对总体最小二乘理论的进一步完善。本文将偏差改正结合到方差分量估计中,然而并未对偏差量级对结果产生影响的程度进行分析,这也是今后将要开展的工作。
| [1] | GOLUB G H, VAN LOAN C F. An analysis of the total least squares problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883–893. DOI:10.1137/0717073 |
| [2] |
王乐洋.
基于总体最小二乘的大地测量反演理论及应用研究[J]. 测绘学报, 2012, 41(4): 629.
WANG Leyang. Research on theory and application of total least squares in geodetic inversion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 629. |
| [3] | FANG Xing. Weighted total least squares solutions for applications in geodesy[D]. Germany: Leibniz Universität Hannover, 2011. |
| [4] |
王乐洋, 许才军.
总体最小二乘研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(7): 850–856.
WANG Leyang, XU Caijun. Progress in total least squares[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 850–856. |
| [5] | AMIRI-SIMKOOEI A, JAZAERI S. Weighted total least squares formulated by standard least squares theory[J]. Journal of Geodetic Science, 2012, 2(2): 113–124. |
| [6] | JAZAERI S, AMIRI-SIMKOOEI A R, SHARIFI M A. Iterative algorithm for weighted total least squares adjustment[J]. Survey Review, 2014, 46(334): 19–27. DOI:10.1179/1752270613Y.0000000052 |
| [7] | FANG Xing. Weighted total least squares:necessary and sufficient conditions, fixed and random parameters[J]. Journal of Geodesy, 2013, 87(8): 733–749. DOI:10.1007/s00190-013-0643-2 |
| [8] | FANG Xing. A structured and constrained total least-squares solution with cross-covariances[J]. Studia Geophysica et Geodaetica, 2014, 58(1): 1–16. DOI:10.1007/s11200-012-0671-z |
| [9] | SCHAFFRIN B, FELUS Y A. On total least-squares adjustment with constraints[M]//SANSÒ F. A Window on the Future of Geodesy. Berlin, Heidelberg: Springer, 2005: 417-421. |
| [10] | SCHAFFRIN B, FELUS Y A. An algorithmic approach to the total least-squares problem with linear and quadratic constraints[J]. Studia Geophysica et Geodaetica, 2009, 53(1): 1–16. DOI:10.1007/s11200-009-0001-2 |
| [11] | MAHBOUB V, SHARIFI M A. On weighted total least-squares with linear and quadratic constraints[J]. Journal of Geodesy, 2013, 87(3): 279–286. DOI:10.1007/s00190-012-0598-8 |
| [12] | WANG Ding, ZHANG Li, WU Ying. Constrained total least squares algorithm for passive location based on bearing-only measurements[J]. Science in China Series F:Information Sciences, 2007, 50(4): 576–586. DOI:10.1007/s11432-007-0023-8 |
| [13] | FANG Xing. Weighted total least-squares with constraints:a universal formula for geodetic symmetrical transformations[J]. Journal of Geodesy, 2015, 89(5): 459–469. DOI:10.1007/s00190-015-0790-8 |
| [14] | FANG Xing. On non-combinatorial weighted total least squares with inequality constraints[J]. Journal of Geodesy, 2014, 88(8): 805–816. DOI:10.1007/s00190-014-0723-y |
| [15] | AYDIN C, MERCAN H, UYGUR S Ö. Increasing numerical efficiency of iterative solution for total least-squares in datum transformations[J]. Studia Geophysica et Geodaetica, 2018, 62(2): 223–242. DOI:10.1007/s11200-017-1003-0 |
| [16] | XU Peiliang, LIU Jingnan, SHI Chuang. Total least squares adjustment in partial errors-in-variables models:algorithm and statistical analysis[J]. Journal of Geodesy, 2012, 86(8): 661–675. DOI:10.1007/s00190-012-0552-9 |
| [17] |
刘经南, 曾文宪, 徐培亮.
整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(5): 505–512.
LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of total least squares methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505–512. |
| [18] |
王乐洋, 余航, 陈晓勇.
Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22–29.
WANG Leyang, YU Hang, CHEN Xiaoyong. An algorithm for partial EIV model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22–29. DOI:10.11947/j.AGCS.2016.20140560 |
| [19] |
王乐洋, 许光煜, 温贵森.
一种相关观测的Partial EIV模型求解方法[J]. 测绘学报, 2017, 46(8): 978–987.
WANG Leyang, XU Guangyu, WEN Guisen. A method for partial EIV model with correlated observations[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 978–987. DOI:10.11947/j.AGCS.2017.20160430 |
| [20] | ZENG Wenxian, LIU Jingnan, YAO Yibin. On partial errors-in-variables models with inequality constraints of parameters and variables[J]. Journal of Geodesy, 2015, 89(2): 111–119. DOI:10.1007/s00190-014-0775-z |
| [21] |
赵俊, 归庆明, 郭飞宵.
基于改进目标函数的partial EIV模型WTLS估计的新算法[J]. 武汉大学学报(信息科学版), 2017, 42(8): 1179–1184.
ZHAO Jun, GUI Qingming, GUO Feixiao. A new algorithm of weighted total least squares estimate of partial EIV model based on an improved objective function[J]. Geomatics and Information Science of Wuhan University, 2017, 42(8): 1179–1184. |
| [22] |
王乐洋, 许光煜, 陈晓勇.
附有相对权比的PEIV模型总体最小二乘平差[J]. 武汉大学学报(信息科学版), 2017, 42(6): 857–863.
WANG Leyang, XU Guangyu, CHEN Xiaoyong. Total least squares adjustment of partial errors-in-variables model with weight scaling factor[J]. Geomatics and Information Science of Wuhan University, 2017, 42(6): 857–863. |
| [23] |
许光煜. Partial EIV模型的总体最小二乘方法及应用研究[D].南昌: 东华理工大学, 2015. XU Guangyu. The total least squares method and its application of partial errors-in-variables model[D]. Nanchang: East China University of Technology, 2015. |
| [24] |
王乐洋, 温贵森.
一种基于Partial EIV模型的多项式拟合解法[J]. 大地测量与地球动力学, 2017, 37(7): 737–742.
WANG Leyang, WEN Guisen. A kind of polynomial fitting method based on partial EIV model[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 737–742. |
| [25] |
王乐洋, 熊露云.
水准测量中尺度比参数的附加系统参数的Partial EIV模型解法[J]. 大地测量与地球动力学, 2017, 37(8): 856–859, 875.
WANG Leyang, XIONG Luyun. The partial EIV model solution for additional systematic parameters of scale parameters in leveling[J]. Journal of Geodesy and Geodynamics, 2017, 37(8): 856–859, 875. |
| [26] | SCHAFFRIN B, WIESER A. On weighted total least-squares adjustment for linear regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [27] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An iterative solution of weighted total least-squares adjustment[J]. Journal of Geodesy, 2011, 85(4): 229–238. DOI:10.1007/s00190-010-0431-1 |
| [28] |
曾文宪.系数矩阵误差对EIV模型平差结果的影响研究[D].武汉: 武汉大学, 2013. ZENG Wenxian. Effect of the random design matrix on adjustment of an EIV model and its reliability theory[D]. Wuhan: Wuhan University, 2013. |
| [29] | BOX M J. Bias in nonlinear estimation[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1971, 33(2): 171–201. DOI:10.1111/rssb.1971.33.issue-2 |
| [30] | GERHOLD G A. Least-squares adjustment of weighted data to a general linear equation[J]. American Journal of Physics, 1969, 37(2): 156–161. DOI:10.1119/1.1975432 |
| [31] | AMIRI-SIMKOOEI A R, ZANGENEH-NEJAD F, ASGARI J. On the covariance matrix of weighted total least-squares estimates[J]. Journal of Surveying Engineering, 2016, 142(3): 04015014. DOI:10.1061/(ASCE)SU.1943-5428.0000153 |
| [32] |
王乐洋, 赵英文, 陈晓勇, 等.
多元总体最小二乘问题的牛顿解法[J]. 测绘学报, 2016, 45(4): 411–417, 424.
WANG Leyang, ZHAO Yingwen, CHEN Xiaoyong, et al. A newton algorithm for multivariate total least squares problems[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 411–417, 424. DOI:10.11947/j.AGCS.2016.20150246 |
| [33] | WANG Leyang, ZHAO Yingwen. Unscented transformation with scaled symmetric sampling strategy for precision estimation of total least squares[J]. Studia Geophysica et Geodaetica, 2017, 61(3): 385–411. DOI:10.1007/s11200-016-1113-0 |
| [34] |
赵英文.总体最小二乘精度评定方法研究[D].南昌: 东华理工大学, 2017. ZHAO Yingwen. Research on precision estimation method for total least squares[D]. Nanchang: East China University of Technology, 2017. |
| [35] |
於宗俦.
方差-协方差分量估计的统一理论[J]. 测绘学报, 1991, 20(3): 161–171.
YU Zongchou. The uniformity theory of estimation of variance-covariance components[J]. Acta Geodaetica et Cartographica Sinica, 1991, 20(3): 161–171. DOI:10.3321/j.issn:1001-1595.1991.03.001 |
| [36] | TEUNISSEN P J G, AMIRI-SIMKOOEI A R. Least-squares variance component estimation[J]. Journal of Geodesy, 2008, 82(2): 65–82. DOI:10.1007/s00190-007-0157-x |
| [37] |
崔希璋, 於宗俦, 陶本藻, 等.
广义测量平差(新版)[M]. 武汉: 武汉大学出版社, 2005.
CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized surveying adjustment (New Edition)[M]. Wuhan: Wuhan University Press, 2005. |
| [38] |
李博峰.
无缝仿射基准转换模型的方差分量估计[J]. 测绘学报, 2016, 45(1): 30–35.
LI Bofeng. Variance component estimation in the seamless affine transformation model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 30–35. DOI:10.11947/j.AGCS.2016.20140676 |
| [39] |
余航.总体最小二乘联合平差方法及其应用研究[D].南昌: 东华理工大学, 2016. YU Hang. Research on the total least squares joint adjustment and its application[D]. Nanchang: East China University of Technology, 2016. |
| [40] | AMIRI-SIMKOOEI A R. Application of least squares variance component estimation to errors-in-variables models[J]. Journal of Geodesy, 2013, 87(10-12): 935–944. DOI:10.1007/s00190-013-0658-8 |
| [41] | WANG Leyang, XU Guangyu. Variance component estimation for partial errors-in-variables models[J]. Studia Geophysica et Geodaetica, 2016, 60(1): 35–55. DOI:10.1007/s11200-014-0975-2 |
| [42] |
王乐洋, 温贵森.
Partial EIV模型的非负最小二乘方差分量估计[J]. 测绘学报, 2017, 46(7): 857–865.
WANG Leyang, WEN Guisen. Non-negative least squares variance component estimation of Partial EIV model[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 857–865. DOI:10.11947/j.AGCS.2017.20160501 |
| [43] | XU Peiliang, LIU Jingnan. Variance components in errors-in-variables models:estimability, stability and bias analysis[J]. Journal of Geodesy, 2014, 88(8): 719–734. DOI:10.1007/s00190-014-0717-9 |
| [44] | RATKOWSKY D A. Nonlinear regression modeling:a unified practical approach[M]. New York: Marcel Dekker Inc, 1983. |


