2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013;
3. 江西省数字国土重点实验室, 江西 南昌 330013;
4. 南昌航空大学, 江西 南昌 330063
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG, Nanchang 330013, China;
3. Jiangxi Province Key Lab for Digital Land, Nanchang 330013, China;
4. Nanchang Hangkong University, Nanchang 330063, China
测绘数据常存在复杂的不确定性,不确定性是不精确性、模糊性、不明确性等概念的总称。不确定性与误差意义接近,但它涵盖的内容更广,如属性不确定性、模糊不确定性等[1]。不确定度是不确定性的度量,是不确定性的一种指标[2]。不确定度与测量界的精度度量方式几乎完全一致,不确定度可以用方差、均方差、误差区间、误差椭圆、误差椭球表示[1]。测量数据的不确定性不再是一个具体的数值,有时仅知道它们各自在一定的区间内变动,有时仅是一个模糊数,沿用随机误差的分布限定会给测量平差数据处理带来困难[3]。在测绘数据处理领域,应用不确定度理论,研究不确定度评定方法,研究有效降低不确定性的影响等成为研究热点[4-7]。文献[8]在不确定度理论下构建海底数字高程模型;文献[9]从几何的角度分析了最大不确定度对数据的影响,并提出不确定性平差模型解算方法;文献[10—11]应用广义拉格朗日法构造目标函数,更为具体地分析了不确定度的各种情况,并推导了相应的求解公式。在传统最小二乘方法中,由于系数矩阵的病态性进而会导致因观测量微小波动而造成解算结果产生巨大波动,参数估值已严重失真,不是最优解[12],很多学者对此展开了研究,诸如提出了Tikhonov正则化法[13-14]、岭估计法[15-16]等解决病态问题的方法。对于病态情形下的EIV模型应用总体最小二乘进行解算,解算受系数矩阵误差和观测值误差的影响将更加严重[17],学者也提出了病态总体最小二乘的正则化法[18-20]、病态加权总体最小二乘的岭估计解法[21],得到参数估值更加稳定。
当不确定性平差模型出现病态,如何解决病态问题的相关研究较少。考虑到不确定性平差模型中系数矩阵可能出现接近于0的奇异值,如何处理此模型的病态问题是本文研究重点。基于对病态G-M模型、EIV模型下的岭估计法和不确定性平差模型的平差准则分析,以及文献[10]对不确定性平差模型迭代解算算法,本文建立了相应的病态不确定性平差模型及平差准则,该准则加入了稳定泛函,对法矩阵的奇异值进行修正,将模型由严重病态变成病态性较弱或无病态,使得法矩阵求逆变得稳定,并推导了病态不确定性平差岭估计法的迭代解算公式,通过算例对算法进行验证及讨论。
1 不确定性平差模型及平差准则不确定平差模型为
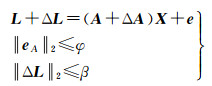 (1)
(1)
式中,ΔA和ΔL分别为系数矩阵A和观测向量L的不确定性误差;φ和β分别是A和L的不确定度;e是L的随机误差;eA=vec(ΔA);‖·‖是向量2-范数。
文献[10]总结出不确定性平差模型的不同情形并对其加以讨论,从而建立的不确定性最小二乘(uncertainty least squares,ULS)平差准则
 (2)
(2)
构造广义拉格朗日目标函数
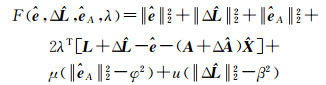 (3)
(3)
式中, λ、μ、u是拉格朗日乘子,ΔA、ΔL的不确定度用代数式表示,整理得到法方程
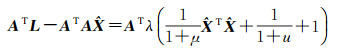 (4)
(4)
令
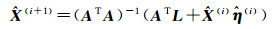 (5)
(5)
用迭代的方法求解参数,可以采用最小二乘估计作为迭代初值,当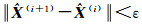
当不确定性平差模型病态时,法方程系数矩阵ATA求逆会变得极不稳定,在以均方误差作为估值参考依据,当法矩阵存在特征值接近于零时,方差将会非常大,导致求解出的参数估值不可靠。
2 病态不确定性平差模型的岭估计根据不确定性平差模型,当系数矩阵A接近0的奇异值,模型的计算公式(5)中,法矩阵求逆将极不稳定,导致求解参数估值可靠性降低。为了降低病态对不确定性平差模型平差结果的影响,在ULS平差准则式(2)中加入稳定泛函,即
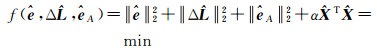 (6)
(6)
式中,α是岭参数。构建广义拉格朗日目标函数
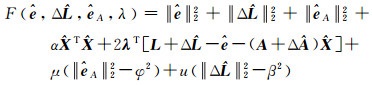 (7)
(7)
求一阶偏导得
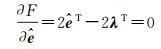 (8a)
(8a)
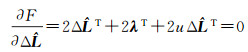 (8b)
(8b)
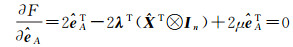 (8c)
(8c)
 (8d)
(8d)
 (8e)
(8e)
 (8f)
(8f)
由式(8)可得
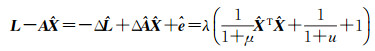 (9)
(9)
根据式(9)可以求得
 (10)
(10)
法方程式
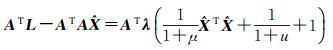 (11)
(11)
从式(8d)可知
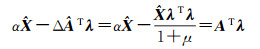 (12)
(12)
将式(12)代入式(11)得
 (13)
(13)
再把式(10)代入式(13)得
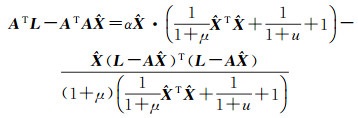 (14)
(14)
在文献[10]中,当φ趋近于正无穷,且β等于零时,式(5)变成总体最小二乘解算方法。同理,当φ趋近于正无穷,且β等于零,根据式(8e)得出μ=0,根据文献[10]中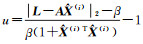

 (15)
(15)
可以看出式(15)为病态总体最小二乘岭估计解算方法,与文献[17]相一致,因此,病态总体最小二乘岭估计是本文病态不确定性平差模型岭估计的特例。
计算前需先确定岭参数α,α常采用L-曲线法确定。根据文献[18]中的介绍,在求总体最小二乘正则化参数时,给定一范围内和步长选择参数并求得结果,再作出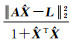


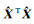
解算步骤如下:
(1) 在计算时先给出系数矩阵A、观测向量L、不确定度φ、β。
(2) 设定迭代初值

(3) 在一范围[a,b]内按一定步长Δd选择α。
(4) 确定u、μ,确定公式参考文献[10]的方法,计算公式为
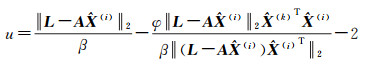 (16a)
(16a)
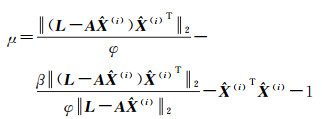 (16b)
(16b)
通过式(16)求出u、μ,要保证迭代值u(i)、μ(i)为非负数,u(i)、μ(i)求解参考文献[10]中的解算步骤部分:
(a)当u、μ均大于0时
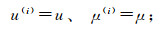
(b) 当u、μ均小于等于0时

(c) 当u>0、μ≤0时

(d) 当u≤0、μ>0时
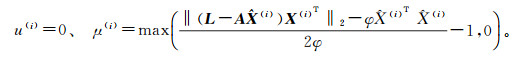
(5) 根据式(14)进行迭代计算
令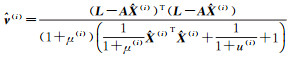
则
 (17)
(17)
当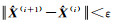
(6) 绘制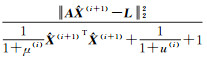

采用文献[17]中的模拟病态问题算例,法矩阵条件数为2.083 8×104,严重病态。未知参数有5个,X=[x1 x2 x3 x4 x5]T,真值为X=[1 1 1 1 1]T。为验证病态不确定最小二乘岭估计法,分别用LS、TLS、ULS、岭估计LS(R-LS)、岭估计TLS(R-TLS)和岭估计ULS(R-ULS)进行解算。由于该数据的不确定度未知,计算时φ、β从不同区间((0,5]、(0,2.5]、(0,1]、(0,0.5]、(0,0.1])随机取值,分别重复计算1000次,比较不同不确定度对结果的影响,结果如表 1所示。
| 方案 | 真值 | LS | TLS | ULS 最优 |
R-LS | R-TLS | R-ULS 最优 |
|
1 | 1.394 4 | 3.305 1 | 2.808 8 | 1.215 7 | 1.210 2 | 1.203 2 |
| 1 | 0.122 3 | -2.804 8 | -2.043 2 | 0.372 8 | 0.377 6 | 0.382 8 | |
| 1 | 0.779 1 | 0.059 6 | 0.247 1 | 0.828 0 | 0.826 1 | 0.822 5 | |
| 1 | 0.262 8 | -3.589 4 | -2.588 3 | 0.598 3 | 0.603 4 | 0.607 9 | |
| 1 | 1.441 4 | 2.903 4 | 2.523 0 | 1.315 7 | 1.313 1 | 1.310 3 | |

|
0 | 1.308 8 | 6.735 0 | 5.319 4 | 0.854 7 | 0.846 8 | 0.838 9 |
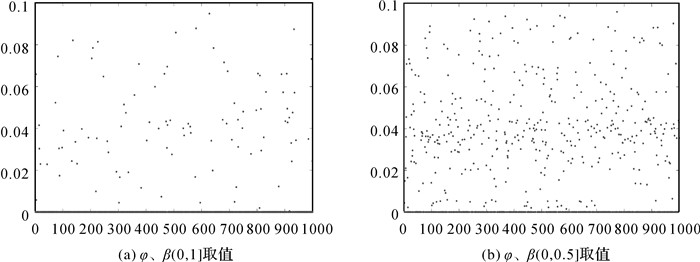
应用L-曲线法确定岭参数,岭参数变化如图 1所示。在确定岭参数α后,φ、β从上述5个给定取值区间随机取值计算试验中发现,R-ULS最低的差值范数

|
| 图 1 各方法L-曲线图 Fig. 1 The L-curve of each methods |

|
| 图 2 不同区间结果 Fig. 2 Different interval results |
|
| 图 3 不同区间结果 Fig. 3 Different interval results |

|
| 图 4 φ、β(0,0.1]结果 Fig. 4 φ、β(0, 0.1) results |
4.2 算例2
采用文献[23]空间测边网算例。P1、P2、…、P10为10个已知点,其坐标具体数据略去。10个已知点到3个未知点P11、P12、P13(假设模拟坐标真值分别为(0,0,0)、(68,-26,9)和(14,41,-11))的距离,以及3个未知点间的距离假定已通过测量得到。设各距离为等精度观测,中误差为±0.01 m。根据33个距离观测值确定3个未知点坐标。计算中3个未知点坐标近似值分别取(0.03 m,-0.025 m,0.01 m)、(68.03 m,-25.97 m,8.98 m)和(14.04 m,40.97 m,-11.04 m)。该测边网所建立观测方程的系数阵A严重病态,法矩阵条件数为89 543。为验证病态不确定最小二乘岭估计法,分别用LS、TLS、ULS、R-LS、R-TLS和R-ULS进行解算,由于该数据的不确定度未知,计算时φ、β也从不同区间((0,5]、(0,2.5]、(0,1]、(0,0.5]、(0,0.1])随机取值重复计算1000次,比较不同不确定度对结果的影响,结果见表 2。
| 方案 | 真值 | LS | TLS | ULS | R-LS | R-TLS | R-ULS 最优 |

|
0 | 0.053 0 | 不收敛 | 不收敛 | 0.052 4 | 0.044 4 | 0.041 2 |
| 0 | -0.084 6 | -0.069 8 | -0.022 8 | -0.012 6 | |||
| 0 | -0.805 3 | -0.681 9 | -0.163 7 | -0.057 5 | |||
| 68 | 68.040 0 | 68.040 6 | 68.039 5 | 68.031 3 | |||
| -26 | -26.030 3 | -25.905 3 | -25.912 9 | -25.930 5 | |||
| 9 | 8.511 3 | 8.947 2 | 8.961 6 | 8.964 4 | |||
| 14 | 14.007 2 | 14.007 8 | 14.006 7 | 14.008 4 | |||
| 41 | 40.808 0 | 40.945 3 | 40.965 4 | 40.968 1 | |||
| -11 | -11.585 7 | -11.131 6 | -11.028 4 | -11.012 2 | |||

|
0 | 1.131 3 | — | — | 0.711 6 | 0.204 8 | 0.116 1 |
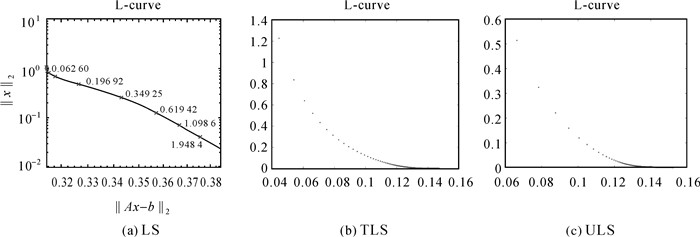
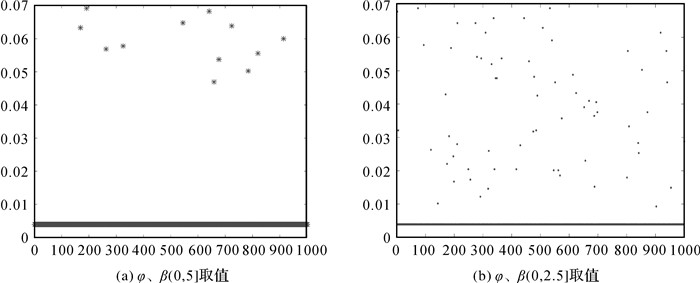
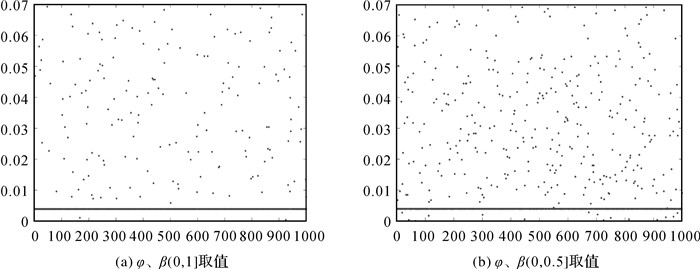
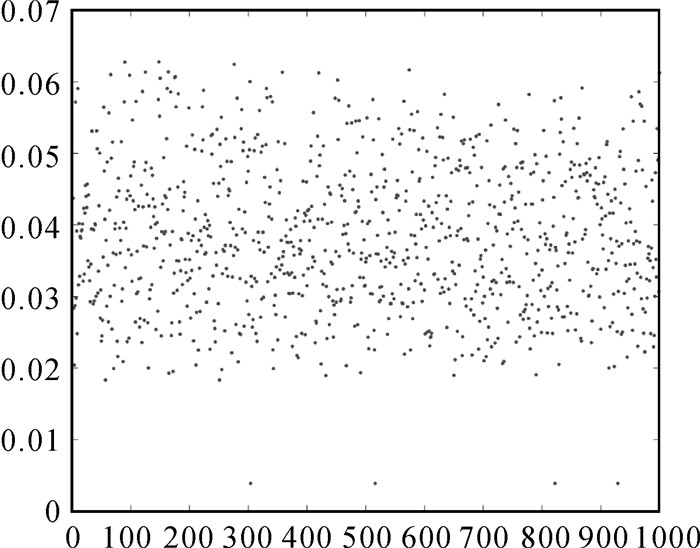
应用L-曲线法确定岭参数,岭参数变化如图 5所示,确定岭参数后,φ、β随机取值计算中发现R-ULS最低的差值范数为0.112 2,但出现的次数太少,而出现最多的差值范数是0.116 1,所以把差值范数为0.116 1时的参数估值作为最优估值。为验证不同不确定度时R-ULS的可行性,本文在给定5个取值区间再次分别重复计算1000次,并将所得差值范数减去0.112 2并作出相应的散点图(横坐标为计算次数,纵坐标为差值范数减0.112 2),纵坐标为0时差值范数则为0.112 2,结果如图 6、图 7和图 8所示。
|
| 图 5 各方法L-曲线图 Fig. 5 The L-curve of each method |
|
| 图 6 不同区间结果 Fig. 6 Different interval results |
|
| 图 7 不同区间结果 Fig. 7 Different interval results |
|
| 图 8 φ、β(0,0.1]结果 Fig. 8 Results of φ、β(0, 0.1) |
4.3 算例分析
病态情况是法矩阵出现几个接近于零的特征值,从而法矩阵求逆将变得极不稳定,导致参数估值与真值偏差较大。在两算例中,岭参数用L-曲线法确定。L-曲线图如图 1、图 5所示,岭参数则为图中的拐点处曲率最大的点对应的值。两算例LS估计差值范数均比TLS、ULS估计低,说明TLS和ULS均比LS受病态情况影响更为严重,对病态性更敏感。
岭估计削弱或消除法矩阵的病态性,使得法矩阵求逆变得稳定,有效地抑制住病态带来的影响。将岭估计运用于病态情况下的LS估计和TLS估计,算例1得到参数估值的差值范数分别是0.854 7、0.846 8,算例2得到结果分别是0.711 6、0.204 8,均优于相应的LS、TLS、ULS方法得到结果。病态不确定性平差模型应用岭估计法可以有效地提高了参数估计解算结果的稳定性。两算例中R-ULS最优的差值范数分别为0.838 9、0.116 1,较R-LS、R-TLS解算结果更优,说明岭估计可用于病态不确定性平差模型解算。
由于不确定度φ、β是未知的,在试验过程中不确定度是上述5个取值区间的随机数,分别重复计算1000次,发现R-ULS存在最优解。根据两算例的散点图,在(0,5]区间中,算例1的0.838 9出现次数最多且最低(纵坐标为参数差值范数减0.838 9);算例2的0.116 1出现次数最多(纵坐标为参数差值范数减0.112 2),存在最低的0.112 2,但出现次数太少。在参数真值已知情况下,可根据差值范数大小确定最优估值。随着区间进一步缩小,最优值出现概率在降低,不同的不确定度得出不同的结果,可从(0,1]、(0,0.5]、(0,0.1]3个取值区间相应图形看出最优值出现概率在降低。此外,从两算例的散点图发现不同不确定度参数估值的差值范数是在一定区间内变化,算例1是在区间范围[0.838 9,0.938 9],算例2是区间范围[0.112 2,0.182 2]。说明病态不确定性平差模型岭估计解受不确定性有界的约束,在不确定度较小时,不确定性约束更为明显。同时进一步说明随着不确定度增大,病态不确定性平差模型岭估计解对不确定度的敏感程度在降低。
5 结论本文分析了当不确定性平差模型出现病态时,ULS受病态情形的影响,提出基于岭估计,同时顾及系数矩阵和观测向量出现不确定性误差,推导了病态不确定性平差模型的岭估计平差准则,推导了迭代算法,以提高解的稳定性。通过算例结果表明,R-ULS能够有效地抑制病态的影响和降低差值范数,说明了提出的病态不确定性平差模型岭估计法具有一定的有效性。同时从算例得出,病态不确定性模型的岭估计解受不确定度影响,影响程度随着不确定度增大而降低。
| [1] |
杨元喜.
卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646–650.
YANG Yuanxi. Some notes on uncertainty, uncertainty measure and accuracy in satellite navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646–650. |
| [2] |
陶本藻.
GIS质量控制中不确定度理论[J]. 测绘学院学报, 2000, 17(4): 235–238.
TAO Benzao. Basic theory of uncertainty of quality control in GIS[J]. Journal of Institute of Surveying and Mapping, 2000, 17(4): 235–238. DOI:10.3969/j.issn.1673-6338.2000.04.001 |
| [3] |
宋迎春, 谢雪梅, 陈晓林.
不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135–141.
SONG Yingchun, XIE Xuemei, CHEN Xiaolin. Adjustment criterion and algorithm in adjustment model with uncertain[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135–141. DOI:10.11947/j.AGCS.2015.20130213 |
| [4] |
杨元喜.
关于"新的点位误差度量"的讨论[J]. 测绘学报, 2009, 38(3): 280–282.
YANG Yuanxi. Discussion on "a new measure of positional error"[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 280–282. DOI:10.3321/j.issn:1001-1595.2009.03.015 |
| [5] |
王新洲.
最小不确定度约束下的极大可能性估计[J]. 测绘工程, 2003, 12(1): 5–8.
WANG Xinzhou. Maximum possibility estimation restricted by least uncertainty[J]. Engineering of Surveying and Mapping, 2003, 12(1): 5–8. DOI:10.3969/j.issn.1006-7949.2003.01.002 |
| [6] |
陶本藻.
精确度和不确定度估计及应用[J]. 勘察科学技术, 2003(5): 24–27.
TAO Benzao. Estimation of accuracy and uncertainty and its application[J]. Site Investigation Science and Technology, 2003(5): 24–27. DOI:10.3969/j.issn.1001-3946.2003.05.009 |
| [7] |
陈伟, 张践.
最小不确定度估计及其在测量数据处理中的应用[J]. 测绘通报, 2013(1): 16–18, 32.
CHEN Wei, ZHANG Jian. Least uncertainty estimation theory and its applications in survey data processing[J]. Bulletin of Surveying and Mapping, 2013(1): 16–18, 32. |
| [8] |
邹永刚, 翟京生, 刘雁春, 等.
利用不确定度的海底数字高程模型构建[J]. 武汉大学学报(信息科学版), 2011, 36(8): 964–968.
ZOU Yonggang, ZHAI Jingsheng, LIU Yanchun, et al. Seabed DEM construction based on uncertainty[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 964–968. |
| [9] |
宋迎春, 金昊, 崔先强.
带有不确定性的观测数据平差解算方法[J]. 武汉大学学报(信息科学版), 2014, 39(7): 788–792.
SONG Yingchun, JIN Hao, CUI Xianqiang. Adjustment algorithm about observation data with uncertain[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 788–792. |
| [10] |
王志忠, 陈丹华, 宋迎春.
具有不确定性平差算法[J]. 测绘学报, 2017, 46(7): 834–840.
WANG Zhizhong, CHEN Danhua, SONG Yingchun. An algorithm in adjustment model with uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 834–840. DOI:10.11947/j.AGCS.2017.20160522 |
| [11] |
王志忠, 宋迎春, 何玲莉.
系数矩阵中部分有界不确定性的混合平差算法[J]. 测绘学报, 2018, 47(9): 1171–1178.
WANG Zhizhong, SONG Yingchun, HE Lingli. Mixed adjustment algorithm for part of the coefficient matrix with uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(9): 1171–1178. DOI:10.11947/j.AGCS.2018.20170344 |
| [12] |
崔希璋, 於宗俦, 陶本藻, 等.
广义测量平差[M]. 武汉: 武汉大学出版社, 2009: 9.
CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized surveying adjustment[M]. Wuhan: Wuhan University Press, 2009: 9. |
| [13] | TIKHONOV A. Solution of incorrectly formulated problems and the regularization method[J]. Soviet Math Dokl, 1963, 5(4): 1035–1038. |
| [14] | TIKHONOV A N, ARSENIN V Y. Solutions of ill-posed problems[M]. New York: John Wiley & Sons, 1977. |
| [15] | HOERL A E, KENNARD R W. Ridge regression:biased estimation for nonorthogonal problems[J]. Technometrics, 1970, 12(1): 55–67. DOI:10.1080/00401706.1970.10488634 |
| [16] | HOERL A E, KENNARD R W. Ridge regression:applications to nonorthogonal problems[J]. Technometrics, 1970, 12(1): 69–82. DOI:10.1080/00401706.1970.10488635 |
| [17] |
鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用[D].武汉: 武汉大学, 2010. LU Tieding. Research on the total least squares and its applications in surveying data processing[D]. Wuhan: Wuhan University, 2010. |
| [18] |
葛旭明, 伍吉仓.
病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372–377.
GE Xuming, WU Jicang. Generalized regularization to ill-posed total least squares problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372–377. |
| [19] |
袁振超, 沈云中, 周泽波.
病态总体最小二乘模型的正则化算法[J]. 大地测量与地球动力学, 2009, 29(2): 131–134.
YUAN Zhenchao, SHEN Yunzhong, ZHOU Zebo. Regularized total least-squares solution to ill-posed error-in-variable model[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 131–134. |
| [20] |
葛旭明, 伍吉仓.
误差限的病态总体最小二乘解算[J]. 测绘学报, 2013, 42(2): 196–202.
GE Xuming, WU Jicang. A regularization method to ill-posed total least squares with error limits[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 196–202. |
| [21] |
王乐洋, 许才军, 鲁铁定.
病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报(信息科学版), 2010, 35(11): 1346–1350.
WANG Leyang, XU Caijun, LU Tieding. Ridge estimation method in ill-posed weighted total least squares adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1346–1350. |
| [22] |
王振杰, 欧吉坤.
用L-曲线法确定岭估计中的岭参数[J]. 武汉大学学报(信息科学版), 2004, 29(3): 235–238.
WANG Zhenjie, OU Jikun. Determining the ridge parameter in a ridge estimation using L-curve method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3): 235–238. |
| [23] |
郭建锋.测量平差系统病态性的诊断与处理[D].郑州: 信息工程大学, 2002. GUO Jianfeng. The diagnosis and process of ill-conditioned adjustment system[D]. Zhengzhou: Information Engineering University, 2002. |



