2. 河南理工大学测绘与国土信息工程学院, 河南 焦作 454000
2. School of Surveying and Land Information Engineering Henan Polytechnic University, Jiaozuo 454000, China
Voronoi图(简称V图)是计算几何学中一个重要的数据结构,具有自然邻近、动态稳定等特性,在计算机图形学、地理信息系统、生态学、分子化学、气象学、机械、医学、艺术等领域得到了广泛应用[1-6]。其中,V图结构的高效、准确生成是其诸多应用顺利实现的关键。国内外学者对V图生成算法进行了许多研究,其成果主要分为矢量算法和栅格算法两类。
经典矢量算法包括分治算法[7]、插入算法[8]、扫描线算法[9]、投影算法[10]等。矢量算法对生长元有一定的局限性[11],只能将点和线段(或半线)作为生长元处理,较难生成线集图[12],对于面和其他更复杂的空间目标要将其分解为点和线后才能处理,这种分解严重地破坏了空间生长目标的完整性。矢量算法不仅算法复杂,而且产生的数据结构复杂,不利于海量数据的处理[13]。
为弥补矢量算法的不足,许多学者提出了基于栅格数据的V图生成算法。栅格V图生成算法的关键是为每个格网找到距其最近的种子点(或线、面)。依据格网得到种子点归属方法的不同,现有栅格V图生成算法可分为3类。第一类算法,是较为传统的通过多边形的扩张和距离变换来得到V图,如距离变换算法[13-14]、扩张算法[15-16]等。这类算法通过使用栅格距离代替欧氏距离来提升效率,所用模板有棋盘距离、城市距离、八角距离等。这些距离指标只是最优距离度量(欧几里得距离)的粗略近似。这类算法的误差很难控制,随着格网和种子点数量增多而加大。第二类算法是利用四叉树等数据结构通过区域划分并判断区域归属的方式来得到V图,如层次算法[17-18]、细分算法[19]等。此类算法大多较为复杂,不同层次、区域拓扑关系不明朗,且很难动态添加删除数据。第三类算法是通过计算与比较格网与种子点之间的距离得到V图,如确定归属算法[20-21]、栅格扫描算法[22]等。此类算法使用欧氏距离作为距离基准,大多具有较好的精度指标。除此之外,一些学者也通过并行计算来对上述各类算法的效率进行改进[16, 21, 23-24],但是通常情况下,计算机技术并不能提升算法的精度。
综合精度和效率因素,栅格扫描算法是最优的栅格V图生成算法之一。此类算法通常利用邻域模板对所有格网进行向前向后两次扫描得到V图。算法既符合计算机离散特征,又优化了欧氏距离算法,在大数据量情况下,较其他第三类栅格V图生成算法具有效率上的优势[25]。但是由于栅格距离与欧氏距离的差异,在扫描过程中部分单元的归属不可避免地产生一定的误差[26]。然而,在地图、军事、医学[3-5]等高精度领域的应用中,V图的误差可能会造成严重的后果。例如,在海洋划界工作中,V图是问题的理想解决办法[6]。不过,在海洋区域的划界中出现任何位置误差,就会增加一个国家的海洋空间,而损害另一个国家的海洋空间。这种情况可能对有关国家的经济、军事活动和国家关系产生严重影响。
为此,本文提出了一种基于横-纵扫描的V图生成改进算法,即根据传统算法产生误差的区域特征,在一个正常周期的水平(横向)扫描后,增加一个周期竖直(纵向)扫描,实现栅格V图的高效、准确生成,并把误差控制在一个格网以内,最后进行了试验对比分析。
1 传统扫描算法原理及缺陷 1.1 传统扫描算法原理与矢量空间Voronoi区域是连续的相同,在栅格空间,一般情况下Voronoi区域也是连续的,即一个栅格格网和它的部分邻近格网属于相同的Voronoi区域。根据这个特点,利用邻近格网之间最近种子点的传递,格网就可以从它邻近格网处得到它所属的Voronoi区域,而不必与所有种子点进行距离比较。
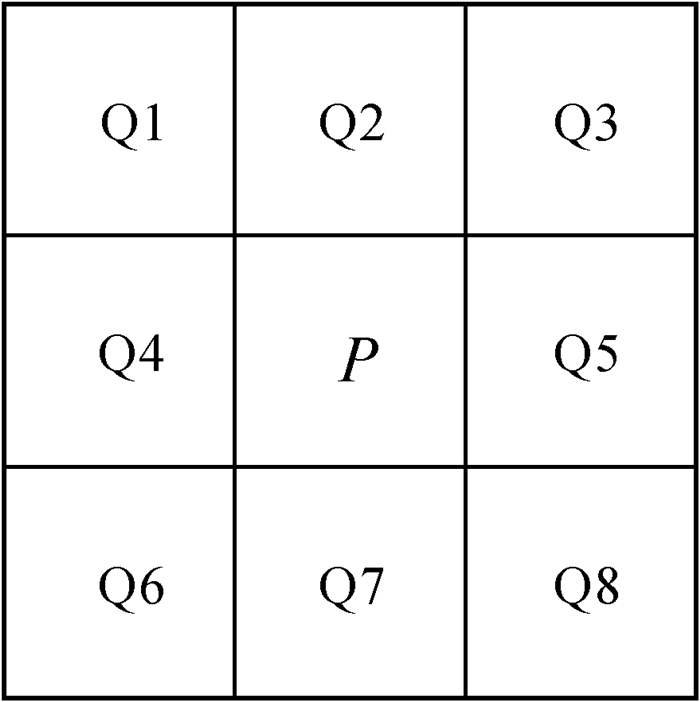
传统栅格扫描算法[22]原理是通过一个3×3的邻域模板将一个格网的信息传递给它的邻近格网(如图 1所示)。首先,进行正反两次扫描:扫描开始之前格网P被赋予一个空值,正向扫描按从左到右、从上到下的顺序逐行进行,扫描过程中格网P分别计算并比较与Q1、Q2、Q3和Q4这4个邻近格网(临时)最近种子点之间的距离,然后将距离最短的种子点作为当前格网P的(临时)最近种子点,可用公式(1)来表示;反向扫描按从右到左、从下到上的顺序逐行进行扫描,通过距离的计算与比较从P的临时最近种子点及Q5、Q6、Q7和Q8的最近种子点中获取P的最终最近种子点。一般情况下,Q1到Q8至少有一个与格网P有相同的最近种子点。在正反两次扫描过程中,格网P通过与其邻近格网的(临时)最近种子点的距离计算与比较得到其最近种子点,这一过程称为格网P得到其正确归属种子点。
|
| 图 1 3×3邻域示意图 Fig. 1 3 × 3 neighborhood diagram |
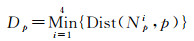 (1)
(1)
式中,Dp为格网P到(临时)最近种子点的距离;Npi为格网P的第i个邻近格网的最近种子点;函数Dist(a, b)的作用为计算种子点a到格网b的距离。
1.2 传统算法缺陷分析本文将一次正向扫描和一次反向扫描称作一个水平周期扫描。按上述算法进行了一个周期扫描之后,大多数的格网单元都得到了正确的种子点,但仍有少数格网单元的归属信息是错误的(如图 2)。
|
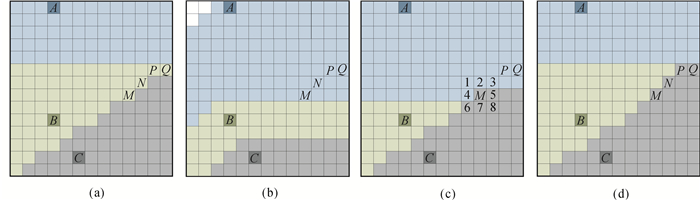
| 图 2 出现错误的原因 Fig. 2 Reason of sweeping errors |
如图 2所示,格网A、B和C为该V图种子点,其正确结果如图 2(a)所示,格网M、N、P和Q的正确归属均为种子点B。但是,一个水平扫描周期后,格网M、N、P和Q没有得到其正确归属,如图 2(d)。这是由于正向扫描为从上到下的逐行扫描,格网M、N、P和Q的扫描顺序在种子点B之前,它们归属判断的种子点并不包括种子点B,正向扫描完成后这4个格网暂时归属于种子点A,如图 2(b)所示;当反向扫描到格网M时,此时它的邻近格网5-8归属于种子点C,格网1-4归属于种子点A,格网M只能从其临近格网的归属(种子点A和C)中进行判断比较,而不能得到其正确归属(种子点B),如图 2(c)。在整个水平扫描周期过程中,正反两次与格网M进行距离计算和比较的种子点中都没有包括其正确的最近种子点(种子点B),造成了错误的出现。
扫描算法核心是在扫描过程中通过每个格网的与部分种子点之间的距离计算和比较得到该格网的最近种子点。然而由于传统算法扫描的不完备,上述错误的出现主要因为在扫描过程中对某一格网(如格网M)所进行的距离计算与比较并没有包括其最近种子点,致使该格网的归属出现错误。图 3(a)为一随机种子点情况下传统栅格扫描算法得到的V图,图 3(c)为确定归属算法得到的正确的V图,可以看出它们之间有较大的差异,如图 3(b)黑色区域所示。

|
| 图 3 一周期水平扫描后出现的误差 Fig. 3 Errors after the horizontal cycle sweeps |
也有学者在扫描算法结果的基础上,进行多周期的相同扫描过程以减少不正确归属格网的数量,但是为得到正确V图,重复扫描周期的次数n是难以控制的。
2 改进算法 2.1 归属出错单元范围界定首先分析种子点经一个周期扫描后错误归属单元的空间分布特征。
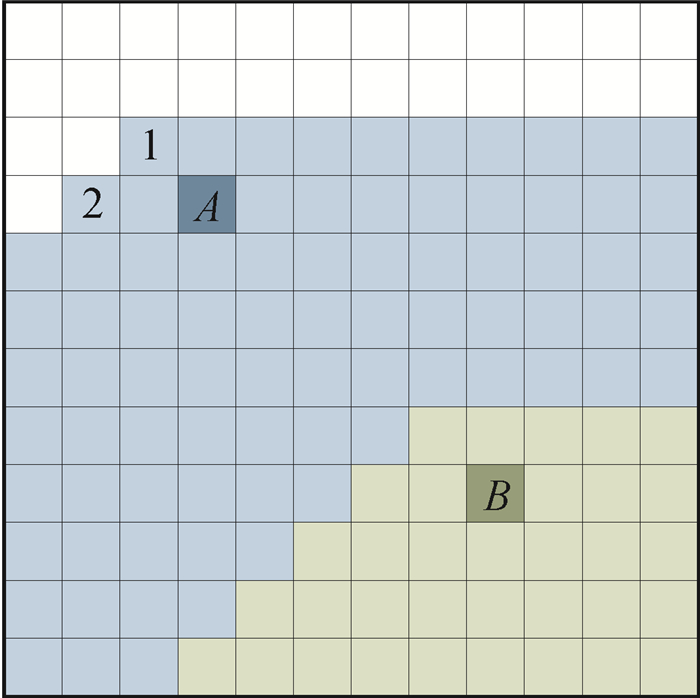
如图 4所示,格网A和格网B为种子点。在进行正向扫描时,扫描顺序为从左到右、从上到下顺序逐行进行扫描。因为所选模板为3×3模板,所以扫描顺序在种子点A左上方格网1之前的格网,都没有计算和比较过与种子点A之间的距离。与格网1为同一行且扫描顺序在格网1之后的格网,都可以从其左侧格网处得到种子点A。种子点A同一行的格网中,最早得到种子点A的是格网2,它是从其右上方格网1处得到的。这样临时归属于种子点A的格网就形成了一个135°的角度,由格网1向左下方延伸。在扫描到达种子点B附近时,经过了与种子点A相同过程。于是在正向扫描结束时,就形成了如图 4所示的临时种子点归属图,其中浅蓝色格网归属于种子点A,浅绿色格网归属于种子点B。
|
| 图 4 单次正向扫描结果 Fig. 4 Result of single positive scan |
单次反向扫描过程与正向扫描过程类似。其结果如图 5所示。

|
| 图 5 单次反向扫描结果 Fig. 5 Result of single reverse scan |
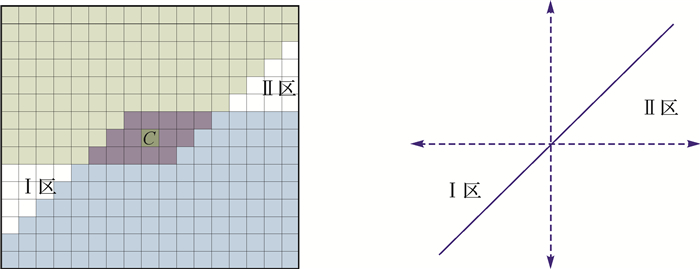
在传统扫描算法中,一个格网需经过正反两次扫描,如果其在任意一次扫描过程中得到正确种子点,那么便能得到正确归属。如图 6所示,蓝色部分格网在正向扫描后必定可以得到种子点C,绿色部分格网在反向扫描时必定可以得到种子点C,紫色部分格网是它们的重合部分。白色部分格网想要得到种子点C就需要反向扫描时蓝色格网的传递,如果传递被阻隔的话(例如图 2),那么部分格网就不能得到其正确归属,造成单元归属出错。从上面的分析可以看出:可能出现归属错误的区域单元(图 6白色单元)位于其正确种子点的左下方(Ⅰ区)与右上方(Ⅱ区)。
|
| 图 6 正反扫描后一定能得到种子点的区域 Fig. 6 The area which can get the seed point after the positive and reverse scanning |
2.2 改进方法
在找到了出现单元归属错误的区域后,本文设计了一种水平扫描后接竖直扫描的解决方案。竖直扫描保持数据结构不变,扫描模板仍为3×3模板(如图 1所示)。竖直扫描方向为竖直方向,扫描顺序为先从左上角开始由下至上的逐列向右扫描一次为正向扫描,模板中心格网P从Q1、Q4、Q6和Q2这4个邻近格网中得到其最近种子点。再从右下角开始从下至上的逐列向左扫描一次为反向扫描,模板中心格网P从Q8、Q5、Q3和Q2这4个邻近格网中得到其最近种子点。正反两次扫描称为一个竖直扫描周期。
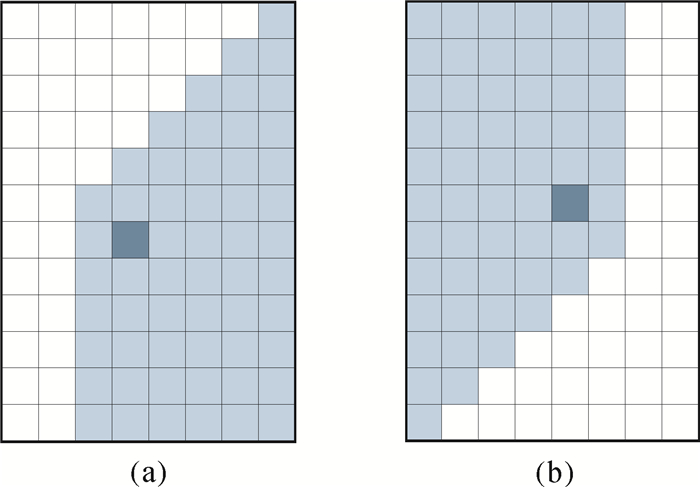
与水平扫描周期相同,竖直扫描周期正反扫描同样具有类似的过程,其结果如图 7所示,其中图 7(a)为单次正向扫描后的结果,图 7(b)为单次反向扫描后的结果。
|
| 图 7 竖直扫描周期单次正反扫描后结果 Fig. 7 The result of single positive and reverse scan of vertical scanning cycle |
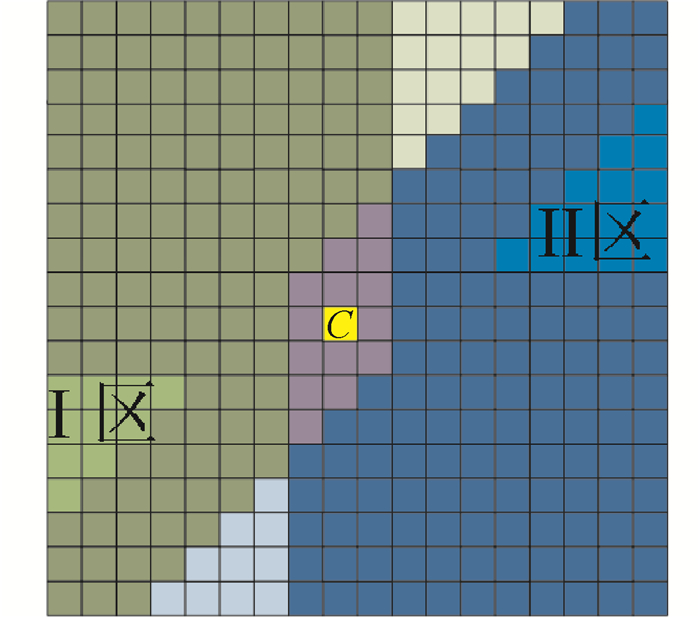
水平扫描后接竖直扫描的解决方案对一个格网进行两个周期共4次扫描,可以完全覆盖该种子点周围所有区域,如图 8所示。蓝色格网为竖直周期正向扫描覆盖区域,绿色格网为竖直周期反向扫描覆盖区域,紫色区域为他们重合区域。左侧的浅绿色区域(Ⅰ区)和右侧的浅蓝色区域(Ⅱ区)为水平周期无法完全覆盖的区域,但是可以被竖直周期覆盖。这样就保证了种子点周围所有区域在经过水平、竖直两个周期扫描后都可以得到该种子点。
|
| 图 8 水平加竖直两周期扫描后结果 Fig. 8 The results of horizontal plus vertical two-period scan |
3 试验与分析
确定归属算法是根据V图定义,计算并比较所有栅格与每一个种子点之间的距离,来确定格网单元的最近种子点。其需要进行大量的距离计算与比较,随着空间分辨率的增大,要处理的数据量急剧上升,算法效率大大降低,实际操作性较差。但是其算法精度高,相较于正确矢量结果,其误差在一个格网以内。因此,本文选择确定归属算法作为算法精度评判的基准。
本文算法所用的编程语言为C++,显示所用的三维图形接口为Microsoft OpenSceneGraph SDK (17.1),硬件环境为Intel(R) Core(TM) i5-3337U CPU @1.80 GHz,2.70 GB内存。并与改正前算法和确定归属算法在精度和效率方面进行了对比,如图 9为改正后算法在10、100和1000种子点数量时生成的结果示意图,表 1为确定归属算法、原扫描算法和改正后的算法在不同格网数和不同种子点数情况下所花费的时间。

|
| 图 9 不同种子点数生成结果示意图 Fig. 9 The results of different seed points |
| 格网数 | 种子点数 | 确定归属算法/ms | 原扫描算法t1/ms | 改进后扫描算法t2/ms | t2/t1 |
| 100×100 | 20 | 18 | 19 | 25 | 1.26 |
| 300×300 | 50 | 177 | 109 | 137 | 1.26 |
| 1000×1000 | 100 | 3232 | 1230 | 1518 | 1.23 |
| 1000×1000 | 1000 | 23 895 | 1239 | 1536 | 1.23 |
| 3000×3000 | 10 000 | — | 14 375 | 17 066 | 1.18 |
| 10 000×10 000 | 50 000 | — | 171 055 | 199 673 | 1.17 |
由表 1可以看出,在格网数和种子点数较少情况下,确定归属算法与扫描算法效率相差不大。但是在数据量较大的情况下,扫描算法具有明显的速度优势,且随着格网数和种子点数量的增加这种优势越来越明显。而改进后扫描算法与原算法效率大体相当。
图 10为在3000×3000格网数情况下,3种算法所需时间随种子点数量增加而变化的情况,确定归属算法在10 000种子点数量情况下由于所需时间太长而无法在图中表示。由图可以看出,确定归属算法那所需时间随种子点数量增加而剧烈增加,而扫描算法时间几乎不变。改正后的算法在时间上略高于原算法,但远低于确定归属算法。

|
| 图 10 各算法效率情况 Fig. 10 The efficiency of different algorithms |
为验证本文算法精度,使用公式(2)对原栅格扫描算法和改进后算法与确定归属算法的结果误差进行了计算。式中,函数Dist(a, b)的作用用于计算种子点与格网之间的距离,Ni和N′ i为分别利用确定归属算法和扫描算法计算得到的最近种子点。结果如表 2所示。
| Δd | 100×100 | 300×300 | 1000×1000 | ||||||
| 0-1 | 1-3 | 3以上 | 0-1 | 1-5 | 5以上 | 0-1 | 1-10 | 10以上 | |
| 原算法 | 75 | 22 | 3 | 28 | 67 | 5 | 2 | 54 | 44 |
| 改进后 | 100 | 0 | 0 | 100 | 0 | 0 | 100 | 0 | 0 |
| 注:表中数字表示100次随机试验中两种算法得到的格网的最大误差在各区间的数量。 | |||||||||
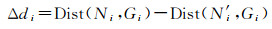 (2)
(2)
由上表可以看出,原算法大概率会出现单元归属错误,且误差随数据量的增加而增加,严重影响了某些需要高精度的应用,而改进后的算法,以确定归属算法生成结果为基准,生成的V图把每个格网的误差都控制在了一个格网以内,所以本文提出的算法达到了与确定归属算法相当的精度。
4 结论本文在深入分析了传统扫描算法产生误差缺陷的原因和区域特征后,在传统栅格扫描算法基础上,提出了一种基于横-纵扫描的V图生成改进算法,并进行了相关效率和精度试验,结果表明:
(1) 改进后的算法保留了扫描算法效率上的优势,在大数据量情况下速度远高于确定归属算法,与原扫描算法的效率基本一致。
(2) 改进后算法弥补了原算法不完备的扫描缺陷,在高效生成的同时把误差限制在一个格网以内,达到了与确定归属算法相当的精度。
| [1] |
周培德.
计算几何:算法分析与设计[M]. 北京: 清华大学出版社, 2000.
ZHOU Peide. Computational geometry:algorithm analysis and design[M]. Beijing: Tsinghua University Press, 2000. |
| [2] |
普雷帕拉塔F P, 沙莫斯M I.计算几何导论[M].庄心谷, 译.北京: 科学出版社, 1990. PREPALATA F P, SHAMOS M I. Computational geometry[M]. ZHUANG Xingu, trans. Beijing: Science Press, 1990. |
| [3] |
刘小凤, 吴艳兰, 胡海.
面状要素的多层次骨架线提取[J]. 测绘学报, 2013, 42(4): 588–594.
LIU Xiaofeng, WU Yanlan, HU Hai. A method of extracting multiscale skeletons for polygonal shapes[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 588–594. |
| [4] |
张雯.医学可视人真彩图像分割技术研究[D].西安: 西北工业大学, 2005. ZHANG Wen. Research on medical visualization of human color image segmentation technology[D]. Xi'an: Northwestern Polytechnical University, 2005. http://cdmd.cnki.com.cn/article/cdmd-10699-2005065131.htm |
| [5] |
陆晓庆.多飞行器协同航路规划与编队控制方法研究[D].南昌: 南昌航空大学, 2014. LU Xiaoqing. Research on route planning and formation control method for multi aircraft cooperative[D]. Nanchang: Nanchang Hangkong University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10406-1014059143.htm |
| [6] | KASTRISIOS C, TSOULOS L. A cohesive methodology for the delimitation of maritime zones and boundaries[J]. Ocean & Coastal Management, 2016(130): 188–195. |
| [7] | SHAMOS M I, HOEY D. Closest-point problems[C]//Proceedings of the 16th Annual Symposium on Foundations of Computer Science. Washington, DC: IEEE Computer Society, 1977: 151-162. |
| [8] | GREEN P J, SIBSON R. Computing dirichlet tessellations in the plane[J]. The Computer Journal, 1978, 21(2): 168–173. DOI:10.1093/comjnl/21.2.168 |
| [9] | FORTUNE S. A sweepline algorithm for voronoi diagrams[J]. Algorithmica, 1987, 2(1-4): 153–174. DOI:10.1007/BF01840357 |
| [10] | BROWN K Q. Geometric transforms for fast geometric algorithms[D]. Pittsburgh: Carnegie Mellon University, 1979. |
| [11] | HELD M. VRONI:An engineering approach to the reliable and efficient computation of Voronoi diagrams of points and line segments[J]. Computational Geometry, 2001, 18(2): 95–123. DOI:10.1016/S0925-7721(01)00003-7 |
| [12] | OKABE A, BOOTS B, SUGIHARA K, et al. Spatial tessellations:concepts and applications of Voronoi diagrams[M]. 2nd ed. London: John Wiley & Sons, Inc, 2000. |
| [13] |
李成明, 陈军.
Voronoi图生成的栅格算法[J]. 武汉大学学报信息科学版, 1998, 23(3): 208–210.
LI Chengming, CHEN Jun. Raster-based method for Voronoi diagram[J]. Geomatics and Information Science of Wuhan University, 1998, 23(3): 208–210. |
| [14] | CHEN J. A raster-based method for computing Voronoi diagrams of spatial objects using dynamic distance transformation[J]. International Journal of Geographical Information Science, 1999, 13(3): 209–225. DOI:10.1080/136588199241328 |
| [15] | RONG Guodong, TAN T S. Variants of jump flooding algorithm for computing discrete Voronoi diagrams[C]//Proceedings of the 4th International Symposium on Voronoi Diagrams in Science and Engineering. Glamorgan, UK: IEEE, 2007: 176-181. |
| [16] | GUO Licai, WANG Feng, HUANG Zhangjin, et al. A fast and robust seed flooding algorithm on GPU for Voronoi diagram generation[C]//Proceedings of 2011 International Conference on Electrical and Control Engineering. Yichang, China: IEEE, 2011: 492-495. |
| [17] |
李佳田, 陈军, 赵仁亮, 等.
基于线性四叉树结构的Voronoi图反向膨胀生成方法[J]. 测绘学报, 2008, 37(2): 236–242.
LI Jiatian, CHEN Jun, ZHAO Renliang, et al. A backward inflation generating method for voronoi diagram based on linear quadtree structure[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 236–242. DOI:10.3321/j.issn:1001-1595.2008.02.019 |
| [18] | LIANG E H, LIN S G. A hierarchical approach to distance calculation using the spread function[J]. International Journal of Geographical Information Science, 1998, 12(6): 515–535. DOI:10.1080/136588198241653 |
| [19] |
寿华好, 袁子薇, 缪永伟, 等.
一种平面点集Voronoi图的细分算法[J]. 图学学报, 2013, 34(2): 1–6.
SHOU Huahao, YUAN Ziwei, MIAO Yongwei, et al. A subdivision algorithm for a planar point set Voronoi grap[J]. Journal of Graphics, 2013, 34(2): 1–6. DOI:10.3969/j.issn.2095-302X.2013.02.001 |
| [20] |
王新生, 刘纪远, 庄大方, 等.
一种新的构建Voronoi图的栅格方法[J]. 中国矿业大学学报, 2003, 32(3): 293–296.
WANG Xinsheng, LIU Jiyuan, ZHUANG Defang, et al. New raster-based method for constructing Voronoi diagrams[J]. Journal of China University of Mining & Technology, 2003, 32(3): 293–296. DOI:10.3321/j.issn:1000-1964.2003.03.019 |
| [21] | MAJDANDZIC I, TREFFTZ C, WOLFFE G. Computation of Voronoi diagrams using a graphics processing unit[C]//Proceedings of 2008 IEEE International Conference on Electro/Information Technology, 2008. Ames, IA: IEEE, 2008: 437-441. https://www.researchgate.net/publication/4347002_Computation_of_Voronoi_diagrams_using_a_Graphics_Processing_Unit |
| [22] | SHIH F Y, WU Yiya. Fast euclidean distance transformation in two scans using a 3×3 neighborhood[J]. Computer Vision and Image Understanding, 2004, 93(2): 195–205. DOI:10.1016/j.cviu.2003.09.004 |
| [23] |
李淑艳, 曹菡, 刘妮玲.
Voronoi图的并行生成算法研究[J]. 郑州轻工业学院学报(自然科学版), 2010, 25(1): 105–109.
LI Shuyan, CAO Han, LIU Niling. Generation parallel algorithm research of Voronoi diagram[J]. Journal of Zhengzhou University of Light Industry (Natural Science), 2010, 25(1): 105–109. DOI:10.3969/j.issn.1004-1478.2010.01.028 |
| [24] |
屠文森, 汪佳佳.
Voronoi图栅格生成算法GPU并行实现[J]. 现代电子技术, 2015, 38(4): 66–68, 72.
TU Wensen, WANG Jiajia. Raster-based method for Voronoi diagram using GPU parallel technology[J]. Modern Electronics Technique, 2015, 38(4): 66–68, 72. DOI:10.3969/j.issn.1004-373X.2015.04.018 |
| [25] | FABBRI R, COSTA L D F, TORELLI J C, et al. 2D Euclidean distance transform algorithms:a comparative survey[J]. ACM Computing Surveys, 2008, 40(1): 1–44. |
| [26] |
王磊.基于QTM的球面Voronoi图生成算法与应用[D].北京: 中国矿业大学(北京), 2016. WANG Lei. QTM-based spherical Voronoi diagram generating algorthms and its application[D]. Beijing: China University of Mining and Technology (Beijing), 2016. http://d.old.wanfangdata.com.cn/Periodical/chxb201811018 |



