2. 昆明理工大学云南省高校高原山区空间信息测绘技术应用工程研究中心, 云南 昆明 650093
2. Surveying and Mapping Geo-Informatics Technology Research Center on Plateau Mountains of Yunnan Higher Education of Kunming University of Science and Technology, Kunming 650093, China
立体像对相对定向是恢复摄影时刻相邻两像片摄影光束的相互关系,从而使同名光线对对相交[1]。相对定向算法研究具有典型的实际意义。
在航空摄影测量中,立体像对相对定向时像片间的旋偏角一般小于6°,可对相对定向元素中的基线分量近似,以简化相对定向模型,在相对定向元素初值为0的前提下,通常采用最速下降法迭代求解[1-2]。随着倾斜摄影测量和低空摄影测量的发展,立体像对相对定向时像片间的旋偏角可能达到甚至超过10°,最速下降法常因相对定向元素初值无法获取而失败[3],一般采用相对定向线性变换法求解[4]。上述两种算法的不足之处是:最速下降法具有线性收敛速度、求解精度高,但过分依赖相对定向元素初值[5-6],使得大角度相对定向时收敛速度减慢、收敛至局部极值甚至不收敛[7];相对定向线性变换是一种直接解法,虽然无须预知相对定向元素的初值,但求解精度不高,一般作为光束法平差的初值[8]。因此,两种算法均较难兼顾收敛性与求解精度两个方面的要求。
关于初值依赖问题,国内外学者已取得丰硕的成果,主要分为代数法和矩阵分解法两类[9]。代数法是根据共面方程的约束关系,将相对定向元素引入约束方程,构造含有未知数的约束方程组[7, 10-16]。其中,文献[7]将计算机视觉中的8点算法引入相对定向中,无须初值,仅需8个同名点即可解算相对定向元素;较之8点算法,5点算法因有较高精度而被关注,因其采用多项式求解,存在多个解及误解排除的问题[13-16]。矩阵分解法是通过分解基础矩阵或本质矩阵解算相对定向元素[17-19]。文献[18]在顾及基础矩阵元素非独立条件下实现无须初值的相对定向元素求解。文献[19]从基础矩阵中直接导出立体像对像片间的平移和旋转量,较难得到精确的相对定向元素。近年来,针对最速下降法具有较高计算精度,依赖于初值的特点,有学者提出混合算法以克服初值依赖并提高相对定向的解算精度。文献[20]通过分解本质矩阵得到相对定向元素初值,然后采用最速下降法迭代求解。文献[21]结合遗传算法的全局收敛性与最速下降法的局部收敛性,利用两者的混合算法求解大角度立体像对相对定向。
初值依赖性、数值收敛性及求解精度是解算相对定向需考虑的3个问题。文献[22]对常规模拟退火法产生新的待估参数及接受概率进行改进,提出了随机爬山(stochastic hill climbing,SHC)算法。它具有全局收敛性,且较之遗传算法与模拟退火法,其具有收敛速度快的优点。因此,为解决大角度相对定向时,最速下降法对相对定向元素初值依赖的问题,并加快算法的收敛速度,本文提出一种基于SHC算法与共轭梯度的混合共轭梯度算法,采用超线性收敛的共轭梯度法替代最速下降法,加快局部收敛速度。当相对定向元素初值未知时,为避免共轭梯度法陷入局部极值并加快全局收敛速度,利用SHC算法为其提供迭代初值。
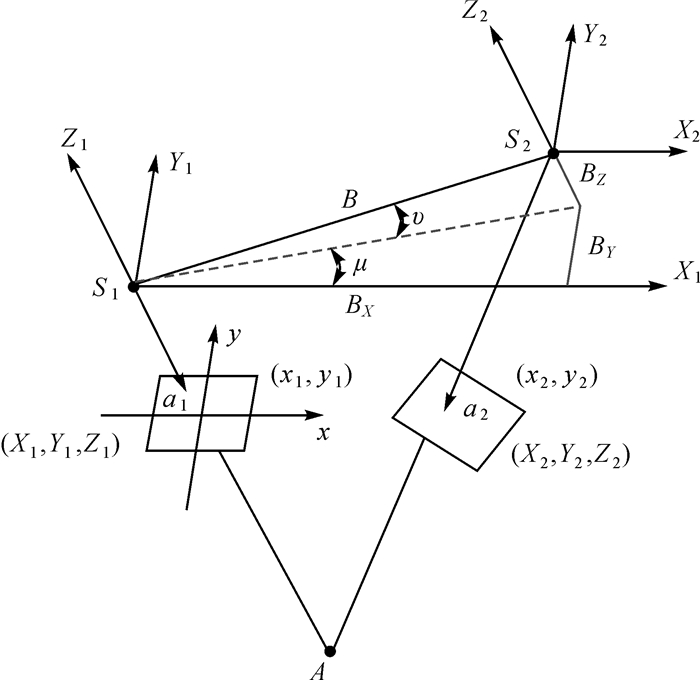
1 混合共轭梯度法解算大角度相对定向 1.1 相对定向模型连续像对相对定向是以左像片为基准,确定右像片相对于左像片的相对定向元素(BX, BY, BZ, φ, ω, κ),如图 1所示。
|
| 图 1 相对定向示意图 Fig. 1 Schematic diagram of relative orientation |
图 1中以左像片的像空间坐标系为像对的像空间辅助坐标系,记为S1-X1Y1Z1,以右摄影中心S2为原点建立另一个像空间辅助坐标系,记为S2-X2Y2Z2。两坐标系互相平行,且左右像点a1, a2在各自像空间辅助坐标系中的坐标分别为(X1, Y1, Z1)和(X2, Y2, Z2),像点坐标分别为(x1, y1)和(x2, y2,S2)在(S1-X1Y1Z1)中的坐标为(BX, BY, BZ),则每对同名像点的共面条件方程为[1]
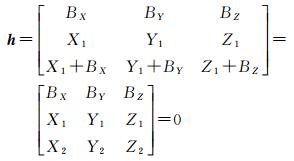 (1)
(1)
式中
 (2)
(2)
式中,f为摄像机焦距;R为相对定向φ、ω、κ角元素方向余弦构成的矩阵。
相对定向中,由于立体像对像片间的旋偏角较小,一般采用简化模型求解,即基线分量BX已知,BY和BZ用小角度μ、ν近似表示
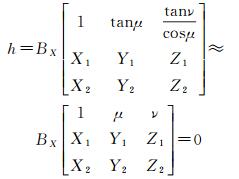 (3)
(3)
对式(3)中5个相对定向元素BY、BZ、φ、ω、κ分别求导,采用最速下降法迭代求解。在大角度相对定向情况之下,存在如下问题:
(1) 立体像对像片间的旋偏角较大,式(3)的简化模型不再适用。
(2) 最速下降法具有线性收敛速度,因此,收敛速率方面仍有改进的空间。
(3) 最速下降法是局部收敛算法,在相对定向元素初值难以获取的情况下,计算会陷入局部极值,甚至不收敛。
1.2 混合共轭梯度法SHC算法是一种改进后的模拟退火法,同样具有全局收敛的性质,它通过对模拟退火算法中新的待估参数产生过程和概率重新修改,获得比模拟退火法更快的收敛速度。设待估参数当前值和新值分别为Xk和Xk+1,f为目标函数,则其只接受f(Xk+1) < f(Xk)的参数,并由下式产生新的待估参数[22]
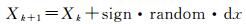 (4)
(4)
式中,random为[0, 1]均匀分布的随机数;当x≥0时,sign=1,否则sign=-1;dx为给定的扰动步长,控制待估参数的修改幅度。
为进一步加快算法收敛速度,在局部搜索过程中,考虑采用共轭梯度法进行计算,即混合共轭梯度算法,计算过程如图 2所示。

|
| 图 2 混合共轭梯度法 Fig. 2 Hybrid conjugate gradient |
(1) 按式(4)扰动当前待估参数值来产生新值。
(2) 判断产生的新值是否符合要求。
(3) 若符合要求,则接受新值,并以新值为初值进行共轭梯度法迭代,否则,返回步骤(1)继续扰动产生新值。
(4) 判断是否满足全局收敛条件,满足则结束计算,否则,则返回(1)。
结合混合共轭梯度算法的特点及1.1节大角度相对定向存在的3个问题,本文具体改进是:
(1) 采用具有全局收敛性的SHC算法进行全局搜索,为局部搜索提供迭代初值。
(2) 不采用小角度μ、ν近似,BX已知的简化模型,而直接对BX、BY、BZ、φ、ω、κ这6个相对定向元素求导。
(3) 采用共轭梯度法代替最速下降法,加快局部搜索的收敛速度。
1.3 共轭梯度法由上文可知,求解式(1)中6个相对定向元素BX、BY、BZ、φ、ω、κ,至少需要6对同名像点。为提高解算精度,常有多余观测。设有n对同名像点(n>6),则有由n个式(1)构成的方程组
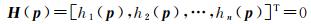 (5)
(5)
式中,p=[BX, BY, BZ, φ, ω, κ]T为相对定向元素。式(5)是典型的非线性优化过程[23]。共轭梯度法的求解思路是:给定一个相对定向元素初值p0,假定初值p0在真值p*邻域内,则相对定向元素可通过式(6)迭代计算
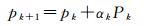 (6)
(6)
式中
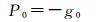 (7)
(7)
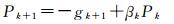 (8)
(8)
式中,αk为1维搜索步长,通过线性搜索获得;Pk为搜索方向;βk为参数。不同的βk对应不同算法,文中采用Polak-Ribiere-Polyak算法[24]
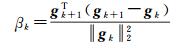 (9)
(9)
式中,gk=∇H(pk)是函数H(p)在当前相对定向元素估计值pk处的梯度矩阵,即
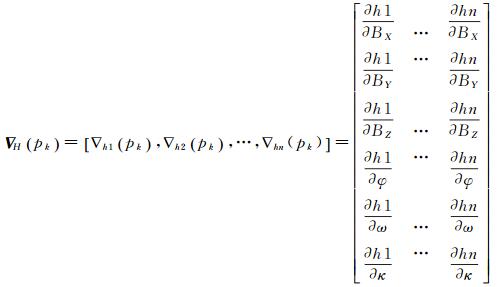 (10)
(10)
进一步由式(1)可得
 (11)
(11)
因此,在给定1维搜索步长αk的情况下,若相对定向元素初值充分接近真值,则相对定向问题可利用共轭梯度法多次迭代式(6)解算。
1.4 SHC算法[25]在大角度相对定向中,若相对定向元素初值充分接近真值,则大角度相对定向问题可由超线性收敛的共轭梯度法解算。但其相对定向元素初值一般较难获取,若将相对定向将初值设为0,则会使共轭梯度法收敛于局部极小值,甚至不收敛。为此,在大角度相对定向元素初值未知的情况下,采用SHC算法计算相对定向元素初值。具体过程如下:
(1) 已知左右像片n对同名像点坐标和摄影机焦距f,给定相对定向元素初值pk。
(2) 由式(2)计算左右像对同名像点在各自像空间辅助坐标系的坐标(X1, Y1, Z1)和(X2, Y2, Z2)。
(3) 由式(1)、式(5)计算得到H(pk)。
(4) 按式(4)修改当前相对定向元素pk以产生新的相对定向元素pnew,计算得到ΔH=H(pnew)-H(pk)。
(5) 若ΔH>0,则拒绝pnew,返回步骤(4);否则接受pnew,即pk=pnew,并以更新后的pk作为初值按共轭梯度法进行相对定向元素计算,直至收敛于局部极值,设收敛的局部极值为pk*,对应的目标函数值为H(pk*)。
(6) 用收敛的局部极值pk*更新当前相对定向元素,即pk=pk*。若未达到全局收敛条件(若真值p*已知,则全局收敛条件为H(pk)=H(p*);若真值未知,则为算法是否达到指定的迭代次数或规定的限差),则返回步骤(3)继续执行;否则计算结束,此时的pk即为所求的相对定向元素。
2 试验与分析为验证本文算法的有效性,分别进行模拟试验和实测试验。
2.1 模拟试验已知摄像机焦距f及立体像对左像片像点坐标,以左像片为基准,采用交向摄影模拟产生3组右像片分别与左像片构成虚拟立体像对,相对定向元素模拟值见表 1,其中仅考虑了大角度相对定向。然后分别计算不同相对定向元素下右像片的像点坐标,并在其中加入均值为0,方差为0.05的高斯噪声。为模拟大角度立体像对,假设成像不受图幅限制。以左右像片的像点坐标、摄像机焦距f为已知条件,采用本文算法、最速下降法及文献[21]中基于最速下降法的混合遗传算法(简称为算法3)分别对相对定向元素求解,并将相对定向元素计算值与模拟值进行比较。试验中,相对定向线元素和角元素的模型扰动步长dx分别为0.05 mm和0.02 rad。
| 基线向量/mm | 旋转角度/rad | |||||
| BX | BY | BZ | φ | ω | κ | |
| 0.989 7 | -0.086 5 | 0.195 2 | 0.808 5 | -0.483 3 | 0.675 1 | |
| -0.956 2 | -0.097 5 | -0.186 2 | 0.390 6 | -0.204 8 | -0.903 6 | |
| 0.975 3 | 0.070 3 | -0.245 9 | -0.949 1 | -0.501 3 | -0.661 8 | |
由表 1可知,由于相对定向元素模拟值倾角较大,为保证最速下降法正确收敛,试验中采用相对定向线性变换法[4]为其提供初值。而本文算法和算法3中相对定向元素初值均设为0,即BX=BY=BZ=φ=ω=κ=0。3种算法计算结果见表 2,本文算法和算法3的迭代次数见表 3。
| 像对编号 | 算法 | 基线向量/mm | 旋转角度/rad | |||||
| BX | BY | BZ | φ | ω | κ | |||
| 左-右1 | 本文算法 | 0.989 6 | -0.086 4 | 0.195 1 | 0.808 4 | -0.483 3 | 0.675 2 | |
| 最速下降法 | 0.989 6 | -0.086 3 | 0.195 0 | 0.808 4 | -0.483 2 | 0.675 2 | ||
| 算法3 | 0.989 5 | -0.086 1 | 0.194 8 | 0.808 3 | -0.483 1 | 0.675 4 | ||
| 左-右2 | 本文算法 | -0.956 3 | -0.097 4 | -0.186 2 | 0.390 6 | -0.204 8 | -0.903 6 | |
| 最速下降法 | -0.956 3 | -0.097 5 | -0.186 1 | 0.390 6 | -0.204 8 | -0.903 6 | ||
| 算法3 | -0.956 0 | -0.097 6 | -0.186 0 | 0.390 7 | -0.204 6 | -0.903 7 | ||
| 左-右3 | 本文算法 | 0.975 2 | 0.070 3 | -0.245 8 | -0.949 1 | -0.501 2 | -0.661 7 | |
| 最速下降法 | 0.975 2 | 0.070 3 | -0.245 8 | -0.949 2 | -0.501 3 | -0.661 8 | ||
| 算法3 | 0.975 5 | 0.070 4 | -0.246 1 | -0.948 9 | -0.501 2 | -0.661 6 | ||
| 像对编号 | 算法 | 迭代次数 |
| 左-右1 | 本文算法 | 45 |
| 算法3 | 56 | |
| 左-右2 | 本文算法 | 40 |
| 算法3 | 62 | |
| 左-右3 | 本文算法 | 43 |
| 算法3 | 60 |
由表 2、表 3可知,本文算法的计算精度高于算法3,与最速下降法相当,但最速下降法依赖于相对定向元素初值,为保证其正确收敛,需预知相对定向元素初值;而本文算法无须提供初值,且较之算法3,收敛速度较快。原因在于:混合共轭梯度算法中采用了共轭梯度法,具有超线性收敛速度,虽然可能陷入局部极值,但由于采用SHC算法通过扰动产生新的随机相对定向元素,并按目标函数值对产生的相对定向元素进行取舍,保证收敛方向和速度。因此,在多次迭代中,能够跳出共轭梯度法陷入的局部极值。试验中,当相对定向元素初值距离模拟值较远时,混合共轭梯度算法在不同极值处进行多次局部优化,并在每次局部搜索过程中,因SHC算法对所产生的相对定向元素进行判断,越来越接近模拟值,经多次迭代后,最终收敛。
2.2 实测试验如图 3所示,为云南省某地居民楼房两条基线下交向摄影获得的3幅像片,构成2对连续立体像对。航拍相机为Canon 5D Mark Ⅱ,镜头焦距为35 mm,相对航高445 m,图像大小为449×300像素,像素大小为6.4 μm。为减少同名点定位带来的外部误差,采用人工量测的8个同名像点来进行相对定向元素的解算。采用最速下降法、算法3和本文算法分别对立体像对进行相对定向元素解算。由于立体像对像片间的旋偏角较大,试验中采用相对定向线性变换法[4]为最速下降法提供初值,而本文算法和算法3中,相对定向元素初值设为0,即BX=BY=BZ=φ=ω=κ=0,3种算法的计算结果见表 4,本文算法和算法3的迭代次数见表 5。试验中相对定向线元素和角元素的模型扰动步长dx分别为0.05 mm和0.02 rad。

|
| 图 3 像片序列 Fig. 3 Sequence of images |
| 立体像对 | 算法 | BX/mm | BY/mm | BZ/mm | φ/rad | ω/rad | κ/rad | 精度/μm |
| 像片2/像片1 | 最速下降法 | -1.367 5 | -0.016 2 | 0.052 4 | -1.064 7 | 0.069 8 | -1.570 8 | 2.1 |
| 算法3 | -1.367 4 | -0.016 2 | 0.052 1 | -1.064 5 | 0.069 8 | -1.570 6 | 2.4 | |
| 本文算法 | -1.367 5 | -0.016 3 | 0.052 5 | -1.064 8 | 0.069 9 | -1.570 7 | 2.2 | |
| 像片3/像片1 | 最速下降法 | -1.391 1 | 0.024 5 | 0.041 1 | -1.029 7 | 0.025 4 | 0.043 6 | 1.8 |
| 算法3 | -1.391 0 | 0.024 5 | 0.041 3 | -1.029 6 | 0.025 4 | 0.043 8 | 2.1 | |
| 本文算法 | -1.391 1 | 0.024 4 | 0.041 0 | -1.029 7 | 0.025 5 | 0.043 7 | 1.8 |
从表 4、表 5可知,本文算法计算精度与最速下降法相当,相对定向达到约±0.5像素的精度,而最速下降法因依赖于相对定向元素初值,需要相对定向线性变换法提供初值;较之算法3,本文算法具有计算精度高且收敛快的优点。
3 结论提出了一种全局收敛的混合共轭梯度算法。试验表明,在无须预知相对定向元素初值的前提下,算法能够正确解算大角度立体像对相对定向,并具有解算精度高和收敛速度快的特点。此外,合理选取SHC算法中的扰动步长将会进一步加快收敛速度。针对大角度相对定向解算,扰动步长的定量分析与选取有待进一步研究。
| [1] |
张剑清, 潘励, 王树根.
摄影测量学原理[M]. 2版. 武汉: 武汉大学出版社, 2009.
ZHANG Jianqing, PAN Li, WANG Shugen. The principles of photogrammetry[M]. 2nd ed. Wuhan: Wuhan University Press, 2009. |
| [2] |
王之卓.
摄影测量原理[M]. 武汉: 武汉大学出版社, 2007.
WANG Zhizhuo. The principles of photogrammetry[M]. Wuhan: Wuhan University Press, 2007. |
| [3] |
张永军, 胡丙华, 张剑清.
基于多种同名特征的相对定向方法研究[J]. 测绘学报, 2011, 40(2): 194–199.
ZHANG Yongjun, HU Binghua, ZHANG Jianqing. Relative orientation based on multiple conjugate features[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 194–199. |
| [4] |
张祖勋, 张剑清.
数字摄影测量学[M]. 2版. 武汉: 武汉大学出版社, 2012.
ZHANG Zuxun, ZHANG Jianqing. Digital photogrammetry[M]. 2nd ed. Wuhan: Wuhan University Press, 2012. |
| [5] |
袁亚湘, 孙文瑜.
最优化理论与方法[M]. 北京: 科学出版社, 1997.
YUAN Yaxiang, SUN Wenyu. Optimal theories and methods[M]. Beijing: Science Press, 1997. |
| [6] |
张光澄.
非线性最优化计算方法[M]. 高等教育出版社, 2005.
ZHANG Guangcheng. Computational methods for nonlinear optimization[M]. Beijing: Higher Education Press, 2005. |
| [7] |
李巍, 董明利, 孙鹏, 等.
大尺寸摄影测量局部参数优化相对定向方法[J]. 仪器仪表学报, 2014, 35(9): 2053–2060.
LI Wei, DONG Mingli, SUN Peng, et al. Relative orientation method for large-scale photogrammetry with local parameter optimization[J]. Chinese Journal of Scientific Instrument, 2014, 35(9): 2053–2060. |
| [8] | TRIGGS B, MCLAUCHLAN P F, HARTLEY R I, et al. Bundle adjustment-a modern synthesis[M]. Berlin: Springer, 2000: 298-372. |
| [9] | STEWÉNIUS H, ENGELS C, NISTÉR D. Recent developments on direct relative orientation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(4): 284–294. DOI:10.1016/j.isprsjprs.2006.03.005 |
| [10] |
陈义, 陆珏, 郑波.
近景摄影测量中大角度问题的探讨[J]. 测绘学报, 2008, 37(4): 458–463, 468.
CHEN Yi, LU Yu, ZHENG Bo. Research on close-range photogrammetry with big rotation angle[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 458–463, 468. DOI:10.3321/j.issn:1001-1595.2008.04.010 |
| [11] |
陆珏, 陈义, 郑波.
多基线近景摄影测量连续像对相对定向[J]. 同济大学学报(自然科学版), 2010, 38(3): 442–447.
LU Jue, CHEN Yi, ZHENG Bo. Research on dependent relative orientation in multi-baseline close-range photogrammetry[J]. Journal of Tongji University (Natural Science), 2010, 38(3): 442–447. |
| [12] | NIST D. An efficient solution to the five-point relative pose problem[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 26(6): 756–770. |
| [13] |
于起峰, 尚洋.
摄像测量学原理与应用研究[M]. 北京: 科学出版社, 2009.
YU Qifeng, SHANG Yang. Videometrics:principles and researches[M]. Beijing: Science Press, 2009. |
| [14] | KUKELOVA Z, BUJNAK M, PAJDLA T. Polynomial eigenvalue solutions to minimal problems in computer vision[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1381–1393. DOI:10.1109/TPAMI.2011.230 |
| [15] | WANG Wenbin, LIU Guihua, LIU Xianyong, et al. Two removal tactics of pseudo solutions for essential matrix five-point algorithm[J]. Opto-Electronic Engineering, 2010, 37(8): 46–52. |
| [16] |
张征宇, 朱龙, 黄叙辉, 等.
基于前方交会的5点相对定向[J]. 光学学报, 2015, 35(1): 231–238.
ZHANG Zhengyu, ZHU Long, HUANG Xuhui, et al. Five-point relative orientation based on forward intersection[J]. Acta Optica Sinica, 2015, 35(1): 231–238. |
| [17] |
袁修孝, 陈时雨, 钟灿.
基于基础矩阵的倾斜航摄影像相对定向方法[J]. 武汉大学学报(信息科学版), 2016, 41(8): 995–1000.
YUAN Xiuxiao, CHEN Shiyu, ZHONG Can. Oblique aerial image relative orientation based on fundamental matrix[J]. Geomatics and Information Science of Wuhan University, 2016, 41(8): 995–1000. |
| [18] | ZHANG Yongjun, HUANG Xu, HU Xiangyun, et al. Direct relative orientation with four independent constraints[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(6): 809–817. DOI:10.1016/j.isprsjprs.2011.09.006 |
| [19] | WANG J, LIN Z, REN C. Relative orientation in low altitude photogrammetry survey[J]. ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012(1): 463–467. |
| [20] |
杨阿华, 李学军, 刘涛, 等.
基于直接解算与迭代优化的相对定向方法[J]. 计算机应用, 2014, 34(6): 1706–1710.
YANG Ahua, LI Xuejun, LIU Tao, et al. Relative orientation approach based on direct resolving and iterative refinement[J]. Journal of Computer Applications, 2014, 34(6): 1706–1710. DOI:10.3969/j.issn.1001-3695.2014.06.024 |
| [21] |
周拥军, 邓才华.
利用HGA和单位四元数的相对定向解法[J]. 武汉大学学报(信息科学版), 2011, 36(6): 670–673.
ZHOU Yongjun, DENG Caihua. A new method for relative orientation with hybrid genetic algorithm and unit quaternion[J]. Geomatics and Information Science of Wuhan University, 2011, 36(6): 670–673. |
| [22] | HUANG Xuri, KELKAR M. Performance comparison of heuristic combinatorial alorithms for seismic inversion[C]//Proceedings of 1995 SEG Annual Meeting. Houston, Texas: Society of Exploration Geophysicists, 1995: 1025-1027. |
| [23] |
席少霖.
非线性最优化方法[M]. 北京: 高等教育出版社, 1992.
XI Shaolin. The method of nonlinear optimization[M]. Beijing: Higher Education Press, 1992. |
| [24] | POLYAK B T. The conjugate gradient method in extremal problems[J]. USSR Computational Mathematics and Mathematical Physics, 1969, 9(4): 94–112. DOI:10.1016/0041-5553(69)90035-4 |
| [25] |
涂进.基于模拟退火算法的聚类分析在数据挖掘中的应用[D].重庆: 重庆大学, 2003. TU Jin. Study on clustering analysis in data mining based on simulated annealing algorithm[D]. Chongqing: Chongqing University, 2003. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y795265 |



