2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Wuhan University, Wuhan 430079, China
激光扫描(light detection and ranging, LiDAR)技术作为一种重要的三维空间数据获取技术,可以直接快速地获取物体表面三维信息[1],广泛应用于测绘[2]、机器人[3]和无人驾驶[4]等领域。SLAM技术源于机器人领域,中文译为同步定位与制图技术[5]。将LiDAR与SLAM相结合,通过集成LiDAR扫描仪、IMU(inertial measurement unit)等传感器可在扫描平台移动过程中实时获取位置、姿态信息以及场景的空间信息。基于SLAM技术的激光扫描可以高效完成室内空间或室外小场景的三维点云数据获取,近年来在测绘领域得到了广泛的关注和应用[6]。
由于SLAM定位对实时性的要求,无法充分利用多余观测信息对位姿信息和点云数据进行优化,致使激光点云数据中存在内部不一致问题,影响点云后续处理与应用。实时SLAM点云优化,通常先对点云进行分段处理,然后通过闭环检测找出重叠点云构成的闭合环,以此构建位姿图进行优化[7-10]。这类算法存在闭合环检测错误的可能,且无法处理局部区域内部的误差[11]。测绘领域对三维激光点云数据精度要求高,对数据实时性要求较低,可以对点云进行离线的全局优化,从而改善点云内部不一致,提高点云的相对精度。目前的点云全局优化主要针对地面静态式扫描激光扫描点云,方法是将一站点云视为一个视图,利用闭合环条件约束对多视点云进行配准和优化。文献[12-13]提出一种基于光束法区域网平差进行点云整体配准方法,但需要利用靶标;文献[14]提出了一种严密的闭合条件约束配准方法,使用点云间的坐标转换参数构建误差方程,进行优化;文献[15-16]提出一种通过将点云分为两份分别配准,比较转换参数的点云配准质量的评价方式;文献[17]提出了一种利用所有重叠点云对应点作为观测值同时解算配准结果的全局优化的算法。
SLAM点云为移动式实时扫描点云,每一帧点云为一个视图,点云视图数多,重叠关系复杂。为了充分利用重叠点云中的冗余信息对SLAM点云进行精度优化,本文提出一种基于位姿图优化理论[18-19]的离线整体精配准方法。该方法以实时获取的平台轨迹的位姿信息为初始条件,通过迭代最近点算法(iterative closest point, ICP)[20]对在不同时刻扫描的重叠点云进行配准,形成对扫描平台轨迹的约束并对其进行优化,利用优化后的轨迹对点云进行修正。为提高计算效率,本文采用分层优化策略,即将优化分解为局部区域优化和整体优化两个层次。
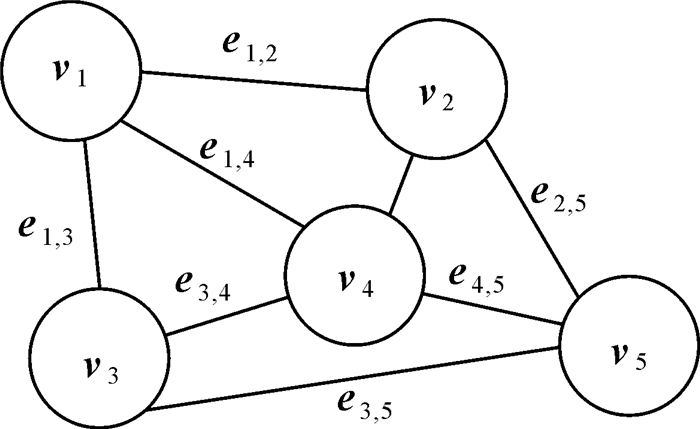
1 位姿图优化理论基础 1.1 位姿图表达图优化理论是一种将图论和非线性优化相结合的理论,通过将优化问题转化为图形式进行表达,从而直观地反映出优化变量与约束条件之间的关系,便于拓扑结构操作和构造目标函数[21]。用G={V, E}表示图结构,V代表图的顶点,E表示边。针对优化问题,图的顶点代表待优化参数,边代表参数之间的约束条件。图优化的目标是最小化所有约束代价,进而通过优化解法获得最佳待求参数。位姿图(见图 1)是优化图的一种具体形式,本文将其用于解决具有复杂点云视图结构的轨迹优化问题。
|
| 图 1 位姿图示例 Fig. 1 Pose graph |
图 1为一个典型的位姿图示例,vi表示一个顶点,ei, j表示一条边。其中,顶点代表扫描平台的位置和姿态,顶点之间的边代表位姿的约束条件。在SLAM激光点云的全局优化中,位姿图的每一个顶点vi都对应于扫描系统的一个轨迹点xi,轨迹点信息包含位置和姿态参数。其中,位置参数使用向量ti=[xi yi zi]T表示,即扫描系统在全局坐标系中的平移位置;姿态参数使用四元数qi=[qwi qxi qyi qzi]T表示,即扫描系统在全局坐标系中的旋转姿态,则顶点vi=[tiT qiT]T。位姿图的每一条边ei, j表示观测值对连接的顶点vi、vj之间相对位姿关系的约束,本文通过对重叠点云进行配准形成约束。由于存在误差,顶点vi、vj无法完全符合边ei, j代表的约束,产生的残差为r(vi, vj, ei, j)。
1.2 优化求解根据最小化位姿图的残差总和的优化准则,获得最优位姿参数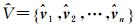
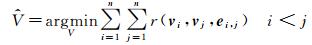 (1)
(1)
式中,n为轨迹中的位姿总数。如果顶点vi、vj间不存在边ei, j作为约束时,则残差r(vi, vj, ei, j)=0。
位姿图优化作为一种全局优化方法,其中每一条边都会直接或间接对所有顶点的估计值产生影响,一个错误的约束就足以导致优化质量的下降,同时降低识别粗差的能力[22]。在构建位姿图的边时,需要对大量点云进行配准,周围环境中存在的对称、重复结构,噪声,点云重叠度低等因素,都会造成配准失败。为提高解算的稳健性,减小异常值对结果的影响,本文通过附加损失函数对式(1)进行改进
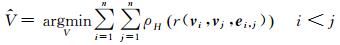 (2)
(2)
式中,ρH为Huber损失函数[23]。
由于目标函数为非线性函数,可使用L-M(Levenberg-Marquardt)优化方法[24]进行解算,获得扫描平台轨迹的最优位姿参数,进而根据优化后的轨迹对点云进行修正,达到改善点云质量的目的。
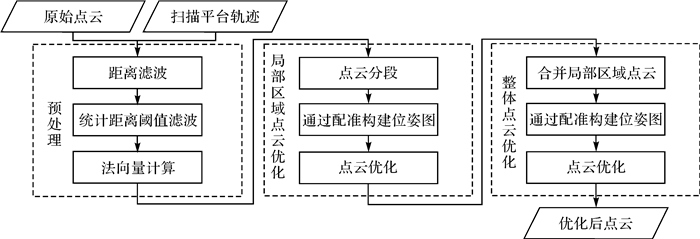
2 基于位姿图的点云优化本文所使用的点云优化方法是通过对扫描平台的轨迹进行全局优化以提高点云精度,方法流程如图 2所示。过程包括数据预处理、局部区域点云优化和整体点云优化3部分。预处理的目的是去除对点云配准贡献小的点,如离群点,并估计点云配准所需的法向量。预处理后按一定的时间间隔将点云和轨迹分为若干小段,每一小段视为一个局部区域,其含有若干帧点云。为了处理局部区域内点云误差,以单帧点云为配准单元,通过外包盒寻找点云之间的重叠关系,对重叠点云进行配准。SLAM激光点云经过实时算法的处理,点云间可认为已经完成粗配准,可以直接使用ICP算法进行配准。利用配准结果对轨迹进行约束,构建位姿图对轨迹进行优化,完成局部区域内点云优化。最后将优化后的局部区域点云合并,合并后的每一段点云视为配准单元,采用类似局部区域优化的方式完成整体点云的全局优化。
|
| 图 2 SLAM点云整体精配准方法 Fig. 2 Global fine registration method of SLAM point |
2.1 预处理
为了提高配准的可靠性和效率,首先采用距离滤波和统计距离阈值滤波对点云数据进行预处理,剔除扫描距离过大点和孤立点。随着扫描距离的增大,点云的精度和密度都会下降,同时噪声增多,根据扫描仪的有效扫描距离和扫描环境,设置距离阈值Dmax,去除扫描距离大于Dmax的点。为了去除孤立点,避免其对之后的法向量计算造成影响,对点云进行统计距离阈值滤波[25]。该方法计算每个点到最邻近点的距离的平均值μ和标准差σ,去除距离最邻近点距离超出μ±σ的点。最后,在预处理中计算每个点的法向量,通过对各点邻域内坐标的协方差矩阵进行特征值分解,其中最小的特征值对应的特征向量为该点的法向量[26]。
2.2 位姿图构建由于SLAM激光点云在获取时存在定位误差,导致对同一区域扫描时获取的不同帧点云之间无法完全重合,通过对这些点云进行配准可以构建对轨迹中位姿的约束。针对室内环境高度结构化的特点,本文选择使用点-切平面ICP算法对点云进行配准[27],通过采用最小化点到目标点云对应点切平面的距离完成配准。作为一种两视点云精配准的方法,相比于普通ICP算法,点-切平面ICP能够建立更精确的同名点,收敛速度较快、精度更高[28],其算法模型为[29]
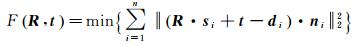 (3)
(3)
式中,si=[six siy siz]T是待配准点云中的点;di=[dix diy diz]T是目标点云中的对应点;R代表旋转矩阵;t代表平移参数;ni=[nix niy niz]T为点si的法向量。
若以点云ci为基准,配准点云cj后获得的转换参数为Ri, j、ti, j,将旋转部分转化四元数的形式与顶点表示形式统一后,转换参数表示为[ti, jT qi, jT]T,转化方法见文献[30],则约束对应顶点vi、vj的边ei, j为
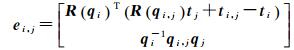 (4)
(4)
式中,R(q)表示四元数q对应的旋转矩阵;边ei, j的实际意义为在点云ci对应的局部坐标系下,两视配准后的点云cj与点云ci的扫描中心的相对位姿关系。
对于顶点vi、vj和边ei, j=[pei, jT qei, jT]T,残差可以分为平移和旋转两部分
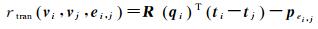 (5)
(5)
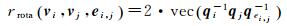 (6)
(6)
式中,rtran(vi, vj, ei, j)、rrota(vi, vj, ei, j)分别为平移和旋转对应的残差;pei, j和qei, j分别为边ei, j的平移和旋转部分;vec(q)为四元数的虚数部分[qx qy qz]。
结合平移和旋转残差的总体残差为
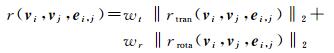 (7)
(7)
式中,wt和wr分别为平移和旋转的权重。
2.3 分层次优化由于SLAM激光点云包含大量的扫描帧数,且相互之间存在大量重叠,若要一次性构建整体点云的位姿图,需要在各帧点云间进行大量配准,导致优化计算耗时过长。因此,通过将点云优化分解为局部区域和整体两个层次进行,以减小构建位姿图时的计算量,提高算法效率,过程如图 3所示。

|
| 图 3 分层次配准过程(每种颜色代表一个分段区域内的点云) Fig. 3 The process of hierarchical registration(each color represents the point cloud in one segmentation |
预处理后,将点云和轨迹按时间间隔ts分段,每一小段视为一个局部区域,其中含有若干帧点云。在局部区域层次上进行点云优化时,首先使用分段后的轨迹构建局部区域内的位姿图顶点。然后,在每个分段区域内通过对每帧点云的外包盒进行相交检测,找出具有重叠关系的点云,使用点到切平面ICP对重叠点云进行配准,每次成功进行重叠点云的配准后,使用2.2节中描述的方法构建位姿图中对应顶点间的一条边。局部区域内的位姿图构建完成后,对位姿图进行解算,获得优化后的分段轨迹,对分段内点云进行修正。
完成局部层次的优化后,对每个分段内的点云进行合并,结果如图 3(b)所示。以合并后的点云为配准单元进行配准,计算配准时建立的同名点对数与目标点云点数的比值α作为有效重叠度,在整体点云位姿图构建时通过阈值αmin去除有效重叠度低的点云间的不可靠配准结果。位姿图解算后,根据优化后的整体轨迹对点云进行修正,完成对整体点云的优化。
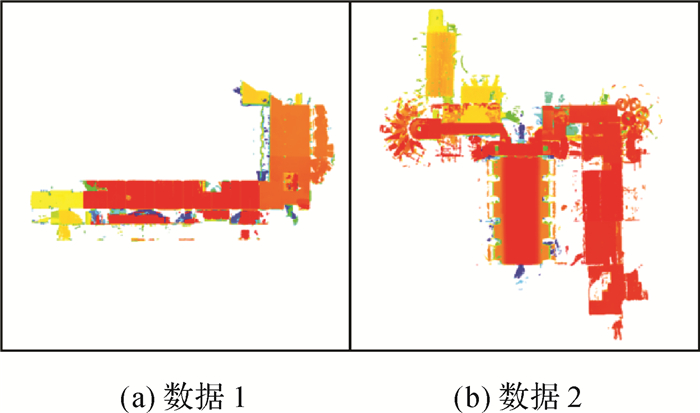
3 试验与分析为了验证本文算法的有效性,本文采用Google公司的Cartographer算法[9]示例数据作为试验数据对本文算法的效果进行验证。该数据包含数据1和数据2两部分,由装备了两个VelodyneVLP-16LiDAR扫描仪和IMU的3D LiDAR背包获取,扫描地点为德意志科技博物馆,图 4为所用试验数据的俯视图。数据1为单个楼层扫描结果,数据2为3个楼层扫描结果,并包含一个大型展厅,数据具体参数如表 1所示。试验的计算机环境为IntelXeonE5-2660 v3 @2.60 GHz,128 GB内存。
|
| 图 4 Google Cartographer算法德意志博物馆示例数据 Fig. 4 Google Cartographer sample data set in Deutsches Museum |
| 数据 | 扫描时长/s | 轨迹长度/m | 包含点云帧数 |
| 数据1 | 382 | 291.2 | 7559 |
| 数据2 | 1466 | 1 300.5 | 21 718 |
在预处理阶段,根据扫描仪的性能和室内环境的尺度,将点云的最大有效距离阈值Dmax设为20 m,去除超出距离阈值的点。局部区域优化时,按时间间隔ts对预处理后的点云和轨迹进行分段,分别在每段点云内部通过ICP配准构建局部区域的位姿图。在位姿图残差计算时,参考Cartographer算法[9]中的设置,将平移和旋转代价的权值wt、wr分别设为1、100,将每段点云中第1帧点云对应的顶点设为基准,使用L-M算法进行解算。整体点云优化时,对局部区域内优化后的点云进行合并,在整体点云范围内搜索重叠点云进行配准,为了保证配准的可靠性,将最小有效重叠度αmin的值设为0.05,进行整体点云的全局位姿图构建。
根据优化后获得的轨迹对点云进行修正,得到整体精配准后的点云。以时间间隔ts=3 s时的点云优化结果为例,图 5、图 6为点云数据优化前后场景的定性对比。从图 5(a)、(b)中1,(c)、(d)中5,图 6(c)、(d)中5、6,(e)、(f)中8、9的对比可知,优化后点云中的物体轮廓更加清晰;从图 5(a)、(b)中3、4,(c)、(d)中6,图 6(c)、(d)中7,(e)、(f)中10、11的对比可知,点云中的墙面的厚度变薄;从图 5(a)、(b)中2,图 6(a)、(b)中1、2、3、4的对比可知,同一物体存在多个扫描结果的现象也得到了消除。

|
| 图 5 数据1优化前后对比 Fig. 5 Data 1 scenes before and after optimization |

|
| 图 6 数据2优化前后对比 Fig. 6 Data 2 scenes before and after optimization |
本文采用重叠点云间的对应点对的距离中误差(root mean square error, RMSE)作为评价标准来定量地分析优化前后点云的相对精度变化。通过优化后的轨迹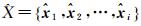
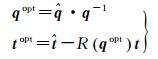 (8)
(8)
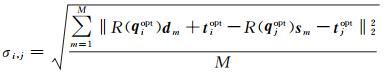 (9)
(9)
式中,q与t分别表示优化前扫描系统位姿的旋转和位移;
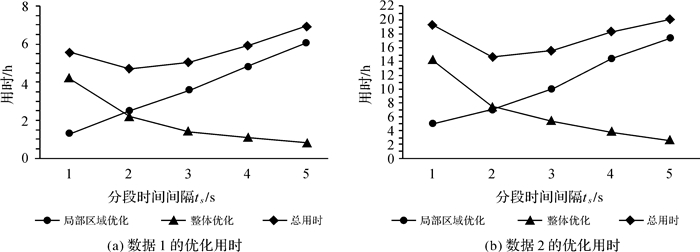
为了分析不同的分段时间间隔ts取值对点云优化的用时和优化精度的影响,以1 s为间隔对ts取值进行点云全局优化,统计优化用时,并计算优化前后整体点云所有重叠帧间的对应点对距离RMSE,结果如图 7和表 2所示。
|
| 图 7 不同时间间隔ts取值下优化用时 Fig. 7 The time cost before and after optimization in different values of ts |
| 分段时间间隔ts/s | 数据1的RMSE/cm | 数据2的RMSE/cm | |||
| 优化前 | 优化后 | 优化前 | 优化后 | ||
| 1 | 10.5 | 4.8 | 14.2 | 6.6 | |
| 2 | 10.5 | 4.5 | 14.3 | 6.7 | |
| 3 | 10.7 | 4.3 | 14.4 | 6.7 | |
| 4 | 10.9 | 4.4 | 14.4 | 6.8 | |
| 5 | 11.0 | 4.5 | 14.5 | 7.0 | |
| 平均值 | 10.7 | 4.5 | 14.4 | 6.8 | |
由图 7(a)、(b)可以看出,局部优化用时随分段时间间隔ts的增大近似线性增长,而整体优化用时则随着时间间隔ts的增大,开始时快速减小,之后减小速度逐渐减慢。在时间间隔ts等于2 s时,数据1和数据2优化总用时最少。从表 2中可以看出,在不同的时间间隔ts下,点云的精度计算结果没有明显变化,说明了本文方法的优化效果受不同时间间隔ts的影较小。其中,优化前的RMSE的变化,是由于时间间隔ts的改变,计算得到的分段点云不同,导致获取的同名点对不同造成的。数据1优化后,不同时间间隔下平均点云RMSE从10.7 cm变为4.5 cm,减小了58%,在ts=3 s时优化后RMSE最小为4.3 cm;数据2优化后,不同时间间隔下平均点云RMSE从14.4 cm变为6.8 cm,减小了53%,在ts=1 s时,优化后RMSE最小为6.6 cm,说明优化后点云精度明显提高,验证了本文方法的有效性。
4 结论基于SLAM技术的激光扫描可以高效地获取目标场景的三维信息,但精度受限,可通过全局优化的方法提高SLAM激光点云的精度。由于SLAM激光点云具有重叠度高,帧数多的特点,导致配准关系复杂,计算量大,传统的点云优化方法不适用于SLAM激光点云的全局优化。本文针对SLAM激光点云相对精度优化问题,提出了一种分层次的点云整体精配准算法。通过对获取的点云进行分段将全局位姿图的构建分为两个层次。首先在分段内部使用点-切平面ICP进行配准,构建局部位姿图对点云进行优化,保证分段内部点云的一致性,再对分段点云进行配准,构建全局位姿图,对整体点云进行优化。通过试验,对算法的可行性和有效性进行了验证。试验结果表明,优化后点云同名点对间的距离中误差减小了约50%,点云中重复扫描间的差异减小,物体轮廓更加清晰,说明点云的内部一致性得以改善。
| [1] |
梅文胜, 周燕芳, 周俊.
基于地面三维激光扫描的精细地形测绘[J]. 测绘通报, 2010(1): 53–56.
MEI Wensheng, ZHOU Yanfang, ZHOU Jun. Fine topographic mapping based on ground three-dimensional laser scanning[J]. Bulletin of Surveying and Mapping, 2010(1): 53–56. |
| [2] |
杨必胜, 董震, 魏征, 等.
从车载激光扫描数据中提取复杂建筑物立面的方法[J]. 测绘学报, 2013, 42(3): 411–417.
YANG Bisheng, DONG Zhen, WEI Zheng, et al. Extracting complex building facades from mobile laser scanning data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 411–417. |
| [3] | TANG Jian, CHEN Yuwei, NIU Xiaoji, et al. LiDAR scan matching aided inertial navigation system in GNSS-denied environments[J]. Sensors, 2015, 15(7): 16710–16728. DOI:10.3390/s150716710 |
| [4] | WANG Heng, WANG Bin, LIU Bingbing, et al. Pedestrian recognition and tracking using 3D LiDAR for autonomous vehicle[J]. Robotics and Autonomous Systems, 2017, 88: 71–78. DOI:10.1016/j.robot.2016.11.014 |
| [5] |
梁明杰, 闵华清, 罗荣华.
基于图优化的同时定位与地图创建综述[J]. 机器人, 2013, 35(4): 500–512.
LIANG Mingjie, MIN Huaqing, LUO Ronghua. Graph-based SLAM:a survey[J]. Robot, 2013, 35(4): 500–512. |
| [6] | LAUTERBACH H, BORRMANN D, HEβ R, et al. Evaluation of a backpack-mounted 3D mobile scanning system[J]. Remote Sensing, 2015, 7(10): 13753–13781. DOI:10.3390/rs71013753 |
| [7] | BOSSE M, ZLOT R. Place recognition using keypoint voting in large 3D LiDAR datasets[C]//Proceedings of 2013 IEEE International Conference on Robotics and Automation. Karlsruhe, Germany: IEEE, 2013: 2677-2684. https://ieeexplore.ieee.org/document/6630945 |
| [8] | ZLOT R, BOSSE M. Efficient large-scale three-dimensional mobile mapping for underground mines[J]. Journal of Field Robotics, 2014, 31(5): 758–779. DOI:10.1002/rob.21504 |
| [9] | HESS W, KOHLER D, RAPP H, et al. Real-time loop closure in 2D LiDAR SLAM[C]//Proceedings of 2016 IEEE International Conference on Robotics and Automation. Stockholm, Sweden: IEEE, 2016. https://ieeexplore.ieee.org/document/7487258 |
| [10] | CAO Jun, ZENG Bi, LIU Jianqi, et al. A novel relocation method for simultaneous localization and mapping based on deep learning algorithm[J]. Computers & Electrical Engineering, 2017, 63: 79–90. |
| [11] | ELSEBERG J, BORRMANN D, NÜCHTER A. 6D of Semi-rigid slam for mobile scanning[C]//Proceedings of 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Vilamoura, Portugal: IEEE, 2012: 1865-1870. https://ieeexplore.ieee.org/document/6385509 |
| [12] |
姚吉利, 马宁, 贾象阳, 等.
光束法区域网平差的地面激光扫描多站点云自动定向方法[J]. 测绘学报, 2014, 43(7): 711–716, 723.
YAO Jili, MA Ning, JIA Xiangyang, et al. Auto-registration for terrestrial laser scanning multi-stations point clouds with bundle block adjustment method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 711–716, 723. DOI:10.13485/j.cnki.11-2089.2014.0099 |
| [13] |
姚吉利, 贾象阳, 马宁, 等.
地面激光扫描多站点云整体定向平差模型[J]. 测绘学报, 2014, 43(8): 835–841.
YAO Jili, JIA Xiangyang, MA Ning, et al. Overall orientation adjustment model of terrestrial laser scanning multi-station point clouds[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 835–841. DOI:10.13485/j.cnki.11-2089.2014.0123 |
| [14] |
闫利, 谭骏祥, 杨容浩, 等.
一种闭合条件约束的全局最优多视点云配准方法[J]. 测绘学报, 2016, 45(4): 418–424.
YAN Li, TAN Junxiang, YANG Ronghao, et al. A method of globally optimal registration for multi-view point clouds constrained by closed-loop conditions[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 418–424. DOI:10.11947/j.AGCS.2016.20150018 |
| [15] | KELBE D, VAN AARDT J, ROMANCZYK P, et al. Marker-free registration of forest terrestrial laser scanner data pairs with embedded confidence metrics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 4314–4330. DOI:10.1109/TGRS.2016.2539219 |
| [16] | KELBE D, VAN AARDT J, ROMANCZYK P, et al. Multiview marker-free registration of forest terrestrial laser scanner data with embedded confidence metrics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 729–741. DOI:10.1109/TGRS.2016.2614251 |
| [17] |
李彩林, 郭宝云, 季铮.
多视角三维激光点云全局优化整体配准算法[J]. 测绘学报, 2015, 44(2): 183–189.
LI Cailin, GUO Baoyun, JI Zheng. Global optimization and whole registration algorithm of multi-view 3D laser point cloud[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 183–189. DOI:10.11947/j.AGCS.2015.20130737 |
| [18] | GRISETTI G, KUMMERLE R, STACHNISS C, et al. A tutorial on graph-based slam[J]. IEEE Intelligent Transportation Systems Magazine, 2010, 2(4): 31–43. DOI:10.1109/MITS.2010.939925 |
| [19] | BORRMANN D, ELSEBERG J, LINGEMANN K, et al. Globally consistent 3D mapping with scan matching[J]. Robotics and Autonomous Systems, 2008, 56(2): 130–142. DOI:10.1016/j.robot.2007.07.002 |
| [20] | BESL P J, MCKAY N D. A method for registration of 3D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239–256. DOI:10.1109/34.121791 |
| [21] | KÜMMERLE R, GRISETTI G, STRASDAT H, et al. G2O: a general framework for graph optimization[C]//Proceedings of 2011 IEEE International Conference on Robotics and Automation.[S.l.]: IEEE, 2011: 3607-3613. |
| [22] | CADENA C, CARLONE L, CARRILLO H, et al. Past, present, and future of simultaneous localization and mapping:toward the robust-perception age[J]. IEEE Transactions on Robotics, 2016, 32(6): 1309–1332. DOI:10.1109/TRO.2016.2624754 |
| [23] | SHEPARD D P, HUMPHREYS T E. High-precision globally-referenced position and attitude via a fusion of visual SLAM, carrier-phase-based GPS, and inertial measurements[C]//Proceedings of 2014 IEEE/ION Position, Location and Navigation Symposium. Monterey, CA, USA: IEEE, 2014: 1309-1328. https://ieeexplore.ieee.org/document/6851506 |
| [24] | MARQUARDT D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431–441. DOI:10.1137/0111030 |
| [25] | RUSU R B, MARTON Z C, BLODOW N, et al. Towards 3D point cloud based object maps for household environments[J]. Robotics and Autonomous Systems, 2008, 56(11): 927–941. DOI:10.1016/j.robot.2008.08.005 |
| [26] | PAULY M, KEISER R, GROSS M. Multi-scale feature extraction on point-sampled surfaces[J]. Computer Graphics Forum, 2003, 22(3): 281–289. DOI:10.1111/cgf.2003.22.issue-3 |
| [27] | POMERLEAU F, COLAS F, SIEGWART R, et al. Comparing ICP variants on real-world data sets[J]. Autonomous Robots, 2013, 34(3): 133–148. DOI:10.1007/s10514-013-9327-2 |
| [28] | PULLI K. Multiview registration for large data sets[C]//Proceedings of the Second International Conference on 3D Digital Imaging and Modeling. Ottawa: IEEE, 1999: 160-168. https://ieeexplore.ieee.org/document/805346 |
| [29] | LOW K L. Linear least-squares optimization for point-to-plane ICP surface registration[R].[S.l.]: University of North Carolina at Chapel Hill, 2004, 4(TR04). |
| [30] |
王永波, 杨化超, 刘燕华, 等.
线状特征约束下基于四元数描述的LiDAR点云配准方法[J]. 武汉大学学报(信息科学版), 2013, 38(9): 1057–1062.
WANG Yongbo, YANG Huachao, LIU Yanhua, et al. Linear-feature-constrained registration of LiDAR point cloud via quaternion[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1057–1062. |



