地球的真实形状是一个不规则的球体[1-2],所以地球的数学模型可分为第一近似模型和第二近似模型。其中第一近似为球体模型,其数学表达式简单,几何误差一般不可忽略,在中低纬度地区多应用于复杂的误差分析。地球的第二近似为椭球模型,参考旋转椭球体更接近地球的真实形状,几何误差可以忽略不计,在中低纬度地区多应用于惯导解算。在极区,地球球体模型的几何误差减小,地球椭球模型的惯导解算复杂度增加,而且由于基于椭球模型的横向坐标系横向经纬线不正交的问题引入了编排原理性误差[3-5],球体模型也被应用于极区惯导解算[6]中。在极区导航算法的进一步研究中,球体模型由于表达式简单得到了更广泛的研究。文献[7]研究了基于球体模型的极区组合导航算法;文献[8-10]分别提出基于球体模型的极区对准方法;文献[11]研究了基于球体模型的中低纬度对极区导航模拟方法。针对具体极区导航应用中选用的地球近似模型类型一直没有明确的界定。惯导极区编排地球近似模型适用性研究对极区导航针对性研究具有重要意义。
为了实现地球近似模型的适用性分析,首先定义适用于极区的第一近似模型和第二近似模型,然后通过误差分析方法,对球近似模型的几何误差进行惯导误差分析,明确球体模型几何误差对惯导编排的影响形式,最后通过仿真对比地球近似模型的惯导误差。仿真结果表明,球近似模型几何误差会随惯导运行时间发散,而椭球近似模型的编排误差随时间变化不大,当惯导运行时间长则球近似模型不再适用于极区。
1 地球近似模型定义 1.1 球近似模型半径的选取当选用球近似模型作为地球模型时,其原点必定位于地心,故地球模型半径的选取关系到模型对地球的拟合程度,直接影响地球模型的几何误差。在不同的应用领域中,地球模型半径选取形式都不同,常用的球体半径有等面积半径Ra、等体积半径Rv、椭球长半轴半径Re、椭球短半轴半径Rp等。在极区应用中,常选取切换位置椭球体曲率半径Rs[12]或椭球短半轴半径作为球体模型的半径[13]。本文通过取N个地球椭球模型上的点p0i(xi, yi)使用最小二乘法拟合出与椭球模型半径误差最小的地球模型。由于椭球表面上的点到地心的距离与所在位置的经度无关,所以本文以过本初子午线的切面为例。
椭球上点到球面距离的平方和M为
 (1)
(1)
式中,R为由最小二乘法确定的球体模型半径。
最小二乘法要求椭球点到地心的距离与球半径的误差值的平方和为最小值,故存在
 (2)
(2)
结合式(1)和式(2)求得
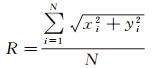 (3)
(3)
在极区范围的椭球弧线上分别取N=1120、N=11 112、N=111 112,得到最小二乘法拟合半径均为R=6 356.968 km,设切换位置为80°N,即取样范围为80°~90°的弧线,通过计算对球体模型半径进行对比,球体模型半径对比参数见表 1。
| 半径类型 | 半径/km | 椭球上点到球面距离的平方和M | ||
| N=1120 | N=11 112 | N=111 112 | ||
| 等表面积半径Ra | 6 371.010 | 219 286.84 | 2 191 386.17 | 21 912 379.48 |
| 等体积半径Rv | 6 371.004 | 219 099.51 | 2 189 514.19 | 21 893 660.90 |
| 椭球长半轴半径Re | 6 378.137 | 498 333.62 | 4 979 895.44 | 49 795 513.57 |
| 椭球短半轴半径Rp | 6 356.752 | 93.61 | 932.85 | 9 325.24 |
| 切换位置椭球体曲率半径Rs | 6 357.398 | 246.49 | 2 464.90 | 24 649.00 |
| 最小二乘法拟合半径R | 6 356.968 | 41.48 | 413.39 | 4 132.45 |
椭球上的点到球面距离的平方和M的大小可以表示为球体模型与椭球体模型在忽略经纬度误差情况下的高度误差平方和。由于在惯导解算中高度误差发散,故选择的M值应尽可能小,椭球上的点到球面距离的平方和M值可以表征球体模型对椭球体模型的拟合程度,由计算结果可知,在极区范围内,与椭球体模型最相近的球体模型的半径为最小二乘法拟合半径R。
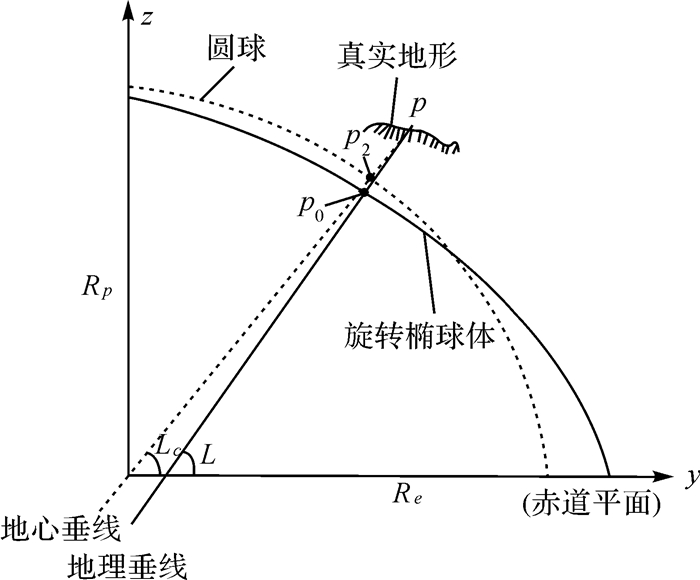
1.2 地球模型定义与对比根据上一节分析结果,地球球体模型定义为以地心为原点,半径为R=6 356.968 km的旋转球体,地球表面为球面。而在导航中,常用的地球椭球模型主要有WGS-84、克拉克等参考椭球体模型[14],其最主要的差别在于参数的不同。由于我国北斗系统采用CGCS2000模型作为参考椭球体模型,为了实际应用中参数转换便利,本文同样选用CGCS2000作为地球椭球模型,即中心位于地心,长半轴Re=6 378.137 km,短半轴Rp=6 356.752 km,扁率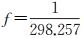
|
| 图 1 球体模型与椭球模型定义对比图 Fig. 1 Comparison diagram between the sphere model and ellipsoid model |
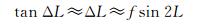 (4)
(4)
由关系式可见两者最大偏差出现在纬度45°处,在极区纬度误差减小[15],故而球体模型在一定的误差范围内可以使用。
2 横向坐标系惯导编排及其误差分析 2.1 横向坐标系惯导编排横向坐标系能解决极点处计算存在奇异值的问题,在极区导航实际应用中横向坐标系的研究具有重要意义。本文使用的横向坐标系如图 2所示,载体位置为横向坐标系(t系)的原点,沿参考球体模型的法线指向天为Zt轴,Xt轴沿横向纬度线指向横向正东,Yt轴沿当地横向子午线指向横向正北,Xt轴与Yt轴均与Zt轴符合右手定则。其横向经纬线如图所示,φ′为横向纬度,λ′为横向经度。

|
| 图 2 横向经纬度与横向坐标系示意图 Fig. 2 A schematic diagram of transverse longitude and latitude and transverse coordinate system |
横向坐标系的编排可分别由以下速度、姿态和位置更新方程确定(具体推导过程从略)
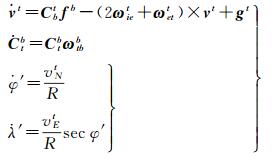 (5)
(5)
式中,vt=[vEt vNt vUt]T为横向速度;Cbt为载体坐标系(b系)到t系的旋转矩阵;fb=[fx fy fz]T为比力;ωiet=[-ωie sin λ′-ωie sin φ′cos λ′ωie cos φ′cos λ′]T为地球自转角速度ωie在t系内的投影;
通过计算值减去真实值推导横向坐标系误差方程(具体推导过程从略)
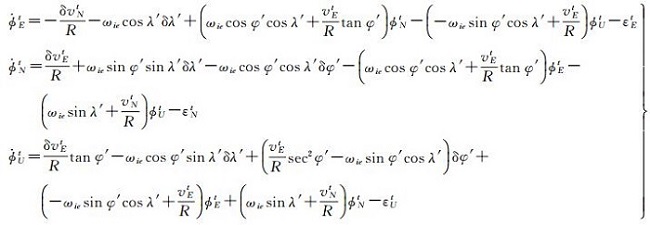 (6)
(6)
 (7)
(7)
 (8)
(8)
式中,ft=[fEt fNt fUt]T=Cbtfb为比力在横向坐标系的投影;∇t=[∇Et ∇Nt ∇Ut]T为导航坐标系下等效加速度计误差,且∇t=Cbt[∇x ∇y ∇z]T,∇x、∇y、∇z分别为b系下x、y、z方向上的加速度计误差;Ctt′= 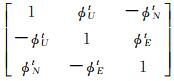
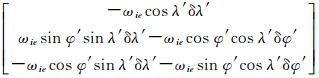
结合1.2节和2.1节可知球近似模型的几何误差会引起解算的位置误差和高度误差。在惯导解算中高度误差是发散的,且姿态误差将影响到垂线偏角误差,即球体模型的选用不仅仅会带来几何误差,还会引起惯导解算误差。本节参考文献[16]中惯导横向坐标系导航性能研究方法,推导球体模型几何误差引起惯导解算误差的具体形式,该误差分析形式与惯导解算中初始误差对惯导系统误差分析基本一致。
为了分析球体模型和椭球模型的几何误差对惯导系统的影响,在静基座条件下进行误差分析,可将误差方程写成矩阵形式
 (9)
(9)
进行拉普拉斯变换得
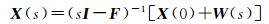 (10)
(10)
式中, X(0)=[δvE0t δvN0t δφ′0 δλ′0 ϕE0t ϕN0t ϕU0t]表示几何误差引起的速度误差、位置误差和失准角;X(s)=[∇Et ∇Nt 0 0 εEt εNt εUt]表示元器件误差。
推导可得其特征
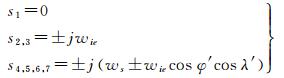 (11)
(11)
式中,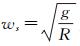
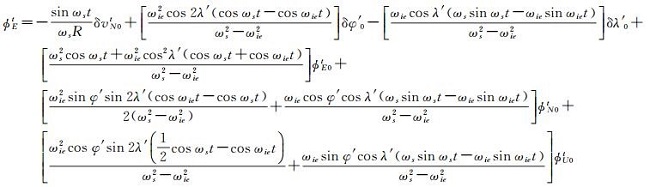
为简化计算,忽略傅科周期成分及元器件误差,推导出由几何误差引起的横向坐标系的系统误差
 (12)
(12)
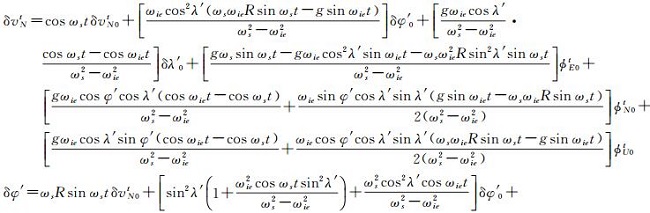 (13)
(13)
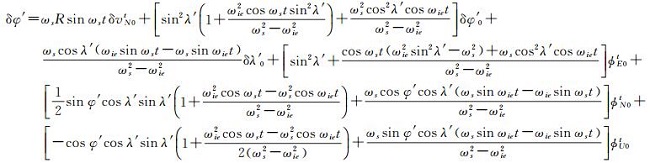 (14)
(14)
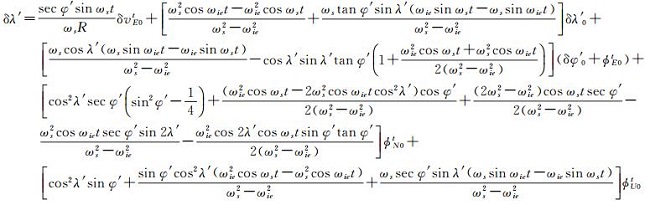 (15)
(15)
 (16)
(16)
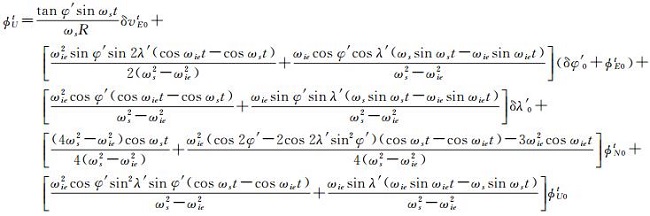 (17)
(17)
 (18)
(18)
分析式(12)-(18),可得如下结论:横向纬度误差会产生δφ′、δλ′和ϕUt常值误差和振荡性误差的叠加。东向失准角会产生δφ′、δλ′和ϕUt常值误差和振荡性误差的叠加。北向失准角会产生δφ′、δλ′和ϕUt常值误差和振荡性误差的叠加。天向失准角会产生δφ′、δλ′和ϕUt常值误差和振荡性误差的叠加。其余项产生振荡性误差。
结合上述分析可知,球体模型的横向纬度几何误差以及姿态几何误差引起的常值误差和振荡性误差的叠加,其余项产生振荡性误差,几何误差影响随时间发散。
3 地球近似模型适用性范围分析球体模型存在几何误差会产生惯导误差,同时在椭球体模型的编排中,为了解决横向经纬线不正交的问题,对编排作了一定的近似,带来了原理性的误差,故在地球模型和椭球体模型的选用中,要考虑两者误差的大小,将两者误差进行比较。
由于器件误差会随时间发散,为了对球体模型的惯导误差和椭球体模型的惯导误差进行对比,本文对无器件误差对球体模型误差和椭球体模型误差进行对比仿真,并通过不同时长的仿真观察球体模型误差发散对模型对比的影响。
本文以航海任务为例,对极区地球近似模型无器件误差惯导编排误差进行仿真,通过不同时长仿真结果对在航海任务中地球近似模型的使用范围进行给定,为极区模型研究提供理论依据。
3.1 无器件误差对比仿真为了对不同地球近似模型误差仿真进行分析,假设载体初始地理位置为(80°N, 125°E),在静基座条件下,仿真周期分别为24、240、360 h。在轨迹发生器中忽略元器件带来的误差。仿真结果如图 3-图 5所示。
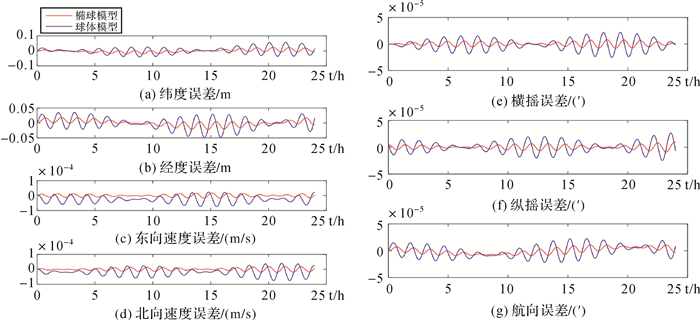
|
| 图 3 极区地球近似模型无器件误差惯导24 h编排误差对比结果 Fig. 3 The comparison result of 24 hours INS arrangement error of non device error with the approximate model in polar region |
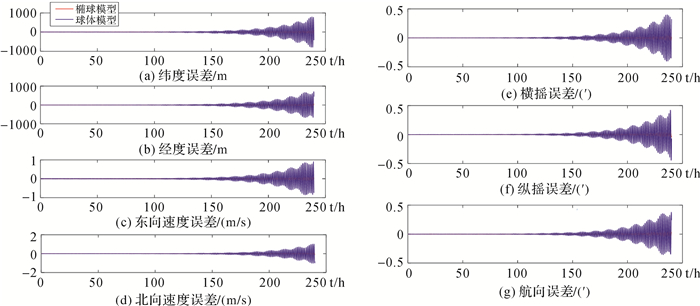
|
| 图 4 极区地球近似模型无器件误差惯导240 h编排误差对比结果 Fig. 4 The comparison result of 240 hours INS arrangement error of non device error with the approximate model in polar region |
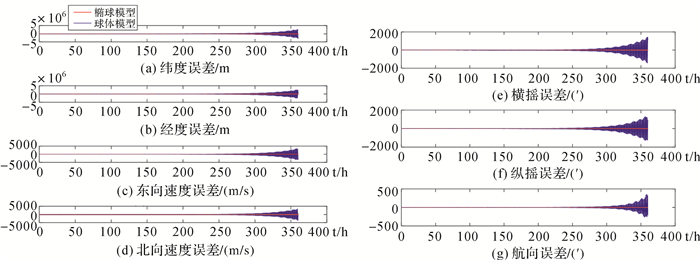
|
| 图 5 极区地球近似模型无器件误差惯导360 h编排误差对比结果 Fig. 5 The comparison result of 360 hours INS arrangement error of non device error with the approximate model in polar region |
为了表示两种模型引起的编排误差差异,定义误差值最大差异为∇,表示球体模型仿真误差的最大值与椭球模型仿真误差的最大值的差值。通过Matlab仿真计算,可得无器件误差不同时长地球近似模型编排误差对比数据,具体数据见表 2。
| 统计量 | 24 h | 240 h | 360 h |
| ∇δφ′/m | 0.033 | 711.2 | 2.59×106 |
| ∇δλ′/m | 0.017 | 638.7 | 2.46×106 |
| ∇δvEt/(m/s) | 7.19×10-6 | 0.81 | 3.23×103 |
| ∇δvNt/(m/s) | 2.12×10-5 | 0.92 | 3.34×103 |
| ∇ϕEt/(′) | 1.39×10-5 | 0.35 | 1.4×103 |
| ∇ϕNt/(′) | 1.72×10-5 | 0.38 | 1.27×103 |
| ∇ϕUt/(′) | 1.19×10-5 | 0.034 | 3.48×102 |
对仿真结果进行分析可知,在极区无器件误差条件下:①24 h内,地球球体模型几何误差和地球椭球模型编排误差引起的惯导误差差异不大,故24 h内地球模型可以使用,极区编排选用球近似模型;②240 h后球体模型和椭球体模型引起的编排误差差异变大,两种模型差异明显,故时长超过240 h,地球模型误差较大,建议极区编排选用椭球近似模型;③在极区无器件误差条件下,地球球体模型几何误差引起的惯导编排随着时间积累,静基座条件下,360 h后球体模型的经纬度误差超过2.4×106 m,速度误差超过3.2×103 m/s,球体模型编排已经发散,不能使用,极区编排选用椭球近似模型。
3.2 实际应用地球近似模型选用分析实际极区导航应用中,元器件误差不可忽略,载体形式不同,元器件误差和惯导运行时长都不一致,本文以舰艇为例,通过对比球体模型和椭球模型横向坐标系编排误差仿真,进一步验证上一节结论,并分析极区导航应用中适用的球体模型。
由于元器件误差会使极区惯导编排发散[17],故当航行时间达到240 h时,基于椭球模型横向坐标系编排和基于球体模型横向坐标系编排均发散,其仿真结果已经不再有效。由于极区特殊的地理环境[18-21],组合导航[22]以及校准模式[23-25]实际应用的可行性还需要得到进一步的验证。为了验证3.1节得出的结论同样适用于存在元器件误差的实际应用,对纯惯导模式分别进行时长24 h和120 h的仿真。假设载体初始地理位置为(80°N, 125°E),地理速度为0.01 m/s,地理航向角为0°,横摇角设置为0.3°sin(πt/4)rad,纵摇角设置为0.3°sin(πt/4)rad。在轨迹发生器中将3个陀螺的常值漂移为0.001(°)/h,随机白噪声标准差为0.001(°)/h,3个加速度计零偏为10-5 g,随机白噪声标准差为10-5 g。仿真周期分别为24、120 h仿真结果如图 6-图 7所示。
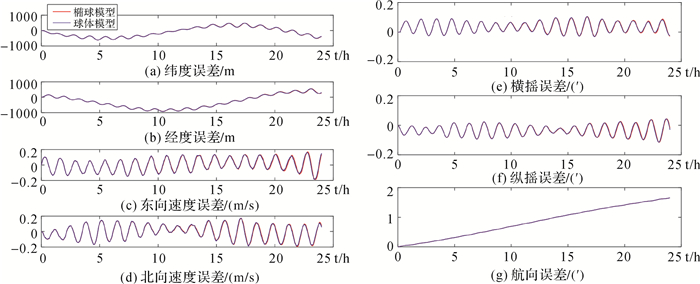
|
| 图 6 极区地球近似模型航海级器件误差24 h编排误差对比结果 Fig. 6 The comparison result of 24 hours INS arrangement error of seafaring level device error with the approximate model in polar region |
|
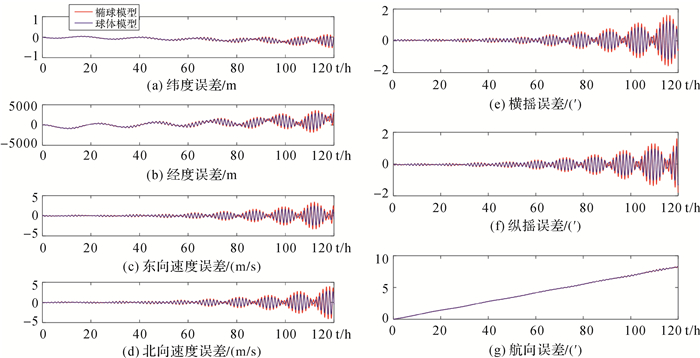
| 图 7 极区航海级器件误差地球近似模型编排误差120 h对比结果 Fig. 7 The comparison result of 120 hours INS arrangement error of seafaring level device error with the approximate model in polar region |
分析以上仿真结果可知,航海级器件误差120 h地球模型差异大于24 h地球模型差异,与3.1节中结论一致。可以证实舰船实际航行中,运行时长超过240 h时必须选用椭球近似模型,时长少于240 h时,可选用球近似模型,以减少编排复杂度。同理,根据表 3数据,飞机和导弹等短时间导航任务载体在极区可以使用球近似模型。在实际航行中,由于元器件误差的存在会使惯导系统随时间发散,一般不会存在运行时长超过240 h的无校准和组合导航的纯惯导导航模式,但元器件误差不会对几何误差引起的惯导误差产生影响,故所得结论不会因为导航模式为组合导航或校准模式而改变。
| 统计量 | 导弹 | 飞机 | 舰船 | 舰船 |
| 5 h | 24 h | 24 h | 120 h | |
| ∇δφ′/m | 0.16 | 76.4 | 2.47 | 348.8 |
| ∇δλ′/m | 1.49 | 153.6 | 2.81 | 516.5 |
| ∇δvEt/(m/s) | 0.001 | 0.08 | 0.007 | 0.59 |
| ∇δvNt/(m/s) | 0.002 | 0.04 | 3.4×10-4 | 0.42 |
| ∇ϕEt/(′) | 9.4×10-5 | 0.06 | 5.8×10-4 | 0.39 |
| ∇ϕNt/(′) | 8.6×10-4 | 0.05 | 3.7×10-4 | 0.19 |
| ∇ϕUt/(′) | 8.2×10-4 | 0.01 | 0.001 3 | 0.01 |
4 结论
本文首先通过不同球体模型半径对比,给出极区地球近似模型的定义。在此基础上,针对球近似模型几何误差,进行横向坐标系惯导编排误差分析,明确球体模型几何误差引起的惯导误差的形式,最后通过对比球体模型几何误差引起的惯性误差仿真和椭球模型编排误差引起的惯性误差仿真差异值,对几种常见的导航载体适用的模型进行判断。得到以下结论:①在极区通过最小二乘法拟合的半径R=6 356.968 km确定的球体模型与椭球模型最相近;②球体模型的横向纬度几何误差以及姿态几何误差会引起常值误差和振荡性误差的叠加,其余几何误差项产生振荡性误差,几何误差影响会随时间发散;③在无器件误差静基座下判断出球体模型适用于时长小于240 h(10 d)的导航任务,椭球体模型适用于时长大于240 h的导航任务;④针对不同载体类型,根据其不同器件误差和不同任务时长对舰船、飞机和导弹进行分析,建议在极区舰船使用椭球模型,而飞机和导弹使用球体模型。
| [1] |
莫里茨.地球形状[M].陈俊勇, 左传惠, 译.北京: 测绘出版社, 1992. MORITZ. Earth shape[M]. CHEN Junyong, ZUO Chunhui, trans. The figure of the Earth. Beijing: Surveying and Mapping Press, 1992. |
| [2] |
孙达, 蒲英霞.
地图投影[M]. 2版. 南京: 南京大学出版社, 2012.
SUN Da, PU Yingxia. Map projection[M]. 2nd ed. Nanjing: Nanjing University Press, 2012. |
| [3] |
刘文超.基于地球椭球的极区惯导格网导航与横向坐标导航技术研究[D].武汉: 海军工程大学, 2016. LIU Wenchao. Research on inertial grid navigation and transverse coordinate navigation based on earth ellipsoid in polar regions[D]. Wuhan: Naval University of Engineering, 2016. |
| [4] | YAO Yiqing, XU Xiaosu, YAO Li. Transverse navigation under the ellipsoidal earth model and its performance in both polar and non-polar areas[J]. Journal of Navigation, 2016, 69(2): 335–352. DOI:10.1017/S0373463315000715 |
| [5] | LI Qian, BEN Yueyang, YU Fei, et al. Transversal strapdown ins based on reference ellipsoid for vehicle in the polar region[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7791–7795. DOI:10.1109/TVT.2015.2497713 |
| [6] | LI Qian, BEN Yueyang, SUN Feng, et al. Transversal strapdown INS and damping technology for marine in polar region[C]//Proceedings of 2014 IEEE/ION Position, Location and Navigation Symposium. Monterey, CA: IEEE, 2014: 1365-1370. https://www.researchgate.net/publication/269297417_Transversal_strapdown_INS_and_damping_technology_for_marine_in_polar_region |
| [7] |
张福斌, 马朋, 王智辉.
基于横坐标系的捷联惯性导航系统/多普勒速度仪极区组合导航算法[J]. 兵工学报, 2016, 37(7): 1229–1235.
ZHANG Fubin, MA Peng, WANG Zhihui. SINS/DVL integrated navigation algorithm based on transversal coordinate frame in polar region[J]. Acta Armamentarii, 2016, 37(7): 1229–1235. DOI:10.3969/j.issn.1000-1093.2016.07.010 |
| [8] | GAO Yanbin, LIU Meng, LI Guangchun. Initial alignment for SINS based on pseudo-earth frame in polar regions[J]. Sensors, 2017, 17(6): 1416. DOI:10.3390/s17061416 |
| [9] |
高伟, 叶攀, 奔粤阳, 等.一种舰船捷联惯导系统极区动基座对准方法: 中国, 103791918A[P]. 2014-05-14. GAO Wei, YE Pan, BEN Yueyang, et al. Polar region moving base alignment method for naval vessel strapdown inertial navigation system: CN, 103791918A[P]. 2014-05-14. |
| [10] | CHENG Jianhua, WANG Tongda, GUAN Dongxue, et al. Polar transfer alignment of shipborne SINS with a large misalignment angle[J]. Measurement Science and Technology, 2016, 27(3): 035101. DOI:10.1088/0957-0233/27/3/035101 |
| [11] | ZHAO C L, WU W Q, LIAN J X. Research on rotating modulation inertial navigation system error characteristics simulation method in polar area[C]//Proceedings of 2014 IEEE Chinese Guidance, Navigation and Control Conference. Yantai, China: IEEE, 2015: 2790-2794. |
| [12] |
郝勇帅, 周爱军, 王海波.
地球模型对横坐标惯导极区导航影响的分析[J]. 舰船电子工程, 2017, 37(7): 37–40.
HAO Yongshuai, ZHOU Aijun, WANG Haibo. Analysis of the influence of the earth model of the transverse coordinate polar inertial navigation[J]. Ship Electronic Engineering, 2017, 37(7): 37–40. DOI:10.3969/j.issn.1672-9730.2017.07.010 |
| [13] | EARLE M A. Sphere to spheroid comparisons[J]. Journal of Navigation, 2006, 59(3): 491–496. |
| [14] |
秦永元.
惯性导航[M]. 2版. 北京: 科学出版社, 2014.
QIN Yongyuan. Inertial navigation[M]. 2nd ed. Beijing: Science Press, 2014. |
| [15] |
李忠美, 李厚朴, 边少锋.
常用纬度差异极值符号表达式[J]. 测绘学报, 2012, 43(2): 214–220.
LI Zhongmei, LI Houpu, BIAN Shaofeng. Symbolic expressions of difference extrema between regular latitudes[J]. Acta Geodaetica et Cartographica Sinica, 2012, 43(2): 214–220. DOI:10.13485/j.cnki.11-2089.2014.0031 |
| [16] |
刘文超, 卞鸿巍, 王荣颖.
惯导系统横向坐标法导航性能研究[J]. 武汉大学学报(信息科学版), 2015, 40(11): 1520–1525.
LIU Wenchao, BIAN Hongwei, WANG Rongying. Navigation performance of SINS transverse coordinate method[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1520–1525. |
| [17] | TITTERTON D H, WESTON J L. Strapdown inertial navigation technology[J]. Aerospace & Electronic Systems Magazine, 2004, 20(7): 33–34. |
| [18] | CHIRCOP A. Regulatory challenges for international arctic navigation and shipping in an evolving governance environment[J]. Ocean Yearbook, 2014, 28(1): 269–290. DOI:10.1163/22116001-02801011 |
| [19] | DEGGIM H. Ensuring safe, secure and reliable shipping in the Arctic ocean[M]//BERKMAN P, VYLEGZHANIN A. Environmental Security in the Arctic Ocean. Dordrecht: Springer, 2013: 241-254. |
| [20] |
余兴光.
中国第四次北极科学考察报告[M]. 北京: 海洋出版社, 2011.
YU Xingguang. The report of 2010 Chinese Arctic research expedition[M]. Beijing: Ocean Press, 2011. |
| [21] |
王有隆.
北极地区飞行中的通信与导航特性[J]. 航空维修与工程, 2016(1): 46–48.
WANG Youlong. Characteristics of communication and navigation on cross-polar routes[J]. Aviation maintenance and Engineering, 2016(1): 46–48. |
| [22] | CLYNCH J R, ALTENBURG R A. Ionospheric residual range error model[C]//Proceedings of International Geodetic Symposium on Satellite Doppler Positioning. Salt Lake City, UT: [s.n.], 1979: 1579-1587. https://www.researchgate.net/publication/258899608_Ionospheric_Residual_Range_Error_Model |
| [23] |
李倩.横坐标系捷联惯导系统极区导航及其误差抑制技术研究[D].哈尔滨: 哈尔滨工程大学, 2014. LI Qian. Research on transversal strapdown INS and error depression technology in polar region[D]. Harbin: Harbin Engineering University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10217-1017245757.htm |
| [24] |
李倩, 孙枫, 奔粤阳, 等.
横坐标系捷联惯导系统极区导航及阻尼设计[J]. 系统工程与电子技术, 2014, 36(12): 2496–2503.
LI Qian, SUN Feng, BEN Yueyang, et al. Transversal strapdown INS and damping design in polar region[J]. Systems Engineering and Electronics, 2014, 36(12): 2496–2503. |
| [25] | LI Qian, BEN Yueyang, YU Fei, et al. System reset of transversal strapdown INS for ship in polar region[J]. Measurement, 2015, 60: 247–257. DOI:10.1016/j.measurement.2014.10.020 |



