在中长基线GNSS相对定位中,如何正确固定模糊度是众多相关领域学者研究的热点问题。我国北斗卫星导航系统BDS(BeiDou navigation satellite system)于2012年底正式提供服务以来,运行稳定[1]。目前北斗系统已进入全球组网新阶段,其在轨卫星均可播发三频信号,可为地面用户提供更多的组合观测量,有助于正确固定模糊度。
经典TCAR算法将原始观测量进行线性组合,经逐级取整固定模糊度参数,但当基线长度达到十几千米甚至几百千米以上时,受电离层延迟和测量噪声的影响,模糊度难以正确固定。因此,如何有效地减小电离层延迟以及测量噪声对模糊度固定的不利影响,是正确固定模糊度需要着重解决的问题。
文献[2]通过构建最优观测量,分3步固定模糊度。文献[3]将经典TCAR模型扩展为几何模型和无几何模型两类。文献[4]通过两个GF和IF组合观测量仅对第3个线性无关的组合观测量进行了研究分析。文献[5]证明基于三频的BDS单历元模糊度解算方法相对于基于双频的模糊度解算方法,模糊度固定正确率有大幅提高。文献[6]对LAMBDA方法、几何TCAR算法、无几何TCAR算法及无几何无电离层TCAR算法进行了实测数据的对比分析。文献[7-8]提出的新算法分别降低了运算量和缩短了窄巷组合的收敛时间,但模糊度固定正确率与传统方法相当。文献[9-10]提出的方法提高了浮点解的精度,但未对固定解作研究分析。文献[11-13]提出的算法提高了中短基线模糊度固定正确率,但对算法在中长基线下的效果未作研究分析。文献[14]提出一种削弱电离层延迟影响的改进TCAR算法,但对窄巷模糊度固定正确率提高有限。文献[15]利用Kalman滤波对BDS多频数据进行处理。文献[16]提出的自适应抗差滤波理论适用于动态导航定位,对于中长基线相对定位具有一定的应用价值。
针对TCAR算法在BDS中长基线下模糊度固定正确率不高的问题,对BDS三频相对定位的解算模型进行了研究并改进。提出一种能减小电离层延迟影响,具有良好自适应抗差特性的BDS改进TCAR算法。在无几何TCAR模型的基础上,通过对模糊度固定的超宽巷进行线性组合得到电离层延迟和宽巷模糊度,再通过构造最优观测量,用自适应抗差滤波求解窄巷模糊度,有效地提高了宽窄巷模糊度的固定正确率。
1 经典TCAR算法 1.1 基本观测量BDS采用双差观测量实现中长基线相对定位,双差伪距和载波相位观测方程表达式为[2]
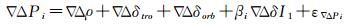 (1)
(1)
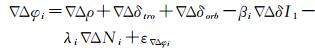 (2)
(2)
式中,∇Δ表示双差运算算子,∇ΔPi和∇Δφi表示在频点i上以m为单位的双差伪距观测量和双差载波相位观测量;∇Δρ表示以m为单位的双差站星几何距离项;∇Δδtro和∇Δδorb分别表示双差对流层延迟误差项和双差轨道误差项;∇ΔδI1表示相对f1频点的一阶电离层延迟项;ε∇ΔPi和ε∇Δφi分别表示fi频点上的双差伪距和载波相位测量噪声;βi表示一阶电离层延迟系数。
三频双差组合观测量表达式为
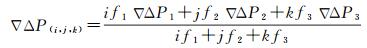 (3)
(3)
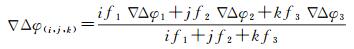 (4)
(4)
式中,i、j、k分别为对应频点f1、f2、f3的组合整数系数。
1.2 计算步骤经典TCAR算法通过对原始伪距和载波相位观测量进行线性组合,可得到最优观测量。按波长由长到短,依次固定超宽巷、宽巷和窄巷模糊度。BDS常用最优载波相位组合观测量见表 1。其中,整数i、j、k分别表示组合观测量的组合系数;λ(i, j, k)表示相应的组合波长;μ(i, j, k)表示以m为单位的观测噪声放大因子;β(i, j, k)为组合观测量一阶电离层延迟系数。
| i | j | k | λ(i, j, k) | μ(i, j, k) | β(i, j, k) |
| 0 | -1 | 1 | 4.884 | 28.529 | -1.591 |
| 1 | 4 | -5 | 6.371 | 172.614 | 0.652 |
| 1 | 0 | -1 | 1.025 | 6.875 | -1.231 |
| 1 | -1 | 0 | 0.847 | 5.575 | -1.293 |
| 0 | 1 | 0 | 0.248 | 1.000 | 1.672 |
| 0 | 0 | 1 | 0.236 | 1.000 | 1.515 |
| 1 | 0 | 0 | 0.192 | 1.000 | 1.000 |
基于无几何模型的TCAR算法分3步对模糊度浮点解进行取整固定。通过对伪距观测量和载波观测量进行线性组合,以消除站星几何距离、对流层延迟及卫星轨道误差等几何相关项。具体步骤如下:
(1) 超宽巷模糊度解算
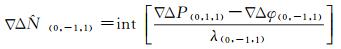 (5)
(5)
式中,int[·]表示取整算子。
(2) 宽巷模糊度解算
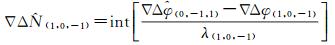 (6)
(6)
(3) 窄巷模糊度解算
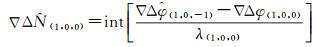 (7)
(7)
式中
 (8)
(8)
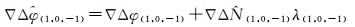 (9)
(9)
根据线性关系,可得到其他原始频点的模糊度
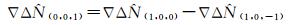 (10)
(10)
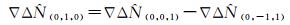 (11)
(11)
电离层延迟是限制中长基线下基于无几何模型的TCAR算法模糊度固定正确率的重要因素。利用两个易于正确固定的超宽巷模糊度求解电离层延迟。根据电离层延迟的大小,调整下述第2步中自适应权因子的大小,固定宽巷模糊度。具体过程如下:
基于无几何模型固定两个超宽巷模糊度分别为[19]
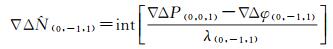 (12)
(12)
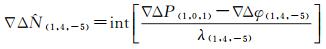 (13)
(13)
由表 1知,BDS超宽巷组合(0, -1, 1)的电离层延迟较小并且测量噪声相比于其他组合最小,其良好的特性被公认是解算模糊度最优的超宽巷组合,又因B3频点上的伪距观测量∇ΔP(0, 0, 1)具有较高精度,可将其用于EWL模糊度解算;BDS超宽巷组合(1, 4, -5)的波长较长,因此十分有利于模糊度的解算;利用伪距组合∇ΔP(1, 0, 1)可由式(13)解得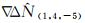
根据得到的超宽巷组合观测量求解电离层延迟及对应精度为
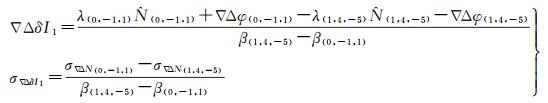 (14)
(14)
构造最优组合观测量求解宽巷模糊度为
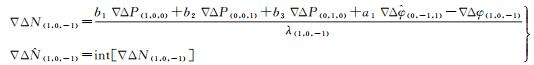 (15)
(15)
式中,实数b1、b2、b3及a1为组合观测量的权因子,应满足以下约束条件
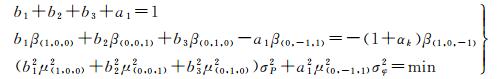 (16)
(16)
式(15)选取了5种观测量的组合,选取原则是消除或减少经典TCAR算法中的残余电离层延迟,尽量减少噪声,实现最佳AR性能。因此引入额外的伪距和模糊度固定的组合,同时也是为了增加线性组合的自由度。具体而言,在式(15)中使用原始伪距和模糊度固定的EWL组合。式(15)中,由观测量组合求得模糊度∇ΔN(1, 0, -1)后,经直接取整固定得到模糊度整数解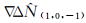
式(16)中组合系数应满足3个条件:无几何条件、无电离层或削弱电离层,以及最小方差条件。为避免将未模型化的误差(如对流层延迟误差、轨道误差等)放大,使几何相关项对应系数之和为1,在消除电离层延迟的情况下得到组合噪声最小的观测量,分别得到约束条件式(16)包含的3个等式。式中,根据经验值,取σφ=0.004 m,σP=0.6 m,αk为自适应权因子, αk取值满足以下函数[14]
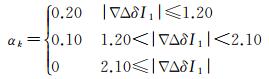 (17)
(17)
按式(17)选取αk可使宽巷模糊度固定正确率最高[14]。因αk可由∇ΔδI1的取值唯一地确定,经对式(16)求极值,可得式(16)存在唯一解。
确定宽巷模糊度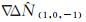
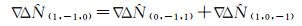 (18)
(18)
由于窄巷观测量波长相对较短,窄巷模糊度对电离层延迟、测量噪声等影响更为敏感,因此窄巷模糊度固定更为困难,而提高窄巷模糊度固定的正确率是提高最终定位精度的关键。模糊度已固定的宽巷可看作是精度优于超宽巷的伪距观测量,可用于窄巷模糊度解算[17]。因此,为了提高窄巷模糊度固定正确率,通过构建最优观测量的方式来降低电离层残差和观测噪声对窄巷模糊度解算造成的不利影响[18]。
将模糊度已固定的超宽巷、宽巷与原始伪距观测量及窄巷观测量经过线性组合,并赋予最优的权重比,得到消电离层、低噪声的最优观测量,用于窄巷模糊度的解算,以提高窄巷模糊度解算的正确率。构建的观测量表达式如下
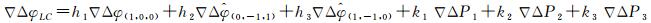 (19)
(19)
式中,组合系数hi和ki(i=1, 2, 3)的选取条件应满足下式所述关系
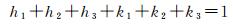 (20)
(20)
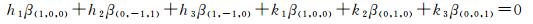 (21)
(21)
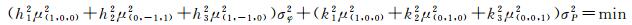 (22)
(22)
为避免将未模型化的误差(如对流层延迟误差、轨道误差等)放大,使几何相关项对应系数之和为1,得到约束条件式(20);在消除电离层延迟的情况下得到组合噪声最小的观测量,分别得到约束条件式(21)和式(22)。对式(22)求极值可得最小噪声,由式(20)、式(21)、式(22)确定的约束关系存在唯一解。
将模糊度固定的宽巷组合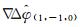
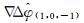
| 最优组合 | h1 | h2 | h3 | k1 | k2 | k3 |
| ∇ΔφLC1 | 0.566 9 | 0.407 6 | 0.017 5 | 0.000 5 | 0.000 7 | 0.006 8 |
| ∇ΔφLC2 | 0.557 5 | 0.403 0 | 0.027 1 | 0.000 8 | 0.001 0 | 0.010 6 |
由表 2可得,因伪距P1和P2的噪声远大于载波噪声,因此赋予k1和k2较小权值。下面用自适应抗差滤波求解窄巷模糊度,过程如下:
(1) 基本模型
窄巷模糊度解算采用优化后的观测量,其载波双差观测方程如下
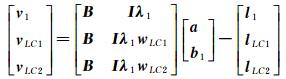 (23)
(23)
式中,a为流动站位置坐标参数(Xr, Yr, Zr);B为基线位置向量a的设计矩阵;b1为双差窄巷模糊度在频点f1上的模糊度参数;v1、vLC1、vLC2表示对应观测量的残差向量;l1、lLC1、lLC2表示对应观测量;wLC1和wLC2分别对应h1不同的取值。求解窄巷模糊度浮点解后经直接取整固定获得窄巷模糊度整数解,以保持窄巷模糊度整数特性。
利用自适应抗差滤波解算位置坐标参数及窄巷模糊度,目的是抵制观测异常误差的影响,构造自适应因子可控制动力学模型误差的影响[19]。其中状态向量为单历元内位置坐标参数及窄巷模糊度,即
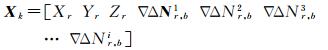 (24)
(24)
式中,Xr、Yr、Zr为流动站的位置坐标参数;Nr, b1~Nr, bi为窄巷模糊度参数。
(2) 等价权计算
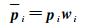 (25)
(25)
式中,pi为观测向量Lk的权矩阵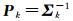
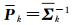
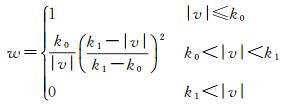 (26)
(26)
式中,k0=1.25;k1=3.75。
(3) 误差判别统计量
采用的误差判别统计量为预测残差统计量
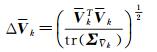 (27)
(27)
式中,Vk表示预测残差向量。
(4) 自适应因子
自适应因子仍采用IGG3方案。即当模型误差统计量小于阈值时,αk等于1;当模型误差大于阈值时,αk等于0;否则,αk大于0,小于1。函数形式为
 (28)
(28)
式中,c0=1.25;c1=3.75。
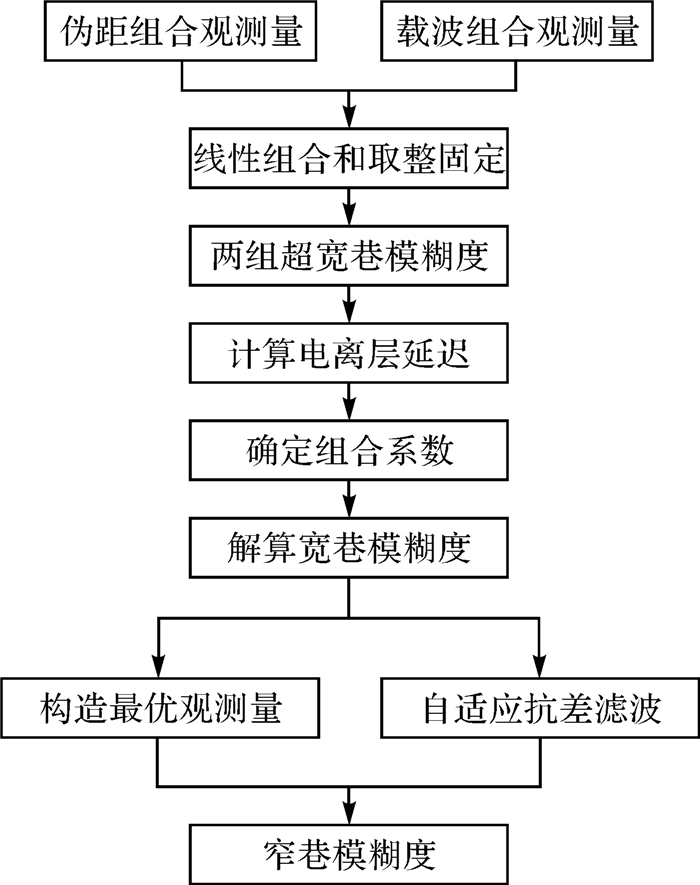
改进TCAR算法总体流程如图 1所示。
|
| 图 1 改进TCAR算法流程 Fig. 1 Flowchart of improved TCAR algorithm |
3 试验分析
为验证改进TCAR算法的可行性和效果,利用多频接收机采集了共3组不同长度的观测数据。所采集数据信息见表 3。
| 采集日期 | 基线长度/km | 采样间隔/s | 观测时长/s | 截止高度角/(°) |
| 2018-03-12 | 25 | 10 | 25 000 | 15 |
| 2018-03-12 | 170 | 10 | 25 000 | 15 |
| 2018-03-12 | 350 | 10 | 25 000 | 15 |
25 km长基线为荥阳-郑州的基线;170 km长基线为平顶山-郑州的基线;350 km长基线为随州-郑州的基线。
利用所采集的3组不同长度基线数据分别对改进TCAR算法进行试验验证。试验采用后处理精密相对定位得到的模糊度固定解作为真值,将每个历元解算得到的模糊度固定解与真值对比,以判断模糊度是否正确固定。图例中以MTCAR表示改进TCAR算法。
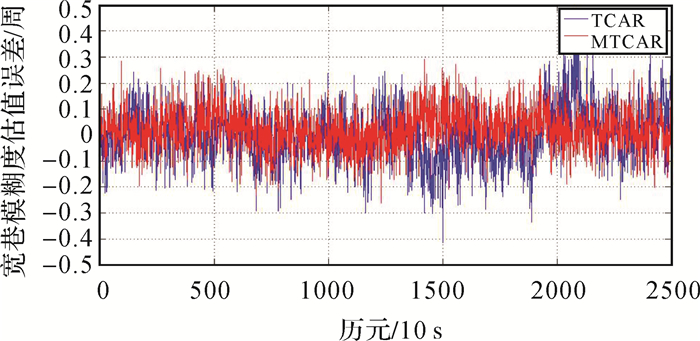
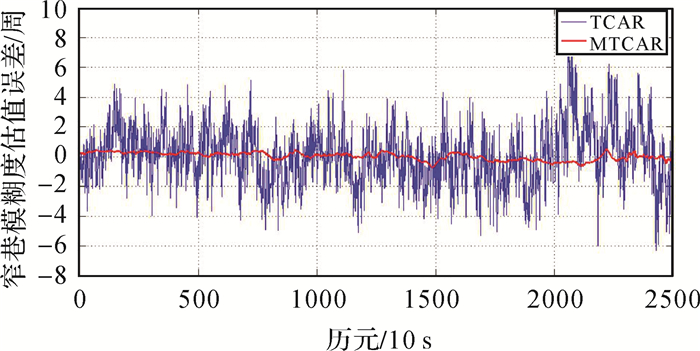
图 2是分别利用经典TCAR算法和改进TCAR算法解算25 km基线时,选取的C01-C10双差卫星相应的宽巷模糊度估值误差。图 3是对应的窄巷模糊度估值误差。
|
| 图 2 宽巷模糊度估值误差(25 km, C01-C10) Fig. 2 Wide-lane ambiguity estimation error(25 km, C01-C10) |
|
| 图 3 窄巷模糊度估值误差(25 km, C01-C10) Fig. 3 Narrow-lane ambiguity estimation error(25 km, C01-C10) |
(1) 25 km基线数据处理结果
由图 2和图 3可以看出,当基线长度为25 km时,采用经典TCAR算法解算模糊度时,宽巷模糊度估值误差可达0.2~0.4周,窄巷模糊度估值误差浮动较大,可达2~5周,窄巷模糊度无法直接取整固定;采用改进TCAR算法解算模糊度时,宽巷模糊度估值误差基本保持在0.1周左右,小于0.2周,窄巷模糊度估值误差基本小于0.4周,可以直接取整固定。
(2) 170 km基线数据处理结果
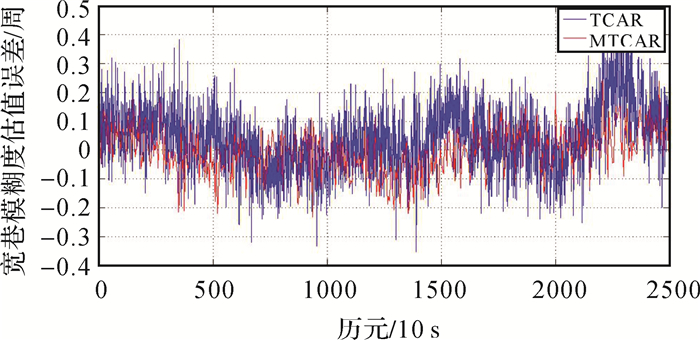
图 4是分别利用经典TCAR算法和改进TCAR算法解算170 km基线时,选取的C01-C10双差卫星相应的宽巷模糊度估值误差。图 5是相应的窄巷模糊度估值误差。
|
| 图 4 宽巷模糊度估值误差(170 km, C01-C10) Fig. 4 Wide-lane ambiguity estimation error(170 km, C01-C10) |

|
| 图 5 窄巷模糊度估值误差(170 km, C01-C10) Fig. 5 Narrow-lane ambiguity estimation error(170 km, C01-C10) |
由图 4和图 5可以看出,当基线长度为170 km时,采用经典TCAR算法解算模糊度时,宽巷模糊度估值误差可达到0.2~0.4周,窄巷模糊度估值误差浮动较大,可达到2~5周,窄巷模糊度无法直接取整固定;采用改进TCAR算法解算模糊度时,宽巷模糊度估值误差基本小于0.2周,窄巷模糊度估值误差基本小于0.6周。
(3) 350 km基线数据处理结果
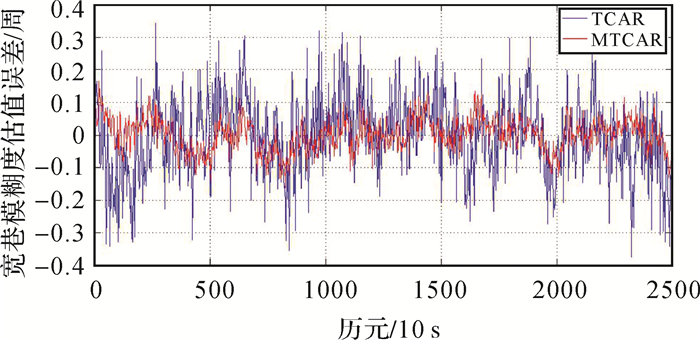
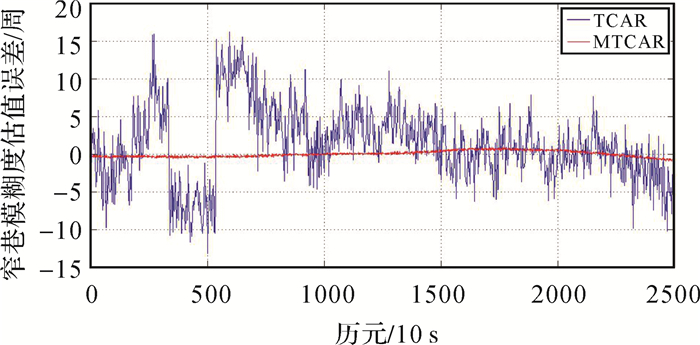
图 6是分别利用经典TCAR算法和改进TCAR算法解算350 km基线时,选取的C01-C06双差卫星相应的宽巷模糊度估值误差。图 7是相应的窄巷模糊度估值误差。
|
| 图 6 宽巷模糊度估值误差(350 km, C01-C06) Fig. 6 Wide-lane ambiguity estimation error(350 km, C01-C06) |
|
| 图 7 窄巷模糊度估值误差(350 km, C01-C06) Fig. 7 Narrow-lane ambiguity estimation error(350 km, C01-C06) |
由图 6和图 7可以看出,当基线长度为350 km时,采用经典TCAR算法解算模糊度时,宽巷模糊度估值误差可达到0.2~0.4周,窄巷模糊度估值误差浮动较大,可达到5~10周,窄巷模糊度无法直接取整固定;采用改进TCAR算法解算模糊度时,宽巷模糊度估值误差基本小于0.2周,窄巷模糊度估值误差小于1周。
对试验结果进行统计,得到上述3种不同长度基线的模糊度固定正确率,统计结果见表 4-表 6。模糊度固定正确率指模糊度固定正确历元数与总历元数的百分比。
| 算法 | 总历元/s | 宽巷固定历元/s | 宽巷固定正确率/(%) | 窄巷固定历元/s | 窄巷固定正确率/(%) |
| 经典TCAR | 25 000 | 24 838 | 99.35 | 5325 | 21.30 |
| MTCAR | 25 000 | 25 000 | 100.00 | 24 370 | 97.48 |
| 算法 | 总历元/s | 宽巷固定历元/s | 宽巷固定正确率/(%) | 窄巷固定历元/s | 窄巷固定正确率/(%) |
| 经典TCAR | 25 000 | 24 470 | 97.88 | 4840 | 19.36 |
| MTCAR | 25 000 | 25 000 | 100.00 | 20 990 | 83.96 |
| 算法 | 总历元/s | 宽巷固定历元/s | 宽巷固定正确率/(%) | 窄巷固定历元/s | 窄巷固定正确率/(%) |
| 经典TCAR | 25 000 | 24 430 | 97.72 | 2623 | 10.49 |
| MTCAR | 25 000 | 25 000 | 100.00 | 19 825 | 79.30 |
本文利用经典TCAR算法解算长度为25 km基线时,宽巷的模糊度固定正确率统计结果是97.72%,窄巷的模糊度固定正确率统计结果是21.3%;文献[11]利用经典TCAR算法解算长度为23 km基线,宽巷模糊度固定率为98.39%,窄巷模糊度固定率为88.17%。本文试验结果与文献[11]相比,宽巷的模糊度固定正确率基本持平,窄巷的模糊度固定正确率偏低。原因如下:①可能是受观测条件的影响,观测数据中包含较多的测量噪声及测量粗差;②即使是等长度的基线,空间相关程度也可能并不相同,本试验采集的数据可能基线间空间相关性较差,双差难以较好消除公共误差项,以上两点导致利用经典TCAR算法解算窄巷模糊度时固定正确率较低。而使用改进的TCAR算法可使窄巷模糊度固定正确率达到83.96%,改进的TCAR算法采用自适应抗差滤波求解窄巷模糊度,因此也可以说明改进的TCAR算法较好地减小测量噪声以及粗差带来的影响。
总体上,随着基线长度不断增加,宽巷和窄巷的模糊度固定正确率均会下降。对于宽巷模糊度,当基线长度为25 km,采用经典TCAR算法时,模糊度固定正确率保持在99.35%,即使基线长度达到350 km,模糊度固定正确率也高达97.72%;采用改进TCAR算法时,模糊度固定正确率均为100%。针对长度分别为25、170、350 km的基线,采用改进TCAR算法相比于经典TCAR算法,宽巷模糊度固定正确率分别提高了0.65%、2.12%、2.28%。
对于窄巷模糊度,当基线长度为25 km,采用经典TCAR算法时,模糊度固定正确率为21.30%,当基线长度达到350 km,模糊度固定正确率仅为10.49%;当基线长度为25 km,采用改进TCAR算法时,模糊度固定正确率高达97.48%,当基线长度达到350 km,模糊度固定正确率为79.30%;针对长度分别为25、170、350 km的基线,采用改进TCAR算法相比于经典TCAR算法,窄巷模糊度固定正确率分别提高了76.18%、64.60%、68.81%。
因多基线数据处理的基础也是单基线处理,对于多基线处理,本文的算法也同样适用于多基线解算,即本文的结论也同样适用。且多基线处理,还可以利用组网由网平差进一步提高基线解算精度。
试验表明,随着基线长度的不断增加,相比于经典TCAR算法,改进TCAR算法能够保持较高的宽巷模糊度固定正确率,且能明显提高窄巷模糊度固定正确率。
4 结论中长基线下模糊度难以正确固定是经典TCAR算法的不足之处。基于自适应抗差滤波的BDS改进TCAR算法在减小电离层延迟的基础上求解宽巷模糊度,在构建最优观测量后,采用自适应抗差滤波求解窄巷模糊度,以提高模糊度固定成功率和可靠性。试验表明,中长基线下窄巷模糊度更难以固定,提出的改进算法仍能保持较高的宽巷模糊度固定正确率,并能明显提高窄巷模糊度固定正确率。
| [1] |
杨元喜.
北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6.
YANG Yuanxi. Progress, contribution and challenges of compass/BeiDou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] | FENG Yanming. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J]. Journal of Geodesy, 2008, 82(12): 847–862. DOI:10.1007/s00190-008-0209-x |
| [3] | FENG Yanming, LI Bofeng. Three carrier ambiguity resolutions:generalised problems, models and solutions[J]. Journal of Global Positioning Systems, 2009, 8(2): 115–123. DOI:10.5081/jgps |
| [4] | WANG K, ROTHACHER M. Ambiguity resolution for triple-frequency geometry-free and ionosphere-free combination tested with real data[J]. Journal of Geodesy, 2013, 87(6): 539–553. DOI:10.1007/s00190-013-0630-7 |
| [5] | TANG Wenming, DENG Chenlong, SHI Chuang, et al. Triple-frequency carrier ambiguity resolution for BeiDou navigation satellite system[J]. GPS Solutions, 2014, 18(3): 335–344. DOI:10.1007/s10291-013-0333-9 |
| [6] | ZHANG Xiaohong, HE Xiyang. Performance analysis of triple-frequency ambiguity resolution with BeiDou observations[J]. GPS Solutions, 2016, 20(2): 269–281. DOI:10.1007/s10291-014-0434-0 |
| [7] |
范建军, 王飞雪.
一种短基线GNSS的三频模糊度解算(TCAR)方法[J]. 测绘学报, 2007, 36(1): 43–49.
FAN Jianjun, WANG Feixue. A method for GNSS three frequency ambiguity resolution based on short baselines[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 43–49. DOI:10.3321/j.issn:1001-1595.2007.01.008 |
| [8] |
梁宵, 黄智刚, 秦红磊, 等.
采用宽窄巷结合的LAMBDA解算方法的北斗多频差分定位技术[J]. 哈尔滨工业大学学报, 2017, 49(11): 46–51.
LIANG Xiao, HUANG Zhigang, QIN Honglei, et al. Multi-frequency BeiDou differential positioning using combination of wide and narrow Lane for LAMBDA resolution[J]. Journal of Harbin Institute of Technology, 2017, 49(11): 46–51. DOI:10.11918/j.issn.0367-6234.201612083 |
| [9] | HENKEL P, GÜNTHER C. Reliable integer ambiguity resolution:multi-frequency code carrier linear combinations and statistical a priori knowledge of attitude[J]. Navigation, 2012, 59(1): 61–75. DOI:10.1002/navi.v59.1 |
| [10] |
谢建涛, 郝金明, 刘伟平, 等.
中长基线的BDS三频线性组合观测量优化[J]. 武汉大学学报(信息科学版), 2017, 42(12): 1779–1784.
XIE Jiantao, HAO Jinming, LIU Weiping, et al. BDS triple frequency linear combination observation optimization for medium-long baseline[J]. Geomatics and Information Science of Wuhan University, 2017, 42(12): 1779–1784. |
| [11] |
谢建涛, 郝金明, 韩聪, 等.
BDS单历元TCAR算法优化研究[J]. 测绘科学技术学报, 2016, 33(1): 6–10, 15.
XIE Jiantao, HAO Jinming, HAN Cong, et al. Research of BDS single-epoch and triple-frequency ambiguity resolution using the modified TCAR method[J]. Journal of Geomatics Science and Technology, 2016, 33(1): 6–10, 15. |
| [12] |
宋玉龙, 廉保旺, 唐成凯.
基于多频模糊度解算的BDS/GPS中基线AEKF RTK算法[J]. 系统工程与电子技术, 2017, 39(8): 1794–1800.
SONG Yulong, LIAN Baowang, TANG Chengkai. BDS/GPS AEKF RTK algorithm utilizing multi-frequency ambiguity resolution for medium baseline[J]. Systems Engineering and Electronics, 2017, 39(8): 1794–1800. |
| [13] |
刘硕, 张磊, 李健.
一种改进的宽巷引导整周模糊度固定算法[J]. 武汉大学学报(信息科学版), 2018, 43(4): 637–642.
LIU Shuo, ZHANG Lei, LI Jian. A modified wide lane bootstrapping ambiguity resolution algorithm[J]. Geomatics and Information Science of Wuhan University, 2018, 43(4): 637–642. |
| [14] | ZHAO Qile, DAI Zhigang, HU Zhigang, et al. Three-carrier ambiguity resolution using the modified TCAR method[J]. GPS Solutions, 2015, 19(4): 589–599. DOI:10.1007/s10291-014-0421-5 |
| [15] |
李金龙.
北斗/GPS多频实时精密定位理论与算法[J]. 测绘学报, 2015, 44(11): 1927.
LI Jinlong. BDS/GPS multi-frequency real-time kinematic positioning theory and algorithms[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1927. DOI:10.11947/j.AGCS.2015.20150254 |
| [16] |
杨元喜.
自适应抗差最小二乘估计[J]. 测绘学报, 1996, 25(3): 206–211.
YANG Yuanxi. Adaptively robust least squares estimation[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 206–211. DOI:10.3321/j.issn:1001-1595.1996.03.009 |
| [17] | LOU Yidong, GONG Xiaopeng, GU Shengfeng, et al. Assessment of code bias variations of BDS triple-frequency signals and their impacts on ambiguity resolution for long baselines[J]. GPS Solutions, 2017, 21(1): 177–186. DOI:10.1007/s10291-016-0514-4 |
| [18] | ZHAO Qile, SUN Binzi, DAI Zhiqiang, et al. Real-time detection and repair of cycle slips in triple-frequency GNSS measurements[J]. GPS Solutions, 2015, 19(3): 381–391. DOI:10.1007/s10291-014-0396-2 |
| [19] | WANG Xing, LIU Wenxiang, SUN Guangfu. An improved geometry-free three carrier ambiguity resolution method for the BeiDou navigation satellite system[J]. Journal of Navigation, 2016, 69(6): 1393–1408. DOI:10.1017/S0373463316000163 |
| [20] |
杨元喜, 任夏, 许艳.
自适应抗差滤波理论及应用的主要进展[J]. 导航定位学报, 2013, 1(1): 9–15.
YANG Yuanxi, REN Xia, XU Yan. Main progress of adaptively robust filter with applications in navigation[J]. Journal of Navigation and Positioning, 2013, 1(1): 9–15. DOI:10.3969/j.issn.2095-4999.2013.01.003 |



