2. 西安测绘研究所, 陕西 西安 710054;
3. 地理信息工程国家重点实验室, 陕西 西安 710054
2. Institute of Surveying and Mapping, Xi'an 710054, China;
3. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China
对于甚长基线干涉测量(very long baseline interferometry,VLBI)、全球导航卫星系统(global navigation satellite system,GNSS)等空间大地测量技术,对流层延迟是其主要误差源之一。在利用这些测量技术求解大地测量参数(包括测站坐标、速度、地球定向参数等)的过程中,一般做法是:将对流层延迟中的主项,即天顶干延迟部分作为延迟的先验值;因干延迟计算精度较高,可达毫米级,远小于天顶湿延迟值,所以可将天顶湿延迟作为干延迟的改正值估计得出;最终,干、湿天顶延迟分别与对应的映射函数相乘并求和得到斜路径延迟[1-2]。以下如不作特殊说明,统一将天顶干、湿延迟简称为干、湿延迟。
这种估计策略并未考虑映射函数的误差,如果选用GMF(global mapping function)、NMF(Niell mapping function)等经验映射函数模型,则干、湿分量有可能存在10-2、10-1量级的误差[3-4],此时与干、湿延迟相乘会产生厘米级甚至分米级的斜路径延迟误差,进而对测站位置等大地测量参数的解算造成不可忽略的影响[5]。虽然VMF(Vienna mapping function)系列模型[6-7]相比GMF和NMF具有更高的精度和时间分辨率,但VMF模型需要利用气象数据事后反算得到,因而在实际观测中无法实时获取。这对未来大地测量产品的快速、高精度发布较为不利[8]。
本文以GMF经验模型为例,分析了该映射函数的误差特点,利用统计方法构建了该误差随高度角变化的函数模型,进而提出了顾及映射函数误差的对流层延迟两步估计法,并用试验证明了该方法的有效性。
1 传统估计方法传统估计方法中,对流层延迟的数学模型如下
 (1)
(1)
式中,L表示斜路径对流层延迟;ZHD、ZWD分别表示天顶对流层干、湿延迟;mfh(el)、mfw(el)表示高度角为el时干、湿分量的映射函数;maz(el)表示高度角为el时对流层水平梯度映射函数,具体形式为[9]
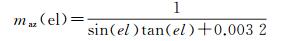 (2)
(2)
式中,α为方位角;Gns、Gew分别被定义为水平梯度的南北、东西分量。
此处需说明的是:①一般情况下,干延迟可按照Saastamonien模型计算[10],当已知地表气压时,认为干延迟误差可忽略;其中,地表气压可通过气象仪器观测获取,或利用数值气象模型等方法得到。本文采用的是后者,具体是欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)提供的分层格网气象数据。除此之外,后文用于评定精度的映射函数、湿延迟等参数的参考值,也根据该数据计算得到。ECMWF数据根据多源气象信息综合得到,在国际气象学研究中具有十分权威的地位,常被学者用作评判对流层延迟精度的参考数据。②映射函数通常是将待求地区的位置和年积日代入GMF等全球经验模型计算得到(具体公式可参照文献[11—12]),并忽略其误差。此时观测方程为
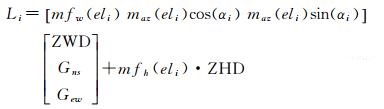 (3)
(3)
式中,下标i表示第i次观测的量。
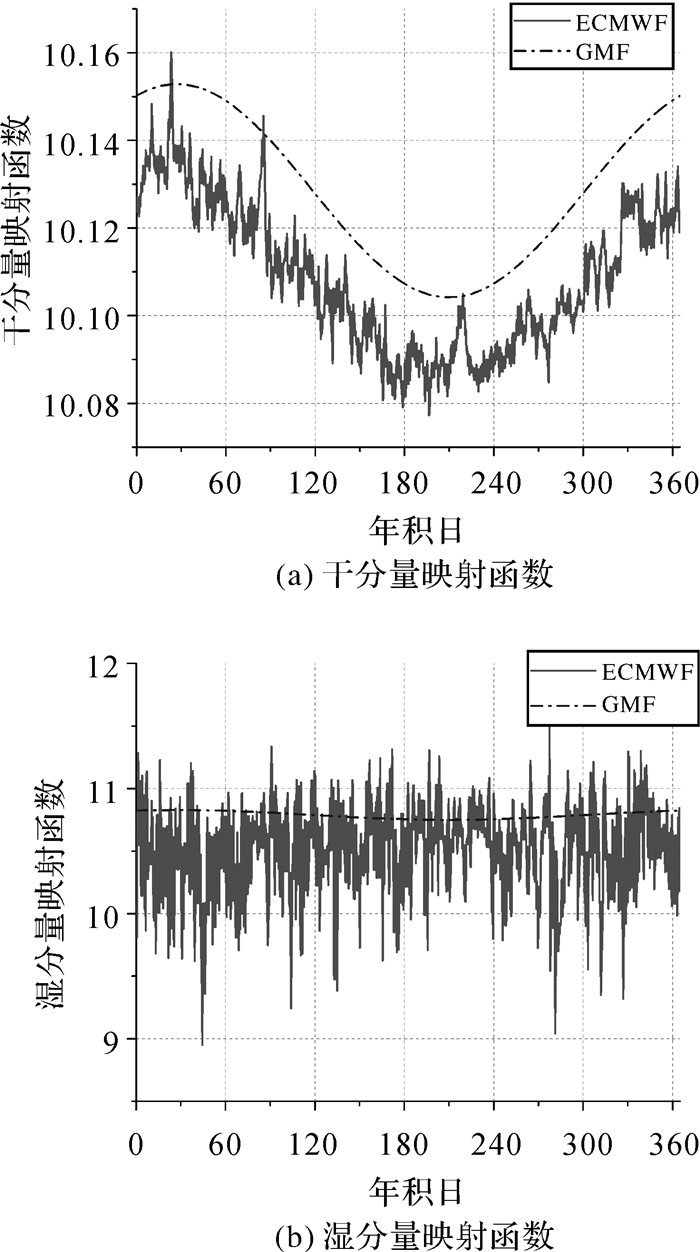
但事实上,映射函数并非准确。以GMF映射函数模型为例,绘出西安地区(大地坐标为34°10′41.74″N,108°59′8.16″E,504.427 m)2016年5°高度角时,GMF与映射函数参考值如图 1(此时暂不考虑方位角对映射函数的影响)。其中映射函数参考值采用ECMWF分层格网气象数据并根据射线追踪方法反算得到[13-14](以下试验的参考值计算方法与之一致)。
|
| 图 1 西安地区2016年5°高度角时干、湿分量映射函数 Fig. 1 Hydrostatic and wet mapping function of Xi'an area during 2016 at elevation of 5° |
统计映射函数各分量误差见表 1。
| 映射函数分量 | 最小值 | 最大值 | 平均值 | 标准差 |
| 干分量 | -0.007 3 | 0.035 6 | 0.019 8 | 0.006 1 |
| 湿分量 | -0.722 1 | 1.873 2 | 0.280 | 0.354 1 |
统计一年当中误差分布频数直方图见图 2。

|
| 图 2 映射函数误差频数直方图 Fig. 2 Histogram of mapping function errors |
从图 1、表 1可知,高度角为5°时,西安地区干、湿分量映射函数均存在明显的系统偏差,湿分量的RMS超过0.3,且最大误差超过1.8;另外由图 2可知,当高度角一定时,一年当中的干、湿分量映射函数误差大体呈正态分布。
2 顾及映射函数误差的估计方法顾及映射函数误差的对流层延迟数学模型如下
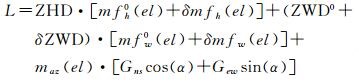 (4)
(4)
式中,mfh0(el)、mfw0(el)、ZWD0表示干、湿映射函数以及湿延迟的先验值;δmfh(el)、δmfw(el)、δZWD表示对应改正项,也即待估参数。忽略上式中的高阶小项,可得观测方程
 (5)
(5)
此处需说明两点:①为避免观测方程中出现两种不同待估参数相乘的现象,式(4)中引入湿延迟先验值,并在式(5)中忽略湿延迟改正与映射函数改正相乘的项;②观测方程待估参数中的映射函数改正项,即δmfh(eli)、δmfw(eli)包含了随高度角而变的量,需将高度角相关项剥离,方可按照最小二乘原理求解。故下文首先对δmfh(eli)和δmfw(eli)(也可将其视为映射函数误差)的变化特性进行分析。
2.1 映射函数误差特性分析在我国境内选取西安、武夷、乌鲁木齐、日喀则、海口5个地区,分别代表温带季风、亚热带季风、温带大陆、高原和热带季风5种主要的气候类型区域进行研究。各地具体位置见表 2。
| 地区 | 纬度 | 经度 | 大地高/m |
| 西安 | 34°10′41.74″ | 108°59′8.16″ | 504.427 |
| 武夷 | 27°37′0.84″ | 117°59′6.21″ | 229.086 |
| 乌鲁木齐 | 42°55′22.44″ | 86°43′9.12″ | 2 609.727 |
| 日喀则 | 29°14′55.29″ | 88°51′54.17″ | 3 858.712 |
| 海口 | 20°1′0.12″ | 110°19′0.12″ | 14.1 |
统计2016年各地区映射函数误差的年均值和标准差随高度角变化的情况见图 3。

|
| 图 3 各地区干、湿分量映射函数误差的平均值和标准差随高度角的变化 Fig. 3 Variation of average and standard deviation of hydrostatic and wet mapping function errors with elevation in different areas |
从图 3可知,该误差的平均值和标准差随高度角增大而迅速减小,当高度角大于40°时,映射函数误差对斜路径延迟的影响将降至亚毫米量级,基本可忽略不计;同时,该误差呈现出较强的地域性,即随地理位置不同而变,尤其是湿分量误差平均值的变化最明显。以下以西安地区为例进一步研究。
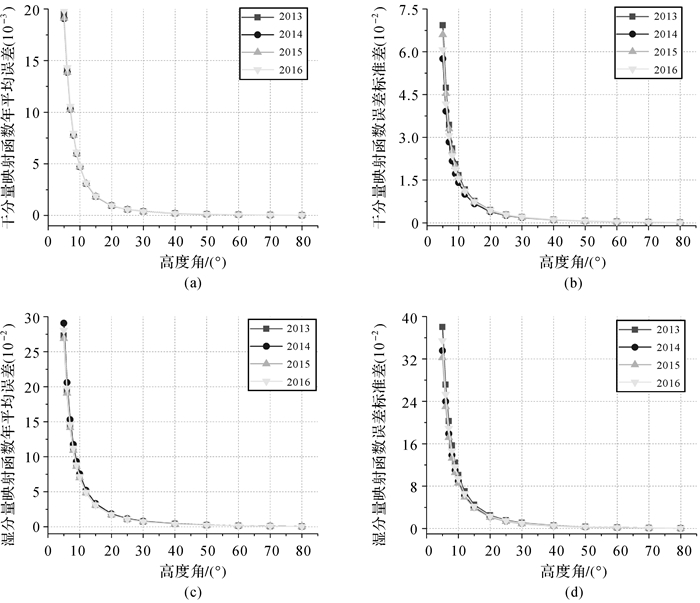
统计西安2013—2016年各年映射函数误差的平均值和标准差随高度角的变化情况见图 4。
|
| 图 4 2013—2016年西安地区干、湿分量映射函数误差的平均值和标准差随高度角的变化 Fig. 4 Variation of average and standard deviation of hydrostatic and wet mapping function errors with elevation in Xi'an during 2013—2016 |
从图 4可知,相比地域性特点,映射函数误差的时域性表现出较强的一致性,即该误差的平均值和标准差各年纵向相比变化趋势十分接近;同时观察各曲线的形状特征,可考虑利用指数函数对其拟合,具体形式如下,其中a1、a2、b1、b2为待拟合系数
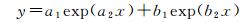 (6)
(6)
统计各年份、各分量的平均值、标准差曲线的拟合系数见表 3。可看出,各年拟合系数十分接近,与上文结论吻合;故考虑利用前3年拟合系数的平均值代表后续年份的情况,即对2013—2015年的a1、a2、b1、b2分别取平均,以其平均值代表 2016年的系数,并统计这种方法的拟合精度,结果见表 4。
| 参数 | 年份 | a1 | a2 | b1 | b2 | 残差标准差 | |
| 干分量 | 平均值 | 2013 | 0.097 6 | -0.346 5 | 0.002 9 | -0.059 0 | 1.044 1e-4 |
| 2014 | 0.093 7 | -0.347 5 | 0.003 4 | -0.067 6 | 7.755 0e-5 | ||
| 2015 | 0.094 0 | -0.346 7 | 0.003 3 | -0.065 3 | 8.527 2e-5 | ||
| 2016 | 0.098 2 | -0.344 3 | 0.002 8 | -0.057 4 | 1.097 1e-4 | ||
| 标准差 | 2013 | 0.038 4 | -0.382 8 | 0.001 5 | -0.066 7 | 9.332 3e-5 | |
| 2014 | 0.032 6 | -0.395 2 | 0.001 6 | -0.075 6 | 8.464 4e-5 | ||
| 2015 | 0.035 0 | -0.365 3 | 0.001 0 | -0.048 4 | 9.332 1e-5 | ||
| 2016 | 0.032 7 | -0.390 6 | 0.001 9 | -0.080 0 | 8.977 0e-5 | ||
| 湿分量 | 平均值 | 2013 | 1.874 2 | -0.462 4 | 0.145 8 | -0.104 1 | 0.001 1 |
| 2014 | 1.987 3 | -0.461 5 | 0.155 1 | -0.104 3 | 0.001 2 | ||
| 2015 | 1.824 8 | -0.462 3 | 0.143 1 | -0.103 6 | 0.001 1 | ||
| 2016 | 1.987 0 | -0.468 3 | 0.149 9 | -0.105 4 | 0.001 2 | ||
| 标准差 | 2013 | 2.468 6 | -0.452 6 | 0.202 4 | -0.101 8 | 0.001 6 | |
| 2014 | 2.178 2 | -0.452 1 | 0.178 7 | -0.101 8 | 0.001 4 | ||
| 2015 | 2.101 0 | -0.452 9 | 0.171 9 | -0.101 9 | 0.001 4 | ||
| 2016 | 2.286 1 | -0.451 7 | 0.188 3 | -0.101 6 | 0.001 5 | ||
| 映射函数分量 | 精度 | 最小值 | 最大值 | 平均值 | 标准差 |
| 干分量 | 平均值 | -7.139 7e-4 | 8.689 9e-5 | -9.846 3e-5 | 1.944 5e-4 |
| 标准差 | -1.101 5e-4 | 3.543 2e-4 | 4.041 1e-5 | 1.3045 e-4 | |
| 湿分量 | 平均值 | -0.004 4 | 0.001 7 | -5.225 4e-4 | 0.001 4 |
| 标准差 | -0.009 2 | 9.073 8e-4 | -0.002 4 | 0.002 5 |
从表 4可知,该方法的精度与直接利用式(6)对2016年拟合的效果相当。此时可近似认为西安地区高度角为el时,干、湿分量映射函数误差中分别包含平均值为μh(el)、μw(el)的系统偏差,同时系数中包含σh(el)、σw(el)乘积项,即映射函数误差可拆分为式(7)形式。式中δmf′h/w表示与高度角无关的映射函数误差,μh(el)、μw(el)、σh(el)、σw(el)的计算公式为式(8)~(11),μh(i)、μw(i)、σh(i)、σw(i)(i=1, 2, 3, 4)的数值详见表 5(μh/w(i)、σh/w(i)的数值可利用Matlab cftool拟合工具箱或1stopt等拟合软件得到)。为叙述方便,后文将该方法称之为映射函数误差模型。
| i | μh(i) | μw(i) | σh(i) | σw(i) |
| 1 | 0.095 10 | 1.895 4 | 0.035 30 | 2.249 27 |
| 2 | -0.346 90 | -0.462 1 | -0.381 10 | -0.452 53 |
| 3 | 0.003 20 | 0.148 0 | 0.001 37 | 0.184 33 |
| 4 | -0.063 97 | -0.104 0 | -0.063 57 | -0.101 83 |
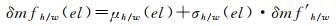 (7)
(7)
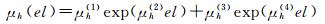 (8)
(8)
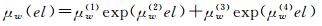 (9)
(9)
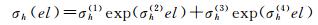 (10)
(10)
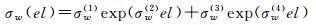 (11)
(11)
根据上文分析,可将观测方程式(5)写作如下形式
 (12)
(12)
此处需说明的是,在利用式(12)求解之前,应首先根据式(3),即传统估计方法解算得到湿延迟先验值,也即ZWD0,同时得ZWD0的权逆阵;进而采用部分参数加权平差[15-16]进行解算。最终参数平差值的计算公式为
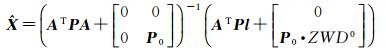 (13)
(13)
式中,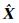
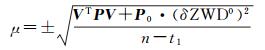 (14)
(14)
式中,V为残差向量;n为观测向量维数;t1为非随机参数维数,此处为4,即除去具有先验信息的湿延迟后的待估参数个数。
此即为顾及映射函数误差的两步估计法,即第一步利用传统估计方法(式(3))对湿延迟进行估计;随后根据部分参数加权平差,利用式(12)得到最终结果。为叙述方便,后文统一将其简称为两步法。
3 在新一代VLBI网观测中的应用效果仿真新一代VLBI全球观测系统(VLBI global observing system,VGOS)建成后,未来大地测量参数的解算精度有望达到1 mm量级[8, 17],将成为毫米级地球科学领域的重要技术基础,然而大气延迟误差依旧会成为制约VGOS测量精度的重要因素[18-19]。故下文通过仿真,研究传统方法与两步法的估计效果。
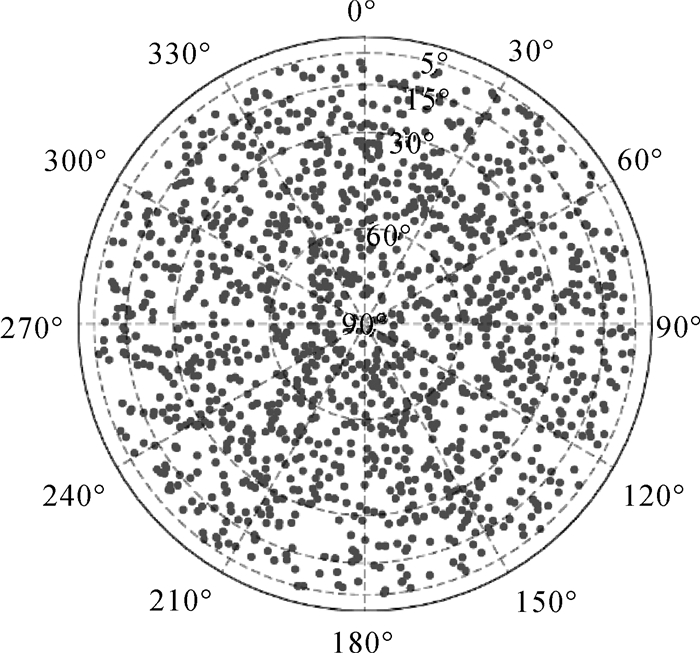
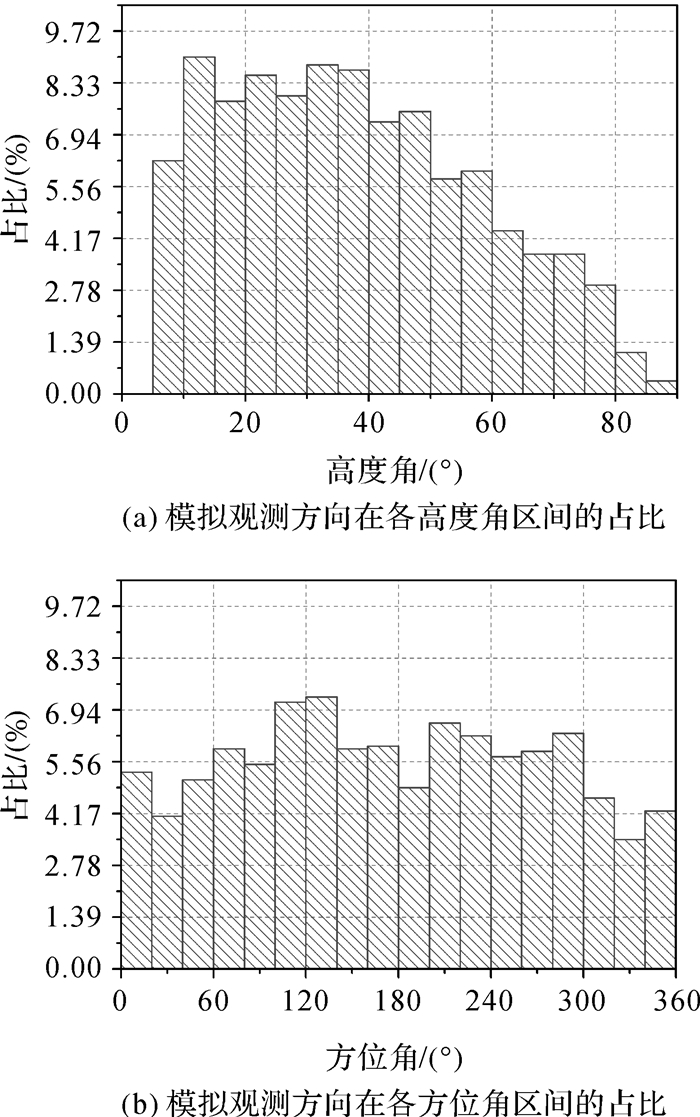
根据未来VGOS网的指标[20-21],每台站单天的观测将达到上千次。故本文首先模拟生成1440个观测方向(平均每分钟1次),即1440组方位角(0°~360°)、高度角(5°~90°)序列,各观测方向具体在测站上空的分布及其在不同高度角、方位角区间的占比可参见图 5、图 6;随后以西安为例,根据该地区2016年年积日185 d的分层格网气象数据(数据来自ECMWF,原始分辨率为6 h,此处通过线性插值生成时间分辨率为1 min的数据),利用射线追踪方法计算各方向斜路径延迟值,并将其作为真实值;接着在该值中加入标准差为4 ps的白噪声和方差为0.3 ps2/sec的随机漫步噪声(分别代表时延测量误差和时钟误差[22],该误差量级与VGOS设备精度一致),以此作为虚拟观测量;最后分别采用传统方法和两步法每60历元估计一次结果,统计两种方法得到的斜路径延迟残差(见图 7,精度统计见表 6)和湿延迟估计值(见图 8,精度统计见表 7)。
|
| 图 5 模拟观测方向在测站上空的分布外圈为方位角轴,向径为高度角轴 Fig. 5 Distribution of simulated observing orientations over the station outer circle represents the azimuthal axis, while inside diameter represents the elevation angle axis |
|
| 图 6 模拟观测方向在各高度角、方位角区间的占比 Fig. 6 Percentages of simulated observing orientations over various elevation angle and azimuth ranges |
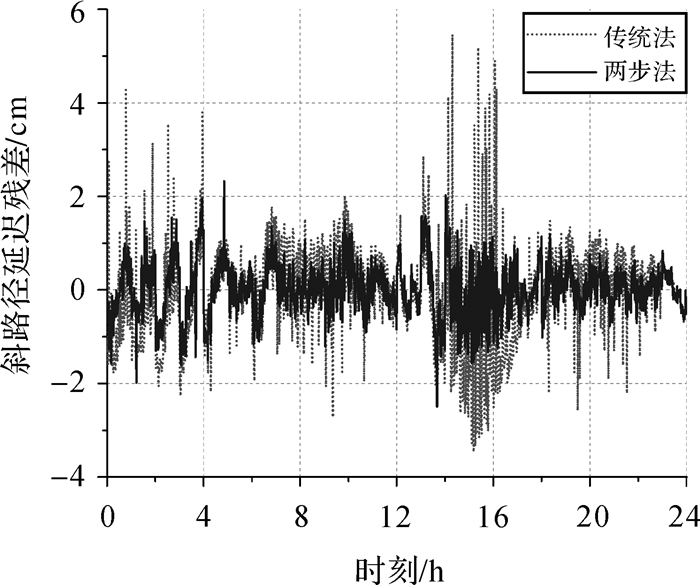
|
| 图 7 两种方法计算的斜路径延迟误差 Fig. 7 Slant path delay errors of two different methods |
| cm | ||||
| 方法 | 最小值 | 最大值 | 平均值 | 标准差 |
| 传统法 | -3.459 3 | 5.456 0 | -0.046 1 | 1.078 3 |
| 两步法 | -2.495 9 | 2.325 0 | 0.007 2 | 0.579 9 |
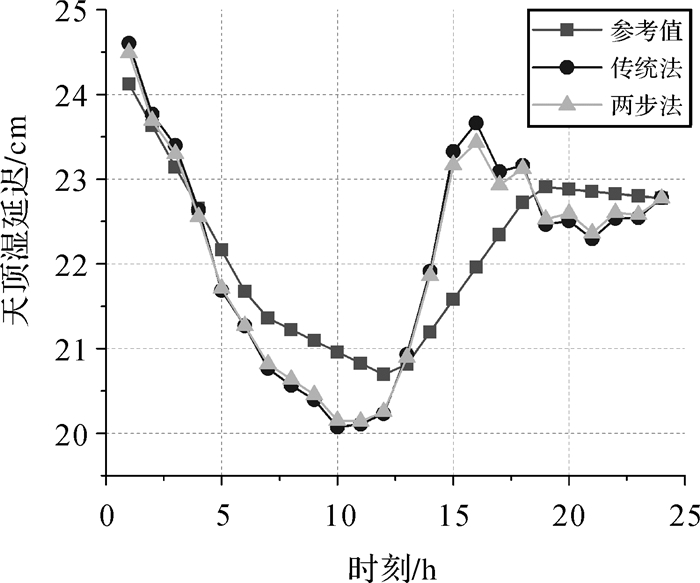
|
| 图 8 湿延迟参考值与两种方法的估计值 Fig. 8 Reference wet delay values and estimated ones by two methods |
| cm | ||||
| 方法 | 最小值 | 最大值 | 平均值 | 标准差 |
| 传统法 | -0.886 6 | 1.748 3 | -0.020 2 | 0.706 9 |
| 两步法 | -0.808 3 | 1.591 5 | -0.035 5 | 0.628 4 |
从图 7、表 6可知,相比传统法,两步法的斜路径延迟残差被大大削减,RMS精度提升至6 mm以内,改善幅度达46.22%,同时最大误差降低54.25%;从图 8、表 7知,湿延迟估计精度有小幅提升,但提升效果十分有限,改善程度在亚毫米级,这主要与第二次平差中湿延迟初值较多依赖第一次平差结果有关。
同理,将上文方法用于其他地区,得到的结果见表 8、表 9。可见该方法在不同地区均有相近的改善效果。
| cm | |||||
| 方法 | 地区 | 最小值 | 最大值 | 平均值 | 标准差 |
| 传统法 | 武夷 | -3.919 4 | 5.955 5 | -0.072 4 | 1.050 2 |
| 乌鲁木齐 | -3.743 5 | 5.354 1 | -0.030 7 | 1.012 5 | |
| 日喀则 | -3.668 4 | 5.465 7 | -0.026 9 | 1.006 7 | |
| 海口 | -3.437 3 | 5.275 7 | 0.003 7 | 1.015 9 | |
| 两步法 | 武夷 | -2.305 4 | 3.172 9 | 0.008 4 | 0.520 7 |
| 乌鲁木齐 | -2.277 6 | 2.281 1 | -0.000 4 | 0.456 8 | |
| 日喀则 | -1.656 0 | 1.834 5 | 0.013 2 | 0.532 3 | |
| 海口 | -2.409 7 | 2.123 4 | 0.025 5 | 0.546 0 | |
| cm | |||||
| 方法 | 地区 | 最小值 | 最大值 | 平均值 | 标准差 |
| 传统法 | 武夷 | -1.317 5 | 1.143 3 | -0.012 4 | 0.691 6 |
| 乌鲁木齐 | -0.874 4 | 1.365 3 | 0.141 9 | 0.632 5 | |
| 日喀则 | -0.588 5 | 1.701 5 | 0.238 6 | 0.668 2 | |
| 海口 | -0.893 1 | 2.016 6 | 0.041 2 | 0.823 4 | |
| 两步法 | 武夷 | -1.255 7 | 1.001 0 | -0.011 4 | 0.662 6 |
| 乌鲁木齐 | -0.704 9 | 1.296 5 | 0.195 6 | 0.578 8 | |
| 日喀则 | -0.476 8 | 1.538 1 | 0.287 0 | 0.586 1 | |
| 海口 | -0.795 5 | 1.817 8 | 0.022 5 | 0.731 7 | |
4 结语
本文首先对对流层映射函数的误差进行研究,利用以往若干年的分层气象格网数据构建了映射函数误差随高度角变化的函数模型,并提出了顾及映射函数误差的对流层延迟两步估计法。试验表明:①本文构建的映射函数误差模型,能精确逼近研究地区映射函数误差在各高度角的情况,可为分析各地区映射函数误差提供依据;②两步法可有效削减斜路径延迟残差,改善幅度达50%左右,这意味着采用该方法可将对流层延迟对VLBI观测结果的影响削弱50%,同时对对流层湿延迟的估计结果也有一定程度的改善。另外,虽然目前VMF系列映射函数精度较高,但模型系数的发布往往滞后期较长,而本文提出的方法可将映射函数改正值和湿延迟一并估计,有利于近实时性地获取映射函数结果。然而本文方法尚存在不足之处,如构建两步法的观测方程时,认定湿延迟改正的量级足够小,故忽略了该改正与映射函数改正相乘的项;但如果先验湿延迟精度不够高(如大于1 cm),则可能会引入毫米级甚至1 cm以上的误差。因此如何选用更合理的湿延迟先验值是进一步提高估计精度的关键。
| [1] | DAVIS J L, ELGERED G, NIELL A E, et al. Ground-based measurement of gradients in the "wet" radio refractivity of air[J]. Radio Science, 1993, 28(6): 1003–1018. DOI:10.1029/93RS01917 |
| [2] | TEKE K, NILSSON T, BÖHM J, et al. Troposphere delays from space geodetic techniques, water vapor radiometers, and numerical weather models over a series of continuous VLBI Campaigns[J]. Journal of Geodesy, 2013, 87(10-12): 981–1001. DOI:10.1007/s00190-013-0662-z |
| [3] |
谢劭峰, 张朋飞, 王新桥, 等.
对流层延迟模型映射函数研究[J]. 大地测量与地球动力学, 2016, 36(11): 941–945, 950.
XIE Shaofeng, ZHANG Pengfei, WANG Xinqiao, et al. Research on mapping functions of troposphere delay model[J]. Journal of Geodesy and Geodynamics, 2016, 36(11): 941–945, 950. |
| [4] |
郭际明, 章迪, 史俊波, 等.
利用射线追踪法分析三种典型对流层映射函数在中国区域的精度[J]. 武汉大学学报(信息科学版), 2015, 40(2): 182–187.
GUO Jiming, ZHANG Di, SHI Junbo, et al. Using ray-tracing to analyse the precision of three classical tropospheric mapping functions in China[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 182–187. |
| [5] | BOEHM J, WERL B, SCHUH H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data[J]. Journal of Geophysical Research:Solid Earth, 2006, 111(B2): B02406. DOI:10.1029/2005JB003629 |
| [6] | ZUS F, DICK G, DOUSA J, et al. Systematic errors of mapping functions which are based on the VMF1 concept[J]. GPS Solutions, 2015, 19(2): 277–286. DOI:10.1007/s10291-014-0386-4 |
| [7] | LANDSKRON D, BÖHM J. VMF3/GPT3:Refined discrete and empirical troposphere mapping functions[J]. Journal of Geodesy, 2018, 92(4): 349–360. DOI:10.1007/s00190-017-1066-2 |
| [8] | HASE H, BEHREND D, MA C, et al. The emerging VGOS network of the IVS[C]//Proceedings of the 7th General Meeting. Madrid, Spain: [s.n.], 2012: 8-12. https://www.researchgate.net/publication/265919856_The_Emerging_VGOS_Network_of_the_IVS |
| [9] | CHEN G, HERRING T A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data[J]. Journal of Geophysical Research, 1997, 102(B9): 20489–20502. DOI:10.1029/97JB01739 |
| [10] | SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J]. Bulletin Géodésique, 1972, 105(1): 279–298. DOI:10.1007/BF02521844 |
| [11] | NIELL A E. Global mapping functions for the atmosphere delay at radio wavelengths[J]. Journal of Geophysical Research, 1996, 101(B2): 3227–3246. DOI:10.1029/95JB03048 |
| [12] | HERRING T A, DAVIS J L, SHAPIRO I I. Geodesy by radio interferometry:the application of Kalman filtering to the analysis of very long baseline interferometry data[J]. Journal of Geophysical Research, 1990, 95(B8): 12561–12581. DOI:10.1029/JB095iB08p12561 |
| [13] | HOFMEISTER A. Determination of path delays in the atmosphere for geodetic VLBI by means of ray-tracing[D]. Vienna, Austria: Vienna University of Technology, 2016: 41-59. |
| [14] | GARCIA-ESPADA S, HAAS R, COLOMER F. Application of ray-tracing through the high resolution numerical weather model HIRLAM for the analysis of European VLBI[C]//Proceedings of the 10th European VLBI Network Symposium and EVN Users Meeting. Hobart, Australia, 2010: 232-236. https://www.researchgate.net/publication/253397012_Application_of_ray-tracing_through_the_high_resolution_numerical_weather_model_HIRLAM_for_the_analysis_of_European_VLBI |
| [15] |
隋立芬, 陶大欣.
有偏估计、参数加权平差及秩亏自由网平差的关系与比较[J]. 解放军测绘学院学报, 1999, 16(4): 257–259.
SUI Lifen, TAO Daxin. The relation and comparison of biased estimation, adjustment of parameter with prior weight and adjustment of free network[J]. Journal of the PLA Institute of Surveying and Mapping, 1999, 16(4): 257–259. |
| [16] |
李全海.
坐标参数加权平差法在线路补测中的应用[J]. 测绘学报, 2002, 31(S1): 77–80.
LI Quanhai. Application of parameter adjustment with weighted coordinates in additional control survey of route[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(S1): 77–80. DOI:10.3321/j.issn:1001-1595.2002.z1.017 |
| [17] | SCHUH H. Geodetic and astrometric very long baseline interferometry (VLBI) the IVS and its future perspectives[R]. Espoo, Finland: EGU and IVS Training School on VLBI for Geodesy and Astrometry, 2013. |
| [18] | PANY A, BÖHM J, MACMILLAN D, et al. Monte Carlo simulations of the impact of troposphere, clock and measurement errors on the repeatability of VLBI positions[J]. Journal of Geodesy, 2011, 85(1): 39–50. DOI:10.1007/s00190-010-0415-1 |
| [19] | NILSSON T, HAAS R. An assessment of atmospheric turbulence for CONT05 and CONT08[C]//Proceedings of the 19th European VLBI for Geodesy and Astrometry Working Meeting. Bordeaux, France: [s.n.], 2009: 39-43. https://www.researchgate.net/publication/253685693_An_Assessment_of_Atmospheric_Turbulence_for_CONT05_and_CONT08 |
| [20] | PETRACHENKO B, NIELL A, BEHREND D, et al. Design aspects of the VLBI2010 system[R]. America: NASA Technical Memorandum, 2009. |
| [21] |
孙中苗, 范昊鹏.
VLBI全球观测系统(VGOS)研究进展[J]. 测绘学报, 2017, 46(10): 1346–1353.
SUN Zhongmiao, FAN Haopeng. Research progress of VLBI global observing system (VGOS)[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1346–1353. DOI:10.11947/j.AGCS.2017.20170326 |
| [22] | SUN Jing, BÖHM J, NILSSON T, et al. New VLBI2010 scheduling strategies and implications on the terrestrial reference frames[J]. Journal of Geodesy, 2014, 88(5): 449–461. DOI:10.1007/s00190-014-0697-9 |


