水汽是地球大气的一种重要组成成分,它主要分布在对流层的底部。水汽在大气中的含量很少,却是大气中最活跃多变的部分,也是最难以描述的气象参数之一[1]。作为温室气体中的重要成分,水汽在近年引起了广泛关注,因为它的变化会对天气和气候产生重要影响[2]。随着全球卫星导航系统(global navigation satellite system, GNSS)的发展,人们开始拓展GNSS的应用面,水汽探测即是其中一项重要的应用。作为一种新的水汽探测手段,GNSS技术拥有其独特的优越性, 包括全天候观测、全球覆盖性、高精度性和高时空分辨率[3]。GNSS信号穿过对流层时会发生弯曲和延迟,将会在伪距或载波相位中引入误差。天顶对流层延迟(zenith tropospheric delay, ZTD)常被用来表示这种误差。ZTD包括天顶静力学延迟(zenith hydrostatic delay, ZHD)和天顶湿延迟(zenith wet delay, ZWD)。高精度的ZHD可以通过经验模型得到[4-6]。将ZHD从ZTD中分离开即可得到ZWD,将ZWD与一个转换因子Π相乘即可得到可降水量(precipitable water value, PWV)。转换因子Π是加权平均温度(weighted mean temperature, 记为Tm)的函数,因为Tm是转换因子中唯一的变量,所以其在GNSS反演水汽的过程中扮演着重要的角色[7]。
Tm可以通过对测站上空的温度和湿度廓线沿天顶方向进行数值积分得到,这些资料通常可以从无线电探空数据、数值天气预报(numerical weather prediction, NWP)产品或者大气再分析资料中获得[3]。因为无线电探空站分布稀疏,其空间分辨率不足以满足GNSS测站的需求,从而大多数GNSS测站都无法获得配套的无线电探空资料,因此NWP产品或者再分析资料成为GNSS测站获取高精度Tm的主要数据源[8]。然而,由于NWP产品的时间分辨率不够高且更新存在延迟的问题,其不能够用作实时/近实时水汽监测[8-9]。为了实现实时/近实时GNSS水汽遥感,必须通过更简便的方法获取Tm,一种常用的获取Tm的简便方法是利用Tm与地表温度(surface temperature, Ts)的线性关系。文献[7]发现Tm与Ts之间存在很强的线性关系,并建立了两者之间的线性回归公式。该方法只需要得到测站地表处的温度即可通过一个简单的线性公式估计出高精度的Tm。然而也有不少学者认为,Tm与Ts之间的关系并不是定值,而是随着季节和地区发生变化的,并由此建立了区域性的线性回归公式[10-14]。
虽然在低海拔地区Bevis公式具有较高精度的Tm估计效果,然而实际应用中不是所有的GNSS测站都处于海拔较低的区域,不少学者已经通过试验发现,Bevis公式随着地表海拔升高精度逐渐降低,在高海拔地区利用Bevis公式计算Tm将会出现较大的误差[15-17]。本文首先在全球范围内对Bevis公式在不同高度面上的适用性进行研究。针对Bevis公式在高海拔地区精度较低的问题,本文提出对Tm与近地大气温度的关系展开研究,利用整个近地空间范围内的大气温度与Tm廓线重新解算线性模型系数(因为对流层范围一般指10 km以下的空间范围,所以本文的近地空间范围指0~10 km的高程范围)的办法来解决该问题。
1 原理和试验数据介绍利用GNSS技术可以估算出高精度的ZTD,它是ZHD和ZWD的总和。ZHD可以通过经验模型和气象参数计算获得,一种广泛应用于GNSS气象学计算ZHD的模型是Saastamoinen模型[4],其形式表达如下
 (1)
(1)
式中,P是测站大气压(hPa);φ为测站纬度;h为测站大地高,单位为km。将ZHD从ZTD中分离后即可得到ZWD。然后PWV可以通过一个转换因子Π从ZWD中恢复出来[3]
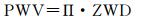 (2)
(2)
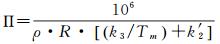 (3)
(3)
式中,ρ是液态水密度;R是水汽压气体常数;k′2和k3是物理常数[3];Tm是大气加权平均温度(K)。因为Π的精度主要是由Tm的误差决定,所以Tm的相对误差可以在一定程度上反映Π的相对误差,这也是为什么提高Tm的估算精度具有重要意义的原因[7]。文献[18]给出了Tm的定义以及精确估计Tm的方法
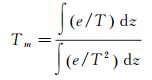 (4)
(4)
式中,e是水汽压(hPa);T是大气温度(K)。利用式(4)计算Tm需要获得整个天顶方向的温度和湿度廓线,在实际应用中,这一点往往难以达到。除了数值积分的方法,Tm还可以利用Bevis关系式和地表温度Ts获得。文献[17]利用美国13个无线电探空站两年观测资料共8712条廓线建立起了适合中纬度地区的Tm与Ts的线性回归公式
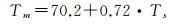 (5)
(5)
文献[19]分析了全球范围内250 000条无线电探空廓线数据后修改了原来的公式, 得到了新的全球范围适用的线性公式。此外,还有不少学者建立了高精度的区域性线性回归公式[10-14]。因为本研究是在全球范围内进行的,并且式(5)是应用最为广泛的Tm-Ts关系式,所以本文主要对式(5)在不同高度面的适用性进行分析。
本文使用的数据包括欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)的再分析资料和全球站点无线电探空资料数据集(integrated global radiosonde archive, IGRA)的无线电探空资料。
ECMWF以格网形式提供了从1979年至今的丰富气象数据,格网最高分辨率可以达到0.125°,时间分辨率可以达到6 h[20-21]。ECMWF再分析资料包括地表的气象数据以及整个大气分层的气象数据,其中的气压分层数据总共可以提供37层从1000 hPa到1 hPa的气象数据。从不同的气压层开始利用式(4)一直积分到顶层即可得到不同气压层的Tm。本文分别将气压从1000 hPa到250 hPa的气压层(高程范围大致为0~10 km)作为底层开始往顶层积分,得到了这些气压层对应高度面的Tm。本文利用全球范围格网分辨率为2.5°的ECMWF气压分层数据来获得Tm廓线和近地大气温度廓线。
探空数据源自美国国家气候数据中心(National Climate Data Center, NCDC), 可以通过IGRA获得,包含了全球超过1500个无线电探空站和测风气球从20世纪60年代开始到现今的高质量观测数据。探空数据通过分层的形式提供气象参数廓线。将不同的层作为底层开始利用式(4)往顶层积分即可得到该层的Tm。本文在全球范围内选取了678个探空站进行试验,其全球分布图如图 1所示,分别将高程范围为0~10 km内的所有高度层作为底层往顶层积分得到对应高程范围的Tm廓线。

|
| 图 1 678个探空站的分布 Fig. 1 Distribution of the 678 radiosonde stations |
2 Bevis公式在不同高度面的适用性
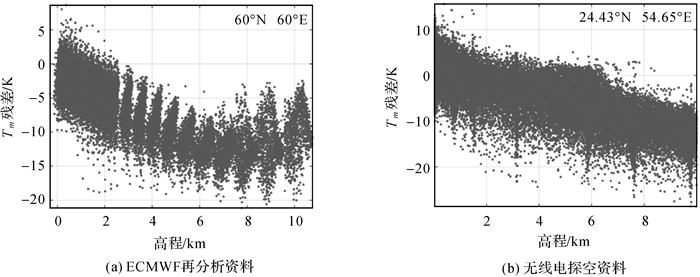
Bevis公式在海拔较低的区域利用地表温度计算Tm时拥有较高的精度,然而在高海拔地区,Bevis公式的适用性需要进一步的验证。本文分别利用ECMWF的一个格网点(60°N 60°E)和一个探空站(24.43°N 54.65°E)3年(2013—2015年)的温度和湿度廓线,利用式(4)进行积分得到Tm廓线并将其作为参考值,然后再根据式(5),利用Bevis公式和分层温度得到Tm廓线,将两条廓线作差即可得到不同高度层的Tm残差。图 2给出了利用两种数据源检验Bevis公式的残差廓线结果,其中图 2(a)是利用ECMWF的再分析资料检验的结果,图 2(b)是利用探空站数据检验的结果。
|
| 图 2 利用多源数据的分层温度检验Bevis公式的残差廓线 Fig. 2 The residual profiles of Bevis formula tested with stratified temperature of multi sources data |
从图 2可以看出,无论是ECMWF还是探空站的计算结果,残差绝对值随高程均存在逐渐上升的趋势,在高海拔高度面,残差主要呈负值,说明在高海拔地区,相比于利用温度和湿度廓线积分得到的Tm,利用Bevis估计得到的Tm会偏大。对ECMWF参与检验的格网点来说,在8 km左右,残差绝对值会达到最大,此时最大残差会达到-20 K左右,可能会引起约3 mm的PWV误差。而对探空站参与检验的测站来说,在10 km时,残差绝对值最大,最大残差会达到-25 K左右,对应的PWV误差约为3.75 mm,此时的残差绝对值已经远远高于低海拔高度面的估计残差。
为了进一步分析全球范围内Bevis公式在不同高度面的适用性,本文首先利用ECMWF再分析资料的气压分层数据得到全球格网点(格网点分辨率2.5°)上Bevis公式在每一个高度面的残差,然后分高度层(高度范围为0~10 km,每1 km为一个高度层)统计每层的偏差(Bias)、均方根误差(root mean square, RMS)和标准差(standard deviation, STD),其中,Bias、RMS和STD的计算公式如下
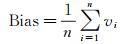 (6)
(6)
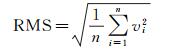 (7)
(7)
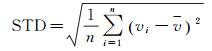 (8)
(8)
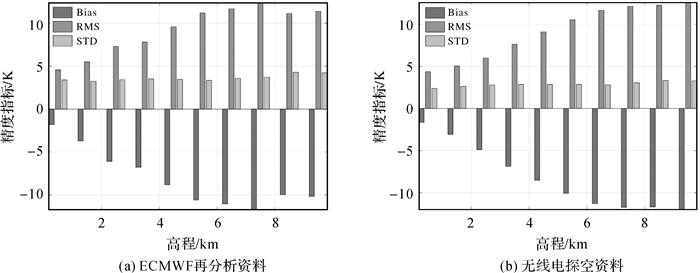
式中,vi为Tm的残差,即用Tm真值减去Tm估计值得到的差值;v代表残差的平均值;n代表观测值总数。用Bias评估Tm的估计值与真值之间的平均偏差度,用RMS评估Tm估计值的总体精准度,用STD评估Tm残差在不同高度层的离散程度。在得到全球格网点的分层Bias、RMS和STD后,对其取平均进行统计,统计结果如图 3(a)所示。接着对全球范围内的678个探空站采取同样的操作得到这些探空站在不同高度层的Bevis公式残差统计值,统计结果如图 3(b)所示。
|
| 图 3 利用多源数据在全球范围内探究Bevis公式在不同高度层的残差统计结果 Fig. 3 The residual statistics of Bevis formula at different levels using multi sources data on a global scale |
从图 3可以看出,无论是对ECMWF资料还是对探空资料来说,Bevis公式在海拔较低时适用性较好,Tm估计精度较高,而随着海拔升高,适用性逐渐降低。具体分析为,在0~1 km的高程范围内,Bevis公式的计算精度可以达到4 K左右,Bias可以维持在-2 K以内,此时的PWV误差只有0.5 mm左右。而在1~8 km的高程范围内,随着海拔升高,Bevis公式估计精度逐渐降低,计算RMS逐渐增大,Bias数值在不断减小,在8 km时,RMS达到12~13 K,Bias达到-12~-11 K,并在之后趋于稳定,在8~10 km的高程范围内,RMS和Bias始终维持在这个水平。然而,这样的精度显然是无法满足Tm的精度要求的,其会在最后的PWV估计结果中引入1.5~2 mm的系统误差。另外,Bevis公式的残差STD始终处在同一水平,所以其在不同高度层的计算残差离散程度并没有很大的差别。通过以上分析可知,Bevis公式在海拔较低的区域可以提供高精度的Tm估计值,然而在高海拔地区利用Ts计算Tm时可能会存在较大误差。
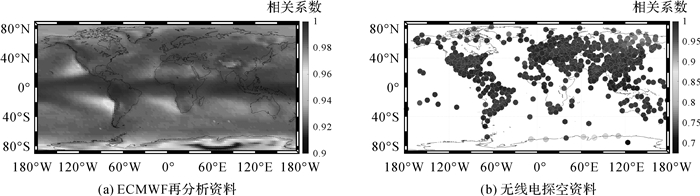
3 基于近地大气温度的全球Tm模型 3.1 近地大气温度与Tm的相关性分析为了解决Bevis公式在高海拔地区适用性较低的问题,本文提出利用ECMWF资料和探空站的分层数据探究近地大气温度与Tm的关系,以构建基于近地大气温度的全球Tm模型。因为对流层顶通常在10 km左右,所以这里的近地大气温度指的是0~10 km高程范围内的大气温度,所以,地表温度Ts是近地大气温度中在地表高度面上的温度。本文首先分析Tm与近地大气温度的相关性,利用ECMWF资料和探空资料3年(2013—2015年)的温度廓线和Tm廓线(廓线高程范围0~10 km)计算全球每一个格网点(格网点分辨率2.5°)和每一个探空站上Tm与近地大气温度的相关系数,其全球分布如图 4所示。
|
| 图 4 由多源数据计算得到的近地大气温度与Tm相关系数全球分布 Fig. 4 The global distribution of correlation coefficients between near-earth atmospheric temperature and Tm obtained from multi sources data |
从图 4可以看出,对两种数据源来说,近地大气温度与加权平均温度在全球范围内都拥有很强的相关性,其在南极区域相对较低,但相关系数依然有0.9左右或0.7左右。对ECMWF的全球格网点来说,相关系数最低为0.904 3,最高为0.997 7,对所有参与检验的探空站来说,相关系数最低为0.672 1,最高为0.995 5。文献[13]利用全球大地观测系统(global geodetic observing system, GGOS)大气的加权平均温度数据和ECMWF的地表温度数据在全球范围内计算了Tm和Ts的相关系数后指出,二者的相关性主要受纬度影响,在高纬度地区较强,在低纬度地区较弱。而通过图 4可以看出,近地大气温度与Tm的相关性在低纬度地区特别是赤道附近较强,而在高纬度地区特别是南极区域较弱。由此可以说明,近地大气温度与Tm的关系和Ts与Tm的关系存在差异。
3.2 模型构建及模型系数求解由上文分析可知,近地大气温度与加权平均温度之间拥有很强的相关性,因此线性回归模型适合用来表示二者之间的关系,该模型如下所示
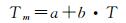 (9)
(9)
式中,T是近地大气温度(K);a是常系数;b是比例系数。因为Tm与Ts之间的关系是随着季节发生变化的,因此Tm与T之间的关系也应具有季节性差异。GPT2w模型采用一个顾及年周期和半年周期的函数表达对流层参数的季节性变化,取得了较高的精度[22-23],本文也使用该函数表示常系数a和比例系数b,其公式如下
 (10)
(10)
式中,A0是平均值;(A1, B1)代表年周期幅值;(A2, B2)代表半年周期幅值;doy是年积日;r(t)代表常系数a和比例系数b。
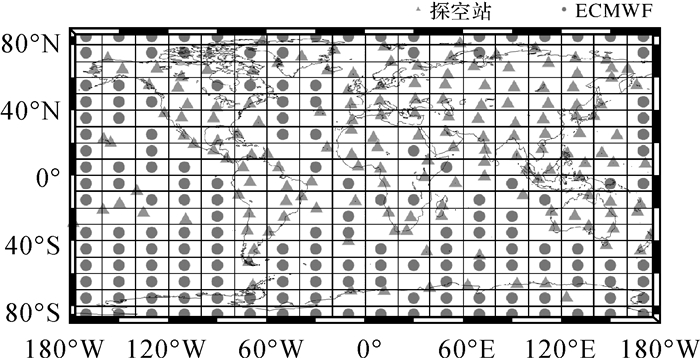
探空站的分层数据是实测数据,因此建模时最好采用探空站的数据作为数据源。探空站大多设置在陆地区域,海洋区域没有探空数据,由此海洋空白区域的数据可以通过ECMWF的再分析资料进行填补。因为海拔较高区域一般在陆地地区,所以海洋区域采用ECMWF作为数据源不会对本模型的应用产生影响。在全球范围内以纬度10°和经度20°划分格子,并在每个格子里选取一个探空站作为建模数据源,对于没有探空站的格子,选取格子中心点的ECMWF数据作为建模数据源,最终选取的164个探空站和160个ECMWF格网点全球分布如图 5所示。
|
| 图 5 选取用来建模的探空站和ECMWF格网点全球分布 Fig. 5 The global distribution of radiosonde stations and ECMWF grid points selected for building model |
考虑到模型不宜采取过多的系数,而且探空站的空间分布具有不均匀性,因此球谐函数比较适合构建该模型。文献[15, 24]采用9阶9次的球谐函数构建全球加权平均温度(global weighted mean temperature, GTm)经验模型时取得了较好的效果,因此本文也使用同样阶次的球谐函数对模型系数进行展开,公式如下
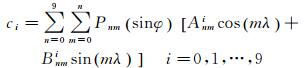 (11)
(11)
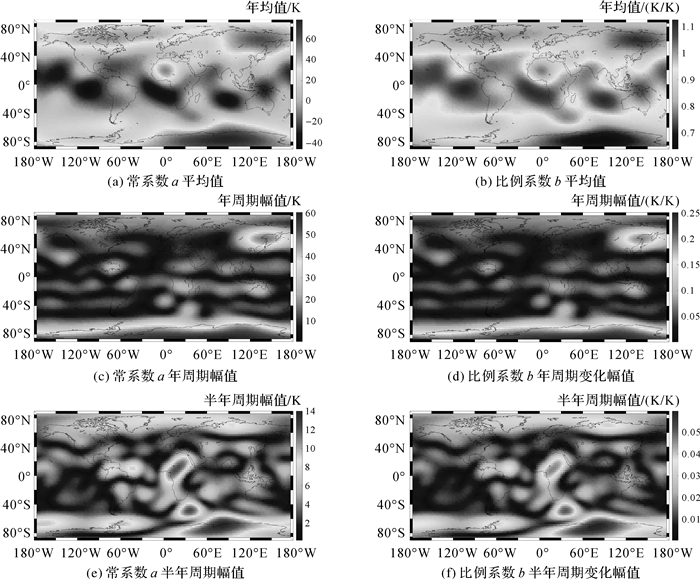
式中,Pmn为勒让德多项式;φ和λ分别为格网点纬度和经度;Anmi和Bnmi为使用最小二乘确定的球谐函数n阶m次系数(共10×110个系数)。图 6为拟合后常系数a的平均值、年周期变化振幅和半年周期变化振幅以及比例系数b的平均值、年周期变化振幅和半年周期变化振幅的全球分布状况。
|
| 图 6 模型系数的平均值、年周期幅值和半年周期幅值全球分布状况 Fig. 6 The global distribution of mean values, annual and semi-annual amplitudes of model coefficients |
由图 6可以看出,常系数a和比例系数b的全球分布存在对应关系,a的平均值大的地方,b的平均值小,而a和b的年周期和半年周期变化幅值则存在一致性。总的来说,a的平均值在低纬度区域较低,在高纬度地区相对较高,而b的平均值情况相反。与Ts和Tm的全球回归系数主要随纬度呈波形变化以及纬度分带明显的特性不同[13],近地大气温度与Tm的回归系数均值在40°S—40°N的区域内具有明显的齿印型分布,这些齿印主要分布在海洋和陆地的交界处且方向与赤道东北信风(北半球)和东南信风(南半球)方向相同[25],这说明近地大气温度与Tm的关系分布不仅与海陆分布、地形有关还受热力环流的影响。回归系数在南极区域具有明显的年周期特性,在该区域,a的年周期幅值可以达到60 K左右,b的年周期幅值可以达到0.25左右,此外,在中西伯利亚高原与太平洋交界的地方也可以观测到较明显的年周期变化特性。而回归系数的半年周期幅值较大值则主要分布于两极区域,这可能与极区的极昼极夜现象有关,在两极地区,a的半年周期幅值可以达到8~14 K,b的半年周期幅值可以达到0.03~0.06。另外撒哈拉沙漠以及非洲和南极洲之间的部分海洋区域也可以观测到较明显的半年周期现象。
在使用本文建立的基于近地大气温度的全球加权平均温度(temperature-based weighted mean temperature, TTm)模型时,首先根据测站的经纬度,利用式(11)得到式(10)的10个参数,再根据该参数和年积日利用式(10)得到线性回归模型的回归系数a和b,最后根据0~10 km高程范围内某一个高度面的温度得到对应高度面的加权平均温度。
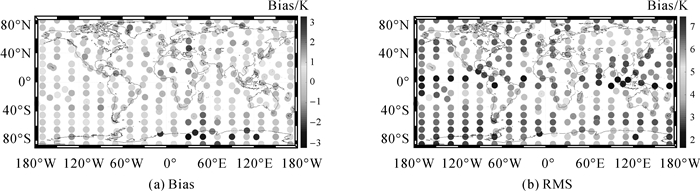
3.3 模型有效性检验 3.3.1 内符合精度检验为了验证本文构建的模型的合理性及建模过程的正确性,利用建模数据(各个建模点2013—2015年的温度和Tm廓线)对本文构建的模型进行内符合精度检验,图 7给出了TTm模型的建模精度,即全球各个建模点的Bias和RMS分布。由图 7可以看出,模型在海洋区域的精度高于陆地区域的精度。根据统计结果显示,其平均Bias为-0.02 K,变化范围为-3.25~3.28 K,平均RMS为3.67 K,变化范围为1.67~7.43 K。从检验结果可以看出,TTm模型的内符合精度较高,说明本文建模过程的合理性。
|
| 图 7 内符合精度检验结果Bias和RMS全球分布图 Fig. 7 The global distribution of bias and RMS results in internal accuracy test |
3.3.2 利用ECMWF和无线电探空分层数据的外符合精度检验
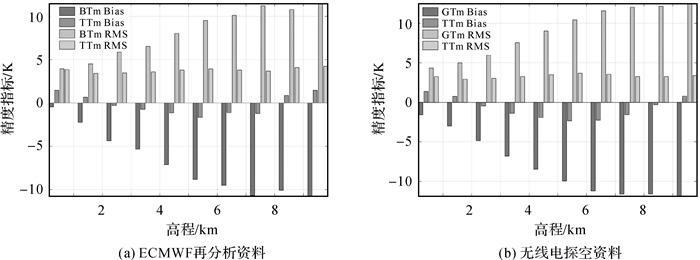
为了验证本文所建立模型的有效性,利用全球格网点(格网点分辨率2.5°)上2016年的ECMWF气压分层数据及678个无线电探空站(分布如图 1所示)上2016年的分层数据对其进行分高度层外符合精度检验。为了进行比较,Bevis公式(式(5))同样被用来进行检验,为了方便表达,Bevis公式将被称为Bevis加权平均温度(Bevis weighted mean temperature, BTm)模型。分别利用两种数据源得到每一个格网点或每一个探空站上两种模型的Tm估计残差廓线(高度范围为0~10 km),然后分高度层(每1 km为一个高度层)统计每个高度层两种模型的Bias和RMS,最后对全球格网点和所有探空站的分层Bias和RMS取平均进行统计,统计结果如图 8所示。
|
| 图 8 利用多源数据的分高度层外符合精度检验结果 Fig. 8 The height-dependent external accuracy test results using multi sources data |
从图 8可以看出,两种数据源的检验结果相似,整体来说,BTm和TTm在0~1 km高程范围内的RMS都在4 K左右,对应约0.6 mm的PWV误差。BTm的RMS随着高程升高逐渐增大,到达8 km时趋于稳定,最后稳定在12~13 K,这会在最后的PWV反演结果中引入1.8~2 mm的误差。而TTm的RMS却一直在4 K左右,不存在误差随高度升高逐渐增大的现象,其PWV误差始终在0.6 mm左右,因此在高海拔高度面上,TTm模型相对于BTm模型精度提升了65%~70%。两种模型的RMS变化存在这样的差异可以从Bias的计算结果看出,两种模型在0~1 km高程范围内的Bias绝对值都较小,其中BTm的Bias为负值,TTm的Bias为正值。随着高度增加,BTm的Bias逐渐减小,其绝对值却在逐渐增大,在8 km时趋于稳定,最后的Bias稳定在-12~-11 K,对应1.5~1.8 mm的PWV误差。而TTm的Bias在0~5 km的范围内随着高度升高逐渐减小,在5~10 km时又随着高度升高逐渐增加,其在0~2 km时为正值,在2~8 km时为负值,在8~10 km时为正值,而其绝对值却一直维持在一个较小的数值。由此可见,相比于Bevis公式,TTm模型可以在近地空间范围内的任意高度面上利用近地大气温度得到高精度的Tm估计值,因此理论上该模型也可以在任何海拔的地表处利用地表温度得到高精度的Tm估计值。
3.3.3 利用高海拔地区无线电探空地表数据的外符合精度检验本文通过引入近地大气温度的概念构造Tm模型,主要目的是为了解决Bevis公式出现的在高海拔地区利用地表温度计算加权平均温度可能精度较低的问题。为此,本文选取了20个高海拔地区(海拔高于1000 m)的探空站对Bevis公式和本文构建的模型进行检验,其中大多数探空站集中在青藏高原地区,最高海拔为4300 m左右。利用这20个探空站2016年的无线电探空地表数据(地表高度约等于探空站海拔)对BTm模型和TTm模型进行检验,将利用温度和湿度廓线积分得到的Tm作为参考值检验利用两个模型和地表温度估计出的Tm,两个模型在这些探空站上的Bias和RMS见表 1。
| 经纬度 | 海拔/m | BTm的Bias/K | TTm的Bias/K | BTm的RMS/K | TTm的RMS/K |
| 15.9°S 47.9°W | 1061 | 0.96 | -0.32 | 2.76 | 2.63 |
| 35.7°N 51.3°E | 1204 | -4.23 | -1.39 | 5.93 | 5.21 |
| 35.5°N 106.7°E | 1348 | -1.81 | 1.61 | 3.95 | 3.93 |
| 38.1°N 46.3°E | 1367 | -4.88 | -2.10 | 6.02 | 4.49 |
| 37.1°N 79.9°E | 1375 | -4.54 | -0.62 | 5.86 | 4.59 |
| 2.8°N 5.4°E | 1377 | -3.99 | -0.44 | 6.26 | 5.03 |
| 32.9°N 59.2°E | 1491 | -5.78 | -3.82 | 6.82 | 5.45 |
| 37.1°N 82.7°E | 1409 | -3.64 | 0.57 | 5.85 | 5.58 |
| 16.4°N 120.6°E | 1500 | 1.60 | 0.25 | 2.76 | 1.81 |
| 41.8°N 97.0°E | 1770 | -4.09 | 1.49 | 5.63 | 4.79 |
| 36.7°N 101.8°E | 2296 | -3.31 | 1.36 | 4.91 | 4.33 |
| 4.7°N 74.2°W | 2547 | -1.04 | -1.02 | 2.19 | 2.06 |
| 36.4°N 94.9°E | 2809 | -6.50 | -1.62 | 7.49 | 4.44 |
| 35.0°N 102.9°E | 2910 | -3.86 | 0.87 | 5.12 | 3.75 |
| 36.3°N 98.1°E | 3190 | -6.89 | -1.81 | 7.62 | 3.72 |
| 31.1°N 97.2°E | 3307 | -5.61 | -1.91 | 6.62 | 4.47 |
| 31.6°N 97.2°E | 3394 | -5.14 | -1.31 | 6.15 | 4.09 |
| 29.7°N 100.0°E | 3650 | -6.27 | -2.89 | 7.31 | 5.02 |
| 33.0°N 97.0°E | 3716 | -5.51 | -0.76 | 6.59 | 4.08 |
| 31.5°N 92.1°E | 4508 | -5.41 | -0.25 | 7.08 | 5.06 |
从表 1可以看出,对这20个参与检验的探空站而言,TTm模型的Tm估计精度都要高于BTm模型。在1~2 km的高程范围内,两个模型的RMS数值相差不大,TTm的RMS略低于BTm。对TTm的计算结果而言,在这一高程范围内,大多数测站的RMS都在4~5 K,对应0.6~0.75 mm的PWV误差。而BTm的计算RMS大多在5~6 K,对应0.75~0.9 mm的PWV误差。因此TTm模型相对于BTm模型在1~2 km的高程范围内水汽反演提升效果为15%~20%。而对于2.5~4.5 km高程范围内的大多数探空站而言,两个模型的RMS却产生了明显的差异。在这一高程范围内,大多数探空站的TTm模型的RMS依然在4~5 K,引起的PWV误差为0.6~0.75 mm。而相应探空站的BTm的RMS却上升到7 K左右,这会在最后的PWV反演中引起约1.05 mm的误差,所以TTm模型相对于BTm模型有25%~40%的精度提升。在这些参与试验的探空站中,两个模型的最大RMS差值达到3.5 K左右,此时TTm模型相对于BTm模型水汽反演精度提升了约0.5 mm。之所以会产生这样的差异,可以从Bias的计算结果看出,由表 1可知,TTm的Bias结果明显优于BTm。BTm的Bias大多呈负值,在1~2.5 km的高程范围内,大多数探空站的BTm的Bias在-4 K左右,对应约0.6 mm的PWV反演误差,而在2.5~4 km的高程范围内时,大多数探空站的Bias却在-6 K左右,对应的PWV误差约为0.9 mm,说明在高海拔地区,利用Bevis估计得到的Tm可能会偏高,这与第2节的结论一致。而TTm的计算Bias绝对值却一直维持在一个较小的数值,大多数探空站的Bias绝对值都在2 K以内,对应的PWV误差只有0.3 mm,相对于BTm模型有一个50%~65%的水汽反演提升效果。
4 结论Bevis公式是GNSS气象学中一个很重要的公式,因为该公式可以利用地表温度和一个简单的线性关系估计出高精度的加权平均温度。然而,不少研究指出,Bevis公式在高海拔地区存在较大误差,本文利用ECMWF再分析资料和无线电探空资料3年(2013—2015年)的气压分层数据,对Bevis公式在不同高度面上的适用性进行探究,并提出了解决Bevis公式在高海拔地区适用性较低问题的可能办法,取得了如下成果:①Bevis公式在海拔较低时适用性较好,Tm估计精度较高,而随着海拔升高,适用性逐渐降低,因为Bevis公式在高海拔地区估计出的Tm可能会偏高,这个偏差值会在到达8 km时趋于稳定,最高偏差会达到11~12 K,这会在最后的PWV反演中引入约1.5~1.8 mm的误差;②提出了近地大气温度的概念,通过研究近地大气温度与加权平均温度的相关性发现,两者在全球范围内都具有很高的相关性,特别是在低纬度地区,相关系数会达到0.97以上;③利用球谐函数建立了基于近地大气温度的全球加权平均温度新模型TTm,并对该模型进行了检验。检验结果表明,该模型在近地空间范围内(0~10 km高程范围)近20个不同的高度层上都可以取得较高的精度,由此可推断,该模型在对应高程范围内的任意高度面上都可以得到高精度的Tm估计值,其在任意高度层的Bias数值都较小,基本都处于-1 K~1 K的区间中,对应约0.15 mm的PWV误差,其RMS始终维持在4 K左右,对应的PWV误差约为0.6 mm,不存在随着高程增加精度逐渐降低的现象。因此也可以推断,该模型在任何地表海拔高度面上都可以利用地表温度提供高精度的加权平均温度估计值。
| [1] | ROCKEEN C, VAN HOVE T, WARE R. Near real-time GPS sensing of atmospheric water vapor[J]. Geophysical Research Letters, 1997, 24(24): 3221–3224. DOI:10.1029/97GL03312 |
| [2] | ALLAN R P. The role of water vapour in earth's energy flows[J]. Surveys in Geophysics, 2012, 33(3-4): 557–564. DOI:10.1007/s10712-011-9157-8 |
| [3] | BEVIS M, BUSINGER S, CHISWELL S, et al. GPS meteorology: mapping zenith wet delays onto precipitable water[J]. Journal of Applied Meteorology, 1994, 33(3): 379–386. DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2 |
| [4] | SAASTAMOINEN J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites[M]. Washington, D.C.: American Geophysical Union, 1972: 247-251. |
| [5] | HOPFIELD H S. Tropospheric effect on electromagnetically measured range: prediction from surface weather data[J]. Radio Science, 1971, 6(3): 357–367. DOI:10.1029/RS006i003p00357 |
| [6] | ASKNE J, NORDIUS H. Estimation of tropospheric delay for microwaves from surface weather data[J]. Radio Science, 1987, 22(3): 379–386. DOI:10.1029/RS022i003p00379 |
| [7] | BEVIS M, BUSINGER S, HERRING T A, et al. GPS meteorology: remote sensing of atmospheric water vapor using the global positioning system[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787–15801. DOI:10.1029/92JD01517 |
| [8] | WANG Xiaoming, ZHANG Kefei, WU Suqin, et al. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend[J]. Journal of Geophysical Research: Atmospheres, 2016, 121(2): 833–852. DOI:10.1002/2015JD024181 |
| [9] | DING Maohua. A neural network model for predicting weighted mean temperature[J]. Journal of Geodesy, 2018, 92(10): 1187–1198. DOI:10.1007/s00190-018-1114-6 |
| [10] | ROSS R J, ROSENFELD S. Estimating mean weighted temperature of the atmosphere for global positioning system applications[J]. Journal of Geophysical Research: Atmospheres, 1997, 102(D18): 21719–21730. DOI:10.1029/97JD01808 |
| [11] | DUAN Jingping, BEVIS M, FANG Peng, et al. GPS meteorology: direct estimation of the absolute value of precipitable water[J]. Journal of Applied Meteorology, 1996, 35(6): 830–838. DOI:10.1175/1520-0450(1996)035<0830:GMDEOT>2.0.CO;2 |
| [12] | WANG Junhong, ZHANG Liangying, DAI Aiguo. Global estimates of water-vapor-weighted mean temperature of the atmosphere for GPS applications[J]. Journal of Geophysical Research: Atmospheres, 2005, 110(D21): D21101. DOI:10.1029/2005JD006215 |
| [13] | YAO Yibin, ZHANG Bao, XU Chaoqian, et al. Analysis of the global Tm-Ts correlation and establishment of the latitude-related linear model[J]. Chinese Science Bulletin, 2014, 59(19): 2340–2347. DOI:10.1007/s11434-014-0275-9 |
| [14] | YAO Y, ZHANG B, XU C, et al. Improved one/multi-parameter models that consider seasonal and geographic variations for estimating weighted mean temperature in ground-based GPS meteorology[J]. Journal of Geodesy, 2014, 88(3): 273–282. DOI:10.1007/s00190-013-0684-6 |
| [15] | YAO Yibin, ZHU Shuang, YUE Shunqiang. A globally applicable, season-specific model for estimating the weighted mean temperature of the atmosphere[J]. Journal of Geodesy, 2012, 86(12): 1125–1135. DOI:10.1007/s00190-012-0568-1 |
| [16] | ZHANG Hongxing, YUAN Yunbin, LI Wei, et al. GPS PPP-derived precipitable water vapor retrieval based on Tm/Ps from multiple sources of meteorological data sets in China[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(8): 4165–4183. DOI:10.1002/2016JD026000 |
| [17] |
于胜杰, 柳林涛.
水汽加权平均温度回归公式的验证与分析[J]. 武汉大学学报(信息科学版), 2009, 34(6): 741–744.
YU Shengjie, LIU Lintao. Validation and analysis of the water-vapor-weighted mean temperature from Tm-Ts relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 741–744. |
| [18] | DAVIS J L, HERRING T A, SHAPIRO I I, et al. Geodesy by radio interferometry: effects of atmospheric modeling errors on estimates of baseline length[J]. Radio Science, 1985, 20(6): 1593–1607. DOI:10.1029/RS020i006p01593 |
| [19] | BEVIS M, BUSINGER S, CHISWELL S. Earth-based GPS meteorology: an overview, american geophysical union 1995 fall meeting[J]. EOS, 1995(76): 46. |
| [20] | SIMMONS A, UPPALA S, DEE D. ERA-interim: new ECMWF reanalysis products from 1989 onwards[J]. ECMWF Newsletter, 2006(110): 25–36. |
| [21] | DEE D P, UPPALA S M, SIMMONS A J, et al. The ERA-interim reanalysis: configuration and performance of the data assimilation system[J]. Quarterly Journal of the Royal Meteorological Society, 2011, 137(656): 553–597. DOI:10.1002/qj.v137.656 |
| [22] | BÖHM J, MÖLLER G, SCHINDELEGGER M, et al. Development of an improved empirical model for slant delays in the troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433–441. DOI:10.1007/s10291-014-0403-7 |
| [23] | LAGLER K, SCHINDELEGGER M, BÖHM J, et al. GPT2: empirical slant delay model for radio space geodetic techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069–1073. DOI:10.1002/grl.50288 |
| [24] | YAO Yibin, ZHANG Bao, YUE Shunqiang, et al. Global empirical model for mapping zenith wet delays onto precipitable water[J]. Journal of Geodesy, 2013, 87(5): 439–448. DOI:10.1007/s00190-013-0617-4 |
| [25] | ACKERMAN S, KNOX J A. Meteorology: understanding the atmosphere[M]. Pacific Grove, CA: Thomson Learning, 2006. |


