2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 信息工程大学, 河南 郑州 450052
2. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China;
3. Information Engineering University, Zhengzhou 450052, China
基于星间链路,导航卫星星座可以实现自主导航,在地面站设施受损的情况下继续提供服务。对于北斗卫星导航系统而言,星间链路的首要功能是确保系统在区域监测站条件下实现设计的定轨和时间同步指标。2015年以来,北斗三号系统(BDS-3)陆续发射了5颗试验卫星[1],2017年11月至今已经陆续发射了18颗北斗工作卫星,这些卫星都搭载了星间链路设备。国内外许多学者开展了利用星间链路观测数据进行星座自主导航或联合地面锚固站或监测站观测数据进行定轨和时间同步的仿真研究[2-8]。针对北斗系统星间链路实际应用的研究成果也非常令人鼓舞[9-14]。北斗三号试验卫星发射之后,最新研究成果显示,在星间测距数据的支持下,轨道径向的精度达到10 cm[9]。
通常星间链路采用时分多址的运行模式,北斗系统的星间链路通过相控阵天线实现信号接收、发射和波束指向控制,提供Ka频段单频伪距观测量[15-16]。在任一时刻(隙)一颗卫星只能按照预先确定的链路规划与另外一颗卫星进行通信和测距。同一卫星对其他卫星的伪距观测量是分别在不同时刻(隙)获得的。已有的利用星间链路数据进行定轨和时间同步的方法[4-5, 7-8, 13, 15-18],都首先将原始的单程测距观测量进行历元归化,得到在指定时刻的虚拟观测量(即归化伪距), 例如将同一时隙内一对卫星相向的两个单程伪距归算到最近的同一个整3 s时刻[9]。然后,进一步构造出无钟差组和无几何组合观测量[5-7, 8, 13, 15-18],分别用于轨道和钟差确定,即定轨和时间同步是独立进行的;或者,另一种方式,直接采用单程归化伪距联合地面监测站数据同时确定导航卫星轨道和钟差[19-21]。后者的最大优势是可以同时确定卫星轨道和钟差,还可估计星间链路设备时延相对于导航信号设备的时延偏差,是进行星间链路设备时延在轨标定的有效方法[19, 21],但还未见有用于BDS-3星间链路实际数据处理的报道。本文延续这一思路,但是更进一步地,无须进行历元归化,直接采用原始单程伪距观测数据联合地面监测站数据同时确定卫星轨道、钟差及星间链路设备时延偏差。
1 观测方程 1.1 星间伪距观测方程由于采用时分多址测量体制,一颗卫星对其他可测卫星的星间测距被分配在不同的时隙进行,假设在ti, j时刻卫星i获得对卫星j的星间测距观测量为Pi, j,观测方程可表示如下[9, 21]
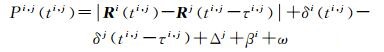 (1)
(1)
式中,τi, j为星间链路信号在空间传播的时间;Ri和Rj分别为卫星i和j在信号接收和发射时刻的位置;δi和δj为以距离表示的卫星i和j的时钟偏差;Δj和βi分别为星间链路设备发射和接收的硬件时延,在一段时间内通常可视为稳定不变量;ω为测量噪声。式(1)省略了信号传播的相对论延迟、卫星天线相位中心偏差等改正项。
1.2 地面接收机伪距和相位观测方程地面监测站的测量型接收机在设定的采样时刻可同时获得多颗卫星多个频点的载波相位和伪距观测量,不妨设tk时刻接收机r对卫星i的消电离层组合载波相位和伪距观测量分别为:Lri(tk)和Pri(tk),观测方程表示如下
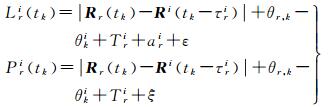 (2)
(2)
式中,k为观测历元计数;τri为信号从卫星到测站的传播时间;Rr为测站r的位置;θr, k=δr, k+br,θki=δki-bi分别为第k历元的测站和卫星钟差参数,包含了各自的时钟偏差(δr, k和δki)及消电离层组合伪距硬件时延(br和bi);ari为消电离层组合模糊度参数(包含了载波和伪码的硬件时延);Tri为测站的对流层延迟;ξ和ε分别为载波相位和伪距观测量的测量误差。式(2)省略了相对论传播时延、相位缠绕效应、卫星天线相位中心偏差等改正项。
1.3 联合观测方程不同测站的接收机通过锁定导航信号进行时钟同步(同步时间差常小于1 us,一般不超过1 ms),因此同一采样历元不同测站对同一卫星的观测量所对应的信号发射时刻的差异也很微小(远小于1 s)。而导航卫星配置了高精度的原子钟,在如此短的时间内卫星钟差的变化可以忽略。因此在处理地面监测站数据时,将同一历元不同观测量对应同一卫星的钟差视为同一个值。
BDS-3卫星为每条链路分配的测量和通信时隙宽度为3 s[9],用于接收和发射信号的时间分别为1.5 s,每颗卫星获得的星间伪距观测量以约3 s的(整数倍)间隔分布在时间轴上,因此每个观测量对应不同时刻的卫星钟差。假设一颗卫星可以对10颗卫星进行星间测距,则该星对第一颗和最后一颗卫星进行观测的时间差可达到30 s。对于高精度的定轨和时间同步,这两个观测量包含的钟差应该视为不同的值。因此,每个星间单程伪距观测量包含独有的两个钟差参数,没有多余观测,不能通过平差以改进轨道和钟差。为此,已有的方法都需要对星间链路数据进行历元归化,得到(至少两个)同时观测的归化伪距观测数据,以便分离轨道和钟差信息[5, 9, 10, 15]。
本文将直接处理原始星间单程伪距数据。为了能够直接对原始的单程伪距观测量进行平差解算,首先需要解决原始观测数据的非同时观测问题。为此,将连续的时间轴划分为离散的互不重叠的时间窗,每个时间窗的宽度为w。在时间窗内,任意时刻t的卫星钟差用多项式表示为
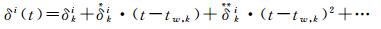 (3)
(3)
式中,tw, k为第k个时间窗的参考时刻,不妨选时间窗的中间点为参考时刻;δki为对应参考时刻tw, k的卫星钟差,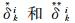
对钟速进行改正,并忽略高次项,则单程星间伪距观测方程可以表示如下
 (4)
(4)
式中,ω包含了预报钟速误差的影响。注意式(4)和式(1)的区别,式(4)中同一时间窗内的不同时刻的星间单程伪距观测量对应的是同一时刻tw, k的钟差,因此可以直接进行平差解算,同时确定轨道和钟差(相当于集中式自主定轨和时间同步,当然需要解决星座定向秩亏问题)[14]。
为了将星间测距数据与地面监测站数据构成联合观测方程,最简单的方法是将地面监测站的观测历元时刻tk作为上述时间窗的参考时刻,即令tw, k=tk。这样钟差多项式的零次项系数就可用tk时刻的卫星钟差替代。省去推导过程,直接给出第k个时间窗(0≤ti, j-tk < w)内单程星间伪距与地面接收机伪距及载波相位的联合观测方程
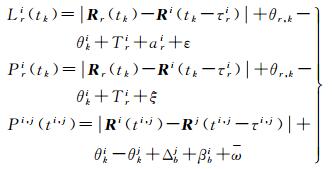 (5)
(5)
式中,Δb*=Δ*-b*和βb*=β*+b*分别为卫星(*=i, j)的星间链路发射和接收设备时延偏差[21],表示星间链路发射和接收设备时延相对于导航信号(伪码)设备时延的偏差[21]。如果没有精确的已知值(通常如此),可以将Δb*和βb*作为未知参数一同解算。以式(5)为观测方程进行模型改正和线性化之后就可采用,如最小二乘方法,同时解算出卫星轨道、钟差和时延偏差等未知参数。
利用观测方程式(5)确定轨道和钟差的数据处理过程与单独处理地面观测网数据的过程几乎完全一致(用时间窗概念代替了历元概念),只是星间伪距观测量的函数模型与地面接收机数据不同。众所周知的,在解算上述方程时,必须在每个时间窗(历元)选择一个钟差参数作为钟差基准。此外,由于时延偏差参数的绝对值也是不可测的,需要选择一个时延偏差参数作为基准以消除方程的秩亏[21]。
2 试验及结果分析 2.1 试验为了验证上述方法,收集2018年5月1—9日(DOY121—129) BDS-3的6颗MEO卫星(B19、B20、B21、B22、B27和B28)的星间伪距数据和国际GNSS监测评估系统(iGMAS)国内6个监测站(西安、武汉、北京、长春、乌鲁木齐、拉萨)的观测数据进行联合定轨和钟差确定试验。为了考察星间链路数据的贡献,进行了以下两组试验:
试验1(EXP1):仅用地面监测站数据。
试验2(EXP2):同时利用地面监测站和星间链路数据。
采用SPODS软件[22]进行解算,定轨弧长为3 d。其中地面接收机数据采用B1I和B3I双频数据,采样间隔为5 min,按照2 m和0.02 m的先验精度对伪距和载波相位进行定权,并根据高度角按照函数sin2e进行降权,截至高度角取10°。测站坐标和地球自转参数固定于已知值,卫星轨道参数包括初始状态矢量和ECOM模型的5个参数(D0, Y0, B0, Bc & Bs),对流层天顶延迟的初值采用Saastamoinen模型计算,采用GMF作为映射函数,对每一个测站,每2 h估计一个天顶对流层延迟参数,每24 h估计一组水平方向的梯度参数。将监测站数据采样时刻作为星间链路各时间窗的参考时刻和中心点,时间窗宽度取为1 min,星间单程伪距数据按照0.1 m精度定权。未知参数还包括每个历元的卫星和接收机钟差、每个无周跳弧段的消电离层组合非差模糊度参数,每颗卫星的星间链路接收和发射时延偏差参数。采用相邻两个处理弧段的重叠段互差来评估轨道和钟差的确定精度,重叠弧长为2 d。
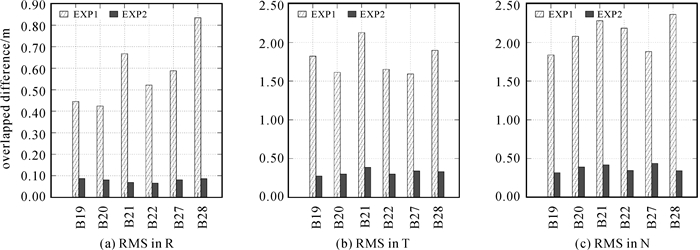
2.2 结果分析图 1显示了两组试验中各颗卫星轨道重叠段互差在R、T和N方向的RMS。可以看出,试验1中,R方向的RMS都超过0.5 m,T方向的RMS超过了1.5 m,N方向的RMS在2 m左右。加入星间伪距数据后,R方向的RMS不超过0.1 m,T和N方向的不超过0.5 m。平均RMS分别为0.078、0.321和0.375 m,改进幅度分别为86.5%、82.0%和82.2%。
|
| 图 1 按卫星统计的卫星轨道重叠互差RMS Fig. 1 RMS of overlap orbit differences for each satellite |
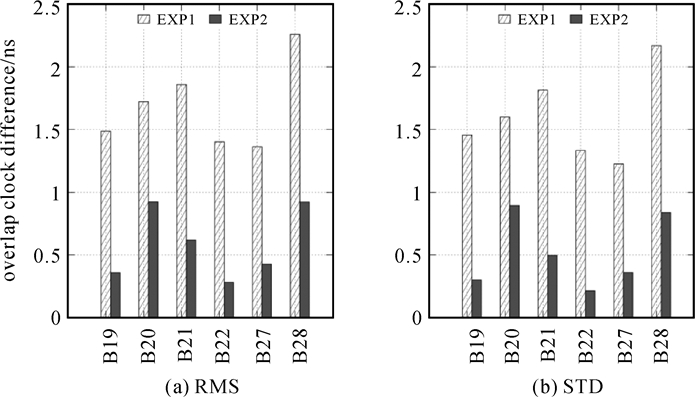
图 2统计了两组试验中各卫星钟差重叠互差的RMS和STD。可以看出,试验1中,各卫星的RMS和STD分别大于1.3和1.2 ns,平均分别为1.682和1.600 ns。试验2中,各卫星的RMS和STD都显著减小,平均值分别为0.589和0.519 ns,改进弧度分别达到65.0%和67.6%。由于每颗卫星的观测链路数量还比较少,钟差精度的改进很可能是直接得益于轨道精度的改进。但星间链路数据的加入使卫星钟差的有效观测(至少有两个以上观测数据)弧段显著增加,例如在本次试验中提高了85.7%。如果星座健全,则很容易实现全弧段跟踪。
|
| 图 2 按卫星统计的卫星钟差重叠互差的RMS和STD Fig. 2 RMS and STD of overlap clock differences for each satellite |
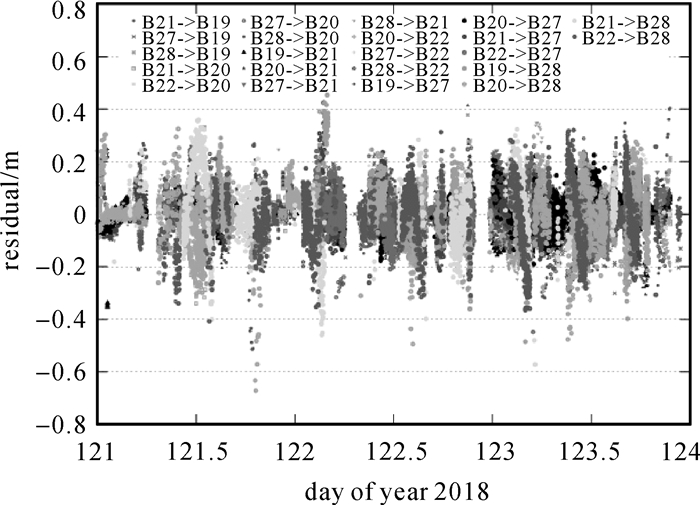
图 3显示了年积日121—124共计3 d弧段星间单程伪距观测量的残差序列。可以看出,绝大部分的残差都小于0.2 m,统计得到RMS为0.082 m。统计7个定轨弧段,各颗卫星接收的星间伪距数据残差的平均RMS分别为:0.067、0.071、0.064、0.067、0.082和0.145 m,其中卫星B28的伪距残差明显比其他卫星大得多,6颗卫星的RMS平均值为0.083 m。
|
| B22->B19表示卫星B22到B19的链路 图 3 单程星间伪距数据的残差序列 Fig. 3 Residual series of inter-satellites pseudorange for each satellite-pair |
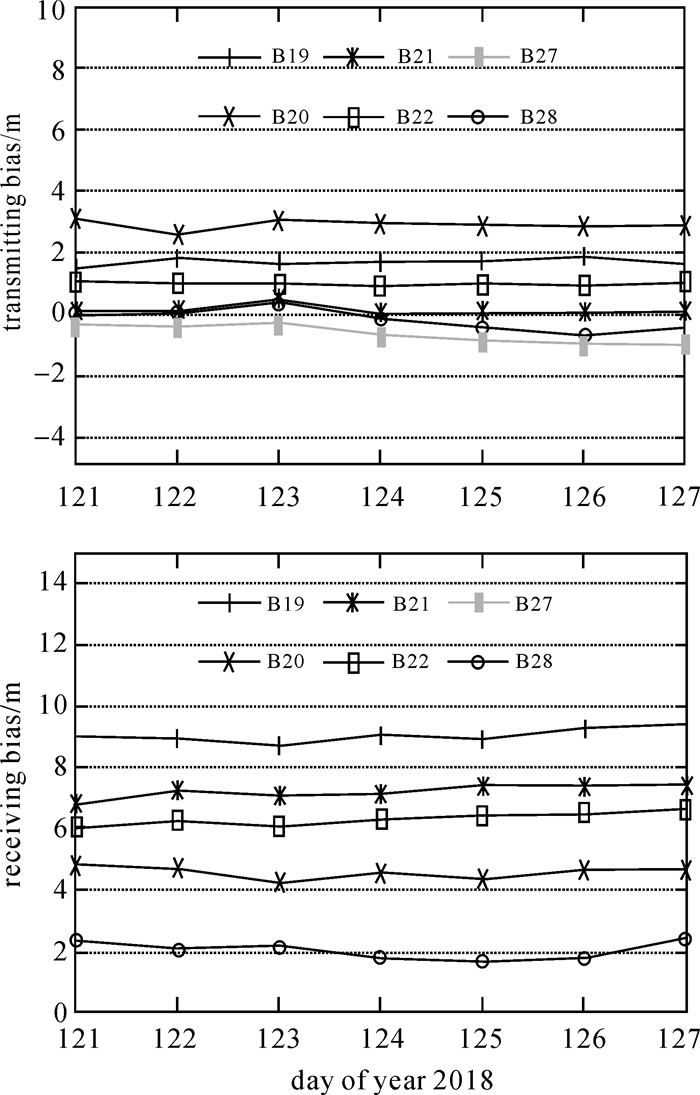
图 4给出各颗卫星接收和发射时延偏差的估值序列(每颗卫星分别扣除一个值)。表 1统计了各颗卫星发射和接收时延偏差的平均值(仅显示个位数以下数值)和标准差。卫星B27和B28同类时延偏差参数的均值相差不超过0.5 m。从标准差来看,除了卫星B28的接收时延偏差之外,STD都小于0.3 m(合1 ns)。卫星B28的接收和发射时延偏差都是所有卫星中最大的,相应的星间单程伪距残差的RMS值也是最大的。
|
| 图 4 星间链路接收和发射时延偏差估值序列 Fig. 4 Estimates of ISL receiving and transmitting hardware delay bias |
| m | |||||
| 卫星 | 接收时延偏差 | 发射时延偏差 | |||
| MEAN | STD | MEAN | STD | ||
| B19 | **1.687 | 0.107 | **9.042 | 0.213 | |
| B20 | **2.890 | 0.168 | **4.597 | 0.181 | |
| B21 | 0.000 | — | **7.234 | 0.230 | |
| B22 | **0.983 | 0.049 | **6.329 | 0.210 | |
| B27 | **9.343 | 0.288 | **2.153 | 0.176 | |
| B28 | **9.793 | 0.345 | **2.070 | 0.281 | |
3 讨论
由于星间链路采用时分多址的测量体制,同一卫星的每个观测量都是在不同时刻测量获得的,每个观测量都包含两个独有的钟差参数,所以没有多余观测,不能通过平差确定轨道和钟差。已有的方法都通过历元归化将(至少两个)不同时刻获得的星间链路数据归算到指定的同一目标时刻,从而能够进行平差处理[21]或者对轨道和钟差信息进行解耦。这种思路最初可能由Ananda(1990)提出[15],被许多学者沿用至今[9-11, 14]。
本文方法的巧妙之处在于:①采用多项式描述卫星钟差,使原本非同时观测的星间单程伪距数据对应于共同的钟差参数——多项式系数,从而能够直接进行平差;②通过合理设置时间窗,控制多项式模型误差。实际上就是用分段多项式描述卫星钟差。该方法无须对星间链路数据进行历元归化,也无需对两颗卫星的相向测距数据进行匹配以分离轨道和钟差信息。数据处理过程非常简洁,与传统地面监测站数据处理过程几乎一致。与现有方法相比,该方法的优点还表现在可以同时解算出卫星轨道、钟差和星间链路设备相对于导航设备的硬件时延偏差,轨道和钟差更加自洽,获得的时延偏差估计值可以用于修正星间链路观测数据,并应用于自主导航。直接处理原始单程伪距数据的另一个好处是可以单独分析每个星间链路发射或接收设备的数据质量或设备性能。
上述用分段多项式表示(卫星)钟差的思想,还可以用于(联合)其他同时或非同步观测数据,如星地双向时间比对数据或锚固站数据的定轨、时间同步及设备时延标定。
4 结论直接利用原始的单程星间伪距数据联合地面监测站数据同时确定BDS-3卫星轨道、钟差和星间链路设备时延偏差,方法相对简单,所有单程星间观测量都可以直接参与计算。利用北斗6颗组网卫星的星间伪距数据和6个iGMAS国内监测站数据进行了试验验证。结果表明,3 d定轨的重叠段互差在R、T和N方向的RMS分别为0.078、0.321和0.375 m;钟差的重叠段互差RMS和STD分别达到0.589和0.519 ns。相比于仅用国内监测站的结果,轨道和钟差的改进幅度分别超过80%和60%。星间链路单程伪距残差的平均RMS为0.083 m,各颗卫星的设备时延偏差估值的稳定度普遍优于1 ns,发射和接收设备时延偏差估值的平均稳定度分别为0.53和0.72 ns。
由于目前掌握数据较少,该方法的稳定性还需要更多数据进行充分验证。
致谢: 感谢国际GNSS监测评估系统(iGMAS)和西安卫星测控中心提供试验数据。
| [1] |
杨元喜, 许扬胤, 李金龙, 等.
北斗三号系统进展及性能预测——试验验证数据分析[J]. 中国科学地球科学, 2017, 48(5): 584–594.
YANG Yuanxi, XU Yangyin, LI Jinlong, et al. Progress and performance evaluation of BeiDou global navigation satellite system:data analysis based on BDS-3 demonstration system[J]. Science China Sciences, 2017, 48(5): 584–594. |
| [2] |
陈金平, 焦文海, 马骏, 等.
基于星间测距/轨道定向参数约束的导航卫星自主定轨研究[J]. 武汉大学学报(信息科学版), 2005, 30(5): 439–443.
CHEN Jinping, JIAO Wenhai, MA Jun, et al. Autonav of navigation satellite constellation based on crosslink range and orientation parameters constraining[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 439–443. |
| [3] |
陈金平, 尤政, 焦文海.
基于星间距离和方向观测的导航卫星自主定轨研究[J]. 宇航学报, 2005, 26(1): 43–46.
CHEN Jinping, YOU Zheng, JIAO Wenhai. Research on autonav of navigation satellite constellation based on crosslink range and inter-satellites orientation observation[J]. Journal of Astronautics, 2005, 26(1): 43–46. DOI:10.3321/j.issn:1000-1328.2005.01.009 |
| [4] |
刘万科.导航卫星自主定轨及星地联合定轨的方法和模拟计算[D].武汉: 武汉大学, 2008: 163. LIU Wanke. Research and simulation on autonomous orbit determination and combined orbit determination of navigation satellitess[D]. Wuhan: Wuhan University, 2008: 163. |
| [5] |
宋小勇. COMPASS导航卫星定轨研究[D].西安: 长安大学, 2009: 169. SONG Xiaoyong. Study on the orbit determination of COMPASS navigation satellites[D]. Xi'an: Chang'an University, 2009: 169. http://cdmd.cnki.com.cn/Article/CDMD-11941-1011185305.htm |
| [6] | HEIN G W. Inter satellite links for GNSS[R]. Munich: University FAF Munich, 2011. |
| [7] |
朱俊.基于星间链路的导航卫星轨道确定及时间同步方法研究[D].长沙: 国防科学技术大学, 2011: 218. ZHU Jun. Research on orbit determination and time synchronizing of navigation satellite based on crosslinks[D]. Changsha: National University of Defense Technology, 2011: 218. http://cdmd.cnki.com.cn/Article/CDMD-90002-1012020138.htm |
| [8] | FERNÁNDEZ F A. Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data[J]. Advances in Space Research, 2011, 47(5): 786–801. DOI:10.1016/j.asr.2010.10.002 |
| [9] | TANG Chengpan, HU Xiaogong, ZHOU Shanshi, et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements[J]. Journal of Geodesy, 2017, 92(10): 1155–1169. |
| [10] | YANG Daoning, YANG Jun, LI Gang, et al. Globalization highlight:orbit determination using BeiDou inter-satellite ranging measurements[J]. GPS Solutions, 2017, 21(3): 1395–1404. DOI:10.1007/s10291-017-0626-5 |
| [11] | PAN Junyang, HU Xiaogong, ZHOU Shanshi, et al. Time synchronization of new-generation BDS satellites using inter-satellite link measurements[J]. Advances in Space Research, 2018, 61(1): 145–153. DOI:10.1016/j.asr.2017.10.004 |
| [12] | REN Xia, YANG Yuanxi, ZHU Jun, et al. Orbit determination of the next-generation BeiDou satellites with intersatellite link measurements and a priori orbit constraints[J]. Advances in Space Research, 2017, 60(10): 2155–2165. DOI:10.1016/j.asr.2017.08.024 |
| [13] |
宋小勇, 毛悦, 冯来平, 等.
BD卫星星间链路定轨结果及分析[J]. 测绘学报, 2017, 46(5): 547–553.
SONG Xiaoyong, MAO Yue, FENG Laiping, et al. The preliminary result and analysis for BD orbit determination with inter-satellite link data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 547–553. DOI:10.11947/j.AGCS.2017.20160203 |
| [14] |
任夏.北斗导航系统自主定轨理论与方法研究[D].郑州: 信息工程大学, 2018: 146. REN Xia. Research on the theory and method of BDS autonomous orbit determination[D]. Zhengzhou: Information Engineering University, 2018: 146. |
| [15] | ANANDA M P, BERNSTEIN H, CUNNINGHAM K E, et al. Global positioning system (GPS) autonomous navigation[C]//IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences. Las Vegas, NV: IEEE, 1990: 497-508. https://www.researchgate.net/publication/3490188_Global_Positioning_System_GPS_autonomous_navigation |
| [16] |
林益明, 秦子增, 初海彬, 等.
基于星间链路的分布式导航自主定轨算法研究[J]. 宇航学报, 2010, 31(9): 2088–2094.
LIN Yiming, QIN Zizeng, CHU Haibin, et al. A satellite cross link-based GNSS distributed autonomous orbit determination algorithm[J]. Journal of Astronautics, 2010, 31(9): 2088–2094. DOI:10.3873/j.issn.1000-1328.2010.09.005 |
| [17] | CAI Zhiwu, HAN Chunhao, DU Yan, et al. Orbit determination method and accuracy analysis utilizing satellite-ground and satellite-satellite links[C]//Proceedings of CSNC2011. Shanghai: [s.n.], 2011: 472-476. |
| [18] |
毛悦, 宋小勇, 贾小林, 等.
星间链路观测数据归化方法研究[J]. 武汉大学学报(信息科学版), 2013, 38(9): 1201–1206.
MAO YUE, SONG Xiaoyong, JIA Xiaolin, et al. Naturalisation method research on inter-satellite link observation data[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1201–1206. |
| [19] | RUAN Rengui, FENG Laiping, JIA Xiaolin, et al. Estimation of crosslink equipment delay and its contribution to GNSS orbit determination and time synchronization[C]//SUN J, LIU J, YANG Y, et al. China Satellite Navigation Conference(CSNC) 2012 Proceedings. Berlin, Heidelberg: Springer, 2012. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-WXDH201205003008.htm |
| [20] | LIU Wanke, GONG Xiaoying, ZHANG Weixing. GPS orbit determination with real ground tracking observations and simulative crosslink ranging observations[C]//Proceedings of CSNC 2011. Shanghai: [s.n.], 2011: 451-455. |
| [21] |
阮仁桂, 冯来平, 贾小林.
导航卫星星地/星间链路联合定轨中设备时延估计方法[J]. 测绘学报, 2014, 43(2): 137–142, 157.
RUAN Rengui, FENG Laiping, JIA Xiaolin. Equipment delay estimation for GNSS satellite combined orbit determination with satellite-ground link and inter-satellite link observations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 137–142, 157. DOI:10.13485/j.cnki.11-2089.2014.0020 |
| [22] |
魏子卿, 阮仁桂, 贾小林, 等.
卫星定位定轨系统SPODS:理论与测试[J]. 测绘学报, 2014, 43(1): 1–4.
WEI Ziqing, RUAN Rengui, JIA Xiaolin, et al. Satellite positioning and orbit determination system spods:theory and test[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 1–4. DOI:10.13485/j.cnki.11-89.2014.0001 |


