2. 信息工程大学, 河南 郑州 450001
2. Information Engineering University, Zhengzhou 450001, China
目前,建立新型LEO(low earth orbit)卫星星座在国际上重新引发了开发和投资热潮[1-2]。国际上,在Orbcomm、Iridium和Globalstar等公司的基础上,OneWeb公司提出在2019年建成648颗卫星组成的LEO星座,SpaceX公司计划在2020年建立4425颗卫星组成的LEO导航星座,其LEO星座的目的是提供真正的全球稳健的宽带互联网覆盖,同时具备作为导航增强系统的功能[3-7]。在国内,中国航天科技集团计划2020年建成由60颗LEO卫星组成的“鸿雁星座通信系统”,中国航天科工集团则提出包括156颗LEO卫星的“虹云工程”(表 1)。航天技术的进步降低了卫星的研制和发射成本,而高精度导航定位服务又催生了LEO导航增强卫星星座建设需求。
| 系统 | Orbcomm | Iridium | Globalstar | OneWeb | SpaceX | 鸿雁星座通信系统 | 虹云工程 |
| 运营商 | 美国Orbcomm | 美国摩托罗拉 | 美国LQSS | 法国OneWeb | 美国SpaceX | 中国航天科技集团 | 中国航天科工集团 |
| 轨道类型 | 圆轨道 | 圆轨道 | 圆轨道 | 圆轨道 | 圆轨道 | 圆轨道 | 圆轨道 |
| 轨道高度/km | 835/725 | 785 | 1414 | 1200 | 1127 | 1200 | 1000 |
| 卫星数目 | 36 | 66+6 | 48 | 648 | 4425 | 60 | 156 |
| 轨道倾角/(°) | 0/45/70/108 | 86.4 | 52 | 88 | - | - | - |
| 覆盖区域 | 全球 | 全球 | ±70° | 全球 | 全球 | 全球 | 全球 |
| 服务时间 | 1997 | 1998 | 1999 | 2019 | 2020 | 2020 | 2022 |
LEO的广播星历参数设计是低轨导航增强系统设计的重要环节[8]。目前导航系统常用的广播星历主要分为两类[9]:一类是以GPS星历为代表的轨道根数型广播星历;另一类是以GLONASS星历为代表的轨道列表型广播星历。由于目前大多数导航系统(如GPS、BDS、Galileo和QZSS)都是使用的轨道根数型星历模型,因此此类星历在通用性上具有较大优势。但是轨道根数型星历包含了经典的开普勒根数,直接用于小偏心率轨道时会出现奇点问题[10]。文献[11]采用第二类无奇点根数,针对GEO卫星将偏心率和轨道倾角相关参数进行改进,解决了GEO卫星小偏心率的问题。文献[12]针对GPS广播星历用于GEO卫星出现的小偏心率奇点问题,基于第一类无奇点根数提出了无旋转倾角的两步法星历参数拟合算法,避免了GEO星历拟合奇点问题,并将GEO卫星2~3 h星历拟合误差降低至毫米级。目前针对星历拟合奇点问题的研究,主要集中在GNSS星座中的GEO卫星,对LEO卫星奇点问题的研究较少。文献[13]根据LEO卫星的轨道特征,基于第二类无奇点根数设计了一套23参数星历拟合法,1000 km高度轨道拟合20 min误差优于5 cm。其拟合误差较小,符合星历URE(user range error)优于10 cm的标准(GPS space segment/navigation user interfaces, Rev.c.TCD-GPS-200C, 2012)。但拟合参数较多,拟合时段不统一;其结果表明卫星沿迹向和径向受摄动力影响明显,拟合误差较大,需要较多参数进行拟合,为LEO星历拟合的改进提供了参考。
针对LEO小偏心率奇点和轨道沿迹向、径向拟合误差较大的问题,基于第一类无奇点根数提出了轨道根数型16/17/18/18*/19参数LEO星历拟合模型;针对拟合时段不统一的问题,将拟合时段设为卫星的地面最大可见时间,减少了用户更新星历的频率。设计的星历模型有效地避免了小偏心率轨道拟合出现的拟合误差增大的问题,有效地减小了卫星沿迹向的拟合误差,使得卫星轨道沿迹向、径向、外法向的拟合误差较为均匀;星历参数占用卫星传输信道的比特位较少,可以有效节约卫星资源;星历拟合误差URE指标保持在厘米级,能够满足LEO导航星座精度需求。
1 星历参数设 1.1 URE贡献因子星历参数拟合误差直接影响着用户导航定位的精度,是评价星历参数设计优劣的重要指标。在评定广播星历拟合误差时一般使用三个标准来评价:三维位置精度、RTN精度、用户测距误差(URE)。在广播星历的实际使用过程中,用户更注重的是星历误差在用户-卫星视线方向上的投影(即URE),URE性能指标综合反映了导航星历误差和预报钟差,是计算星历和钟差误差对定位影响的一个重要评价指标[14]。
URE的来源主要是轨道外推误差和钟差误差,这里仅分析星历参数拟合误差的单项影响,钟差误差在此不作考虑,简化后的URE计算公式为[11]
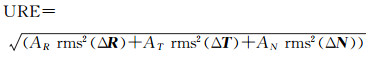
式中,ΔR、ΔT和ΔN分别为卫星径向、沿迹向和外法向位置分量的拟合误差;AR、AT和AN是分别对应3个方向的贡献因子。
GPS卫星URE的RTN 3方向的贡献因子值分别为:0.96/0.02/0.02,显然,绝大部分是卫星径向误差的贡献。值得注意的是,LEO的贡献因子与GPS的规律完全不同。图 1给出了高度在300-1500 km的低轨卫星URE贡献因子变化(用户最小观测仰角设置为0)[15-16],可以看出:

|
| 图 1 RTN 3方向贡献因子随轨道高度变化 Fig. 1 Change of weight factors with track height in RTN directions |
(1) 与MEO相比,LEO的3方向贡献因子相差不再悬殊,每个方向分量的影响均不超过0.45。
(2) 随着轨道高度降低,径向贡献因子快速减小,沿迹向和外法向贡献因子逐渐增大;在1000 km轨道高度,3个方向URE贡献因子基本相当。
1.2 星历参数分析设计LEO星历参数的首要原则是,在满足URE指标要求的前提下,尽量与经典的广播星历参数保持一致。以GPS为例,其NAV/CNAV广播星历参数主要由3部分构成:轨道基本参数(如

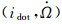
短时段内,影响低轨LEO卫星轨道外推误差的主要摄动力包括地球扁率摄动、大气阻力摄动、日月引力摄动和光压等。与中轨GPS相比:①轨道更低,地球扁率摄动影响更大,因此,半轨道周期的调和项仍为主周期项;②随轨道高度降低(< 600 km),大气阻力成为摄动主项,对轨道半长轴和偏心率(a, e)有长期累积效应;③扁率摄动引起的轨道面进动更大,日月引力摄动和光压的影响随轨道高度降低而有所减弱。
因此,根据LEO受力特点,对LEO的星历参数的改造,可集中在轨道面内长期摄动参数上。一方面是吸收大气阻力引起的轨道变低变圆的长期效应;另一方面,低轨卫星URE的贡献因子中AT显著增大,需要加强轨道沿迹向位置分量的参数表征。
1.3 轨道面内星历参数表征和位置分量计算通过增减轨道径向和沿迹方向的参数,对GPS16/18参数模型进行改进(表 2),以解决GPS星历用于LEO时径向和沿迹向拟合误差较大的问题。
| 参数个数 | 16 | 17 | 18 | 18* | 19 |
| 轨道沿迹方向长期摄动参数 | Δn | Δn Δṅ | Δn Δṅ | Δn Δṅ 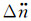 |
Δn Δṅ 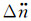 |
| 轨道径向长期摄动参数 | - | - | ȧ | - | ȧ |
表 2对应的完整星历模型参数集为

与GPS16/18星历的卫星位置计算相比,LEO星历模型的用户算法基本相同,仅在轨道半长轴和卫星平均角速度的计算上有所区别,表 3给出了其具体计算方法。
| 参数个数 | 轨道半长轴 | 卫星平均角速度 |
| 16 | 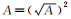 |
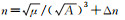 |
| 17 | 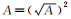 |
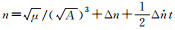 |
| 18 |  |
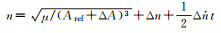 |
| 18* | A=Aref+ΔA |  |
| 19 | 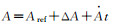 |
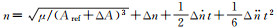 |
| 注:μ=3.986 005×1014 m3/s2;Aref为轨道半长轴参考值,文中取为不同高度轨道的近地点和远地点半长轴的平均值。 | ||
1.4 第一类无奇点根数及拟合参数
针对小偏心率引起的奇点问题,星历模型参数的求解采用两步法。参考文献[17-18],引进第一类无奇点根数σ1=[a, e1, i, Ω, u],其与开普勒根数的关系为
 (1)
(1)
式中,二维偏心率矢量e1的大小等于偏心率,方向指向近点,并且椭圆运动方向的快变量采用新的组合量u,组合量去除了ω和M的负相关性。
综上,星历参数的两步法拟合算法流程如下:
(1) 将标准星历参数(e, ω, M0)替换为无奇点拟合参数(ex, ey, u0),则有对应的一套拟合参数集。
(2) 采用拟合时段的卫星位置向量序列,计算拟合参数。
(3) 通过式(2)将无奇点拟合参数(ex, ey, u0)转换为标准星历参数(e, ω, M0),得到经典轨道根数型星历。
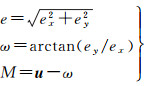 (2)
(2)
参数拟合计算中,需要给出ECEF下卫星位置向量R对3个无奇点根数(ex, ey, u0)的偏导数,即
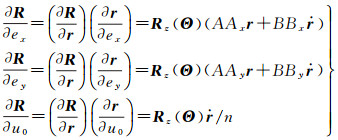 (3)
(3)
式中,Rz(Θ)表示ECEF转换至准地心惯性系的地球自转旋转矩阵,Θ是toe时刻之后的格林尼治恒星时角
 (4)
(4)
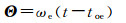 (5)
(5)
式中,ωe是地球自转角速度;n为卫星平均角速度;r和ṙ分别表示t时刻卫星的地心惯性系位置和速度向量,可通过拟合的轨道参数概略计算;系数(AAx, BBx)与(AAy, BBy)计算方法类似,式(6)给出了(AAx, BBx)计算方法[19]
 (6)
(6)
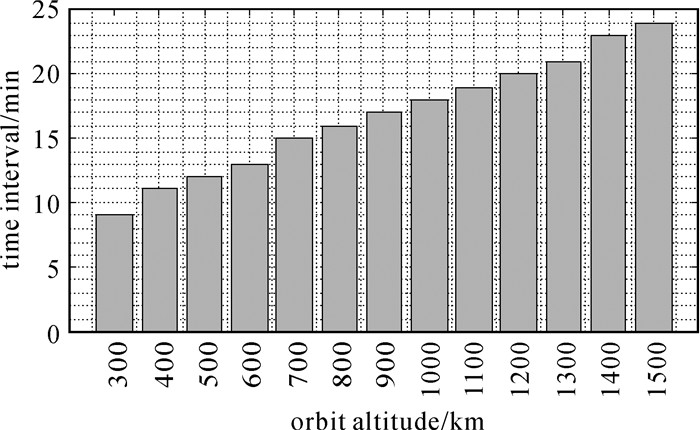
对于低轨卫星而言,拟合时段相同时,轨道高度越低,星历拟合误差越大。由于URE标准为优于10 cm,为保证用户URE需求,应适当缩短较低轨道的星历拟合时段。将拟合时长设置为卫星最大可见时间附近的整分钟数(如图 2所示),这样对于较低的轨道,使用拟合时间也较短,从而可以减小较低轨道的星历拟合误差,并且可以减少用户的星历更新频率。
|
| 图 2 不同高度卫星的最大可见时间 Fig. 2 Max time in view of satellites in different altitudes |
2.2 仿真数据拟合
将16/17/18/18*/19参数星历模型用于不同高度近圆轨道低轨卫星的星历拟合,轨道高度为300~1500 km,倾角45°,偏心率为0.001。摄动力包括100×100的地球非球形摄动、大气阻力摄动、第三体引力摄动和光压摄动等;计算大气阻力摄动的大气密度模型采用Harris-Priester密度模型,卫星面质比为0.02 m2/kg;采用IERS发布的地球定向参数将外推轨道转换到ECEF坐标系下。300~1500 km高度LEO卫星轨道周期为90~116 min,仿真数据从2017年5月1日至5月31日共一个月时间,数据点间隔为30 s,按照拟合时段进行分组,历元时刻取每组的中间时刻,星历更新时间和拟合时间一致。
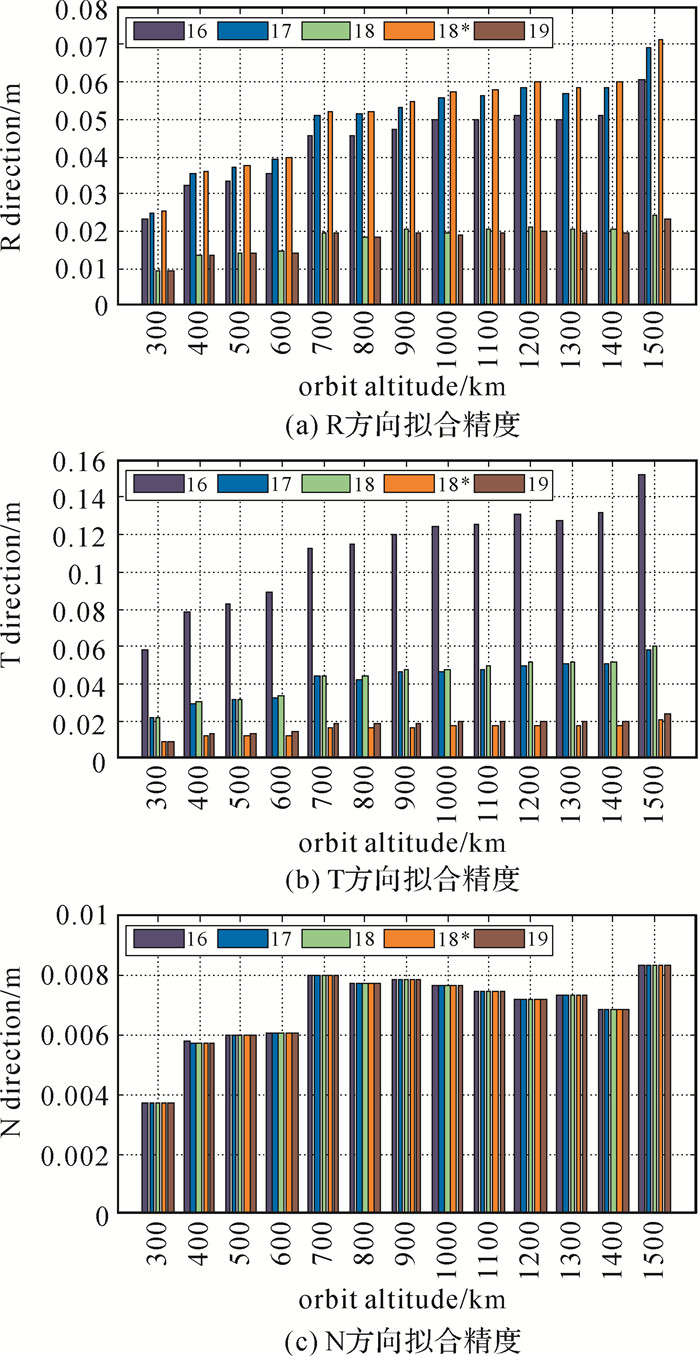
图 3为300~1500 km高度轨道在RTN 3个方向的拟合误差统计。试验过程中,没有出现迭代发散的情况,拟合成功率为100%,拟合迭代次数均稳定为3或4次。可以看出,5种星历模型在R方向拟合精度均优于8 cm,T方向优于16 cm,N方向优于1 cm。结合表 2可知:
|
| 图 3 RTN 3方向拟合误差统计 Fig. 3 Statics of fitting errors in RTN directions |
(1) 18和19参数模型由于在R方向增加了长期摄动参数ȧ,该方向拟合误差减小了50%以上。
(2) 17和18参数模型在T方向增加了Δṅ,该方向拟合误差相对于16参数模型减少了50%以上。
(3) 19和18*参数模型在T方向增加了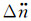
(4) N方向由于参数并没有改变,各参数拟合误差相同。
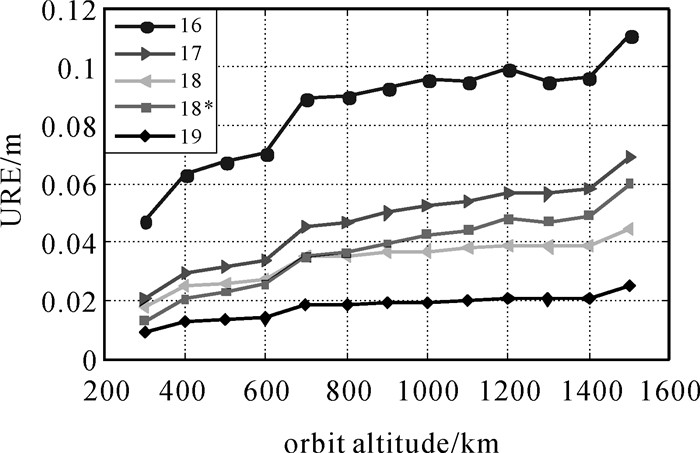
图 4为LEO 16~19参数星历拟合试验的URE结果。可以看出:
|
| 图 4 星历拟合试验URE结果 Fig. 4 UREs of ephemerides fitting experiments |
(1) 星历拟合精度随着参数个数增加而提高,16参数星历URE优于12 cm,而17~19参数模型由于在轨道R或者T方向增加了参数,拟合精度提高明显,URE均优于7 cm。
(2) 随着轨道升高,拟合时段延长,各模型的URE均逐渐降低。若要求拟合误差小于10 cm,16参数星历模型的适用轨道高度要控制在1400 km以内。
(3) 虽然18和18*参数模型的参数个数相同,但是在轨道径向和沿迹方向的拟合参数不同,所以适用高度也不尽一致。可以看出,两模型的URE在700 km轨道高度基本一致。若低于700 km,建议采用18*参数模型。
需要说明的是,文献[21]的试验条件是统一的拟合时段(20 min),因此,其结论是轨道越高,URE越小。注意这与本文的结果不矛盾。
2.3 实际数据拟合为验证设计星历在实际数据中的拟合效果,使用AVISO数据中心提供的Envisat卫星轨道实测数据进行了拟合试验。Envisat卫星于2002年发射入轨,2013年3月停止服务,其设计轨道高度为800 km,轨道周期约为101 min,轨道倾角98°,偏心率为0(文献[21])。试验数据从2010年1月1日至2011年12月31日共两年时间,数据点间隔为30 s,星历更新时间与拟合时间一致。由于大气阻力对轨道的影响,在试验时间段内,Envisat卫星轨道高度在758~776 km之间。
图 5为Envisat卫星实测轨道拟合试验的URE结果统计,图中均方根误差(root mean square,RMS)为每个星历模型在试验时间段内的所有URE值的统计结果。RMS的计算方法为: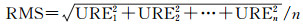

|
| 图 5 Envisat实测轨道拟合试验URE结果及统计 Fig. 5 UREs and their statistics of fitting experiments of the Envisat orbits |
3 接口设计
接口设计是广播星历设计中的重要环节,选取合适的参数量化单位和比特位不仅可以减少用户接收到的星历的精度损失,也可节约卫星在星历广播时的传输信道[22-23]。对于广播星历而言,其接口设计主要是根据星历精度需求,设计合适的量化因子(least significant bit, LSB)对拟合得到的星历参数进行量化来舍弃参数冗余的数据位,然后广播给用户,广播过程中参数所占用的信道宽度即为其占用的比特位(n)。其中参数比特位的设计原则为:根据参数的实际变化范围,设计一定的冗余量,得到参数的有效变化范围(effective range, ER),防止出现参数超限的情况;根据量化因子和参数有效变化范围设计合适的比特位。其中参数有效变化范围与量化因子、比特位的关系为
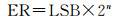 (7)
(7)
根据用户精度需求,对设计的星历模型进行了接口设计,试验使用数据与2.3节相同,结果如表 4所示。可以看出:LEO 16/17/18/18*/19参数星历模型总共分别占用329/343/376/379/396比特位(包含符号位);除了增加或减少的参数外,16~19参数星历的其他参数占用比特位相当。LEO 16/17参数星历模型比特位相对于GPS16参数模型减少了29/15个(GPS16/18参数广播星历总共分别占用358/437比特位,参见文献[24]);LEO 18/18*/19参数星历模型比特位相对于GPS18参数星历模型减少了64/61/41个。
| 参数 | 16参数 | 17参数 | 18参数 | 18*参数 | 19参数 | 量纲 | |||||||||
| LSB | bits | LSB | bits | LSB | bits | LSB | bits | LSB | bits | ||||||
| toe | 24 | 16 | 24 | 16 | 24 | 16 | 24 | 16 | 24 | 16 | s | ||||
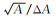 |
2-17 | 29 | 2-5 | ±18 | 2-5 | ±22 | 2-5 | ±19 | 2-6 | ±19 | 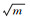 |
||||
| e | 2-28 | 23 | 2-29 | 19 | 2-29 | 24 | 2-29 | 22 | 2-30 | 22 | - | ||||
| i0 | 2-29 | ±29 | 2-30 | ±28 | 2-30 | ±30 | 2-30 | ±28 | 2-30 | ±28 | π | ||||
| Ω0 | 2-29 | ±29 | 2-30 | ±31 | 2-30 | ±30 | 2-30 | ±31 | 2-30 | ±31 | π | ||||
| ω | 2-29 | ±29 | 2-30 | ±31 | 2-30 | ±30 | 2-30 | ±31 | 2-31 | ±32 | π | ||||
| M0 | 2-29 | ±29 | 2-30 | ±31 | 2-30 | ±30 | 2-30 | ±31 | 2-31 | ±32 | π | ||||
| Ȧ | - | - | - | - | 2-14 | ±18 | - | - | 2-14 | ±19 | m/s | ||||
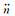 |
- | - | - | - | - | - | 2-56 | ±18 | 2-38 | ±15 | π/s3 | ||||
| idot | 2-37 | ±15 | 2-37 | ±14 | 2-38 | ±15 | 2-38 | ±15 | 2-39 | ±15 | π/s | ||||
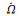 |
2-37 | ±17 | 2-38 | ±17 | 2-38 | ±18 | 2-38 | ±17 | 2-39 | ±18 | π/s | ||||
| Δn | 2-38 | ±17 | 2-39 | ±19 | 2-38 | ±17 | 2-39 | ±22 | 2-47 | ±18 | π/s | ||||
| ṅ | - | - | 2-48 | ±17 | 2-46 | ±17 | 2-48 | ±17 | 2-54 | ±19 | π/s2 | ||||
| Cuc | 2-27 | ±14 | 2-28 | ±15 | 2-28 | ±16 | 2-28 | ±18 | 2-28 | ±17 | π | ||||
| Cus | 2-27 | ±14 | 2-28 | ±16 | 2-28 | ±17 | 2-28 | ±18 | 2-28 | ±16 | π | ||||
| Crc | 2-4 | ±15 | 2-5 | ±16 | 2-5 | ±17 | 2-5 | ±17 | 2-5 | ±17 | m | ||||
| Crs | 2-4 | ±13 | 2-5 | ±14 | 2-5 | ±16 | 2-5 | ±16 | 2-5 | ±17 | m | ||||
| Cic | 2-27 | ±14 | 2-27 | ±13 | 2-27 | ±13 | 2-27 | ±13 | 2-28 | ±14 | rad | ||||
| Cis | 2-27 | ±14 | 2-27 | ±13 | 2-28 | ±14 | 2-28 | ±14 | 2-28 | ±14 | rad | ||||
| 总比特位数(包含符号位) | - | 329 | - | 343 | - | 376 | - | 379 | - | 396 | - | ||||
3.2 数据截断误差
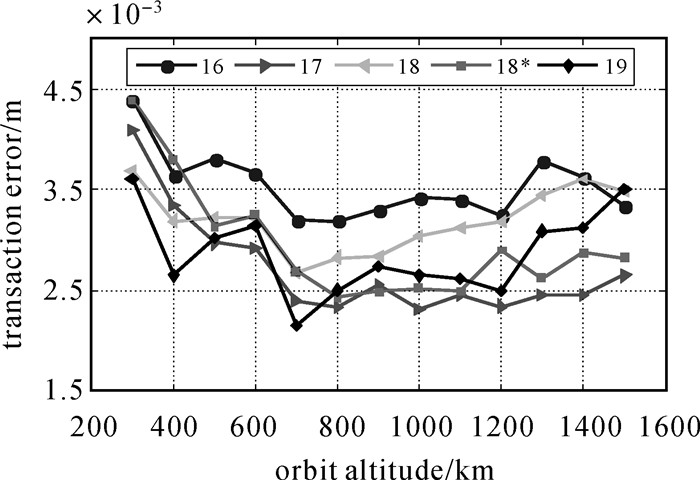
图 6为LEO 16~19参数星历参数截断引起的URE误差统计。对于300~1500 km高度的低轨卫星,16~19参数星历模型的数据截断误差相当,均在5 mm以内,远小于星历拟合产生的误差,证明了选取的量化单位的合理性。
|
| 图 6 16~19参数星历模型接口设计数据截断误差 Fig. 6 Transaction errors of the interfaces for 16~19 elements ephemerides |
4 总结
本文设计的适用于近圆低轨卫星的16/17/18/18*/19参数星历拟合模型,有效地解决了LEO轨道径向和沿迹向拟合效果差的问题。星历模型基于第一类无奇点根数,有效避免了轨道根数型星历用于近圆轨道时出现的奇点问题。通过将拟合时段设置为卫星的地面最大可见时间,在保证较高的拟合误差的同时,有效地减少用户的星历更新频率。通过设计合理的量化因子,在保证星历截断引起的URE误差为毫米级的同时,减少了星历占用比特位,节约了星历传输过程中占用的卫星信道资源。
基于300~1500 km高度LEO轨道的拟合试验表明,LEO16/17/18/18*/19参数星历URE分别优于10/6/4/5/2.5 cm,分别占用329/343/376/379/396比特位,LEO16/17参数星历模型比特位相对于GPS16参数模型分别减少了29/15个,LEO18/18*/19参数星历模型比特位相对于GPS18参数星历模型减少了64/61/41个,数据截断对URE的影响均为保持在5 mm以内。基于Envisat实测数据拟合试验表明,LEO16/17/18/18*/19参数星历URE的RMS统计值分别为1.5/2.7/2.8/3.5/6.7 cm,误差小于同样高度的仿真数据拟合结果。若星座高度在700 km以内,建议采用18*/19参数星历模型;若星座高度高于700 km,建议采用17/18/19参数星历模型。
| [1] | DE SELDING P B. Virgin, qualcomm invest in OneWeb satellite internet venture[EB/OL]. (2015-01-15). https: //spacenews.com/virgin-qualcomm-invest-in-global-satellite-internet-plan/. |
| [2] | DE SELDING P B. SpaceX to build 4, 000 broadband satellites in seattle[EB/OL]. (2015-01-20). https: //www.space.com/28305-spacex-satellite-internet-seattle.html |
| [3] | REID T G R, NEISH A M, WALTER T F, et al. Leveraging commercial broadband LEO constellations for navigation[C]//Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR: [s.n.], 2016. |
| [4] | MAINE K, DEVIEUX C, SWAN P. Overview of IRIDIUM satellite network[C]//Conference Record. 'Microelectronics Communications Technology Producing Quality Products Mobile and Portable Power Emerging Technologies'. San Francisco, CA: IEEE, 1995: 483. |
| [5] | FOSSA C E, RAINES R A, GUNSCH G H, et al. An overview of the IRIDIUM (R) low earth orbit (LEO) satellite system[C]//Proceedings of the IEEE 1998 National Aerospace and Electronics Conference. Dayton, OH: IEEE, 1998: 152-159. |
| [6] | JOERGER M, NEALE J, PERVAN B. Iridium/GPS carrier phase positioning and fault detection over wide areas[C]//Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah, GA: ION, 2009: 1371-1385. |
| [7] | JOERGER M, GRATTON L, PERVAN B, et al. Analysis of iridium-augmented GPS for floating carrier phase positioning[J]. Navigation, 2010, 57(2): 137–160. |
| [8] | YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass satellite navigation system to global PNT Users[J]. Chinese Science Bulletin, 2011, 56(26): 2813–2819. DOI:10.1007/s11434-011-4627-4 |
| [9] |
胡松杰.
GPS和GLONASS广播星历参数分析及算法[J]. 飞行器测控学报, 2005, 24(3): 37–42.
HU Songjie. Research on the broadcast ephemeris parameters of GPS and GLONASS[J]. Journal of Spacecraft TT&C Technology, 2005, 24(3): 37–42. |
| [10] |
阮仁桂, 贾小林, 吴显兵, 等.
关于坐标旋转法进行地球静止轨道导航卫星广播星历拟合的探讨[J]. 测绘学报, 2011, 40(S1): 145–150.
RUAN Rengui, JIA Xiaolin, WU Xianbing, et al. Broadcast ephemeris parameters fitting for GEO satellites based on coordinate transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 145–150. |
| [11] |
张中凯, 杜兰, 刘利, 等.
GEO广播星历参数设计的无奇点根数法[J]. 测绘学报, 2014, 43(5): 452–457.
ZHANG Zhongkai, DU Lan, LIU Li, et al. Parameter design of GEO broadcast ephemeris based on the nonsingular orbital elements[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 452–457. |
| [12] | DU Lan, ZHANG Zhongkai, ZHANG Jin, et al. An 18-element GEO broadcast ephemeris based on non-singular elements[J]. GPS Solutions, 2015, 19(1): 49–59. DOI:10.1007/s10291-014-0364-x |
| [13] |
王鼎蔚, 杜兰, 郑勇, 等.
LEO广播星历参数设计的无奇点根数法[J]. 测绘科学技术学报, 2017, 34(1): 31–37.
WANG Dingwei, DU Lan, ZHENG Yong, et al. Parameter design of LEO broadcast ephemeris based on the nonsingular orbital elements[J]. Journal of Geomatics Science and Technology, 2017, 34(1): 31–37. |
| [14] |
郭睿, 周建华, 胡小工, 等.
一种地球静止轨道卫星的快速恢复定轨方法[J]. 测绘学报, 2011, 40(S1): 19–25.
GUO Rui, ZHOU Jianhua, HU Xiaogong, et al. A strategy of rapid orbit recovery for the geostationary satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 19–25. |
| [15] |
罗璠, 李建文, 黄海, 等.
BDS广播星历的轨道误差分析[J]. 测绘通报, 2015(2): 70–72, 91.
LUO Fan, LI Jianwen, HUANG Hai, et al. Error analysis of orbit determined by BDS broadcast ephemeris[J]. Bulletin of Surveying and Mapping, 2015(2): 70–72, 91. DOI:10.13474/j.cnki.11-2246.2015.0045 |
| [16] |
袁晓波, 张超, 杜兰.
基于第一类无奇点根数的LEO历书参数设计[J]. 测绘科学技术学报, 2016, 33(6): 572–576.
YUAN Xiaobo, ZHANG Chao, DU Lan. Parameter design of LEO almanac ephemeris based on the first class of non-singularity variables[J]. Journal of Geomatics Science and Technology, 2016, 33(6): 572–576. |
| [17] |
杜兰, 刘泽军, 周佩元, 等.
无旋转倾角的NAV/CNAV型GEO广播星历拟合[J]. 测绘学报, 2017, 46(3): 297–306.
DU Lan, LIU Zejun, ZHOU Peiyuan, et al. GEO NAV/CNAV-type broadcast ephemeris fitting without rotation of inclination[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 297–306. DOI:10.11947/j.AGCS.2017.20160393 |
| [18] |
韩星远, 向开恒, 王海红.
第一类无奇点变量的广播星历参数拟合算法[J]. 航天器工程, 2011, 20(4): 54–59.
HAN Xingyuan, XIANG Kaiheng, WANG Haihong. Research on broadcast ephemeris parameters fitting algorithm based on the first class of no singularity variables[J]. Spacecraft Engineering, 2011, 20(4): 54–59. DOI:10.3969/j.issn.1673-8748.2011.04.009 |
| [19] |
黄华.导航卫星广播星历参数模型及拟合算法研究[D].南京: 南京大学, 2012. HUANG Hua. Research on the broadcast ephemeris parameters model and its fitting algorithm[D]. Nanjing: Nanjing University, 2012. http://cdmd.cnki.com.cn/article/cdmd-10284-1012376108.htm |
| [20] |
方善传, 杜兰, 周佩元, 等.
低轨导航增强卫星的轨道状态型星历参数设计[J]. 测绘学报, 2016, 45(8): 904–910.
FANG Shanchuan, DU Lan, ZHOU Peiyuan, et al. Orbital list ephemerides design of LEO navigation augmentation satellite[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 904–910. DOI:10.11947/j.AGCS.2016.20160091 |
| [21] |
赵小阳, 李建成, 金涛勇, 等.
ENVISAT-1卫星测高数据编辑标准的研究[J]. 海洋测绘, 2006, 26(6): 65–67.
ZHAO Xiaoyang, LI Jiancheng, JIN Taoyong, et al. The research on data editing criteria of ENVISAT-1 satellite altimeter[J]. Hydrographic Surveying and Charting, 2006, 26(6): 65–67. DOI:10.3969/j.issn.1671-3044.2006.06.019 |
| [22] |
常志巧, 胡小工, 杜兰, 等.
第二类无奇点根数的北斗历书参数设计[J]. 宇航学报, 2016, 37(11): 1298–1303.
CHANG Zhiqiao, HU Xiaogong, DU Lan, et al. Almanac designing with second class of nonsingular orbital elements for BeiDou navigation satellite system[J]. Journal of Astronautics, 2016, 37(11): 1298–1303. DOI:10.3873/j.issn.1000-1328.2016.11.003 |
| [23] |
陈刘成, 李静, 马瑞, 等.
工程化广播星历参数拟合算法与接口设计[J]. 武汉大学学报(信息科学版), 2011, 36(1): 18–23.
CHEN Liucheng, LI Jing, MA Rui, et al. The Engineering design for broadcast ephemeris parameters fitting arithmetic and their interfaces[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 18–23. |
| [24] |
肖琴琴.广播星历参数及拟合算法性能研究[D].长沙: 中南大学, 2013. XIAO Qinqin. The performance study of broadcast ephemeris parameters and fitting method[D]. Changsha: Central South University, 2013. http://d.wanfangdata.com.cn/Thesis/Y2423737 |



