2. 中国科学院计算地球动力学重点实验室, 北京 100049;
3. 中国地质大学(北京)土地科学技术学院, 北京 100083
2. Key Laboratory of Computational Geodynamics, Chinese Academy of Sciences, Beijing 100049, China;
3. School of Land Science and Technology, China University of Geosciences(Beijing), Beijing 100083, China
地球重力场是地球的基本物理场之一,在确定大地水准面上起着决定性作用。通常,重力场是用球谐级数来表示,即通过给出球谐级数的位系数来构建重力场模型。由于大地水准面更接近于某个旋转椭球面(参考椭球面),因此文献[1-2]建议以参考椭球面为边界来解算重力场。特别是文献[2]研究了以参考椭球面作为边界时重力边值问题的求解方法,同时严格推导了重力场椭球谐系数与球谐系数之间的转换公式,这就使得椭球谐函数在重力场研究中成了与球谐函数同样重要的数学工具。由于椭球谐函数的表达式是由第二类Legendre函数来表示的,因此出现了诸多关于第二类Legendre函数计算的研究工作[3-10]。尽管上述列举的研究工作出发点不同,但结论都是使用迭代方法来计算第二类Legendre函数。这里值得提及的是文献[11]的工作,他们使用解析函数Laurent展开式给出了第二类Legendre函数的表达式,因而无须进行迭代就可以直接使用第二类Legendre函数。
借助于旋转椭球面在大地测量学中的应用思路,也有学者引入了三轴椭球面作为大地边值问题的边界面。但由于此时需要计算Lamè函数,其计算公式较为复杂,加上大地坐标系是以参考椭球面作为基准的原因,故三轴椭球面在研究地球重力场中没有被详细研究。
总体而言,研究椭球谐函数的主要目标体现在以下两个方面:①如何在保证所需的精度下给出第二类Legendre函数的计算;②在满足精度要求下寻求椭球谐系数与球谐系数之间便于计算的转换关系。本文的主要任务是:在保留椭球扁率量级的前提下实现上述两个目标。之所以仅保留扁率量级,是因为大地边值问题都来自于扰动位的线性化,即:舍去的量级是O(T2),这里T是扰动位;而保留扁率量级意味着舍去的量级是O(T·ε4),这里ε2≈0.006。这意味着保留扁率量级基本能够保证大地边值问题的线性化精度。
1 第二类Lengenre函数与Laurent展开式在物理大地测量中,常用的边界面是大地水准面或参考椭球面,如果忽略掉O(T2)量级,大地水准面可以用参考椭球面来替代。记∑:(x2+y2)/a2+z2/b2=1是参考椭球面在直角坐标系下的表达式,这里a是赤道半径,b是半短轴。再引入记号:E2=a2-b2以及ε2=E2/b2,这里ε2就是参考椭球面的第二偏心率。扰动位T作为∑外的调和函数,根据Laplace方程的性质,扰动位有下列椭球谐级数展开式
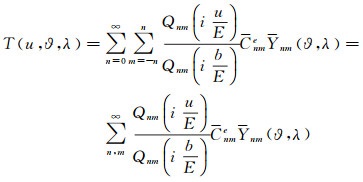 (1)
(1)
式中,Qnm是第二类Legendre函数;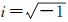

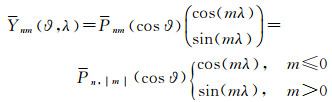 (2)
(2)
式中,Pnm为归一化连带Legendre函数。
从式(1)可知,第二类Legendre函数Qnm的计算是椭球谐级数的核心问题,为此令
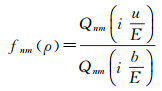 (3)
(3)
式中,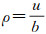
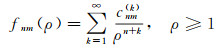 (4)
(4)
事实上,式(4)就是解析函数的Laurent展开式。
由于Qnm满足Legendre微分方程,所以可导出式(4)中的系数cnm(k)满足:cnm(2k)=0以及
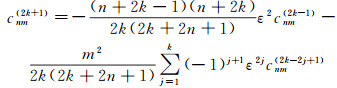 (5)
(5)
特别舍去ε4以上量级时,式(5)简化为
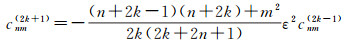 (6)
(6)
以及fnm(ρ)可写成
 (7)
(7)
将式(7)代入式(1),并调整系数cnm(1)Cnme仍为Cnme,则∑外扰动位的椭球谐级数表达式是
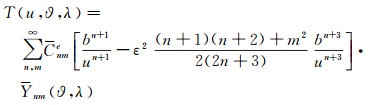 (8)
(8)
事实上,式(8)便是在保留ε2的精度下参考椭球面∑外扰动位的椭球谐级数表达式。至此,得到了便于计算的扰动位椭球谐级数表达式。需要说明的是,在将扰动位的表达式(8)用于求解大地边值问题时,其边值问题的求解精度是O(T·ε4),该精度与线性化精度O(T2)基本上是一致的。
2 椭球谐系数与球谐系数之间的转换关系根据Runge延拓定理[17],扰动位T也可展开为球谐级数
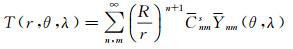 (9)
(9)
式中,Cnms是球谐系数;R是地球平均半径;(r, θ, λ)是球坐标系,r是原点距、θ是余纬,λ仍是经度。事实上,形如式(9)的球谐级数是重力场最重要的表示形式之一,目前主要的重力场模型都是以该形式给出的。
如何建立椭球谐系数Cnme与球谐系数Cnms之间的关系呢?事实上,文献[2]曾导出它们之间的转换公式,但该公式中涉及无穷级数的求和,因而不便于应用。本节的目标是在保留ε2的精度下给出Cnme与Cnms之间的转换关系。根据Legendre函数正交性,有如下公式存在
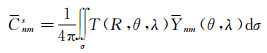 (10)
(10)
和
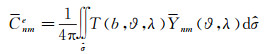 (11)
(11)
式中,σ、
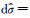
在推导转换关系之前,先写出直角坐标系、球坐标系、椭球坐标系之间的转换关系
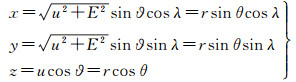 (12)
(12)
在保留至ε2量级下,根据式(12)的前两式,可以得出
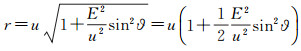 (13)
(13)
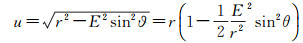 (14)
(14)
当r=R时,u=b,根据式(12)的第3式,有
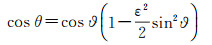 (15)
(15)
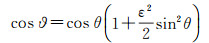 (16)
(16)
此外根据Legendre函数性质,存在如下递推关系[11, 17]
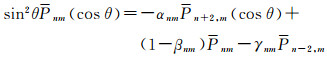 (17)
(17)
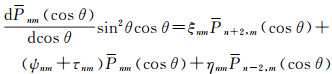 (18)
(18)
式中
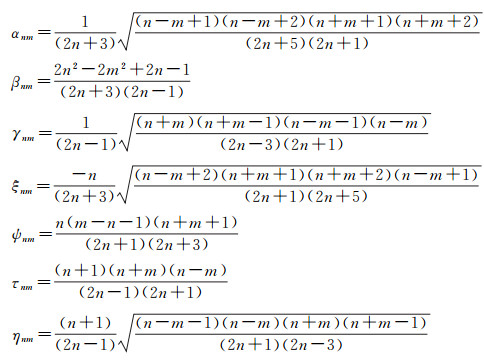
首先推导球谐系数转换到椭球谐系数,根据式(11),将扰动位T用球谐展开式代入,便有
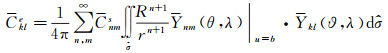 (19)
(19)
将式(13)和式(15)代入式(19),可得
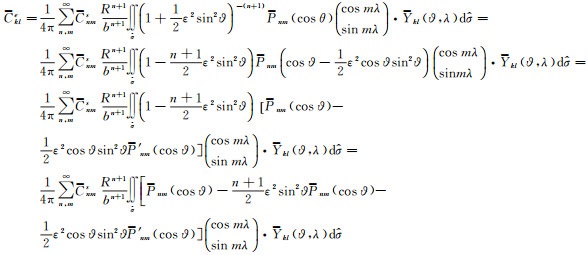 (20)
(20)
式(17)和式(18)代入式(20),便有
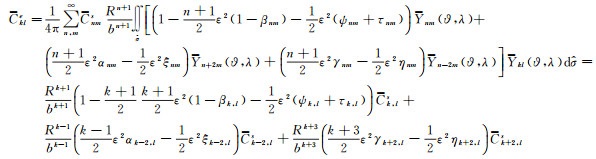 (21)
(21)
可得球谐系数到椭球谐系数的转换公式。
同理可以导出椭球谐系数到球谐系数的转换,根据式(10)则有
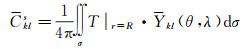 (22)
(22)
利用式(8)与式(16),保留至ε2量级,则有
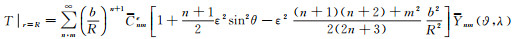 (23)
(23)
再将式(14)、式(23)代入式(22)中,便有
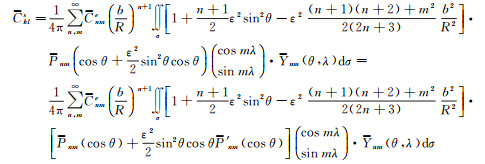 (24)
(24)
再次运用式(17)和式(18),便得
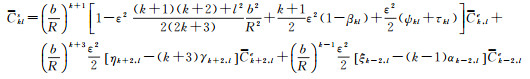 (25)
(25)
总之,在顾及ε2量级下,球谐系数转换到椭球谐系数可按照式(21)得到,椭球谐系数转换到球谐系数可按照式(25)计算。
3 算例为了验证本文推导的椭球谐系数与球谐系数转换公式的精度,本文采用EGM2008超高阶次重力场模型进行模拟计算。选取的阶数为2160阶,模拟计算的设计如下:①从EGM2008模型计算出大地水准面S,并给出S上相应的重力值g;②利用严格的Stokes边值问题的建立过程,在参考椭球面上得到边值问题;③使用球近似方法变换Stokes边值问题来还原EGM2008模型的位系数;④直接在椭球面上利用式(8)求解Stokes边值问题,然后再利用文中给出的系数转换式(25)来还原EGM2008的位系数;最后绘制了还原位系数的误差阶方差图(见图 1)。
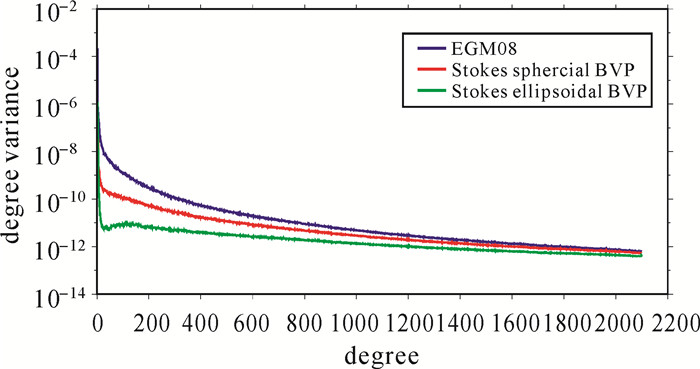
|
| 图 1 阶方差比较 Fig. 1 Degree variances comparison |
从图 1可见,直接在椭球面上求解Stokes边值问题具有更高的精度,特别是这里使用了从椭球谐系数到球谐系数的转换式(25),这意味着,本文导出的转换公式具有较好的精度,可以用于超高阶次的重力场模型的计算。
4 总结与分析本文研究的目的是利用Legendre函数的正交性,在保留ε2量级下导出椭球谐系数与球谐系数相互之间简单转换关系,具有下列优点:①对于第二类Legendre函数的计算,采用Laurent级数的形式,使得对第二类Legendre函数的计算更为简单;②由于物理大地测量中的边值问题都是基于扰动位的线性化问题,即精度为O(T2),因此在实际解算这些边值问题时顾及精度O(T·ε2)就基本能够满足线性化问题的精度要求,本文推导的系数转换式(21)和式(25)保留了ε2量级,相对于文献[2]的结果要简单得多;③通过处理EGM2008超高阶次重力场模型可知,文中给出的转换公式能用于求解物理大地测量中的边值问题。
| [1] | HEISKANEN W A, MORITZ H. Physical geodesy[M]. San Francisco: W. H. Freeman and Company, 1967. |
| [2] | JEKELI C. The exact transformation between ellipsoidal and spherical harmonic expansions[J]. Manuscripta Geodaetica, 1988, 13: 106–113. |
| [3] | CLAESSENS S J, FEATHERSTONE W E. The Meissl scheme for the geodetic ellipsoid[J]. Journal of Geodesy, 2008, 82(8): 513–522. DOI:10.1007/s00190-007-0200-y |
| [4] | CLAESSENS S J. Spherical harmonic analysis of a harmonic function given on a spheroid[J]. Geophysical Journal International, 2016, 206(1): 142–151. DOI:10.1093/gji/ggw126 |
| [5] | THONG N C, GRAFAREND E W. A spheroidal harmonic model of the terrestrial gravitational field[J]. Manuscripta Geodaetica, 1989, 14(5): 285–304. |
| [6] | SONA G. Numerical problems in the computation of ellipsoidal harmonics[J]. Journal of Geodesy, 1995, 70(1-2): 117–126. DOI:10.1007/BF00863423 |
| [7] | MARTINEC Z, GRAFAREND E W. Solution to the Stokes boundary-value problem on an ellipsoid of revolution[J]. Studia Geophysica et Geodaetica, 1997, 41(2): 103–129. DOI:10.1023/A:1023380427166 |
| [8] | GIL A, SEGURA J. A code to evaluate prolate and oblate spheroidal harmonics[J]. Computer Physics Communications, 1998, 108(2-3): 267–278. DOI:10.1016/S0010-4655(97)00126-4 |
| [9] | SEBERA J, BOUMAN J, BOSCH W. On computing ellipsoidal harmonics using Jekeli's renormalization[J]. Journal of Geodesy, 2012, 86(9): 713–726. DOI:10.1007/s00190-012-0549-4 |
| [10] | FUKUSHIMA T. Recursive computation of oblate spheroidal harmonics of the second kind and their first-, second-, and third-order derivatives[J]. Journal of Geodesy, 2013, 87(4): 303–309. DOI:10.1007/s00190-012-0599-7 |
| [11] | YU Jinghai, CAO Huasheng. Elliptical harmonic series and the original stokes problem with the boundary of the reference ellipsoid[J]. Journal of Geodesy, 1996, 70(7): 431–439. DOI:10.1007/BF01090818 |
| [12] | BUCHDAHL H A, BUCHDAHL N P, STILES P J. On a relation between spherical and spheroidal harmonics[J]. Journal of Physics A:Mathematical and General, 1977, 10(11): 1833–1836. DOI:10.1088/0305-4470/10/11/011 |
| [13] | DECHAMBRE D, SCHEERES D J. Transformation of spherical harmonic coefficients to ellipsoidal harmonic coefficients[J]. Astronomy & Astrophysics, 2002, 387(3): 1114–1122. |
| [14] | GLEASON D M. Comparing ellipsoidal corrections to the transformation between the geopotential's spherical and ellipsoidal spectrums[J]. Manuscripta Geodaetica, 1988, 13(2): 114–129. |
| [15] | HU Xuanyu, JEKELI C. A numerical comparison of spherical, spheroidal and ellipsoidal harmonic gravitational field models for small non-spherical bodies:examples for the Martian moons[J]. Journal of Geodesy, 2015, 89(2): 159–177. DOI:10.1007/s00190-014-0769-x |
| [16] | KONOPLIV A S, ASMAR S W, BILLS B G, et al. The Dawn gravity investigation at Vesta and Ceres[J]. Space Science Reviews, 2011, 163(1-4): 461–486. DOI:10.1007/s11214-011-9794-8 |
| [17] | MORITZ H. Advanced physical geodesy[M]. Karlsruhe: Herbert Wichmann, 1980. |
| [18] | PARK R S, KONOPLIV A S, ASMAR S W, et al. Gravity field expansion in ellipsoidal harmonic and polyhedral internal representations applied to Vesta[J]. Icarus, 2014, 240(6): 118–132. |
| [19] | PEARSON J. Computation of hypergeometric functions[D]. Oxford: University of Oxford, 2009. |
| [20] | SANSÒ F, TSCHERNING C C. Fast spherical collocation:theory and examples[J]. Journal of Geodesy, 2003, 77(1-2): 101–112. DOI:10.1007/s00190-002-0310-5 |
| [21] | VERSHKOV A N. Determination of the spherical harmonic coefficients from the ellipsoidal harmonic coefficients of the Earth's external potential[J]. Artificial Satellites, 2002, 37(4): 157–168. |
| [22] | WALTER H G. Association of spherical and ellipsoidal gravity coefficients of the Earth's potential[J]. Celestial Mechanics, 1970, 2(3): 389–397. DOI:10.1007/BF01235139 |
| [23] | HU Xuanyu. The exact transformation from spherical harmonic to ellipsoidal harmonic coefficients for gravitational field modeling[J]. Celestial Mechanics and Dynamical Astronomy, 2016, 125(2): 195–222. DOI:10.1007/s10569-016-9678-z |
| [24] |
于锦海, 曾艳艳, 朱永超, 等.
超高阶次Legendre函数的跨阶数递推算法[J]. 地球物理学报, 2015, 58(3): 748–755.
YU Jinhai, ZENG Yanyan, ZHU Yongchao, et al. A recursion arithmetic formula for Legendre functions of ultra-high degree and order on every other degrees[J]. Chinese Journal of Geophysics, 2015, 58(3): 748–755. |
| [25] |
于锦海.
地球重力场椭球谐模型的建立[J]. 解放军测绘学院学报, 1994(4): 309–317.
YU Jinhai. Elliptical harmonic model about the Earth's gravity field[J]. Journal of the PLA Institute of Surveying and Mapping, 1994(4): 309–317. |
| [26] |
张传定.
大地测量应用卫星的轨道设计——椭球谐引力场下卫星的运动[J]. 测绘学报, 2000, 29(z1): 80–85.
ZHANG Chuanding. Orbital design of satellite for geodetic applications[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(z1): 80–85. DOI:10.3321/j.issn:1001-1595.2000.z1.017 |
| [27] |
于锦海.
O(T2)精度下椭球界面Dirichlet边值问题的积分解[J]. 地球物理学报, 2004, 47(1): 75–80.
YU Jinhai. The integral solution of the Dirichlet's boundary value problem on the ellipsoid interface with the accuracy of O(T2)[J]. Chinese Journal of Geophysics, 2004, 47(1): 75–80. DOI:10.3321/j.issn:0001-5733.2004.01.011 |
| [28] | YU Jinghai, WU Xiaoping. The solution of mixed boundary value problems with the reference ellipsoid as boundary[J]. Journal of Geodesy, 1997, 71(8): 454–460. DOI:10.1007/s001900050113 |



